随着城市现代化建设的不断发展,有限的城市地面空间已不能满足人们日益增长的生活和工作需要,地下综合管廊作为集中敷设电力、通信、广播电视、给水、排水、热力、燃气等市政管线的公共隧道,是城市基础设施的重要组成部分.其中,盾构井工程是地下管廊建设中重点的系统工程,它与场地工程地质勘查、支护结构设计、施工开挖、基坑稳定、降水、施工管理、现场监测、相邻场地施工相互影响等密切相关[1].类似于盾构井支护这种深基坑工程施工影响因素众多,如建筑场地的工程地质条件、场区的周边环境、施工技术、施工机械等,各种因素相互制约、相互关联而又不断变化.目前,国内基坑支护和支撑技术在我国相对还比较落后,基坑工程的设计和施工技能的钻研和实行,成为了近几年来国内土木工程建设项目的热点问题.形式各异的挡土结构,如排桩、水泥土搅拌桩支护、SMW工法和地下连续墙,取代了单桩维护的模式,形成了多样化施工方法比选[2].国内并没有一套成型的理论模型能解决在施工方案比选中存在的问题,必须综合运用多门学科知识和丰富的实践经验.本文将物元分析理论结合层次分析法,构建盾构井支护施工方案的评价指标模型,将定性分析和定量分析相结合,对盾构井的支护技术方案进行了系统分析和综合评价研究,对盾构井施工方案优选具有一定的指导意义.
1 物元分析理论基础及模型建立
我国学者蔡文创立了物元分析理论,通过研究事物的可变性,合理地解决了不相容问题,经过多年的发展,物元分析理论已经在很多领域的综合评判中成功得到应用.该理论基本步骤为确定待评物元,将物元划分为不同指标级别、经典域、节域,确定关联函数以及不同指标级别,通过层次分析法计算不同目标的权重,最终计算关联度、综合关联度以及确定评价等级[3].
1.1 物元基本理论
物元理论形成的基础是物元,用来描述事物基本元素.在此理论中,以有序三元组R=(N,C,V)来描述事物的基本元素,其中,N为质,C为量,V为质和量的反映.在本文中,N为事物的名称,C为事物的特征,V为事物N特征C的量值,将事物的名称、事物的特征、事物的量值称之为物元的三元素[4],N、V、C体现了一种数学函数关系,即V=C(N).物元的一般形式可表示为
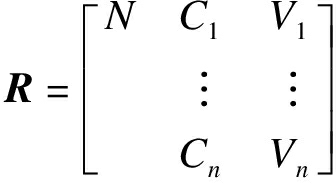
1.2 盾构井施工方案物元分析模型建立
1)物元表示.若该施工技术方案有n个特征C1,C2,C3,…,Cn,则对应有n个量值,即V1,V2,V3,…,Vn,该方案可表示为
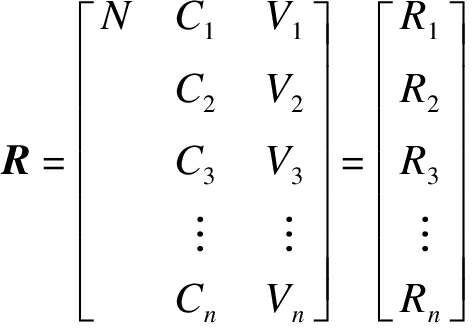
式中:N为施工技术方案;C为特征;V为量值.R的分物元可表示为Ri=(N,Ci,Vi)(i=1,2,…,n).
2)确定经典域、节域.盾构井的施工技术方案综合评价的经典域矩阵可以表示为
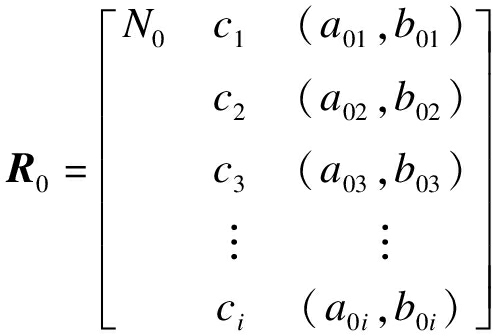
式中:R0为评定等级的物元模型;N0为评定等级的待评物元;ci为N0的第i个特征.v01,v02,…,v0i为N0关于ci的取值范围,即经典域,其寓意是指各个评价指标量值的变化区间,v0i的取值范围为(a0i,b0i),其中,i=1,2,…,n[5].盾构井施工方案综合评价的节域矩阵为
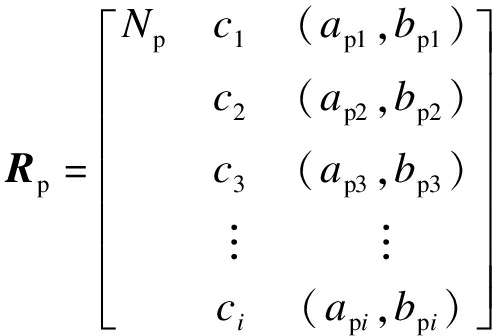
式中,Rp为施工技术方案评定等级经典域的物元模型.vp1,vp2,…,vpi分别为Np关于ci的取值范围,即Np的节域,vpi的取值范围为(api,bpi).
对盾构井施工方案的综合评价是一个繁杂的过程,可以看作是对各个方面进行评价的过程,涉及到工程质量、经济目标、施工效率和安全环保等多重复杂因素[6].在对各指标进行评价时,针对不同施工方案以及突发事件,并且结合专家组论证,对各评价指标的量值确定取值范围,这样就可以对施工方案中各个要素进行评级,从而得到经典域和节域,最后对方案进行综合评定,选出最优方案.
3)计算关联函数.关联函数的计算公式为
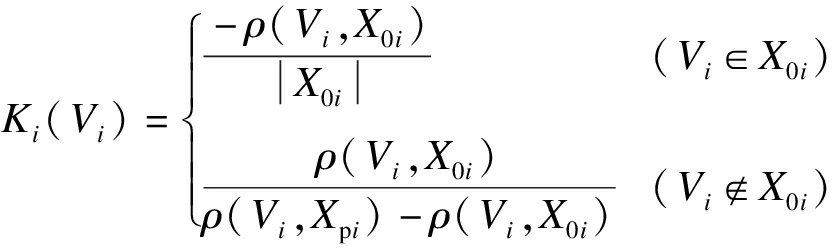
(1)
(2)
(3)
式中:Vi为待评物元;(a0i,b0i)为经典域;(api,bpi)为节域,i=1,2,…,n.
对于待评对象盾构井施工技术方案N,可以得到其关于等级j的关联度,即
(4)
式中:ωi为各个指标的权重;Ki(Vi)为由关联函数确定的关联函数值;Kj(N)为综合关联度.
4)综合评价.该支护施工方案的综合评价等级公式为
Kj=max Kj(N) (j=1,2,…,m)
(5)
式中,max Kj(N)为最大综合关联度.由此可知,盾构井施工方案的评价等级由综合关联度的最大值确定,最大值所在的评定等级即为综合评价的最终评定等级.
2 盾构井评价指标体系的建立及权重计算
2.1 评价指标建立原则及确定
评价指标的建立是科学综合评价的基础,评价指标好坏程度直接影响其评价结果的合理性与准确性.建立评价指标,应充分尊重其科学性、准确性、整体性、独立性、结构的层次性等原则.
由于盾构井支护系统施工技术方案的影响因素众多,其施工工序较为复杂,受多重影响因素的制约,在满足安全性、经济性和可行性的同时,必须兼顾环境保护和施工效率.经过查阅相关资料[7-9],结合自身周围环境条件,最终确定的指标如表1所示.
表1 盾构井施工综合评价体系
Tab.1 Comprehensive evaluation system for shield well construction

目标层一级评价指标二级评价指标盾构井施工综合评价指标P工程质量P1经济合理P2施工效率P3环境保护P4工程安全P5设计质量P11施工质量P12综合造价P21施工难易程度P31施工工期P32施工目标相互干扰程度P33变形及影响范围P41环境保护措施P42“三废”及噪声P43整体稳定安全系数P51施工技术可靠度P52支护系统破坏及其危害P53
2.2 计算指标权重
评价指标的权重,主要是采用层次分析法进行计算,其主要步骤为:目标层确定、构造判断矩阵以及一致性检验.目标层由表1确定.现将目标层、一级指标与二级指标之间两两进行对比分析,根据标度的含义和专家评判,对Pij采用1~9标度赋予其相对数值,确定判断矩阵,标度含义及其取值如表2所示.
表2 标度定义及其含义
Tab.2 Definition of scale meaning

标度含义1表示两因素相比,具有同样的重要性3表示两因素相比,前一个因素(i)比后一个因素(j)稍微重要5表示两因素相比,前一个因素(i)比后一个因素(j)明显重要7表示两因素相比,前一个因素(i)比后一个因素(j)强烈重要9表示两因素相比,前一个因素(i)比后一个因素(j)极端重要2,4,6,8上述两相邻判断中间值
通过对一级指标进行评估,为了使判断矩阵能近似反映权重情况,将得到的一级评价指标进行归一化处理,再将归一化的数字相加所得向量乘以1/n得出权重,其表达式为
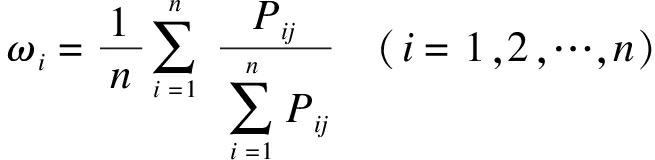
(6)
相应的判断矩阵为

经计算所得一级权重结果如表3所示.
表3 一级指标权重
Tab.3 Weight of primary indexes

一级指标P1P2P3P4P5权重ωi0.21910.19050.09520.10450.4186
根据一级指标权重可以得出,对于施工而言,工程安全最为重要,所占权重最多为0.418 6;施工的质量问题也是大家较多关注的重点问题之一,所占权重为0.219 1;经济合理性权重占比为0.190 5.随着国家政策的不断改进,以及对环境保护越来越重视,政府出台了相应的法律条文来限制施工单位对环境的污染,因此,对于环境保护所占权重比施工效率略高为0.104 5,施工效率所占权重最低,为0.095 2.
对专家提供的二级指标数据进行整理分析,结合文献进行判断,可得到二级指标的判断矩阵,如表4所示.
表4 二级指标权重
Tab.4 Weight of secondary indexes
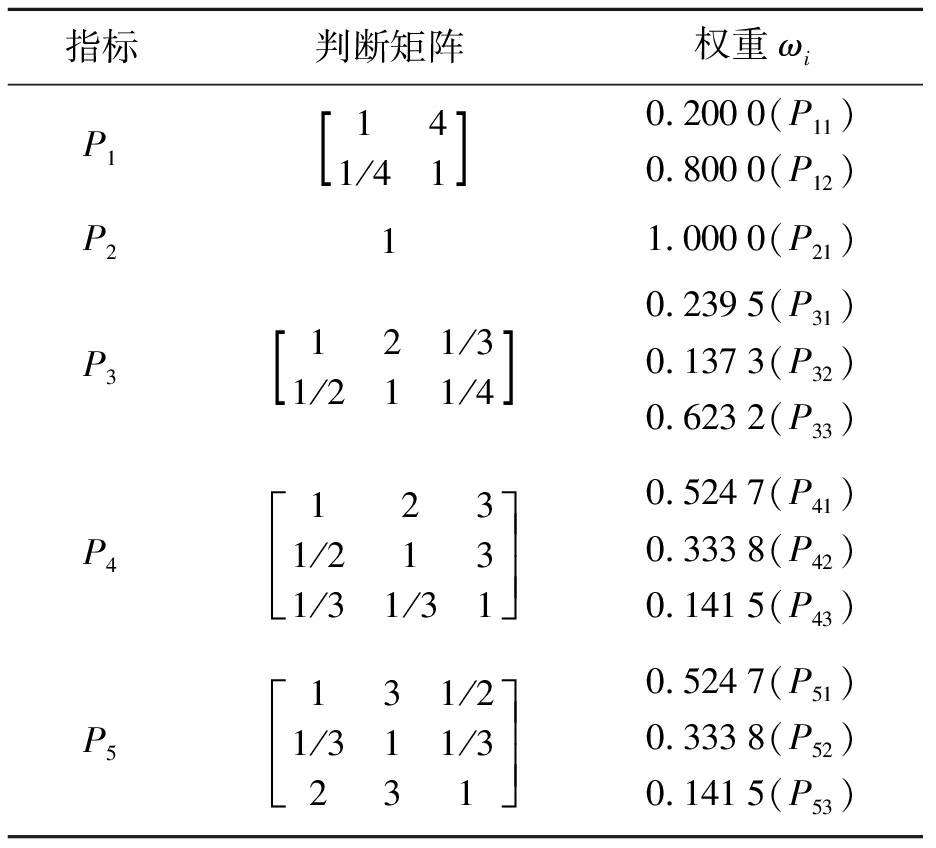
指标判断矩阵权重ωiP1141/41[]0.2000(P11)0.8000(P12)P211.0000(P21)P3121/31/211/4[]0.2395(P31)0.1373(P32)0.6232(P33)P41231/2131/31/31éëêêùûúú0.5247(P41)0.3338(P42)0.1415(P43)P5131/21/311/3231éëêêùûúú0.5247(P51)0.3338(P52)0.1415(P53)
2.3 一致性检验
判断矩阵是各因素之间进行两两比较得到的,由于客观事物具有认识多样性和问题复杂性,往往会出现一些偏差,因此有必要进行一致性检验.一致性检验需要引入随机偏移指标RI,其数值如表5所示.经过对平均偏移指标CI和随机偏移指标RI进行比较,确定其一致性,CI越大,判断矩阵的一致性越大,其检验公式为
(7)
(8)
其中,λmax由方根法比较求出,其计算公式为
(9)
(10)
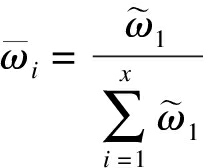
(11)
(12)
式中:λmax为最大特征值;x为矩阵的阶数;y为矩阵的行数;aij为方案i与方案j的比较,具体数值由表2确定;![]() 为向量的分量开x次方后的值;
为向量的分量开x次方后的值;![]() 为正规化后的特征值.若CR<0.1或x<3,则一致性通过,如表6所示.其中,P1、P2中矩阵阶数小于3,则一致性通过.由表6可以看出,各级指标一致性检验均满足,说明其判断矩阵符合要求,可以作为评判施工方案的标准.
为正规化后的特征值.若CR<0.1或x<3,则一致性通过,如表6所示.其中,P1、P2中矩阵阶数小于3,则一致性通过.由表6可以看出,各级指标一致性检验均满足,说明其判断矩阵符合要求,可以作为评判施工方案的标准.
表5 随机偏移指标(RI)
Tab.5 Random offset indexes(RI)

阶数123456789RI000.580.901.121.241.321.411.45
表6 各级指标一致性检验
Tab.6 Consistency check of indexes at each level
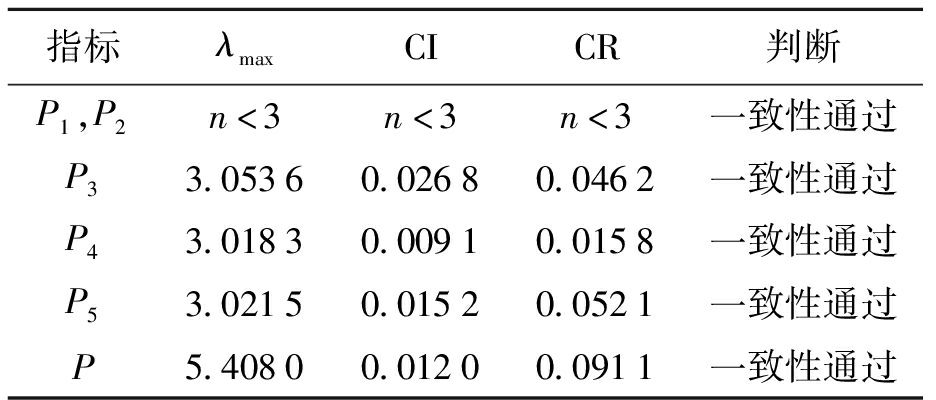
指标λmaxCICR判断P1,P2n<3n<3n<3一致性通过P33.05360.02680.0462一致性通过P43.01830.00910.0158一致性通过P53.02150.01520.0521一致性通过P5.40800.01200.0911一致性通过
3 应用实例
以沈阳市地下管廊J25盾构井工程为例.J25节点井位于小河沿路与北方街桥交汇处西南侧绿化带内,沿南运河北侧布置.本盾构井中心里程为右K10+481.000 m,结构形式采用四层三跨的箱形框架结构,顶板覆土约4.1 m,采用明挖顺做法施工.经过专家评选,共有三个方案:地下连续墙;支护桩+锚索+止水帷幕;钢结构内支撑+支护桩+止水帷幕.通过物元模型综合判断三种施工方案,最终选取最优施工技术方案.
3.1 物元模型矩阵的建立
1)经典域、节域物元矩阵的确定.在三种施工方案的综合评价中,以专家评审意见为主,配合相关文献和国家标准,对指标进行定量分析,本文采用9分制打分法,根据各个指标不同性质,确定其经典域取值范围.通过工程专家组的评议打分,各个评价等级的经典物元矩阵为RA、RB、RC、RD.其中,A、B、C、D分别代表优、良、合格、不合格,各物元矩阵为


盾构井施工方案的节域由其经典域来确定,其物元矩阵为
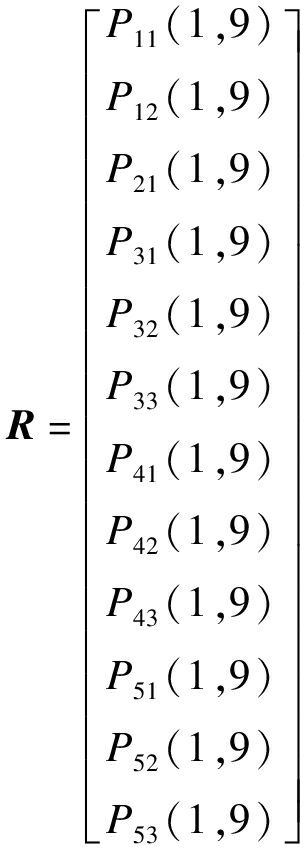
2)待评物元的确定.分别以三种不同的施工方案为研究对象,根据工程所在位置的特点以及专家打分情况,建立待评物元矩阵,具体如表7所示.
表7 待评物元矩阵
Tab.7 Matrix of matter element for evalution
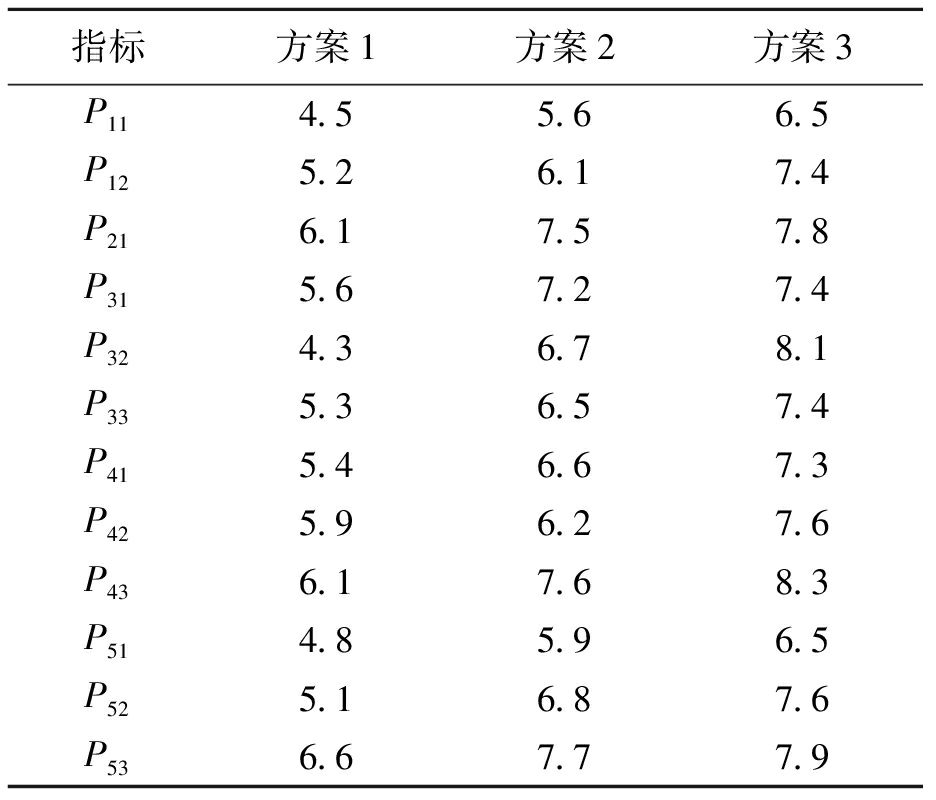
指标方案1方案2方案3P114.55.66.5P125.26.17.4P216.17.57.8P315.67.27.4P324.36.78.1P335.36.57.4P415.46.67.3P425.96.27.6P436.17.68.3P514.85.96.5P525.16.87.6P536.67.77.9
3)综合各指标的关联度计算.根据式(1)~(3)进行计算,可以得到三种施工方案各指标对应等级的关联度值,表8为方案1的各指标关联度值,表9为方案2的各指标关联度值,表10为方案3的各指标关联度值.
表8 方案1的各指标关联度值
Tab.8 Associated degree of each index in scheme 1
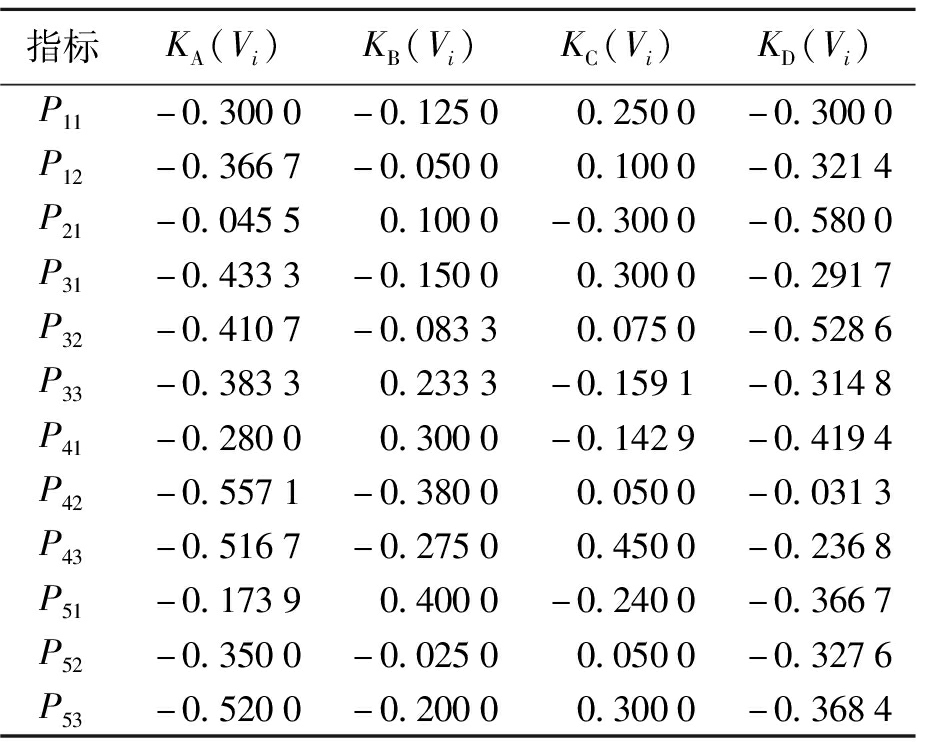
指标KA(Vi)KB(Vi)KC(Vi)KD(Vi)P11-0.3000-0.1250 0.2500-0.3000P12-0.3667-0.05000.1000-0.3214P21-0.04550.1000-0.3000-0.5800P31-0.4333-0.15000.3000-0.2917P32-0.4107-0.08330.0750-0.5286P33-0.38330.2333-0.1591-0.3148P41-0.28000.3000-0.1429-0.4194P42-0.5571-0.38000.0500-0.0313P43-0.5167-0.27500.4500-0.2368P51-0.17390.4000-0.2400-0.3667P52-0.3500-0.02500.0500-0.3276P53-0.5200-0.20000.3000-0.3684
表9 方案2的各指标关联度值
Tab.9 Associated degree of each index in scheme 2
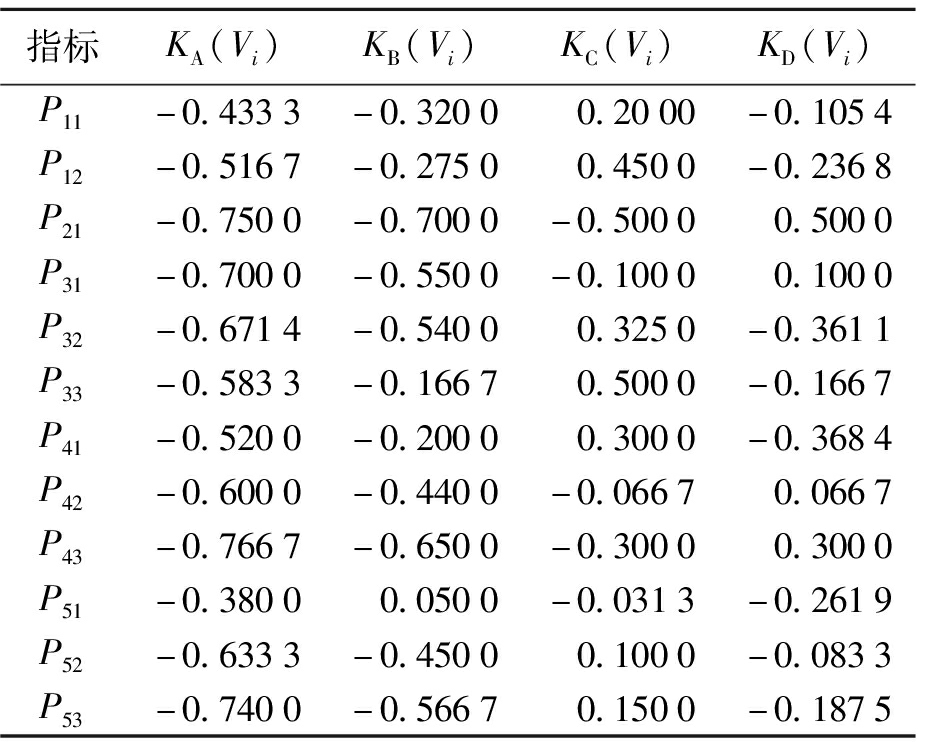
指标KA(Vi)KB(Vi)KC(Vi)KD(Vi)P11-0.4333-0.3200 0.2000-0.1054P12-0.5167-0.27500.4500-0.2368P21-0.7500-0.7000-0.50000.5000P31-0.7000-0.5500-0.10000.1000P32-0.6714-0.54000.3250-0.3611P33-0.5833-0.16670.5000-0.1667P41-0.5200-0.20000.3000-0.3684P42-0.6000-0.4400-0.06670.0667P43-0.7667-0.6500-0.30000.3000P51-0.38000.0500-0.0313-0.2619P52-0.6333-0.45000.1000-0.0833P53-0.7400-0.56670.1500-0.1875
表10 方案3的各指标关联度值
Tab.10 Associated degree of each index in scheme 3
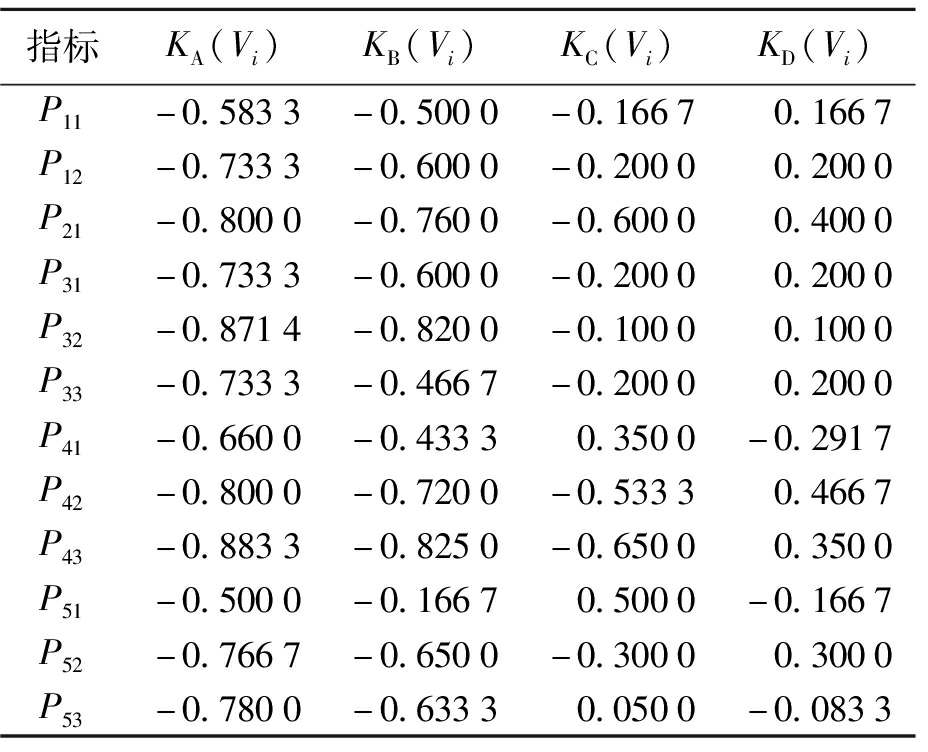
指标KA(Vi)KB(Vi)KC(Vi)KD(Vi)P11-0.5833-0.5000-0.1667 0.1667P12-0.7333-0.6000-0.20000.2000P21-0.8000-0.7600-0.60000.4000P31-0.7333-0.6000-0.20000.2000P32-0.8714-0.8200-0.10000.1000P33-0.7333-0.4667-0.20000.2000P41-0.6600-0.43330.3500-0.2917P42-0.8000-0.7200-0.53330.4667P43-0.8833-0.8250-0.65000.3500P51-0.5000-0.16670.5000-0.1667P52-0.7667-0.6500-0.30000.3000P53-0.7800-0.63330.0500-0.0833
3.2 评定等级
在确定各个指标的关联度后,由式(5)可以得出各个方案的综合关联度,并对方案进行最终评级.其中,方案1的综合关联度为
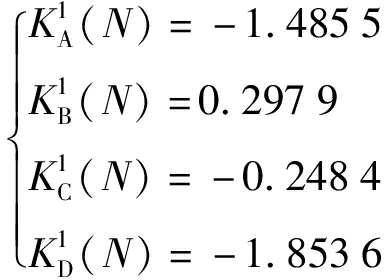
求得![]()
方案2的综合关联度为
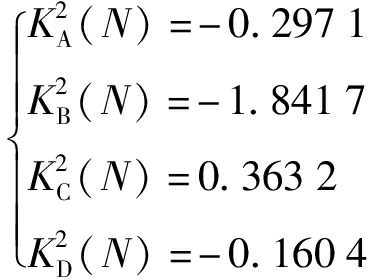
求得![]()
方案3的综合关联度为
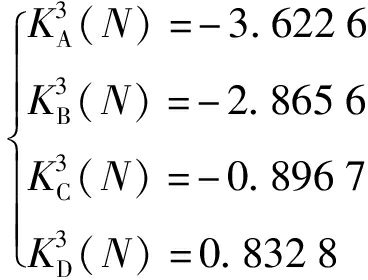
求得![]()
综合计算结果,![]() 综合关联度越大,代表方案综合性越好,即方案3为A级“优”.
综合关联度越大,代表方案综合性越好,即方案3为A级“优”.
4 结 论
本文以沈阳地下管廊实际工程为例,在施工过程中对各种因素进行综合分析,建立物元模型,通过计算各个指标的关联度,最终对三种施工方案进行了优选对比,得到了相应方案的评价等级,确定了最优方案.通过实例验证可知,相比于多目标函数随机搜索最佳方案的整体优化法、灰色系统理论、层次分析法等方法,本文模型能有效处理复杂多样的指标系统,可以反映各种不利因素具体的影响程度,把定性与定量分析有机结合起来,弱化了评价过程中人为的影响[10].由于物元要素的多样性以及发散性,符合施工方案中各种因素复杂性的特点,因此,本文方法在实际工程中具有一定的可行性.
[1] 冯谦.深基坑支护结构设计及优化方法研究[D].武汉:武汉理工大学,2006.
(FENG Qian.Study on the design and optimization of support structure of deep foundation pit[D].Wuhan:Wuhan Polytechnic University,2006.)
[2] 齐宁.深基坑支护方案优选与施工管理[D].石家庄:石家庄铁道大学,2016.
(QI Ning.Optimization of supporting scheme for deep foundation pit and construction management[D].Shijiazhuang:Shijiazhuang Tiedao University,2016.)
[3] 黄辉玲.基于物元分析的土地生态安全评价[J].安全工程学报,2010,26(3):316-321.
(HUANG Hui-ling.Land ecological safety evaluation based on material element analysis[J].Journal of Safety Engineering,2010,26(3):316-321.)
[4] 赵博,徐卫亚,张冬梅.基于安全监测信息的岩石高边坡稳定性评价[J].沈阳工业大学学报,2013,36(1):100-105.
(ZHAO Bo,XU Wei-ya,ZHANG Dong-mei.Stability evaluation of high slope of rock based on security monitoring information[J].Journal of Shenyang University of Technology,2013,36(1):100-105.)
[5] 范树平,刘友兆,张红梅.基于层次模糊物元模型的承接产业用地空间适宜评价[J].农业工程学报,2015,31(6):266-276.
(FAN Shu-ping,LIU You-zhao,ZHANG Hong-mei.Evaluation of the space suitability of industrial land for undertaking industry based on hierarchical fuzzy object element model[J].Journal of Agricultural Engineering,2015,31(6):266-276.)
[6] 李建峰,郑永伟,李彬.地铁车站施工方案优选决策模型[J].西安科技大学学报,2009,29(2):159-164.
(LI Jian-feng,ZHENG Yong-wei,LI Bin.Optimization decision model of construction scheme for subway station[J].Journal of Xi’an University of Science and Technology,2009,29(2):159-164.)
[7] 谷昀.基于模糊综合评判法的地铁施工风险评估研究[D].北京:中国铁道科学研究院,2013.
(GU Yun.Study on risk assessment of subway construction based on fuzzy comprehensive evaluation[D].Beijing:China Railway Science Institute,2013.)
[8] 肖武权,冷伍明.深基坑支护结构设计的优化方法[J].岩土力学,2007,28(6):1201-1205.
(XIAO Wu-quan,LENG Wu-ming.Optimization method of support structure design for deep foundation pit[J].Rock and Soil Mechanics,2007,28(6):1201-1205.)
[9] 龚云成.模糊综合评价法在基坑支护方案选型中的应用[J].山西建筑,2007,33(35):6-7.
(GONG Yun-cheng.Application of fuzzy comprehensive evaluation method in selection of type of base pit support scheme[J].Shanxi Construction,2007,33(35):6-7.)
[10] 马世骁,孙彦,许萍.基于物元分析模型的工程项目风险评价[J].沈阳建筑大学学报(社会科学版),2012,14(12):157-160.
(MA Shi-xiao,SUN Yan,XU Ping.Risk evaluation of engineering projects based on a physical element analysis model[J].Journal of Shenyang University of Architecture(Social Sciences),2012,14(12):157-160.)