近年来，我国500 kV及以上的高压直流输电系统正在快速发展建设中，随着电压等级的提高，电网某些部位的电场畸变更为严重[1].由于直流电阻分压器的端部表面电场强度较高，在运行中极可能出现电晕放电现象，出现电晕损失、局部过热、泄漏电流增大等恶性情况，最终导致分压器的准确度降低[2]，且电晕损失是高压直流输电线路和直流电阻分压器设计的一项重要经济技术指标，所以进行直流电压互感器的外绝缘设计，研究如何平衡端部表面过高的场强尤为关键.
最优化设置均压环的尺寸和安装位置可以降低最大电场强度，改善电场畸变问题，但目前针对均压环的尺寸和安装位置设计存在以下3个问题：1)目前大部分学者选择的方法是试凑和实际实验验证，即罗列若干组均压环的尺寸数据并进行仿真测试，选出仿真结果中最大电场强度最小的一组，实验结果不具备科学性；2)我国没有针对均压环尺寸和安装位置的统一标准和方法[3]；3)由于世界能源环境的变化和我国能源战略的调整，节能减排的压力越来越大，对电能计量的准确度要求在不断提高，这必然要求进一步提高高压直流分压器的测量精确度水平.本文针对以上问题，基于ANSYS有限元仿真软件搭建了±500 kV直流电阻标准分压器模型，如图1所示，提出了迭代-正交实验法用以高效求解均压环最优尺寸和位置，并给出了500 kV直流电阻标准分压器均压环安装尺寸和位置的参考值.该方法可明显缩短求解时间，并可应用于特高压直流输电工程的设计.
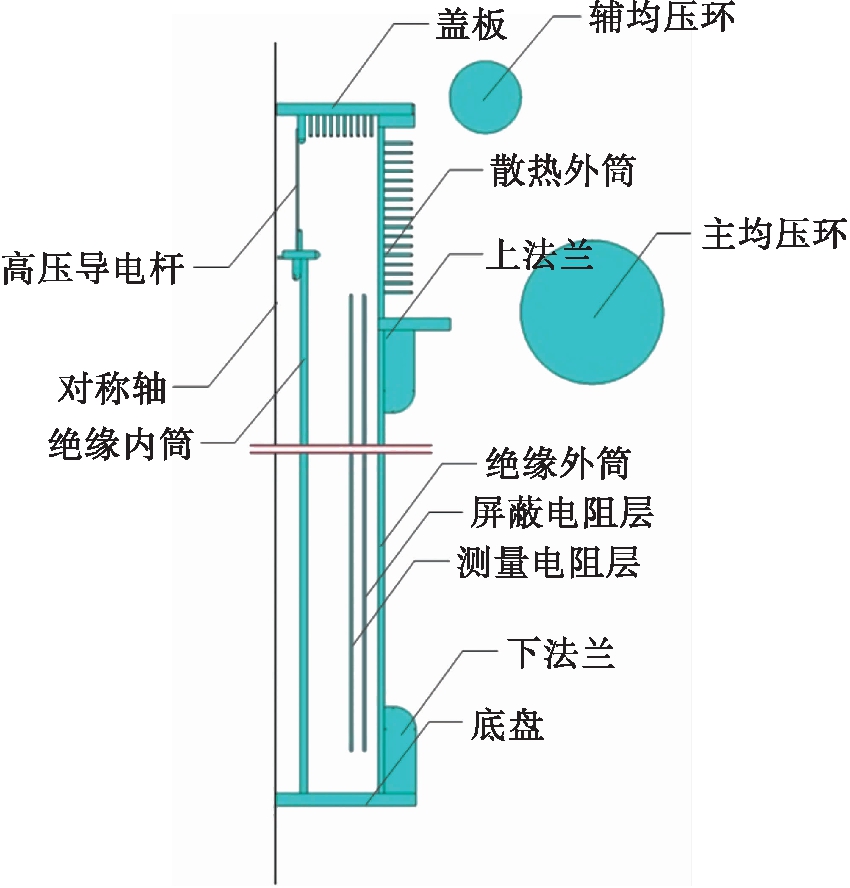
图1 500 kV直流电阻标准分压器模型
Fig.1 Model for 500 kV standard voltage divider with DC resistance
模型的绝缘内筒、绝缘外筒、测量电阻层和屏蔽电阻层的相关信息如表1所示.
表1 500 kV直流电阻标准分压器部分数值选择
Tab.1 Value selection for parts of 500 kV standard voltage divider with DC resistance
部位材料内直径/mm壁厚/mm高度/mm相对介电常数绝缘内筒有机玻璃160203522.04绝缘外筒环氧玻璃纤维600163550.04测量电阻层-42053392.41×106屏蔽电阻层-49073392.41×106
1 迭代-正交实验法基本原理
将数理统计学中的正交实验法和迭代法相结合，设计了如图2所示的基于迭代-正交实验法计算模型.第一轮迭代-正交实验的目标函数为
y=f(x1，x2，…，xn)
(1)
正交实验的目标函数为正交实验取的n个实验因素xi的函数；ANSYS仿真得出的结果称为实验结果，在后文中用符号表示为yi；实验中需要考察的可控条件变量称为因素，用符号表示为A、B、C；这些需要考察的可控条件变量取不同状态的值称为水平，例如因素A的r个水平分别为A1，A2，…，Ar，设ybest为第一轮正交实验后的最优结果，对应的各因素取值为x1best，x2best，…，xnbest，第一轮正交实验第i个因素的水平之间差值为ΔQi.
第二轮正交实验的目标函数为
y′=f(x′1，x′2，…，x′n)
(2)
第二轮正交实验的目标函数为正交实验取n个实验因素x′i的函数.第二轮正交实验各因素的水平与第一轮有差异，如第二轮正交实验因素A的水平取A′1，A′2，…，A′r，则这些因素所对应的新一轮不同水平取值为
(3)
式中：ε为偏移系数；ΔQ′i为第二轮迭代-正交实验法的迭代步长，即新一轮第i个因素水平之间的差值，其表达式为
ΔQ′i=μΔQi (μ≤1)
(4)
其中，μ为迭代系数，具体取值需按照工程经验制定.因为需要以上一次迭代-正交实验的最佳点为中心，所以应有一个偏移系数，偏移系数的取值视情况而定.值得注意的是，主、辅均压环之间、均压环与分压器之间不能有空间上的重合，所以，在设置参数时应当尤其注意.
由于目标函数的全局最优点可能不止一个，所以初始求解时，应使初始群体的范围覆盖面尽可能广[4].本案例中均压环不能与分压器本体重合，因此均压环的尺寸和安装位置的可行域是容易被限制的，而正交实验法恰好可以固定初始种群[5]，且正交实验法覆盖范围比较广，这保证了初始水平的广泛性和多样性.第一次实施正交实验后可以快速收敛到较优区域[6]，同时还可以分析出影响最大的因素和交互作用，这些最优水平即是这个因素的所有水平中自适应度最高的[7].传统正交实验法到此完成，但有可能得到的实验结果不满足工程需要，此时应该再次复制上一次正交实验中的因素，重置各因素的水平，选择新一轮交互作用，即使用迭代实验对目标函数的种群进行优化[8].
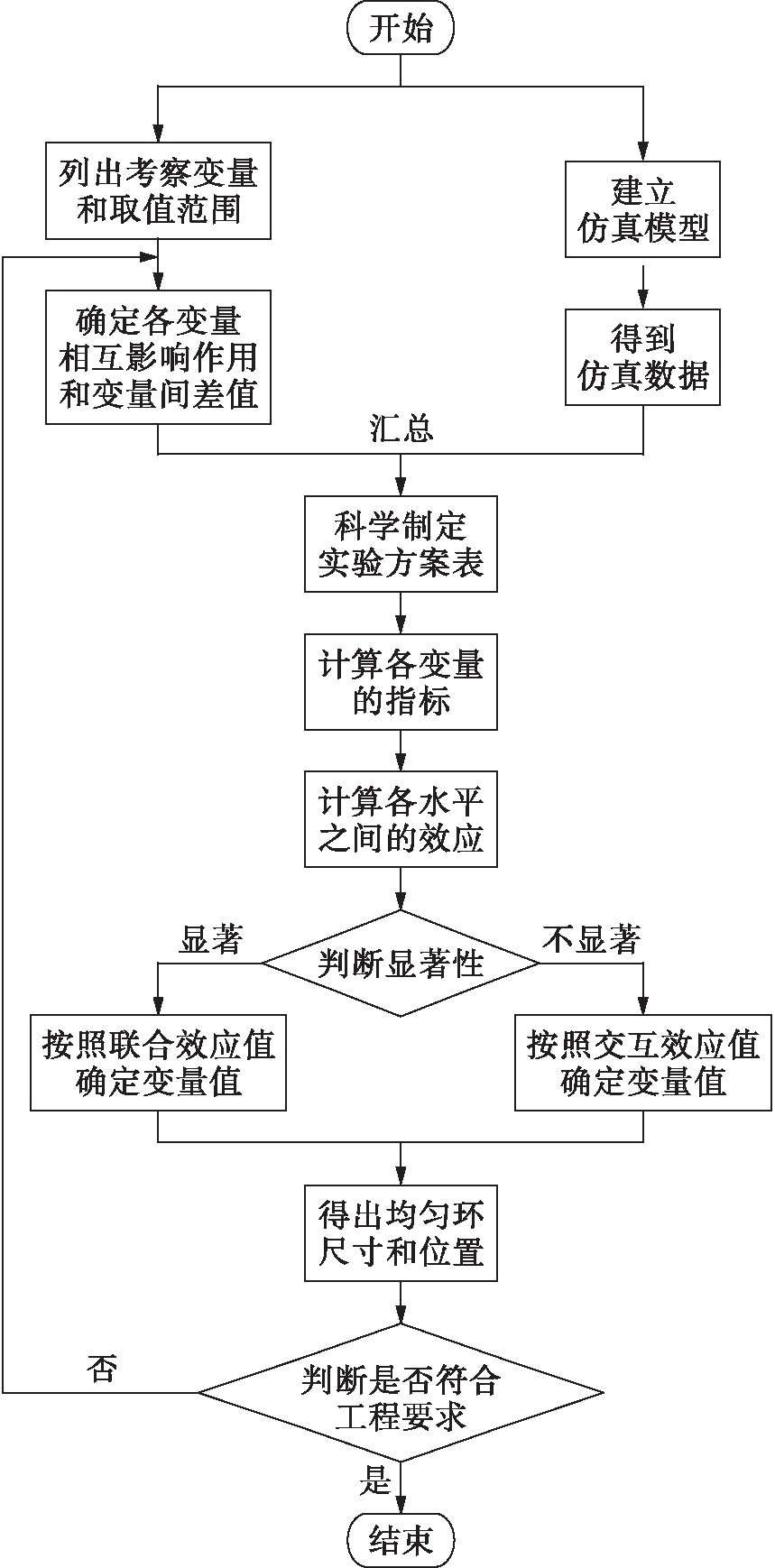
图2 迭代-正交实验法流程图
Fig.2 Flow chart of iterative-orthogonal test method
2 实验仿真应用
本文将所提出的迭代-正交实验法应用于500 kV直流电阻标准分压器周围均压环最佳尺寸的求解中.若500 kV直流电阻标准分压器周围未安装均压环，则其周围最大电场强度为4 212.5 V/mm，如图3所示.而本实验的目的是确保分压器周围最大电场强度尽可能低，以满足工程所需.
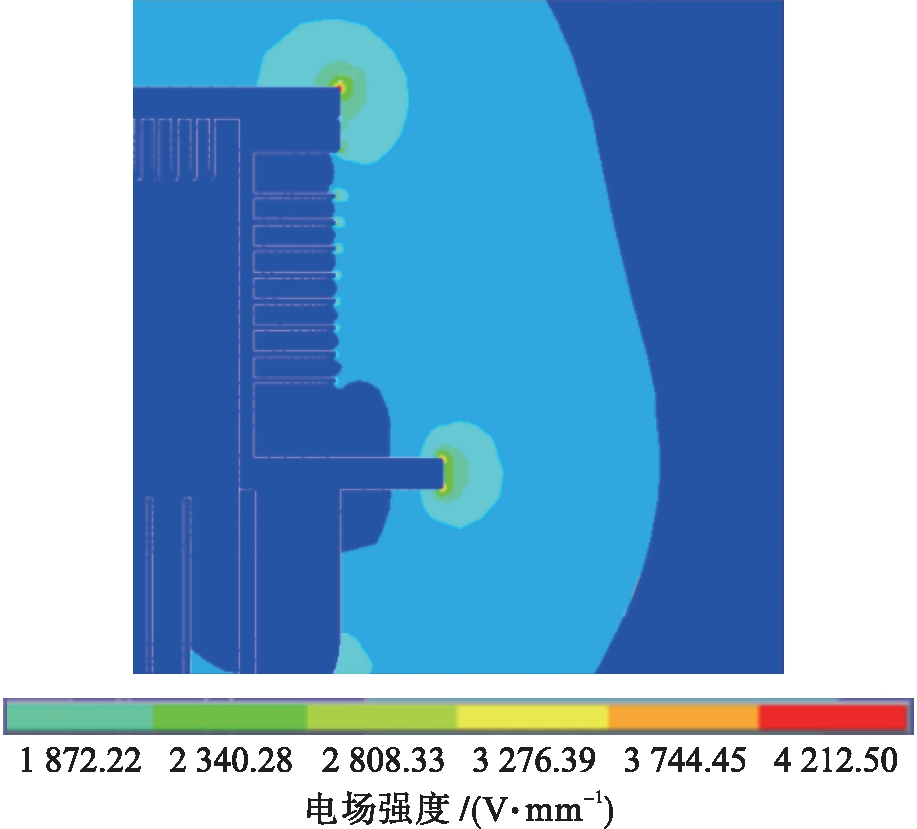
图3 未安装均压环时分压器周围电场分布
Fig.3 Distribution of electric field around voltage divider without grading ring
2.1 第一轮迭代-正交实验
本轮实验的目标函数为y=f(x1，x2，…，x6)，本方案设计了6个变量，即6个因素，具体包括：辅均压环的内环半径A、辅均压环圆心到对称轴的距离B、辅均压环圆心到地面的距离C、主均压环的内环半径D、主均压环圆心到对称轴的距离E、主均压环圆心到地面的距离F.本文使用等重复实验，给每个实验因素取了3个等差值，即3个水平.各变量的取值分别为Ai、Bi、Ci、Di、Ei、Fi，如表2所示.第一轮实验各水平每次取的差值为ΔQ，本文ΔQA、ΔQB、…、ΔQF分别取10、10、20、10、10、100.
表2 第一轮迭代-正交实验各变量的取值
Tab.2 Variable values in first round of iterative-orthogonal test mm
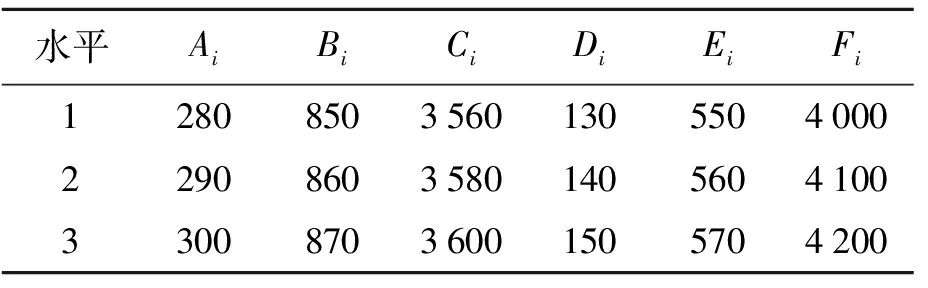
水平AiBiCiDiEiFi128085035601305504000229086035801405604100330087036001505704200
本文案例是6因素3水平实验，若做全因素实验需要完成36=729次实验，选择L27(313)的正交表安排实验[9]，可以有效减少实验次数至27次.给出各变量相互影响作用表，并安排实验，在众多计算条件中按一定规则选出少数代表性强的计算方案，确定各变量相互影响作用表.
由于需要寻找最小值，即确定最优均压环尺寸和位置使分压器周围最大电场强度减小，本文将实验结果取相反数，变为寻找最大值.使用方差分析法对实验结果进行分析，判断设计变量对实验结果影响显著与否，找出本轮实验最优解[10].
首先定义以下计算参数值，即
(5)
(6)
(7)
(8)
式中：Kij为第j列上第i个水平的计算结果总和；
为总和平均值；t为第j列上变量号i出现的次数；Sj为第j列因素的偏差平方和；ST为计算实验结果的总偏差平方和；T为所有实验结果的总和；gi为所有实验结果总和的平均值；
为各均方和[11]；fj为偏差平方和的自由度.
为了用方差分析法对正交实验结果进行解析，需要构造检验统计量，即
(9)
式中：Se为误差平方和，即求和所有空白列的偏差平方和；fe为误差平方和Se的自由度.构造检验统计量时，需要分以下两种情况[12].如果各列的
则直接继续之后的步骤；若存在某些列的
说明误差列的影响可能比某些列的影响更大，则需要把这些列的Sj加起来并与Se求和，当作新的误差平方和，记符号为
这些列的自由度也要相加并与fe求和，当作新的误差列自由度，记符号为
此时，构造的新检验统计量为
(10)
计算出各Fj，列出方差分析表，用各F值与所查得的F分布表临界值相比可知各个变量影响结果的显著程度，若认为该因素对实验结果有显著影响，则用*号表示.
计算因素A第i个水平的效应，即得效应ai，其表达式可记为
(11)
按照式(11)的方法可以定义Bi、Ci的效应bi、ci.定义水平Ai与Bj的组合对实验结果产生的总效应为联合效应，其表达式为
[ab]ij=μij-μ
(12)
式中：μij为水平Ai与Bj组合下的均值；μ为所有水平组合的总均值.定义水平Ai与Bj的交互作用对实验结果产生的影响值为
(ab)ij=[ab]ij-ai-bj
(13)
选择最佳生产条件时，应该大致符合以下原则：
1)如果因素A、因素B、因素A×B对实验结果均有显著影响，则应该用二元表列出[ab]ij、ai和bi，选择[ab]ij中的最大者；
2)如果因素A、因素A×B对实验结果有显著影响，因素B对实验结果的影响不显著，则应该用二元表列出(ab)ij、ai和bi，选择交互效应(ab)ij和效应ai中的最大者.
本文中，因素A、因素C和交互作用A×B、交互作用B×C对实验结果影响显著，因素B和因素A×C对实验结果的影响并不显著，所以应该选择交互效应(ab)ij和效应ai中的最大者、交互效应(bc)ij和效应ci中的最大者.计算所得因素A、因素B的二元表如表3所示.因素A与因素B之间交互效应表如表4所示.
表3 第一轮迭代-正交实验因素A和因素B的二元表
Tab.3 Binary list of factors A and B in first round of iterative-orthogonal test
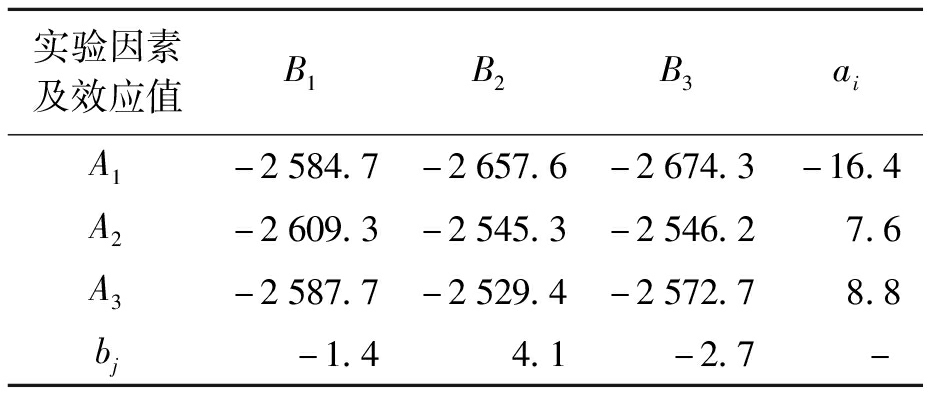
实验因素及效应值B1B2B3aiA1-2584.7-2657.6-2674.3-16.4A2-2609.3-2545.3-2546.27.6A3-2587.7-2529.4-2572.78.8bj-1.44.1-2.7-
表4 第一轮迭代-正交实验因素A和因素B之间交互效应
Tab.4 Interaction effect between factors A and B in first round of iterative-orthogonal test
实验因素B1B2B3A1 19.5-10.3-9.1A2-12.73.19.6A3-6.77.2-0.5
由表3可见，ai中的最大值为a3=8.8，所以因素A应取A3，与A3搭配的最大交互作用为B3B2=7.2，故因素B取B2.
类似于求解因素A、B的方法，计算出因素A、因素C的二元表和因素A、因素C之间联合效应表.效应ai的最大值为a3=8.8，效应ci的最大值为c3=13.2，联合作用[ac]ij的最大值为A3C3=21.0，所以因素C应取水平C3.
其他影响显著的因素包括因素D、因素F，分别取最优值，通过对比得到因素D应取水平D3，因素F应取水平F2.因素E由于对实验结果的影响不显著，因此可通过再做3组实验，即组合A3B2C3D3ExF2重新计算.当x分别取1、2、3时，得到的实验结果分别为827.756、836.132、831.318 V/mm，则ybest=827.756 V/mm，因此，本次实验的最佳生产条件为A3B2C3D3E1F2.在该条件下进行ANSYS仿真实验结果如图4所示.
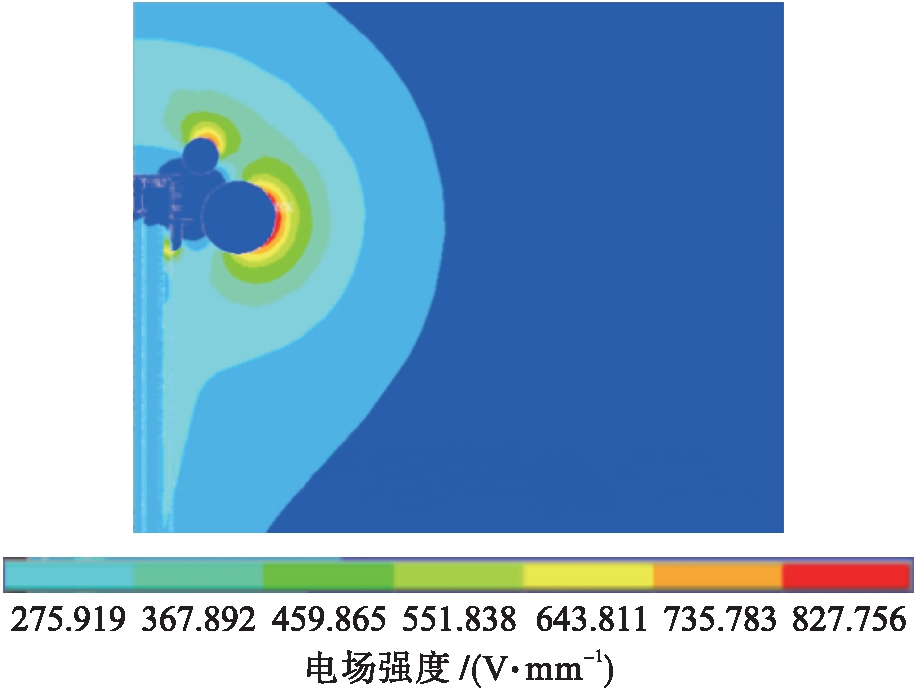
图4 第一轮迭代-正交法求解的最佳生产条件仿真结果
Fig.4 Simulation results of optimal production conditions obtained by first round of iterative-orthogonal method
2.2 第二轮迭代-正交实验
有时一次正交实验不能完全满足工程需要，可能最大电场强度仍大于起晕场强，所以可使用正交实验-迭代法在求得的最佳生产条件附近迭代，以更精细地划分因素水平，直到满足工程要求为止.
第二轮迭代-正交实验法的目标函数为y′=f(x′1，x′2，…，x′6)，其中x′1∈(A′1，A′2，A′3)，x′2∈(B′1，B′2，B′3)，…，x′6∈(N′1，N′2，N′3).
第二轮正交实验各因素水平的差值记为ΔQ′A、ΔQ′B、ΔQ′C、ΔQ′D、ΔQ′E、ΔQ′F，分别取ΔQ′A=|A′1-A′2|=|294-299|=5，ΔQ′B=|B′1-B′2|=|854-859|=5，ΔQ′C=|C′1-C′2|=|3 590-3 601|=11，ΔQ′D=|D′1-D′2|=|146-151|=5，ΔQ′E=|E′1-E′2|=|546-551|=5，ΔQ′F=|F′1-F′2|=|4 060-4 110|=50.第二轮迭代各水平具体取值如表5所示.
由第一轮正交实验分析可知，因素C′和交互作用B′×C′对实验结果影响显著，因素B′对实验结果的影响不显著，所以应选择交互效应(bc)′ij、效应c′i中的最大者.c′i中的最大值为c′1=2.9，水平c′1下交互作用[bc]′ij的最大值为[bc]′31=6.2，所以因素B′应取B′3，因素C′应该取C′1.
表5 第二轮迭代各变量的取值
Tab.5 Variable values in second round of iteration
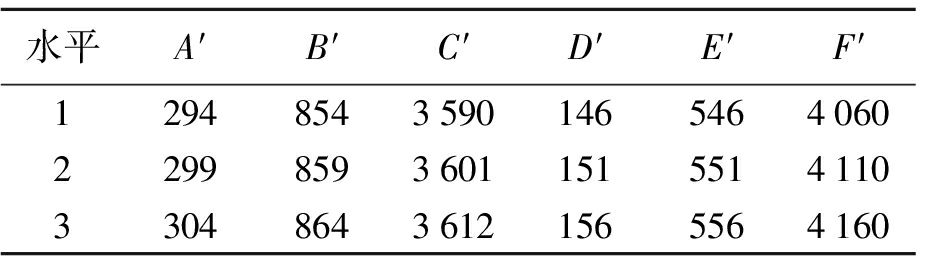
水平A′B′C′D′E′F′129485435901465464060229985936011515514110330486436121565564160
由于因素D′和因素E′对实验结果的影响不显著，因此可以通过再做9组实验，即组合A′3B′3C′1D′xE′yF′1进一步分析.当x、y分别排列组合水平1、2、3时，得到的最优实验结果为820.719 V/mm，因素D′和因素E′的最优水平组合为D′3E′2.因此，本次实验的最佳生产条件y′best为A′3B′3C′1D′3E′2F′1.在该条件下进行ANSYS仿真实验结果如图5所示.
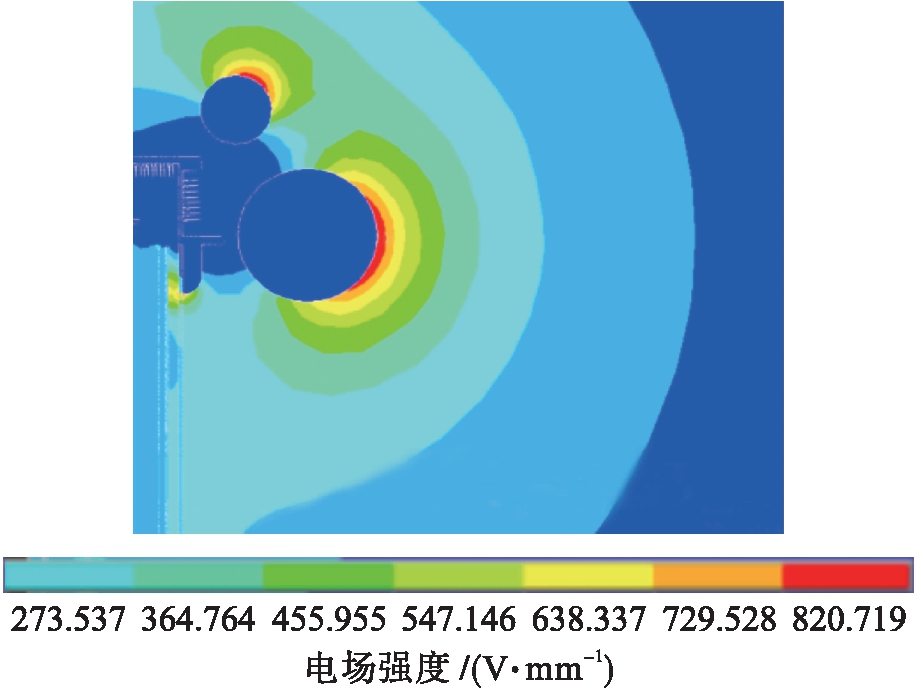
图5 第二次迭代-正交法求解的最佳生产条件仿真结果
Fig.5 Simulation results of optimal production conditions obtained by second round of iterative-orthogonal method
分析第二轮迭代-正交实验结果可以发现，此次实验结果整体而言比第一轮正交实验法的实验结果更优.通过此次迭代后，分压器周围的最大电场强度降到了820.719 V/mm，发生电晕放电的可能性变小.
本文提出的迭代-正交实验法从本质上讲是一种逼近最优值的方法，该算法不仅可应用于求解500 kV直流电阻标准分压器周围均压环的尺寸和安装位置问题上，还可以应用于其他电压等级分压器的均压环设计，或应用于电气工程领域涉及的其他需要逼近最优值的问题.
3 结 论
本文提出了一种迭代-正交实验最优分析方法，利用迭代-正交实验法来求解500 kV直流电阻标准分压器周围均压环的尺寸和安装位置信息，得到了以下结论：
1)通过第一轮迭代-正交实验得到了一组最佳组合方案，使分压器周围最大电场强度从4 212.5 V/mm下降到827.756 V/mm；在该组最佳组合方案附近进行第二轮迭代实验，使分压器周围最大电场强度又从827.756 V/mm下降到了820.719 V/mm.
2)对比分析第一轮和第二轮迭代-正交实验结果可以发现，此次实验结果整体而言比单纯正交实验法的实验结果更优，证明了本文提出的迭代-正交实验法可以在有效减小500 kV直流电阻标准分压器周围初始电场强度的同时，还能快速确定均压环安装位置和尺寸参数的寻优范围与方向，有效减少了实验次数及迭代次数，并提高了生产效率.
3)本算法不仅可应用于求解500 kV直流电阻标准分压器周围均压环的尺寸和安装位置问题上，还可应用于其他电压等级分压器的均压环设计.尤其适用于电气工程领域实验次数多、寻优范围广的取最优值问题.
[1] 王宇，李丽，汤龙华，等.基于ANSYS分析的典型500 kV电流互感器电场分布计算[J].广东电力，2014，27(2)：73-78.
(WANG Yu，LI Li，TANG Long-hua，et al.Calculation on electric field distribution of typical 500 kV current transformer based on ANSYS analysis[J].Guangdong Electric Power，2014，27(2)：73-78.)
[2] 黄道春，阮江军，刘守豹.特高压交流复合绝缘子电位和均压环表面电场分布计算[J].高电压技术，2010，36(6)：1442-1447.
(HUANG Dao-chun，RUAN Jiang-jun，LIU Shou-bao.Potential distribution along UHV AC transmission line composite insulator and electric field distribution on the surface of grading ring[J].High Voltage Engineering，2010，36(6)：1442-1447.)
[3] 曾三友，魏巍，康立山，等.基于正交设计的多目标演化算法[J].计算机学报，2005(7)：1153-1162.
(ZENG San-you，WEI Wei，KANG Li-shan，et al.A multi-objective evolutionary algorithm based on orthogonal design[J].Chinese Journal of Computers，2005(7)：1153-1162.)
[4] Clautiaux F，Carlier J，Moukrim A.A new exact method for the two-dimensional orthogonal packing problem[J].European Journal of Operational Research，2007，183(3)：1196-1211.
[5] Zhao C，Chen X，Zhao C.Study on CO capture using dry potassium-based sorbents through orthogonal test method[J].International Journal of Greenhouse Gas Control，2010，4(4)：655-658.
[6] 宫照煊，王莉.基于正交设计的免疫克隆遗传算法[J].辽宁科技大学学报，2010，33(5)：552-554.
(GONG Zhao-xuan，WANG Li.Immune cloning genetic algorithm with orthogonal design[J].Journal of University of Science and Technology Liaoning，2010，33(5)：552-554.)
[7] 孙海霞，李冬敏，孔志鹏.基于ABAQUS和正交实验法的基坑支护桩优化[J].沈阳工业大学学报，2016，38(4)：457-460.
(SUN Hai-xia，LI Dong-min，KONG Zhi-peng.Optimization of foundation pit supporting piles based on ABAQUS and orthogonal experimental method[J].Journal of Shenyang University of Technology，2016，38(4)：457-460.)
[8] 王雷，蔡劲草，李明.基于正交实验的遗传算法参数优化[J].南京师范大学学报(工程技术版)，2016，16(2)：81-85.
(WANG Lei，CAI Jin-cao，LI Ming.Parameter optimization of genetic algorithm based on orthogonal experiment[J].Journal of Nanjing Normal University(Engineering and Technology Edition)，2016，16(2)：81-85.)
[9] 张屹，万兴余，郑小东，等.基于正交设计的元胞多目标遗传算法[J].电子学报，2016，44(1)：87-94.
(ZHANG Yi，WAN Xing-yu，ZHENG Xiao-dong，et al.Cellular genetic algorithm for multi-objective optimization based on orthogonal design[J].ACTA Electronica Sinica，2016，44(1)：87-94.)
[10] 黄玲，文习山，蓝磊，等.基于改进遗传算法的特高压绝缘子均压环优化[J].高电压技术，2009，35(2)：218-224.
(HUANG Ling，WEN Xi-shan，LAN Lei，et al.Optimization of grading rings for UHV composite insulator by the improved GA[J].High Voltage Engineering，2009，35(2)：218-224.)
[11] Gong W.An improved multiobjective differential evolution based on pareto-adaptive-dominance and or-thogonal design[J].European Journal of Operational Research，2009，198(2)：576-601.
[12] 吴浩扬，常炳国，朱长纯.遗传算法的一种特例：正交实验设计法[J].软件学报，2001(1)：148-153.
(WU Hao-yang，CHANG Bing-guo，ZHU Chang-chun.A special case of genetic algorithm：orthogonal experimental design[J].Journal of Software，2001(1)：148-153.)