近年来,磁致伸缩/压电(简称磁电)复合材料因具有磁电转换系数大、结构简单、易于制备和低成本等优点已成为磁传感器研究的热点[1].磁电复合材料的磁电电压系数与磁致伸缩材料的压磁系数成正比,而压磁系数是偏置磁场的函数,因此可通过测量磁电电压系数测量磁场强度[2].由于压电材料的电容特性,磁电复合材料的磁电输出电压会随着磁场频率的降低而急剧减小,因此,利用磁电复合材料测量静态磁场通常需要利用线圈产生一定频率和幅值的交变磁场激励[3].但是,通过线圈产生交变磁场的激励方式可能会对电路造成电磁干扰,并且存在发热问题.
利用磁致伸缩材料的ΔE效应使磁电复合振动元件的谐振频率随着磁场强度的变化产生偏移,再根据振动元件的阻抗或者导纳变化测量磁场,采用这种技术路线不需要线圈产生交变激励磁场.例如Jahns等人提出的SiO2/Pt/AlN/FeCoSiB叠层复合磁传感器以及Nan等人提出的AlN/(FeGaB/Al2O3)异质结构磁传感器[4-5].但是上述磁电复合磁传感器的输出信号均为微弱模拟信号,需要采用锁定放大器或低噪声信号放大器、滤波器、A/D转换器等装置进行信号处理.此外,受磁致伸缩材料品质因数(Q值)的影响,磁电复合振动元件的Q值较低[6].
谐振式传感器利用振动元件把被测参量转换为频率信号,故又称频率式传感器,其具有精度高、分辨力高、抗干扰能力强、便于长距离数据传输、能直接与数字设备相连接等优点[7-8].Bian等人提出采用磁致伸缩/压电/音叉复合的谐振磁传感器[9].在静态或准静态磁场作用下,磁致伸缩材料产生的应变通过陶瓷支座传递至音叉,使音叉受到纵向拉伸作用,谐振频率随之变化,无需通过线圈施加交变激励磁场.但由于采用单件磁电复合材料与音叉复合的非对称结构,音叉会在偏心拉伸作用下产生弯曲变形.这不仅会削弱磁电材料对音叉的纵向拉伸作用,还会使音叉偏离其最优振动模态.本文提出一种改进结构的磁致伸缩/压电/音叉复合谐振磁传感器,通过采用对称的传感器复合结构增强对音叉的纵向拉伸并且抑制偏心拉伸引起的弯曲变形,显著提高磁传感器的灵敏度.
1 谐振式磁传感器原理
1.1 磁传感器结构
改进后的磁传感器结构如图1所示(单位:mm),磁传感器由音叉振动元件、压电薄膜以及磁电复合材料三部分组成.音叉为对称结构,具有三个两端固定的振动梁;两片压电薄膜粘附在音叉中间梁的两端,分别用于振动激励(Y方向)与信号采集;两片压电材料短薄片粘结在一片磁致伸缩材料长薄片的两端,组成一件磁电复合材料,其中磁致伸缩材料沿长度方向(X方向)磁化;两件磁电复合材料从上下两侧对称地夹持一件音叉振动元件并通过环氧树脂胶固结,形成对称的三明治结构.
图1中,在静态磁场作用下,磁致伸缩材料发生形变并通过压电层传递至音叉,使后者受到纵向(X方向)拉伸作用,音叉的谐振频率随之升高.由于采用对称的叠层复合结构,上下磁电复合材料对音叉拉伸作用力的合力保持在音叉中性轴方向而不会产生所谓偏心拉伸问题,因此音叉不会因为弯矩的作用发生横向弯曲(Y方向).通过引进上述的改进结构设计,作用在音叉上的纵向拉伸作用力得以加强,同时抑制了弯曲变形对音叉振动梁的干扰,因此磁传感器可以达到更高的灵敏度.
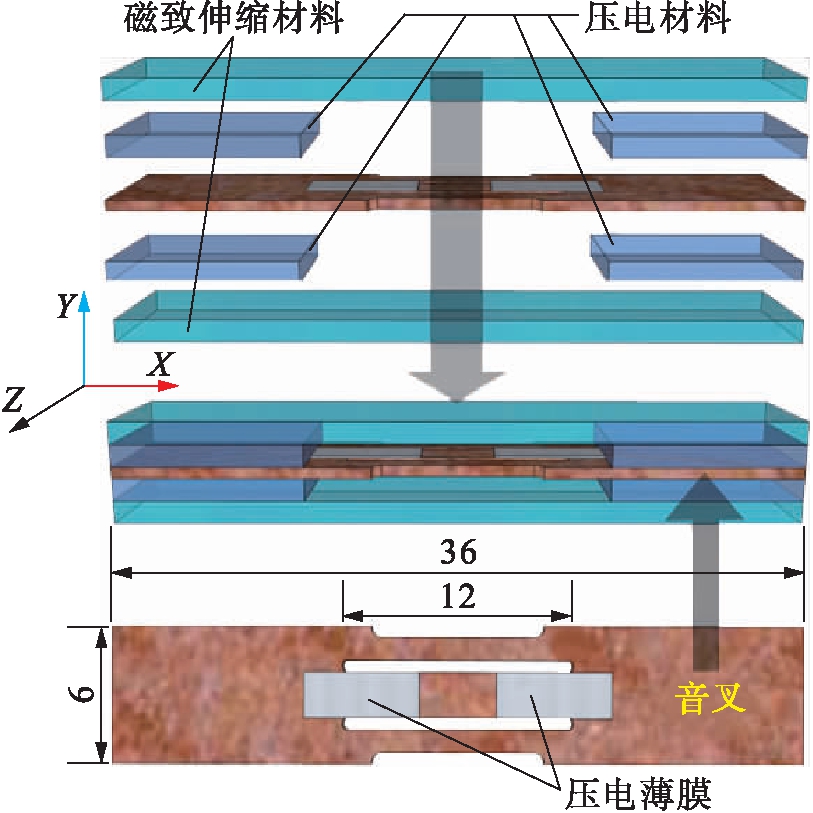
图1 谐振磁传感器结构示意图
Fig.1 Schematic structure of resonant magnetic sensor
1.2 基于有限元的改进仿真
利用COMSOL有限元仿真软件对磁传感器的应力与应变分布以及音叉的振动模态进行仿真[10].模型的参数与属性如下:音叉材质为铍青铜,泊松比为0.38,杨氏模量为130 GPa,密度为8.26×103 kg/m3,相对磁导率为1,几何尺寸为36 mm×6 mm×0.3 mm,其中振动梁长度为12 mm,中间梁和外侧两个梁的宽度分别为2和1 mm,相邻梁的距离为0.5 mm;磁致伸缩材料采用Terfenol-D,几何尺寸为36 mm×6 mm×1 mm,泊松比为0.3,杨氏模量为40 GPa,密度为9.25×103 kg/m3,初始磁化率为12,饱和磁化强度为0.637×106 A/m,饱和磁致伸缩系数为0.008%;压电材料采用PZT5,泊松比为0.36,杨氏模量为56 GPa,密度为7.5×103 kg/m3,几何尺寸为10 mm×6 mm×0.5 mm;环氧树脂胶层厚度为30 μm,泊松比为0.38,杨氏模量为3 GPa.对赋予属性的磁传感器模型进行网格划分,加载的静态磁场强度为0.12 T.仿真得到磁传感器应力分布如图2所示,音叉的最优工作模态如图3所示.
单件磁电复合材料与音叉复合的情况如图2a所示,受偏心拉伸作用影响,磁传感器发生弯曲变形,音叉与压电粘结部分的应力较为集中,而振动梁处的应力较小,大小约为4×106 N/m2.两件磁电复合材料上下对称地与音叉复合的情况如图2b所示,磁传感器没有发生弯曲变形,音叉振动梁处的应力显著增强且分布较为均匀,大小约为1.6×107 N/m2.仿真结果表明,采用磁传感器的改进结构设计能够有效抑制弯曲变形并显著增强对振动梁的纵向拉伸作用.图3中,音叉中间振动梁的相位与外侧两个振动梁的相位相反,可降低振动梁在固定端的耦合振荡损耗,从而提高谐振器的Q值[11-12].将此定义为音叉的最优工作模态,仿真得到与之对应的谐振频率为7.219 kHz.
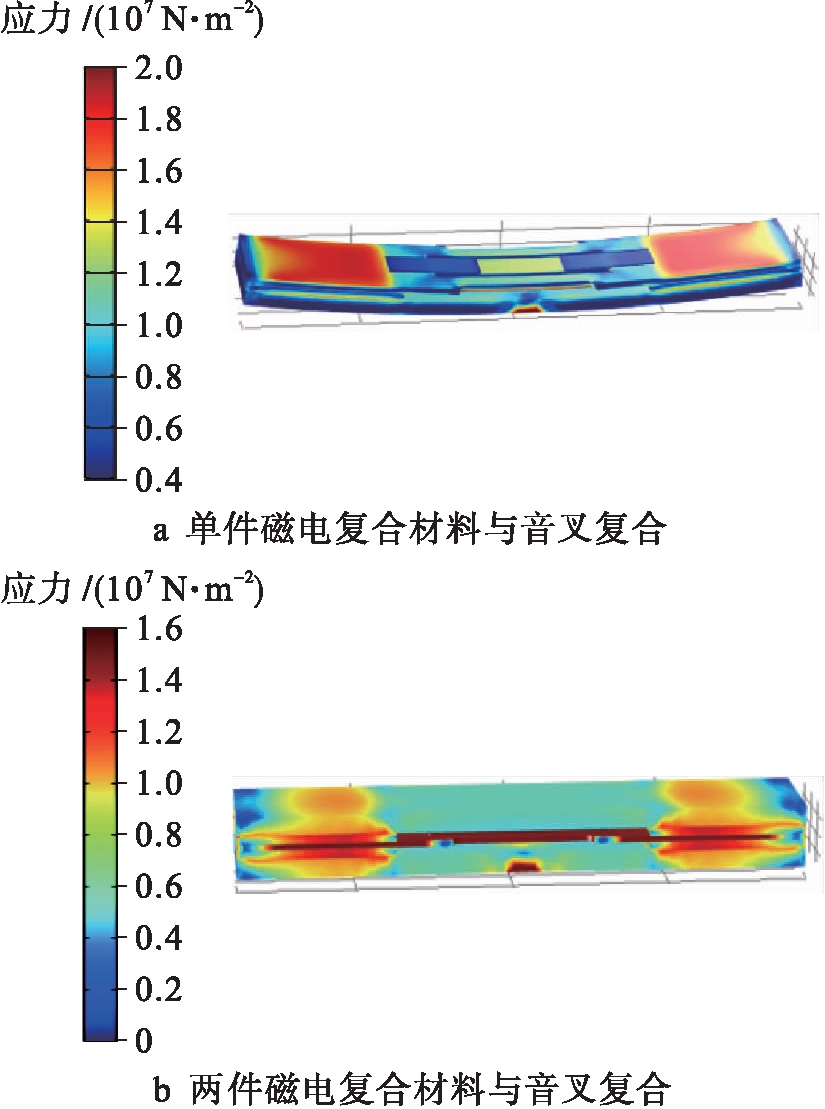
图2 磁传感器的应力分布
Fig.2 Stress distribution of magnetic sensor
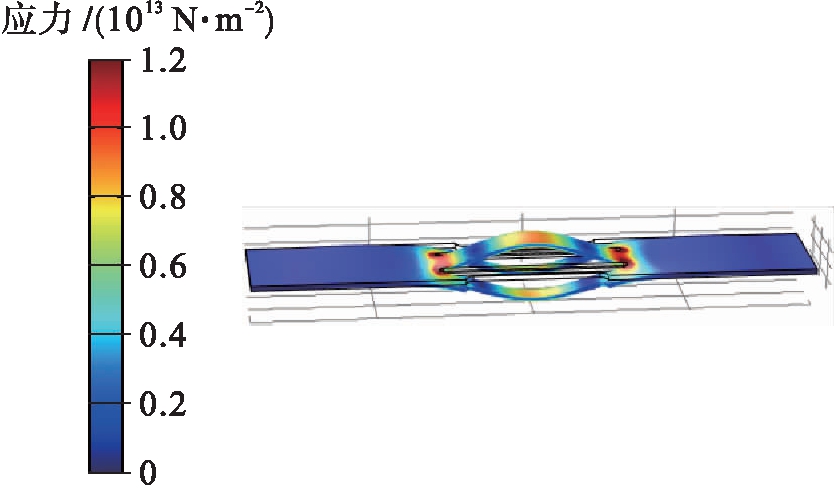
图3 音叉的最优工作模态
Fig.3 Optimal working mode of tuning-fork
1.3 谐振频率与磁场强度的关系
在静态磁场作用下,磁致伸缩材料在X方向产生的应变为
(1)
式中:d为压磁系数;H为磁场强度;σm为磁致伸缩应力;![]() 为在静态磁场S下的杨氏模量.
为在静态磁场S下的杨氏模量.
磁致伸缩材料在静态或频率远低于其谐振频率的准静态磁场作用下,磁致伸缩应力(应变)近似为均匀分布,输出的力和形变位移为
Fm=σmAm
(2)
ΔLm=εmLm
(3)
式中:Am和Lm分别为磁致伸缩材料的横截面积和长度;εm为磁致伸缩系数.由于压电层和胶层的剪切形变,音叉受纵向拉伸作用产生的形变位移小于磁致伸缩材料的形变位移,引入比例系数β(0<β<1),则音叉的拉伸形变可以表示为
ΔLT=βΔLm
(4)
两件磁电复合材料对音叉的拉伸作用合力与音叉弹性恢复力的平衡方程可表示为
2σmAm=KaβεmLm
(5)
式中,Ka为音叉纵向拉伸的弹性系数.
根据式(1)和(5),音叉受到磁电复合材料的纵向拉伸作用力可表示为
Ft=2Fm=C1H
(6)
(7)
设音叉初始谐振频率为f0,在纵向拉伸作用力下谐振频率为fr,谐振频率的偏移[9]可表示为
(8)
(9)
式中:l、b和h分别为振动梁的长度、宽度和厚度;Eb为杨氏模量;在基本振动模态下,γ0为0.295.
根据式(6)和(8),Δf可用幂级数近似地表示为
(10)
谐振频率偏移量随磁场强度的增加近似线性递增.
2 实验验证
2.1 实验测试系统
实验测试系统如图4所示,采用一对环形钕铁硼永磁体产生通过磁传感器的静态磁场,采用高斯计测量不同永磁体间距条件下的磁场强度.
图4中,PC端的Labview程序控制锁定放大器Stanford SR830输出交流信号激励音叉中间梁一端的压电薄膜产生振动,同时接收中间梁另一端的压电薄膜输出的响应信号.为了验证传感器改进结构的有效性,首先对改进结构前的磁传感器实施正弦扫频实验,得到在不同磁场强度下的频率响应以及谐振频率随磁场强度的变化发生偏移的规律;然后增加第二件磁电复合材料与音叉组成改进结构的磁传感器,在相同条件下重复正弦扫频实验.
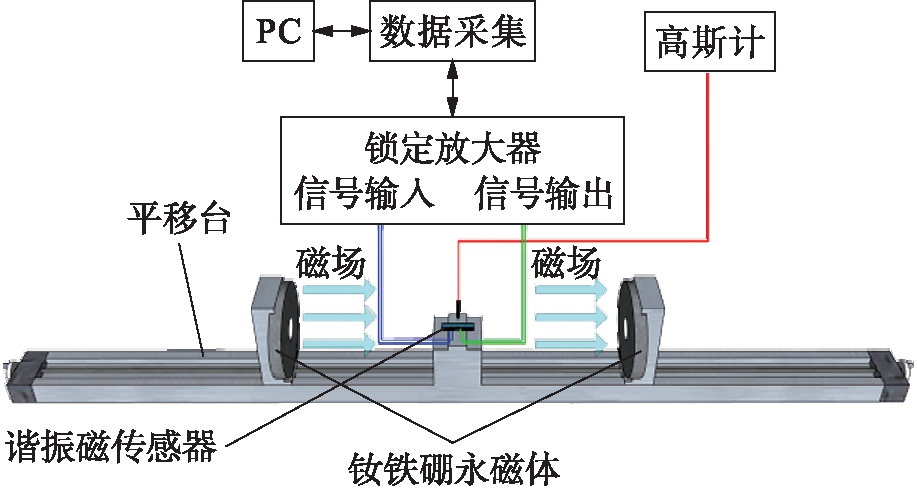
图4 实验测试系统示意图
Fig.4 Schematic diagram of experimental testing system
2.2 实验结果
图5为不同磁场强度条件下磁传感器的幅频响应.通过平移台逐步减少永磁体的间距,从而增大通过磁传感器的磁场强度,得到一系列谐振频率逐步偏离无外加磁场条件下初始谐振频率的幅频响应.传感器Q值随磁场强度变化规律如图6所示,其中,Q值为谐振频率除以相应谐振峰的3 dB带宽.
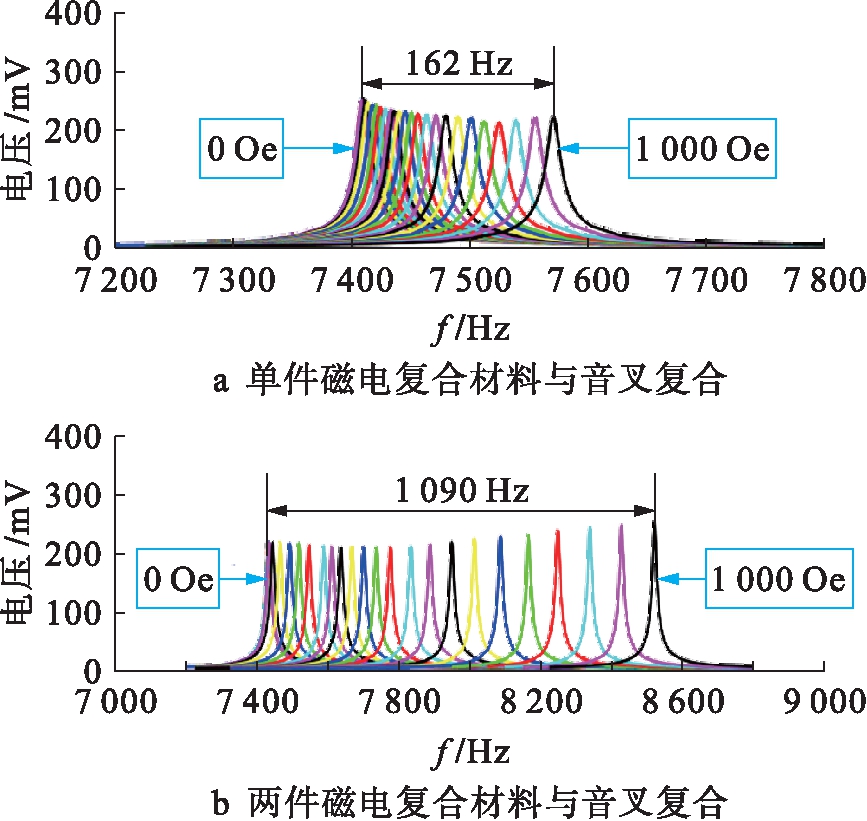
图5 传感器幅频响应
Fig.5 Amplitude-frequency response of sensor
磁传感器改进结构前的幅频响应如图5a所示.在0~1 000 Oe的范围内,谐振频率从7.408 kHz逐步增加至7.570 kHz,频率偏移幅度达162 Hz.磁传感器改进结构后的频率响应如图5b所示,在同等条件下谐振频率从7.432 kHz增加至8.522 kHz,频率偏移幅度达1 090 Hz.谐振频率的变化范围明显扩展,原因包括:一方面采用两件磁电复合材料显著增大了磁致伸缩引起的对音叉的纵向拉伸作用力;另一方面改进后的结构消除了偏心拉伸引起的弯曲变形,磁致伸缩材料的磁化方向能够保持与外部磁场方向一致,能够产生更大的磁致伸缩位移,进一步增强对音叉的纵向拉伸作用力.图6中,Q值随磁场强度变化的曲线在传感器正行程(磁场强度增大)和反行程(磁场强度减小)过程中差异较小,且改进结构后Q值仍保持较高水平,说明两件磁电材料对称地与音叉复合的结构对Q值影响较小.
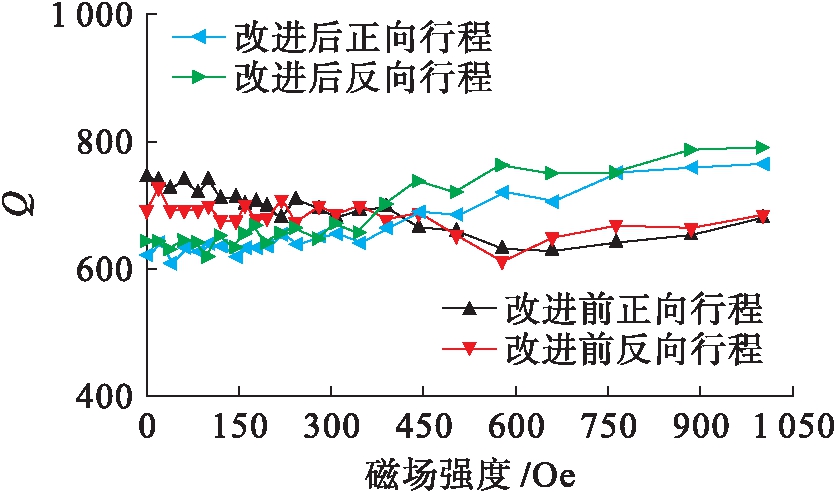
图6 Q值随磁场的变化
Fig.6 Q values changing with magnetic field
谐振频率随磁场强度变化的曲线如图7所示.在0~1 000 Oe范围内,传感器改进结构前后的谐振频率都随着磁场强度的增加近似线性递增.
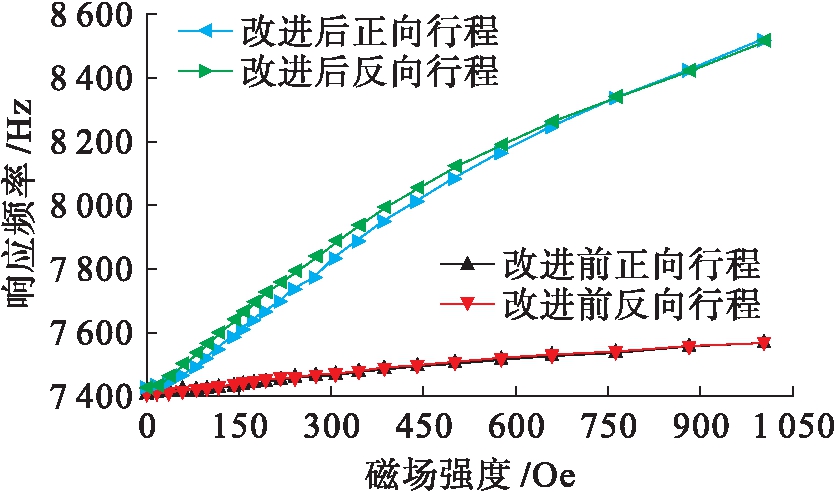
图7 谐振频率随磁场的变化
Fig.7 Resonance frequencies changing with magnetic field
改进结构前传感器的灵敏度在正向行程达到0.211 3 Hz/Oe,在反向行程达到0.236 7 Hz/Oe;改进结构后,灵敏度在正向行程达到1.595 4 Hz/Oe,在反向行程达到1.750 5 Hz/Oe.在正向和反向行程中,改进结构后的灵敏度与改进结构前相比均提高了7倍以上,与有限元仿真中音叉振动梁应力显著增强的结果相符.此外,在线性度方面,图7中改进结构前正向行程为3.83%,反向行程为4.43%;改进结构后,正向行程的线性度为4.84%,反向行程为5.96%.传感器改进结构前后保持了较好的线性度.在回程误差方面,改进结构前为4.02%,改进结构后为2.54%,回程误差明显减小.
3 结 论
本文提出磁致伸缩/压电/音叉复合谐振磁传感器的改进结构设计,采用两件磁电复合材料对称地与音叉复合增强磁传感器的灵敏度.应用COMSOL仿真软件对传感器改进结构前后的工作模态进行对比分析.结果表明,音叉受到的纵向拉伸作用显著增强,偏心拉伸引起的弯曲变形得到有效抑制.采用Terfenol-D/PZT磁电复合材料与铍青铜音叉制备谐振磁传感器样品.实验测试结果表明,传感器改进结构后的灵敏度在正反向行程中分别达到1.595 4和1.750 5 Hz/Oe,是改进结构前的7倍以上,验证了传感器改进结构设计的有效性.为了实现谐振磁传感器的工程实际应用,将来可采用Q值更高、稳定性更好的材料(例如石英)制备音叉谐振器,以进一步提高传感器更高的精度和分辨力.
[1] Guo L,Zhang H,Lu R,et al.Magnetoelectric analysis of a bilayer piezoelectric/magnetostrictive composite system with interfacial effect[J].Composite Structures,2015,134:285-293.
[2] Burdin D A,Chashin D V,Ekonomov N A,et al.High-sensitivity DC field magnetometer using nonlinear resonance magnetoelectric effect[J].Journal of Magnetism & Magnetic Materials,2016,405:244-248.
[3] Li P,Wen Y,Huang X,et al.Wide-bandwidth high-sensitivity magnetoelectric effect of magnetostrictive/piezoelectric composites under adjustable bias voltage[J].Sensors & Actuators A:Physical,2013,201(5):164-171.
[4] Jahns R,Zabel S,Marauska S,et al.Microelectro-mechanical magnetic field sensor based on ΔE effect[J].Applied Physics Letters,2014,105(5):1671-1681.
[5] Nan T,Hui Y,Rinaldi M,et al.Self-biased 215 MHz magnetoelectric MEMS resonator for ultra-sensitive DC magnetic field detection[J].Scientific Reports,2013,3:1-6.
[6] Wang Y,Li J,Viehland D.Magnetoelectrics for magnetic sensor applications:status,challenges and pers-pectives[J].Materials Today,2014,17(6):269-275.
[7] Lee E Y,Bahreyni B,Seshia A A.An axial strain modulated double-ended tuning fork electrometer[J].Sensors & Actuators A:Physical,2008,148(2):395-400.
[8] Kiser J,Finkel P,Gao J,et al.Stress reconfigurable tunable magnetoelectric resonators as magnetic sensors[J].Applied Physics Letters,2013,102(4):350-358.
[9] Bian L,Wen Y,Li P,et al.Magnetostrictive stress induced frequency shift in resonator for magnetic field sensor[J].Sensors & Actuators A:Physical,2016,247(3):453-458.
[10] 杨理践,郭天昊,高松巍,等.油气管道特殊部件的漏磁检测信号特征分析[J].沈阳工业大学学报,2017,39(1):43-47.
(YANG Li-jian,GUO Tian-hao,GAO Song-wei,et al.Feature analysis on magnetic flux leakage detection signal for special parts of oil and gas pipeline[J].Journal of Shenyang University of Technology,2017,39(1):43-47.)
[11] Yan T,Jones B E,Rakowski R T,et al.Design and fabrication of thick-film PZT-metallic triple beam resonators[J].Sensors & Actuators A:Physical,2004,115(2):401-407.
[12] Zhang W,Lee E Y.Frequency-based magnetic field sensing using Lorentz force axial strain modulation in a double-ended tuning fork[J].Sensors & Actuators A:Physical,2014,211(5):145-152.