我国输配电网络规模日益扩大,逐渐朝着超高压和远距离方向发展[1],同时,电力系统的结构、运行方式以及电网中的不确定因素也变得日趋复杂,这对电网的影响日益明显,并造成了巨大的经济损失.因此,评估电网调度的风险可以有效减少电力系统的故障概率,从而降低损失[2].
要保证电网运行风险评估的有效性和精确性,需要根据电力系统的发电站、变电站、输电子系统和配电子系统等各功能部分的特点使用不同的评估方法,以实现最优的评估效果[3].目前,常用的电网调度风险评估方法主要分为模拟法和解析法两类,其中,解析法通过建立严格、精确的数学模型来求取各种风险指标;而模拟法利用计算机和随机数的产生原理,采用重复模拟一个过程的实现、随机抽样和统计的方法来计算调度系统风险指标的近似值[4].模拟法使用随机数来模拟物理和数学问题,以解决确定性问题与带有随机性的问题,包括非序贯模式和序贯模式两种[5-6].其中,非序贯蒙特卡洛模拟不需要考虑系统的实际运行顺序,只通过抽取大量的样本数据即可评估系统运行风险指标;而序贯模式则需要按照系统运行的时间顺序和运行历史来计算风险指标.解析法则需要根据系统设计和元件的故障数据来推导系统的风险指标,主要包括状态空间法、网络分析法、状态枚举法和故障树分析法[7-8].
模拟法与解析法均包括状态选择、状态估计和指标计算三个步骤.其中,解析法使用枚举的方法进行状态选择,并计算风险指标的解析解[9];而模拟法使用抽样的方法进行状态选择,用统计法计算风险指标[10].解析法通常具有清晰的物理模型和概念,并能获得较高的评估精度,但其需要处理复杂的关联事件,且在模拟实际控制策略时会遇到较大困难;而模拟法的采样次数与系统的规模无关,易于处理各种实际运行策略,但需要进行多次模拟来获取较高的评估精度,且当系统参数变化时需要重新模拟[11].
针对上述问题,本文结合解析法和模拟法的特点提出了一种基于非序贯蒙特卡洛的电网调度风险评估方法.首先在非序贯蒙特卡洛模拟的基础上结合解析法来提高计算效率,然后提出了一种等分散抽样法来减小采样方差,从而提高收敛效率,最后,在IEEE RTS系统上进行仿真测试来验证所提出方法的有效性.
1 解析法与非序贯蒙特卡洛模拟
本文通过在模拟过程中结合解析法和蒙特卡洛模拟来解析判断采样状态,从而减少系统评估所需的时间,充分发挥解析法计算精度高和蒙特卡洛模拟法计算量小的优势,在蒙特卡洛模拟过程中使用解析法来减少采样次数.
假设电网调度系统只考虑供电线路和发电机的故障,则可将随机采样后的系统状态划分为如图1所示的4个区域.
图1中GF和GN分别表示发电机处于故障状态和正常运行状态,TF和TN分别表示输电线路处于故障状态与正常运行状态.图1中Ⅰ区为正常运行状态,其他区域为故障状态,其中,Ⅳ区表示同时出现发电机和线路故障.由于配电系统在不同故障状态出现系统切负荷的概率不同,故本文将Ⅱ、Ⅲ和Ⅳ区划分为不引起系统切负荷的状态集合和可能引起系统切负荷的状态集合.本文首先计算判断采样状态是否属于不引起系统切负荷的状态,若属于则不会影响配电系统的风险指标,立即转入下次采样;否则会影响系统的风险指标,需应用削减负荷.
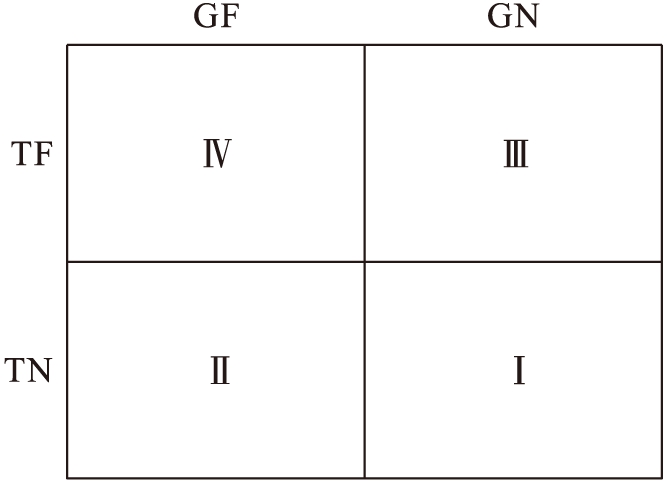
图1 系统状态划分图
Fig.1 Partition diagram of system states
解析法判断流程如图2所示.其中,GF=1和GN=1分别表示发电机与输电线路故障;GF=0和GN=0分别表示发电机和输电线路正常工作.
当出现发电机故障时,该发电机节点备用容量能够弥补故障,导致有功出力损失时需重置GF=0,即
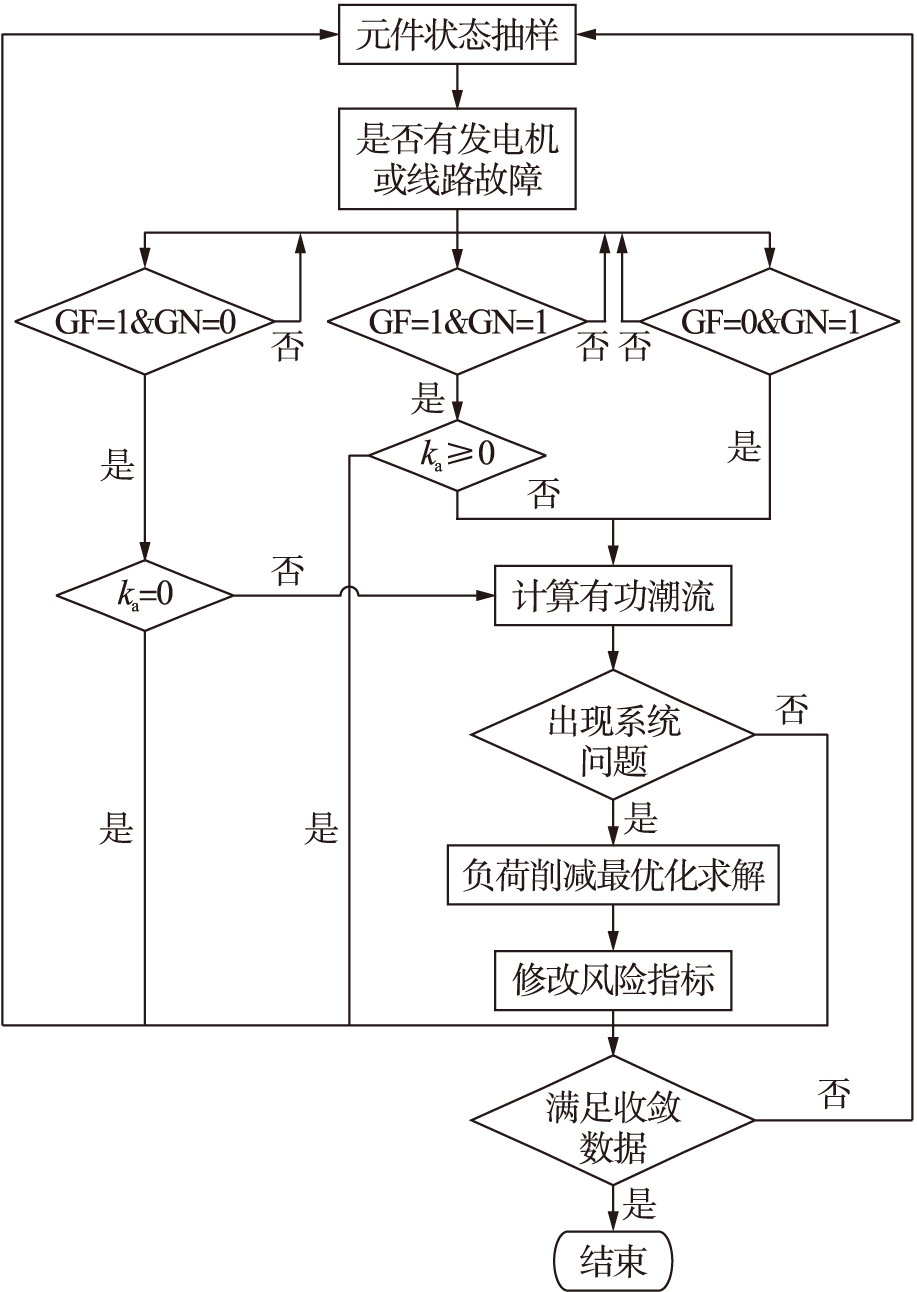
图2 解析法判断流程
Fig.2 Flow chart of judgment with analytic method
ka=∑P′c-Pc+P′gc-Pgc
(1)
式中:P′c和Pc分别为发电机的有功功率上限和实际有功功率;P′gc和Pgc分别为发生故障前后的有功功率;ka≥0表示该节点的有功注入功率不变.本文通过在发电机或线路故障时计算各线路的有功潮流来判断线路是否过负荷,从而判定是否需要削减负荷.
2 抽样方差减小技术
在进行电网调度风险评估时,为了获得更高的风险指标,通常需要对数目庞大的系统随机状态进行评估,需要花费较长的计算时间.本文提出了一种等分散抽样方法,通过降低抽样方差在保证计算精度的前提下,显著减少采样次数来提升计算速度.
等分散抽样法将采样区间[0,1]等分成k个不同长度的子区间,其中k满足max(f1,f2,…,fm)≤k<1,f1,f2,…,fm为m个系统元件的强迫失效概率.
对于某一元件i的状态值xi,可按照式(2)在k个子区间中采样k个状态变量xi1,xi2,…,xij,…,xik,即
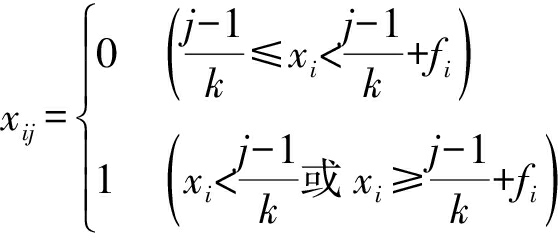
(2)
由式(2)可知,每随机抽样一次可以根据抽样结果得到k个状态,从而有效提高了采样效率.本文将k个状态的风险指标值F(x1),F(x1),…,F(xi),…,F(xk)的平均值作为随机变量xi的风险指标值.
本文采用系统停电功率期望EP和停电概率TP作为风险指标,其定义分别为
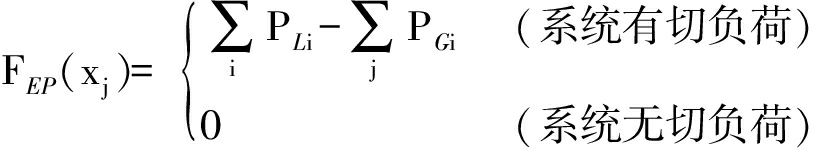
(3)
(4)
式中:PLi为负荷总量;PGi为发电出力总量.可以得到本文的风险指标为
(5)
其期望值为
(6)
式中,![]() 为第j次抽样得到的风险指标值,则F*(x)的方差为
为第j次抽样得到的风险指标值,则F*(x)的方差为
(7)
3 电网调度风险评估流程
本文将解析法和方差减小技术加入到传统的非序贯蒙特卡洛模拟法中,以实现更高的评估效率.其中,通过引入解析法来减少单次抽样模拟所需的时间,并采用等分抽样法在保证计算精度的同时减少抽样次数.所提出改进方法的计算流程如图3所示.
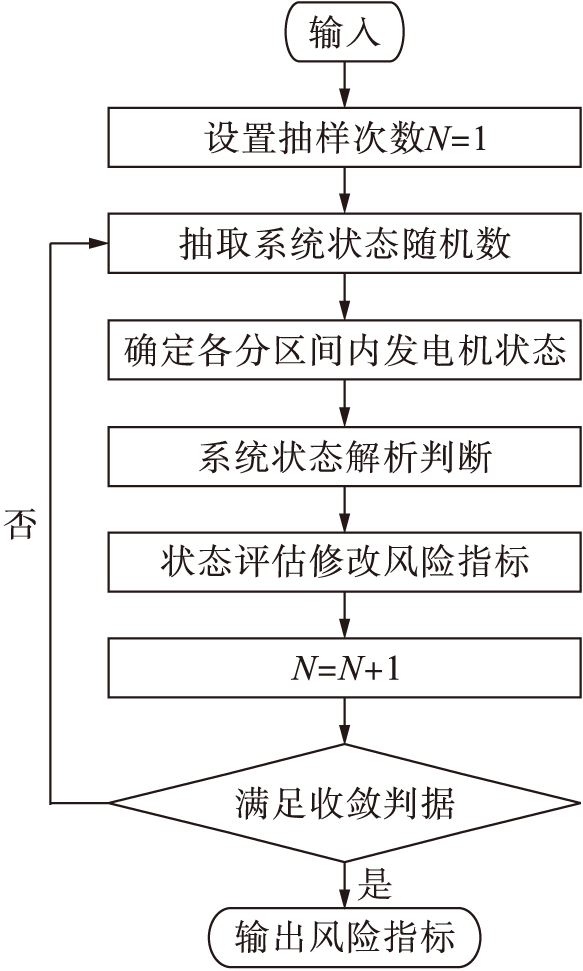
图3 改进的非序贯蒙特卡洛模拟法计算流程
Fig.3 Calculation flow chart of improved non-sequentialMonte Carlo simulation method
改进的非序贯蒙特卡洛模拟法采用等分散抽样的方法随机抽取系统的状态.假设该调度控制系统包含N个元件,当进行均匀抽样时每次抽取只能得到一个系统状态;而采用等分散抽样后,每次抽样可以生成元件的k个状态,并得到k个系统状态,从而大幅提高抽样效率.该方法在系统状态抽样结束后,先进行解析判断再评估系统状态与计算风险指标,由此便能减少单次抽样模拟所需的时间,从而提高效率.
4 算例分析
本文使用如图4所示的IEEE RTS系统进行仿真测试,来验证所提出方法的有效性.该系统包含32台发电机、33条输电线路和24条母线,以及17个装机总容量为3 410 MW,平均负荷率为62.44%的电源.
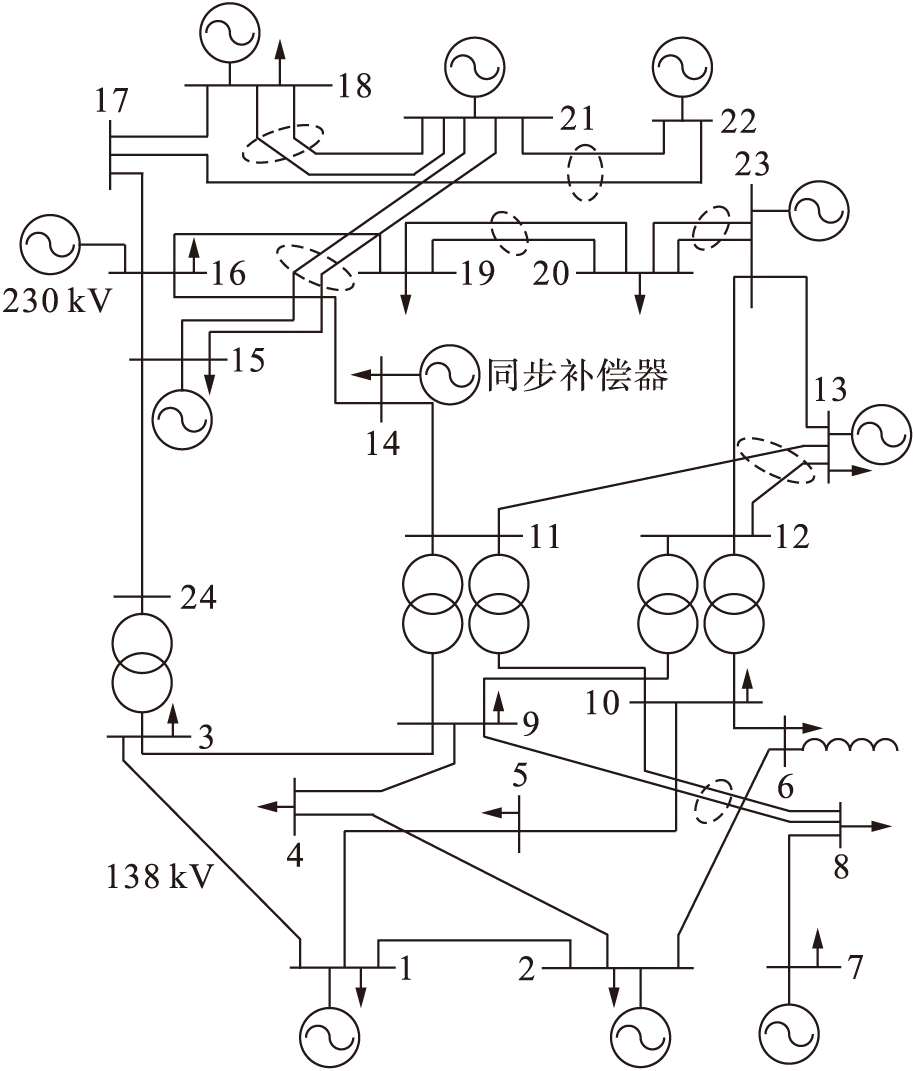
图4 IEEE RTS系统网络图
Fig.4 Diagram of IEEE RTS system network
将所提出的方法(方法Ⅲ)与传统采用分散抽样的非序贯蒙特卡洛模拟法(方法Ⅰ)和采用均匀抽样的非序贯蒙特卡洛模拟法(方法Ⅱ)进行比较,以验证所提出的方法具有更高的计算效率.使用系统停电功率期望EP和停电概率TP作为该系统的风险指标.
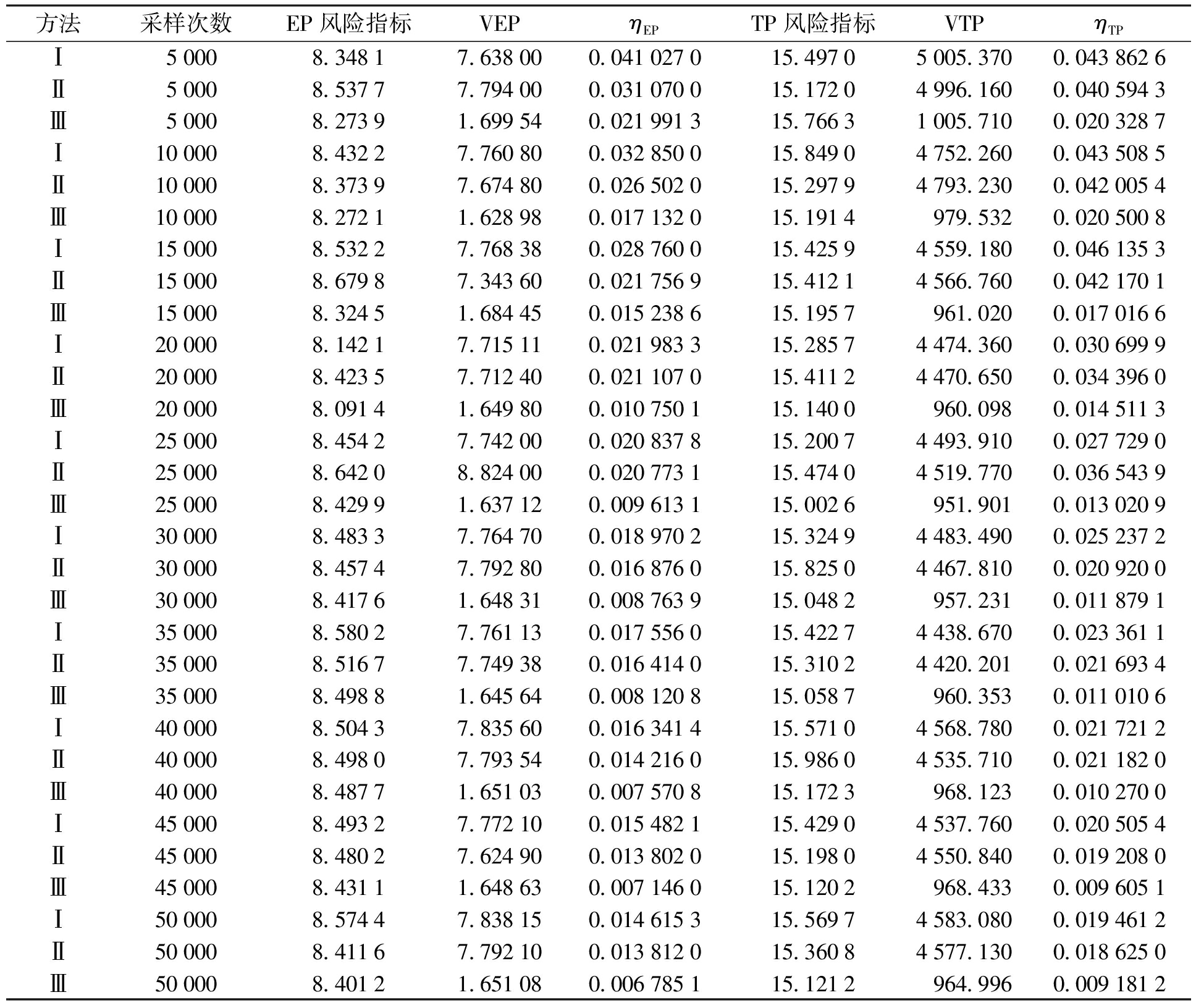
表1为3种方法的风险评估结果,其中,VEP和VTP分别为系统停电功率期望EP与停电概率TP的方差;ηEP和ηTP分别为其对应的方差系数.本文分别比较了抽样次数为5 000、10 000、15 000、20 000、25 000、30 000、35 000、40 000、45 000和50 000时,各方法的风险指标值.从表1中可以看出,在相同的抽样次数下,本文方法能明显降低抽样方差,并能提高收敛速度.在采样次数为50 000时,本文方法所获得的ηEP和ηTP分别为方法Ⅰ的20.06%和21.18%,方法Ⅱ的21.05%和21.08%,表明本文方法的收敛性能更优.
表1 各方法风险评估结果
Tab.1 Risk assessment results of various methods
方法采样次数EP风险指标VEPηEPTP风险指标VTPηTPⅠ50008.34817.638000.041027015.49705005.3700.0438626Ⅱ50008.53777.794000.031070015.17204996.1600.0405943Ⅲ50008.27391.699540.021991315.76631005.7100.0203287Ⅰ100008.43227.760800.032850015.84904752.2600.0435085Ⅱ100008.37397.674800.026502015.29794793.2300.0420054Ⅲ100008.27211.628980.017132015.1914979.5320.0205008Ⅰ150008.53227.768380.028760015.42594559.1800.0461353Ⅱ150008.67987.343600.021756915.41214566.7600.0421701Ⅲ150008.32451.684450.015238615.1957961.0200.0170166Ⅰ200008.14217.715110.021983315.28574474.3600.0306999Ⅱ200008.42357.712400.021107015.41124470.6500.0343960Ⅲ200008.09141.649800.010750115.1400960.0980.0145113Ⅰ250008.45427.742000.020837815.20074493.9100.0277290Ⅱ250008.64208.824000.020773115.47404519.7700.0365439Ⅲ250008.42991.637120.009613115.0026951.9010.0130209Ⅰ300008.48337.764700.018970215.32494483.4900.0252372Ⅱ300008.45747.792800.016876015.82504467.8100.0209200Ⅲ300008.41761.648310.008763915.0482957.2310.0118791Ⅰ350008.58027.761130.017556015.42274438.6700.0233611Ⅱ350008.51677.749380.016414015.31024420.2010.0216934Ⅲ350008.49881.645640.008120815.0587960.3530.0110106Ⅰ400008.50437.835600.016341415.57104568.7800.0217212Ⅱ400008.49807.793540.014216015.98604535.7100.0211820Ⅲ400008.48771.651030.007570815.1723968.1230.0102700Ⅰ450008.49327.772100.015482115.42904537.7600.0205054Ⅱ450008.48027.624900.013802015.19804550.8400.0192080Ⅲ450008.43111.648630.007146015.1202968.4330.0096051Ⅰ500008.57447.838150.014615315.56974583.0800.0194612Ⅱ500008.41167.792100.013812015.36084577.1300.0186250Ⅲ500008.40121.651080.006785115.1212964.9960.0091812
图5、6分别为各种方法的停电功率期望EP和停电概率TP的方差系数变化曲线.从图5、6中可以看出,随着抽样次数的增加,各方法的方差系数均在减小,且相比于采用分散抽样的非序贯蒙特卡洛模拟法和采用均匀抽样的非序贯蒙特卡洛模拟法,本文方法具有更小的方差系数.
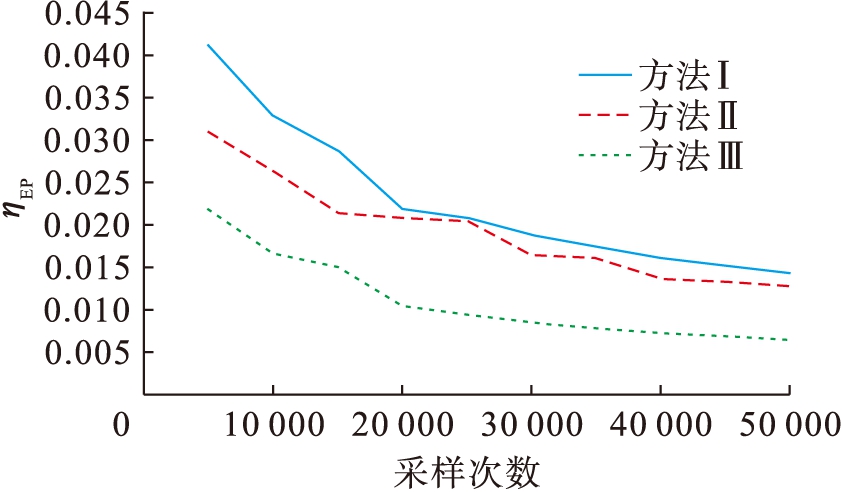
图5 停电功率期望方差系数变化曲线
Fig.5 Expected variance coefficient change of power outage
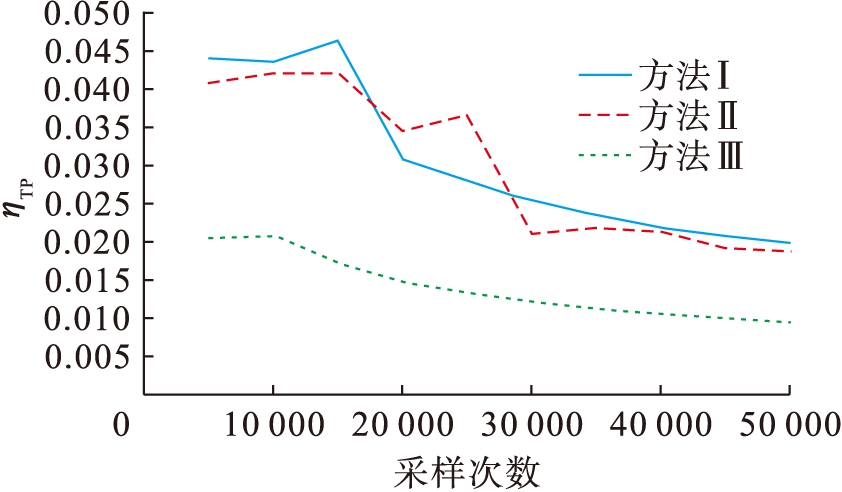
图6 停电概率方差系数变化曲线
Fig.6 Variance coefficient change of power outage probability
采用分散抽样的非序贯蒙特卡洛模拟法和采用均匀抽样的非序贯蒙特卡洛模拟法进行风险评估时,在不同的抽样次数下所耗费的时长占比均为100%.而本文进行5 000~50 000次采样时,所耗费的时长占比分别为29.39%、32.12%、31.76%、32.4%、31.78%、32.7%、32.47%、32.21%、31.41%和32.3%,由此表明,本文所提出的方法可以节省70%以上的计算时间.
5 结 论
本文结合解析法和模拟法的特点,提出了一种基于非序贯蒙特卡洛的电网调度风险评估方法.该方法在非序贯蒙特卡洛模拟的基础上结合解析法来提高计算效率,同时使用方差减小技术来提高收敛效率.基于IEEE RTS系统的仿真测试与实验结果表明,所提出的方法能节省70%以上的计算时间,且具有更高的计算效率.
[1]晏鸣宇,何宇斌,姚伟,等.基于时变结构可靠性理论的覆冰电网风险调度 [J].电网技术,2017,41(6):1873-1879.
(YAN Ming-yu,HE Yu-bin,YAO Wei,et al.Risk dispatch of iced grid based on time-varying structure reliability theory [J].Grid Technology,2017,41(6):1873-1879.)
[2]侯广松,高军,徐珂,等.基于远程监控技术的电力调度设计与实现 [J].电子设计工程,2016,24(17):107-110.
(HOU Guang-song,GAO Jun,XU Ke,et al.Design and implementation of power dispatching based on remote monitoring technology [J].Electronic Design Engineering,2016,24(17):107-110.)
[3]Kaabi S S A,Zeineldin H H,Khadkikar V.Planning active distribution networks considering multi-DG configurations [J].IEEE Transactions on Power Systems,2014,29(2):785-793.
[4]Xing H,Yang F,Cheng H.Active distribution network expansion planning integrating practical operation constraints [J].Electric Power Components & Systems,2018,45(16):1-11.
[5]Sang H L,Son K S,Jung W,et al.Risk assessment of safety data link and network communication in digital safety feature control system of nuclear power plant [J].Annals of Nuclear Energy,2017,108(5):394-405.
[6]Pukhrem S,Basu M,Conlon M F.Probabilistic risk assessment of power quality variations and events under temporal and spatial characteristic of increased PV integration in low voltage distribution networks [J].IEEE Transactions on Power Systems,2018,9:1-7.
[7]王秀,孙忠林,姜莉.任务定时调度在企业级开发中的研究 [J].电子科技,2015,28(10):100-104.
(WANG Xiu,SUN Zhong-lin,JIANG Li.Research on task timing scheduling in enterprise development [J].Electronic Science and Technology,2015,28(10):100-104.)
[8]葛维春,刘前卫,刘富家,等.高比例清洁能源电网灵活调节方法 [J].沈阳工业大学学报,2018,40(5):481-485.
(GE Wei-chun,LIU Qian-wei,LIU Fu-jia,et al.Fle-xible adjustment method for power grid with high-proportion clean energy [J].Journal of Shenyang University of Technology,2018,40(5):481-485.)
[9]刘辛,张坦通.面向MANETs按需路由协议的黑洞攻击解析改进模型 [J].重庆邮电大学学报(自然科学版),2017,29(2):245-250.
(LIU Xin,ZHANG Tan-tong.Improved black hole attack analytical model for MANETs on demand routing protocols [J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2017,29(2):245-250.)
[10]Cusumanotowner M F,Mansinghka V K.Measuring the non-asymptotic convergence of sequential Monte Carlo samplers using probabilistic programming [J].IEEE Transactions on Power Systems,2017,32(9):1988-1999.
[11]Smith R A,Ionides E L,King A A.Infectious disease dynamics inferred from genetic data via sequential Monte Carlo [J].Molecular Biology & Evolution,2017,34(8):2065-2084.