近几十年,空气质量的评价和预报研究获得了较大进展,指数法、层次决策法、主成分分析法、模糊理论和灰色系统分析等被很多学者应用于空气质量评价和预报.随着计算机技术的发展和一些新学科的创立,国内外又产生和提出很多新的方法和理论进行多种空气质量的评价和预报,这些方法主要有物元可拓法[1]、投影寻踪分析法、集对分析法、新的指数评价法、遗传优化法及多种方法的耦合模型[2-3]等.由于上述评价和预报方法的数学基础不同,因此它们的适用范围和适用对象差异也较大,各有优缺点,这些方法是在原有空气质量评价和预报方法的基础上改进、丰富和发展而来.由于受到多种因素的影响,大气污染物浓度的变化具有较强的非线性特性,很难用确定的数学模型描述,要对其进行较为准确的预测,就必须采用能捕捉非线性变化规律的预报方法,传统统计预报方法或数值预报局限性很大[4].
神经网络具有独特的联想、记忆和学习功能,因此得到广泛应用.由于空气质量指数变化具有很强的非线性特征,结合神经网络强大的泛化能力和非线性刻画能力,本文运用极限学习机神经网络模型对A市空气质量进行预报研究,并针对标准极限学习机神经网络存在收敛速度慢和局部最优的问题,运用粒子群算法优化极限学习机神经网络的权值和阀值,提高了A市空气质量预报结果的准确率.
1 极限学习机神经网络
极限学习机(ELM)是一种新型的单隐含层前馈神经网络(single-hidden layer feed-forward neural networks,SLFNs),是在Moore-Penrose矩阵理论基础上所提出的快速学习算法,其结构示意图如图1所示.
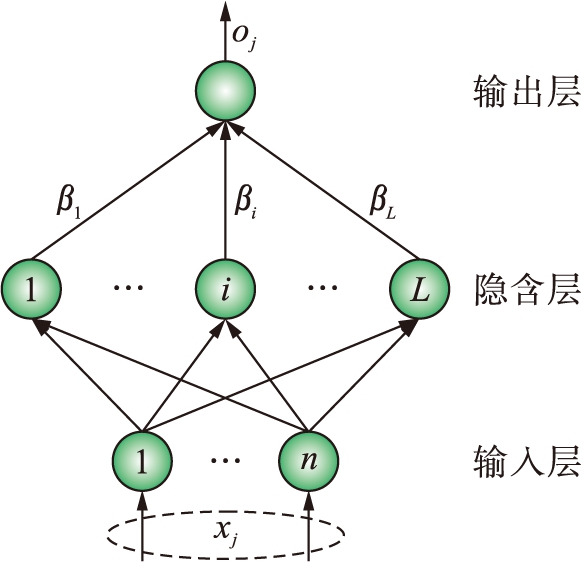
图1 ELM结构示意图
Fig.1 Schematic structure of ELM
对于N个不同样本(xi,ti),其中xi=[xi1,xi2,…,xin]T∈Rn,ti=[ti1,ti2,…,tim]T∈Rm,一个隐藏层结点数目为![]() 激励函数g(x)的SLFN统一模型[5-6]为
激励函数g(x)的SLFN统一模型[5-6]为
![]()
(j=1,2,…,N)
(1)
式中:ai=[ai1,ai2,…,ain]T为连接第i个隐藏层结点的输入权值;bi为第i个隐藏层结点的偏置;βi=[βi1,βi2,…,βim]T为连接i个隐藏层结点的输出权值.上述N个方程的矩阵形式可写为
Hβ=T
(2)
式中:
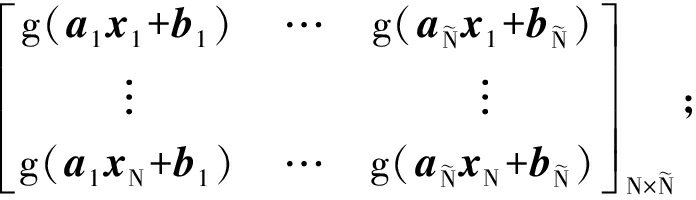
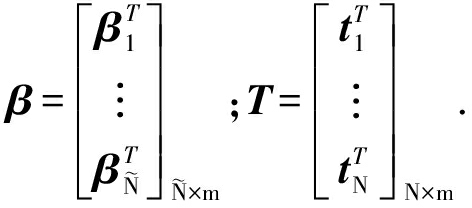
E(W)表示期望值和实际值之间的误差平方和,问题求解就是寻找最优的权值W=(a,b,β)使代价函数E(W)最小,其数学模型[7-9]可表示为
(j=1,2,…,N)
(3)
式中,εj=[εj1,εj2,…,εjm]为第j个样本的误差.
2 PSO优化ELM空气质量预报
2.1 PSO算法
粒子群算法是一种模拟鸟群觅食的群体智能算法,每个粒子表示一个可能解向量,粒子的好坏根据适应度函数值进行判断,并通过向全局和个体最优解学习实现粒子位置和速度的不断更新,最终实现全局寻优的目的.若Xi=(Xi1,Xi2,…,Xid)和Vi=(Vi1,Vi2,…,Vid)分别表示粒子的位置和粒子的速度,粒子的速度和位置的更新策略表达式[10-11]为
(4)
(5)
式中:![]() 分别为迭代次数t时刻粒子的个体最优解和全局最优解;r1、r2为0~1之间的随机数;c1、c2为学习因子.
分别为迭代次数t时刻粒子的个体最优解和全局最优解;r1、r2为0~1之间的随机数;c1、c2为学习因子.
2.2 适应度函数
在保证空气质量指数预报误差最低的情况下,通过PSO优化ELM的权值和阀值.由于ELM需要优化的参数为权值和阀值,其适应度函数[12-13]可用式(3)进行表示,但权值和偏置的取值范围均在0~1之间.
2.3 算法步骤
PSO优化ELM的空气质量预报算法流程如下:
1) 归一化空气质量样本数据,建立训练样本和测试样本;
2) 设定PSO算法的种群大小,最大迭代次数及学习因子c1、c2;
3) 将构建出的训练样本输入ELM,根据目标函数式(3)计算粒子个体的适应度函数值,寻找粒子个体和全局最优粒子的位置和最优值;
4) 更新粒子速度和位置;
5) 计算适应度同时更新位置和速度;
6) 运用PSO优化ELM获取的最优参数ai、βi、bi,实现空气质量预报.
3 实证分析
3.1 评价指标
为了评价空气质量预测结果的优劣,选择平均绝对百分比误差(mean absolute percentage error,MAPE)、均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)作为预测结果的评价指标,评价公式为
(6)
(7)
(8)
式中:yi为某一时刻的空气质量实际值;![]() 为某一时刻的空气质量预测值;M为预测时刻的长度.
为某一时刻的空气质量预测值;M为预测时刻的长度.
3.2 数据来源
为了验证本文算法的有效性和可靠性,本文选择A市2016年9月14日~2017年3月31日的空气质量指数数据为研究对象,剔除无效数据,剩余数据141组.将样本数据分成两个部分,前97组作为训练数据,用来建立A市空气质量预报模型,后44组作为测试数据集,用来验证所建立模型的效果.粒子群算法参数设置如下:最大迭代次数为100,种群规模为10,学习因子c1=c2=2.极限学习机参数设置如下:输入神经元个数为3,隐含层神经元个数为30,输出层神经元个数为1,ELM神经网络训练次数为10 000,学习速率为0.05,训练误差目标为0.001.PSO-ELM的训练结果和预测结果对比图分别如图2、3所示.
为了验证PSO-ELM算法的优越性,将PSO-ELM算法与GA-ELM、SOA-ELM、DE-ELM及ELM算法进行对比.GA算法参数设置如下:种群规模10,最大迭代次数100,交叉概率0.7,变异概率0.1;SOA算法参数设置如下:种群规模10,最大迭代次数100,最大隶属度值Umax=0.950 0,最小隶属度值Umin=0.011 1,权重最大值Wmax=0.9,权重最小值Wmin=0.1;DE算法参数设置如下:种群规模10,最大迭代次数100,缩放因子0.5,交叉概率0.7.不同算法预测结果分别如图4~11所示.
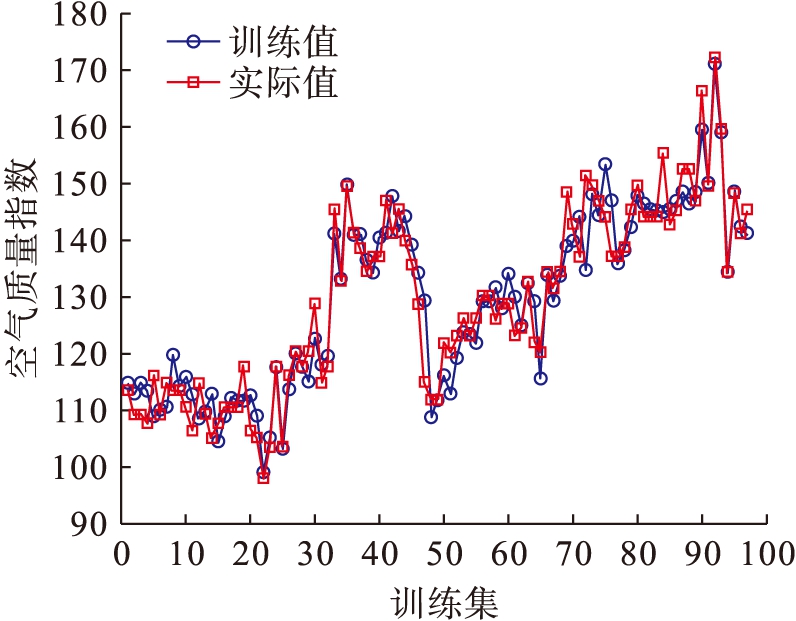
图2 PSO-ELM训练结果和实际值对比图
Fig.2 Comparison between training results and actual values by PSO-ELM
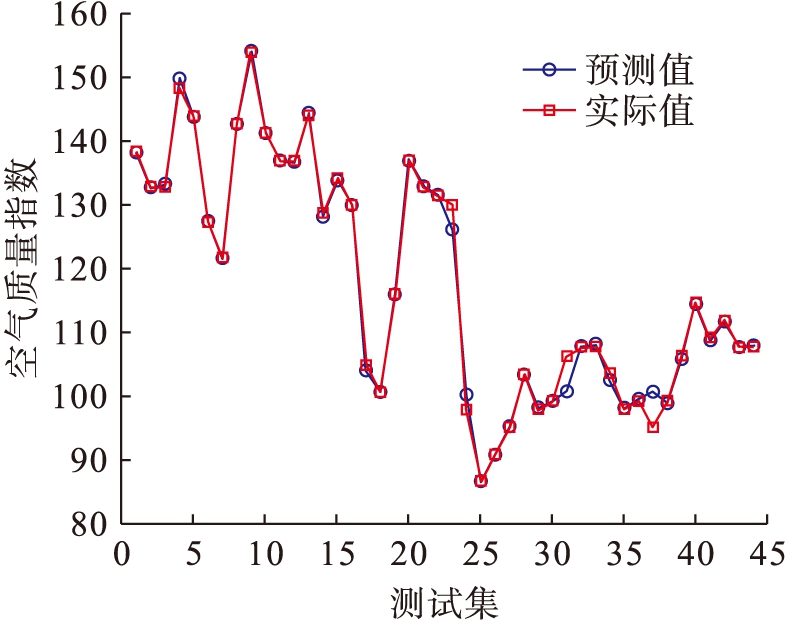
图3 PSO-ELM预测结果和实际值对比图
Fig.3 Comparison between predicted results and actual values by PSO-ELM
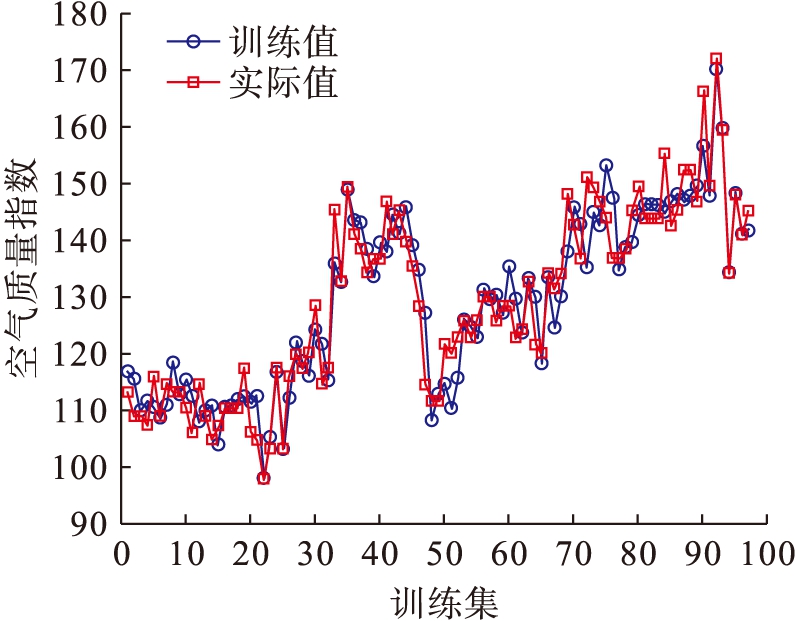
图4 GA-ELM训练结果和实际值对比图
Fig.4 Comparison between training results and actual values by GA-ELM
由表1不同算法空气质量预测结果对比可知,在RMSE、MAE和MAPE三个评价指标上,PSO-ELM的预测精度最高,优于GA-ELM、SOA-ELM、DE-ELM和ELM;其次,GA-ELM的预测精度优于SOA-ELM、DE-ELM和ELM;ELM的预测精度最差.通过对比可知,运用群智能算法对ELM的输入权值、输出权值和偏置进行优化,可以有效提高ELM的预测精度,其中PSO算法对ELM的优化效果最好,较其他智能算法相比具有更高的预测精度.
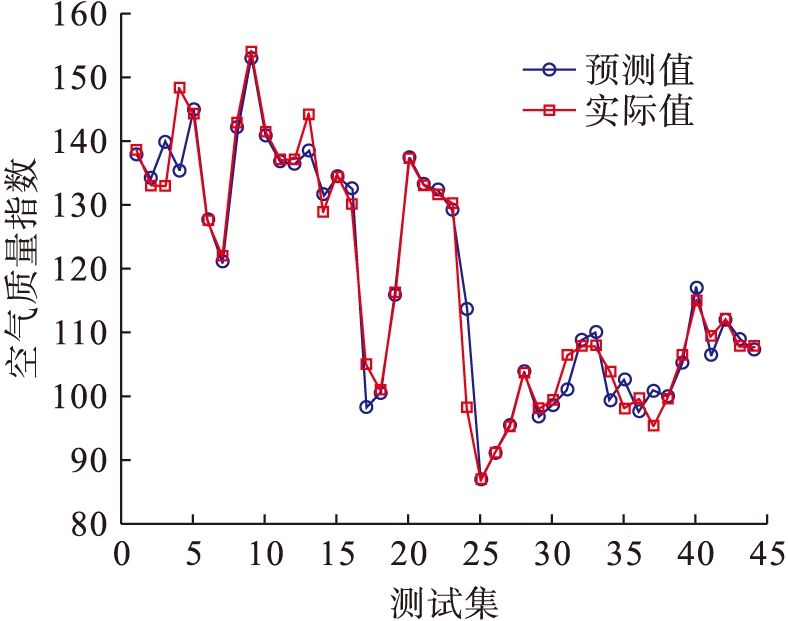
图5 GA-ELM预测结果和实际值对比图
Fig.5 Comparison between predicted results and actual values by GA-ELM
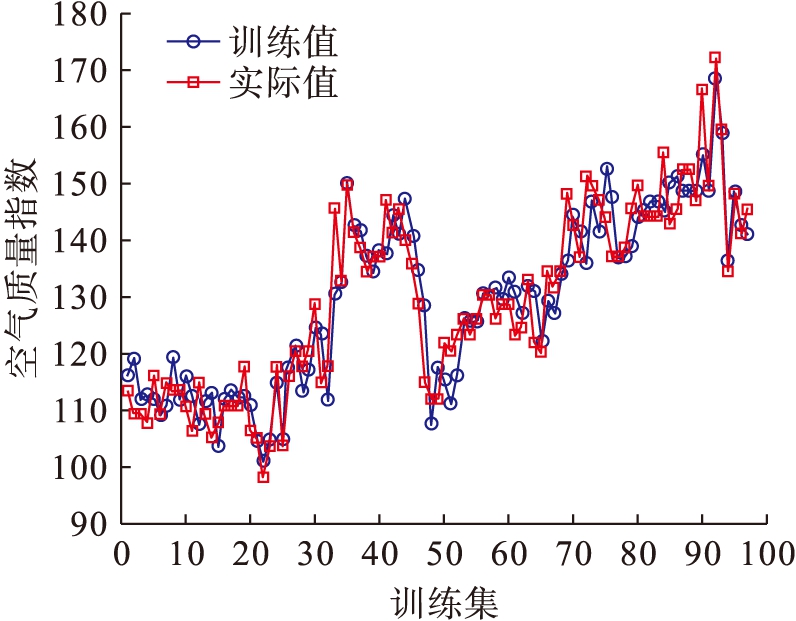
图6 SOA-ELM训练结果和实际值对比图
Fig.6 Comparison between training results and actual values by SOA-ELM
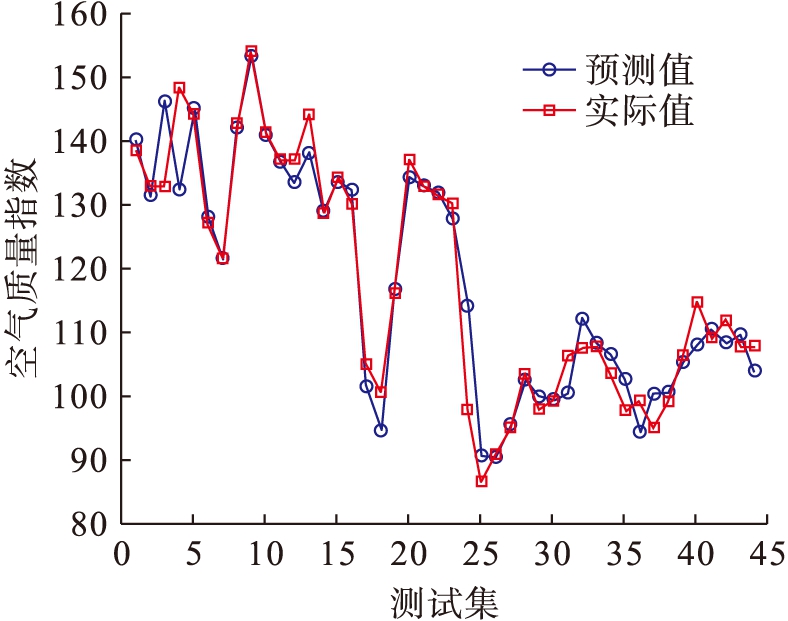
图7 SOA-ELM预测结果和实际值对比图
Fig.7 Comparison between predicted results and actual values by SOA-ELM
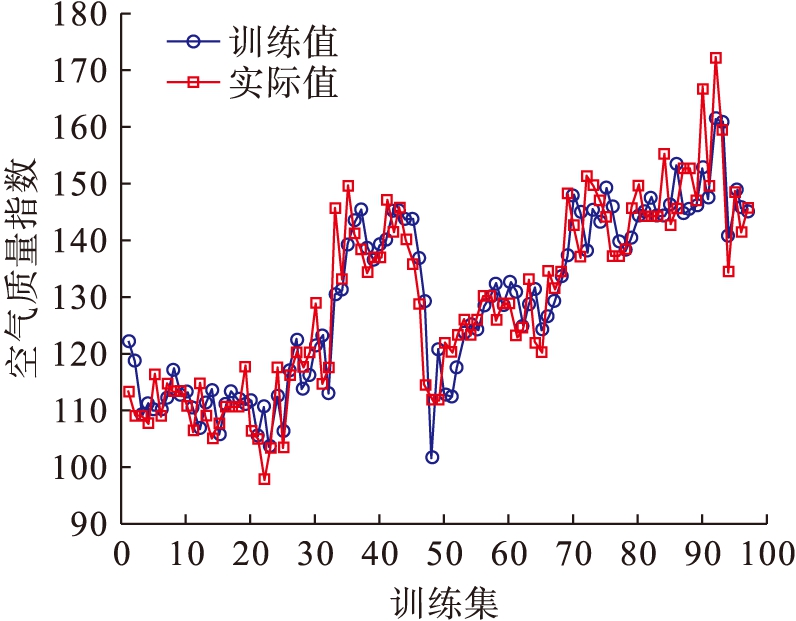
图8 DE-ELM训练结果和实际值对比图
Fig.8 Comparison between training results and actual values by DE-ELM
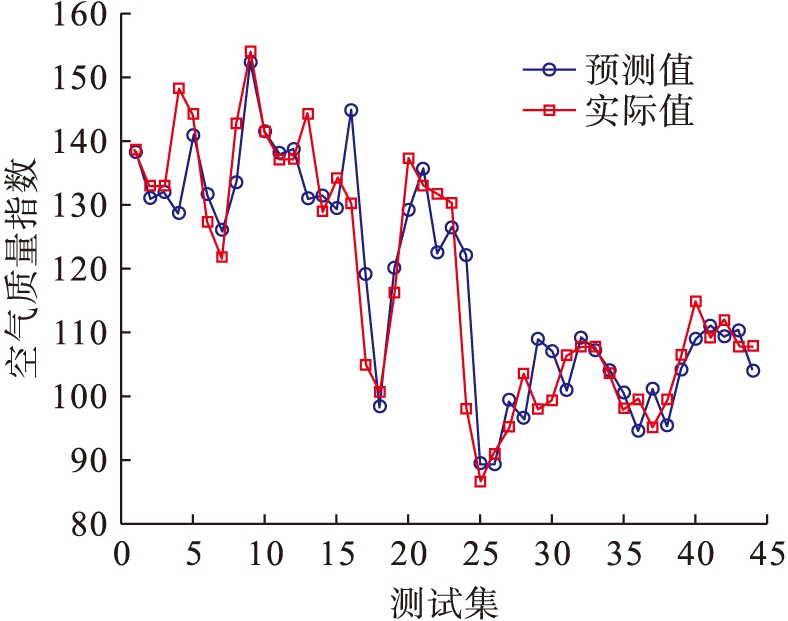
图9 DE-ELM预测结果和实际值对比图
Fig.9 Comparison between predicted results and actual values by DE-ELM
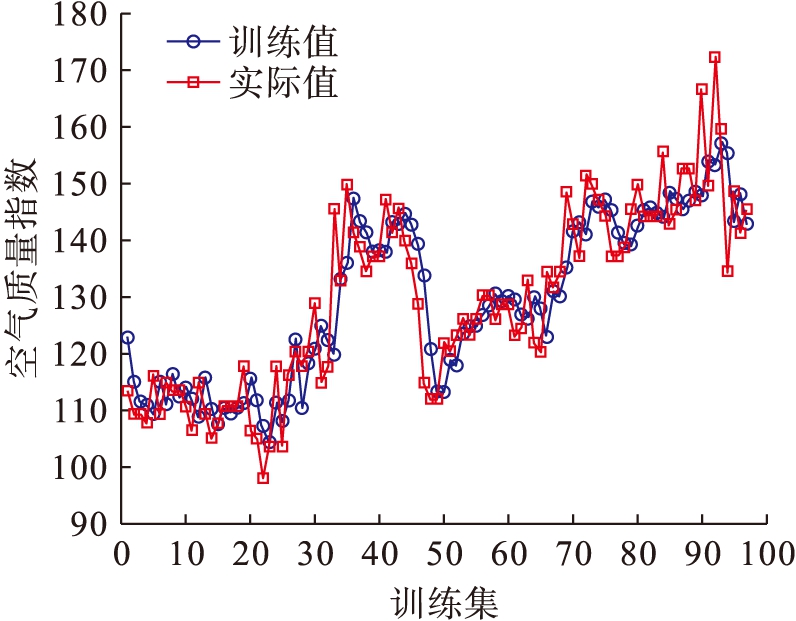
图10 ELM训练结果和实际值对比图
Fig.10 Comparison between training results and actual values by ELM
4 结 论
空气质量指数变化具有很强的非线性特征,为避免标准极限学习机陷入局部最优,提出一种基于粒子群算法优化极限学习机的空气质量预测模型.运用粒子群算法优化极限学习机神经网络的权值和阀值,实现极限学习机的权值和阀值的最优选择.研究结果表明,与ELM相比,PSO-ELM可以有效提高空气质量预测精度,具有较好的工程应用前景和价值.
图11 ELM预测结果和实际值对比图
Fig.11 Comparison between predicted results and actual values by ELM
表1 不同算法的对比结果
Tab.1 Comparison results of different algorithms
方法RMSEMAE/%MAPE/%PSO-ELM1.43670.64720.5844GA-ELM3.97212.27941.9703SOA-ELM4.88373.11412.7034DE-ELM7.32625.22434.4427ELM8.14836.10767.4534
[1]王国胜,郭联金,董晓清,等.深圳市区空气污染的人工神经网络预测 [J].环境工程学报,2015,9(7):3393-3399.
(WANG Guo-sheng,GUO Lian-jin,DONG Xiao-qing,et al.Artificial neural network prediction of air pollutants in Shenzhen city [J].Journal of Environmental Engineering,2015,9(7):3393-3399.)
[2]花晓蕾,唐慧强,张红燕,等.基于RBF神经网络的空间插值法在空气质量监测中的应用 [J].传感器与微系统,2015,34(1):157-160.
(HUA Xiao-lei,TANG Hui-qiang,ZHANG Hong-yan,et al.Application of spatial interpolation method in air quality monitoring based on RBF neural network [J].Sensor and Microsystem,2015,34(1):157-160.)
[3]谢超,马民涛,于肖肖,等.多种神经网络在华北西部区域城市空气质量预测中的应用 [J].环境工程学报,2015,9(12):6005-6009.
(XIE Chao,MA Min-tao,YU Xiao-xiao,et al.Forecasting model of air pollution index based on multi-artificial neural network in western region of Northern China [J].Journal of Environmental Engineering,2015,9(12):6005-6009.)
[4]李媛,武岩岩,王思琪.基于混沌时间序列的Elman神经网络工业用电预测 [J].沈阳工业大学学报,2016,38(2):196-200.
(LI Yuan,WU Yan-yan,WANG Si-qi.Elman neural nnetwork for forecasting industrial electricity consumption based on chaotic time series [J].Journal of Shenyang University of Technology,2016,38(2):196-200.)
[5]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications [J].Neurocompu-ting,2006,70(1/2/3):489-501.
[6]Im U,Bianconi R,Solazzo E,et al.Evaluation of ope-rational on-line-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2 [J].Atmospheric Environment,2015,115(2):404-420.
[7]Feng X,Li Q,Zhu Y,et al.Artificial neural networks forecasting of PM 2.5,pollution using air mass trajectory based geographic model and wavelet transformation [J].Atmospheric Environment,2015,107:118-128.
[8]郭平.大数据分析中基于 MapReduce 的空间权重创建方法研究 [J].重庆邮电大学学报(自然科学版),2016,28(4):533-538.
(GUO Ping.Research on construction method of spatial weights based on MapReduce in analysis of big data [J]Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2016,28(4):533-538.)
[9]刘锋,李春燕,谭祥勇,等.基于机器学习在空气质量指数中的应用 [J].重庆工商大学学报(自然科学版),2017(3):82-87.
(LIU Feng,LI Chun-yan,TAN Xiang-yong,et al.App-lication of machine learning in air quality index [J].Journal of Chongqing Technology and Industry University (Natural Science Edition),2017(3):82-87.)
[10]南亚翔,李红利,修春波,等.基于卡尔曼滤波的空气质量指数预测方法 [J].环境科学导刊,2016,35(3):80-84.
(NAN Ya-xiang,LI Hong-li,XIU Chun-bo,et al.Based on Kalman filter’s air quality index forecasting method [J].Environmental Science Guide,2016,35(3):80-84.)
[11]杨阳,沈泽昊,郑天立,等.中国当前城市空气综合质量的主要影响因素分析 [J].北京大学学报(自然科学版),2016,52(6):1102-1108.
(YANG Yang,SHEN Ze-hao,ZHENG Tian-li,et al.Analysis of the main influencing factors of air quality in China [J].Journal of Peking University (Natural Science Edition),2016,52(6):1102-1108.)
[12]周家师.基于多元统计和智能算法的上海市空气质量指数评价分析 [D].兰州:兰州大学,2016.
(ZHOU Jia-shi.Evaluation and analysis of Shanghai air quality index based on multiple statistics and intelligent algorithms [D].Lanzhou:Lanzhou University,2016.)
[13]Iosifidis A,Tefas A,Pitas I.Graph embedded extreme learning machine [J].IEEE Transactions on Cybernetics,2016,46(1):311-314.