电容层析成像(electrical capacitance tomography，简称ECT)技术是过程层析成像技术中的一种，其研究始于上世纪80年代末期.该技术基于电容敏感原理，通过测量放置在封闭管道或容器外不同极板间的电容值作为投影数据，采用适当的图像重建算法重建出封闭物场内部介质(介电常数)分布情况的二维或三维图像[1-2].ECT技术在诸多方面得到广泛应用，例如鼓泡硫化床气/固两相流成像、流动的油/水两项介质的动态分布成像、循环流化床气/固两相流动三维成像以及热虹吸管冷凝实验成像等[3-6].该技术具有结构简单、费用低、响应速度快、安全无辐射等优点，被认为是一种极具发展前景的可视化测量技术.
传统的ECT重建图像是管道的二维截面图.近几年兴起的三维ECT重建图像以三维图像形式给出.由于三维ECT可以获得介质分布的几何形状、相对位置和体积等信息，因此受到广泛关注.但是与传统的二维ECT相比，三维ECT系统测量信号的动态范围和敏感场强度差异较大，导致灵敏度矩阵的条件数变大，病态问题也更严重[7]，因此对于重建算法的要求就更高.
工业中对重建速度与精度要求同等重要，因此，对ECT图像重建算法的速度和精度要求更高[8].目前，电容层析成像技术的图像重建算法总体上可分为非迭代算法和迭代算法两大类.迭代算法相比非迭代算法在大多数情况下可获得较好的重建效果，但是其也具有两个比较显著的缺点：1)运算时算法的收敛速度比较慢，通常需要很多次的迭代运算才能获得比较高质量的重建图像；2)在灵敏度比较高的成像区域，重建图像会产生伪迹现象.特别是在三维ECT图像重建时，这两个问题就变得更为严重.目前，国内外学者对于算法的研究主要集中在算法迭代公式的改进或灵敏度矩阵的优化上，如Gunes等[2]采用离散傅里叶方法进行伪三维成像；吴新杰等[9]将卷积神经网络应用在ECT图像重建上；张立峰[10]将压缩感知理论和快速傅里叶变换用于图像重建；Moura等[11]提出了一种稀疏重建方案，采用冗余灵敏度矩阵来改善重建效果等.而阈值滤波是减少伪迹的一种简单而有效的方法，目前，迭代滤波方面的研究工作相对较少，并且将各改进算法与传统Landweber迭代算法重建结果进行比较，而传统Landweber迭代算法均采用简单的0-1方式进行阈值滤波.
本文将Landweber迭代算法和阈值滤波技术相融合，提出了一种基于自适应阈值滤波的三维ECT重建算法(three-dimensional reconstruction algorithm based on adaptive threshold filtering，简称ATF算法).在迭代重建过程中使用阈值滤波对重建图像进行强化伪迹抑制操作，并定期自动更新滤波阈值.为了获得最佳滤波阈值，首先定义基于香农熵函数的图像模糊度量，然后找到使图像模糊度量最小的阈值作为最佳滤波阈值.
1 三维ECT图像重建系统和原理
电容层析成像系统由传感器系统、数据采集系统和图像重建系统三部分组成，如图1所示.
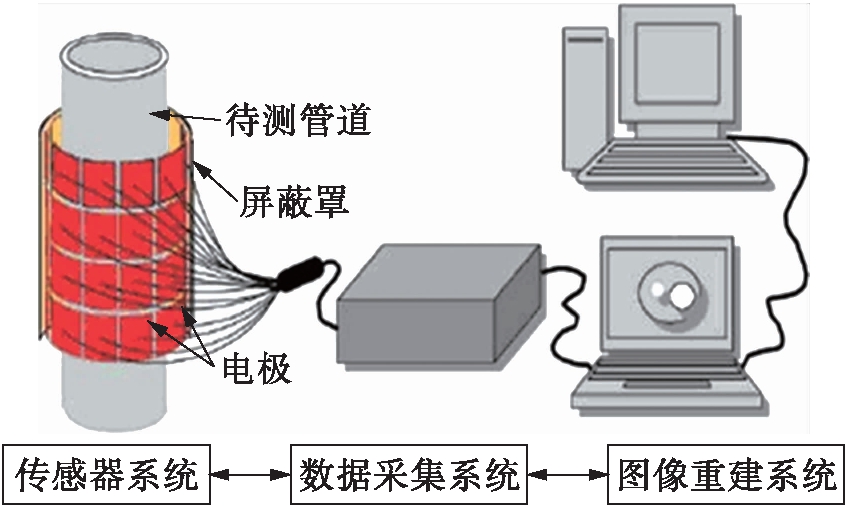
图1 ECT系统结构示意图
Fig.1 Schematic ECT system structure
假设屏蔽罩内没有自由电荷，则ECT传感器的静电场由拉普拉斯方程[12]描述，即
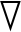·(ε0ε(x，y，z)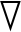φ(x，y，z))=0
(1)
式中：ε0为真空介电常数；ε(x，y，z)为相对介电常数分布；φ(x，y，z)为电势分布.电容与介电常数之间的关系式为
(2)
式中：C0为电容值；Q为检测极板上的电荷；U为电势差；E为电场强度；Γ为包围极板的封闭曲面.测量电容值和介质分布之间的关系是非线性的，为了计算方便，将二者的非线性关系按照线性化近似可得
C=SG
(3)
式中：C∈RN×1为归一化的电容矢量；G∈RM×1为归一化的介电常数矢量；S∈RN×M为归一化的灵敏度矩阵.对于J极板构成的ECT系统，可获得独立测量电容数目为N=J(J-1)/2.
2 带自适应阈值滤波的三维ECT重建算法
本文算法的重建公式可描述为
G0=P(STC)
(4)
Gk=P(Gk-1+αST(C-SGk-1))
(5)
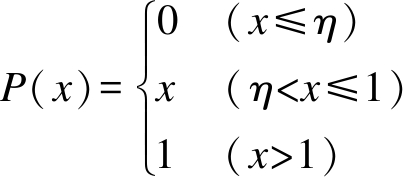
(6)
式中：η为滤波阈值；ST为M×N维的归一化灵敏度矩阵的转置阵；α为迭代步长.本文取α=2/λmax，λmax为STS的最大特征值，当α<1时，则取α=1.5.式(4)用来获取重建图像的初始值，式(5)为迭代重建公式，式(6)为阈值滤波算子，算法具体实施步骤如下：
1) 令η=0，用式(4)、(5)计算图像初始值G0=[G0(1)，G0(2)，…，G0(M)]，并令k=1，其中，M为归一化的介电常数矢量个数.
2) 计算Gk=P(Gk-1+αST(C-Gk-1)).
3) 如果((k))q≠1，((k))q表示k对q取余数，q为预先设定好的一个正整数，则转到步骤4)；否则按下述方法求η.
将0～1的灰度值均匀地划分为0～L-1，即L(L为预先设定好的一个正整数，且为2的幂指数)个灰度级；令gmax、gmin分别为图像的最大、最小灰度级，h(g)为灰度级g在图像中出现的次数；对于给定阈值t，基于香农熵定义阈值t所对应的图像模糊度量E(t)为
(7)
F(g)=-μ(g)ln[μ(g)]-[1-μ(g)]·
ln[1-μ(g)]
(8)
(g=0，1，…，gmax-1)
(9)
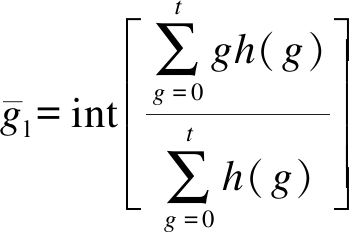
(10)
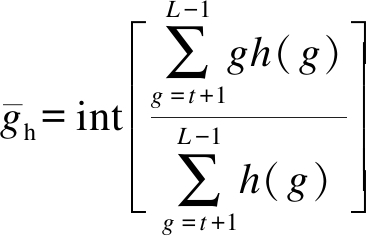
(11)
式中，int[x]为对实数x四舍五入取整数值.令E=1、t=gmin、topt=gmin，取值采用如下步骤：
① 利用式(7)～(11)计算阈值t所对应的图像模糊度量E(t)，如果E(t)<E，则令E=E(t)，topt=t.
② 如果t=gmax-1，则转到步骤③；如果t<gmax-1，则令t=t+1，转到步骤①.
③ 令
当求得的最小熵值同时与几个大小不同的灰度级对应时，则应选取这些灰度级中的最大灰度级作为topt.
4) 利用式(12)对图像Gk进行强化伪迹抑制，其表达式为
Gk=P(Gk)
(12)
通过仿真实验发现，η值计算时间的长短与灰度级L的大小有关，即灰度级L的取值越大，η值的计算时间就越长.但是算法的重建精度并不总是随着灰度级L的取值增大而减少.因此，通过仿真实验确定灰度级L=64.
本文中，q值越小，对伪迹抑制效果越好，但是所消耗的重建时间也越长.通过仿真实验，本文取q=10.
3 算法验证
对本文提出的三维重建方法分别进行了仿真和实验验证.采用12极板三维ECT传感器，实物图如图2所示.传感器的极板轴向上分为三层，每一层上布置4个极板，相邻两层极板水平方向上旋转45°.每一个极板均由宽为32.725 mm，高为9 mm的铜箔构成，水平方向上两个相邻极板间的距离为6.545 mm，轴向上相邻两层极板间的距离为9 mm；实验使用的绝缘有机玻璃管道内半径为23 mm，外半径为25 mm，管壁厚度为2 mm，管壁相对介电常数约为4；外部屏蔽罩的内半径为33 mm.
图2 三层ECT传感器实物剖面图
Fig.2 Profile of three-layer ECT sensor
3.1 仿真重建
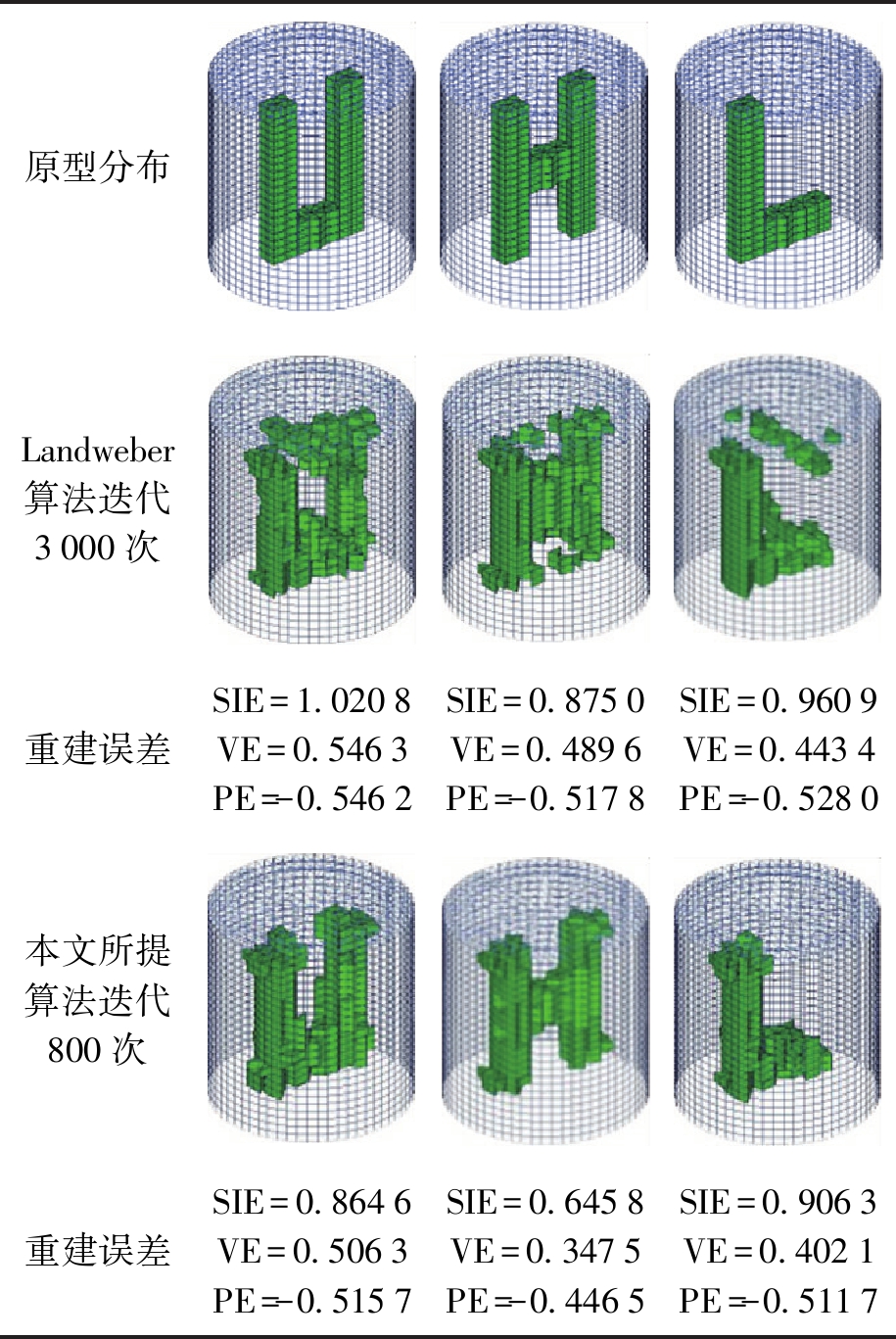
为了验证算法的有效性，采用本文算法与传统的Landweber迭代算法对U、H、L三种字母型复杂分布进行了仿真重建.表1为原型分布图，以及传统Landweber迭代算法和本文算法的重建图像.其中，传统Landweber迭代算法的迭代次数为3 000次，本文算法迭代次数为800次.两种算法的迭代步长皆为α=1.334 2.表1列出了两种算法的空间图像误差(SIE)、体积误差(VE)和介电常数误差(PE).
表1 仿真成像及误差
Tab.1 Simulated images and errors
原型分布Landweber算法迭代3000次重建误差SIE=1.0208VE=0.5463PE=-0.5462SIE=0.8750VE=0.4896PE=-0.5178SIE=0.9609VE=0.4434PE=-0.5280本文所提算法迭代800次重建误差SIE=0.8646VE=0.5063PE=-0.5157SIE=0.6458VE=0.3475PE=-0.4465SIE=0.9063VE=0.4021PE=-0.5117
极板覆盖区域称为成像区域，设e为成像区域中的第e个像素单元，T为成像区域内总的像素单元数，即e=1，2，…，T，则空间图像误差(SIE)的计算公式为
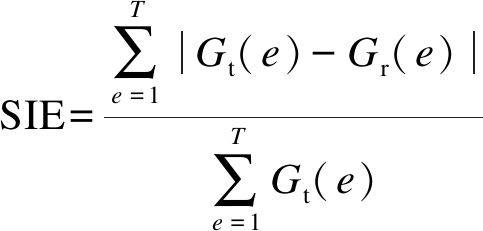
(13)
式中：
空间图像误差(SIE)包括重建物体在形状、位置和体积上的空间误差信息，因此，SIE的值越小越好.
体积误差(VE)反映了实际物体和三维重建物体在体积上的差异.VE的绝对值越小越好，其计算公式为
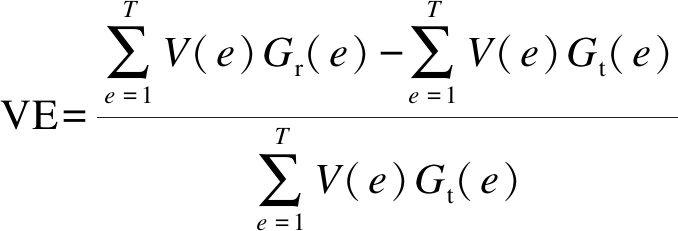
(14)
式中，V(e)为成像区域内第e个像素单元的体积.
介电常数误差(PE)反映了实际物体的归一化介电常数平均值与三维重建物体归一化介电常数之间的差异.介电常数误差的绝对值越小，重建图像的质量就越好，其计算公式为
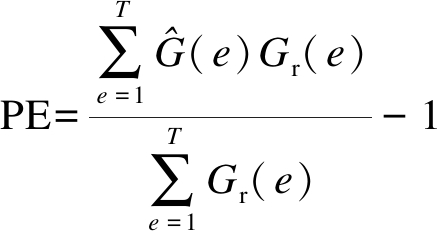
(15)
式中，
为三维重建归一化介电常数矢量
中的第e个元素.
本文提出的三维重建算法迭代800次的重建伪迹明显少于Landweber算法迭代3 000次时的重建伪迹，重建图像更接近于原型分布.从重建误差来看，本文提出的三维重建算法的SIE、VE和PE值均优于Landweber算法值.通过仿真分析，本文提出的三维重建算法迭代800次和Landweber算法迭代3 000次时，对于同一重建对象的程序运行时间比值约为1∶3.因此，本文提出的三维重建算法对于伪迹抑制是有效的，既提高了重建图像的质量，又加快了重建速度.
3.2 实验重建
实验所用ECT系统如图3所示，实验所使用的测试物是由U、H、L型字母分布的介电常数约为3.7的石英砂构成.图4为三种字母型测试物的形状以及在管道中与极板的相对位置.
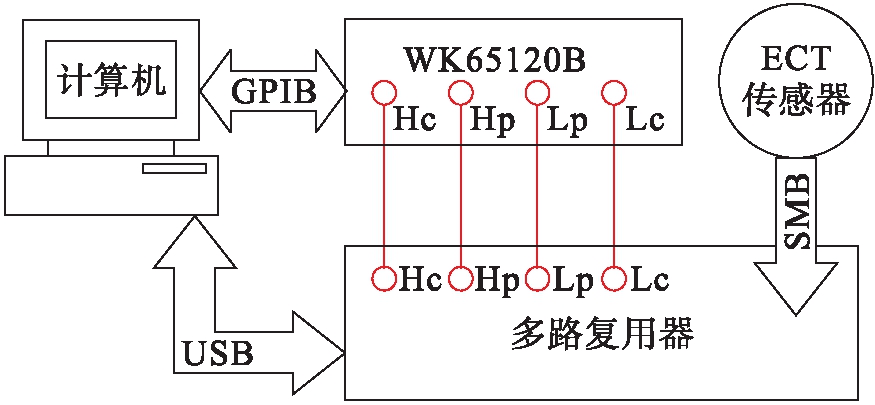
图3 基于WK65120B的ECT系统
Fig.3 ECT system based on WK65120B
表2为传统Landweber迭代算法和本文所提三维重建算法的重建图像，可以看出，两种算法均可以重建出复杂分布的基本形状.相比之下，本文所提算法的重建伪迹相对较少，进一步验证了本文所提算法是有效的、可行的.
4 结 论
本文将Landweber迭代算法和模糊阈值滤波技术相结合，提出了基于自适应阈值滤波的三维ECT重建算法，在迭代过程中采用阈值滤波方式
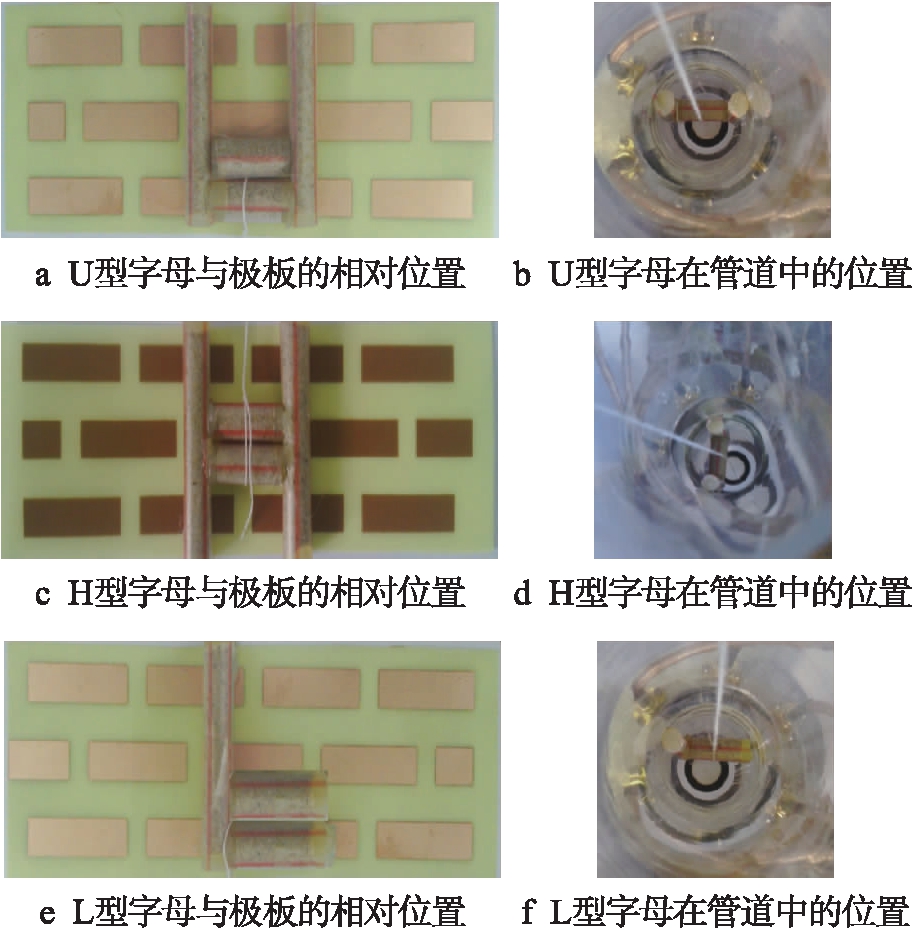
图4 重建实物图
Fig.4 Reconstruction of real objects
表2 实验重建图像
Tab.2 Reconstructed images in experiments
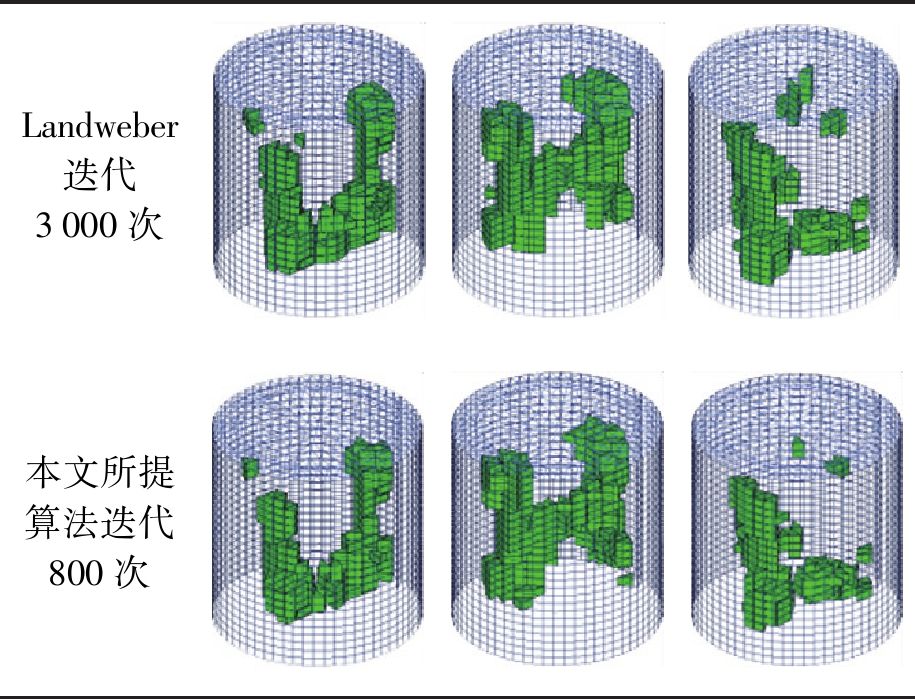
Landweber迭代3000次本文所提算法迭代800次
对所获得的重建图像进行强化伪迹抑制操作，并定期调整滤波阈值.仿真和实验结果表明，与传统Landweber迭代算法相比，具有伪迹抑制作用的重建算法能够显著减少重建图像中的伪迹，缩短重建时间，该方法具有良好的应用潜力.
[1]Cao Z，Li J，Xu L J.Iterative reconstruction algorithm for electrical capacitance tomography based on calderon’s method [J].IEEE Sensors Journal，2018，18(20)：8450-8462.
[2]Gunes C，Acero D O，Marashdeh Q M，et al.Accelera-tion of electrical capacitance volume tomography imagingby Fourier-based sparse representations [J].IEEE Sensors Journal，2018，18(23)：9649-9659.
[3]Li X X，Jaworski A J，Mao X A.Comparative study of two non-intrusive measurement methods for bubbling gas-solids fluidized beds：electrical capacitance tomography and pressure fluctuations [J].Journal of Thermal Science，2018，62：255-268.
[4]Perera K，Pradeep C，Mylvaganam S，et al.Imaging of oil-water flow patterns by electrical capacitance tomography [J].Flow Measurement and Instrumentation，2017，56：23-34.
[5]Mao M X，Ye J M，Wang H G，et al.Investigation of gas-solids flow in a circulating fluidized bed using 3D electrical capacitance tomography [J].Measurement Science and Technology，2016，27(9)：1-13.
[6]Han Z X，Mu H P，Zhang J Y，et al.Experimental study on the condensation of a thermosyphon by electrical capacitance tomography [J].Journal of Thermal Science，2016，25(2)：171-177.
[7]Haddadi M B，Maddahian R.A new algorithm for image reconstruction of electrical capacitance tomography based on inverse heat conduction problems [J].IEEE Sensors Journal，2016，16(6)：1786-1794.
[8]王莉莉，刘洪波，陈德运，等.基于谱投影梯度的电容层析成像图像重建算法 [J].哈尔滨理工大学学报，2018，23(4)：64-68.
(WANG Li-li，LIU Hong-bo，CHEN De-yun，et al.Image reconstruction algorithm based on spectral projected gradient pursuit for electrical capacitance tomography [J].Journal of Harbin University of Science and Technology，2018，23(4)：64-68.)
[9]吴新杰，李红玉，梁南南.卷积神经网络在ECT 图像重建上的应用 [J].辽宁大学学报，2018，45(1)：28-33.
(WU Xin-jie，LI Hong-yu，LIANG Nan-nan.Application of convolutional neural network in ECT image reconstruction [J].Journal of Liaoning University，2018，45(1)：28-33.)
[10]张立峰.压缩感知在电容层析成像中的应用 [J].北京航空航天大学学报，2017，43(11)：2316-2321.
(ZHANG Li-feng.Compressed sensing application to electrical capacitance tomography [J].Journal of Beijing University of Aeronautics and Astronautics，2017，43(11)：2316-2321.)
[11]Moura H L D，Pipa D R，Wrasse A D N，et al.Image reconstruction for electrical capacitance tomography through redundant sensitivity matrix [J].IEEE Sensors Journal，2017，17(24)：1-9.
[12]王伊凡，颜华，孙延辉.直接三维ECT 传感器灵敏度计算 [J].沈阳工业大学学报，2015，37(1)：80-86.
(WANG Yi-fan，YAN Hua，SUN Yan-hui.Calculation of sensitivity for direct 3D ECT sensor [J].Journal of Shenyang University of Technology，2015，37(1)：80-86.)