地下连续墙基础起源于欧洲，发展于日本.所谓地下连续墙，就是利用各种挖槽机械，向地下开挖出一条既窄又深的沟槽，在泥浆护壁的作用下成型，并在沟槽之内浇筑适当的建筑材料，形成兼具防渗、挡土和承重功能的一道墙体[1].近年来，一种新型的自立式复合支护结构——格形地下连续墙在国内的一些船坞基坑和水电工程已得到了应用，例如桐子林水电站导流明渠地基基础原设计为“十”字形格式地下连续墙，但其存在槽壁不稳定的情况，通过分析研究决定优化为单室格栅墙桩组合式地下连续墙，开创了单室格栅式地下连续墙成功应用的先例.广东某过江隧道由于在施工阶段原有护岸不能保证稳定性要求，对护岸进行的支护设计方案就是格栅式地下连续墙支护.南京青奥轴线J匝道区段深基坑施工围护结构亦采用格栅式地下连续墙，分析表明其可有效降低基坑坑底变形[2-7].格栅形地下连续墙不仅可以作为挡土墙和防渗结构使用，亦可作为竖向承载结构.在日本，格形地下连续墙是一种新型的桥梁基础，被称为“格栅式地下连续墙”(lattice-shaped diaphragm wall，LSDW).日本新干线饭坂彻高架桥工程中采用了单室闭合地连墙基础取代传统的沉井式基础；日本青森大桥主墩P9、P10亦采用了单室闭合型地连墙基础，取得了较好的经济效益[8].虽然格形地下连续墙已经在实际工程中被设计为竖向承载结构使用，但目前国内关于格形地下连续墙竖向承载特性的研究尚处于起步阶段.数值模拟近年来在基础工程中应用广泛，可借助数值模型代替原位试验[9].本文基于ABAQUS有限元分析软件[10]，设定工况为格栅式地下连续墙基础应用在工民建基础中，墙顶不设承台盖板，地下室底板作为盖板，墙体顶端钢筋锚固于地下室底板内，这对于工民建基础形式的创新具有一定意义.
1 数值计算及模型
受施工技术和成槽设备的限制，目前地下连续墙成槽的厚度为50～120 cm，最大厚度为320 cm，入土深度一般为10～50 m，最大深度为170 m[4].为了研究格栅式地下连续墙基础承载特性，比较不同几何尺寸的格栅式地下连续墙承载性状，需要建立数值模型进行模拟，位于模型外侧的竖向边界约束其水平向位移，模型底部约束所有方向的位移，基于场地土边界效应的考虑，本文设置格栅式地下连续墙基础的水平向计算边界为6D(D为格栅式地下连续墙的埋深)，且大于3倍的地下连续墙的最长边，竖向计算区取为2D.为方便模拟简化计算又符合实际工程应用，外围墙体埋深取为10 m，墙厚为0.5 m，分别建立三组格栅式地下连续墙基础模型：第一类模型的内墙体埋深为8 m，墙间距为2 m，如图1所示；第二类模型的内墙体埋深为10 m，墙间距为4 m，如图2所示；第三类模型的内墙体埋深为12 m，墙间距为6 m，如图3所示.
假定格栅式地下连续墙为弹塑性材料，为了分析基础模型间的差异，墙体材料均采用强度等级为C30的混凝土，由于以往静载试验中地连墙内部应力并未超出钢筋混凝土的屈服极限，因此，该假定是合理的[9].
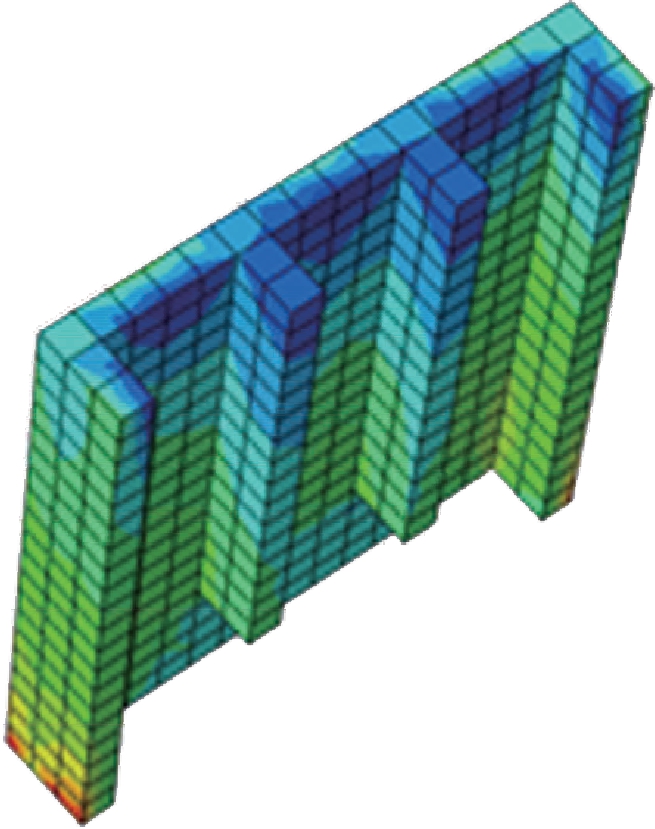
图1 第一类地连墙
Fig.1 First type of diaphragm walls
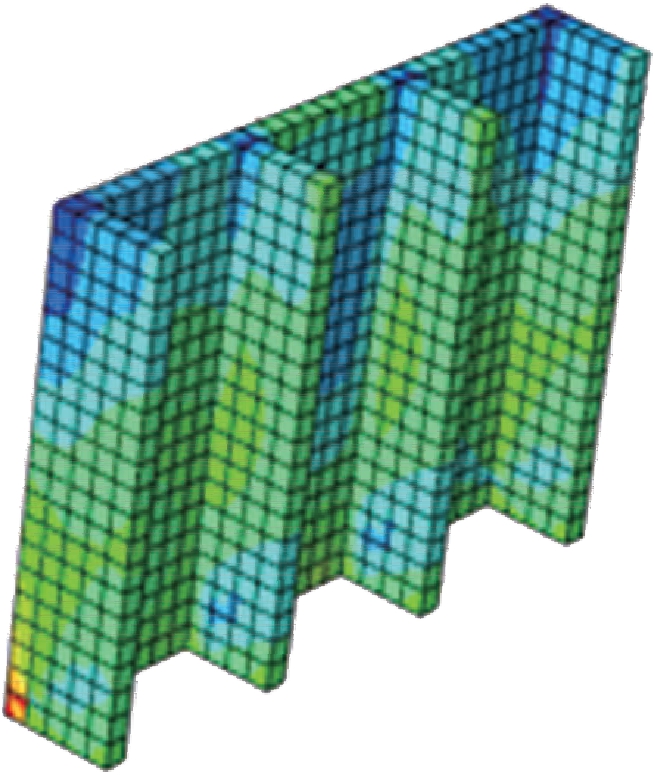
图2 第二类地连墙
Fig.2 Second type of diaphragm walls
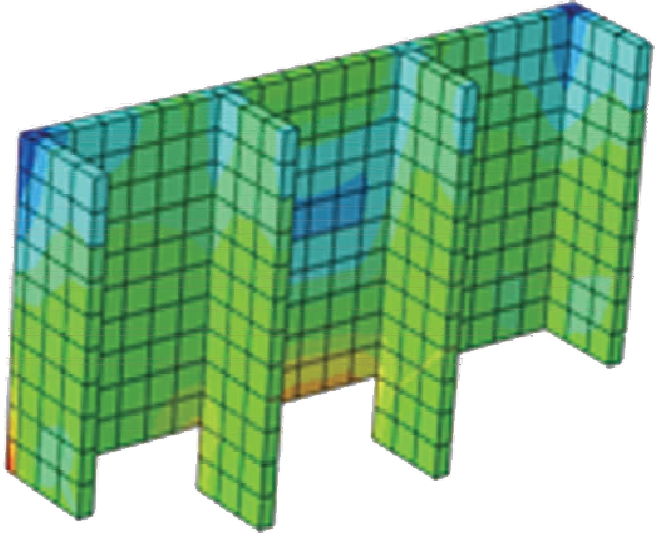
图3 第三类地连墙
Fig.3 Third type of diaphragm walls
土体采用Mohr-Coulomb弹塑性本构模型，根据文献[11]，为了达到简化计算的目的，土体采用单层土体，具体参数如表1所示.
表1 数值分析中墙体及地层参数
Tab.1 Parameters for numerical analysis of walls and strata
项目弹性模量MPa粘聚力kPa内摩擦角(°)密度(kg·m-3)墙体30000--2200土体3020301800
地应力平衡分析结果[10]如图4所示.平衡结果符合要求，ABAQUS提供了多种加载方式，其中均布荷载加载是最接近实际情况的加载形式.为了比较三个模型在同等承载条件下的承载力特性，本文在三个模型墙顶施加单位均布荷载1 000 kPa.
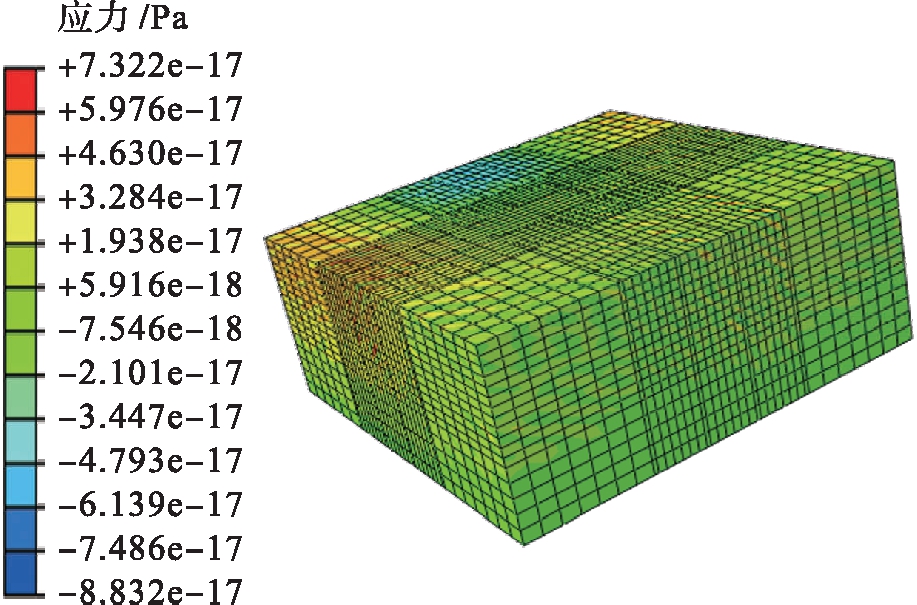
图4 地应力平衡
Fig.4 Equilibrium of in-situ stress
2 数值计算结果分析
为了更加清晰地对比3个不同模型承载性状，3个模型选取截面相同位置延深度方向进行比较，分析点位置选取如图5、6所示.
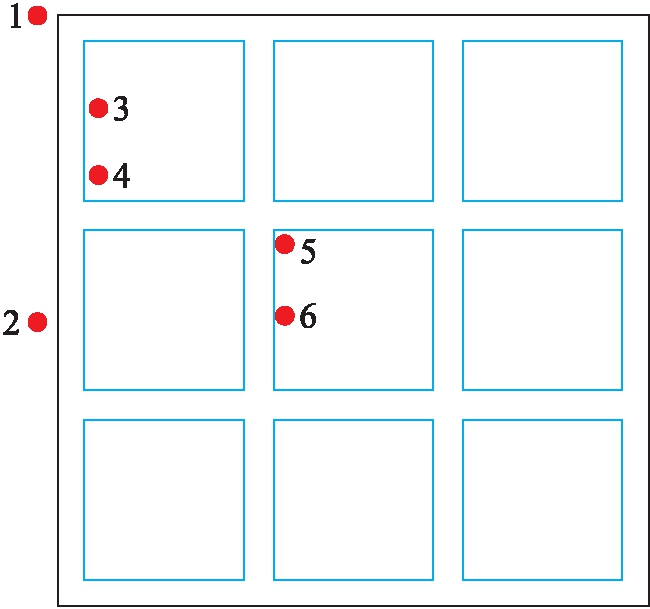
图5 沉降与侧摩阻力分析点位置
Fig.5 Point locations for analysis of settlement and lateral friction resistance
2.1 沉降
深度曲线分析
针对竖向荷载导致的格栅式地下连续墙基础的沉降，将3个不同几何形状的连续墙选取相同的位置作为检测和重点分析对象.不同点沉降深度曲线如图7～12所示(Ⅰ、Ⅱ、Ⅲ表示第一、二、三类格栅式地下连续墙).在相同单位均布荷载作用下，内墙深为12 m，墙间距为6 m的第三类格栅式地下连续墙基础总体沉降量最小，沉降量最大值为26.18 mm，出现在6点位置处；内墙深为10 m，墙间距为4 m的第二类格栅式地下连续墙基础总体沉降量最大，沉降量最大值为28.88 mm，同样出现在6点位置处.说明在相同荷载下，内墙间距大，内外墙有埋深深度差的格栅式地连墙基础沉降量较小.内墙深为8 m，墙间距为2 m的第一类格栅式地下连续墙基础总体沉降量介于第二类与第三类地下连续墙之间，沉降量最大值为27.59 mm，出现在3点位置处，由于第一类地连墙墙间距为2 m，内墙埋深为8 m的地连墙沉降量介于第三类和第二类地连墙基础之间，且对所用施工场地尺寸要求小，浇筑的混凝土体积量少，在对于施工场地有尺寸限制，对沉降有要求的工况下，可以选用第一类格栅式地下连续墙基础，这样既满足了施工条件，又节省了预算.
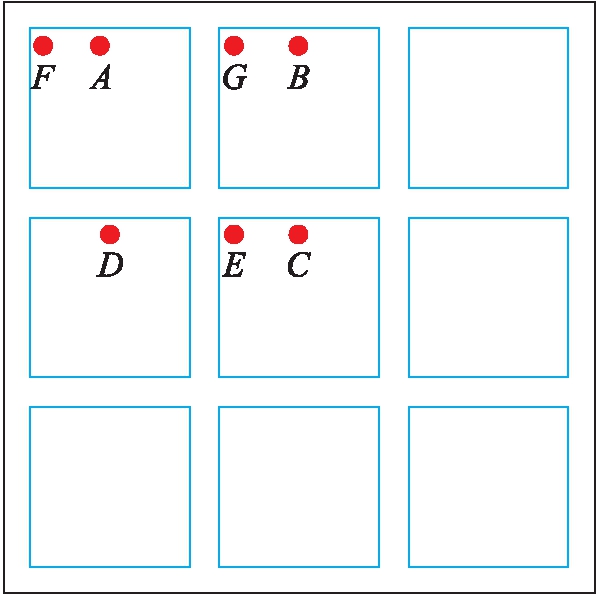
图6 墙端阻力分析点位置
Fig.6 Point locations for analysis of toe resistance
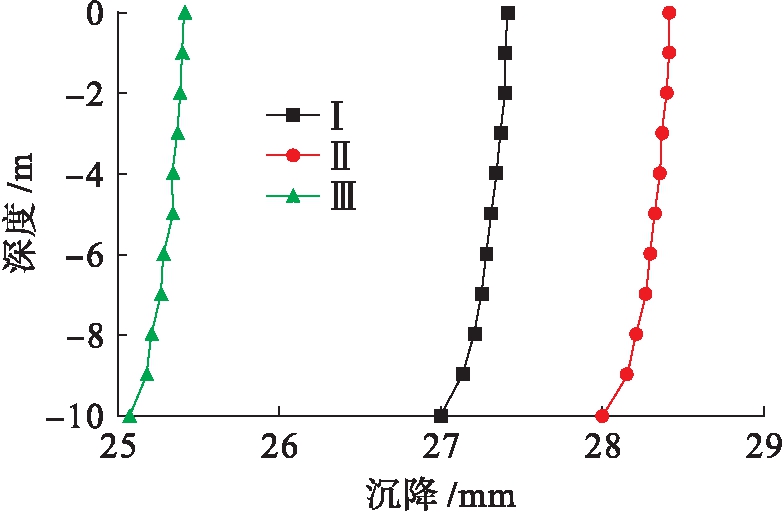
图7 1点处沉降深度曲线
Fig.7 Settlement-depth curves of point 1
2.2 侧摩阻力深度曲线分析
格栅式地下连续墙基础的侧摩阻力随深度的变化而不同，侧摩阻力深度曲线如图13～18所示(Ⅰ、Ⅱ、Ⅲ表示第一、二、三类格栅式地下连续墙).三类地下连续墙侧摩阻力发展趋势都是先随深度的增加而增加，到某一深度出现拐点，而后随深度的增加而减小.其中内墙深度为12 m，墙间距为6 m的第三类格栅式地下连续墙基础承受的单位侧摩阻力最小，如表2所示.产生这样现象的原因是第三类地下连续墙内墙埋深大，内外墙有深度差，内墙间距大，造成墙土接触面积大，承受单位侧摩阻力小，而第一类地下连续墙虽然间距小但内外墙有深度差，底部相当于一个单室地连墙，所以在相同荷载下所受单位侧摩阻力和第二类地连墙相近，这也与吴九江群墙效应[12]相吻合.综上，越靠近中心内墙，墙身承受的单位侧摩阻力越小，这样施工时中心部分内墙可适当降低混凝土的强度标号，也可根据拐点深度适当调整中心内墙的埋置深度.总体上内墙间距大，内外墙存在深度差的第三类地下连续墙基础更有承载优势.
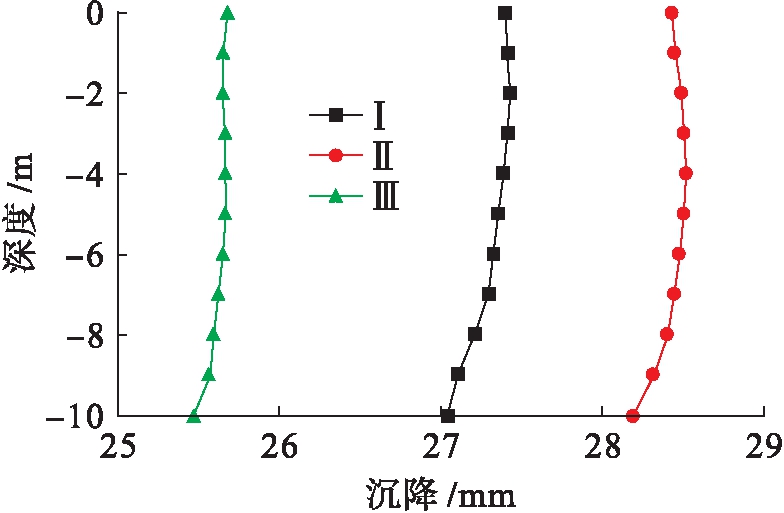
图8 2点处沉降深度曲线
Fig.8 Settlement-depth curves of point 2
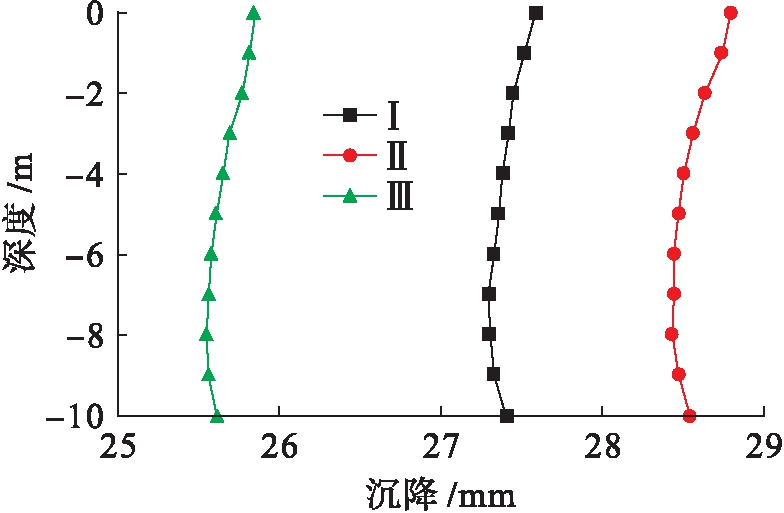
图9 3点处沉降深度曲线
Fig.9 Settlement-depth curves of point 3
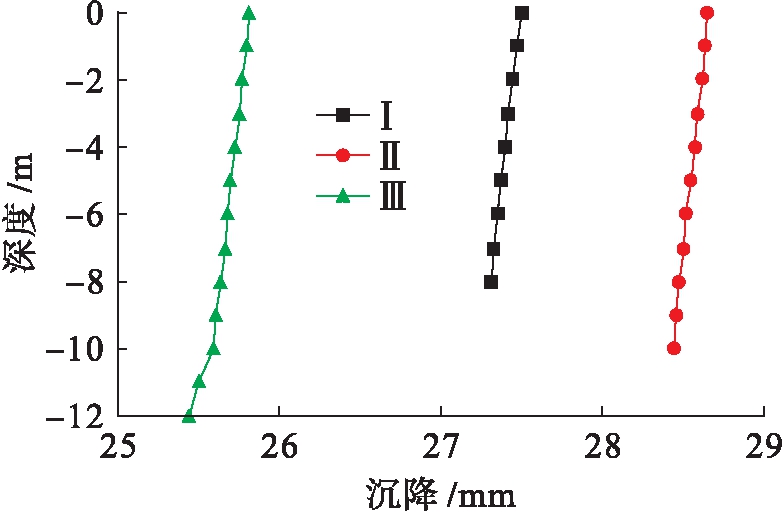
图10 4点处沉降深度曲线
Fig.10 Settlement-depth curves of point 4
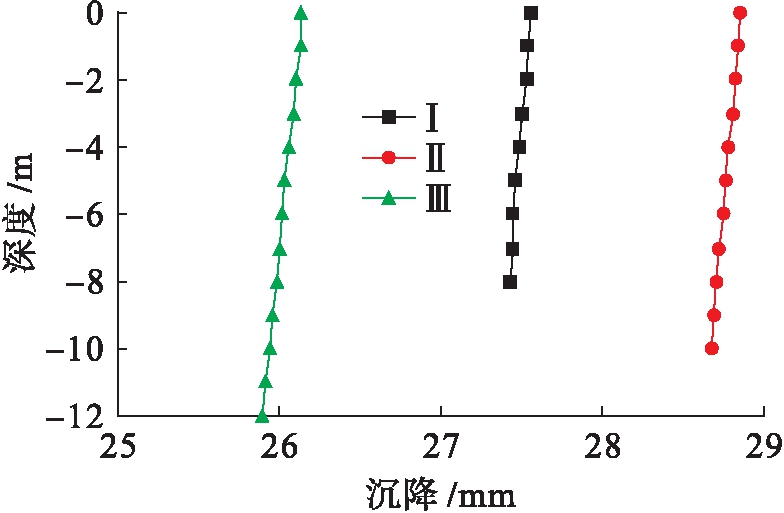
图11 5点处沉降深度曲线
Fig.11 Settlement-depth curves of point 5
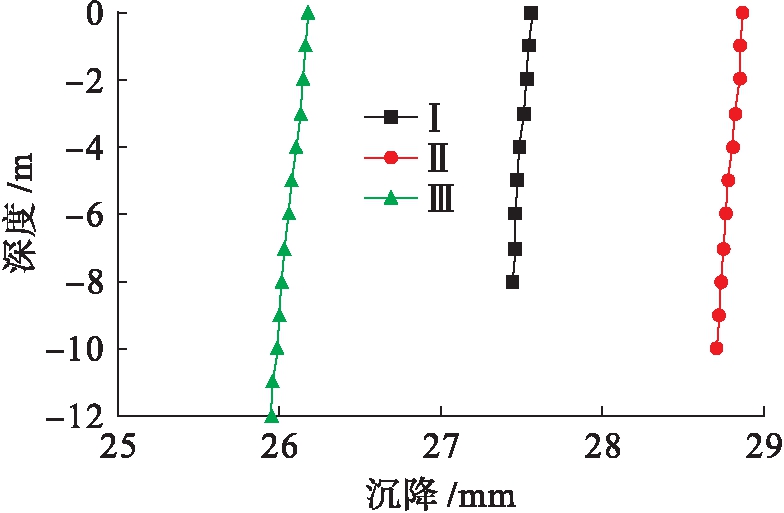
图12 6点处沉降深度曲线
Fig.12 Settlement-depth curves of point 6
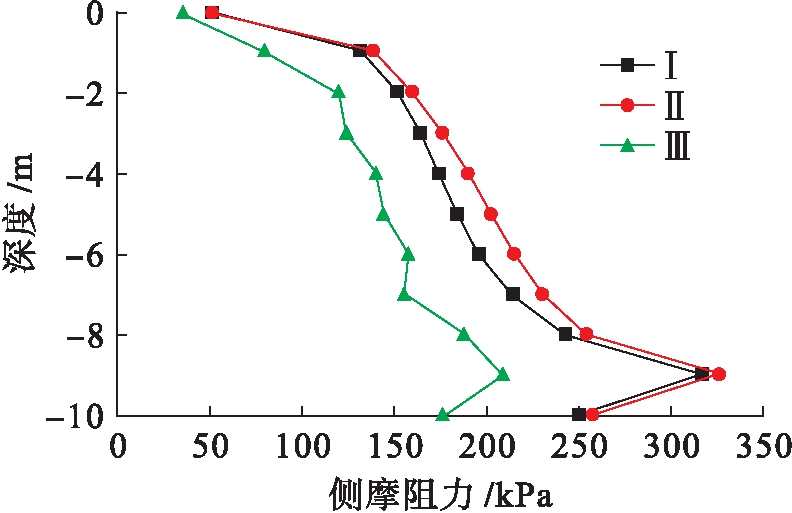
图13 1点处侧摩阻力深度曲线
Fig.13 Lateral friction resistance-depth curves of point 1
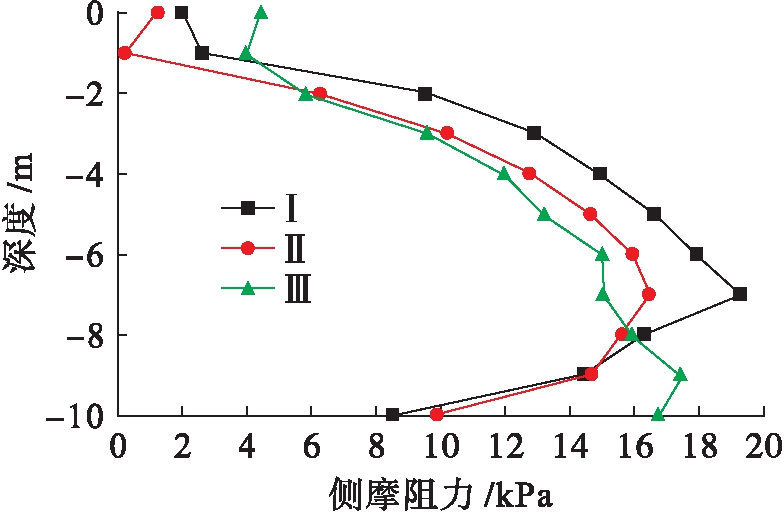
图14 2点处侧摩阻力深度曲线
Fig.14 Lateral friction resistance-depth curves of point 2
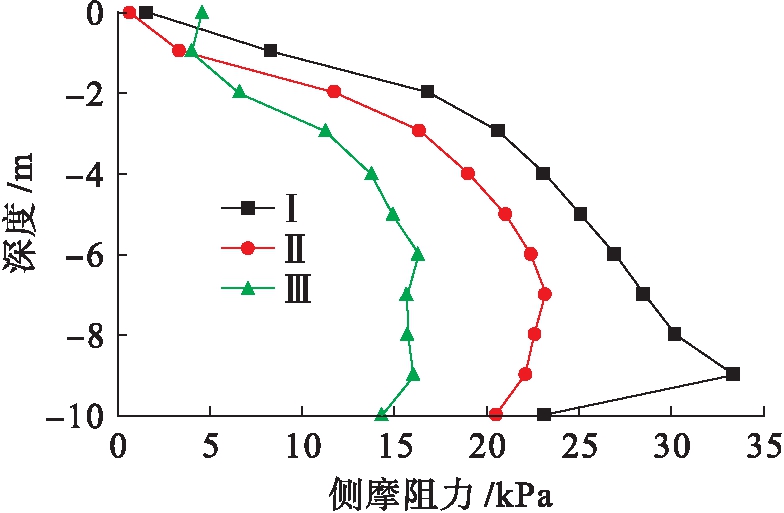
图15 3点处侧摩阻力深度曲线
Fig.15 Lateral friction resistance-depth curves of point 3
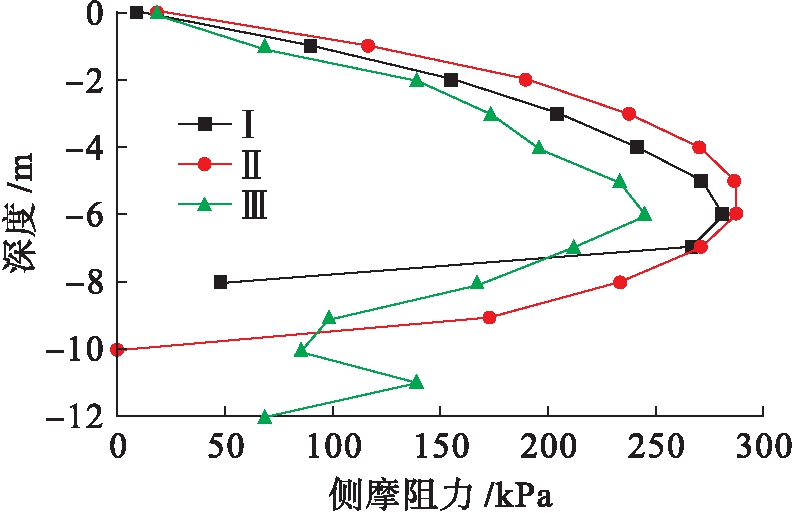
图16 4点处侧摩阻力深度曲线
Fig.16 Lateral friction resistance-depth curves of point 4
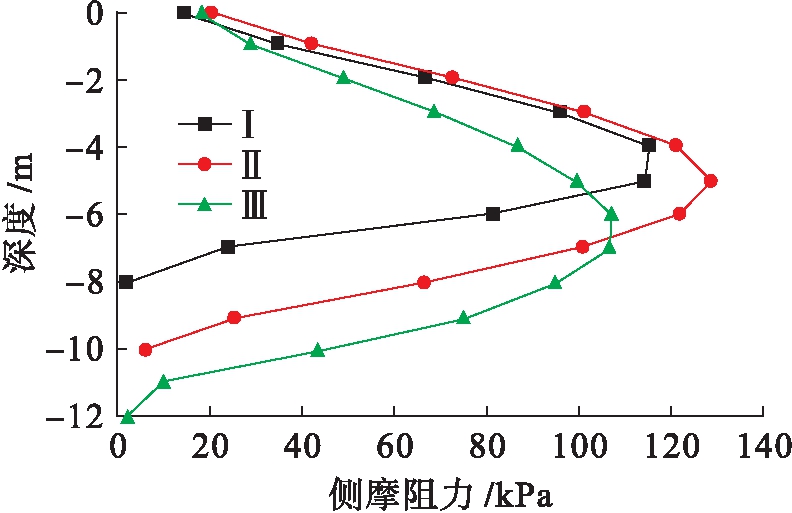
图17 5点处侧摩阻力深度曲线
Fig.17 Lateral friction resistance-depth curves of point 5
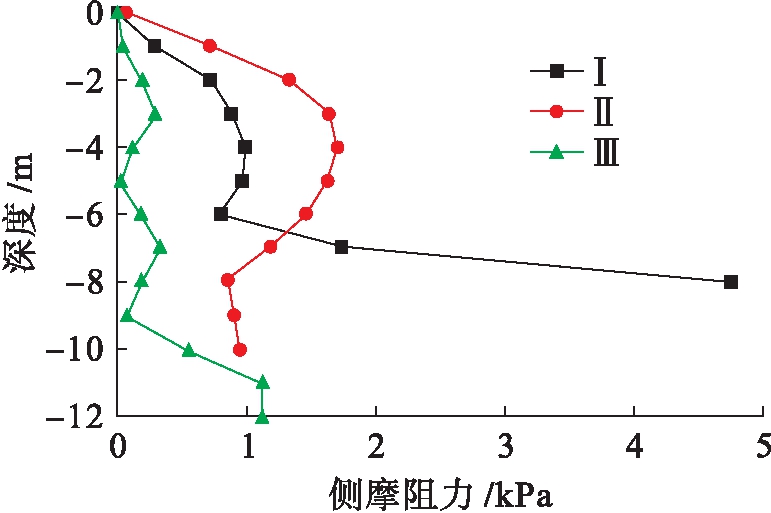
图18 6点处侧摩阻力深度曲线
Fig.18 Lateral friction resistance-depth curves of point 6
表2 拐点位置与单位侧摩阻力最大值
Tab.2 Inflexion positions and maximum values of unit lateral friction resistance
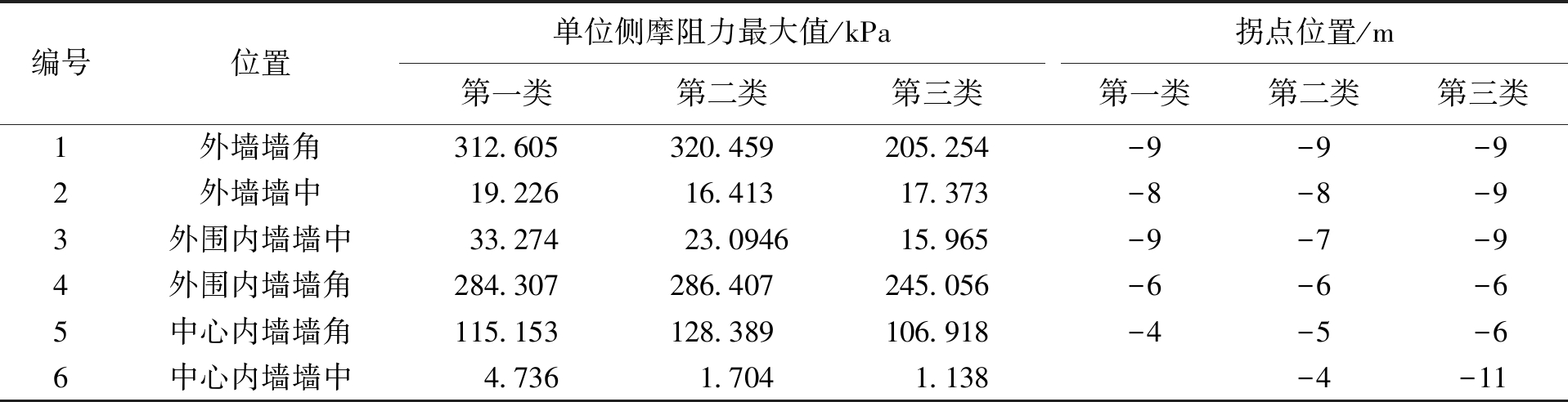
编号位置单位侧摩阻力最大值/kPa第一类第二类第三类拐点位置/m第一类第二类第三类1外墙墙角312.605320.459205.254-9-9-92外墙墙中19.22616.41317.373-8-8-93外围内墙墙中33.27423.094615.965-9-7-94外围内墙墙角284.307286.407245.056-6-6-65中心内墙墙角115.153128.389106.918-4-5-66中心内墙墙中4.7361.7041.138-4-11
2.3 墙端阻力曲线分析
相同单位均布荷载下三类地连墙在A、B、C、D、E、F、G七个点处墙端阻力的位置曲线如图19所示(Ⅰ、Ⅱ、Ⅲ表示第一、二、三类格栅式地下连续墙)，第三类地连墙各点曲线值最小，这说明在相同单位均布荷载作用下墙端承受的单位端阻力最小，在同等荷载条件下，第三类地连墙墙端不宜破坏更有优势，施工设计过程中墙端部可适当降低混凝土强度标号与钢筋用量，节约施工成本.第一类与第二类地连墙各点所受单位端阻力相当，在施工工况受限的条件下可优先考虑第一类地连墙；三类地连墙基础中心内墙所受单位端阻力大于外墙单位端阻力.三类地连墙同时在E点处墙端阻力达到最大，角部单位端阻力大于墙中单位端阻力，在施工过程中要注意掌控.
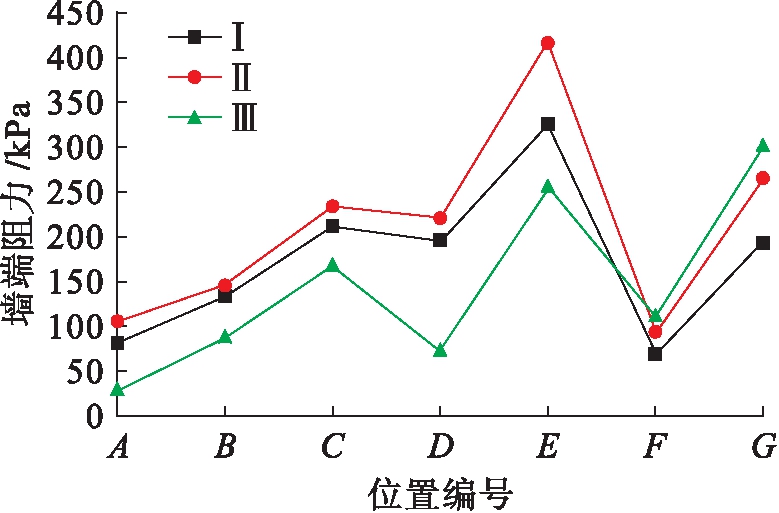
图19 A～G点墙端阻力曲线
Fig.19 Toe resistance curves of A to G points
3 结 论
通过对三类不同几何形式九室格栅式地下连续墙基础的竖向荷载模型进行数值模拟，研究了格栅式地下连续墙基础的承载特性，得出在相同单位均布荷载作用下，内墙间距大，内外墙有埋深深度差的格栅式地连墙基础沉降量小.
三类格栅式地下连续墙侧摩阻力发展趋势大体为沿深度先增大后减小.内墙间距大，内外墙存在深度差，在承受相同单位侧摩阻力作用时，地连墙承载能力更大.分析三类不同格栅式地下连续墙基础七个点，内外墙存在深度差，内墙深度大，间距大的格栅式地下连续墙基础承受的单位墙端阻力最小.
[1]殷成龙.格栅式地下连续墙桥梁基础物理模型试验研究 [D].成都：西南交通大学，2014.
(YIN Cheng-long.Model test of lattice shaped dia-phragm wall as bridge foundation [D].Chengdu：Southwest Jiaotong University，2014.)
[2]吴九江，程谦恭，文华.格栅式地下连续墙竖向荷载模型试验研究 [J].岩土力学与工程学报，2015，34(12)：2581-2592.
(WU Jiu-jiang，CHENG Qian-gong，WEN Hua.Mo-del study of the vertical bearing behaviours of lattice shaped diaphragm wall as bridge foundation in soft soil [J].Chinese Journal of Rock Mechanics & Engineering，2015，34(12)：2581-2592.)
[3]王旭辉.框格式地下连续墙在水利水电工程中的应用 [J].工程建设与设计，2011(4)：172-175.
(WANG Xu-hui.Frame format in the underground continuous wall of wall resources and hydropower engineering [J].Construction and Design for Project，2011(4)：172-175.)
[4]侯永茂.软土地层中格形地下连续墙围护结构形状研究 [D].上海：上海交通大学，2010.
(HOU Yong-mao.Behavior of cellular diaphragm wall in soft deposit [D].Shanghai：Shanghai Jiaotong University，2010.)
[5]时爱祥，邓祥吉，仇建春.格形地下连续墙的三维有限元分析 [J].南水北调与水利科技，2015，13(3)：571-574.
(SHI Ai-xiang，DENG Xiang-ji，QIU Jian-chun.Three-dimensional finite element analysis of cellular diaphragm wall [J].South-to-North Water Science & Techology，2015，13(3)：571-574.)
[6]张玉成，杨光华，胡海英.格栅式地下连续墙在沉管隧道护岸工程支护中的应用 [J].岩土工程学报，2012，34(增刊)：440-446.
(ZHANG Yu-cheng，YANG Guang-hua，HU Hai-ying.Application of grillage shaped diaphragm wall in support of revetment project of immersed tube tunnel [J].Chinese Journal of Geotechnical Engineering，2012，34(Sup)：440-446.)
[7]卞少帅，谭跃虎，李二兵.格栅式地下连续墙在南京青奥轴线中的应用研究 [J].施工技术，2015，44(增刊)：80-82.
(BIAN Shao-shuai，TAN Yue-hu，LI Er-bing.Application research on grille diaphragm wall in the Nanjing youth Olympic axis [J].Construction Technology，2015，44(Sup)：80-82.)
[8]吴九江.软土地基格栅式地下连续墙桥梁基础竖向承载性状研究 [D].成都：西南交通大学，2015.
(WU Jiu-jiang.Vertical bearing behavorior of lattice-shaped diaphragm wall as bridge foundations in soft soil [D].Chengdu：Southwest Jiaotong University，2015.)
[9]侯永茂.格形地下连续墙竖向承载特性的研究 [J].岩土工程学报，2012，34(4)：701-708.
(HOU Yong-mao.Vertical bearing behaviors of cellular diaphragm wall [J].Chinese Journal of Geotechnical Engineering，2012，34(4)：701-708.)
[10]徐伟，左玉柱，张平.大型格形地下连续墙三维数值模拟受力分析 [J].建筑施工，2010，32(10)：1070-1071.
(XU Wei，ZUO Yu-zhu，ZHANG Ping.Force analysis of 3D numerical simulation for lattice shaped diaphragm wall [J].Building Construction，2010，32(10)：1070-1071.)
[11]徐凌，陈格际，刘帅.基于FLAC3D的基坑开挖与支护数值模拟应用 [J].沈阳工业大学学报，2016，38(1)：91-96.
(XU Ling，CHEN Ge-ji，LIU Shuai.Application of numerical simulation for excavation and supporting of deep foundation pit based on FLAC3D [J].Journal of Shenyang University of Technology，2016，38(1)：91-96.)
[12]吴九江，程谦恭，汤文理.格形地下连续墙桥梁基础格室效应数值分析 [J].施工技术，2016，45(17)：60-63.
(WU Jiu-jiang，CHENG Qian-gong，TANG Wen-li.Numerical analysis of the chamber effect of lattice shaped diaphragm wall as bridge foundation in sand [J].Construction Technology，2016，45(17)：60-63.)