随着国家基础设施建设的不断发展,混凝土对自然资源的占用及对环境造成了严重的负面影响,如何对拆旧建新过程中产生的大量废弃混凝土进行有效的资源化处置具有重要的现实意义[1-2],解决废弃混凝土最有效的措施就是再生混凝土技术[3].随着我国经济快速发展,我国对桥梁等基础设施开展了大规模建设,预应力混凝土结构作为主要受力构件得到了广泛应用.综合自密实混凝土具有的流动性、填充性、间隙通过性和抗离析性等方面的性能优势和再生混凝土的节能环保特点,以及预应力混凝土梁的构造形式,利用再生骨料和粉煤灰等材料配制成自密实再生混凝土,并将其应用于预应力混凝土梁中,具有良好的应用前景.
我国目前使用的规范《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)(以下简称《规范》)规定的弹性刚度折减系数为0.95[4],自密实再生混凝土存在脆性较大、弹性模量较小的缺陷[5-6],在实际应用时,现行《规范》规定的弹性刚度折减系数是否适用是一个迫切需要研究的问题.因此,可通过对预应力自密实再生混凝土梁的试验研究,对其弹性刚度进行详细分析.
1 试验概况
1.1 配合比设计
试验所用再生粗骨料为实验室科研试验废弃的C30混凝土块体,采用颚式破碎机破碎后经人工筛分而制得,粒径范围为5.00~20.00 mm,实测试验用再生骨料的表观密度为2 730 kg/m3,吸水率为3.70%,压碎指标为16.2%;试验用细骨料均采用含泥量小于1%的天然水洗中砂,其表观密度为2 620 kg/m3;试验用水泥为山水工源牌水泥,配制C40混凝土时采用PO42.5级普通硅酸盐水泥,其表观密度为3 100 kg/m3;粉煤灰采用沈西热电厂生产的I级粉煤灰,其表观密度为2 200 kg/m3;减水剂采用辽宁省建筑科学研究院生产的LJ612型聚羧酸高效减水剂.试验混凝土具体配合比取水∶水泥∶粉煤灰∶砂子∶再生骨料=190∶375∶125∶870.4∶816,粗骨料取代率为100%.新拌混凝土的坍落扩展度为690 mm,J型环扩展度为680 mm,扩展度达到500 mm的时间T500为3.0 s.扩展度试验如图1所示.

图1 扩展度试验
Fig.1 Test for extending degree
1.2 试件设计
试验对2组共12根有粘结后张法现浇预应力自密实再生混凝土简支梁进行张拉阶段的受力监测,试验梁混凝土强度均为C40,其中,A组试验梁5根,尺寸均为200 mm×300 mm×3 000 mm,立方体抗压强度为48.57 MPa,混凝土弹性模量为3.25×104 N/mm2;B组试验梁7根,尺寸均为140 mm×200 mm×1 600 mm,立方体抗压强度为47.02 MPa,混凝土弹性模量为4.01×104 N/mm2.普通纵向受力钢筋采用HRB400级钢筋,箍筋为HPB300级钢筋,弹性模量为2.1×105 N/mm2,预应力筋采用低松弛1860级钢绞线,公称直径为15.2 mm,弹性模量为1.95×105 N/mm2,张拉控制应力均为0.75fptk,预应力筋采用直线布筋形式.部分试验梁的钢筋布置如图2所示(单位:mm),试验参数如表1所示.
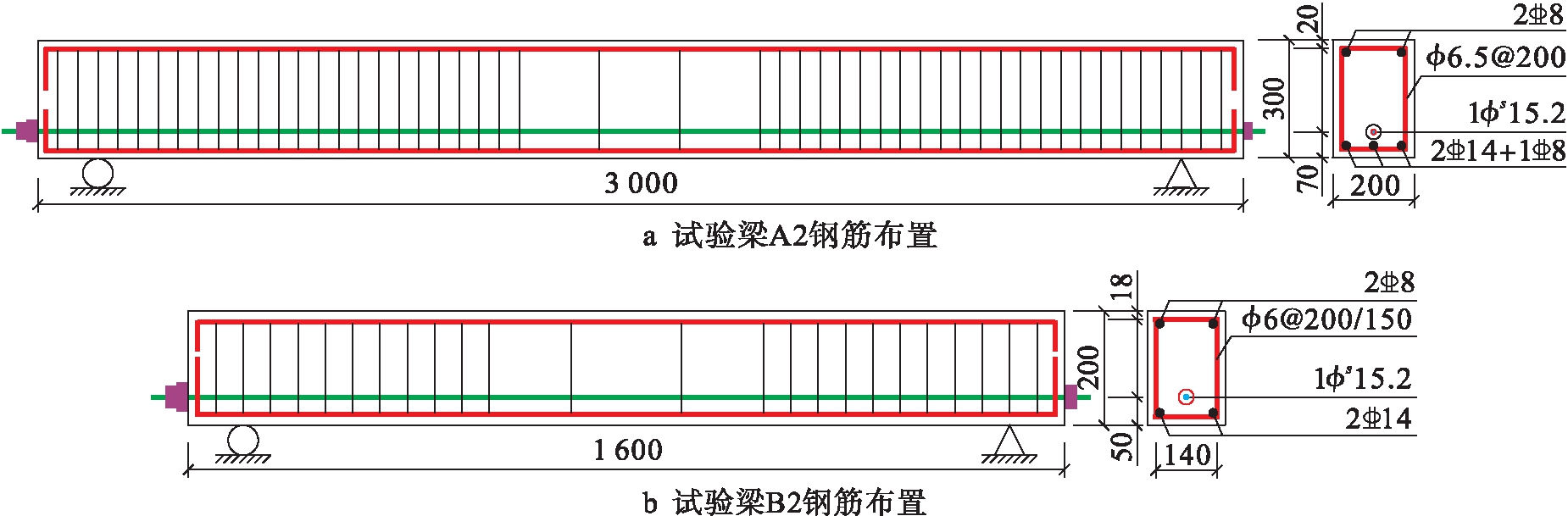
图2 梁试件尺寸图
Fig.2 Dimension of beam specimens
表1 试验梁设计参数
Tab.1 Design parameters for test beams
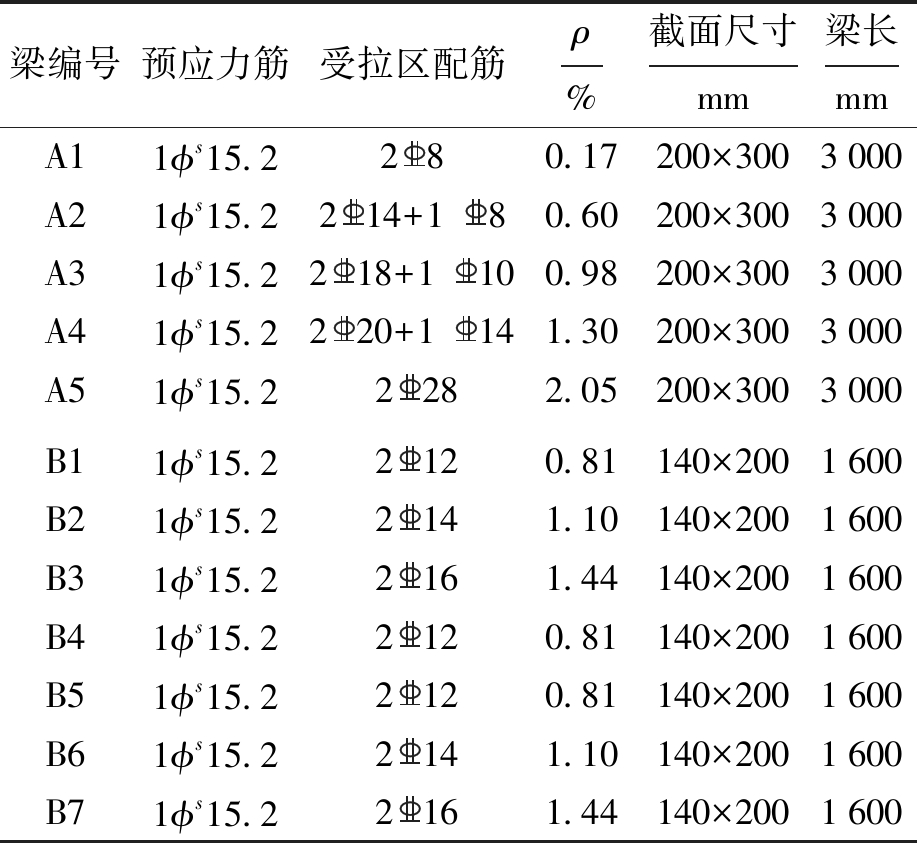
梁编号预应力筋受拉区配筋ρ%截面尺寸mm梁长mmA11ϕs15.2280.17200×3003000A21ϕs15.2214+180.60200×3003000A31ϕs15.2218+1100.98200×3003000A41ϕs15.2220+1141.30200×3003000A51ϕs15.22282.05200×3003000B11ϕs15.22120.81140×2001600B21ϕs15.22141.10140×2001600B31ϕs15.22161.44140×2001600B41ϕs15.22120.81140×2001600B51ϕs15.22120.81140×2001600B61ϕs15.22141.10140×2001600B71ϕs15.22161.44140×2001600
注:ρ为非预应力筋配筋率.
1.3 测点布置及加载方案
试验梁的加载及测点布置如图3所示.张拉过程采用270 kN的穿心式千斤顶加载,为了精确控制张拉荷载的大小,在千斤顶后放置300 kN的穿心式拉压传感器进行实时监控.为获得张拉后受压区混凝土的有效压应力,在试验梁受压区边缘粘贴标距为100 mm的混凝土应变片.此外,为了获得试验梁的反拱值,在试验梁的跨中及两端支座处分别安装位移计测量张拉过程中各点的位移变化,设两端读数分别为a和b,跨中的读数为c,单位为mm,则张拉阶段试验梁的反拱值计算式为c-(a+b)/2.
由于试验梁较短,为了减小预应力损失,采用低回缩锚具及辅助张拉装置结合二次张拉工艺方法[7]进行张拉.在正式加载前,先进行两次预加载,以消除支座及加载装置间隙对变形的影响.第一次张拉时,每级荷载为张拉控制应力的10%(即10%σcon),共十级,每级荷载持载3 min,然后缓慢放张,第二次张拉将辅助张拉装置,即中空、立面局部开口的圆柱型层铰放置在穿心千斤顶前段,然后将预应力筋一次性张拉至σcon,同时拧紧低回缩锚具的锚环以弥补张拉端锚具变形和钢筋的回缩量.两次张拉的荷载、混凝土应变以及试验梁的变形值均通过IMC动态数据采集仪自动采集.

图3 试验梁加载及测点布置图
Fig.3 Loading of test beams and layout of measuring points
2 预应力自密实再生混凝土梁刚度分析
2.1 反拱值计算
根据文献[8],预应力混凝土梁的上拱变形又称反拱,是由预加力Np作用引起的,它与外荷载引起的挠度方向相反,对张拉阶段的试验梁而言,外荷载即为试验梁自重.在预加力作用下,预应力混凝土梁的上拱值可根据给定的构件刚度用结构力学的方法计算,故后张法预应力自密实再生混凝土简支梁跨中的反拱值为
(1)
式中:Mpe为由有效预加力在任意截面x处所引起的弯矩值;![]() 为跨中作用单位力时任意截面x处所产生的弯矩值;Bs为构件弹性刚度,计算时按实际受力阶段取值,因试验梁张拉阶段为弹性阶段,故取Bs=EcIn,其中,Ec为混凝土的弹性模量,In为试验梁净截面惯性矩;α为弹性刚度折减系数;L为试验梁的计算跨度.
为跨中作用单位力时任意截面x处所产生的弯矩值;Bs为构件弹性刚度,计算时按实际受力阶段取值,因试验梁张拉阶段为弹性阶段,故取Bs=EcIn,其中,Ec为混凝土的弹性模量,In为试验梁净截面惯性矩;α为弹性刚度折减系数;L为试验梁的计算跨度.
由试验梁自重引起的下挠度为
(2)
式中,MG为由自重在跨中截面处所产生的弯矩值.因试验梁的梁长较短、自重较轻,导致fG≪δpe,故由试验梁自重产生的弯矩可以忽略不计,因此,f总=δpe-fG≈δpe.
2.2 有效预加力计算
根据试验得到的混凝土受压区应变值,可获得预应力自密实再生混凝土梁的有效预加力为
(3)
式中:σ为由预加力产生的混凝土法向应力;Np为预应力自密实再生混凝土梁的有效预加力;An为试验梁净截面面积;epn为净截面重心至预应力钢筋和普通钢筋合力点的距离;yn为净截面重心至所计算纤维处的距离;ε为计算纤维处混凝土的应变值;Ec为混凝土的弹性模量.
2.3 刚度折减系数计算
由于Np是考虑第一批预应力损失的预应力筋和普通钢筋的合力,因此,试验梁在施加预应力后,在不考虑梁体自重的情况下,得出作用在预应力自密实再生混凝土梁上的等效荷载为
Mp=Npepn
(4)
将式(3)、(4)代入式(1)得到弹性刚度折减系数表达式,即
(5)
根据上述方法对本文12根预应力自密实再生混凝土梁弹性刚度折减系数进行计算,具体计算结果如表2所示.
表2 弹性刚度折减系数计算结果
Tab.2 Calculated reduction factors of elastic stiffness
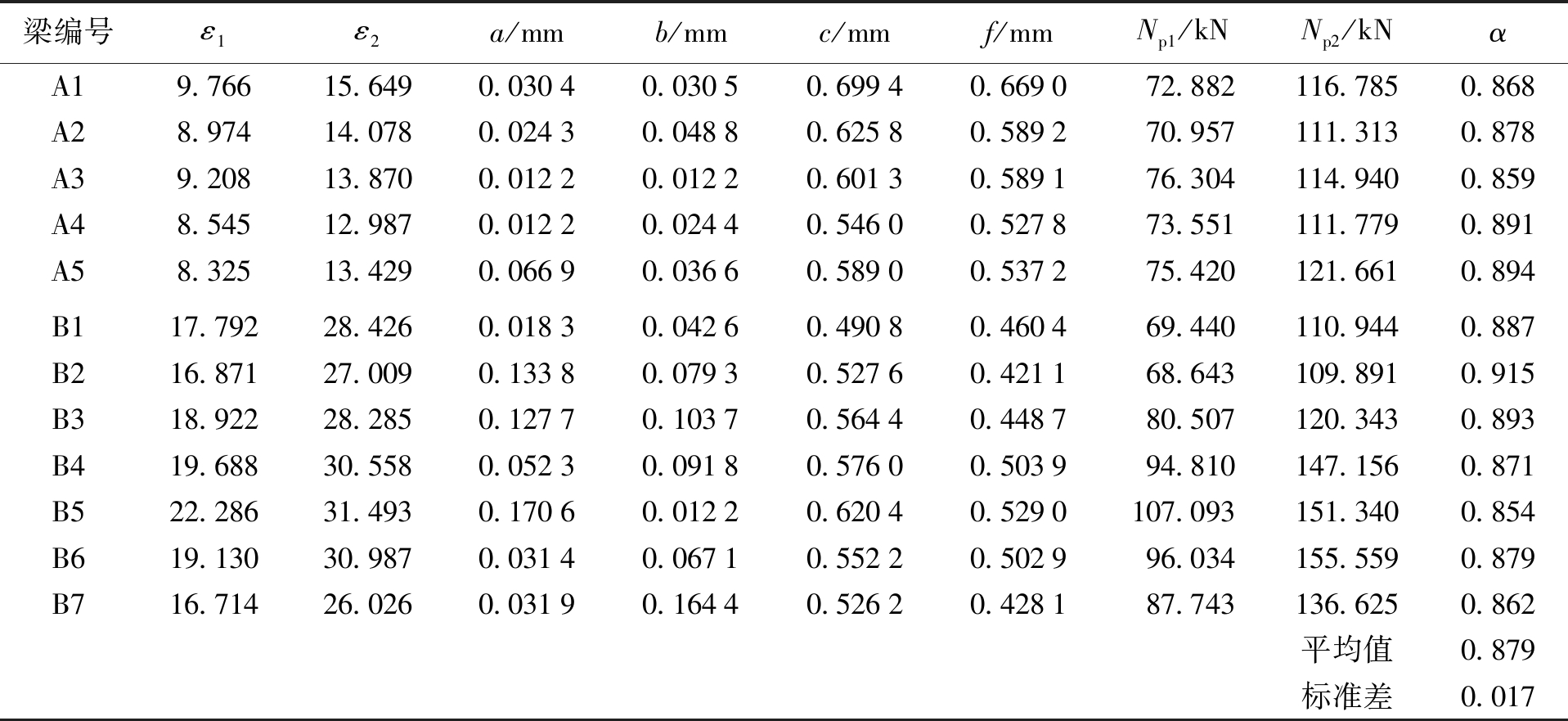
梁编号ε1ε2a/mmb/mmc/mmf/mmNp1/kNNp2/kNαA19.76615.6490.03040.03050.69940.669072.882116.7850.868A28.97414.0780.02430.04880.62580.589270.957111.3130.878A39.20813.8700.01220.01220.60130.589176.304114.9400.859A48.54512.9870.01220.02440.54600.527873.551 111.7790.891A58.32513.4290.06690.03660.58900.537275.420121.6610.894B117.79228.4260.01830.04260.49080.460469.440110.9440.887B216.87127.0090.13380.07930.52760.421168.643109.8910.915B318.92228.2850.12770.10370.56440.448780.507120.3430.893B419.68830.5580.05230.09180.57600.503994.810147.1560.871B522.28631.4930.17060.01220.62040.5290107.093151.3400.854B619.13030.9870.03140.06710.55220.502996.034155.5590.879B716.71426.0260.03190.16440.52620.428187.743136.6250.862平均值0.879标准差0.017
注:ε1为第一次张拉混凝土应变;ε2为第二次张拉混凝土应变;a为第二次张拉端位移计实测值;b为第二次张拉锚固端位移计实测值;c为第二次张拉跨中位移计实测值;f为实测反拱值;Np1为第一次张拉有效预加力;Np2为第二次张拉有效预加力.
由表2可以看出,第二次张拉后的有效预加力均大于第一次张拉后的有效预加力,增幅为41.3%~61.9%,说明使用低回缩锚具及辅助张拉装置结合二次张拉工艺方法能够有效地降低由于张拉端锚具变形和预应力筋内缩引起的预应力损失.本文经试验所得到的预应力自密实再生混凝土梁的弹性刚度折减系数为0.854~0.915,而文献[9]根据预应力超高强混凝土梁的试验结果所得到的弹性刚度折减系数为0.998~1.089;文献[10]根据A类预应力混凝土梁及未开裂的B类预应力混凝土梁的试验结果所得到的弹性刚度折减系数为0.91~1.06.《规范》规定的预应力混凝土构件弹性阶段的弹性刚度折减系数为0.95.通过对比可以看出,本文经试验所得到的弹性刚度折减系数小于文献[9-10]的试验值及《规范》的规定值,这主要是因为本文试验所采用的自密实再生混凝土的弹性模量、抗拉强度较超高强混凝土及普通混凝土小的缘故.因此,《规范》建议的弹性阶段刚度折减系数不适用于预应力自密实再生混凝土梁,需要对刚度折减系数进行修正.本文得到的试验梁弹性刚度折减系数平均值为![]() 若取保证率为95%,则有
若取保证率为95%,则有
(6)
式中,D为标准差.根据式(6)计算可以得到预应力自密实再生混凝土梁的弹性刚度折减系数修正值α为0.85.
3 弹性阶段挠度实测值与计算值对比分析
为了验证本文给出的刚度计算公式的适用性,研究人员对其他3根不同设计参数下的预应力自密实再生混凝土梁进行了受弯性能试验,并将弹性阶段的跨中挠度实测值按照现有规范公式计算值与按本文公式计算值进行对比,其对比结果如表3所示.
表3 实测挠度与计算挠度比较
Tab.3 Comparison between measured and calculated deflections
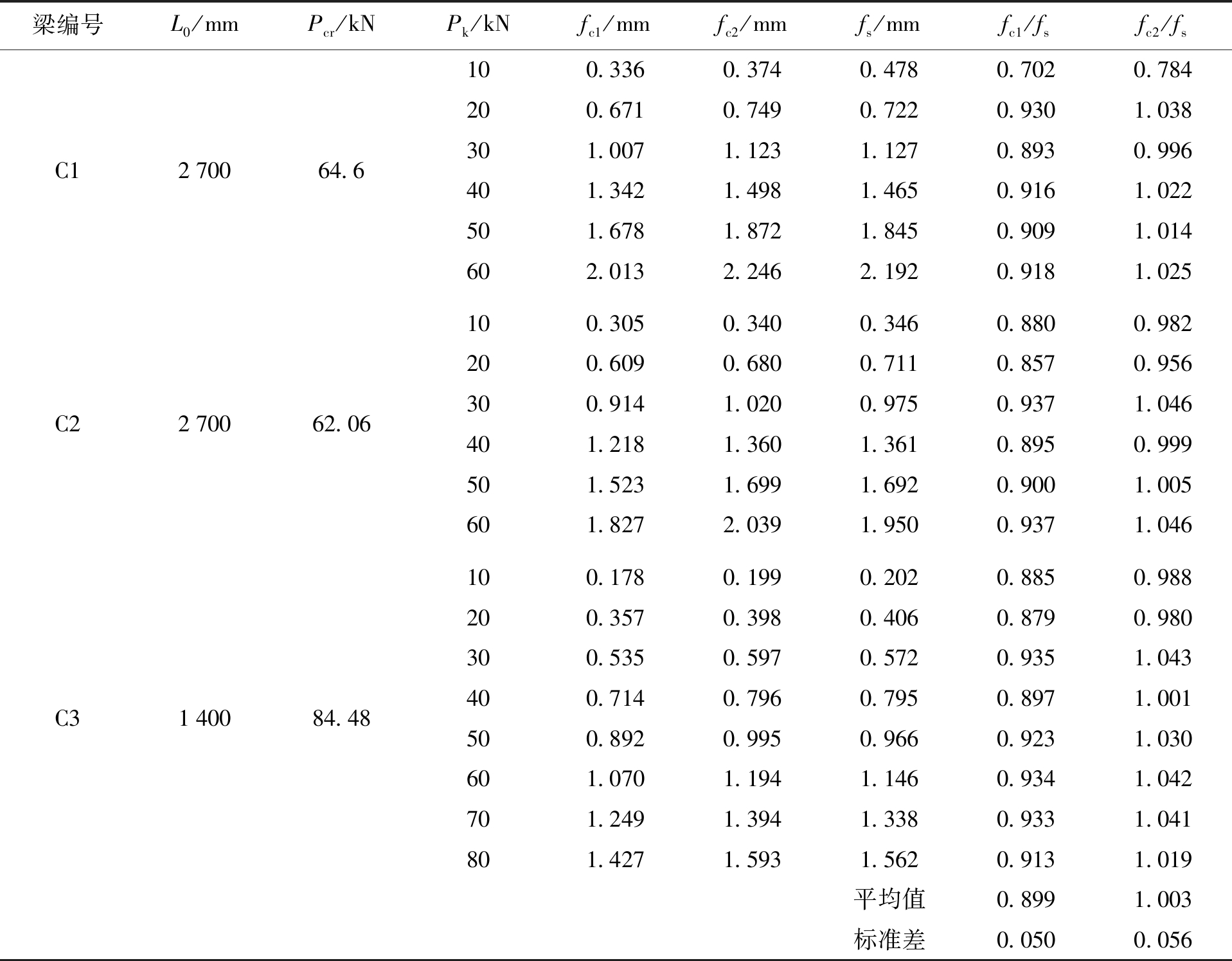
梁编号L0/mmPcr/kNPk/kNfc1/mmfc2/mmfs/mmfc1/fsfc2/fsC1270064.6C2270062.06C3140084.48100.3360.3740.4780.7020.784200.6710.7490.7220.9301.038301.0071.1231.1270.8930.996401.3421.4981.4650.9161.022501.6781.8721.8450.9091.014602.0132.2462.1920.9181.025100.3050.3400.3460.8800.982200.6090.6800.7110.8570.956300.9141.0200.9750.9371.046401.2181.3601.3610.8950.999501.5231.6991.6920.9001.005601.8272.0391.9500.9371.046100.1780.1990.2020.8850.988200.3570.3980.4060.8790.980300.5350.5970.5720.9351.043400.7140.7960.7950.8971.001500.8920.9950.9660.9231.030601.0701.1941.1460.9341.042701.2491.3941.3380.9331.041801.4271.5931.5620.9131.019平均值0.8991.003标准差0.0500.056
注:L0为计算跨度;Pcr为开裂荷载;Pk为工作荷载;fc1为按《规范》建议公式计算挠度;fc2为按本文建议公式计算挠度;fs为挠度实测值.
由表3可知,按规范建议公式所得的计算挠度与实测挠度之比的平均值为0.899,标准差为0.050,而按本文建议公式所得的计算挠度与实测挠度之比的平均值为1.003,标准差为0.056,说明在预应力自密实再生混凝土梁的任一弹性加载阶段,挠度实测值较按规范公式所得的挠度计算值偏大,而本文建议公式所得的挠度计算值与实测值符合较好.因此,建议对《规范》中弹性刚度折减系数进行修正,本文建议公式适用于预应力自密实再生混凝土梁的计算.
4 结 论
本文通过分析得出以下结论:
1) 使用低回缩锚具及辅助张拉装置结合二次张拉工艺的方法能够有效降低由于张拉端锚具变形和预应力筋内缩引起的预应力损失.
2) 通过12根试验梁的预应力张拉试验结果结合现有理论,推导出预应力自密实再生混凝土梁的弹性刚度计算公式,并基于概率论方法,给出了预应力自密实再生混凝土梁弹性刚度折减系数建议值,其值为0.85.
3) 通过部分试验梁的受弯试验结果,对比了预应力自密实再生混凝土梁按规范公式和本文建议公式在弹性阶段的挠度计算结果.结果表明,按本文建议公式所得的弹性阶段挠度计算值与实测值符合较好,本文建议公式适用于预应力自密实再生混凝土梁的计算.
[1]邹毅松,徐亦冬,王银辉.高性能再生骨料混凝土的物理力学性能及耐久性 [J].沈阳工业大学学报,2014,36(4):459-463.
(ZOU Yi-song,XU Yi-dong,WANG Yin-hui.Physical and mechanical properties and durability of high performance recycled aggregate concrete [J].Journal of Shenyang University of Technology,2014,36(4):459-463.)
[2]杨焜,汪俊杰,喻展展,等.再生混凝土国内外研究现状综述 [J].山西建筑,2018,44(5):100-101.
(YANG Kun,WANG Jun-jie,YU Zhan-zhan,et al.A summary of the research status of recycled concrete at home and abroad [J].Shanxi Architecture,2018,44(5):100-101.)
[3]程东辉,羌震.再生混凝土梁受力性能研究现状 [J].山西建筑,2019,45(3):40-41.
(CHENG Dong-hui,QIANG Zhen.Overview on mechanical behavior of recycled concrete beams [J].Shanxi Architecture,2019,45(3):40-41.)
[4]中华人民共和国交通部.JTG D62-2004 公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].北京:人民交通出版社,2004.
(Ministry of Communications of the People’s Republic of China.JTG D62-2004 Design specification for highway reinforced concrete and prestressed concrete bridges and culverts [S].Beijing:China Communications Press,2004.)
[5]吴波,刘璐,赵霄龙.自密实再生混合混凝土的单轴受压试验研究 [J].建筑结构学报,2016,37(增刊2):73-78.
(WU Bo,LIU Lu,ZHAO Xiao-long.Test study on uniaxial compressive behaviors of compound concrete made of normal-strength demolished concrete lumps and high-strength self-compacting concrete [J].Journal of Building Structures,2016,37(Sup2):73-78.)
[6]吴春杨,马剑,潘志宏,等.非连续级配再生粗骨料自密实混凝土基本力学性能试验研究 [J].建筑结构,2015,45(10):69-73.
(WU Chun-yang,MA Jian,PAN Zhi-hong,et al.Experimental study on basic mechanical properties of self-compacting recycled concrete with discontinuous graded recycled coarse aggregate [J].Building Structure,2015,45(10):69-73.)
[7]姚大立,余芳,鲍文博,等.试验用超短预应力梁的预应力锚具及其张拉工艺:中国专利,CN104453100A [P].2015-03-25.
(YAO Da-li,YU Fang,BAO Wen-bo,et al.Prestressed anchors for testing ultra-short prestressed beams and their tensioning process:Chinese patent,CN104453100A [P].2015-03-25.)
[8]叶见曙.结构设计原理 [M].北京:人民交通出版社,2014.
(YE Jian-shu.Principles of structural design [M].Beijing:People’s Communications Press,2014.)
[9]姚大立,贾金青,涂兵雄,等.预应力超高强混凝土梁弹性刚度分析 [J].武汉理工大学学报(交通科学与工程版),2013,37(1):74-76.
(YAO Da-li,JIA Jin-qing,TU Bing-xiong,et al.Analysis of elastic stiffness of prestressed ultra high strength concrete beams [J].Journal of Wuhan University of Technology(Transportation Science & Engineering),2013,37(1):74-76.)
[10]张克波.静载和疲劳荷载作用下PPC受弯构件的挠度 [J].长沙交通学院学报,1990,6(4):59-68.
(ZHANG Ke-bo.The deflection of PPC flexural members under static load and fatigue loading [J].Transactions of Changsha Communications College,1990,6(4):59-68.)