与三相电机相比,多相电机驱动系统具有转矩脉动小,系统可靠性高,可以实现低压大功率等优点,在电动汽车、风力发电、航空航天和船舶推进等领域受到关注[1-3].在各种多相电机中,相移30°双三相电机由于可以抑制六次谐波转矩脉动而得到广泛应用.
磁场定向控制(field oriented control,FOC)是电机驱动最常用的方法[4],定子相电流谐波含量小,然而旋转变换比较复杂,很难得到理论分析的结果.模型预测控制(model predictive control,MPC)作为一种新的控制策略被应用于多相电机[5],能够获得较好的动态性能,但存在对电机参数敏感、计算量大等缺点.直接转矩控制(direct torque control,DTC)结构简单、转矩动态响应快,被广泛应用于三相电机,但低速转矩脉动大[6].电机相数的增加有利于将直接转矩控制推广到多相电机系统.文献[7]将空间矢量调制(space vector modulation,SVM)应用到直接转矩控制中,但计算复杂,失去了传统DTC控制简单的优点.文献[8]在分析转矩增减不对称的基础上,设计了一种滞环宽度可调的转矩控制器,可以有效减小转矩稳态误差,但需要在线计算以及额外增加一个PI调节器.文献[9]通过构造中间矢量可以很好地抑制谐波电流.占空比DTC能有效降低转矩和磁链脉动,与SVM-DTC相比,计算量和复杂性都减小很多[10].
为同时抑制双三相PMSM的转矩脉动和谐波电流,本文提出了一种合成矢量和占空比相结合的直接转矩控制策略.分析了合成矢量对转矩变化率的影响,并对磁链扇区和电机转速进行离散化,引入电压矢量评价函数和转速评价函数,用于占空比的计算.
1 数学模型
双三相永磁同步电机的相量图如图1所示.α-β为静止坐标系,d-q为转子坐标系,x-y为定子坐标系,其中永磁体磁链ψf和d轴同向,定子磁链ψs和x轴同向.
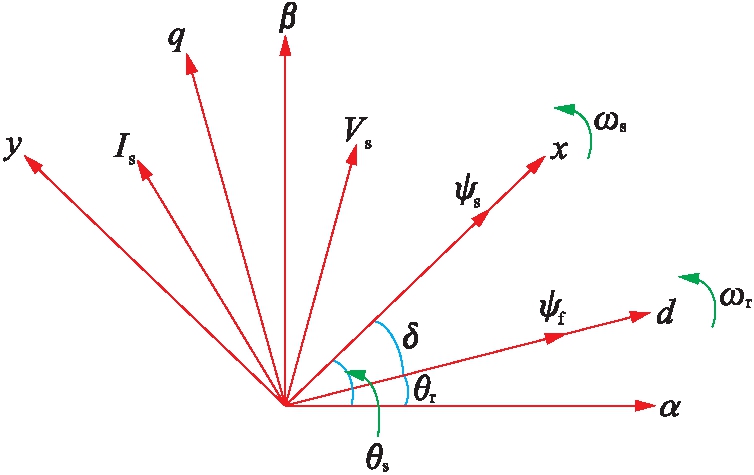
图1 空间相量图
Fig.1 Space vector diagram
表贴式永磁同步电机各参量可表示为
Usx=RsIsx+ρψs
(1)
Usy=RsIsy+ωsψs
(2)
ψsd=LdId+ψf
(3)
ψsq=LqIq
(4)
Te=3npψfIq
(5)
式中:Usx、Usy为定子电压x、y分量;Isx、Isy为定子电流x、y分量;ψs为定子磁链幅值;ψf为转子永磁体磁链幅值;ωs为定子磁链的电角速度;Rs为定子电阻;Ld、Lq为定子电感的d、q分量;ψsd、ψsq为定子磁链幅值的d、q分量;Id、Iq为定子电流的d、q分量;np为电机的极对数;Te为电磁转矩;ρ为微分算子.
2 逆变器电压矢量
双三相永磁同步电机是一个强耦合的六维系统,根据空间矢量解耦[11],可以将双三相电机分解为三个相互正交的二维子空间:αβ、z1z2和o1o2,三个子空间中只有αβ空间的分量会在气隙中产生旋转磁动势,参与机电能量转换.当电机两套三相绕组的中性点互相隔离时,o1o2子空间的电流分量全为零.
逆变器总共有64个开关状态,αβ子空间和z1z2子空间的电压矢量如图2所示,每一个子空间包含60个有效电压矢量和4个零矢量.将每个电压矢量用一个十进制数编号,Ui=SWSVSUSCSBSA.
αβ平面的有效电压矢量构成了四个不同幅值的正十二边形,按幅值从大到小依次为大变量UL、中变量UM、原始变量UB和小变量US,幅值分别为:0.644Udc、0.471Udc、0.333Udc和0.173Udc,其中,Udc为直流母线电压.
3 虚拟矢量的占空比直接转矩控制
3.1 合成虚拟矢量
传统直接转矩控制中,只对αβ平面的电压矢量进行控制,而没有考虑z1z2谐波平面.实际上,由于z1z2平面的阻抗很小,会产生较大的谐波电流[9],造成损耗,因此必须对谐波平面同时进行控制.
根据图2中两个平面的矢量分布,αβ平面中同一方向的大矢量和中矢量对应于z1z2平面中方向相反的小矢量和中矢量.通过控制两个矢量的作用时间,可以使z1z2平面的合成电压矢量为零.假设在一个控制周期Ts内,αβ平面中同一方向的大变量UL、中变量UM的作用时间分别为TL、TM.当虚拟矢量满足在z1z2平面上幅值为零的约束时,则有
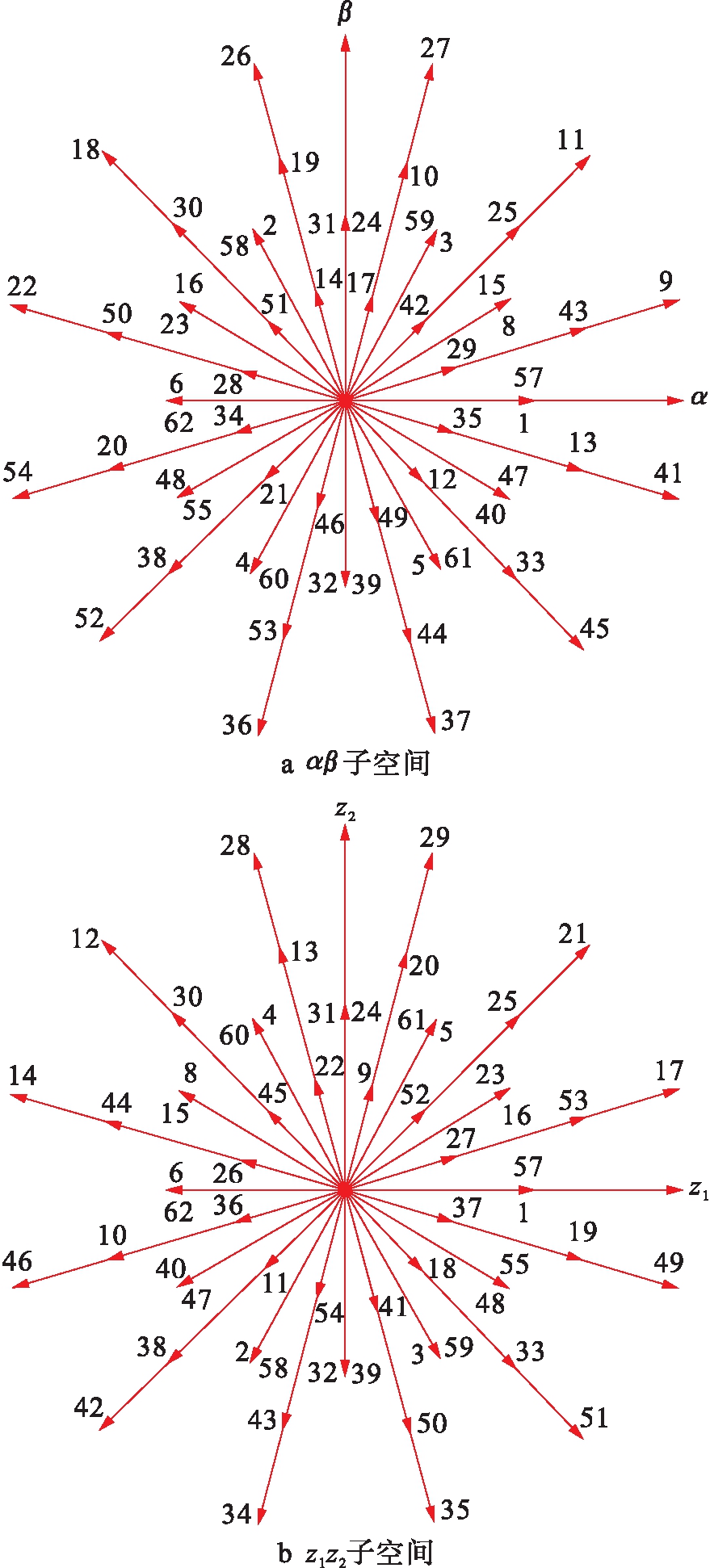
图2 电压矢量空间分布
Fig.2 Space distribution of voltage vectors
(6)
将矢量的幅值代入式(6)可得
(7)
上述方法保证z1z2平面的电压矢量幅值为零,能有效抑制谐波电流,此时合成虚拟矢量在αβ平面的幅值为
UU=ULTL+UMTM=0.928UL
(8)
本文所提控制策略中,使用12个虚拟矢量UUi(i=1,2,…,12)来替代传统直接转矩控制中使用的12个大变量,在有效抑制谐波的情况下,保持较高的电压利用率.
3.2 转矩变化率
由式(4)、(5)可得
(9)
对式(9)求导可得
(10)
式中:ωr为转子电角速度;δ为转矩角.
将式(2)代入式(10)化简可得
ΔT1+ΔT2+ΔT3
(11)
式中:![]() 与负载有关;
与负载有关;![]() 与电机转速有关;
与电机转速有关;![]() 与电压矢量有关.
与电压矢量有关.
图3a为本文所用电机在额定转速和额定负载运行时,在不同虚拟矢量和零矢量作用下的转矩变化率.可以看出,零矢量作用下转矩的变化率为-9.287×104 N·m/s,总是使转矩减小.合成虚拟矢量对转矩的作用与磁链的位置有关,最小转矩变化率为-3.885×105 N·m/s,最大转矩变化率为2.027×105 N·m/s,转矩减小的速率比转矩增加的速率要大.电压矢量引起转矩增加的变化率和减小的变化率存在明显的不对称,这是产生转矩脉动的一个主要原因.图3b为定子磁链位于第一扇区,电机在不同转速和负载运行时,合成矢量UU7和零矢量对转矩变化率的影响.可以看出,电机转速对转矩变化率的影响要比负载大得多.
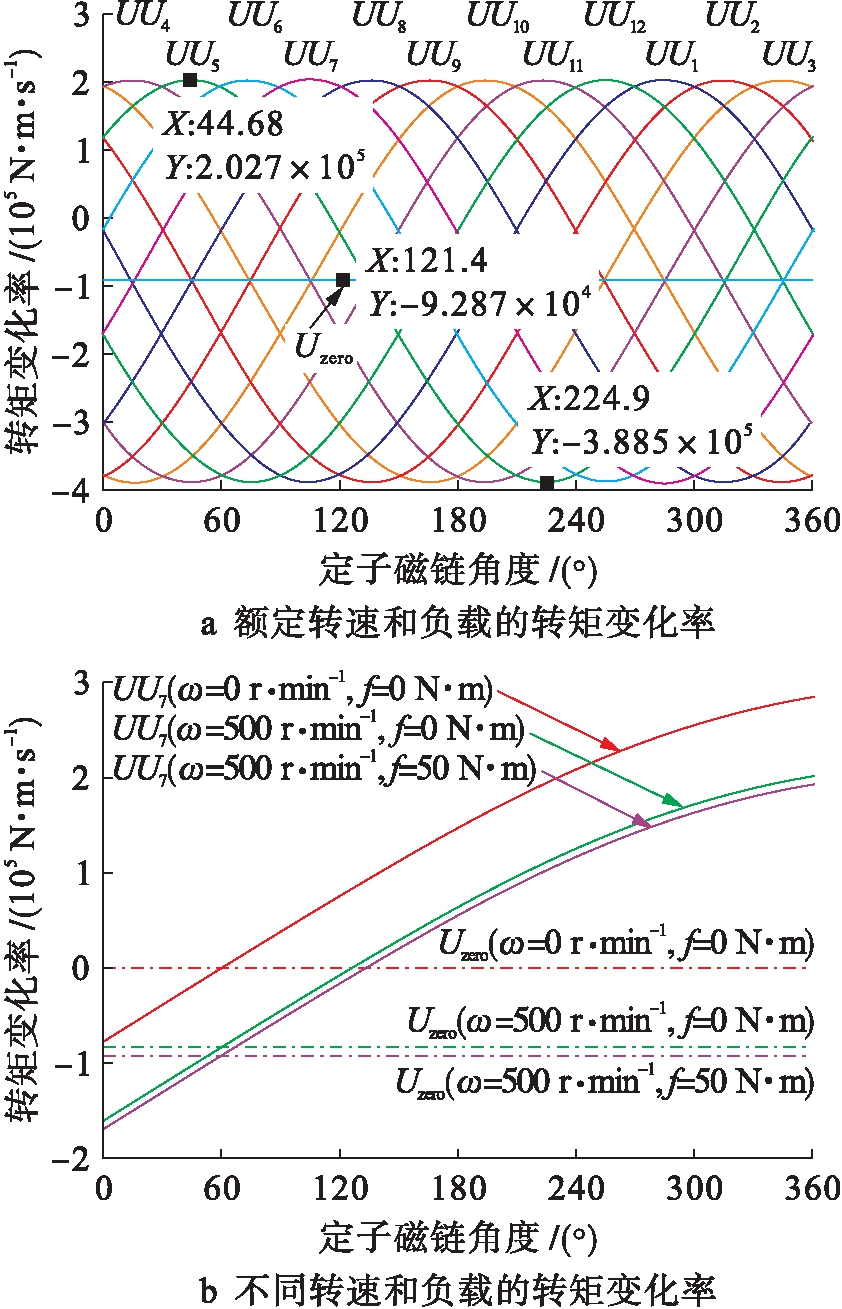
图3 转矩变化率
Fig.3 Torque variation rate
3.3 占空比计算
占空比控制的原理是:在一个控制周期中,有效电压矢量仅作用一部分时间,其余时间由零矢量作用.定义有效电压矢量作用时间和整个周期的比值为占空比D.
由3.2节的分析可知,转矩变化率主要取决于作用的虚拟电压矢量以及电机转速,根据式(11)可知,定义虚拟矢量对转矩影响的评价函数及电机转速对转矩影响的评价函数分别为
Te_V=Usy=UUsin(θi-θs) (i=1,2,…,12)
(12)
Te-s=-ψsωr
(13)
式中:θi为UUi与α轴的夹角;θs为定子磁链与α轴的夹角.
为定量分析虚拟矢量和电机转速对转矩的相对作用效果,将定子磁链角度θs和电机额定转速ωN离散化.如图4所示,在12个扇区的基础上,每个扇区逆时针被三等分(以扇区S1为例,变为S1a、S1b、S1c),一共得到36个扇区.同时,将额定转速ωN等分为10个区间.
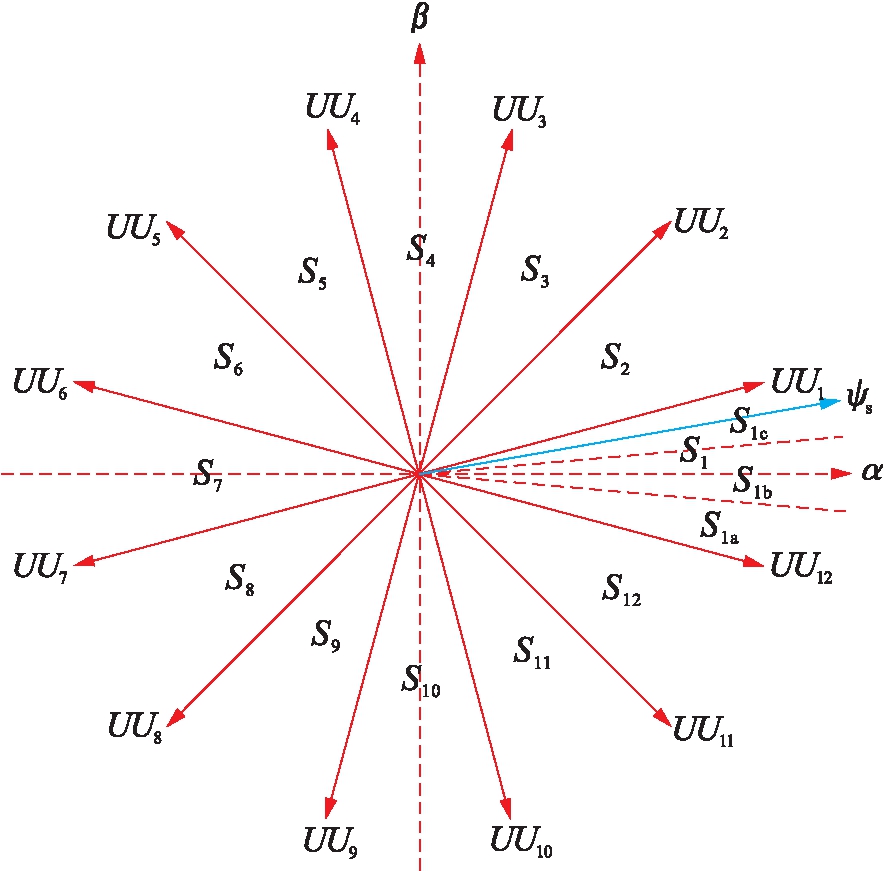
图4 虚拟矢量和定子磁链分区
Fig.4 Virtual vectors and partition of stator flux
式(12)、(13)在一个区间内的平均值可以表示为
(14)
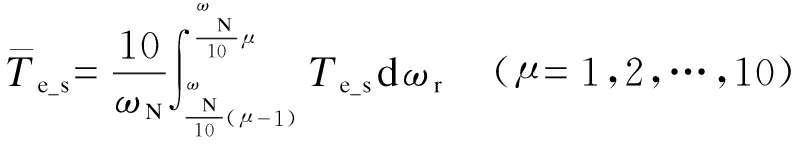
(15)
式中:λ为磁链扇区编号;μ为转速区间编号.
以平均值作为整个区间内变量对转矩影响的评价值,当定子磁链位于图4的扇区Sk(k=1,2,…,12)时,合成虚拟矢量和电机转速的评价值分别如表1、2所示.表1中,数值均以虚拟矢量评价值的最小值进行标幺.
表1 合成矢量的评价值
Tab.1 Evaluation values of resultant vector

扇区磁链增加转矩增大转矩减少磁链减少转矩增大转矩减少Ska146-100100-146Skb128-128128-128Skc100-146146-100
表2 转速的评价值
Tab.2 Evaluation values of rotating speed
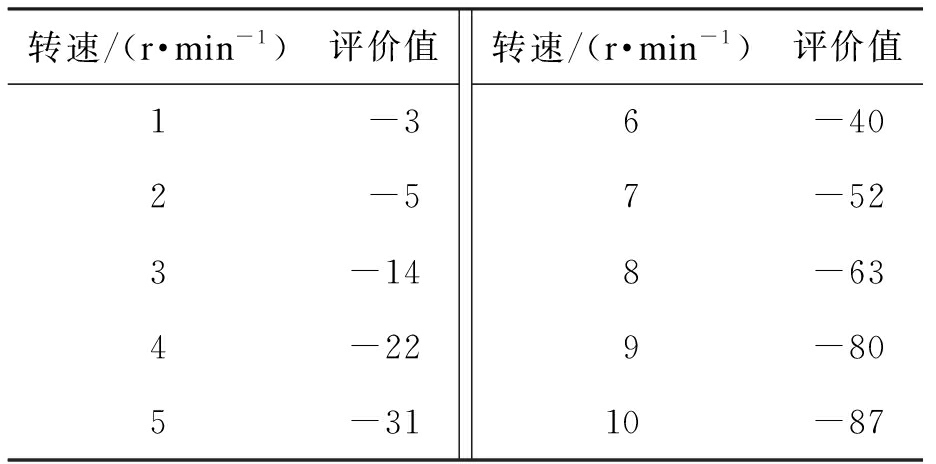
转速/(r·min-1)评价值1-32-53-144-225-31转速/(r·min-1)评价值6-407-528-639-8010-87
根据当前的转矩误差、电机转速,推算下一周期作用的合成虚拟矢量的占空比D为
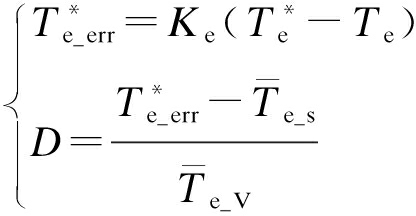
(16)
式中:![]() 为转矩参考值;Te为转矩瞬时采样值;Ke为转矩误差的增益系数.基于合成虚拟矢量的占空比直接转矩控制系统框图如图5所示.
为转矩参考值;Te为转矩瞬时采样值;Ke为转矩误差的增益系数.基于合成虚拟矢量的占空比直接转矩控制系统框图如图5所示.
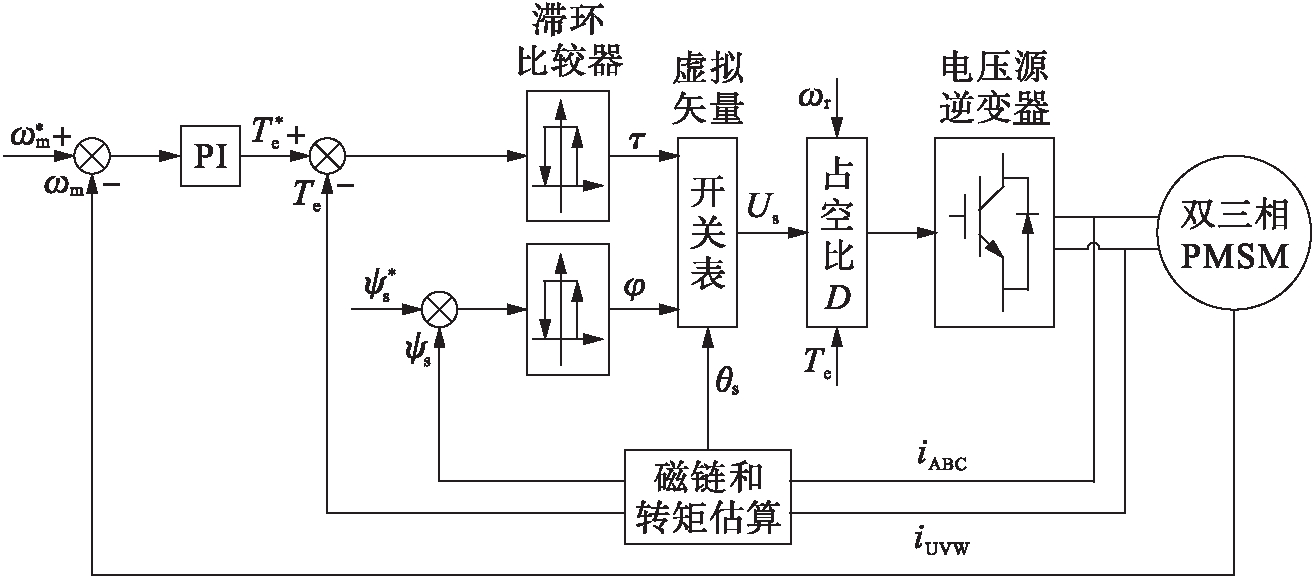
图5 占空比DTC系统框图
Fig.5 Block diagram of DTC based on duty ratio
4 仿真结果与分析
为了验证所提算法的正确性,在Matlab/Simu-link中进行仿真分析,电机参数如表3所示.将文献[9]给出的传统DTC算法和本文所提基于合成矢量的占空比DTC算法的控制周期分别设置为100、150 μs,以保证两种算法的开关频率相近.系统定子磁链给定0.7 Wb,转矩和磁链滞环宽度分别为4 N·m和0.007 Wb,参数Ke=7.
表3 永磁同步电机参数
Tab.3 Parameters of PMSM

定子电阻RsΩ直交轴电感Ld、LqmH转子永磁体磁链ψfWb额定转速ωN(r·min-1)额定转矩TN(N·m)极对数np直流母线电压UdcV1.480.68500503300
4.1 稳态性能
图6、7分别给出了传统DTC和本文所提占空比DTC的稳态运行结果.电机的给定转速为400 r/min,负载转矩为40 N·m.
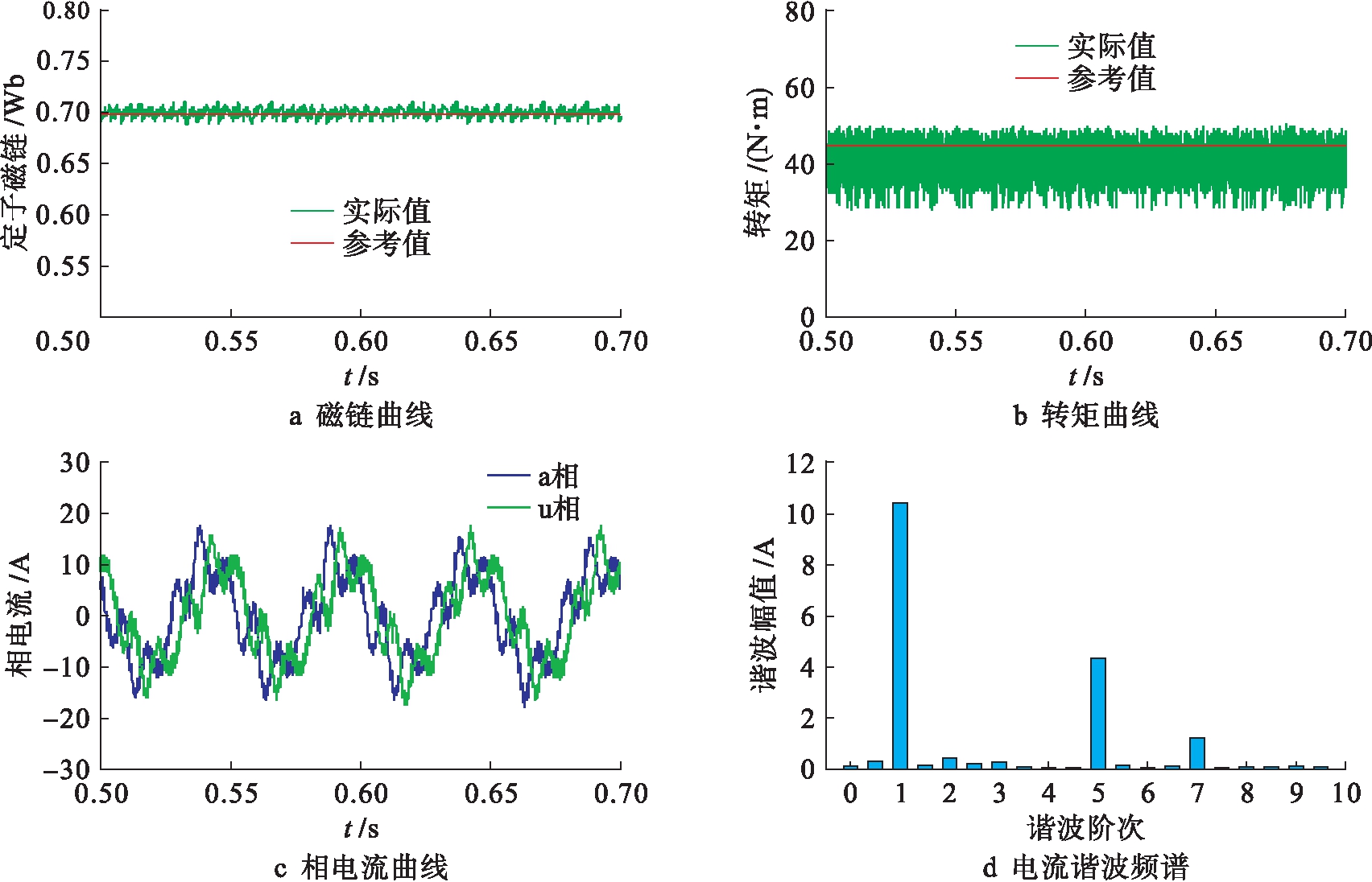
图6 传统DTC仿真结果
Fig.6 Simulation results of traditional DTC
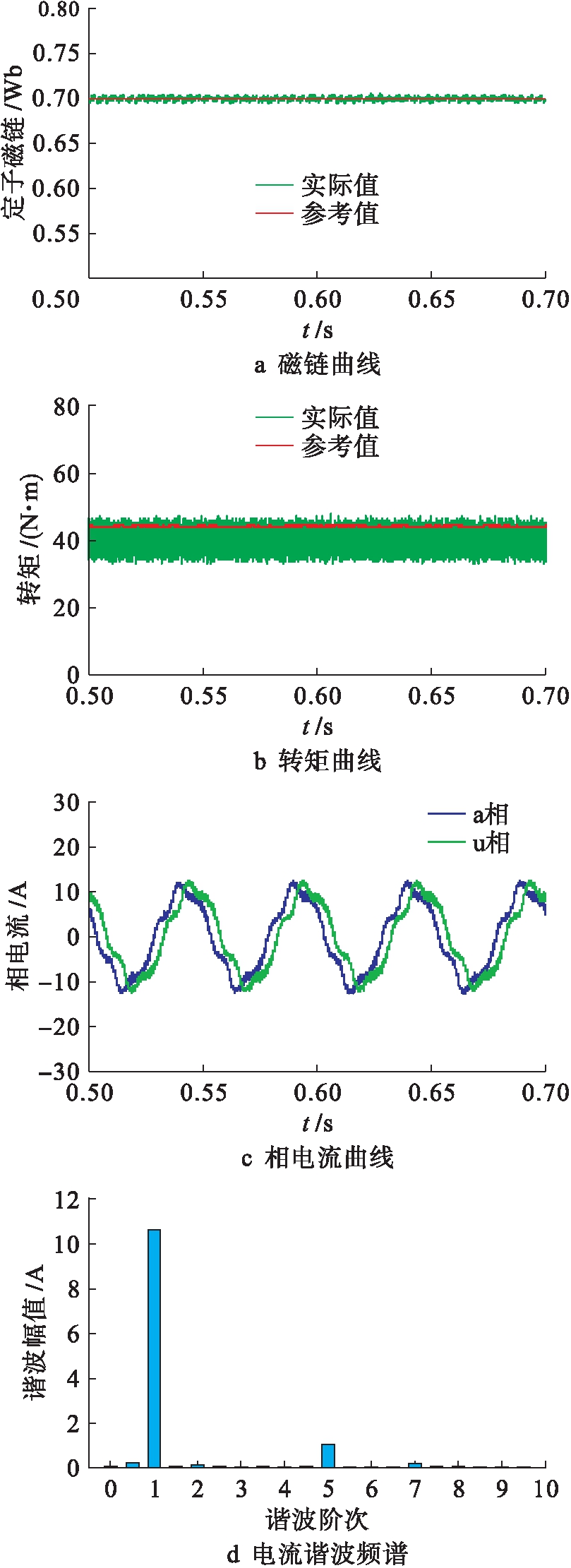
图7 所提DTC仿真结果
Fig.7 Simulation results of as-proposed DTC
由图6a和图7a可以看出,通过设置较小的磁链滞环宽度,传统DTC和占空比DTC都能保持良好的磁链性能.图6b和图7b对比表明,占空比DTC可以明显地减小转矩脉动.传统DTC未对z1z2平面的谐波电流(主要是5、7次)进行控制,导致相电流含有大量谐波,相电流波形畸变严重.占空比DTC中通过引入合成矢量,可以有效地抑制谐波电流.
表4给出了两种算法的定量结果,其中转矩和磁链脉动的计算公式为
(17)
(18)
式中:ψs_j和Τe_j为磁链和转矩的采样瞬时值;ψs_av和Te_av为磁链和转矩的采样平均值.
从表4中可以看出,在两种算法开关频率相近的情况下,相比于传统DTC,占空比DTC的转矩脉动减小了33.81%,相电流的总谐波量减小了69.78%.
表4 两种DTC算法的结果
Tab.4 Results of two DTC algorithms
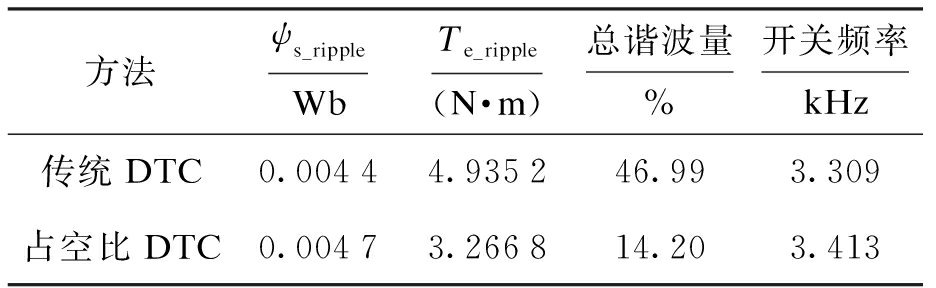
方法ψs_rippleWbTe_ripple(N·m)总谐波量%开关频率kHz传统DTC0.00444.935246.993.309占空比DTC0.00473.266814.203.413
4.2 动态性能
图8给出了占空比DTC突加负载时的结果,电机给定转速保持在400 r/min,在1 s时负载转矩由0 N·m变为40 N·m.从仿真结果可以看出,转矩能很快地跟踪参考值,转速恢复时间约为0.2 s.
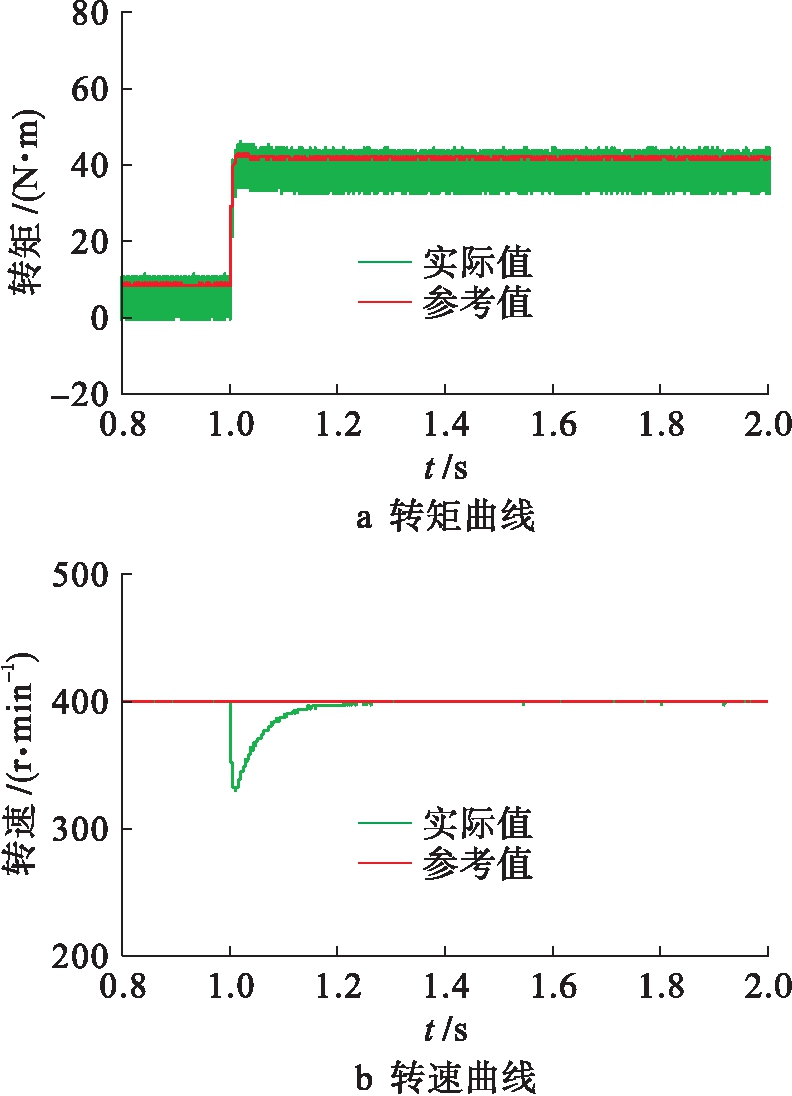
图8 所提DTC加载响应
Fig.8 Response to load disturbance of as-proposed DTC
4.3 转速对占空比的影响
图9给出了电机在不同转速下占空比的仿真结果,条件为:0~1 s为50 r/min,1~2 s为250 r/min,2~3 s为450 r/min,负载转矩一直为空载.从图9中可以看出,在电机启动阶段和转速突然变化时,占空比的值为1,表明有效矢量作用整个控制周期,从而使转矩能迅速达到给定值.稳定后,占空比的大小与电机转速密切相关,0~1 s低速运行时,占空比的平均值约为0.1,这也说明了传统直接转矩控制中低速性能差的原因;2~3 s高速运行时,占空比的平均值约为0.6.结果表明,电机转速对占空比有很大影响.
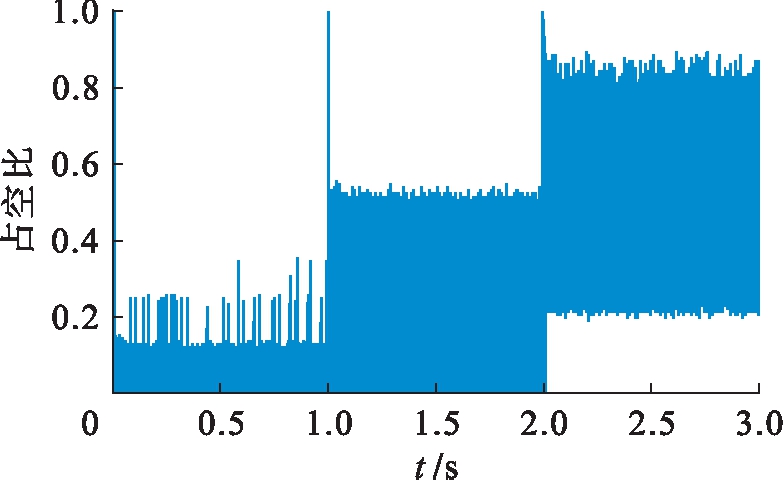
图9 不同转速下的占空比
Fig.9 Duty ratios at different rotating speeds
5 结 论
本文以双三相永磁同步电机为研究对象,提出了基于虚拟矢量的占空比直接转矩控制算法.该算法根据PWM调制原理,使得到的虚拟矢量在z1z2平面的幅值为零,实现了对谐波电流的抑制.将12个合成的虚拟矢量组成新的开关表,利用转矩误差来计算虚拟电压矢量在一个控制周期内的作用时间.将磁链划分为36个扇区,转速分为10个等级,每一个区间内用平均值进行近似,占空比计算简单.仿真结果表明,与传统DTC算法相比,基于占空比DTC的双三相PMSM转矩脉动和谐波电流分别减小了33.81%和69.78%.所提算法的正确性和有效性均得到了验证.
[1]张红伟.新能源汽车的发展现状及前景分析 [J].汽车实用技术,2016(9):22-24.
(ZHANG Hong-wei.Analysis of development status and prospect of new energy vehicles [J].Automobile Applied Technology,2016(9):22-24.)
[2]张炳义,张霄霆,姜珊珊.电动汽车永磁同步驱动电机优化波形质量方法 [J].沈阳工业大学学报,2017,39(5):481-485.
(ZHANG Bing-yi,ZHANG Xiao-ting,JIANG Shan-shan.Optimization method for waveform quality of permanent magnet synchronous motor for electric vehicles [J].Journal of Shenyang University of Technology,2017,39(5):481-485.)
[3]杨金波,杨贵杰,李铁才.六相电压源逆变器PWM算法 [J].电工技术学报,2012,27(7):205-211.
(YANG Jin-bo,YANG Gui-jie,LI Tie-cai.PWM techniques for six-phase voltage-source inv erters [J].Transactions of China Electrotechnical Society,2012,27(7):205-211.)
[4]孟超,欧阳红林,刘伟候,等.双Y移30°永磁同步电机的空间矢量调制 [J].中国电机工程学报,2010,30(3):90-98.
(MENG Chao,OUYANG Hong-lin,LIU Wei-hou,et al.Space-vector PWM techniques for dual Y shift 30 degree permanent-magnet synchronous motor [J].Proceedings of the CSEE,2010,30(3):90-98.)
[5]Guzman H,Duran M J,Barrero F,et al.Comparative study of predictive and resonant controllers in fault-tolerant five-phase induction motor drives [J].IEEE Transactions on Industrial Electronics,2016,63(1):606-617.
[6]夏加宽,毕亮,李瑞泽,等.车用永磁同步电机MT坐标系下DTC控制 [J].沈阳工业大学学报,2018,40(3):241-247.
(XIA Jia-kuan,BI Liang,LI Rui-ze,et al.DTC in MT coordinate system for permanent magnet synchronous motor used in electric vehicle [J].Journal of Shen-yang University of Technology,2018,40(3):241-247.)
[7]Tahen A,Rahmati A,Kaboli S.Comparison of effi-ciency for different switching tables in six phase induction motor [J].Journal of Power Electronics,2012,12(1):128-135.
[8]Zhu Z Q,Ren Y,Liu J M.Improved torque regulator to reduce steady-state error of torque response for direct torque control of permanent magnet synchronous machine drives [J].IET Electric Power Applications,2014,8(3):108-116.
[9]周长攀,苏健勇,杨贵杰.双三相永磁同步电机直接转矩控制谐波电流抑制研究 [J].电机与控制学报,2015,19(9):46-53.
(ZHOU Chang-pan,SU Jian-yong,YANG Gui-jie.Harmonic currents suppression in direct torque control of dual three-phase permanent magnet synchronous motor [J].Electric Machines and Control,2015,19(9):46-53.)
[10]Hoang K D,Ren Y,Zhu Z Q,et al.Modified switching-table strategy for reduction of current harmonics in direct torque controlled dual-three-phase permanent magnet synchronous machine drives [J].IET Electric Power Applications,2015,9(1):10-19.
[11]Levi E,Barrero F,Duran M J.Multiphase machines and drives-revisited [J].IEEE Transactions on Industrial Electronics,2016,63(1):429-432.