体育成绩的建模与预测,不但可以指定锻炼计划[1],还能够增加锻炼效率[2].一般来说,对体育成绩的建模与预测将一定时间段内的体育成绩数据看作是时间序列数据,可采用多元线性回归对其完成非线性建模,通过计算预测参数对某个个体的体育成绩进行估计[3].为了解决传统方法在体育成绩预测中的缺陷,近年来快速发展的模糊理论和灰色理论成为了研究热点[4],灰色预测过程可以看作是一个黑盒子,虽然对普通大众部分不规则的体育成绩预测有良好效果,但是预测结果缺乏一定的解释性[5].此外,机器学习模型也逐渐引用至体育成绩预测过程中,相比于传统计算模型,机器学习模型能够通过自组织、非线性的方式从已有体育成绩数据中学习出映射关系,获得精准的成绩预测结果,同时还有较强的解释性[6].
目前为止,传统机器学习体育成绩预测方法已经无法面对海量的大数据[7].为了解决海量数据背景下的体育成绩预测问题,本文在GM(1,1)模型和GOM模型基础上提出了一种改进的等维动态GOM模型提取体育成绩时间序列中的灰度特征,并构建深度卷积神经网络完成对体育成绩时间序列的回归与预测,获取更精确、稳定的体育成绩预测.
1 体育成绩灰度预测特征模型的构建
经典的灰度预测特征模型为GM(1,1)模型[8]和GOM模型[9],通常情况下,随着时间序列长度的增加,当预测的时刻越远时,灰度特征区间越大,相应的预测精度也会降低.不同的预测问题将会有不同的区间范围选择,为了使体育成绩预测获得最优化的灰度特征预测区间,引入等维动态GOM灰度特征模型进行预测区间构建[10],该模型的构建步骤如下:
1) 假设体育成绩时间序列为![]() 基于该时间序列构建GOM模型,通过该模型可以得到下一时间段相应的预测值
基于该时间序列构建GOM模型,通过该模型可以得到下一时间段相应的预测值![]()
2) 将预测结果加入到时间序列中,为了保证时间序列长度相同,需要去掉位于时间序列首部的结果![]() 构建新的时间序列
构建新的时间序列![]() 通过新的时间序列可以重新构建GOM模型,并计算出下一个预测值
通过新的时间序列可以重新构建GOM模型,并计算出下一个预测值![]()
3) 再次将新的预测值加入到时间序列数据中,并重复步骤2),直到预测的特征能够达到预测目标或满足给定的精度要求后停止.
2 基于CNNs的体育成绩预测算法
2.1 体育成绩预测的CNNs模型
目前为止,体育成绩数据量大且体育科目分布广泛,采用机器学习模型通常无法解决海量灰度特征分析.因此,本文引入深度卷积神经网络(convolutional neural networks,CNNs)模型完成对日益增长的体育成绩数据及提取的灰度特征进行识别与回归[11].图1给出了本文体育成绩灰度特征分析的CNNs模型.
从图1中可以看出,整体深度CNNs由5层网络组成,每层网络的详细设计如下:
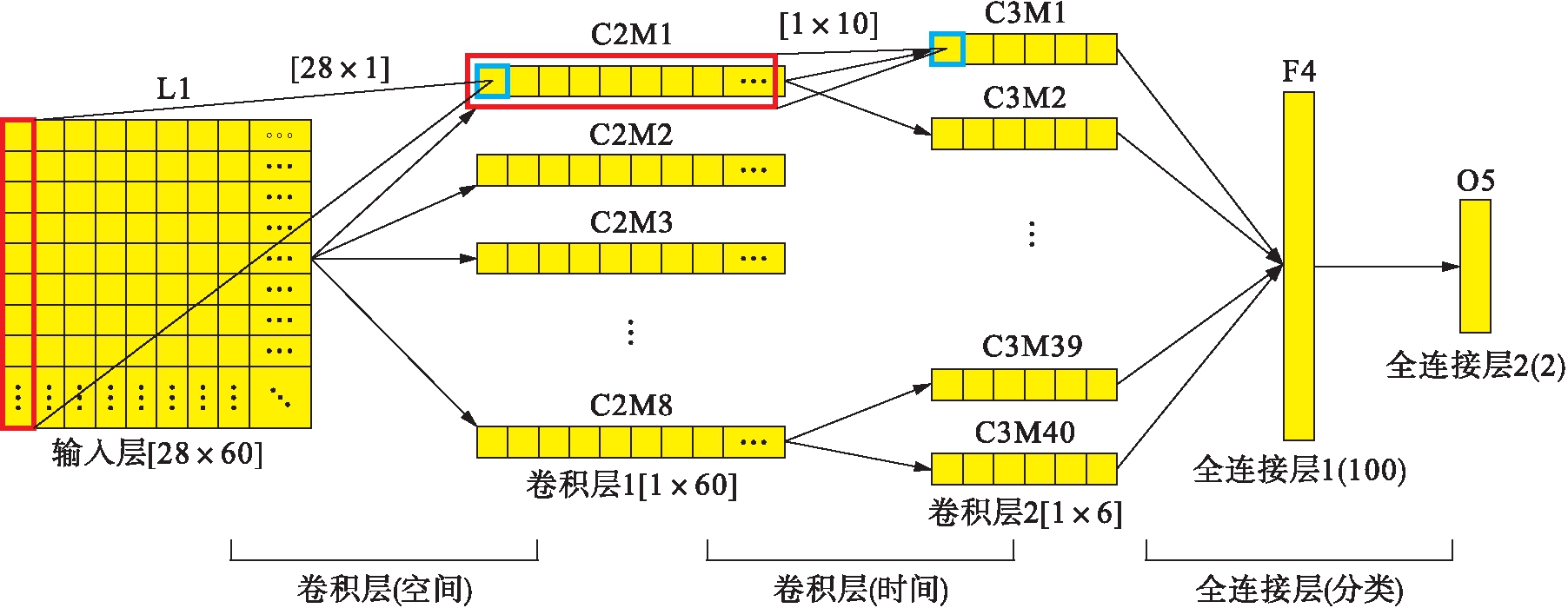
图1 体育成绩灰度特征分析的CNNs模型
Fig.1 CNNs model for analysis of gray scale features of sport performance
第一层(L1):输入层输入的GOM主变量样本大小为[28×60].
第二层(C2):第一个卷积层的作用是实现纵向的空间滤波用于提取体育特征的灰度空间特征.空域特征的卷积核大小为[28×1],卷积输出的特征图大小为[1×60],卷积核采用向量卷积方式.
第三层(C3):第二个卷积层的作用是实现横向的时间域滤波用于体育成绩的时域特征,使用了5组横向滤波器,产生40个空域上的特征图.
第四层(F4):第一个全连接层用于将两层卷积产生的40个特征图进行合并,由于一共产生了240个输出结果,用100个神经元作为过渡,将产生的特征降维.
第五层(O5):第二个全连接层也是输出层,将降维后的时域特征和灰度空间特征进行分回归,获得回归后的体育成绩预测值.
在训练过程中,设置训练的最大次数为10 000次,并根据误差产生的loss曲线判断网络是否收敛,作为迭代的终止标准.
2.2 体育成绩预测过程
对于体育成绩X0及其相应的影响因子X1,X2,…,Xp,假设存在N个时刻的真实数据,现在需要预测第n+1,n+2,…时刻的体育成绩值,基于融合模型的体育成绩预测算法构建步骤如下:
1) 根据动态影响因素模型计算出关于体育成绩量的时间序列,并按照关联顺序进行排序,假设排序后的指标为X1,X2,…,Xp,其中,p为筛选后的指标个数.
2) 根据体育成绩影响因素构建的等维动态GOM模型,对各个影响因子分别预测第n+1,n+2,…时刻的体育成绩值,加入预测值后的影响因子向量,采用X1,X2,…,Xp来表示.
3) 根据数据特征选定出影响因素范围[L,H],L和H均为正整数,且L≥1,H不超过样本个数.
4) 设置阈值范围Lmin,选择前L个影响因子经过主成分分析算法生成主成分,假设获得的前M个主成分的得分为F1,F2,…,Fm,对应的荷载因子为μ1,μ2,…,μm.
5) 将相同年份的F1,F2,…,Fm与X0的时间序列数据值归一化至[-1,1],并划分为训练集和测试集,将N个样本划分为n1个训练集样本,n2个测试集样本.
6) 构造如图1所示的深度CNNs模型.
7) 将测试集输入至训练好的BP网络中,计算网络的预测值与真实值之间的平均相对误差e1,其中,e1为拟合误差.
8) 根据等维动态GOM模型计算出各个影响因子在n-n2,n-n2+1,…,n年的预测值和相应的荷载因子μ1,μ2,…,μm,计算出各个主成分F1,F2,…,Fm对应年份的体育成绩值,并将体育成绩归一化至[-1,1],输入至已经训练好的CNNs中,计算网络预测值与实际值之间的平均相对误差e2,其中,e2为综合误差,包括了等维动态GOM模型的预测误差和CNNs的拟合误差,作为评价算法的最终指标.
9) 将F1,F2,…,Fm在n+1,n+2,…年的预测值归一化后输入至已训练好的CNNs中,再将网络的输出值进行逆归一化,即可获得在n+1,n+2,…时刻体育成绩的预测值.
3 仿真实验与结果分析
为了验证本文提出算法的可行性与有效性,从网络上抓取百米赛跑体育成绩为研究目标,分别记录百米赛跑每秒成绩达标的人数,在12~20 s的时间段内分别记录体育成绩达标人数.在数据采集过程中,满足横向平等的比较原则,且收集数据均来自我国各大赛事的网络成绩公布结果.
3.1 体育成绩达标人数预测实验结果
在灰度预测特征的对比实验中,采用网络收集到的数据,构建了GM(1,1)模型,将GOM模型和等维动态GOM模型进行灰度预测特征对比.表1给出了12~20 s内百米赛跑达标人数体育成绩结果.
表1 12~20 s内百米赛跑达标人数体育成绩结果
Tab.1 Sport performance results of qualified person number with completion time from 12 s to 20 s in 100-metre race

时间/s121314151617181920达标人数/人211982124723087270612876434531473415538664029
根据灰度预测特征模型的构建过程,可以计算出
28 764,34 531,47 341)
根据GM(1,1)模型和GOM模型的构建过程,可计算出模型中的发展系数a和常数b以及平移值c,结果如下:a=-0.165 37,b=13 823.47,c=17 947.38,由此获得百米赛跑体育成绩达标人数的预测模型,即
GM(1,1)模型:
GOM模型:
采用这两个模型拟合并预测20 s后百米赛跑体育成绩达标的人数.表2为对比的预测结果.
表2 GM(1,1)模型与GOM模型的拟合结果比较
Tab.2 Comparison of fitting results between GM(1,1) and GOM models
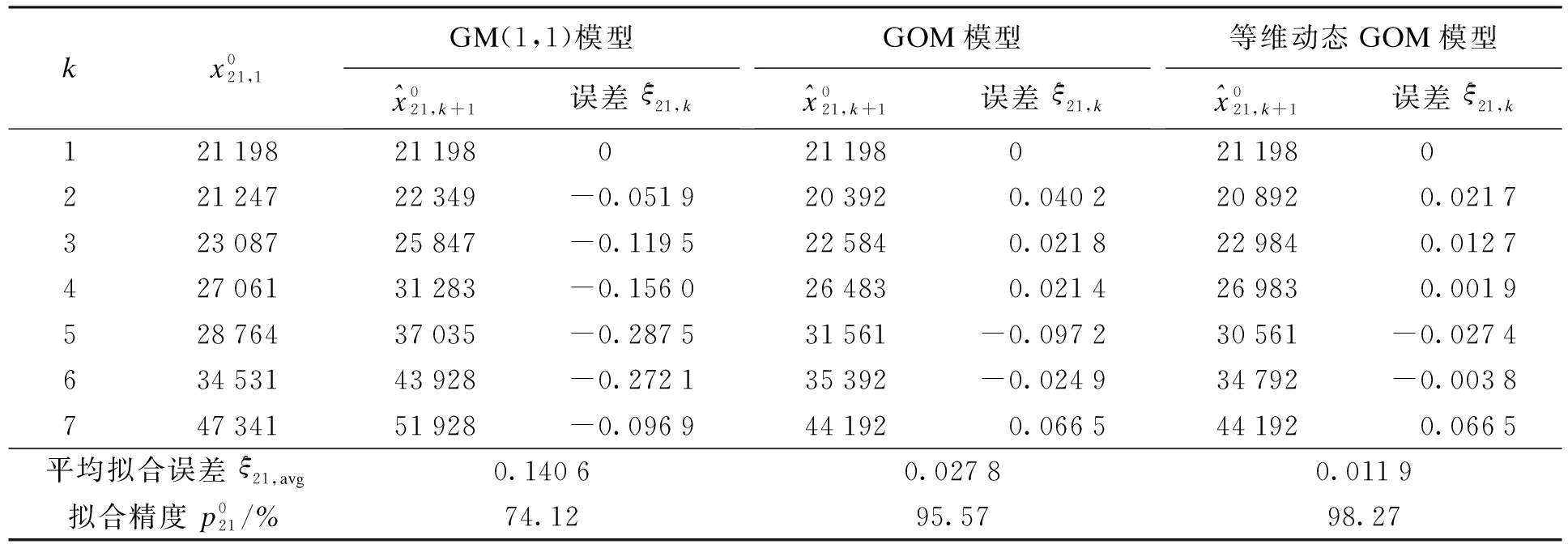
kx021,1GM(1,1)模型^x021,k+1误差ξ21,kGOM模型^x021,k+1误差ξ21,k等维动态GOM模型^x021,k+1误差ξ21,k12119821198 021198 021198 022124722349-0.051920392 0.040220892 0.021732308725847-0.119522584 0.021822984 0.012742706131283-0.156026483 0.021426983 0.001952876437035-0.287531561-0.097230561-0.027463453143928-0.272135392-0.024934792-0.003874734151928-0.096944192 0.066544192 0.0665平均拟合误差ξ21,avg0.14060.02780.0119拟合精度p021/%74.1295.5798.27
由表2可以看出,在GM(1,1)模型下,误差绝大部分都大于10%,有些甚至会高于20%,拟合的精度也较小,不高于75%.结果表明,GM(1,1)模型能够适用于体育成绩达标人数的预测,但是预测的精度偏低.相反,在GOM模型下的误差均没有超过10%,且拟合精度高于95%,远比GM(1,1)模型高,在条件数的比较上也可以看出,GOM模型比GM(1,1)模型拥有更好的稳定性和鲁棒性.
另外,本文还比较了GM(1,1)模型、GOM模型和等维动态GOM模型预测5、10、15、21和22 s内的百米赛跑体育成绩达标人数预测结果.表3为三种灰度特征提取模型的对比预测结果.
表3 三种灰度特征提取模型的对比预测结果
Tab.3 Comparison and prediction results by three extraction models for gray scale features
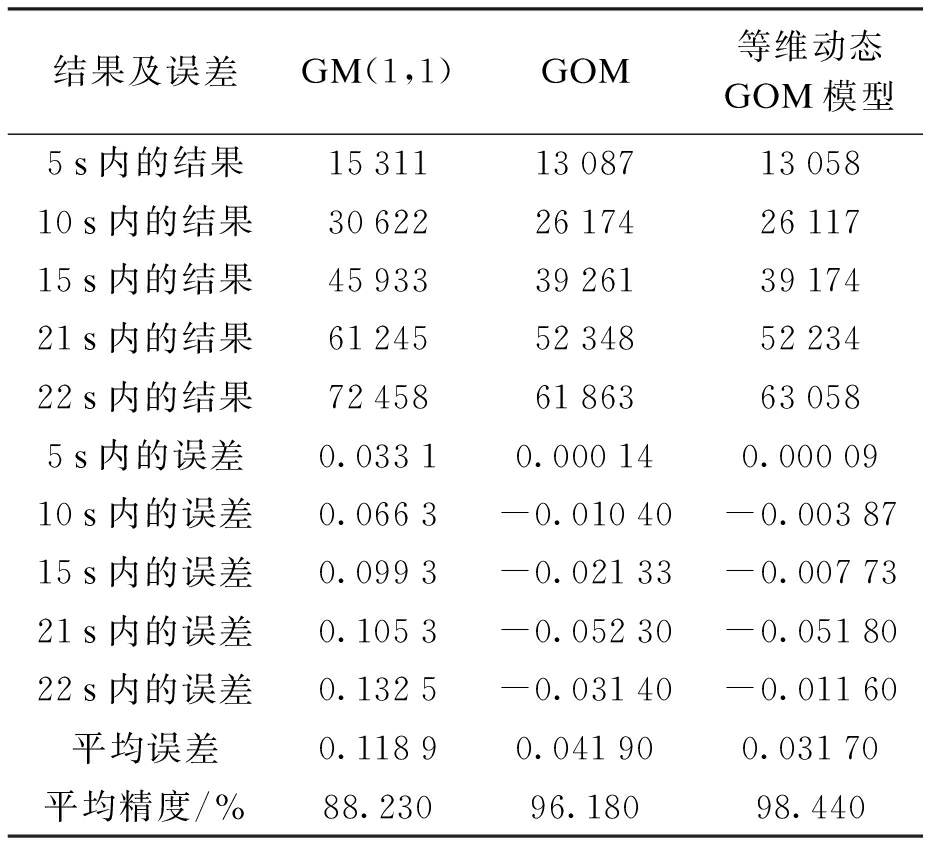
结果及误差GM(1,1)GOM等维动态GOM模型5s内的结果15311130871305810s内的结果30622261742611715s内的结果45933392613917421s内的结果61245523485223422s内的结果7245861863630585s内的误差0.03310.000140.0000910s内的误差0.0663-0.01040-0.0038715s内的误差0.0993-0.02133-0.0077321s内的误差0.1053-0.05230-0.0518022s内的误差0.1325-0.03140-0.01160平均误差0.11890.041900.03170平均精度/%88.23096.18098.440
比较三个模型的预测结果可以看出,GM(1,1)模型的平均预测精度小于90%,而GOM模型和等维动态GOM模型的预测精度均大于95%,取得了更为优秀的体育成绩达标人数预测结果.无论是21 s内还是22 s内的预测结果,等维动态GOM的预测精度均高于GOM模型.因此,经过白化过程,可以使得灰度预测特征提取模型获得更好的预测结果和更高的预测精度.
3.2 深度CNNs体育成绩预测实验结果
在体育成绩的预测上,采用20 s内的64 029个百米跑的成绩完成模型训练.针对21 198个样本,将其中的60%样本作为训练集,20%作为验证集,剩下的20%作为测试集.通过图1定义的CNNs完成对训练集的训练,并通过测试集完成对已经训练好的体育成绩预测模型的测试.为了可视化测试结果,图2给出了测试难度最大的500个样本.
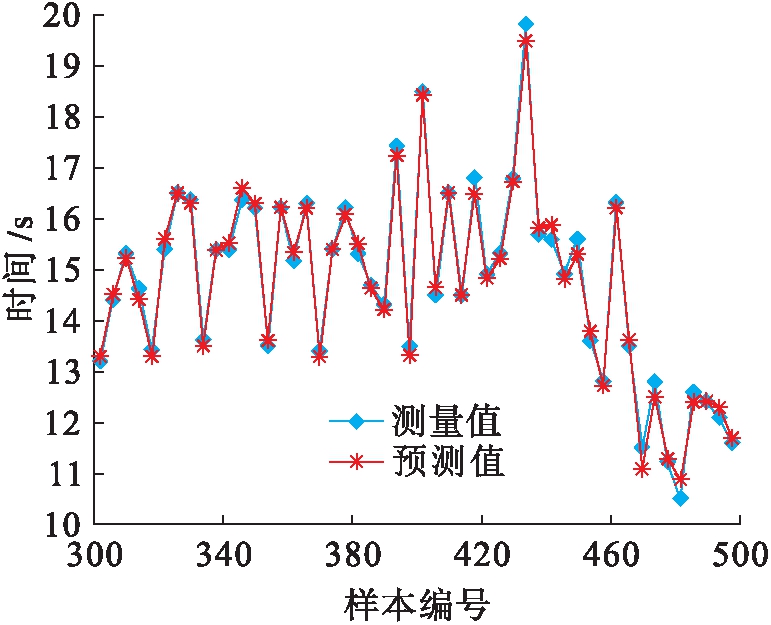
图2 测试难度最大体育成绩预测结果
Fig.2 Prediction results of sport performance with maximum difficulty
从图2中的结果可以看出,经过CNNs的预测,百米跑成绩预测结果与真实结果差距较小,算法精度较高,误差变化区间比较窄,二者之间的误差几乎可以忽略不计.该结果验证了CNNs对体育成绩时间序列预测的可行性与有效性,预测结果良好,并且整体的预测误差较小.
为了横向比较本文提出的CNNs性能,采用相同数量的训练集、验证集和测试集,分别比较本文算法与当前主流算法.图3为百米跑体育成绩预测平均精度对比结果.从图3中的对比结果可以看出:1)多元线性回归对于百米跑体育成绩预测精度最低,该模型不能反映普通大众的体育成绩变化特点,构建出的预测模型误差较大,在大群体数据的预测中几乎没有应用价值.2)遗传算法和粒子群算法等群智能算法结果优于多元线性回归,但是此类算法更适合小样本的数据分析,对于海量样本的体育成绩预测结果不理想.虽然获得了较为不错的平均预测精度,但是在极个别特殊情况下的体育成绩预测效果一般.3)本文提出的CNNs属于深度学习模型,该模型在海量数据样本中的识别能力较强,综合图2、3中的结果可以看出,深度CNNs拥有海量的权重和阈值完成对特殊情况的预测,因此,不论是整体预测的平均精度还是特殊极端结果的预测都获得了良好的效果,更适合体育成绩时间序列数据的预测.
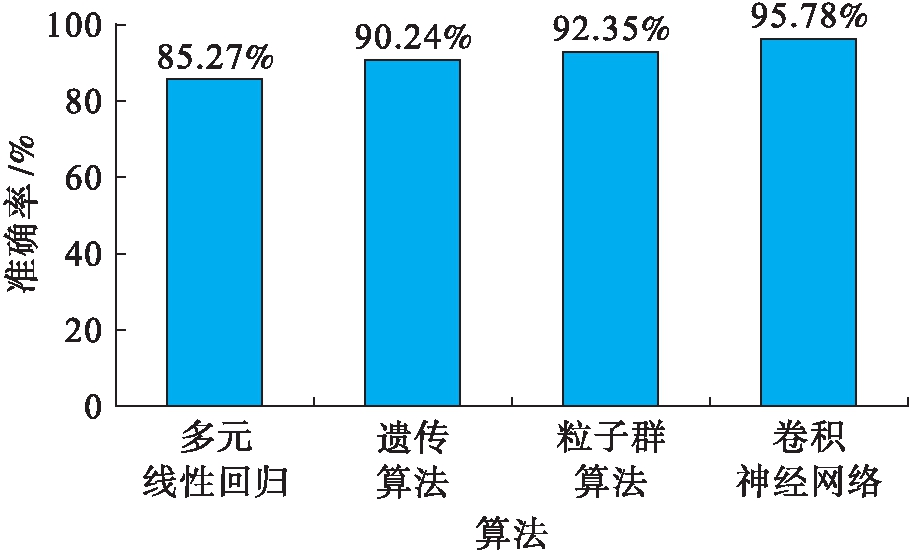
图3 百米跑体育成绩预测平均精度对比结果
Fig.3 Comparison results of average accuracy for sport performance prediction in 100-meter race
4 结 论
通过改进的等维动态GOM模型,在体育成绩达标人数预测中取得了最优预测结果.在体育成绩预测中,本文提出的CNNs超越了传统的多元线性回归、遗传算法和粒子群算法,不但在平均预测精度上取得了最好的效果,而且在极端数据的成绩预测中也获得了最佳的结果,预测值与真实值之间的误差可忽略.今后的工作集中在构建更精确的深度模型,从海量大数据中提取更精确的灰度预测特征,对体育成绩和达标人数完成更为精确的预测.
[1]张文,牟艳,高振兴,等.基于果蝇算法优化极限学习机的体育竞赛成绩预测研究 [J].微型电脑应用,2018,34(3):58-61.
(ZHANG Wen,MU Yan,GAO Zhen-xing,et al.Research on the performance prediction of the sport competition based on the optimization learning machine [J].Microcomputer Application,2018,34(3):58-61.)
[2]刘昊.基于GM(1,1)与反向传输神经网络的大学生体育成绩预测 [J].南京理工大学学报,2017,41(6):760-764.
(LIU Hao.Sports performance prediction for college students based on GM(1,1) and back propagation neural network [J].Journal of Nanjing University of Science and Technology,2017,41(6):760-764.)
[3]Moheb A H,Robert B H.Developing talent from a supply-demand perspective:an optimization model for managers [J].Logistics,2017,1(1):51-59.
[4]刘昊.基于组合核函数相关向量机的体育成绩预测 [J].统计与决策,2015(23):81-84.
(LIU Hao.Sports achievement prediction based on combined kernel function correlation vector machine [J].Statistics and Decision-Making,2015(23):81-84.)
[5]Sinha A,William P,He Y,et al.Matching supply with demand in supply chain management education [J].The International Journal of Logistics Management,2016,27(3):837-861.
[6]Kui D,Liu X,Liang X,et al.Prediction model of sports performance based on grey BP neural network [J].International Journal of u-and e-Service,Science and Technology,2016,9(8):87-96.
[7]Geng W,Dong Y,Li J C,et al.The employment forecasting after the reform of logit model-based gra-duation project on university engineering cost program [J].Journal of Residuals Science & Technology,2016,12(2):13-19.
[8]Zhao M.The gray prediction GM(1,1) model in traffic forecast application [J].Mathematical Modelling of Engineering Problems,2015,2(1):17-22.
[9]Gao N,Cai Y G.Optimized grey model for forecast on deformation of dangerous rock [J].Science of Surveying and Mapping,2014,4(1):18-26.
[10]Zhao H.Grey verhulst model and application based on background value and initial value optimization [J].Systems Engineering,2014,3(1):22-29.
[11]刘芳,冯丹,宫雪然.基于IACO-BP算法的洪涝灾害应急物资需求预测 [J].沈阳工业大学学报,2019,41(3):332-338.
(LIU Fang,FENG Dan,GONG Xue-ran.Flood emergency material demand forecast based on IACO-BP algorithm [J].Journal of Shenyang University of Technology,2019,41(3):332-338.)