综合能源系统通常是指能够根据区域能源结构与能源储备,对能源资源进行优化配置的综合性系统[1].其作为加速全球可持续能源转型的重要途径,近年来备受关注.精确的负荷预测不仅对能源系统的综合规划、运行、管理与梯级利用起到决定性作用,而且是推动能源市场发展的关键技术[2].
目前负荷预测技术的发展比较成熟,然而,对综合能源系统的应用仍存在一定的局限性,原因如下:1)用户需求和负荷特性随着分布式能源的综合而发生改变;2)电力市场的开放性重组增大了随机因素对预测结果的影响;3)在电力零售市场机制下,绩效考核体系通常按月进行.综上所述,对综合能源系统月度负荷预测的深入研究具有实际意义[3-4].
时间序列形式的月度负荷数据通常受季节、用户行为和经济发展等因素的影响,因此,可将负荷序列分解为代表各种影响因素的分量[5].目前,基于分解技术的时间序列预测方法已被应用于包括负荷预测在内的多个领域[6].文献[7]将时间序列分解为趋势分量与季节分量,并采用季节自回归积分移动平均(seasonal auto regressive integral moving average,SARIMA)与加权方法对各分量进行预测.文献[8]采用X12乘子模型分解月负荷序列,并建立不同的模型来预测每个分量.X12模型不仅克服了传统组合模型无法估计开始与结束时多个样本趋势值的缺点,且对于预测性质随时间变化的序列具有更大的优势,但X12模型也存在无法控制季节分量变化率的局限性.文献[9]采用基于拟合的季节性与趋势性预测方法(seasonal and trend decomposition using loess,STL)对负荷序列进行预测,但没有考虑季节拐点对季节分量变化率的影响.上述基于分解的负荷预测方法虽然考虑了对负荷预测的季节因素与趋势因素,但均无法控制季节分量的变化率与趋势分量的平滑度,且对异常值的鲁棒性较低.
本文提出了一种基于STL分解的月度负荷预测方法.将负荷序列分解为趋势、季节与随机分量,对各月份设定不同的季节变化率,分别进行周期性与非周期性的季节分量分解,利用X12模型提取经济数据拟合中的趋势分量.分别采用向量自回归模型(vector auto regression,VAR)、最小二乘支持向量回归(least square support vector regression,LSSVR)与平均法对趋势分量、季节分量与随机分量进行预测,采用分量投影重建法预测月度负荷.通过某高校园区的实际月用电量数据验证分析了所提方法的有效性.
1 综合能源系统负荷预测相关因素
利用历史数据对某区域的月度负荷进行预测时,预测结果受当地气候、季节、用户类型、节假日情况以及经济条件等因素影响.在本文预测过程中,将月度负荷分解成若干分量,分别代表对负荷造成影响的各个因素,之后对各分量采用合适的模型进行预测.
1.1 月份因素相关性分析
月份因素是月度用电量的主要影响因素.其中每个月份中不仅包括社会行为信息(例如学校的寒暑假),也包括以季节为代表的自然信息.由于短假期对月度负荷造成的影响较小,因此,本文仅考虑寒暑假以及春节对月度用电量的影响[10].除了长假期以外,负荷曲线的拐点与季节的变化也存在相关性,例如在我国北方,四个季节变化的拐点通常发生在1、3、7及10月份.
1.2 经济因素相关性分析
由于国内生产总值(GDP)是衡量区域经济水平的一个重要指标,本文通过GDP分析经济水平与月度用电量之间的定性关系.由于目前无法获取月度GDP数据,因此,本文选用与月度GDP最为相似的季度GDP代表经济因素.由于经济因素对用电量的时滞效应,季度GDP增长率峰值总是高于月度用电量增长率的峰值.然而,GDP的波动可以反映在一段时间后的用电量波动上,因此,季度GDP与月度用电量的关系可以间接反映经济发展与用电量的关系.
2 基于特征分解的月度负荷预测
由于各影响因素存在本质区别,导致各组分在时间序列上的变化特征也存在一定差异.其中,趋势分量主要受经济因素影响,反映较长时期的发展方向;季节分量是长度与振幅固定的周期性波动;随机分量则是由各种偶然因素共同组成的.本文利用分解技术对单个分量进行预测,且对于不同月份的用电量预测采用不同的分解策略,之后将所有分量的预测值重构为月度负荷值.本文提出的月度负荷预测方法流程图如图1所示.
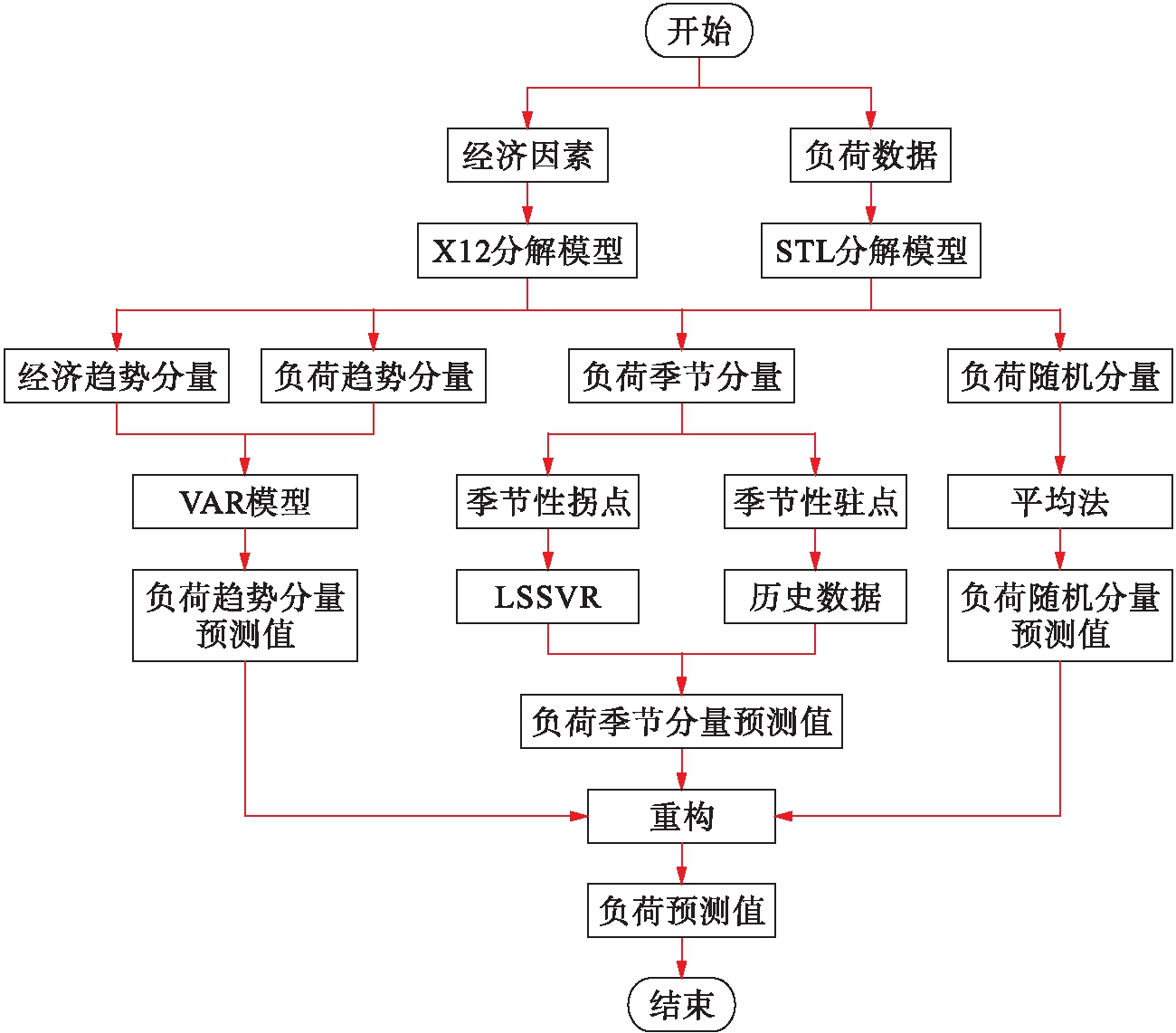
图1 月度负荷预测方法流程图
Fig.1 Flow chart of monthly loading forecast method
所提出的负荷预测方法采用X12分解模型提取经济数据中的趋势分量,通过VAR模型拟合经济因素与用电量的趋势分量.考虑时间因素包括季节与节假日信息,进而从用电量历史数据中提取出季节分力量,并建立LSSVR对其进行预测.当随机分量变化不规律时,则采用平均值法直接计算.
2.1 基于STL模型的月度负荷分解
STL模型是一种时间序列分解方法,采用鲁棒局部加权回归作为平滑方法.在对响应变量进行估计时,从预测变量附近选择一个子集,之后使用加权最小二乘法在子集中执行线性回归或二次回归,以减小远离估计点数值的权重,最后通过局部回归模型估计响应变量的数值.通常采用逐点拟合的方法拟合整条曲线,实现对时间序列的精确分解.
分解模型主要分为乘积形式和相加形式,其中相加形式的分解模型假设各分量的影响是相互独立的,且各分量以绝对值的形式表示;而乘积形式的分解模型假设各分量的影响是相互关联的,趋势分量作为绝对数值,其他分量按照比例表示.由于各因素对负荷产生交互影响,因此,本文分解模型采用乘法模型.月度负荷由三部分分量的乘积组成,分别代表趋势、季节与随机因素.因此,将原始时间序列分解为
Y=YtYsYr
(1)
式中:Y为用电量的时间序列;Yt为趋势分量;Ys为季节分量;Yr为随机分量.
在季节分量分解过程中,若某月份季节分量在季节的拐点处且存在较大波动性,则需要对其进行非周期性的分解;而非季节拐点处的月份季节分量几乎是恒定的,可对其采取周期性的分解.
2.2 基于X12模型的经济因素分解
经济因素与用电量均受季节变化与随机因素的影响,而经济因素对用电量的影响主要体现在趋势分量上.为避免冗余分量的影响,本文采用X12模型对GDP数据进行季节调整,剔除季节分量与随机分量,剩余部分用于预测用电量的趋势分量.X12模型是美国商务部人口普查局提出的一种季节性分解模型[11].由于各因素对GDP的影响是相互关联的,因此,本文选择乘法分解模型将GDP序列表示为趋势因素、季节因素和随机因素的乘积,即
E=EtEsEr
(2)
式中:E为月度GDP的时间序列;Et为趋势分量;Es为季节分量;Er为随机分量.
2.3 三组分月度负荷预测模型
本文提出三组分月度负荷预测模型,其中趋势分量是长期经济增长形成稳定的发展方向,季节分量是受季节交替影响的周期性波动,随机分量是一种微小扰动,在偶然因素的影响下,其特性无明显变化.本文采用三种不同模型对趋势分量、季节分量与随机分量进行预测.
2.3.1 趋势分量的VAR预测模型
本文将GDP数据作为月度用电量的经济影响因素,采用VAR模型对用电量进行趋势预测.VAR模型是分析和预测经济指标最常用的计量模型之一,该模型根据数据的统计特性,将系统内生变量作为外生变量的滞后值,VAR模型可表示为
yt=A1yt-1+…+Apyt-p+BXt+εt
(3)
式中:yt为k维内生变量;Xt为d维外生变量;A与B为系数矩阵;εt为k维的扰动量.假设εt的协方差矩阵为k维正定矩阵,则式(3)可表示为
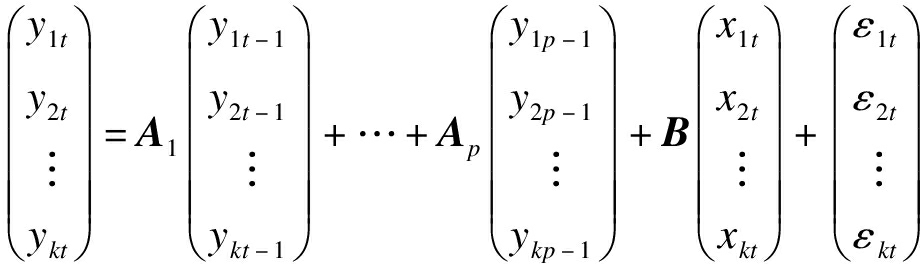
(4)
由式(4)可看出,带有k个时间序列变量的VAR(p)模型由k个等式组成,且内生变量滞后于VAR(n)模型n个序列,则式(4)可简化为
(5)
式中,![]() 为yt关于外生变量Xt回归过程的残差,即
为yt关于外生变量Xt回归过程的残差,即
(6)
其中:A(L)=Ik-A1L-A2L2-…-ApLp为滞后算子L的k阶参数方阵;![]() 为白噪声向量.
为白噪声向量.
当考虑无外生变量的无限制VAR模型时,VAR模型表达式为
yt=A1yt-1+…+Apyt-p+εt
(7)
如果det[A(L)]满足稳定性条件,则可表示为无穷阶的动态平均形式,即
yt=C(L)εt
(8)
式中,C(L)=A(L)-1.
可通过最小二乘法对VAR模型进行估计.在估计VAR参数时,假定A(L)C(L)=Ik,进而获取相应的动态平均模型的参数估计.由于不存在同时的相关问题,因此VAR模型的估计量可以通过标准最小二乘法获取.
2.3.2 季节分量预测模型
对季节分量的预测,需要考虑当前月份属于季节拐点还是季节平稳点.根据月份属性的不同采用相应方法进行预测.
1)季节平稳点月份.对于季节平稳点的月份,对其进行周期性分解,待预测月份的季节分量与历史同时期的季节分量相同.
2)季节拐点月份.对于季节拐点处的月份,本文采用LSSVR对此时的季节分量进行预测.LSSVR是对SVM的改进算法,将传统SVM中的不等式约束转化为等式约束,且将误差平方和损失函数作为训练集的经验损失,进而将解二次规划问题转化为求解线性方程组问题,以提高求解问题的速度与精度[12-13].回归的LSSVR预测模型为
(9)
式中:K(x,xi)=φ(x)φ(xi)为核函数;ai为回归系数;b为偏差.
2.3.3 随机分量的平均预测模型
随机分量的数值通常小于1且变化趋势不明显,本文采用平均值法对随机分量进行预测,即待预测月份的随机分量等于历史数据相同月份中随机分量的平均值.
2.4 月度负荷预测值重构
对各分量的预测值采取指数相乘的方式进行重构,将所得结果作为每个月用电量的最终预测值,即
Yfi,j=eYti,jeYsi,jeYri,j
(10)
式中:Yfi,j为第i年第j个月用电量的预测值;Yti,j为趋势分量预测值;Ysi,j为季节分量预测值;Yri,j为随机分量预测值.
3 实例与分析
本文实验数据来自北方某高校8年间的实测月度用电量,用于验证本文所提出的月度负荷预测方法可行性.其中使用前7年的月度用电量数据作为训练数据,使用第8年的月度用电量数据作为测试数据.
3.1 月度负荷分解
首先,将拐点月份与普通月份的季节分量进行分离.根据1.1节中对季节分量的分析,将1~3月、7~8月与11月的季节分量进行非周期性分解,而将4~6月、9~10月、12月进行周期性分解.由于STL函数仅能处理加性模型,因此可通过对数变换将原乘法模型Y转化为对数可加模型Yd.
以3月与4月的训练数据为例,利用STL函数绘制序列Yd的变化曲线,并将曲线分解为趋势Yt、季节分量Ys与随机分量Yr.各分量的变化趋势如图2所示.由图2可见,拐点月份的季节分量Ys随时间逐渐变化,而非拐点月份的季节分量Ys随时间周期性变化.Yt有稳定的增长趋势,Yr则没有明显的变化规律.
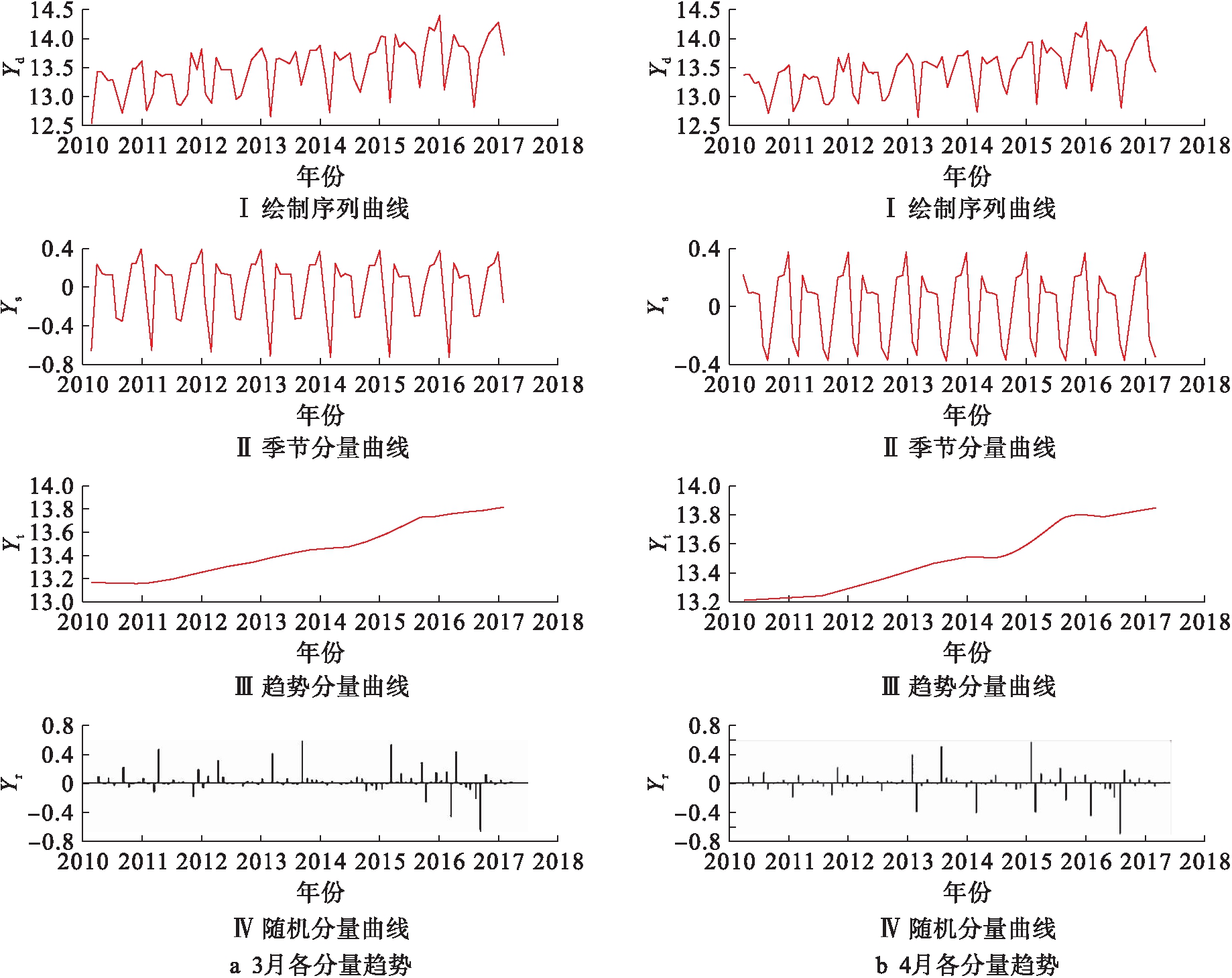
图2 原始负荷数据各分量趋势
Fig.2 Trends of each component of original loading data
3.2 月度负荷趋势分量预测
本节利用Eviews软件包,使用2010年1月至2016年12月的数据进行月用电量趋势分量预测.
3.2.1 数据分解
将各季度GDP平均分成3份,作为近似月度GDP数据,以保证经济因素的样本量与月度用电量一致.之后利用X12模型对月GDP数据进行分解,得到GDP的趋势分量数据.对趋势分量的自然对数进行数据处理并建立VAR模型,以保证数据的稳定性.GDP的趋势分量曲线如图3所示.
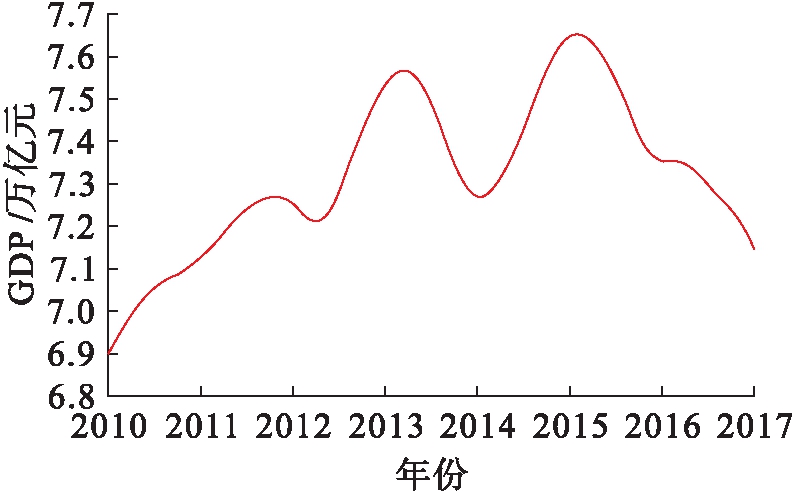
图3 GDP趋势分量曲线
Fig.3 Component curve of GDP trend
3.2.2 VAR模型建立
利用Eviews中的Granger外生变量检验功能,分析GDP与用电量的相关性.通过校验,Prob值为0.013,小于置信度0.05,因此,可以判定GDP对电量的影响显著,进而证明了VAR模型具有实际意义.
考虑货币政策的滞后时间通常为6~12个月,因此,将滞后因子的上限设置为12,分别计算之后因子在0~12时的置信度,当滞后因子选择11时,能够得到最好的结果,因此将时滞因子值设为11.
对VAR模型的参数进行估计,并通过Forecast选项中的静态预测得到月度用电量趋势分量的预测值.
3.3 月度负荷季节分量与随机分量预测
在季节分量预测中,对季节平稳的月份,可直接将历史同期值作为待预测月份的季节分量预测值.对季节拐点处的月份,采用LSSVR进行预测,利用MATLAB中的工具箱toolbox LS-SVM lab完成对数据样本的训练与预测,LSSVR中的乘法系数与核参数通过PSO方法优化,优化结果为[76,0.135 9].将前12个月的数值作为输入,待预测月份作为输出.对随机分量的预测值则通过历史随机分量的平均值获取.
3.4 对比方法与结果分析
将本文所提负荷预测方法与其他3种对比算法的预测结果进行对比,各算法的描述如下:
1)利用ARIMA模型,仅根据用电量的时间序列特征,不考虑其他因素的影响,采用线性回归方法预测月用电量.
2)利用SARIMA模型,通过季节差法消除季节因素对时间序列的影响,即仅考虑影响月度用电量的季节因素,对月度用电量进行预测.
3)根据月度用电量的时间序列特征,用代表趋势、季节和随机因素的3个分量的乘积表示月度用电量序列,同时考虑不同因素的影响,对3个分量进行建模和预测.
4)本文所提方法设定了季节分量变化率,根据不同月份用电量的时间序列特征,利用STL模型对时间序列进行分解.同时考虑不同因素的影响,对月度用电量进行预测.
实际值与各方法预测值的对比结果如图4所示.选取相对误差、平均绝对误差(MAE)、均方根误差(RMSE)与平均绝对百分比误差(MAPE)值评价负荷预测模型的性能.统计4种预测方法的各类误差,结果如表1所示.
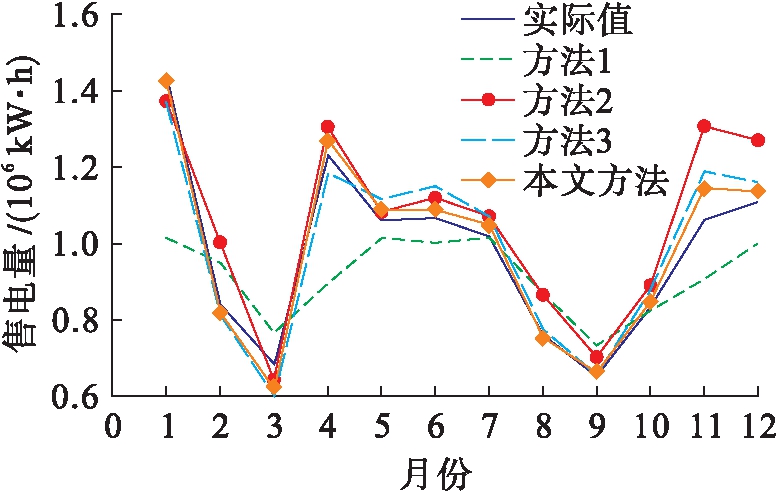
图4 2017年月度用电量预测结果
Fig.4 Forecasting results of monthly electricity consumption in 2017
表1 2017年月度用电量预测结果评估
Tab.1 Assessment of forecasting results for monthly electricity consumption in 2017 %
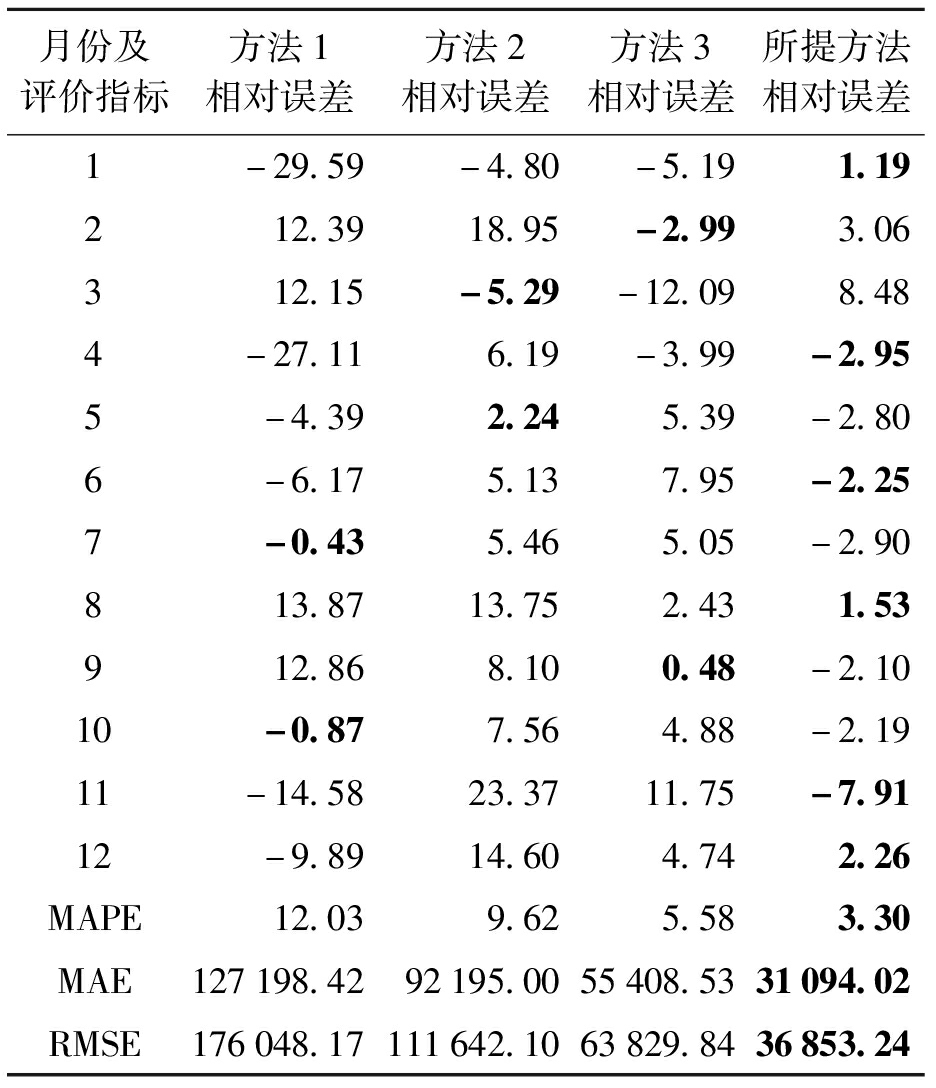
月份及评价指标方法1相对误差方法2相对误差方法3相对误差所提方法相对误差1-29.59-4.80-5.191.19212.3918.95-2.993.06312.15-5.29-12.098.484-27.116.19-3.99-2.955-4.392.245.39-2.806-6.175.137.95-2.257-0.435.465.05-2.90813.8713.752.431.53912.868.100.48-2.1010-0.877.564.88-2.1911-14.5823.3711.75-7.9112-9.8914.604.742.26MAPE12.039.625.583.30MAE127198.4292195.0055408.5331094.02RMSE176048.17111642.1063829.8436853.24
注:各类误差的最小值用粗体表示.
通过预测结果可以看出,对于大部分月份,所提方法均能得到最小的相对误差,且所提方法的MAPE、MAE和RMSE数值均低于其他三种对比方法,说明所提方法的预测值与实际值吻合度最高,即预测准确率高于其他对比算法.此外,对于季节分量非周期分解的1月、3月、7月、8月和11月,所提方法的预测误差均小于方法3,验证了对不同月份的季节分量的修正是有效的.另一方面,虽然所提方法的预测结果总体上优于其他三种对比方法,但对3月和11月的预测误差仍然较大,这是由于在季节拐点处数据存在突变,而ARIMA模型在处理突变数据时容易产生误差.
本文所提出的区域综合能源系统月度负荷预测模型将负荷的时间序列数据分解为季节分量、趋势分量以及随机分量.其中趋势分量由区域经济因素决定,而季节分量中的季节拐点月份由地区的气候因素决定,对于不同的用电单位可根据自身用电特性,通过历史运行数据预测非拐点月份的用电量,通过合适的非线性预测模型预测拐点月份的用电量,通过相似的重构方法可获得最终的月度用电量的预测值,因此,本文所提方法可扩展到其他用电单位的使用中.
4 结 论
现有月度负荷预测方法往往直接对历史数据进行建模与预测,忽略了在不同月份中季节因素和经济因素对预测结果的影响.本文分析了与月度负荷相关的特征分量,并在此基础上提出一种新的预测方法,将STL与X12模型相结合作为预测模型的框架.对北方某高校的用电量预测实例分析实验结果表明,与其他三种对比方法相比,所提方法具有更高的预测精度,验证了所提方法在综合能源系统需求预测方面的应用潜力.
[1] 高滢,王芃,薛友,等.计及需求侧管理的电-气集成能源系统协同规划[J].电力系统自动化,2018,42(13):3-11.
(GAO Ying,WANG Feng,XUE You,et al.Collabora-tive planning of integrated electricity-gas energy systems considering demand side management[J].Automation of Electric Power Systems,2018,42(13):3-11.)
[2] 张明理,宋卓然,梁毅,等.基于饱和负荷密度的城市远景空间负荷预测[J].沈阳工业大学学报,2018,40(1):12-18.
(ZHANG Ming-li,SONG Zuo-ran,LIANG Yi,et al.Forecasting for urban prospective spatial load based on saturated load density[J].Journal of Shenyang University of Technology,2018,40(1):12-18.)
[3] Vu D H,Muttaqi K M,Agalgaonkar A P.A variance inflation factor and backward elimination based robust regression model for forecasting monthly electricity demand using climatic variables[J].Applied Energy,2015,140(15):385-394.
[4] Melo J D,Carreno E M,Aida C,et al.Determining spatial resolution in spatial load forecasting using a grid-based model[J].Electric Power Systems Research,2014,111(2):177-184.
[5] 张强,王毅,李鼎睿,等.基于X-12-ARIMA季节分解与年度电量校正的月度电量预测[J].电力建设,2017,38(1):76-83.
(ZHANG Qiang,WANG Yi,LI Ding-rui,et al.Monthly electricity forecast based on X-12-ARIMA seasonal decomposition and annual electricity correction[J].Electric Power Construction,2017,38(1):76-83.)
[6] 龙勇,苏振宇,盖晓平.成分分解方法预测月度电力负荷[J].电力系统及其自动化学报,2017,29(5):35-40.
(LONG Yong,SU Zhen-yu,GAI Xiao-ping.Monthly load forecasting using component decomposition method[J].Proceedings of the CSU-EPSA,2017,29(5):35-40.)
[7] Abdoulaye C,Wang F,Liu X.Energy consumption forecasting using seasonal ARIMA with artificial neural networks models[J].International Journal of Busi-ness and Management,2016,11(5):231-246.
[8] 颜伟,程超,薛斌,等.结合X12乘法模型和ARIMA模型的月售电量预测方法[J].电力系统及其自动化学报,2016,28(5):74-80.
(YAN Wei,CHENG Chao,XUE Bin,et al.Forecasting for monthly electricity consumption using X12 multiplication method and ARIMA model[J].Proceedings of the CSU-EPSA,2016,28(5):74-80.)
[9] Lu Q Y,Cai Q N,Liu S J.Short-term load forecasting based on load decomposition and numerical weather forecast[C]//Proceedings of the IEEE Conference on Energy Internet and Energy System Integration.Beijing,China,2017:1-5.
[10] Hyndman R J,Fan S.Density forecasting for long-term peak electricity demand[J].IEEE Transactions on Power Systems,2010,25(2):1142-1153.
[11] 张妍,韩璞,王东风,等.基于变分模态分解和LSSVM的风电场短期风速预测[J].太阳能学报,2018,39(1):194-202.
(ZHANG Yan,HAN Pu,WANG Dong-feng,et al.Short-term prediction of wind speed for wind farm based on vibrational mode decomposition and LSSVM model[J].Acta Energiae Solaris Sinica,2018,39(1):194-202.)
[12] Lin W M,Tu C S,Yang R F,et al.Particle swarm optimization aided least-square support vector machine for load forecast with spikes[J].Generation Transmission and Distribution Iet,2016,10(5):1145-1153.
[13] 李红丽,马耀锋.基于多特征融合和混合核SVM的目标识别方法[J].沈阳工业大学学报,2018,40(4):441-446.
(LI Hong-li,MA Yao-feng.Target recognition method based on multi feature fusion and hybrid kernel SVM[J].Journal of Shenyang University of Technology,2018,40(4):441-446.)