无线传感器网络是集成了嵌入式计算、无线通信、微电子和传感器等技术的综合平台，能够实现信息采集、数据分布式处理和传输、信息融合、区域检测等多种功能，可对网络分布区内的监测对象和环境变化信息实时感知[1-3].无线传感器网络(wireless sensor network，WSN)是由面向任务的大量分布式传感器构成的无线传感网络，以其低成本、低功耗突出优点获得广泛应用[4-6].无线传感器网络主要包括路由协议、节点定位、拓扑控制等基本部分[7-8].实现目标监测和实时跟踪的节点定位技术是传感器网络的核心技术，具有关键和基础性的作用.在生物医疗、工农业、军事等领域有广泛的应用.位置信息获取的一般办法是采用GPS定位，但其成本高、功耗大，且卫星信号在有建筑物遮挡地方不一定被传感器网络收到，在节点定位中存在困难.非测距定位质心算法只需将定位设备安装在少数节点上，通过这些相互连通的节点实现定位，具有环境抗干扰，硬件成本和能耗要求低的优点.但多边定位方程的常态方程中传统质心算法使用权值相等的各组数据坐标估计，无区别处理定位误差大小不同情况，影响定位准确性.对此，本文提出了改进加权质心算法的节点定位方法，权值使用常态方程代入解得坐标后的误差值倒数，改进传统质心算法，准确性不同的数据通过不同权值对应不同的影响力，提高定位精度.通过在实际环境中利用传统质心定位算法和提出的加权质心定位算法对未知节点进行定位的实验表明，提出的加权质心定位算法的定位精度有显著提高.
1 质心算法
基于非测距的质心定位算法对已知参考节点坐标值进行中和计算，运算简单，易于实现，其定位过程取决于节点的分布和密度.质心定位利用节点在组网区域中的互通性[9]，基本原理为：参考节点向周围定期广播包含自身位置和ID信息的信号，当未知节点在网络中收到数量达到某预设门限K的信号个数时，待定位未知节点的估计坐标就用这K个参考点组成的多边形质心表示.算法示意图如图1所示.
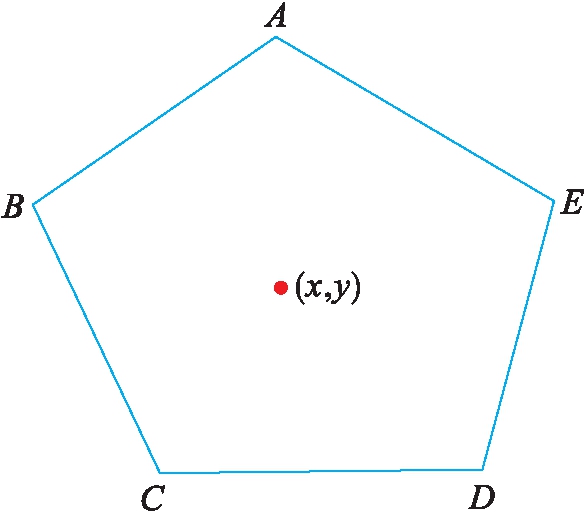
图1 质心算法示意图
Fig.1 Schematic diagram of centroid algorithm
五边形ABCDE的五个顶点坐标分别表示为(x1，y1)、(x2，y2)、(x3，y3)、(x4，y4)、(x5，y5)，若这五个参考节点均在定位节点的通信范围内，这时五边形的几何质心就是所求节点的估算位置(x，y)，其表达式为
(1)
传统质心算法的优点是运算简单，不需要进行节点之间协调，便于实现.在基于测距的传统质心定位算法中，由于随机误差等原因，单靠某一组数据的定位结果可能有较大误差.所以一般是在基于n组数据的传统质心算法中，最后结果取n个估计位置的平均值，考虑到计算复杂度和通信开销的状况，n一般宜取3.传统的质心算法计算过程为
(2)
式中：
为利用多边定位算法估计的第i组数据坐标值；(x0，y0)为采用传统质心算法对三个估算坐标确定的坐标值.可见传统质心算法在坐标定位估计中对各组数据估计坐标进行权值相等的处理，对误差不同的各组数据没有差别处理，影响了定位精度的提高.
2 改进加权质心算法
传统质心算法在坐标定位估计中默认了各组数据估计坐标的权值相等，对误差不同的各组数据没有差别处理.多边定位算法在理想情况下，b为准确值，解方程得到使AX=b两边相等的正确无误的估计坐标值X.但b在实际情况下是包含误差的，且最小二乘法解方程时b的误差越大，得到的估计坐标值X误差越大，降低了定位精度.基于此，本文提出了改进的加权质心算法，引入权值的概念差别处理具有不同误差的数据，提高定位精度.改进的加权质心算法在解得坐标后代入方程得到相应误差值，权值使用该误差值的倒数，即
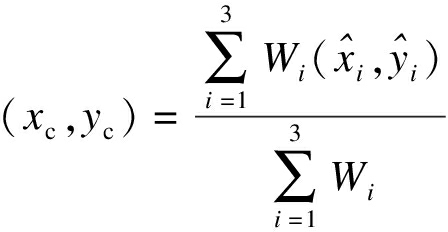
(3)
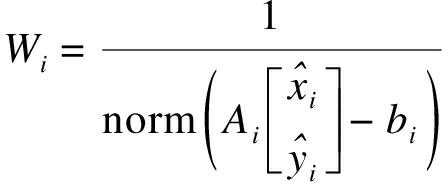
(4)
式中：(xc，yc)为利用改进加权质心算法对三个估算坐标确定的坐标值；Wi为估计坐标值的第i组数据的权值；Ai，bi为对应于第i组数据确定的线性方程参数；norm(X)用来衡量解得坐标的误差，即X的二范数，其表达式为
(5)
在改进的加权质心算法中，利用权值差别处理具有不同定位误差的不同定位结果，较小误差的倒数对应较大的权值，较大误差的倒数对应较小的权值，优化了传统质心算法，提高了定位准确性.
3 实验结果及分析
实验中，随机布置1个定位节点和7个参考节点，其位置坐标如表1所示.利用多边定位的极大似然估计法[10]随机选取三组数据的坐标值，采用传统质心算法和加权质心算法二次处理求出三个坐标更精确的解.
表1 节点位置
Tab.1 Node locations m
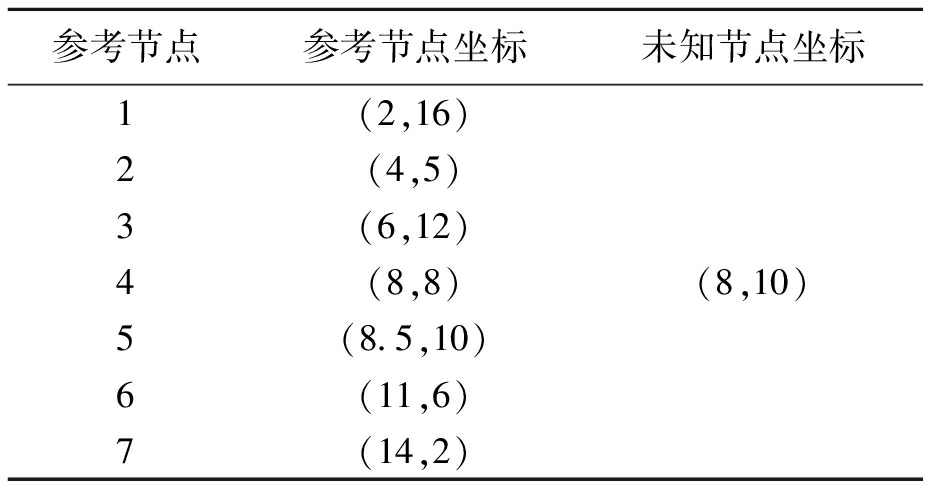
参考节点参考节点坐标未知节点坐标1(2,16)2(4,5)3(6,12)4(8,8)(8,10)5(8.5,10)6(11,6)7(14,2)
方程AX=b在每组数据点数为3时不能使用加权质心算法，只能采用传统质心二次求解.方程AX=b在每组选取4、5、6个点时，利用传统质心算法和加权质心算法分别计算三个坐标.由均方根误差(RMSE)来评价定位算法的准确性和精度.
表2为定位过程中的选点分布情况.表3为多边定位的极大似然法估算分组数据坐标值.利用传统质心算法和改进加权质心算法优化估计的未知节点坐标对数据进行处理，两种算法的定位结果如表4所示.
表2 选点分布
Tab.2 Distribution of selected points
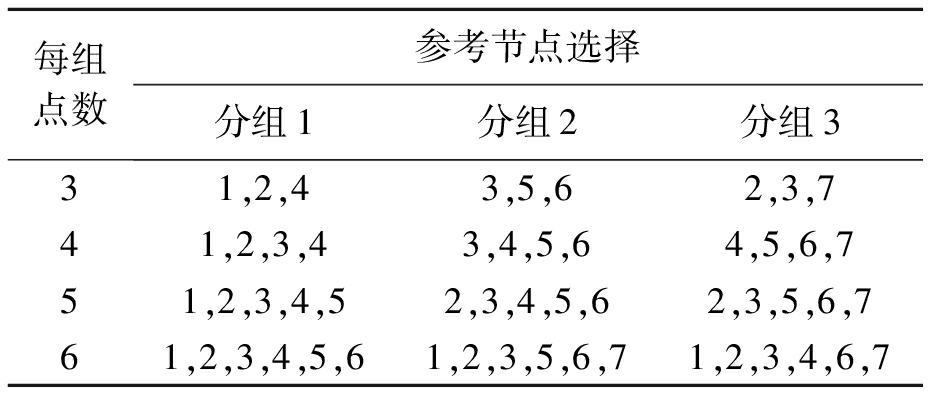
每组点数参考节点选择分组1分组2分组331,2,43,5,62,3,741,2,3,43,4,5,64,5,6,751,2,3,4,52,3,4,5,62,3,5,6,761,2,3,4,5,61,2,3,5,6,71,2,3,4,6,7
表3 各组数据的估计坐标值
Tab.3 Estimated coordinate values of each group data m
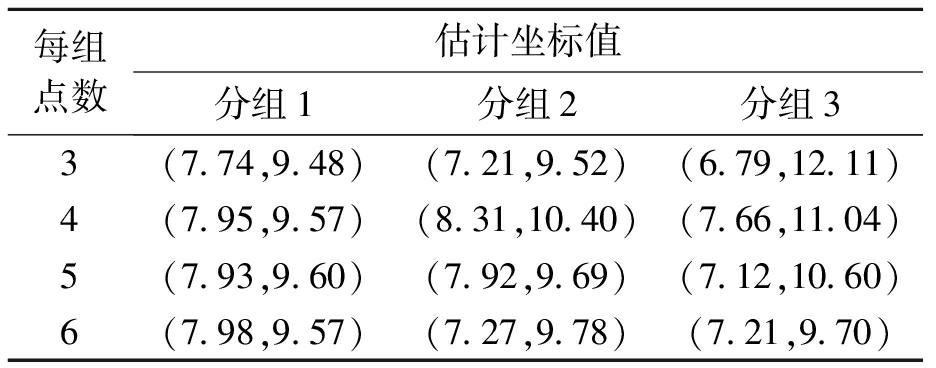
每组点数估计坐标值分组1分组2分组33(7.74,9.48)(7.21,9.52)(6.79,12.11)4(7.95,9.57)(8.31,10.40)(7.66,11.04)5(7.93,9.60)(7.92,9.69)(7.12,10.60)6(7.98,9.57)(7.27,9.78)(7.21,9.70)
表4 定位结果
Tab.4 Localization results m
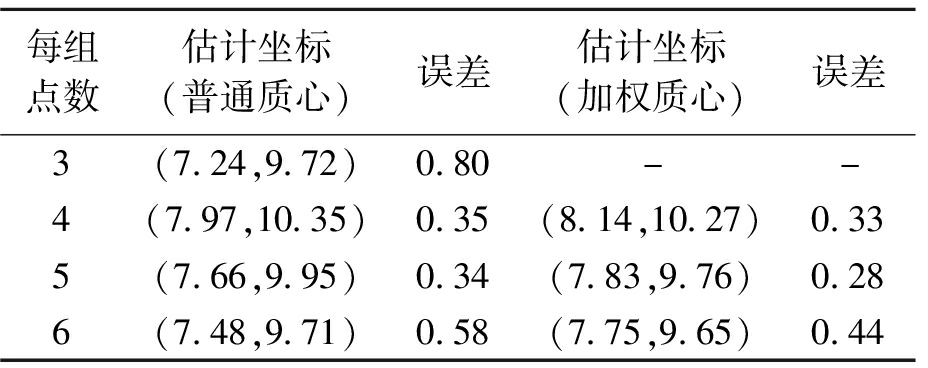
每组点数估计坐标(普通质心)误差估计坐标(加权质心)误差3(7.24,9.72)0.80--4(7.97,10.35)0.35(8.14,10.27)0.335(7.66,9.95)0.34(7.83,9.76)0.286(7.48,9.71)0.58(7.75,9.65)0.44
由表4定位结果可以看出，改进加权质心算法定位误差小于传统质心算法的定位误差，定位精度有显著提高.
图2为误差与参考点个数的关系图.从图2中可以看出，误差随参考节点数的增加先减小后增大.当参考节点数由3逐渐增大到5的过程中，定位误差逐渐变小，但当参考节点数由5逐渐变大到6或7时，定位误差又逐渐增大，选择5个参考节点时的定位误差最小，综合考虑节点成本和计算开销等因素，参考节点个数最优为5个.
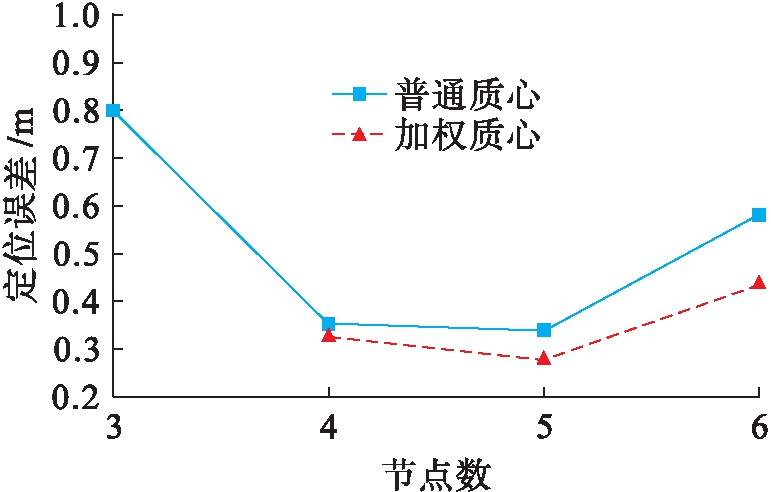
图2 参考点个数与误差关系
Fig.2 Relationship between number of reference points and errors
在通信范围内，从表1中的7个参考节点坐标中任意选取5组，每组有5个不同参考节点，首先分别利用多边定位算法得出未知节点坐标，再利用传统的质心算法和改进加权的质心算法优化未知节点坐标.图3为两种算法定位误差对比图.由图3可以看出，加权质心算法相较传统的质心算法显著改善了定位误差，提高了定位精度，定位准确性改善尤为明显.
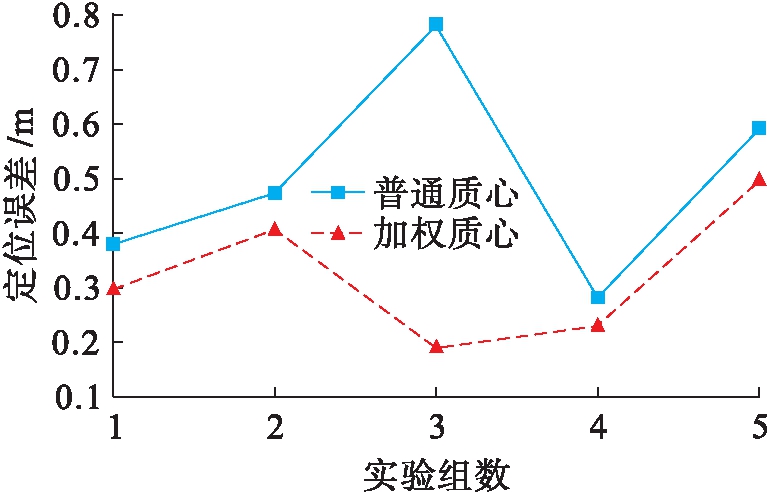
图3 传统质心和改进加权质心算法误差对比
Fig.3 Comparison of errors between traditional and improved weighted-centroid-algorithms
在上述五组随机选取的通信范围内待测节点中，对应于2、3组的定位数据，节点所在位置的横纵坐标值分别用坐标轴中的x、y表示，其真实坐标值分别为(9，5)和(6，6)，得到的定位坐标结果如图4所示.
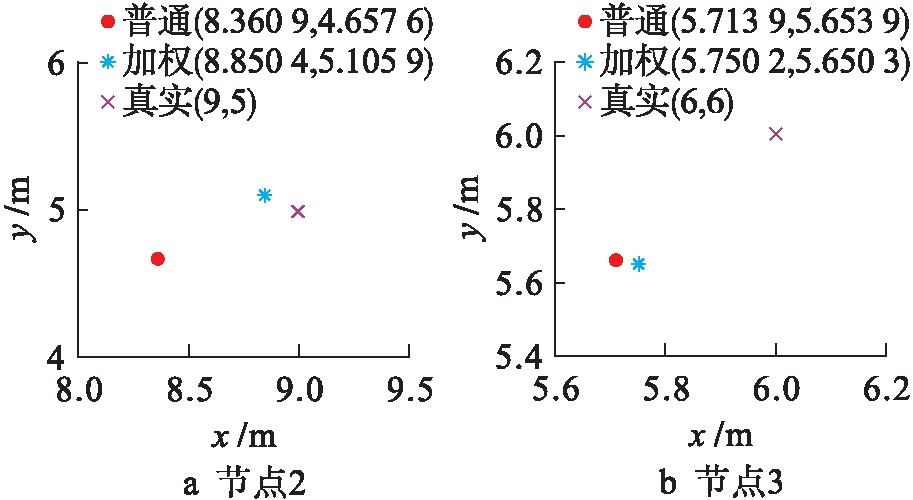
图4 坐标定位结果
Fig.4 Results of coordinate localization
通过定位结果可以看出，改进加权质心算法的定位精度高于传统质心算法，更接近于真实值，改进加权质心算法差别处理具有不同误差的数据，可以提高定位精度，从而优化定位结果.图5为采用普通质心算法和加权质心算法分别测试6组数据，每组5个节点的时间对比.从图5中可以看出，加权质心算法用时更少，效率更高.
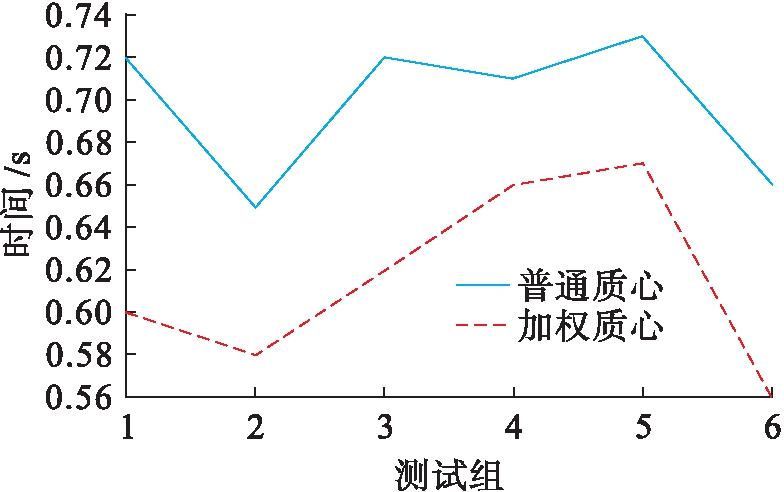
图5 效率对比
Fig.5 Efficiency comparison
4 结 论
由于无线传感网络中传统质心定位算法代入各组数据后定位精度较低，提出了改进加权质心算法的节点定位方法.权值使用常态方程代入解得坐标后误差值的倒数，准确性不同的数据通过不同权值对应不同的影响力，提高了定位精度.分别用传统质心算法和改进加权质心算法进行MATLAB仿真，最终估测出定位节点的位置坐标.结果表明，改进加权质心算法使用坐标解代入方程后误差值的倒数为权值，相较传统质心算法定位误差小，定位精度高.
[1] Yick J，Mukherjee B，Ghosal D.Wireless sensor network survey[J].Computer Networks，2008，52(12)：2292-2330.
[2] Wang H.Wireless sensor networks for an extended city intelligent transportation system[J].International Journal of Advancements in Computing Technology，2011，3(5)：300-307.
[3] Eisenbarth T，Meyerowitz A，Steinwandt R.On the security margin of MAC striping[J].Information Processing Letters，2015，115(11)：899-902.
[4] Elhoseny M，Yuan X，El-Minir H K，et al.An energy efficient encryption method for secure dynamic WSN[J].Security & Communication Networks，2016，9(13)：2024-2031.
[5] Lu R，Lin X，Zhu H，et al.BECAN：abandwidth-efficient cooperative authentication scheme for filtering injected false data in wireless sensor networks[J].IEEE Transactions on Parallel & Distributed Systems，2012，23(1)：32-43.
[6] 任鹏飞，谷灵康.基于粒子群进化的输电网络WSN节点定位算法[J].沈阳工业大学学报，2018，40(5)：541-546.
(REN Peng-fei，GU Ling-kang.WSN node localization algorithm for power transmission networks based on particle swarm optimization[J].Journal of Shen-yang University of Technology，2018，40(5)：541-546.)
[7] Li Y X，Shi H S，Zhang S P.An energy-efficient MAC protocol for wireless sensor network[J].Lecture Notes in Electrical Engineering，2012，143(9)：163-170.
[8] Huang C F.The coverage problem in a wireless sensor network[J].Mobile Networks & Applications，2005，10(4)：519-528.
[9] 安恂，蒋挺，周正.一种用于无线传感器网络的质心算法[J].计算机工程与应用，2007，43(20)：136-138.
(AN Xun，JIANG Ting，ZHOU Zheng.Centroid loca-lization algorithm for wireless sensor networks[J].Computer Engineering and Applications，2007，43(20)：136-138.)
[10] 陈虹，黄忠贤.应用混合极值理论及最大似然法估计中国大陆地震危险性[J].地震学报，1995，17(2)：264-269.
(CHEN Hong，HUANG Zhong-xian.Estimating the earthquake risk in mainland China based on the mixed extremum theory and maximum likelihood method[J].Acta Seismologica Sinica，1995，17(2)：264-269.)