随着桥梁结构建设的不断发展，大跨度桥梁不断出现在人们的视野中，而悬索桥是特大跨径桥梁的主要形式之一.该类桥梁是一种柔性风敏结构，其经济性能良好，适应性较强，但由于其结构本身的特性，该类桥梁的抗风计算不可忽略[1].抗风研究主要有风洞试验和数值模拟两类方法.风洞试验技术要求高，经费高昂[2]；数值模拟方法[3]方便快捷，操作简单，可进行多次模拟比较，得到广泛应用.目前，风速时程数值模拟方法主要有谐波叠加法、线性滤波法[4]以及小波分析法等[5].每种方法都有不同的特点，其中，线性滤波法具有计算量小和速度快的特点，同时能够考虑时间相关性，处理非线性的问题[6-7].根据结构特性，本文采用线性滤波法中的自回归(AR)模型，结合AIC准则确定了该模型的阶数，编制了脉动风速时程模拟程序.
1 风基本特征
在风时程曲线中，一般包括平均风和脉动风两个部分.结构坐标为(x，y，z)处，其风速v(x，y，z，t)为平均风速
和脉动风速vf(x，y，z，t)之和[2]，即
(1)
1.1 平均风
平均风是在一定的观测时间段内，风压值大小和方向等不随时间而改变的量.Davenport等人对现场实测结果进行分析，认为平均风速沿高度变化的规律可用指数函数来表示[8]，即
(2)
式中：
和z为任意高度处的风速和高度；
和z10为标准高度处风速和高度，本文取10 m；α为地面粗糙度.
1.2 脉动风
风的不规则性运动是脉动风形成的原因，所以脉动风的强度变化是随机的.这种强度的变化通常用功率谱密度函数来表达.Kaimal提出了沿高度变化的水平脉动风功率谱[9]，即
(3)
式中：x=nz/vz，vz为高度z处的平均风速；n为脉动风频率；u*为剪切速度.
空间不同点在同一时刻，同时还具有空间相关性，对大跨度桥梁结构而言，应采用三维空间互相关密度函数rij(f)表示，即
(4)
式中，衰减系数cx、cy、cz分别取为16、8和10[10].
2 基于AR模型的脉动风速时程模拟
脉动风可作为零均值的平稳高斯随机过程来考虑.脉动风速时程向量vf(x，y，z，t)可以表示为
(5)
式中：Ψk为AR模型的自回归系数矩阵；p为AR模型阶数；N(t)为给定方差的随机过程向量；Δt为模拟风速的时间步长.
AR模型模拟风速时程采用一种处理时间序列的方法，即用同一风速之前各个时刻的数值，来预测本时刻的表现，并假设它们为线性.其中，自回归系数矩阵Ψk的求解是一项重要内容.
2.1 求解自回归系数Ψk
脉动风过程的协方差矩阵R与回归系数矩阵Ψ之间的关系[11]为
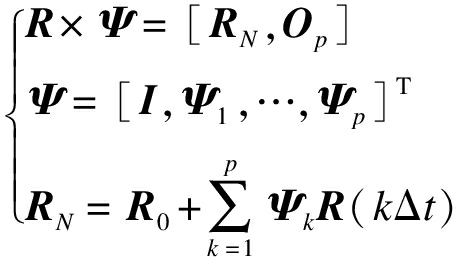
(6)
式中：I为M阶单位矩阵；Op为零矩阵.R作为自相关矩阵，其表达式为
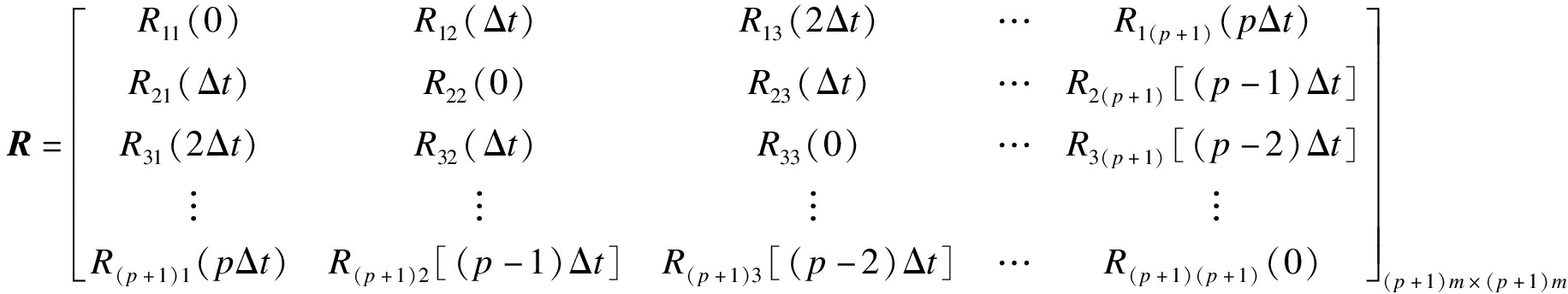
(7)
自相关矩阵R可由功率谱密度函数和相干函数之间满足的维纳-辛钦公式求出，即
Rij(t)=
Sij(f)cos(2πft)df (i，j=1，2，…，m)
(8)
式中，
当i=j时，称为自谱密度函数；当i≠j时，称为互谱密度函数.将式(3)、(4)代入式(8)中求出自相关矩阵R.求解方程组(6)，可得自回归系数Ψk和矩阵RN.
2.2 求随机过程N(t)和M个随机过程
对得到的矩阵RN进行Cholesky分解，可得
(9)
式中，n(t)=[n1(t)，n2(t)，…，nM(t)]T，ni(t)为均值为0、方差为1彼此相互独立的随机过程.进而得到独立的随机过程向量N(t)，最终的M个随机过程可以表示为
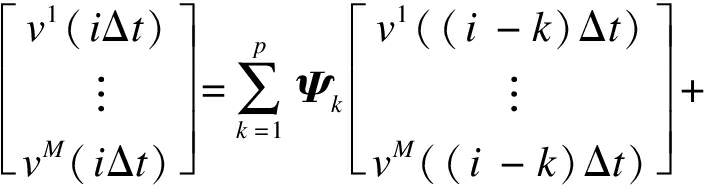
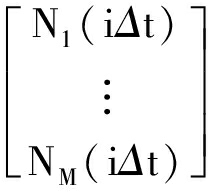
(10)
式中，当t≤0时，v(t)=0.
3 AR模型阶数p的确定
根据AIC准则，又称为最小信息准则[12]，脉动模拟风速时程模拟优先考虑AIC值最小的那一阶，因此，从p=1时开始试算，经过迭代法试算，随着p的增大，AIC值会逐渐减小，当其值趋于稳定时，p值即为所求模型的阶数.AIC准则函数为
AIC(p)=Qln(σ2)+2p
(11)
式中：Q=T，T为周期；σ2=2R(0)-R(Q).
4 工程实例模拟
沈阳东塔自锚式悬索桥的主桥部分长400 m，主桥为三跨自锚式悬索桥，主塔从桥面算起高50 m.基于MATLAB平台，依据前文所述过程和方法，编制模拟程序，对该桥的主梁、主缆及桥塔上的多点脉动风速时程进行数值模拟.
该工程地处沈阳市王家湾桥下游2 km处，地形平坦，地貌单元属河流冲积阶地，周围有庄稼地，未有高楼林立，MATLAB平台模拟需要的主要参数，均参考该工程实际得到，如表1所示.
表1 主要参数
Tab.1 Main parameters
10m高度多年平均最大风速(m·s-1)地面粗糙度α截断频率Hz模拟时间步长s模拟时间s模拟点数29.70.1120.160078
为了与模拟多点的特性相符，本文目标谱采用Kaimal谱.根据结构分析需要，共模拟了78个点的脉动风速时程，点的位置如图1所示.图1中主桥部分共模拟了78个点，包括主梁、主缆各37个点，两主塔塔底和塔顶4个点，本文列出了其中几个点的脉动风速时程.根据AIC准则，确定模型阶数，针对阶数1～8进行计算，绘制出AIC值的变化曲线，如图2所示.从图2中可以看出，当p=4时，AIC值趋于稳定，所以本文AR模型阶数取p=4.
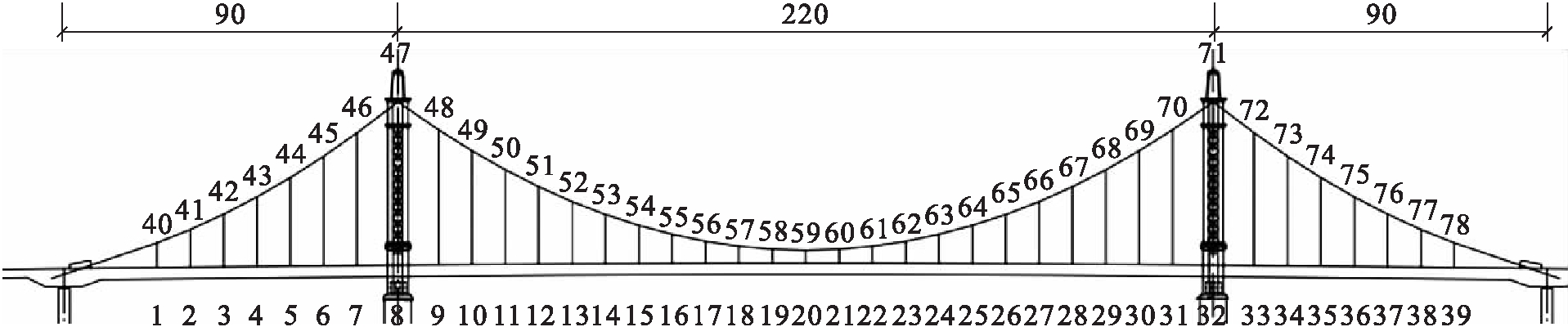
图1 悬索桥主桥风速模拟节点图
Fig.1 Wind speed simulation nodes on main structure of suspension bridge
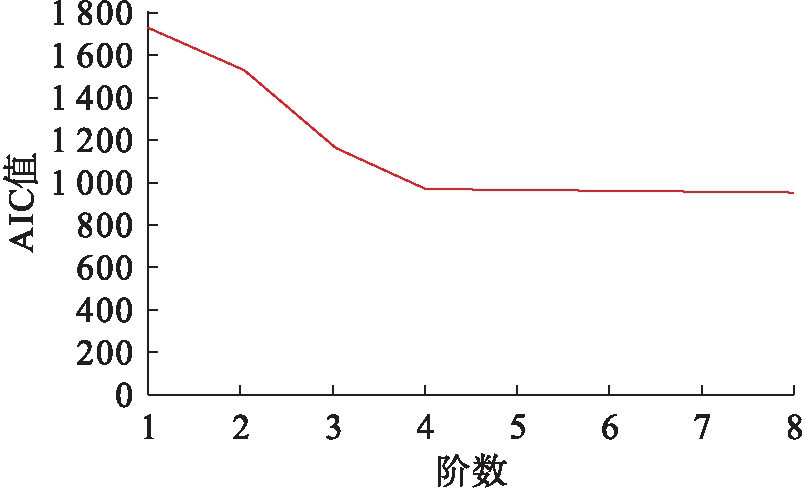
图2 AIC值变化曲线
Fig.2 Change curve of AIC value
4.1 关键点风速时程曲线
图3～5分别为桥梁的主梁、主塔及主缆的脉动风速时程曲线.
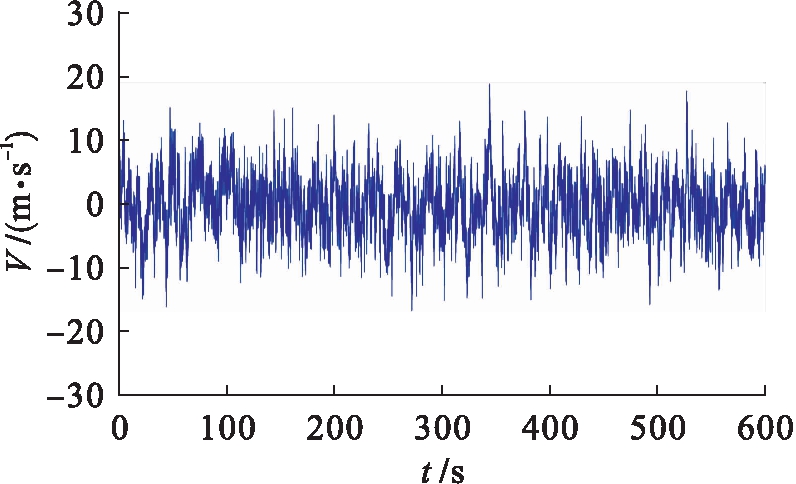
图3 20点(主梁中)脉动风速时程曲线
Fig.3 Time-history curve of fluctuating wind speed for point 20(main beam)
4.2 功率谱密度函数对比
图6～8分别为主梁中点、主缆中点及主塔顶点功率谱密度函数的模拟谱与目标谱的比较.从图中可以看出，拟合较好.
4.3 互相关函数对比
图9为主梁上18点与20点的互相关函数曲线.从图9中可以看出，互相关系数的最大值约为0.51，对模拟值和目标值进行了对比，曲线拟合较好，模拟的空间相关性合理.图10为主梁18点和27点的互相关函数目标值和模拟值对比曲线，可以看出相关性同样合理，最大值约为0.40，由此可知，距离越近的两个点空间相关性越强.
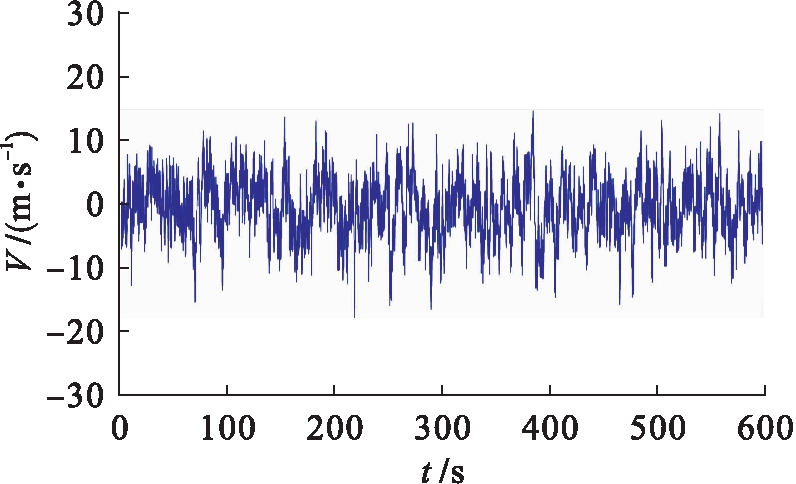
图4 59点(主缆中)脉动风速时程曲线
Fig.4 Time-history curve of fluctuating wind speed for point 59(main cable)
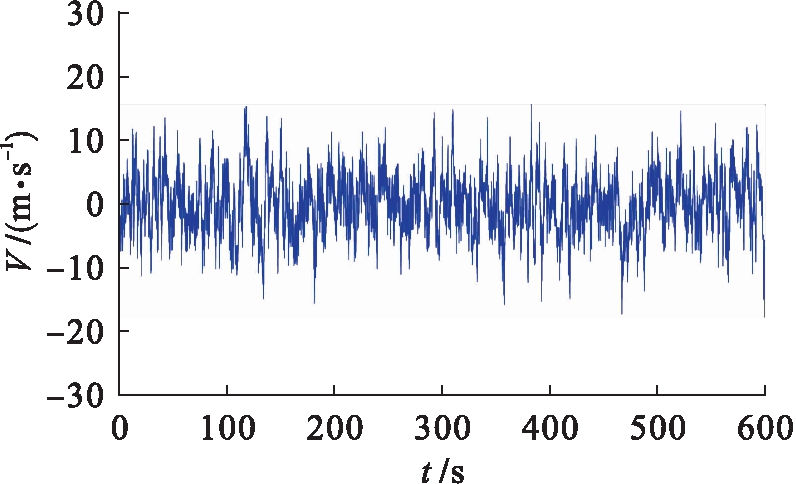
图5 71点(主塔顶)脉动风速时程曲线
Fig.5 Time-history curve of fluctuating wind speed for point 71(main tower top)
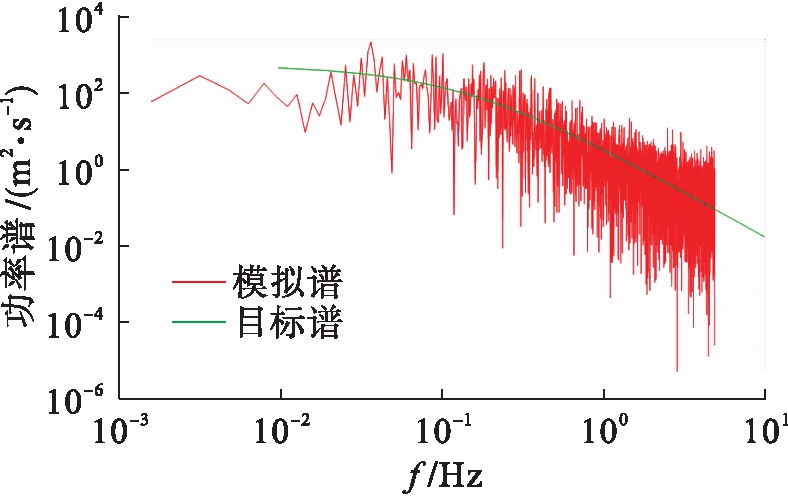
图6 20点(主梁中)功率谱
Fig.6 Power spectra for point 20(main beam)
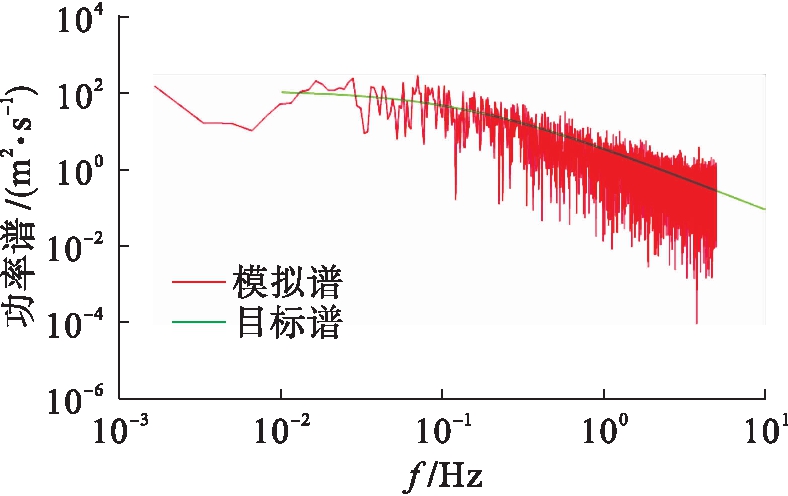
图7 59点(主缆中)功率谱
Fig.7 Power spectra for point 59(main cable)
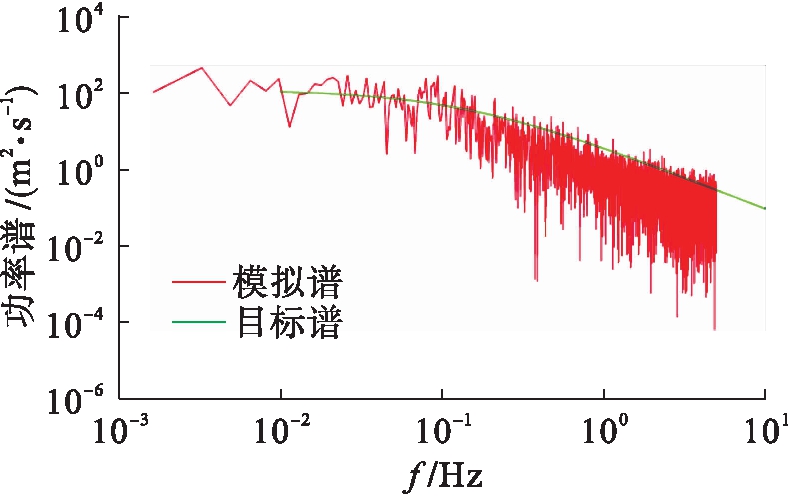
图8 71点(主塔顶)功率谱
Fig.8 Power spectra for point 71(main tower top)
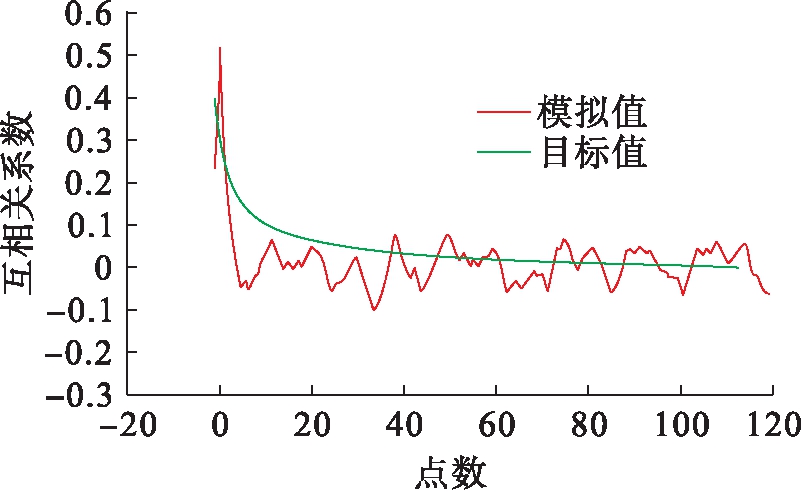
图9 主梁18和20点互相关函数
Fig.9 Cross-correlation function for points 18 and 20 on main beam
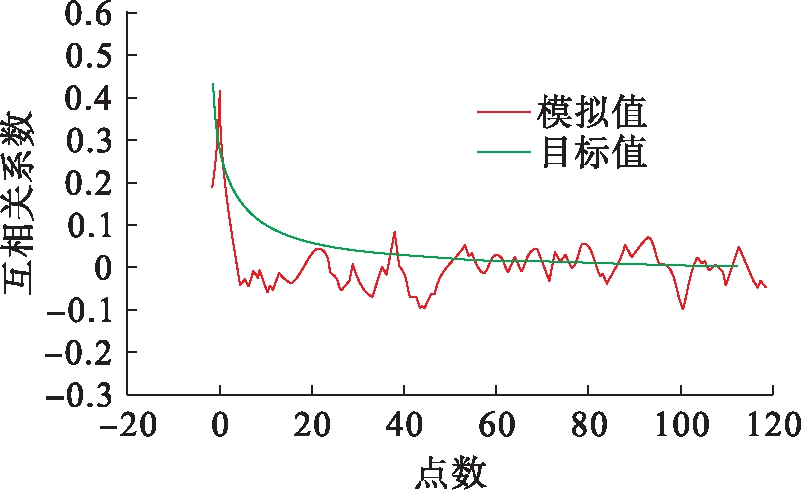
图10 主梁18和27点互相关函数
Fig.10 Cross-correlation function for points 18 and 27 on main beam
5 结 论
本文基于线性滤波法，编制了具有时间和空间相关性的脉动风速时程程序，根据工程实际确定了特定参数的取值，算例表明：
1)该程序采用AR模型计算速度快，使用方便，功率谱密度函数模拟谱与目标谱拟合较好，模拟精确；
2)模拟的脉动风互相关系数同目标互相关系数拟合较好，距离近的两点相关系数越大，空间相关性越强，距离越远的两点相关系数越小，空间相关性越弱；
3)用AIC准则确定了模型阶数，使得模拟更加准确、高效；
4)该方法可以推广到此类吊索结构和大跨度结构风速时程模拟，为工程结构抗风分析提供荷载输入.
[1] 韩兴，黄博，祝兵.基于谱分解法的自锚式悬索桥桥梁风致抖振计算分析[J].铁道标准设计，2017，61(9)：82-86.
(HAN Xing，HUANG Bo，ZHU Bing.Buffeting ana-lysis self-anchored suspension bridge wind resistance based on spectral representation method[J].Raiway Standard Design，2017，61(9)：82-86.)
[2] 杨波.随机脉动风场的数值模拟[D].兰州：兰州大学，2016.
(YANG Bo.Numerical simulation of stochastic fluctuating wind field[D].Lanzhou：Lanzhou University，2016.)
[3] Li J H，Li C X.Simulation of non-gaussian stochastic process with target power spectral density and lower-order moments[J].Journal of Engineering Mechanics ASCE，2012，138(5)：391-404.
[4] 方治华，李晨.斜拉索上瞬时风速与风荷载的数值模拟[J].振动与冲击，2010，29(7)：210-212.
(FANG Zhi-hua，LI Chen.Numerical simulation for instantaneous wind and load on a stayed cable[J].Journal of Vibration and Shock，2010，29(7)：210-212.)
[5] 白泉，朱浮声，边晶梅.基于正交小波逆变换的空间相关性风场数值模拟[J].四川建筑科学研究，2008，34(6)：30-33.
(BAI Quan，ZHU Fu-sheng，BIAN Jing-mei.Simulation of wind field with spatial correlation based on orthogonal basis inverse wavelet transform[J].Sichuan Building Science，2008，34(6)：30-33.)
[6] 刘文洋，张文福.三维空间相关风场的计算机模拟及Matlab程序实现[J].空间结构，2008，14(2)：14-17.
(LIU Wen-yang，ZHANG Wen-fu.Computer modeling on wind histories with spatial correlativity and the program in Matlab[J].Spatial Structures，2008，14(2)：14-17.)
[7] 张文福，马昌恒，肖岩.风场模拟中AR模型的若干问题[J].计算力学学报，2009，26(1)：124-130.
(ZHANG Wen-fu，MA Chang-heng，XIAO Yan.Some issues on AR models for wind field simulation[J].Chinese Journal of Computational Mechanics，2009，26(1)：124-130.)
[8] 刘欣鹏，李正良，焦红伟，等.基于改进的线性滤波法自回归模型法的大跨空间结构风荷载模拟[J].防震减灾工程学报，2015，35(6)：712-717.
(LIU Xin-peng，LI Zheng-liang，JIAO Hong-wei，et al.Numerical simulation of wind loads acting on long-span spatial structures based on modified linear filter auto-regressive model method[J].Journal of Disaster Prevention and Mitigation Engineering，2015，35(6)：712-717.)
[9] Kaimal J C.Spectral characteristics of surface-layer turbulence[J].Royal Meteorol，1972，98：563-589.
[10] 马骏，周岱，李磊，等.风时程模拟的高效高精度混合法[J].工程力学，2009，26(2)：53-59.
(MA Jun，ZHOU Dai，LI Lei，et al.The composite approach for wind time series simulation[J].Engineering Mechanics，2009，26(2)：53-59.)
[11] 李春祥，谈雅雅，李锦华.基于ARMA模型模拟高架桥的脉动风速时程[J].振动与冲击，2009，28(6)：46-51.
(LI Chun-xiang，TAN Ya-ya，LI Jin-hua.Simulation of fluctuating wind speed time series applied on overpass with bridges with resorting to ARMA model[J].Journal of Vibrtion and Shock，2009，28(6)：46-51.)
[12] 姜浩，童申家，李纲，等.基于AIC准则的脉动风速时程模拟[J].交通科技与经济，2008(3)：10-11.
(JIANG Hao，TONG Shen-jia，LI Gang，et al.The simulation of wind speed time series by the AIC rule[J].Technology & Economy in Areas of Communications，2008(3)：10-11.)