随着现代桥梁向大跨径的方向发展,过去传统的混凝土箱梁桥由于在运营一段时间后,普遍出现腹板开裂和跨中挠度过大的问题已难以满足使用要求[1].近几年来,具有截面抗扭刚度大、整体性好、自重轻、跨越能力大等特点的鱼腹式钢箱梁越来越多地进入了人们的视野,特别在城市桥梁中取得普遍应用.相比于混凝土梁桥,钢箱梁的翼缘板和腹板都很薄,这样可以有效地降低桥梁的自重,而且抗弯刚度很小,但在箱梁尺寸较大的情况下,其剪力滞效应会更加明显.混凝土箱梁剪力滞效应的研究已获得一些成果[2-8],但目前各国学者关于钢箱梁剪力滞效应方面的研究相对较少,特别对于鱼腹式钢箱梁的研究更少.
直腹板箱梁剪力滞系数在横向分布所得的结果与传统计算方法所得的结果较为接近,但是鱼腹式箱梁由于截面形状和空间受力与直腹板箱梁呈现不同的剪力滞分布[9].本文通过使用有限元模拟分析软件Midas/civil对鱼腹式钢箱梁进行了剪力滞效应研究,并对其剪力滞系数的横向分布规律做出具体分析.
1 剪力滞效应
1.1 剪力滞定义
箱梁的剪力滞效应是指箱梁在对称荷载作用下,由于顶、底板剪切变形而造成截面正应力沿板横向分布不均匀的现象.当翼缘板和腹板交接处的正应力大于远离腹板的正应力时,则为正剪力滞;若当翼缘板和腹板交接处的正应力小于远离腹板的正应力时,则为负剪力滞[10].
1.2 剪力滞系数
剪力滞系数λ的定义为考虑剪力滞影响所求得的正应力与初等梁理论所求得的正应力的比值,其中,按初等梁理论所求得的正应力是根据翼板实际应力图下的面积除以翼板的宽度而近似得到的[11-12].
2 研究背景
本文以沈阳某高架桥钢箱梁为研究背景,跨径45 m,桥梁总宽23.5 m,双向6车道,单箱五室,梁高2.295 m,横坡均为双向1.5%,底板水平,横坡通过调整腹板高度形成,如图1所示(单位:mm).顶板厚度为16~30 mm,顶板纵肋采用刚度较大的闭口U形肋,间距600 mm,钢板厚为8 mm.底板厚度为16~30 mm,跨中底板厚度为20 mm.腹板间距4 m,板厚16 mm.横隔板采用两种形式,一种为挖空率较大的,一种为挖空率较小的,横隔板厚度为10~24 mm.钢材采用Q345钢,桥面铺装层厚度为7.5 cm.
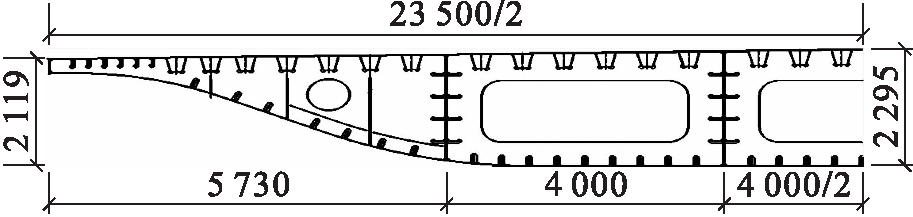
图1 1/2钢箱梁横断面图
Fig.1 Cross section diagram of 1/2 steel box girder
3 空间有限元模型建立
3.1 有限元模型
采用有限元分析软件Midas/civil将结构离散为空间板壳单元,建立鱼腹式钢箱梁板壳有限元模型,钢箱梁中各构件均按实际结构赋予其截面,以反映结构的真实受力.空间有限元板壳模型如图2所示.该模型共划分为56 827个节点,65 664个单元,模型的坐标系原点在桥面端部,X轴沿顺桥向,Y轴沿横桥向,Z轴为垂直向上.

图2 空间板壳模型
Fig.2 Space shell model
3.2 材料参数
钢箱梁采用Q345钢,弹性模量取值为E=2.06×105 MPa,泊松比取值为μ=0.3,容重取值为γ=76.98 kN/m3.
4 横向剪力滞效应分析
为了说明不同荷载情况对鱼腹式钢箱梁剪力滞效应的影响,计算时主要讨论三种荷载形式:对称均布荷载(按6车道加载)、跨中集中荷载和偏载(按3车道加载).为了解在均布荷载、集中荷载、偏载、改变顶板纵向加劲肋厚度这四种情况下的剪力滞系数横向分布规律,取L/8、L/4、L/2横断面作为均布荷载、集中荷载和偏载情况下分析截面,取L/2截面作为改变顶板纵向加劲肋厚度情况下的分析截面,以截面右边缘为参考点1,计算关键点处顶板剪力滞系数,绘制剪力滞系数折线图,从而得到各个截面处顶板剪力滞系数横向分布规律.为了使论述更加方便,将横断面上缘关键部位的点分别用数字标识,各点位置如图3所示.

图3 横截面各点示意图
Fig.3 Schematic diagram of each point of cross section
4.1 均布荷载下横向剪力滞效应分析
均布荷载下各截面正应力分布图,如图4所示.经过计算整理得出三个截面顶板沿横向剪力滞系数分布,如图5所示.
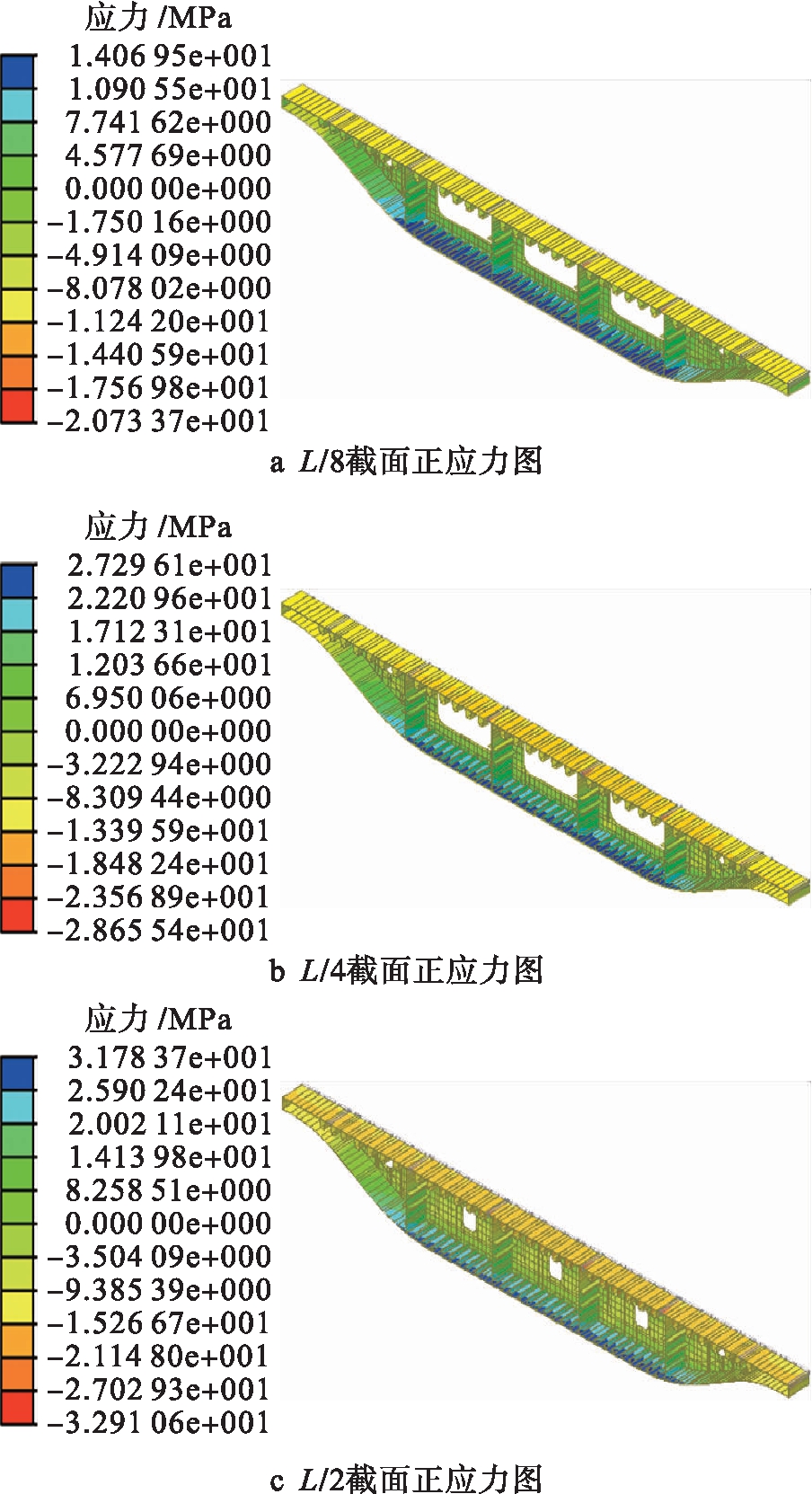
图4 均布荷载下各截面正应力分布图
Fig.4 Normal stress distribution in each section under uniform load
通过整理得出三个截面处顶板压应力最大值分别为20.7、28.7、32.9 MPa,压应力平均值为8.5、15.2、19.8 MPa.通过图5可以看出,剪力滞系数沿横向分布并不均匀,同一截面不同位置呈现出不同的剪力滞效应,例如,L/8截面处的顶板剪力滞系数最大值出现在5号腹板,其值为2.43,与3号腹板的0.87相差较大.边腹板(3号腹板)与端部侧板之间一直处于负剪力滞效应阶段,尤其在三个截面的端部负剪力滞效应最为明显.三个截面的顶板剪力滞系数最大值为2.43、1.88、1.65,说明所选截面远离端部向跨中靠近的时候,正剪力滞系数逐渐下降.所选的三个截面中,负剪力滞系数逐渐趋近于1,说明随着所选截面逐渐远离端部向跨中靠近的过程中,负剪力滞效应逐渐降低,但仍有剪力滞效应发生.
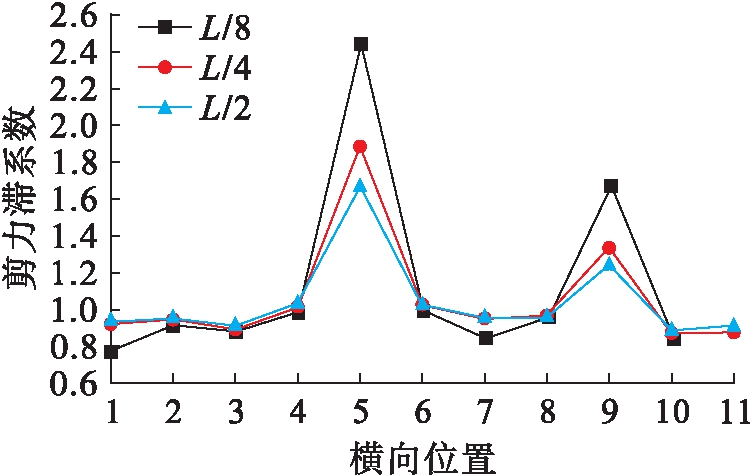
图5 均布荷载下剪力滞系数横向分布
Fig.5 Lateral distribution of shear lag coefficient under uniform load
4.2 集中荷载下横向剪力滞效应分析
集中荷载下各截面正应力分布图,如图6所示.
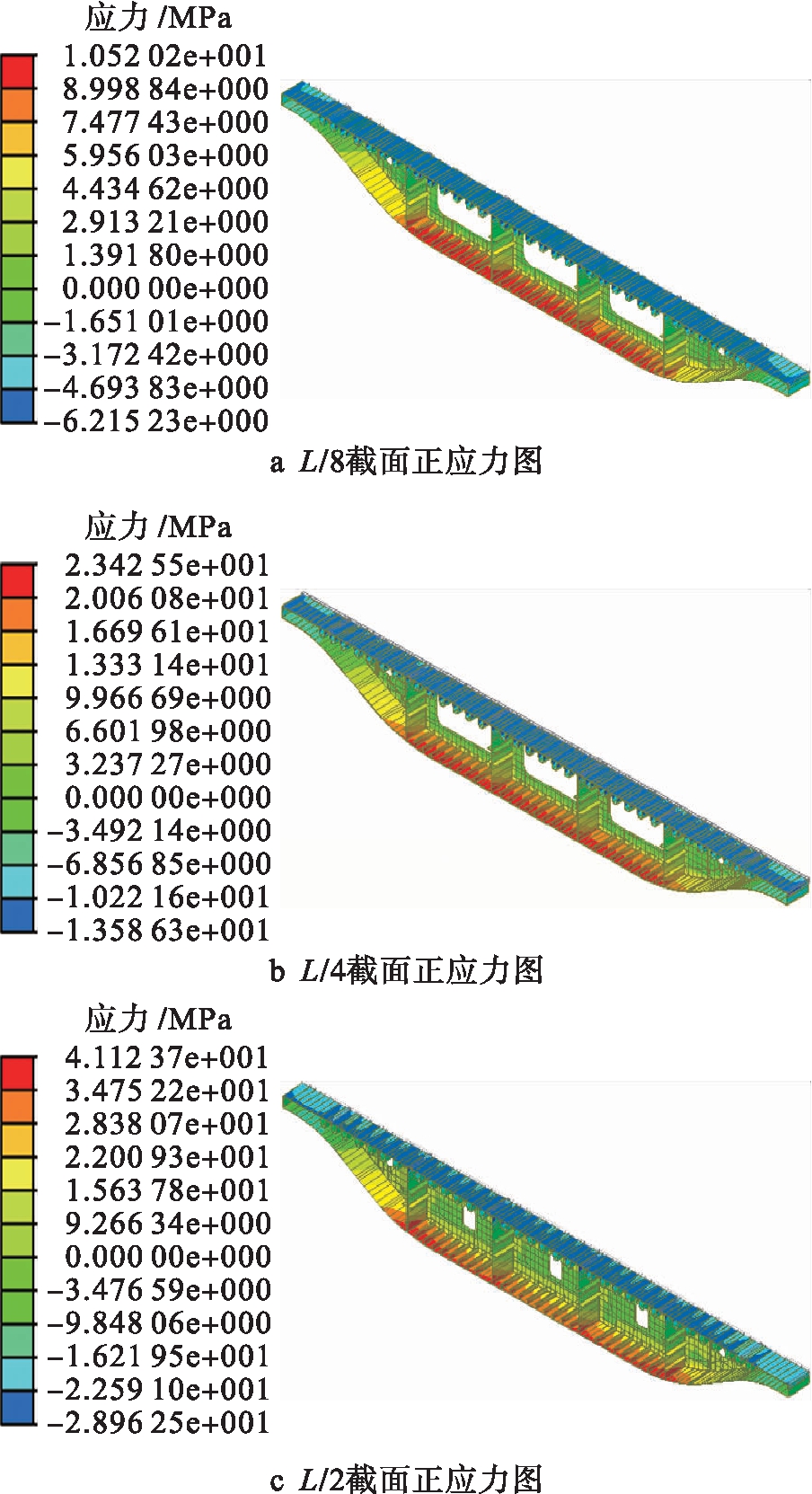
图6 集中荷载下各截面正应力分布图
Fig.6 Normal stress distribution in each section under concentrated load
经过计算整理出三个截面顶板沿横向剪力滞系数分布,如图7所示.
通过整理得出三个截面顶板压应力最大值分别为6.2、13.6、29 MPa,压应力平均值为5.89、12.85、25.84 MPa.由图7可以看出,三个截面的横向剪力滞系数走向不尽相同,L/8截面的剪力滞系数分布规律与另外两个截面有所不同,剪力滞系数最大值出现在顶板中点处,而另外两个截面的剪力滞系数最大值出现在顶板与腹板交界处.不同截面同一位置的剪力滞系数差距不大,在集中荷载作用下,正剪力滞效应明显,仅在边腹板(3号位置和9号位置)与侧板(1号位置和11号位置)之间出现了负剪力滞效应.同时,还可以看出剪力滞系数均与1较为接近,说明在集中荷载作用下,顶板各部分应力值与初梁等理论平截面假定时的应力较为接近,但仍有剪力滞效应发生.
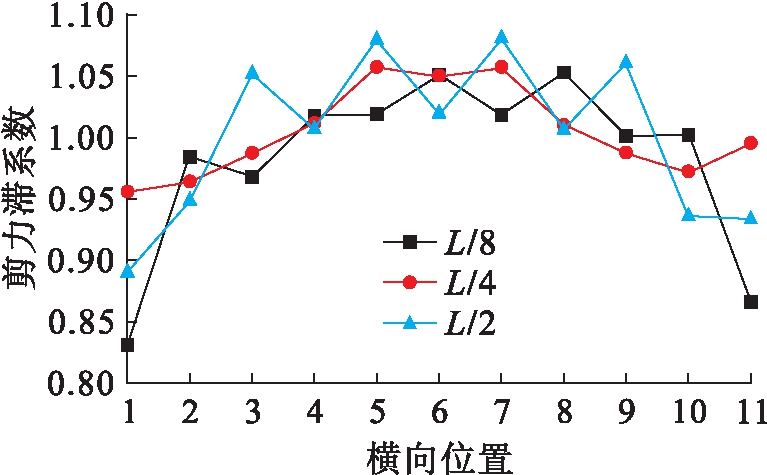
图7 集中荷载下剪力滞系数横向分布
Fig.7 Lateral distribution of shear lag coefficient under concentrated load
4.3 偏载下横向剪力滞效应分析
偏载下各截面正应力分布图,如图8所示.
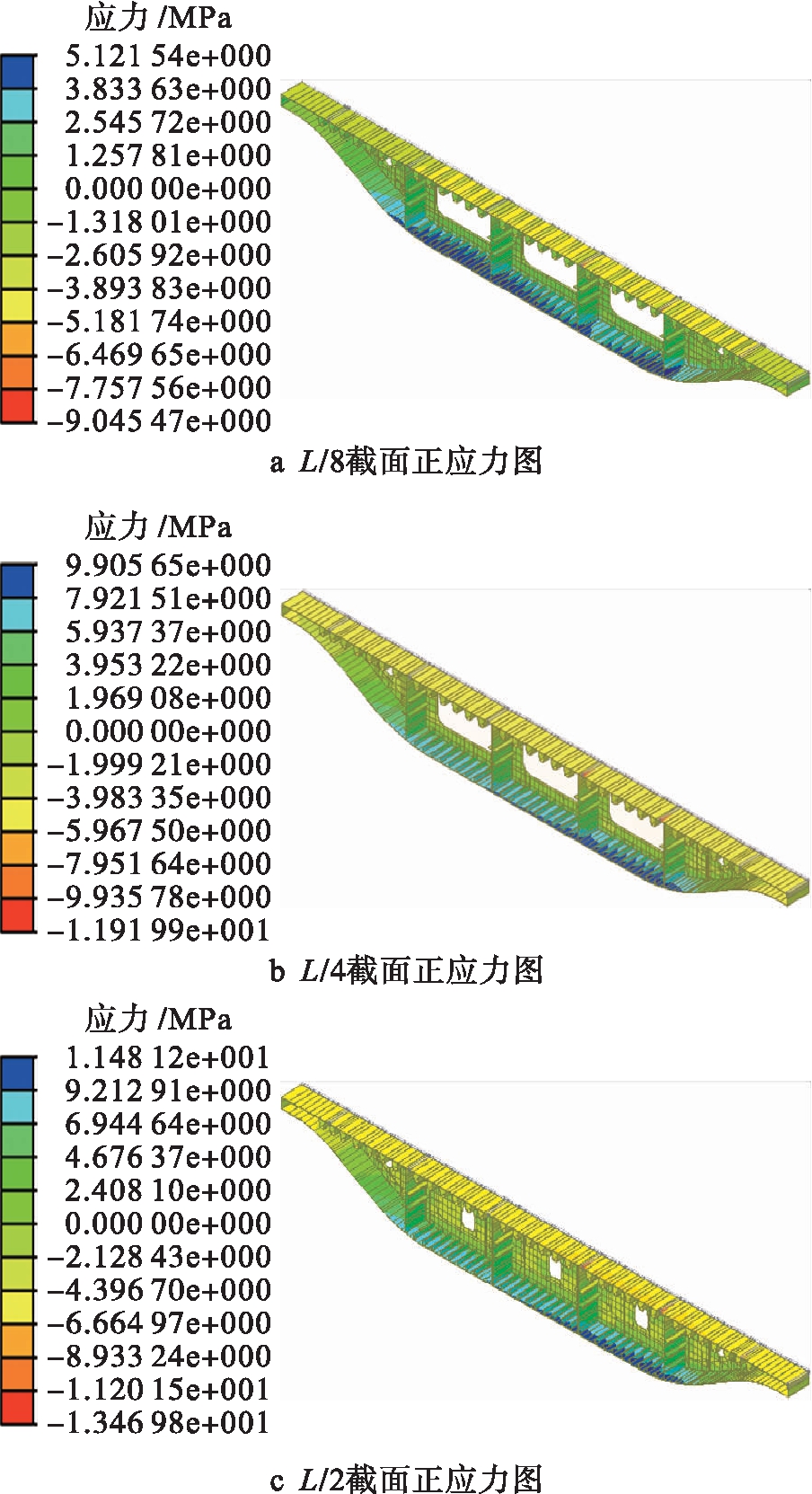
图8 偏载作用下各截面正应力分布图
Fig.8 Normal stress distribution in each section under partial load
经过计算整理得出三个截面顶板沿横向剪力滞系数分布,如图9所示.
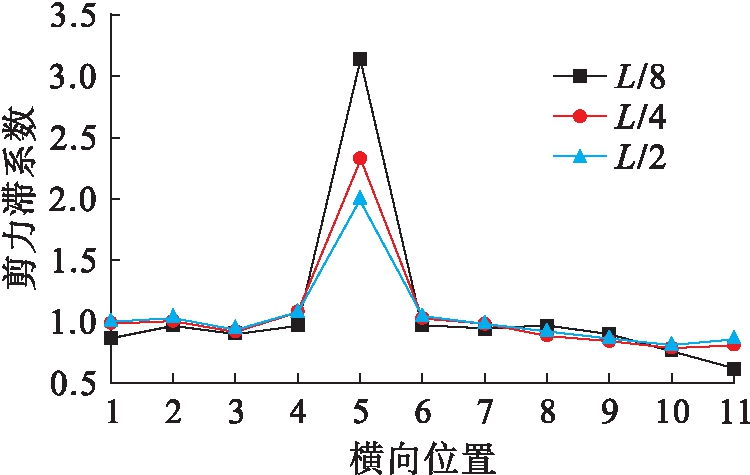
图9 偏载作用下剪力滞系数横向分布
Fig.9 Lateral distribution of shear lag coefficient under partial load
压应力最大值分别为9、11.9、13.5 MPa,压应力平均值为2.87、5.09、6.675 MPa.由图9可以看出,1号位置到4号位置剪力滞系数变化幅度不大,最大剪力滞系数为1.07,最小剪力滞系数为0.87,差距为0.2.从4号位置到6号位置这个阶段,剪力滞系数变化最为明显,其中三个截面的顶板剪力滞系数最大值均出现在5号位置,分别为3.14、2.34、1.99.说明在偏载作用下,5号位置(腹板)应力过于集中,导致出现裂缝,实际工程中应采取相应措施来降低剪力滞系数.6号位置至11号位置剪力滞系数趋于平缓,没有太大的变化,但均处于负剪力滞效应阶段.
4.4 纵向加劲肋厚度对钢箱梁剪力滞效应影响
为研究顶板纵向加劲肋(U形肋、腹板、侧板)厚度对钢箱梁剪力滞效应的影响,将纵肋厚度分别增加4和8 mm,则构件参数取值分别为:U形肋厚度为8、12、16 mm;腹板厚度为16、20、24 mm;侧板厚度为12、16、20 mm;其他结构尺寸保持不变.不同纵肋厚度的钢箱梁跨中截面应力分布如图10所示.
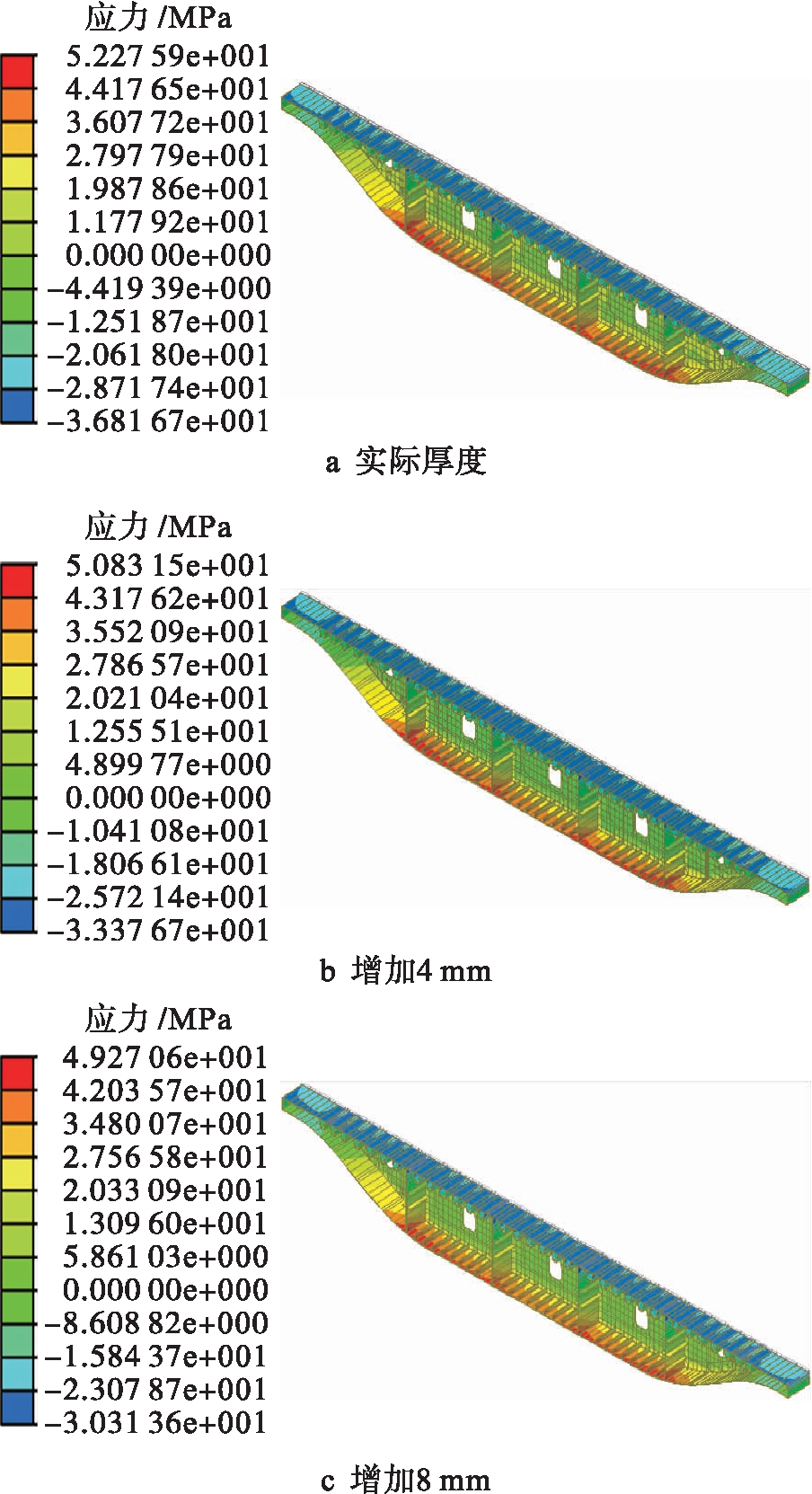
图10 不同厚度跨中截面应力图
Fig.10 Stress diagram for mid-span section with different thicknesses
通过计算整理得出三种纵肋厚度的钢箱梁跨中截面顶板剪力滞系数横向分布,如图11所示.随着纵肋厚度增加,跨中截面顶板压应力最大值从36.8 MPa降低到30.3 MPa,减小了17.7%.由图11可以看出,随着纵肋厚度增加,最大剪力滞系数从1.17降低到1.11,减小了5.1%,由于纵肋承担了大部分剪力,纵肋厚度增加,则纵肋刚度增加,荷载作用下纵肋中的剪力流亦减小,相应地由纵肋传递到顶板上的剪力流减小,顶板剪力滞效应减小,所以板厚的增加对提高钢箱梁纵肋的刚度是有效的.
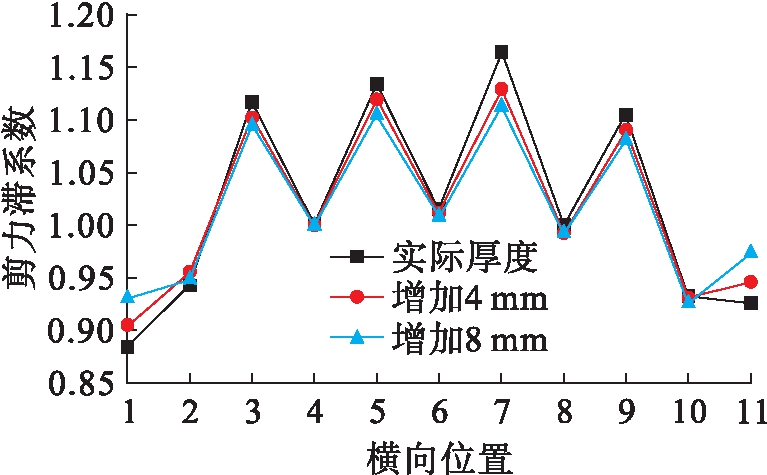
图11 不同厚度剪力滞系数横向分布
Fig.11 Lateral distribution of shear lag coefficient with different thicknesses
5 结 论
本文通过分析得出以下结论:
1)均布荷载作用下剪力滞系数横向分布并不均匀,同一截面不同位置呈现出不同的剪力滞效应.通过对数据处理发现,在三个截面中,负剪力滞系数逐渐趋近1,说明随着所选截面逐渐远离端部向跨中靠近的过程中,负剪力滞效应逐渐降低.
2)集中荷载作用下三个截面顶板剪力滞系数走向不尽相同,L/8截面顶板剪力滞系数走向与另外两个截面不同.同时,集中荷载作用下,正剪力滞效应明显,仅在截面两侧出现了负剪力滞效应.
3)偏载作用下三个截面顶板剪力滞系数最大值均出现在5号位置(腹板),分别为3.14、2.34、1.99,说明随着所选截面向跨中靠近的过程中,剪力滞系数逐渐减小,剪力滞效应降低.同时由于最大剪力滞系数出现在5号位置(腹板),说明此处应力过于集中,容易导致出现裂缝,工程中应采取相应措施来降低剪力滞效应.
4)通过对数据的整理和计算发现,适当地增加顶板纵向加劲肋的厚度,可以提高纵向加劲肋的刚度,从而减小剪力滞系数,降低剪力滞效应.
[1] 吕志涛,潘钻峰.大跨径预应力混凝土箱梁桥设计中的几个问题[J].土木工程学报,2010,43(1):70-76.
(LÜ Zhi-tao,PAN Zuan-feng.Issues in design of long span prestressed concrete box girder bridges[J].China Civil Engineering Journal,2010,43(1):70-76.)
[2] Zhang Y H.Improved finite-fegment method for analyzing shear lag effect in thin-walled box girders[J].Journal of Structural Engineering,2014,138(10):1279-1284.
[3] 蔺鹏臻,方炜彬,杨子江,等.预应力作用下箱梁桥的剪力滞效应研究[J].中国公路学报,2015,28(5):101-107.
(LIN Peng-zhen,FANG Wei-bin,YANG Zi-jiang,et al.Shear lag effect analysis of box girder bridge under prestressing effect[J].China Journal of High Way and Transport,2015,28(5):101-107.)
[4] 蔺鹏臻,刘应龙,孙理想,等.预应力作用下简支箱梁桥的剪力滞效应分析[J].铁道工程学报,2014,31(11):54-58.
(LIN Peng-zhen,LIU Ying-long,SUN Li-xiang,et al.Shear lag analysis of simply supported box gir-ders under prestressing effect[J].Journal of Railway Engineering Society,2014,31(11):54-58.)
[5] 方炜彬,蔺鹏臻.逐跨施工混凝土连续钢箱梁考虑徐变的剪力滞效应研究[J].世界桥梁,2015,43(4):53-57.
(FANG Wei-bin,LIN Peng-zhen.Study of shear lag effect in continuous concrete box beam erected span by span taking into account of creeping effect[J].World Bridges,2015,43(4):53-57.)
[6] 张元海,胡玉茹,林丽霞.基于修正翘曲位移模式的薄壁箱梁剪力滞效应分析[J].土木工程学报,2015,48(6):44-50.
(ZHANG Yuan-hai,HU Yu-ru,LIN Li-xia.Analysis on shear lag effect of thin-walled box girders based on a modified warping displacement mode[J].China Civil Engineering Journal,2015,48(6):44-50.)
[7] 孙志伟,刘英,邬晓光,等.连续刚构宽箱梁剪力滞效应分析及有效分布宽度研究[J].铁道科学与工程学报,2016,13(7):1347-1351.
(SUN Zhi-wei,LIU Ying,WU Xiao-guang,et al.Analysis of shear lag effect on box girder of continuous rigid frame bridge and its effective distribution width[J].Journal of Railway Science and Engineering,2016,13(7):1347-1351.)
[8] 雒敏,蔺鹏臻.单箱三室箱梁剪力滞效应的试验研究[J].实验力学,2015,30(5):621-628.
(LUO Min,LIN Peng-zhen.Experimental study of shearing force lag effect of three-cell box girder[J].Journal of Experimental Mechanics,2015,30(5):621-628.)
[9] 张海,金玉佳.多室鱼腹式箱梁剪力滞效应分析[J].沈阳工业大学学报,2017,39(6):710-715.
(ZHANG Hai,JIN Yu-jia.Shear lag effect analysis for multi-cell fish-bellied box beam[J].Journal of Shenyang University of Technology,2017,39(6):710-715.)
[10] 李建国,孙逢坤,徐良.均布荷载作用下简支箱梁的剪力滞效应分析[J].山西建筑,2014,40(5):188-190.
(LI Jian-guo,SUN Feng-kun,XU Liang.The analysis of shear lag effect of simply-supported box beam loaded by the uniform[J].Shanxi Architecture,2014,40(5):188-190.)
[11] Dai Y W,Wang Y Y.A research to cable force optimizing calculation of cablestayed arch bridge[J].Procedia Engineering,2012,37:155-160.
[12] 张元海,林丽霞.薄壁箱梁剪力滞效应分析的初参数法[J].工程力学,2013,30(8):205-211.
(ZHANG Yuan-hai,LIN Li-xia.Initial parameter method for analyzing shear lag effect of thin-walled box girders[J].Engineering Mechanics,2013,30(8):205-211.)