基于耗散哈密顿系统的控制方法是一种从能量角度研究控制策略的方法[1].不同于传统的控制方法,端口受控哈密顿系统从能量存储、消耗和转换的角度,利用网络中的独立储能元件建模,在此基础上实现对系统的控制.由于其优良的稳定性,基于哈密顿系统的控制方法在电力系统[2-4]、航空航天[5-6]及电机控制[7-8]等方面均有着广泛的应用.
文献[9]在电力有源滤波的基础上,采用互联和阻尼配置无源控制的方法设计了一种无源混合控制器,用于补偿电网电流并抑制谐波,从而获得优良的直流电压动静态性能;文献[10]将端口受控哈密顿控制方法应用于无人驾驶船只螺旋桨驱动控制,实现了船只驱动技术的输出优化,同时提升了无人驾驶船只系统的续航能力;文献[11]利用端口受控耗散哈密顿系统优良的稳定性,并结合反步法协调控制技术的快速性,利用指数协调函数提出了一种二自由度SCARA机器人位置控制技术,实现了对机器人的跟踪定位.
永磁同步电机伺服系统作为目前广泛使用的一种电机系统,在数控机床、工业机器人、航空航天等领域均有着重要应用[12-14],因此,本文研究了基于端口受控耗散哈密顿系统的永磁同步电机无源控制实现方法,将传统的闭环控制函数转变为能量李雅普诺夫函数,进一步提高了永磁同步电机控制系统的精度和稳定性.
1 端口耗散哈密顿系统
端口受控的耗散哈密顿系统(PCHD)通过寻找某一个反馈控制函数,使得控制系统能够达到能量上的平衡,即利用整定控制输入函数u=β(x),使系统的能量函数Hd(x)在平衡点x处取极小值.
一般情况下,工程中采用系统互联和阻尼结构配置的方式来实现耗散哈密顿系统的建模.端口受控耗散哈密顿系统定义为
(1)
式中:J为反对称参数矩阵,反映了系统内部的互联关系;R为半正定对称参数矩阵,反映了端口上附加的阻结构;H为该系统的一个哈密顿能量函数;G为和状态变量有关的函数.
对系统的控制实质就是通过对参数矩阵的调整,即利用两个端口之间的互联和阻尼配置(IDA-PBC)实现对系统的无源控制.假设两个受控的耗散哈密顿系统分别为A与B,将两系统通过一个标准反馈形式互联,则互联之后的闭环耗散哈密顿系统的参数分别为
(2)
(3)
(4)
(5)
闭环系统的哈密顿能量函数满足
H=HA+HB
(6)
对于给定的哈密顿系统及平衡点x′,若存在一个向量函数K(x)满足
(7)
(8)
同时,在平衡点x′处有![]() 则平衡点x′为闭环系统的一个稳定平衡点.
则平衡点x′为闭环系统的一个稳定平衡点.
2 永磁同步电机控制模型
2.1 电机PCH模型建模
d-q坐标系下,永磁同步电机的电压方程和机械特性方程为
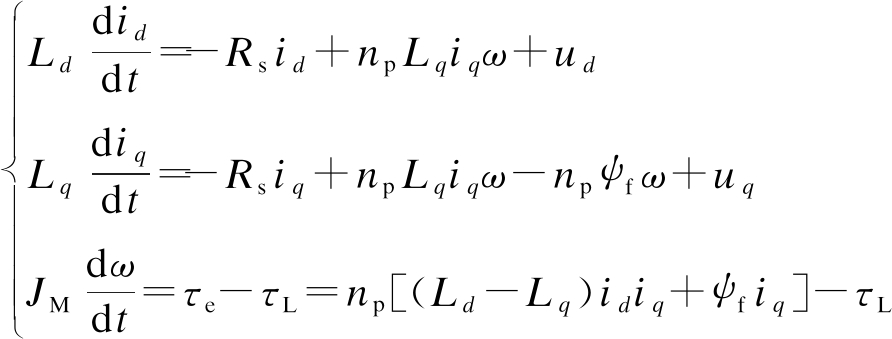
(9)
式中:id、iq为电流;Rs为定子绕组电阻;Ld和Lq为等值电枢电感,对于隐极机有Ld=Lq;ω为角速度;ψf为转子磁链;np为极对数;JM为转动惯量;τe为电磁转矩;τL为负载转矩.
控制系统的状态变量x、输入变量u和输出变量y表示为
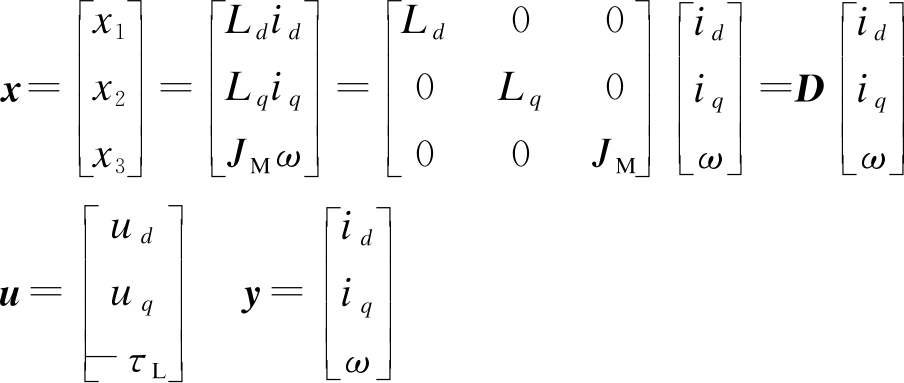
(10)
在上述条件下,同步电机哈密顿函数可以表示为
(11)
根据端口受控耗散哈密顿系统的要求,电机的数学模型可以描述为
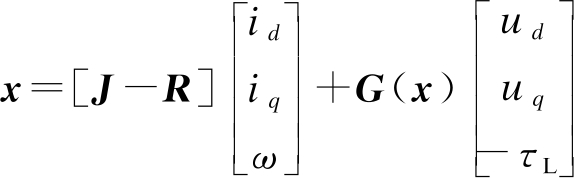
(12)
y=[id,iq,ω]T
(13)
式中:
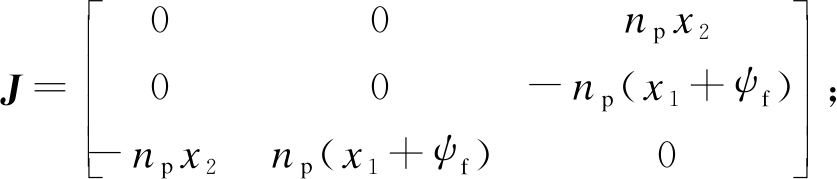
G=diag(1,1,1)
2.2 稳定平衡点和控制器设计
为了寻找电机PCH模型的稳定运行平衡点x′,假设
x′=[x′1,x′2,x′3]T
(14)
在此基础上,构造一个能量函数Hd(x),使得其在x′处取得最小值,并寻找反馈控制规律u=β(x),使得闭环系统满足
(15)
就隐极机而言,一般采用直轴电枢电流id=0 A控制策略时,稳定运行条件下则有
x′3=np[(Ld-Lq)i′di′q+ψfi′q]-τL=0
(16)
当i′d=0 A时,进一步得到
(17)
即在平衡点处有
(18)
加入控制策略u=β(x)后,选取闭环控制系统的哈密顿函数Hd(x)为
(19)
不失一般性,考虑选择
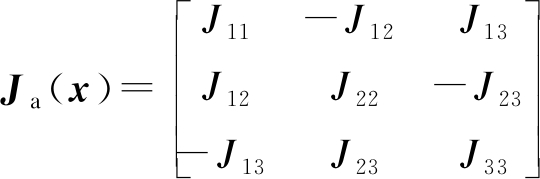
(20)
Ra=diag(r1,r2,0)
(21)
![]() (x)=D-1x
(x)=D-1x
(22)
(23)
式中:J11、J22、J33为0;J12、J13、J23、r1和r2为待定的互联与阻尼参数,则有
[J+Ja-(R+Ra)]K(x)=
(24)
求解方程组可得
(J13+npLqiq)ω′
(25)
[J23+np(x1+ψf)]ω′
(26)
(27)
将平衡点方程代入式(27)可得
(28)
在平衡点运行时,满足τ=τ′=τ′L,则参数J12、J13、J23为
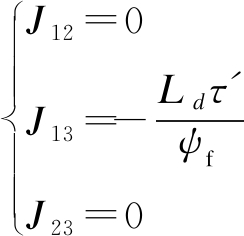
(29)
得到反馈控制ud,uq分别为
(30)
(31)
式中,e1和e2为增益系数,则在x=x′时,可得
![]() (x)=0
(x)=0
(32)
且有Hd(x)的海森矩阵满足
![]() (x)=D-1>0
(x)=D-1>0
(33)
因此满足稳定判别条件,闭环控制系统为渐进稳定系统.
3 系统仿真分析
3.1 同步电机速度控制仿真分析
基于上文分析,本文在MATLAB的Simulink环境中搭建了系统仿真平台,控制框图如图1所示,仿真电机参数设置如表1所示.实验过程中通过调节增益参数e1,e2,使系统达到预期运行目标.
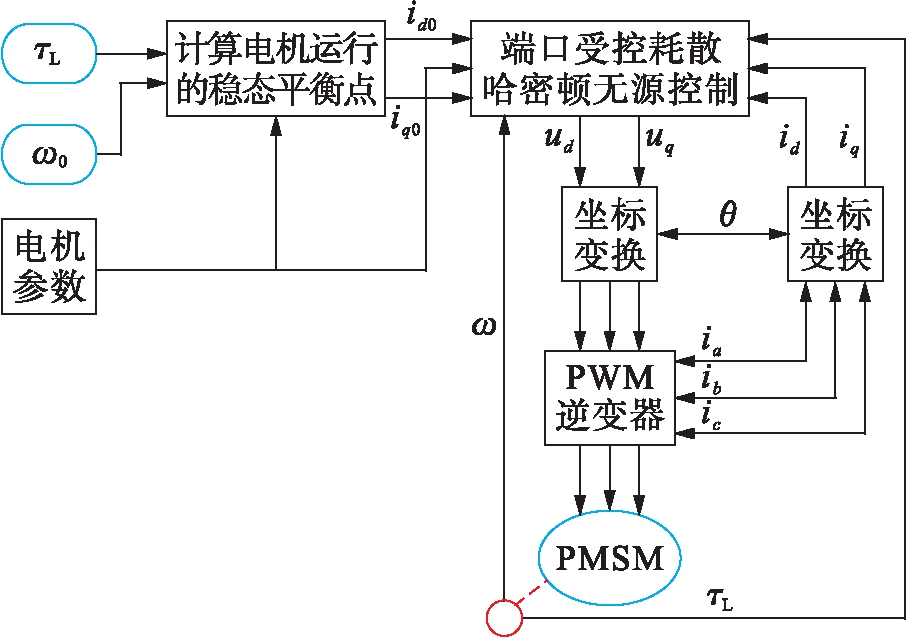
图1 端口耗散哈密顿控制框图
Fig.1 Control diagram of port dissipative Hamiltonian
表1 电机仿真参数设置
Tab.1 Setting of simulation parameters for motor

定子电阻Rs/Ω极对数np转动惯量JM/(kg·m-2)磁链ψf/Wb定子电感Ld,Lq/H0.4530.00210.710.0142
设置同步电机额定转速为100 r/min,增益参数e1为15,e2分别为5、10、15、20,电机转速响应仿真结果如图2所示.
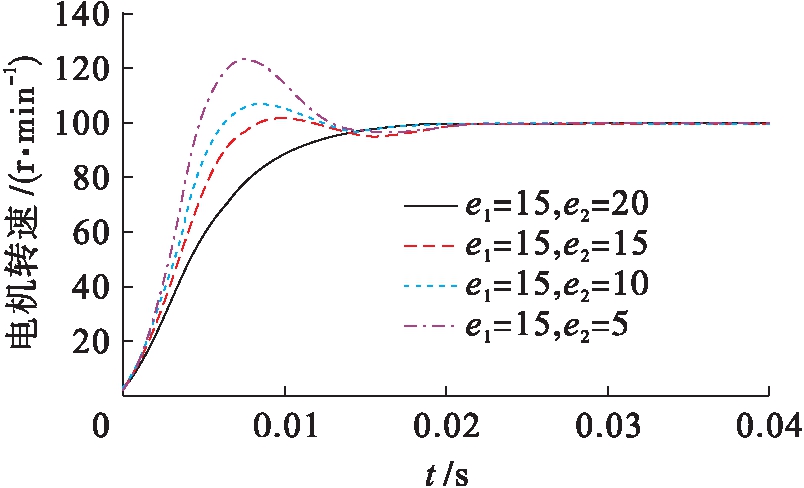
图2 不同增益参数下电机转速响应
Fig.2 Response of motor speed with different gain parameters
不同增益参数e1、e2下,基于端口耗散哈密顿系统的电机转速控制方法能够使得电机转速达到其额定速度.由仿真结果可知,控制参数会影响系统的响应速度,即参数e1不变的条件下,e2较小,系统会产生超调;e2较大,系统动态响应时间延长.
负载突加后的速度响应特性是衡量系统稳定性的又一标准.本文设置初始负载转矩为0 N·m,参数e1=15,e2=15,在t=0.04 s时刻,负载转矩突加10 N·m,转速及电磁转矩响应曲线如图3所示.由仿真结果可以看出,在突加负载的情况下,在0.02 s内系统即恢复稳定运行,电机转速等于额定转速,电磁转矩等于负载转矩.一般的PI控制方法需要调节6个参数[15],而基于端口耗散哈密顿系统的电机控制方法只需要调节两个参数即可实现对电机的控制,减少了系统复杂性.
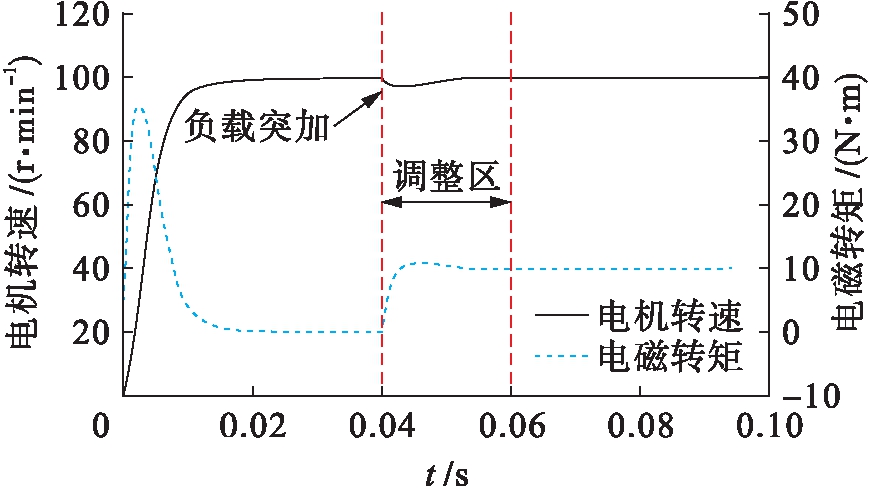
图3 电机转速和电磁转矩响应曲线
Fig.3 Response curves of motor speed and electromagnetic torque
3.2 负载扰动观测器设计
电机控制系统中负载扰动时有发生,且不可直接测量,从而导致了电机速度的波动,造成系统性能的下降.为了避免这一问题,本文设计了基于卡尔曼滤波器的负载扰动观测器,使系统保持稳定运行.负载扰动状态观测器的状态方程为
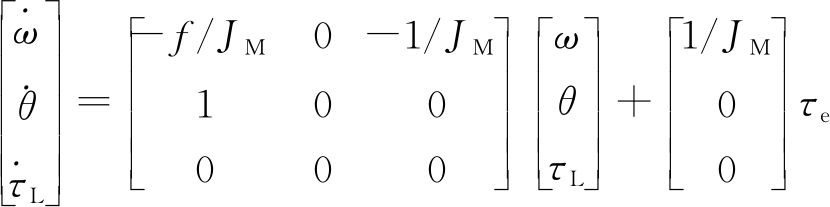
(34)
写成标准形式有
(35)
式中,A、C为系数矩阵.
用欧拉法将式(35)展开进行迭代,迭代误差采用卡尔曼滤波器的反馈校正补偿,则
xn=xn-1+(Axn-1+Gun-1)Ts
(36)
式中,Ts为迭代转化矩阵,整理后可得
xn=Kn-1xn-1+Fn-1un-1
(37)
式中:K=I+ATs;F=GTs.
计算状态变量的估计值和协方差阵的估计值为
x′n=Kn-1xn-1+Fn-1un-1
(38)
(39)
式中:P为状态估计误差的协方差矩阵;Q为系统噪声的协方差矩阵.卡尔曼滤波器增益为
(40)
在此基础上计算状态变量的最优估计值为
xk=x′k+Nn(yk-Cx′k)
(41)
电机额定转速为100 r/min,控制参数e1=15,e2=15.为了研究负载扰动对电机控制系统的影响,在t=0.04 s突加大小为10 N·m的负载,将观测转矩作为参考转矩的前馈补偿,在突加负载的条件下,有补偿和无补偿的转速及转矩仿真结果如图4、5所示.
由图4、5的仿真结果可知:系统中添加了以卡尔曼滤波器为基础的负载转矩观测器之后,将观测转矩作为参考转矩的前馈补偿,可以有效降低噪声的影响,同时加快了系统的响应速度,进一步提高了电机运行的稳定性.
3.3 增益参数切换控制
为了使系统具有良好的响应特性,满足电机在不同工况下的应用需求,需要对电机的增益参数进行切换控制.事实上,增益参数切换控制属于一种分段控制的方法,当电机系统采用基于端口耗散的哈密顿控制方法时,参数e1和e2决定了系统运行暂态过程的变换情况.
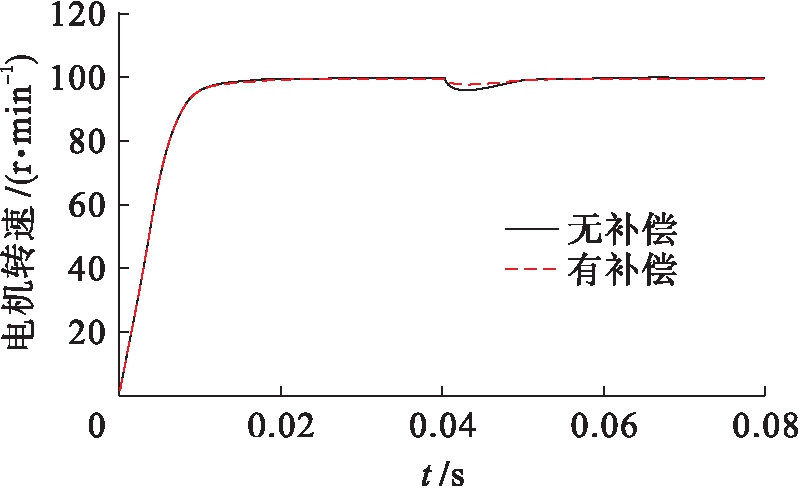
图4 电机转速响应仿真曲线对比
Fig.4 Comparison of simulation curves for motor speed response
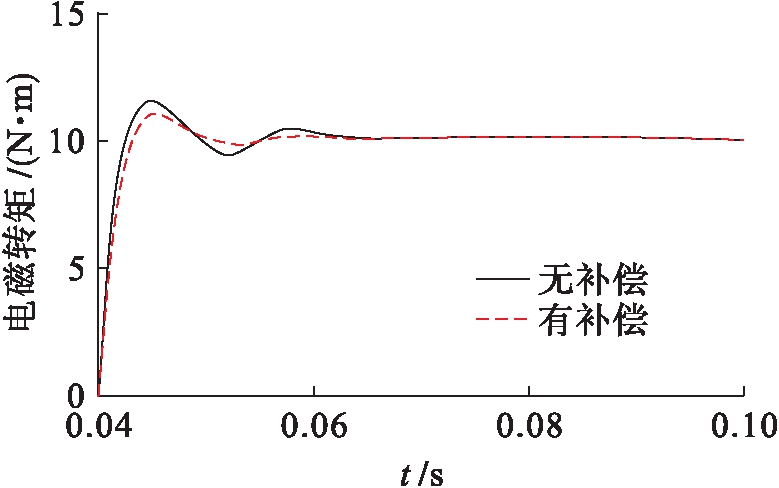
图5 电磁转矩变化仿真曲线对比
Fig.5 Comparison of simulation curves for electromagnetic torque change
当运行偏差大于临界运行偏差时,为了减小电机速度调整的时间,采用具有快速响应的参数;当运行偏差小于临界运行偏差时,为了避免发生超调,应采用相对稳定的运行参数,因此本文选择的参数切换方案如表2所示.
表2 电机运行参数切换方案
Tab.2 Switching schemes of motor operating parameters

编号运行偏差参数选择1ε≥15%e1=15,e2=5210%≤ε<15%e1=15,e2=1035%<ε<10%e1=15,e2=154ε≤5%e1=15,e2=20
电机运行的额定速度在t=0 s时设定为100 r/min,基于上述切换方案的转速响应仿真如图6所示.
图6为选择e1=15,e2=10和e1=15,e2=20仿真结果与参数切换时电机运行仿真结果的对比.由仿真结果可以看出,当电机运行速度较低时,采用参数切换的控制方法具有较高的响应速度,能够在短时间内提升电机的运行速度;当运行速度接近额定转速时,采用参数切换的控制方法能使系统保持稳定而不发生超调.
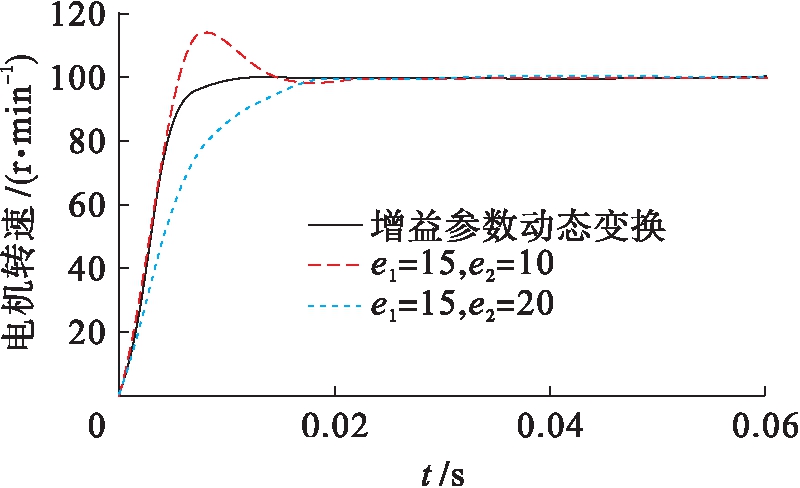
图6 不同切换参数下电机转速响应仿真曲线
Fig.6 Simulation curves of motor speed response with different switching parameters
4 结 论
本文介绍了端口受控耗散哈密顿系统,并对d-q坐标系下的永磁同步电机进行了哈密顿系统建模.此外,通过互联和阻尼配置对电机的速度控制器进行了设计.在此基础上,利用负载扰动观测器作为前馈补偿,降低了噪声影响,加快了系统的响应速度.同时,采用增益参数切换的控制方法提高了系统运行的稳定性.
[1]Ortega R,der Schaft,Mareels I,et al.Putting energy back in control [J].IEEE Control Systems Magazine,2001,21(2):18-33.
[2]冉岩,刘鸿鹏,刘宽,等.改进Y源并网逆变器的能量成型控制策略 [J].电网技术,2018,42(10):54-59.
(RAN Yan,LIU Hong-peng,LIU Kuan,et al.Energy-shaping control strategy of improved Y-source inverter [J].Power System Technology,2018,42(10):54-59.)
[3]马燕峰,俞人楠,刘会强,等.基于Hamilton系统方法的VSG控制研究 [J].电网技术,2017,41(8):2543-2552.
(MA Yan-feng,YU Ren-nan,LIU Hui-qiang,et al.The analysis of VSG control algorithm based on Ha-milton system [J].Power System Technology,2017,41(8):2543-2552.)
[4]程启明,谭冯忍,程尹曼,等.电网不平衡下DFIG网侧变换器侧基于PCHD模型的无源控制 [J].电网技术,2017,41(5):1627-1635.
(CHENG Qi-ming,TAN Feng-ren,CHENG Yin-man,et al.Research on passivity-based control based on PCHD model for DFIG grid-side converter under unbalanced grid voltage conditions [J].Power System Technology,2017,41(5):1627-1635.)
[5]霍伟.基于无源性的航天器姿态跟踪控制设计 [J].空间控制技术与应用,2008,34(2):3-8.
(HUO Wei.Passivity-based control design for spacecraft attitude tracking [J].Aerospace Control and Application,2008,34(2):3-8.)
[6]王青,龚立纲,董朝阳.基于PCH模型的航天器姿态无源控制 [J].北京航空航天大学学报,2017,43(6):1061-1071.
(WANG Qing,GONG Li-gang,DONG Chao-yang.Spacecraft attitude passivity control based on PCH model [J].Journal of Beijing University of Aeronautics and Astronautics,2017,43(6):1061-1071.)
[7]孙宜标,王亚朋,刘春芳.永磁直线电机自适应区间二型模糊滑模控制 [J].沈阳工业大学学报,2017,39(6):601-606.
(SUN Yi-biao,WANG Ya-peng,LIU Chun-fang.Adaptive interval two-type fuzzy sliding mode control for permanent magnet linear motors [J].Journal of Shenyang University of Technology,2017,39(6):601-606.)
[8]程启明,黄伟,程尹曼,等.双级矩阵变换器驱动永磁同步电机的混合非线性控制系统 [J].电工技术学报,2017,32(4):101-111.
(CHENG Qi-ming,HUANG Wei,CHENG Yin-man,et al.Hybrid nonlinear control system of permanent magnet synchronous motor driven by two stage matrix converter [J].Transactions of China Electro Technical Society,2017,32(4):101-111.)
[9]郑成才,王久和,慕小斌,等.基于PCHD模型的APF自适应模糊无源控制研究 [J].电力系统保护与控制,2018,46(2):8-15.
(ZHENG Cheng-cai,WANG Jiu-he,MU Xiao-bin,et al.Self-adaption fuzzy-passivity based hybrid control strategy of active power filter based on port-controlled Hamiltonian with dissipation model [J].Power System Protection and Control,2018,46(2):8-15.)
[10]吕成兴,于海生,周忠海,等.端口受控哈密顿方法的电力双推进无人船航向航速控制 [J].海洋科学,2018,343(1):136-140.
(LÜ Cheng-xing,YU Hai-sheng,ZHOU Zhong-hai,et al.Speed and heading control of unmanned surface vehicles system based on port-controlled Hamiltonian (PCH) control method [J].Marine Science,2018,343(1):136-140.)
[11]李鹏,杨杰,迟洁茹,等.二自由度SCARA机器人位置的端口受控哈密顿与反步法协调控制 [J].测控技术,2018,37(3):41-46.
(LI Peng,YANG Jie,CHI Jie-ru,et al.Position tracking control system of 2-D of SCARA robot based on the hybrid control of port-controlled Hamiltonian and backstepping [J].Measurement & Control Technology,2018,37(3):41-46.)
[12]夏加宽,毕亮,李瑞泽,等.车用永磁同步电机MT坐标系下DTC控制 [J].沈阳工业大学学报,2018,40(3):241-247.
(XIA Jia-kuan,BI Liang,LI Rui-ze,et al.DTC in MT coordinate system for permanent magnet synchronous motor used in electric vehicle [J].Journal of Shen-yang University of Technology,2018,40(3):241-247.)
[13]朱国昕,雷鸣凯,赵希梅.永磁同步电机伺服系统自适应迭代学习控制 [J].沈阳工业大学学报,2018,40(1):6-11.
(ZHU Guo-xin,LEI Ming-kai,ZHAO Xi-mei.Adaptive iterative learning control of permanent magnet synchronous motor servo system [J].Journal of Shen-yang University of Technology,2018,40(1):6-11.)
[14]陈敬灿,汪旭东,许孝卓,等.初级永磁型直线电机矢量控制对比研究 [J].电子科技,2018,31(7):19-22.
(CHEN Jing-can,WANG Xu-dong,XU Xiao-zhuo,et al.Comparative study on vector control of primary permanent magnet linear motor [J].Electronic Science and Technology,2018,31(7):19-22.)
[15]王莉娜,朱鸿悦,杨宗军.永磁同步电机调速系统PI控制参数整定方法 [J].电工技术学报,2014,29(5):104-117.
(WANG Li-na,ZHU Hong-yue,YANG Zong-jun.Tuning method for PI controllers of PMSM driving system [J].Transactions of China Electrotechnical Society,2014,29(5):104-117.)