空间对接技术中,根据结构方式的不同可以将对接机构分为杆锥式对接机构和周边式对接机构[1].对接机构在两个航天器进行空间对接时会发生接触和撞击的现象,为了确保航天器安全和对接成功,需要采用一种有效的手段来对撞击能量进行阻尼与缓冲.一般情况下采用缓冲阻尼系统完成上述功能,根据不同的缓冲阻尼元件,系统可分为独立式液压缓冲阻尼系统和差动式机电缓冲阻尼系统[2].差动式机电缓冲阻尼系统被人们所重视,被广泛使用到国际空间站中,但差动式机电缓冲阻尼系统的结构较为复杂,在该系统中存在上百个能够运动的部件.相关专家学者对缓冲阻尼动力学性能进行了研究,并取得了良好的研究成果,文献[3]进行了嵌入式共固化网格阻尼结构复合材料的动力学性能研究,建立嵌入式共固化网格阻尼结构复合材料的有限元数值模拟模型,用改进的应变能法分析了该网格结构的阻尼特性.文献[4]进行了非线性阻尼非线性刚度隔振系统随机动力学特性研究,通过求解FPK方程等效非线性随机振动方程来研究非线性隔振系统在随机激励下的隔振性能,并使用路径积分和Monte-Carlo数值法进行验证.
采用当前方法研究机电缓冲阻尼系统缓冲阻尼动力学性能时,并不能准确得到机电加工系统的动力学方程和运动约束方程.为了解决上述问题,本文提出了机电加工系统缓冲阻尼动力学性能分析方法.
1 机电加工系统结构组成与运动方程
1.1 机电加工系统结构组成
差动式缓冲阻尼系统作为传动、阻尼和缓冲的直接控制机构,由驱动装置、捕获环、副杆联系组合和丝杆联系组合四个功能单元组成,机电加工系统的结构如图1所示.
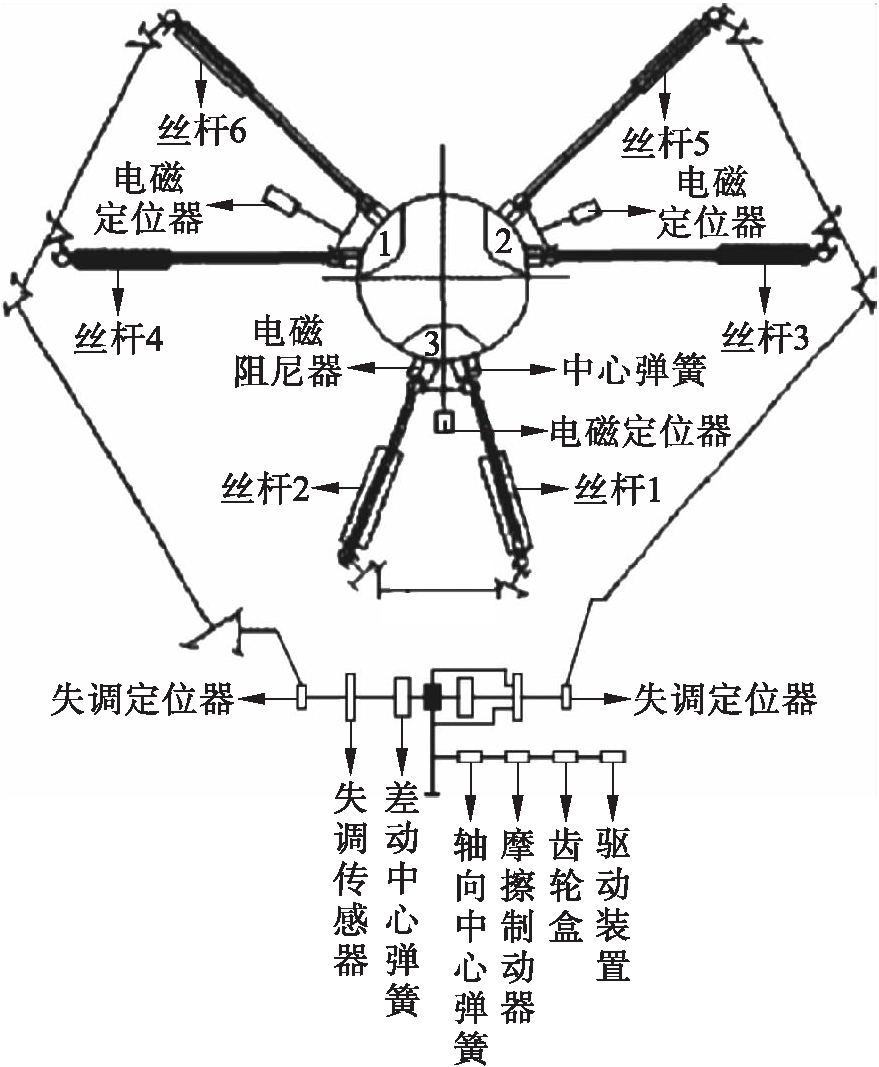
图1 系统的基本部件分布示意图
Fig.1 Schematic diagram of basic part distribution in system
丝杠联系组合是由联系齿轮和滚珠丝杠转换器构成的差动组合;电磁阻尼器和弹簧分别与丝杠联系;副杆联系是一个差动组合,通常由中间传动轴和差速器构成,在差速器中装置双轴弹簧机构,将始端弹簧集合和摩擦制动器放置在驱动装置前[5].利用传动轴和中间齿轮连接各个单元,形成差动式缓冲阻尼系统.通过上述部件并根据合适的运动组合完成对接开始、对接过程中和对接结束后捕获环的伸出和拉紧,在对接时保证在6个自由度方向捕获环的灵活运动,为捕获连接提供便利,进而提供有效的阻尼和缓冲,吸收航天器空间对接时由于接触和撞击而产生的动能[6].
1.2 机电缓冲阻尼机构的运动方程
1.2.1 弹簧机构
在机电加工系统中总共设置了6个采用平面蜗卷弹簧的弹簧机构.机电加工系统中存在两种工作形式不同的弹簧,一种是安装在丝杠组合处的单轴双向旋转弹簧K1;另一种是安装在摩擦制动器前和连接差速器两端的双轴双向旋转弹簧K2、K3[7].单轴双向旋转弹簧和双轴双向旋转弹簧在机电加工系统中的受力变形可分别表示为
(1)
(2)
式中:ki为弹簧的刚度;φ、φ1、φ2为旋转轴对应的转角.
1.2.2 电磁制动器
电磁制动器是一种阻尼元件,存在于丝杠联系组合中.当电磁制动器的转速不高时,转子转速ω实际上与制动力矩成正比.构建动力学方程时,可用速度的线性函数代替制动器的阻尼力,用速度的二次齐次函数代替耗散函数,动力学方程表达式为
(3)
式中:n为电磁制动器在丝杠联系组合中的数量;cij为耗散系数.
1.2.3 摩擦制动器
摩擦制动器在机电加工系统中作为能量吸收元件,由摩擦片、钢球压力调整器和旋转轴构成.摩擦片在钢球压力调整器工作下的额定扭矩为Mn,与差速器外壳连接的齿轮在撞击力的作用下,将扭矩转移到摩擦制动器前端的弹簧K2中,利用旋转轴将弹簧产生的力矩传送到摩擦片上.当额定扭矩Mn大于力矩时,摩擦片保持不动;当额定扭矩Mn小于力矩时,摩擦片随着旋转轴开始传动,撞击能量通过滑动摩擦消耗.设θ为齿轮在差速器外壳上工作的转角;k4为弹簧K4对应的刚度,则差速器传输力矩可表示为Mk3=k4θ.
如果Mk3<Mn,则摩擦制动器停止工作,弹簧K4此时对应的弹性势能可表示为
(4)
式中,f为摩擦系数.如果Mk3≥Mn,摩擦制动器开始工作,旋转轴此时的转角为θ2,此时弹性势能可表示为
(5)
2 缓冲阻尼动力学性能分析
2.1 运动学分析
当丝杠不围着轴线转动时,丝母转速ω1和丝杠沿轴线运动速度v之间的关系可表示为
v=ω1d/2π
(6)
式中,d为螺旋导程.
根据速度合成定理,丝杠沿轴线的平均速度与丝杠轴线上任意一点运动速度对应的投影相同[8].假设在丝杠轴线中存在上铰点和下铰点,则运动速度可表示为
(7)
式中:β为机电加工系统轴线与丝杠轴线之间的夹角;![]() 为沿机电加工系统轴线上铰点分布平面对应的平均运动速度.
为沿机电加工系统轴线上铰点分布平面对应的平均运动速度.
设![]() 为始端弹簧角在机电加工系统中的速度,其表达式为
为始端弹簧角在机电加工系统中的速度,其表达式为
(8)
式中,isd为传动比.将式(6)、(7)代入式(8)可以得到
(9)
cos β=H/L
(10)
式中:H为下铰点分布平面与上铰点分布平面之间的距离;L为下铰点和上铰点之间在机电加工系统中的距离,其计算公式为
(11)
其中,Lyz为下铰点分布平面中距离L的投影距离.
将式(10)、(11)代入式(9)中得到
(12)
式中,θ0、L0为积分常数.
2.2 动力学方程
假设轴向力Fx作用于机电加工系统中,此时摩擦制动器的状态为锁定状态.设m为在不考虑其他构件质量基础上固联构件和捕获环的质量,由虚功率原理和达朗贝尔原理可得
(13)
式中:δ为刚性系数;TB为始端弹簧在机电加工系统中的力矩.
将式(9)转变为变分形式,并将转变结果代入式(13)中,得到机电加工系统的动力学方程为
(14)
设始端弹簧在机电加工系统中为线性弹簧,其力矩表达式为
Tg=T0+CSθ
(15)
式中:CS为弹簧刚度;T0为弹簧预紧力矩.
当始端弹簧处于极限行程时,继续增加轴向力会造成摩擦制动器出现打滑的现象[9].假设始端弹簧机构在此时转变为刚性传动机构,不考虑摩擦制动器在机电加工系统中的传动惯量,则可得到机电加工系统动力学方程对应的变分形式为
(16)
式中,![]() 分别为摩擦制动器对应的转动角和滑转摩擦力.
分别为摩擦制动器对应的转动角和滑转摩擦力.
设if为丝母转速ω1与摩擦制动器角速度![]() 之间的传动比,三者之间的关系表达式为
之间的传动比,三者之间的关系表达式为
(17)
在式(11)和式(12)的基础上,将变分形式导入,则可得输出机电加工系统的动力学方程为
(18)
3 实例与仿真分析
根据得到的动力学方程对机电加工系统缓冲阻尼动力学性能进行分析,获得捕获环在不同撞击力影响下机电加工系统的运动学响应.实验分为实际实验与仿真实验两部分,实验持续时间为一个月,通过实际实验获取机电加工系统捕获环角位移对应的位移响应、丝杆铰链在阶跃型撞击下的约束响应等实验参数.仿真实验软件为MATLAB7.0软件,操作系统为Windows 10,内存为24 GB,机电加工系统基本参数如表1所示.
同轴拉紧或同轴推出时,机电加工系统要求各个丝杆构件在机电加工系统中的受力均匀.各个丝杆构件在机电加工系统联系齿轮、弹簧轴锁定且同轴推出情况下的受力情况如图2所示.
表1 复杂机电加工系统基本参数
Tab.1 Basic parameters for complex electromechanical machining system

质量kg惯性矩(kg·m-2)六个自由度最大耗能J弹簧和阻尼器旋转角(°)摩擦制动器旋转角(°)阻尼系数(N·M)摩擦制动器刚度(N·M)摩擦制动器刚度饱和值(N·M)x:214000x:174.622Φ:11.673x:0x:26.413800y:102000y:57.276Θ:44.100y:24.44y:3.050.0370.2916.17z:102000z:56.766ϕ:44.100z:24.44z:3.05
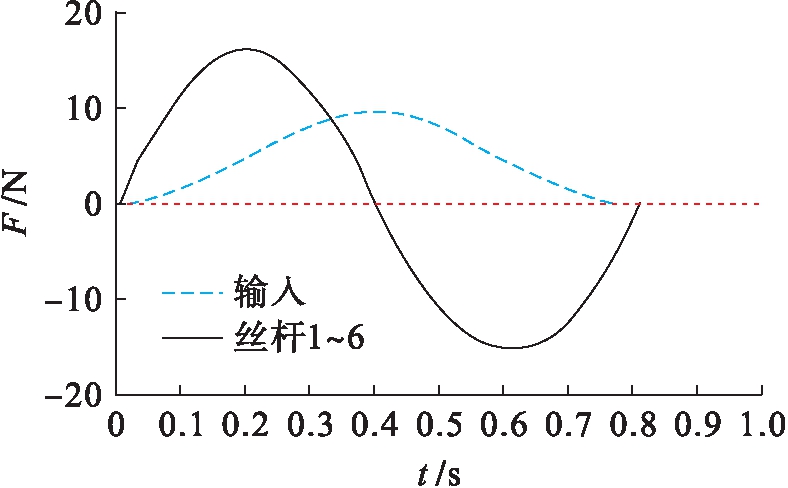
图2 各个丝杆构件的受力情况
Fig.2 Stress condition of each screw component
由图2可知,6根丝杆工作变化曲线是完全重合的,表明在这种工况下,各个丝杆在机电加工系统中的受力是均匀的,机电加工系统的缓冲阻尼符合特殊功能的要求.
在滚动方向撞击力的影响下,机电加工系统中捕获环角位移对应的位移响应曲线如图3所示.
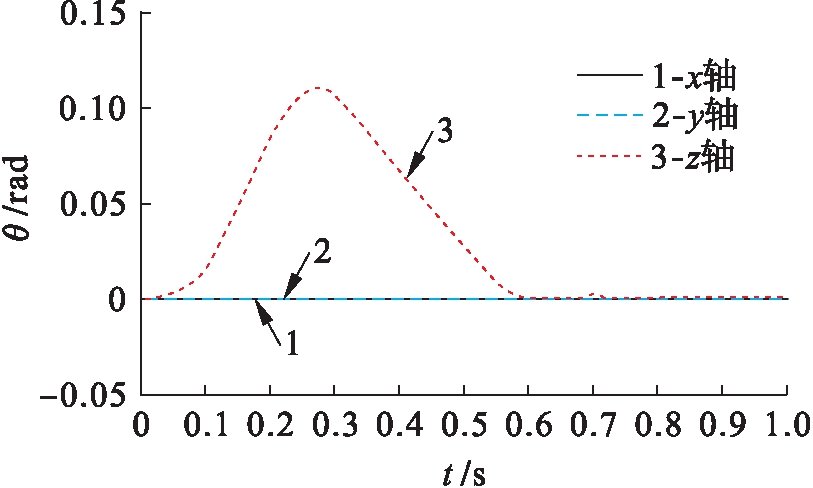
图3 捕获环位移对应的响应曲线
Fig.3 Response curves corresponding to capture ring displacement
由图3可知,在x轴方向和y轴方向捕获环的角位移都是零,只存在捕获环绕z轴得到的角位移.捕获环的运动响应特征在机电加工系统中为纯滚动,通常情况下还在z轴方向中存在极小的线位移.通过进一步的分析和计算可知,相同丝杆组中存在的两个丝杆在机电加工系统中的受力情况不同,但在不同丝杆组中的构件存在相同受力响应情况,表明机电加工系统在滚动方向撞击影响下的响应较为单纯.
图4和图5为机电加工系统在阶跃型函数影响下捕获环角位移的响应和丝杆铰链约束力的响应,其中阶跃型力函数G(t)的表达式为
G(t)=N(s1,0,0,0.1,200)-
N(s2,0.2,0,0.3,2 000)
(19)
式中:N为一阶导数对应的阶跃函数;s1为丝杆铰链约束力的初始响应参数;s2为捕获环角位移的初始响应参数.
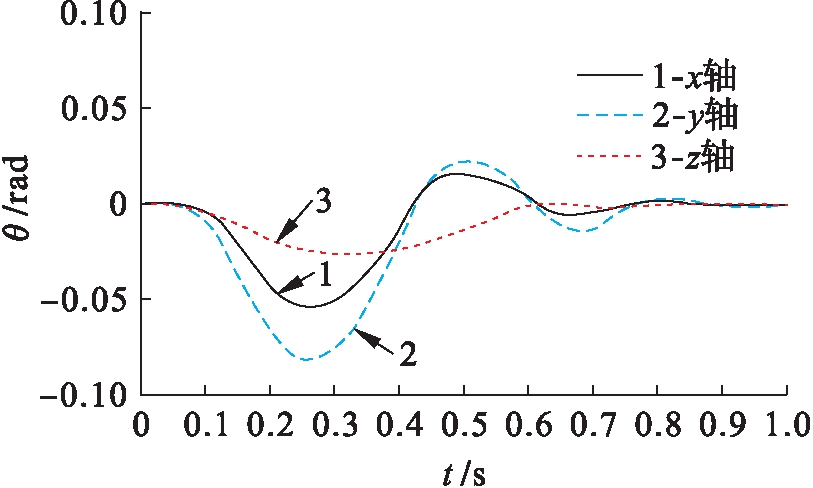
图4 捕获环在阶跃型撞击力下的角位移响应曲线
Fig.4 Angle displacement response curves of capture ring under step impact force
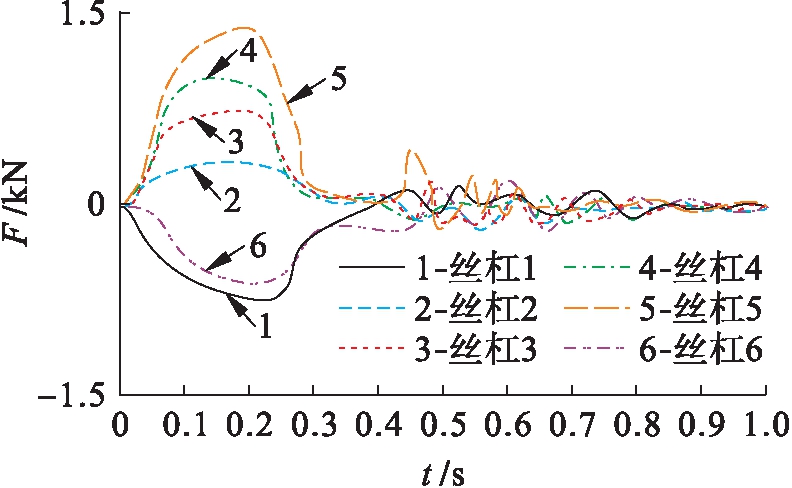
图5 丝杆铰链在阶跃型撞击力下的约束响应曲线
Fig.5 Constrained response curves of screw hinge under step impact force
由图4和图5可知,在不同工况下机电加工系统能够起到缓冲衰减外部作用力的效果,在合理参数配置前提下可以有效地耗散和吸收空间6个自由度方向的作用能量.
4 结 论
本文分析了机电加工系统缓冲阻尼动力学性能,并利用对应的分析方法得到机电加工系统的运动学方程,根据方程进行实例分析,证明了机电加工系统可以有效地吸收并缓冲空间6自由度方向的作用能量.采用机电加工系统缓冲阻尼动力学性能分析方法可以有效、准确地分析机电加工系统的运动情况,本文将机电加工系统的阻尼特性和刚度特征作为机电加工系统开发和设计的依据,为该系统的进一步发展奠定基础.
[1]刘长钊,秦大同,廖映华.采煤机截割部机电传动系统动力学特性分析 [J].机械工程学报,2016,52(7):14-22.
(LIU Chang-zhao,QIN Da-tong,LIAO Ying-hua.Dynamic analysis for the cutting electromechanical transmission system in the long-wall shearer [J].Journal of Mechanical Engineering,2016,52(7):14-22.)
[2]张艳龙,王丽,唐斌斌.含改进LuGre动摩擦的非光滑振动系统的动力学分析 [J].振动与冲击,2018,37(6):212-217.
(ZHANG Yan-long,WANG Li,TANG Bin-bin.Dynamical analysis of a non-smooth vibration system with modified LuGre dynamic friction [J].Journal of Vibration and Shock,2018,37(6):212-217.)
[3]李雪,梁森,梁天锡.嵌入式共固化网格阻尼结构复合材料的动力学性能研究 [J].兵器装备工程学报,2016,37(3):132-137.
(LI Xue,LIANG Sen,LIANG Tian-xi.Dynamic pro-perty analysis of embedded co-cured gridded damping structure composites [J].Journal of Ordnance Equipment Engineering,2016,37(3):132-137.)
[4]黎崛珉,陆泽琦,陈立群.非线性阻尼非线性刚度隔振系统随机动力学特性研究 [J].应用数学和力学,2017,38(6):613-621.
(LI Jue-min,LU Ze-qi,CHEN Li-qun.An investigation on nonlinear-damping and nonlinear-stiffness vibration isolation systems under random excitations [J].Applied Mathematics and Mechanics,2017,38(6):613-621.)
[5]韩爱红,胡伟鹏,邓子辰.偏心冲击下阻尼薄圆板动力学响应的广义多辛分析 [J].振动工程学报,2016,29(6):971-975.
(HAN Ai-hong,HU Wei-peng,DENG Zi-chen.Dynamic analyzing of thin damping circular plate under eccentric impact load by generalized multi-symplectic method [J].Journal of Vibration Engineering,2016,29(6):971-975.)
[6]李培强,胡泽,李欣然,等.基于阻尼转矩分析法的光伏发电系统小信号建模分析 [J].电力系统及其自动化学报,2017,29(6):13-20.
(LI Pei-qiang,HU Ze,LI Xin-ran,et al.Small-signal stability analysis of photovoltaic power generation system based on damping torque analysis method [J].Proceedings of the CSU-EPSA,2017,29(6):13-20.)
[7]李德源,张世亮,池志强,等.地震波传播方向对风力机动力响应的影响 [J].沈阳工业大学学报,2019,41(1):12-18.
(LI De-yuan,ZHANG Shi-liang,CHI Zhi-qiang,et al.Influence of propagation direction of seismic wave on dynamic response of wind turbine [J].Journal of Shen-yang University of Technology,2019,41(1):12-18.)
[8]徐忠四,刘卫新,杜文建.胶泥缓冲器的非线性刚度的控制机理研究 [J].火力与指挥控制,2016,41(6):95-99.
(XU Zhong-si,LIU Wei-xin,DU Wen-jian,Research on control mechanism for nonlinear damping of elastomer damper [J].Fire Control & Command Control,2016,41(6):95-99.)
[9]丁勇为,张子豪,魏小辉,等.油孔几何参数对起落架落震动力学的影响研究 [J].航空计算技术,2018,48(1):30-33.
(DING Yong-wei,ZHANG Zi-hao,WEI Xiao-hui,et al.Influence of orifice geometry parameters on landing gear drop dynamics [J].Aeronautical Computing Technique,2018,48(1):30-33.)