由于计算机网络技术和互联网技术的飞速发展，网络通信业务越来越多，为了满足网络用户对不同业务的通信需求，需要对当前网络通信流量进行有效管理[1].网络流量预测模型的构建是实现网络管理和流量控制的基础工作，高精度的预测模型不仅能够准确地提供未来时段的流量数据，同时也可应用于拥塞控制、僵尸检测等多个方面[2].高精度预测模型具有精确描述网络流量变化特性的能力，例如非线性、周期性和长相关性等.当前的流量预测模型仅能对线性网络流量进行预测，无法准确描述网络流量变化特性，应用范围有限，已不适用于大规模网络流量的预测和分析[3].组合模型能够拟合多个单一预测模型的优点，更精确地描述网络流量特征，已成为该领域的研究热点，受到了广泛关注[4-5].
国内学者在网络流量预测方面已取得较好成果[6].殷荣网[7]采用最小二乘支持向量机(LSSVM)算法构建了网络流量预测模型，利用模糊均值聚类算法对网络流量聚类进行划分，并去除其中孤立样本点，将聚类结果构建成训练集，将其输入至LSSVM中进行学习并构建网络流量预测模型，利用人工蜂群算法优化LSSVM模型.大规模网络流量具有非线性和突发性特点，采用该模型难以精确地描述非线性网络流量变化趋势，预测精度较低.
为了解决上述模型存在的问题，提高网络流量的预测精度，提出基于大数据分析的非线性网络流量组合预测模型.根据实验结果可知，运用所提模型对网络流量进行预测时预测精度较高，能够满足大规模网络环境流量预测精度的要求，有效解决了传统方法存在的问题.
1 网络流量数据特性分析
网络流量是指网络上传输的数据量，由于其数据量规模较大，存在易拥塞、易受攻击等问题，会导致网络异常现象的发生.网络异常，即网络服务器带宽不满足网络用户使用流量需求时导致的带宽拥塞和病毒入侵等，使得真实的网络流量具有混沌特性[8-9].本文在Matlab环境下搭建实验平台，利用NS2仿真软件获取网络流量模拟数据，图1为采集到的网络流量时间序列.
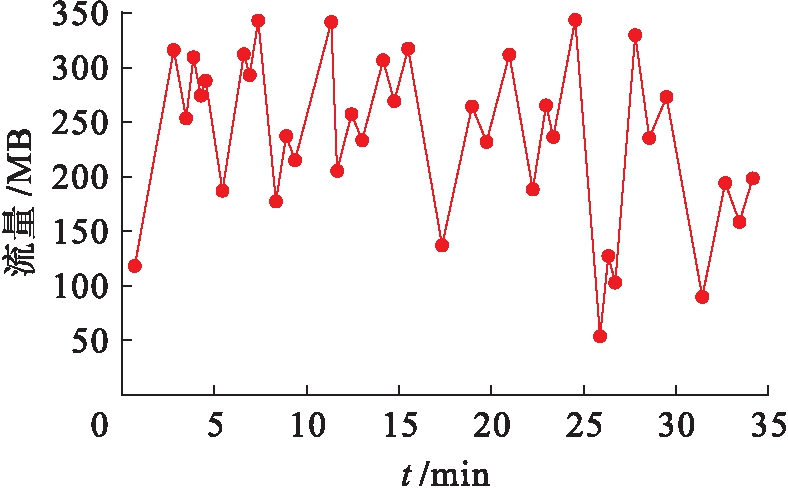
图1 网络流量原始时间序列
Fig.1 Original time series of network flow
通过对该时间序列进行观测和分析，可以发现网络流量数据具有如下特性：1)突发性.受到相同局域网内网络带宽的影响，实际采集的网络流量数据具有突发特性.2)周期性.实际采集的网络流量数据在采集周期内呈现出阶段性变化.3)长相关性.图1所示的网络流量数据具有相同的统计特性.4)非线性.网络流量的变化与用户数量、用户使用高峰期、网络路由协议等相关，造成网络流量的非线性.
综上可知，网络流量数据具有突变性、非线性等特点.对非线性网络流量进行高精度预测，需要对网络流量数据进行分解，从原始非线性网络流量时间序列中提取其变化规律.
2 非线性网络流量组合预测模型
2.1 网络流量数据分解及重构
对采集的大规模网络流量数据进行小波分解，获得多尺度分量，采用混沌理论对分解的多个尺度分量进行重构，获得网络流量子序列，具体过程如下：实际采集的网络流量数据具有混沌特性，从原始非线性网络流量数据提取其变化规律，重构出等效的分布空间[10].对于实际采集的网络流量数据xi(i=1，2，…，n)，可通过分析其变化规律重构出一个多维分布空间yi=(xi，xi+θ，…，xi+(m-1)θ)，θ为时间维度，网络中的流量数据普遍存在噪声.
对采集的网络流量数据进行小波分解，即
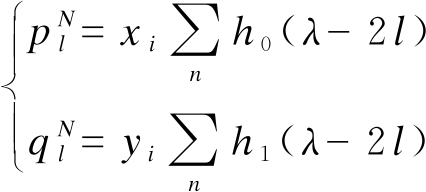
(1)
式中：h0(λ-2l)和h1(λ-2l)为滤波器系数；
和
分别为非线性网络流量数据的高、低频部分；l为小波分解尺度；N为训练样本数量.
利用混沌理论对式(1)分解出的不同分量进行相空间重构，重构出的非线性网络流量子序列为
(2)
式中，g为相空间维度.
非线性网络流量时间序列经过快速小波分解，将网络信号的高低频部分有效分离，可从中挖掘出网络流量数据周期性变化趋势，消除其中突变部分，剩余的高频部分能够精确地描述网络流量数据的变化特征.采用混沌理论对分解的多个尺度分量进行重构，降低了大规模非线性网络流量数据的预测误差及计算复杂度.
2.2 模型构建
采用改进鸟群算法优化核极限学习机模型参数，利用优化后的核极限学习机模型分别对重构后的网络流量子序列进行预测，将各个子序列的预测值进行组合，获得最终的网络流量预测结果.
采用改进鸟群算法通过种群个体之间的信息共享机制以及搜索策略最终获得最优解，具体寻优步骤如下：
1) 觅食行为.鸟类成群觅食时比个体觅食收集到的信息更多，并且觅食效率更高.根据这个原则将网络单元模拟为种群个体，整体网络体系模拟为种群.通过混沌映射初始化种群个体τ在D维搜索空间内的初始位置，每个个体依据历史搜索经验以及种群经验觅食.在种群个体位置更新阶段，引入随机惯性权重避免陷入局部最优，同时根据随机惯性权重值对种群中个体的认知因子C，C∈(Cmin，Cmax)，以及加速因子S，S∈(Smin，Smax)进行动态调整，即
(3)
ω=ωmin+(ωmax-ωmin)rand(0，1)+
σrand(0，1)
(4)
(5)
(6)
式中：
为种群中个体τ在t′时刻所处的位置；pτ为个体τ当前最优位置；gτ为种群当前阶段的最优位置；ω为迭代次数，ω∈(1，2，…，n)；ωmax、ωmin分别为最大迭代次数、最小迭代次数；rand(0，1)为期望为0，标准差为1的高斯分布随机数；Smin为加速因子最小值；Smax为加速因子最大值；Cmin、Cmax分别为认知因子最小值、最大值；σ为最佳适应度值.
2) 警惕行为.种群中的每只鸟在搜索过程中，都会试图靠近种群中心位置飞行.警惕性强的个体相比警惕性低的个体更容易向种群个体中心飞行，彼此之间相互竞争，根据此原则可得
(7)
式中：A1为搜索空间影响因子，A1∈(0，1)；A2为搜索空间干扰影响因子；meanj为群体第j维平均位置；pk，j为种群中搜索空间第j维的平均位置.
3) 个体飞行行为.鸟群会有规律地飞向某个地点，在飞行过程中，个体会在生产者与索取者之间进行切换，警惕性较低的个体寻找食物属于生产者，警惕性较高的个体获取食物属于索取者，生产者以及索取者能够脱离种群，根据此原则可得
(8)
基于改进的鸟群算法网络流量子序列预测模型可得
Lrand(0，1)
(9)
式中：L为索取者通过生产者寻找食物的因子；f为正则化参数.
基于改进的鸟群算法构建的网络流量子序列模型可以最小化输出权值和训练误差，即
(10)
式中：LE为核极限学习机模型输出权值；β为隐含层输出权值向量，β∈[0，2]；h(xτ)为隐含层输出结果；ξτ为训练输出误差.依据模型最优化条件可求解获得
(11)
式中：H为隐含层输出矩阵；T为目标值矩阵.依据Mercer’s条件对重构后的网络流量子序列进行预测，其子序列流量预测矩阵为
ΩE=βh(xτ)h(xj)=K(xτ，xj)
(12)
式中，K(xτ，xj)为子序列流量数据预测函数.利用改进的鸟群算法整合各个子序列的预测值，并对正则化参数进行优化，提升预测精度，最终的网络流量预测模型为
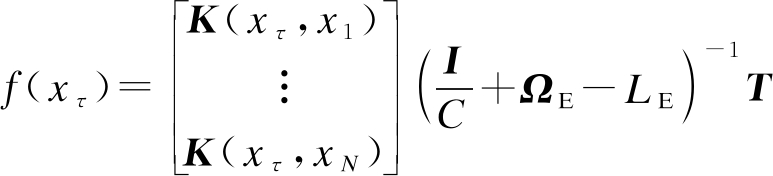
(13)
3 实验结果与分析
为了测试基于大数据分析的非线性网络流量组合预测模型的性能，仿真实验在Intel四核2.8 GHz CPU，4 GB内存，操作系统为Windows7硬件配置电脑下进行，利用VC++软件实现仿真实验.仿真实验来自NS2软件提供的实际网络流量数据，共2 000个数据点，如图2所示.将实际采集的网络流量数据划分为两组，第一组含有1 500个流量数据，将其作为训练数据集；第二组含有500个流量数据，将其作为测试数据集.
分析图2a可知，训练数据集中的网络流量数据具有非线性的特点，数值变化幅度较大，并且变化幅度较大的流量数据会掩盖变化幅度较小的流量数据；图2b测试训练集中的网络流量数据虽少，但是也呈现出非线性的变化特点.为了从采集的网络流量数据样本中获取其变化规律，对图2中的流量进行归一化处理，即
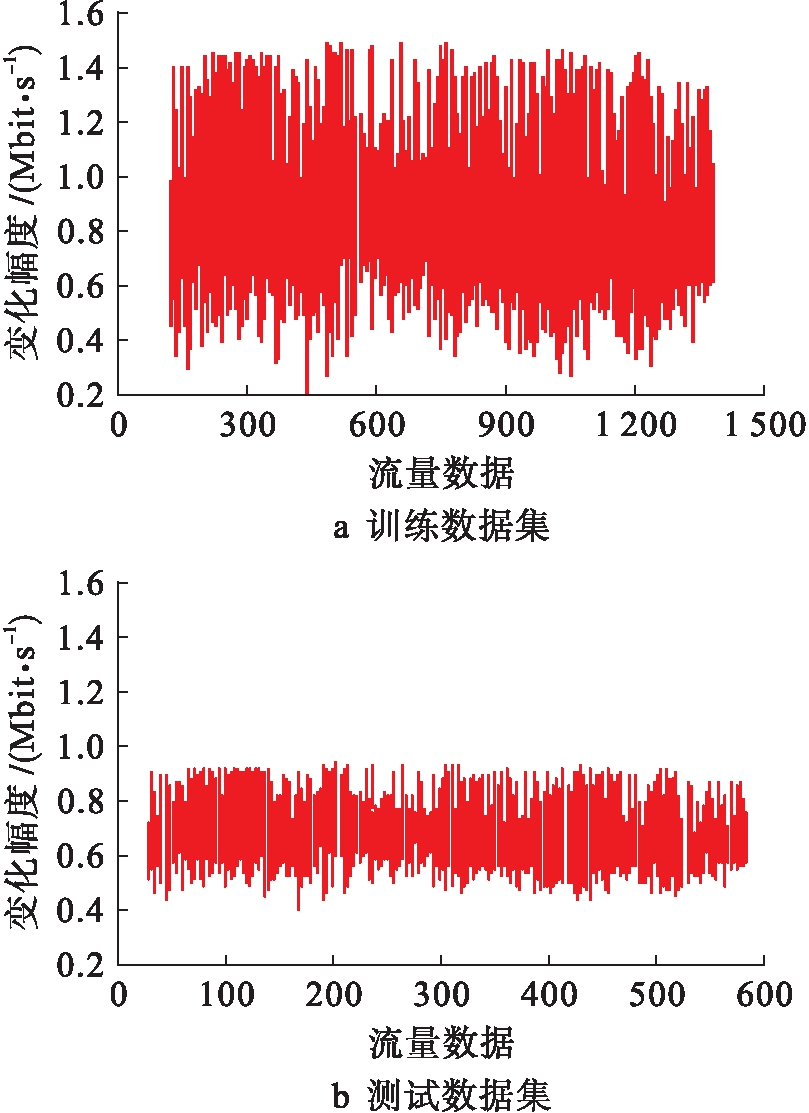
图2 实验数据变化情况
Fig.2 Change of experimental data
(14)
式中：xmax和xmin分别为归一化处理后的流量数据最大值和最小值；x为原始网络流量数据值.
为了使仿真实验的验证结果更具有说服力，选取文献[7]模型、文献[8]模型作为对比模型，将均方根误差(RMSE)、平均相对百分比误差(MAPE)作为评价指标对不同预测模型的性能进行评价，其表达式分别为
(15)
(16)
式中：n为网络流量数据样本数量；
为实际结果；x(i)为预测结果.
网络流量受到用户所属局域网网络带宽、浏览行为、业务种类以及上网时段等因素的影响，具有混沌性、非线性、突变性.针对这些特性，在构建网络流量组合预测模型前，利用混沌理论计算仿真对象的延迟时间以及嵌入维度，得到的最优延迟时间t以及嵌入维度m结果如图3所示.
分析图3可知，最优延迟时间为t=5，最优嵌入维度为m=4.选定t=5、m=4对网络流量数据进行重构，获得网络流量样本数据，并将其划分为训练集和测试集.
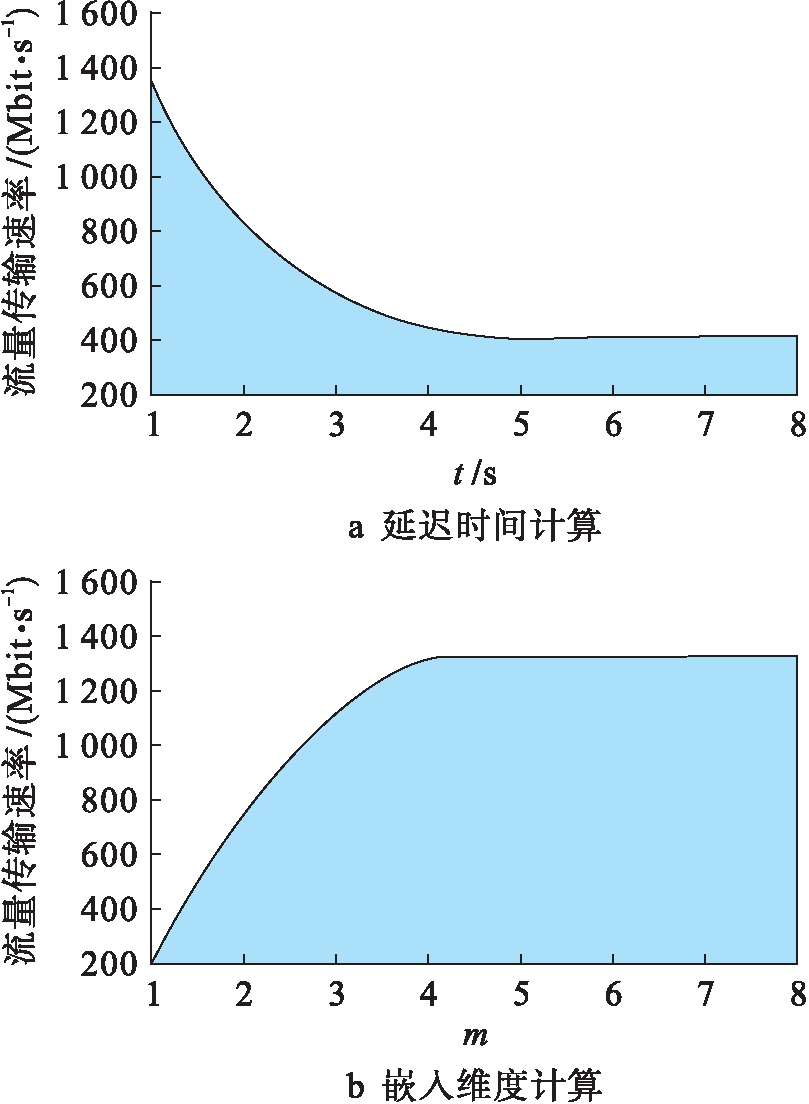
图3 延迟时间和嵌入维度的计算
Fig.3 Calculation of delay time and embedded dimensions
将非线性网络流量训练集输入到核极限学习机模型中进行学习，采用改进鸟群算法优化核极限学习机模型，并构建组合预测模型，预测结果以及预测误差的变化如图4所示.
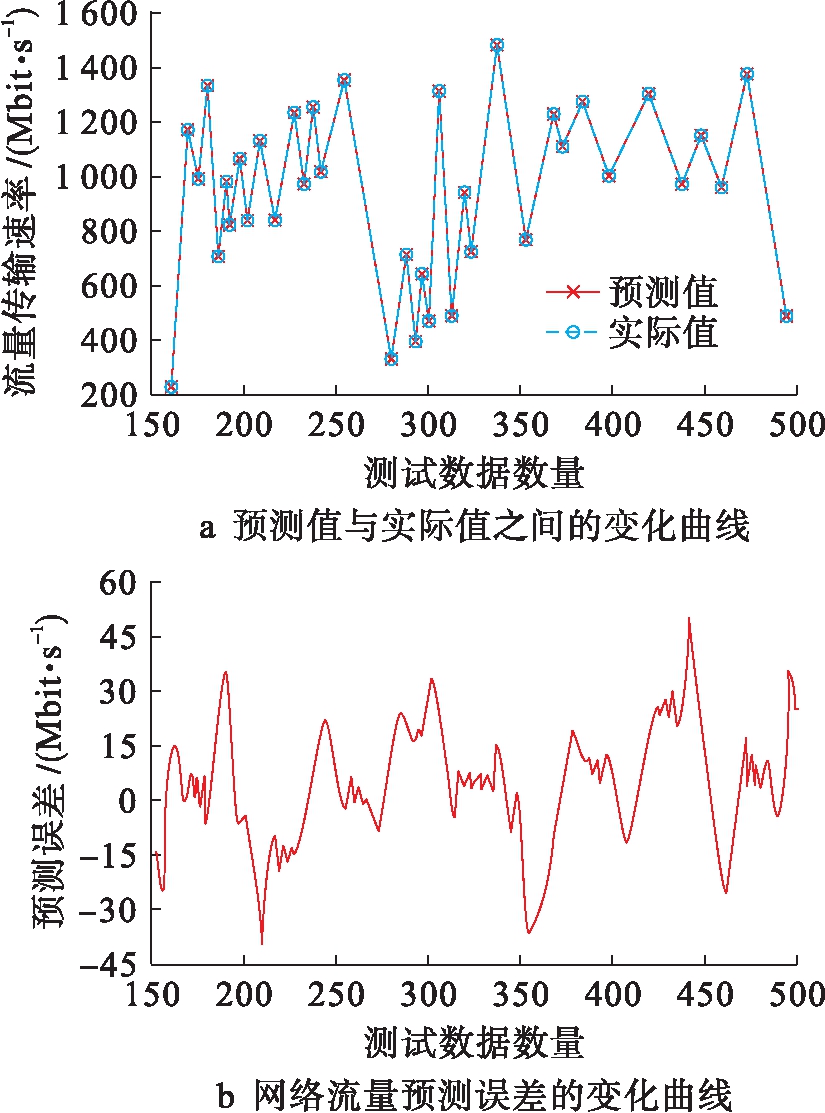
图4 所提模型单步预测结果
Fig.4 One-step prediction results of as-proposed model
分析图4可知，采用本文模型所得单步预测的流量值与实际网络流量值较为接近，可高精度地描述网络流量数据非线性变化特点，预测精度较高.结果表明，通过对采集的网络流量数据进行小波分解，将分解后的网络流量子序列进行相空间重构，并将重构结果输入至核极限学习机中，利用改进鸟群算法对核极限学习机模型进行优化，构建的组合预测模型是有效的.
所提模型与文献[7]模型、文献[8]模型所得的多步预测误差结果如表1所示.
表1 不同模型单步预测精度对比
Tab.1 Comparison of single-step prediction accuracy obtained by different models
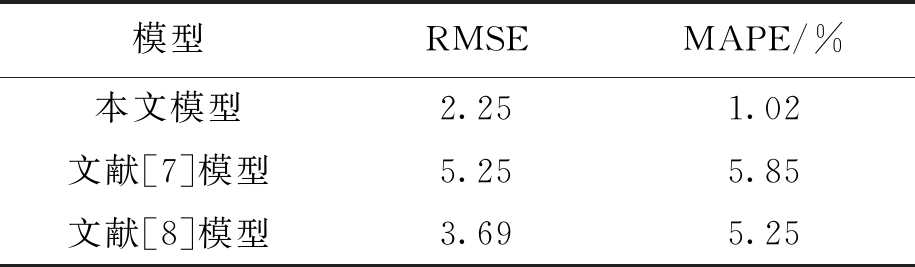
模型RMSEMAPE/%本文模型2.251.02文献[7]模型5.255.85文献[8]模型3.695.25
分析表1结果可知，与文献[7]模型以及文献[8]模型相比，本文模型预测误差最小，有效提高了预测精度，更适用于具有复杂特性的网络流量预测.
对于具有非线性突变特性的网络流量数据，对其进行高精度预测需要提前一定的时间，多步预测网络流量数据具有实际意义.采用本文模型对网络流量数据进行多步预测，获得的预测结果与预测误差变化曲线如图5所示.
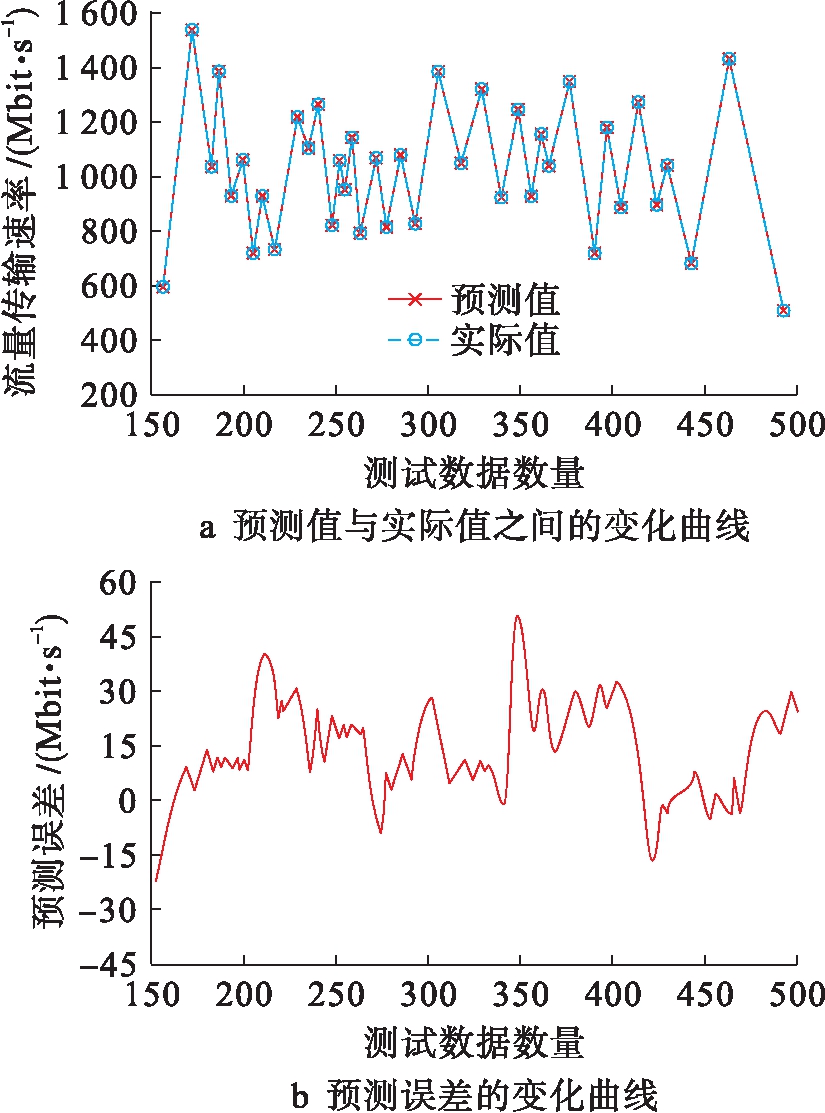
图5 本文模型多步流量预测结果
Fig.5 Prediction results of multi-step flow obtained by as-proposed model
分析图5可知，在先获知前几步流量数据变化趋势的前提下，本文模型预测结果与实际网络流量变化趋势几乎完全吻合，两者之间差值较小，且变化较为平稳，能够将预测误差控制在8%以下，满足大规模网络环境流量预测精度的要求.
本文模型、文献[7]模型以及文献[8]模型的多步预测误差结果如表2所示.
表2 不同模型多步预测误差结果对比
Tab.2 Comparison of multi-step prediction error results obtained by different models
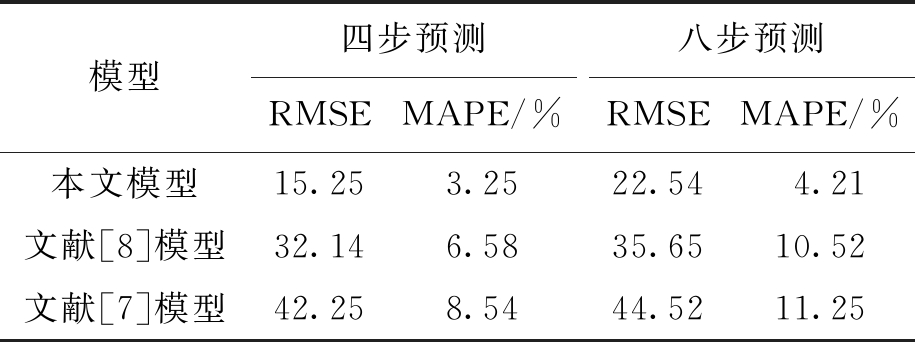
模型四步预测RMSEMAPE/%八步预测RMSEMAPE/%本文模型15.253.2522.544.21文献[8]模型32.146.5835.6510.52文献[7]模型42.258.5444.5211.25
通过对表2结果进行分析可获得以下结论：随着网络流量预测步数的不断增加，本文模型以及对比模型的预测误差逐渐增加，其中文献[7]模型预测误差增加的幅度较大，直到第八步预测时，该模型预测误差达到了11.25%，难以精确地描述网络流量数据阶段性变化趋势，且预测误差较大，所得结果没有实际应用价值.相对于文献[7]模型，文献[8]模型的预测精度较高，降低了网络流量预测误差，但该模型存在计算复杂度高、训练时间长等问题，难以满足大规模网络流量数据的在线预测要求.
4 结 论
网络流量受到带宽拥塞和病毒入侵等多种因素的影响，具有非线性、周期性、长相关性等变化特征，传统的预测模型预测精度较低，针对此问题，提出一种组合预测模型.通过对预测结果进行分析得到以下结论：
1) 相对于文献[7]、文献[8]模型，本文模型预测结果的评价指标均更优，说明所提方法克服了当前预测模型存在的精度低的问题，更适用于大规模网络流量预测.
2) 相对于文献[7]、文献[8]模型，本文模型预测精度有所提高，这表明采用快速小波分析算法对网络流量进行多尺度分解，可以准确挖掘出网络流量数据阶段性变化特征，通过网络流量子序列表示网络流量的多层次变化特性.
3) 从图4～5中给出的网络流量预测结果来看，所提模型获得的网络流量预测值与实际值几乎完全吻合，变化趋势基本相同，说明所提模型预测精度较高.
[1]李军，黄杰.基于自组织映射神经网络的局部自回归方法在网络流量预测中的应用 [J].信息与控制，2016，45(1)：120-128.
(LI Jun，HUANG Jie.Prediction of network traffic using local auto-regressive methods based on self-organizing map neural network [J].Information and Control，2016，45(1)：120-128.)
[2]张洋，吴斌，张继革，等.基于组合模型的网络流量预测 [J].华中科技大学学报(自然科学版)，2016，44(增刊1)：29-34.
(ZHANG Yang，WU Bin，ZHANG Ji-ge，et al.Network traffic forecasting based on combined model [J].Journal of Huazhong University of Science and Technology (Nature Science Edition)，2016，44(Sup1)：29-34.)
[3]张敬磊，王晓原.交通流灰色RBF网络非线性组合预测方法 [J].数学的实践与认识，2011，41(19)：1-7.
(ZHANG Jing-lei，WANG Xiao-yuan.Non-linear combined approach to traffic flow prediction based on gray RBF network [J].Mathematics in Practice and Theory，2011，41(19)：1-7.)
[4]肖汉杰，桑秀丽.相关向量机超参数优化的小时间尺度网络流量非线性预测方法 [J].计算机应用研究，2016，33(6)：1882-1885.
(XIAO Han-jie，SANG Xiu-li.Nonlinear prediction method for small time scale network traffic with optimized ultra parameters of relevance vector machine [J].Application Research of Computers，2016，33(6)：1882-1885.)
[5]段谟意.基于小波分解和支持向量机的网络流量组合预测 [J].微电子学与计算机，2012，29(9)：193-196.
(DUAN Mo-yi.Network traffic combination forecasting by wavelet decomposition and support vector machine [J].Microelectronics & Computer，2012，29(9)：193-196.)
[6]赵会敏，雒江涛，杨军超，等.集成BP神经网络预测模型的研究与应用 [J].电信科学，2016，32(2)：60-67.
(ZHAO Hui-min，LUO Jiang-tao，YANG Jun-chao，et al.Research and application of prediction model based on ensemble BP neural network [J].Telecommunication Science，2016，32(2)：60-67.)
[7]殷荣网.基于FCM-LSSVM网络流量预测模型 [J].计算机工程与应用，2016，52(1)：105-109.
(YIN Rong-wang.Network traffic predicting model based on FCM-LSSVM [J].Computer Engineering and Applications，2016，52(1)：105-109.)
[8]王洪蕾，双凯，柴琦，等.网络流量监控系统的概述与实现 [J].电子设计工程，2017，25(11)：27-30.
(WANG Hong-lei，SHUANG Kai，CHAI Qi，et al.The summary and realization of the network flow monitoring system [J].Electronic Design Engineering，2017，25(11)：27-30.)
[9]赵晓静，舒勤，黄宏光.高速公路交通流量预测模型仿真 [J].计算机仿真，2017，34(6)：169-173.
(ZHAO Xiao-jing，SHU Qin，HUANG Hong-guang.Simulation of freeway traffic flow forecasting model [J].Computer Simulation，2017，34(6)：169-173.)
[10]段华琼，唐宾徽.基于线性多尺度模型的计算机网络数据流量预测 [J].沈阳工业大学学报，2017，39(3)：322-327.
(DUAN Hua-qiong，TANG Bin-hui.Prediction of data flow in computer network based on linear multi-scale model [J].Journal of Shenyang University of Techno-logy，2017，39(3)：322-327.)