应变曲线与试验曲线吻合较好，混凝土单轴压缩过程各阶段吻合度较高，混凝土单轴压缩损伤本构模型具有一定的合理性.建筑工程
摘 要： 为了研究混凝土单轴压缩状态下的损伤演化过程，利用声发射设备采集试样破坏过程的声发射数据，基于声发射信号建立声发射能量表述的损伤本构方程，对损伤程度进行量化表述，提出了损伤因子在启裂强度和损伤强度的取值区间.基于连续介质损伤力学，对微裂纹的发育过程和声发射能量数综合分析.结果表明，理论应力应变曲线与试验曲线吻合较好，混凝土单轴压缩过程各阶段吻合度较高，混凝土单轴压缩损伤本构模型具有一定的合理性.
声发射(acoustic emission，AE)是材料在外部载荷或者其他外部作用下材料内部裂隙产生和裂隙发育的过程中，能量以弹性波释放的过程.作为材料损伤的无损探测方法之一，声发射具有其独特的优越性，设备轻便，可以多参数综合分析，数据直观，监测简单，监测对象既可以取回实验室，也可现场进行，被广泛应用于隧道工程、水电工程、采矿工程、航空航天工程等重要领域.周辉等[1]基于声发射监测数据进行了硬岩启裂强度和损伤强度取值方法的探讨；纪洪广等[2]研究了花岗岩在常规三轴压缩下的声发射特征，发现了振铃计数、能量累计数在岩石破裂过程中的整体变化趋势基本相同，与岩石力学过程形成良好的对应；吴贤振等[3]研究了岩石不同破坏模式下声发射特征及其参数与应力、应变、损伤变量之间的关系；郭清露等[4]研究了大理岩热损伤声发射力学特性，通过声发射数据建立了损伤变量及大理岩本构模型；曾正文等[5]研究了单节理岩体变形与破坏过程中声发射能量的特征，发现了岩石破裂过程中，声发射能量率越大，裂隙扩展越大；Rusch[6]研究了混凝土受压破坏时的Kaiser效应；郭庆华等[7]对混凝土声发射信号频率与强度指标的关系进行了研究，认为混凝土强度指标影响混凝土声发射信号频率特征参数；赖于树等[8]研究了受载混凝土破坏全过程声发射信号频带能量特征，通过FFT变换及小波变换研究了不同破坏阶段声发射信号频率分布、频带能量的变化规律，并从声发射信号频率变迁与裂纹扩展关系角度阐释了混凝土破坏机理；杨跃飞等[9]对单轴多级循环加载条件下混凝土进行了研究，通过分析试验过程中的能量演化规律，引入活跃系数Act对声发射现象发生的活跃程度进行表述.
通过上述研究成果可以看出，声发射监测技术可以揭示岩土材料在外部作用下的裂隙产生及扩展过程.对混凝土材料而言，其声发射参数变化反映了混凝土的损伤变化，与混凝土内部缺陷的演化程度直接相关.本文结合声发射参数变化特征，对试验加载过程中混凝土试样的损伤演化规律进行分析，研究混凝土内部裂隙的扩展规律，通过定义损伤变量，定量描述混凝土的损伤程度，研究成果对工程安全性评价与灾害预防具有重要意义.
试验采用的设备组件如图1所示.加载系统采用RMT-150C岩石力学试验系统，该系统通过电液伺服试验机进行加载，垂直液压缸最大出力1 000 kN，试验加载速率为0.002 mm/s，为减小试样与试验机压头的摩擦效应，在接触面涂抹凡士林作为润滑剂.试验声发射监测采用The AE Sensor Highyway ⅡTM，前置放大器为45 dB，门阈值为45 dB，振谐频率为1 kHz～1 MHz，采用其中三个通道(86、87、88)进行信息采集，声发射探头与试样之间采用真空润滑脂作为耦合剂，用乳胶套将声发射探头固定在试样表面，以保证探头与岩样始终接触良好.声发射设备与加载设备同时开始与结束，以保证数据时间节点上的对应性.试验开始前用断铅法检验传感器是否正常工作.
图1 试验系统组件
Fig.1 Test system components
针对武汉长江隧道支护管片，试验采用C50混凝土，材料配合比为水泥∶粉煤灰∶砂∶石子∶水∶减水剂=2.53∶0.67∶4.61∶7.50∶1∶0.05.试样制备参考《公路工程岩石力学试验规范》(JTG-E41-2005)[10]，利用钻机取出直径50 mm、高100 mm的圆柱体，对两端细致打磨，保证试样两端面平面度公差小于0.05 mm.
为研究混凝土加载过程中的损伤演化规律，在对混凝土试样进行单轴压缩试验时，使用声发射设备采集整个试验过程中的声发射信号，试验过程及结果如图2所示.通过综合分析试样受压全过程中裂隙的产生、发育与声发射的计数、能量等特征参数的对应关系，利用总能量的释放规律来建立连续介质损伤本构方程，对比验证试验数据，分析试样破坏过程中的损伤系数演化规律.
由图2可以看出，试样破坏方式基本以40°～60°斜裂纹贯通方式而失去承载能力.表1为试样参数.图3为试验过程的应力应变曲线.为了更全面地描述混凝土的力学损伤演化规律，采用体应变等效假设，参照应力等效性假设[11]：对于受损材料的应力应变关系可以用虚拟的无损状态下的应力应变关系代替，但仍需用有效应变ε代替真实应变
即对于一维情况，真实损伤状态的应力应变关系为
图2 混凝土单轴压缩试验过程及结果
Fig.2 Process and results of uniaxial compression test of concrete
(1)
虚拟的无损状态应力应变关系为
(2)
则有
(3)
式中：E′为杨氏模量；
为等效杨氏模量.本文用有效应变εv替换虚拟的体应变σ1/K，其中，K为体积模量.根据广义胡克定律，真实损伤状态的真实体积应变虚拟体积应变关系表达式为
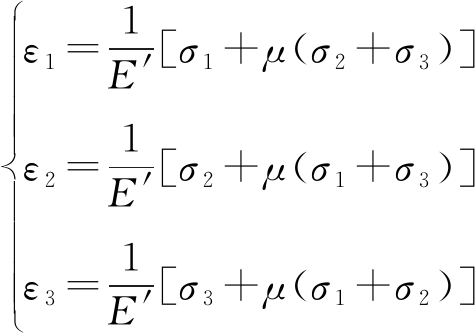
(4)
式中，μ为泊松比.体积应变为
εv=ε1+ε2+ε3
(5)
体积模量
(6)
裂隙体应变为
(7)
将式(6)代入式(7)则有
(8)
表1 试样参数
Tab.1 Specimen parameters
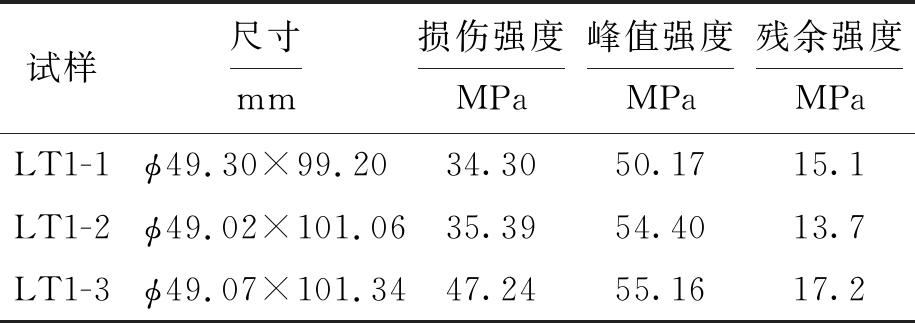
试样尺寸mm损伤强度MPa峰值强度MPa残余强度MPaLT1-1ϕ49.30×99.2034.3050.1715.1LT1-2ϕ49.02×101.0635.3954.4013.7LT1-3ϕ49.07×101.3447.2455.1617.2
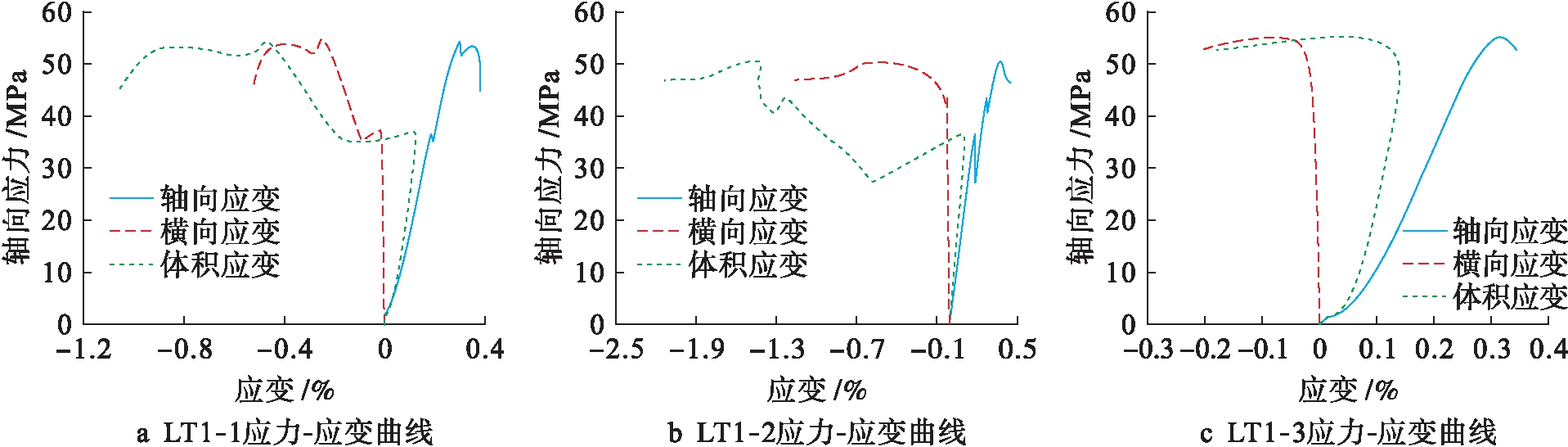
图3 轴向应力轴向应变曲线
Fig.3 Axial stress-axial strain curves
图4为轴向应力应变曲线、体积应变轴向应变曲线和裂隙体积应变轴向应变曲线.分析可以看出，试样经历了压密(OA)、弹性(AB)、裂纹稳定扩展(BC)、裂纹不稳定扩展(CD)和峰后(DE)五个阶段：1)OA阶段为孔隙压缩、闭合阶段，体积应变和裂隙体积应变增大，试样被轴向压缩，微裂隙被压实，应力应变曲线呈现上凹形非线性变化，试样体积应变与裂隙体积应变数值逐步增加；2)AB段为弹性段，该阶段应力应变曲线近似为直线，应力应变近似符合胡克定律，理论上无微裂隙萌生，试样体积应变逐步上升，裂隙体积应变趋近于水平，水平线段结束点即为启裂强度点(B点对应的应力值)；3)BC段为裂纹稳定扩展段，该段裂隙体积应变逐渐减小，内部微裂隙萌生并逐步扩大，启裂强度即为试样开始发生损伤的阈值，B点后变形为弹塑性变形；4)CD段为裂纹非稳定扩展段，轴向应力增加到损伤强度(C点对应的应力值)后，裂隙体积应变和试样体积应变值减小，说明在该段，裂纹扩展造成的体积应变已经大于轴向压缩造成的弹性体积应变；5)DE段为峰后段，应力达到峰值点(D点对应的应力值)后，试样体积应变和裂隙体积应变值继续减小，局部宏观裂隙形成并扩展，直至整体宏观裂隙贯通，试样失去承载能力.
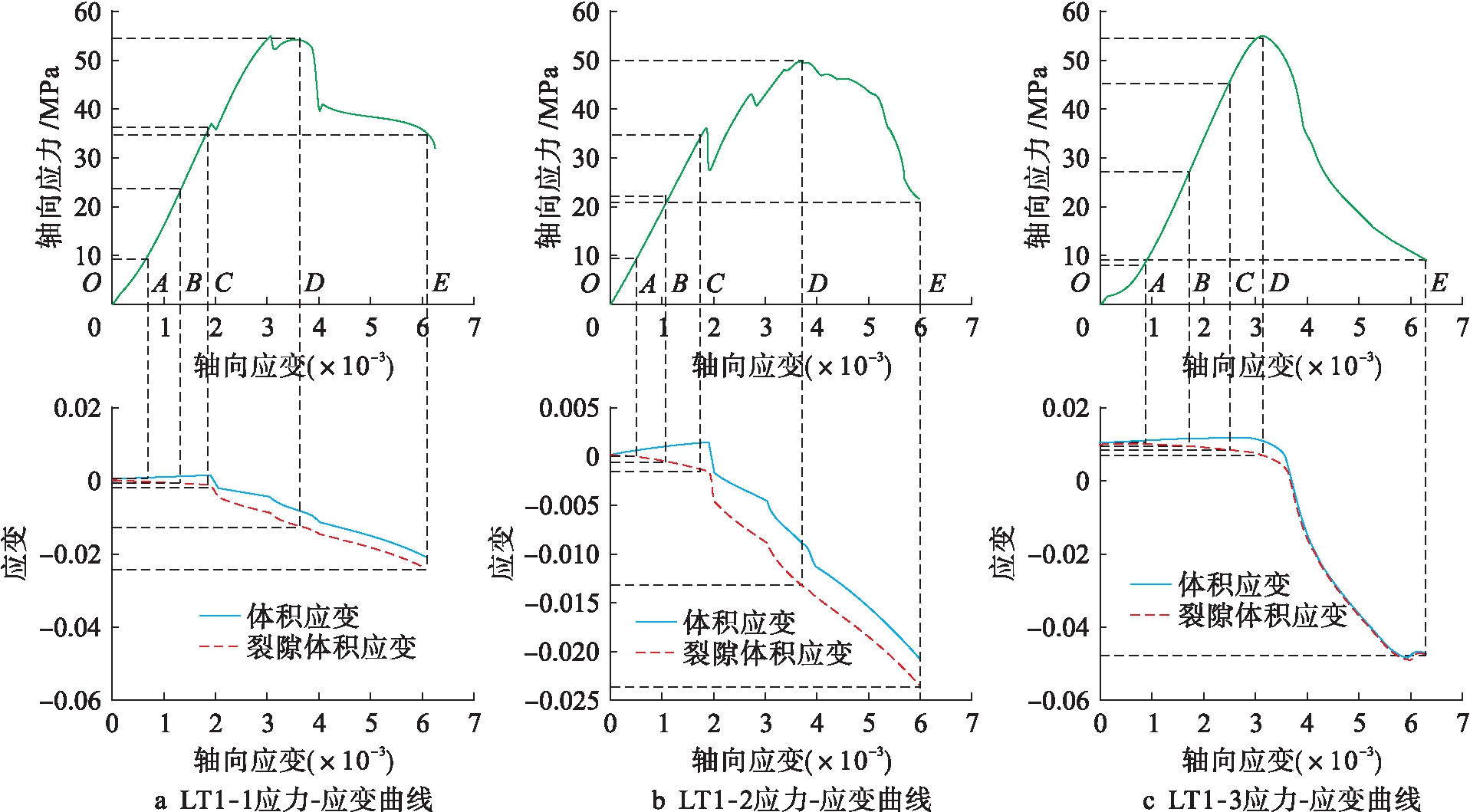
图4 应力应变曲线
Fig.4 Stress-strain curves
声发射撞击数是单位时间内捕捉并记录下的幅值超过门阈的信号次数，能量率是单位时间内捕捉到的能量之和.本文对微裂隙发育过程中产生的低于阈值而未记录的极小部分能量损失不予考虑.
基于连续介质损伤力学基本理论，参照刘保县等[12]定义的损伤变量.本文将能量与裂隙扩展演化联系起来，假设应力达到应力残余值前声发射捕捉到的累计释放的总能量为Pc，应力残余值前第i段释放的能量为Pi，且为了便于计算，取试样失去承载力时对应的损伤变量D′为1，保证D′是不可逆的增函数，定义D′c为损伤临界值，由于试样达到残余强度时未全部破坏，故D′c值可记为
(9)
式中，σc为残余应力.定义损伤变量为
(10)
则为
(11)
图5～7为应力、通道计数、能量、损伤变量与时间的关系曲线.结合图5～7分析可得：1)在OA压密段，孔隙逐渐闭合，微裂隙被压密，理论上无声发射事件，损伤变量接近0；2)在弹性阶段BC段，应力应变曲线呈线性关系，且为弹性变形，故理论上无声发射现象，损伤变量依然接近于0；3)在裂纹稳定扩展段BC段，随着微裂隙的扩展，声发射事件开始增多，损伤变量开始增大，在BC段后期声发射事件数激增，激增的原因是有宏观裂隙形成并稳定扩展，声发射激增点在启裂强度σci附近，表明激增点和启裂强度值有关；4)在非稳定扩展阶段CD段，当超过损伤强度σcd时，声发射事件进入相对平稳区段，该区段声发射事件时间变化曲线与应力时间变化趋势具有很好的对应关系，说明能量释放密集；5)在峰后阶段DE段，随着损伤程度增加，局部宏观裂缝进一步向整体扩张，导致试样整体承载力迅速降低，声发射事件逐渐减少，能量率降低，该区间的损伤变量曲线斜率减小，直至试样破坏，损伤变量时间曲线逐渐趋近于水平.图7中，试样LT1-1、LT1-2、LT1-3启裂强度发生在损伤因子平均值为0.02处；损伤强度发生在损伤因子平均值为0.20处；峰值强度发生在损伤因子平均值为0.45处.由此可知，理论本构模型中的损伤变量可以定量描述混凝土结构的损伤程度.
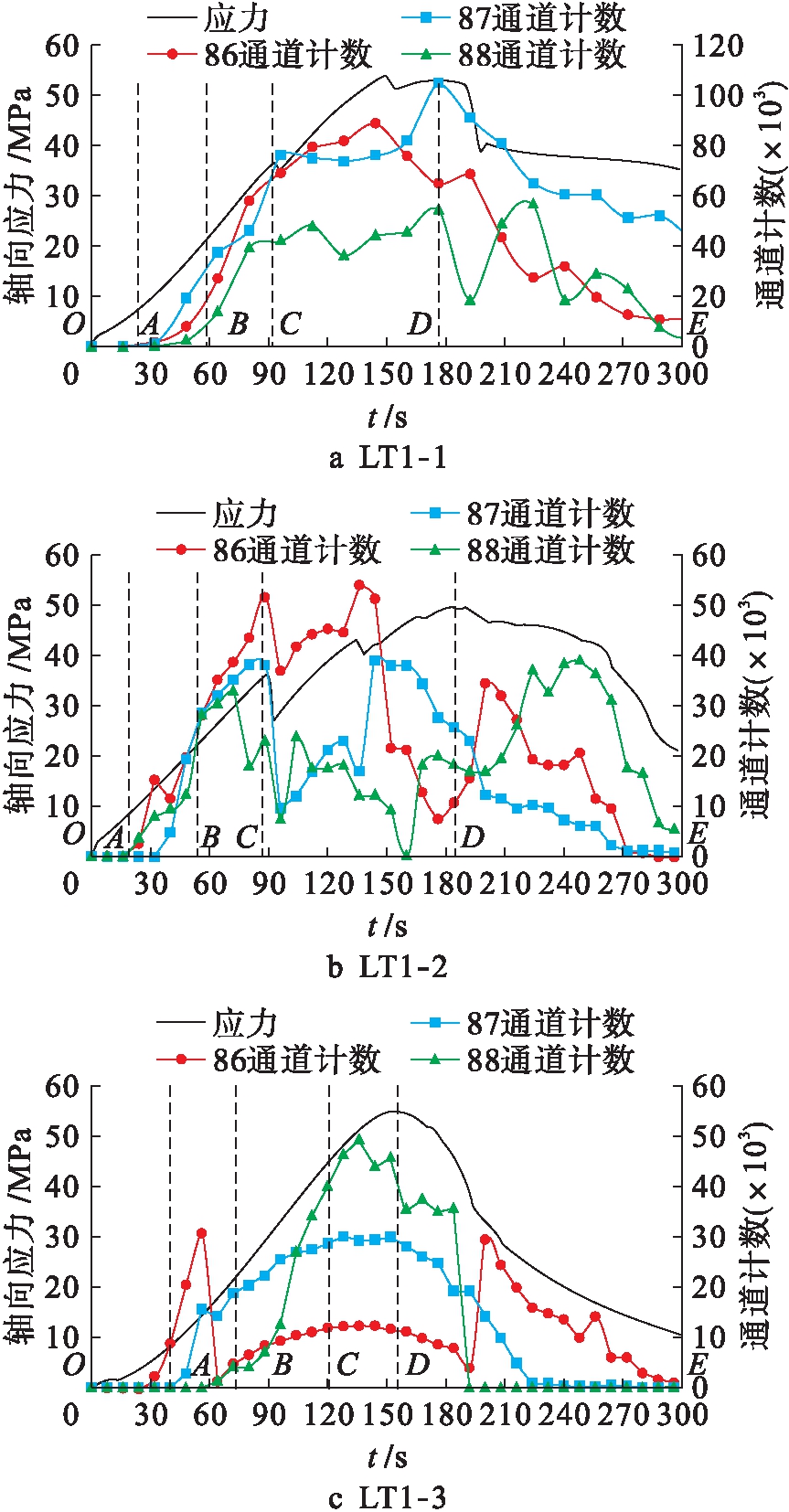
图5 轴向应力时间曲线和通道计数时间曲线
Fig.5 Axial stress-time curves and channel count-time curves
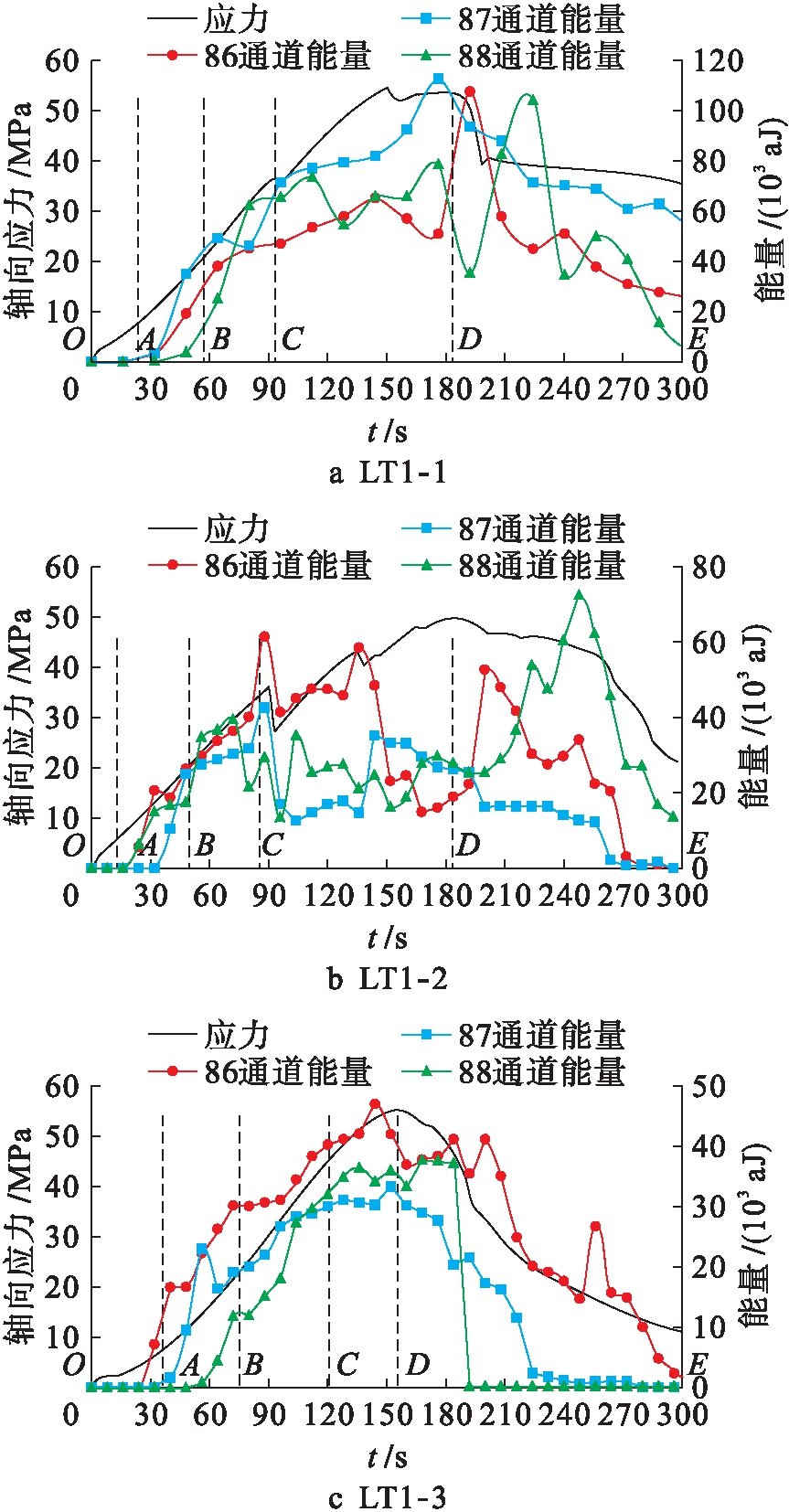
图6 轴向应力时间曲线和能量时间曲线
Fig.6 Axial stress-time curves and energy-time curves
基于等效连续介质力学原理，将混凝土单轴压缩力学模型分为两段讨论，其应力应变关系可以表示为
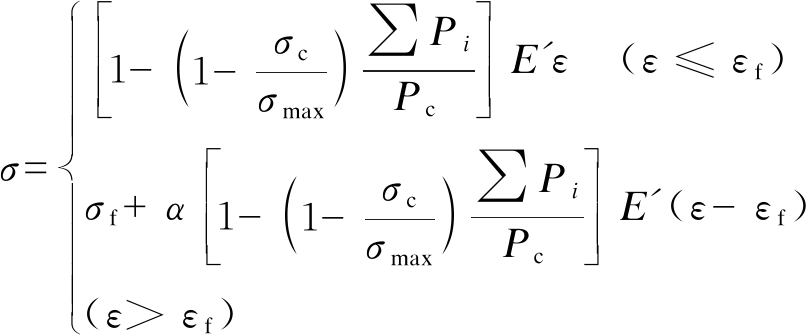
(12)
式中：σf和εf为σmax对应的轴向应力和应变；α为考虑裂隙扩张而定义的应变扩张系数.基于试验数据，计算分析得到，当α=-1.45时，理论应力应变曲线与试验结果最为吻合，故式(12)可写为
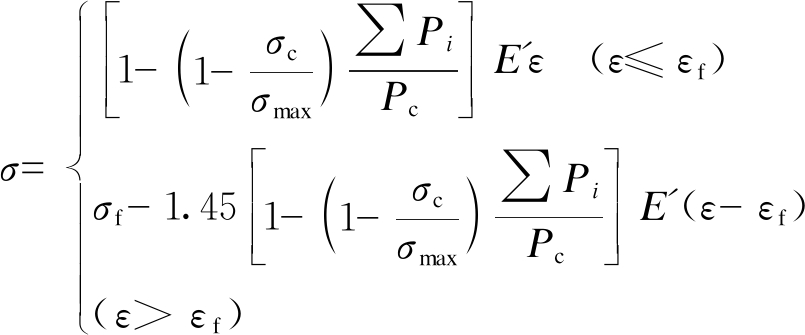
(13)
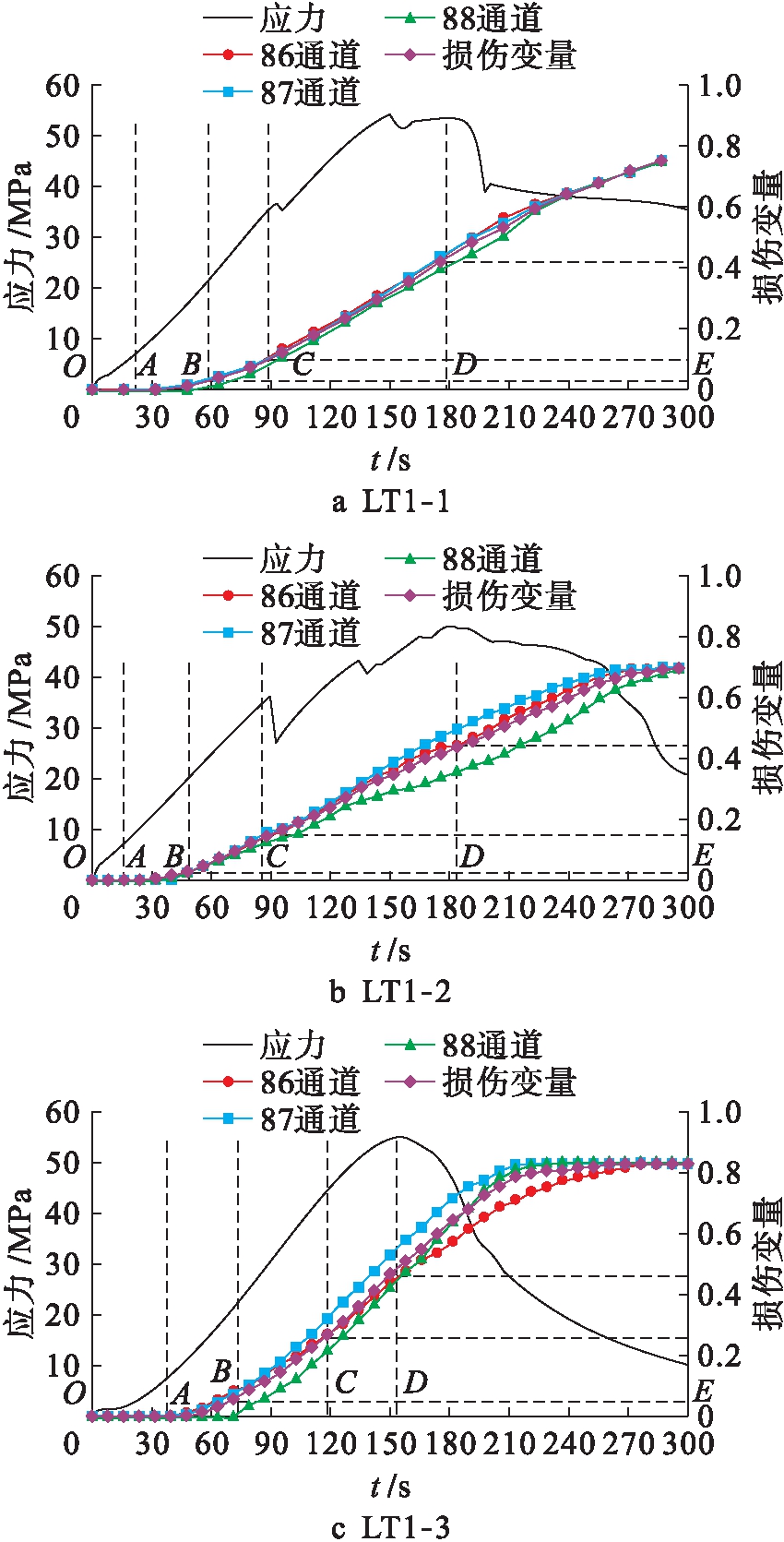
图7 轴向应力时间曲线和损伤变量时间曲线
Fig.7 Axial stress-time curves and damage variable-time curves
由式(13)可得到模型应力应变曲线和损伤变量应变曲线，如图8所示.根据理论方程可得理论应力应变曲线，如图9所示.根据图9，引入声发射能量定义损伤变量的理论应力应变曲线与试验曲线吻合程度较高，说明该理论本构模型能够将混凝土单轴受压过程中裂隙的萌生、扩展及贯通这一裂隙的演化行为较为准确地描述出来.
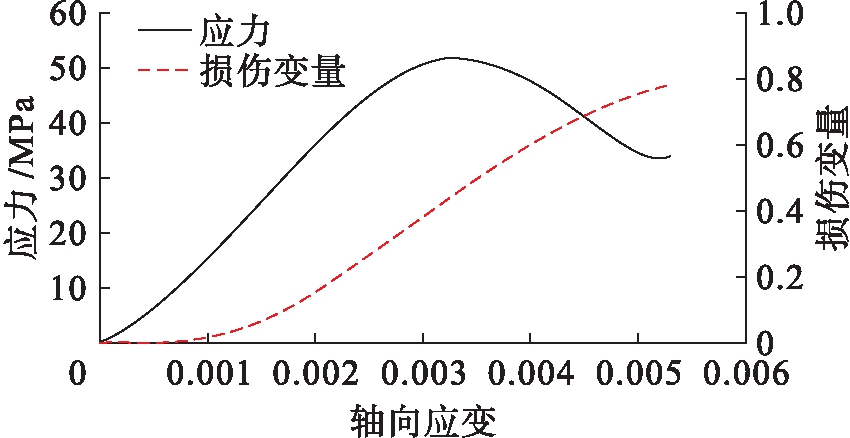
图8 模型应力应变曲线和损伤变量应变曲线
Fig.8 Model stress-strain curves and damage variable-strain curves
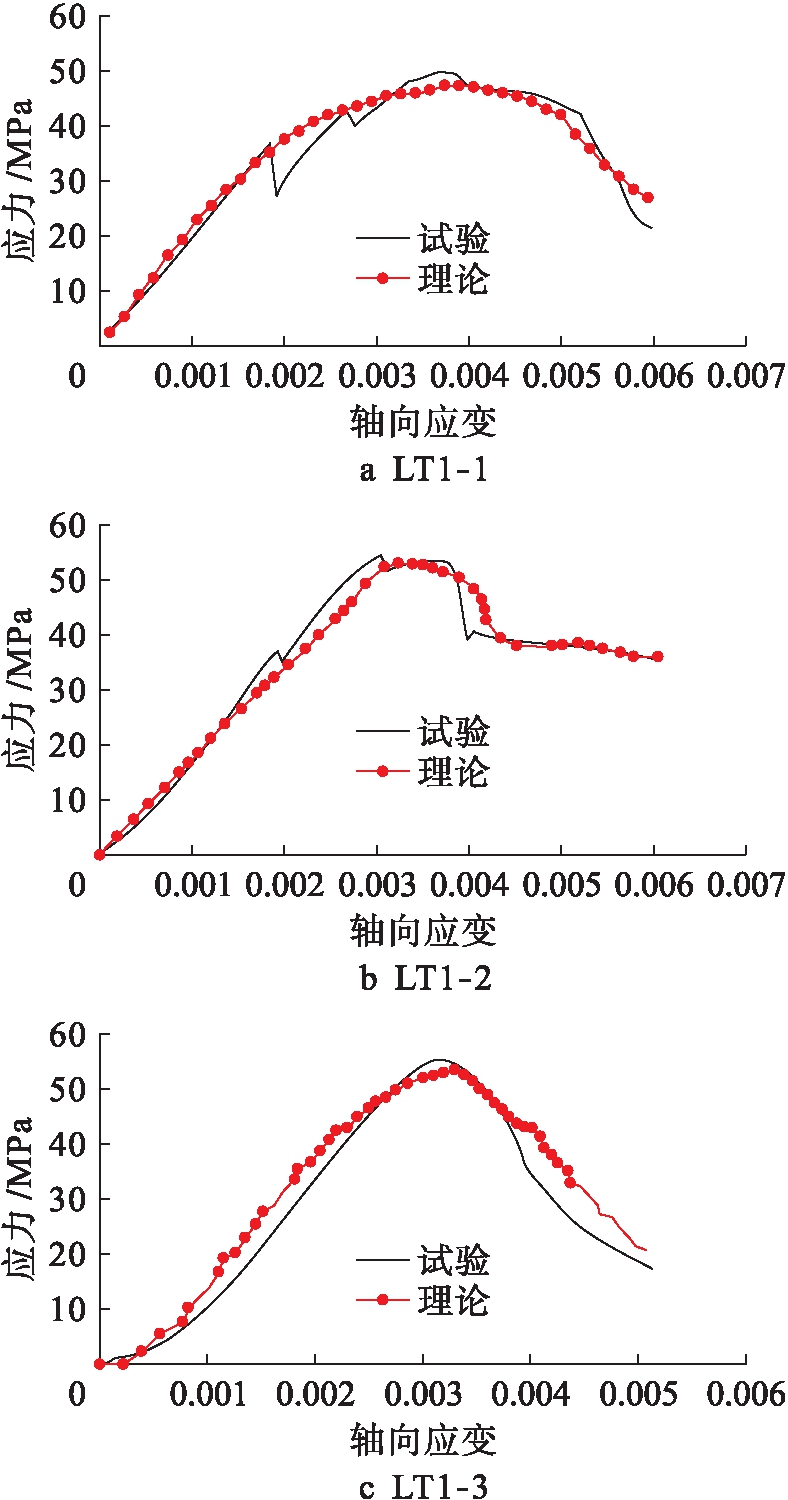
图9 试验应力应变曲线和理论应力应变曲线
Fig.9 Experimental stress-strain curves and theoretical stress-strain curves
本文通过混凝土试样的单轴压缩试验及声发射监测，综合分析了试验过程中裂隙的发育、扩展和对应的声发射特征.通过声发射能量，建立了描述混凝土试样加载过程力学性质的损伤本构模型，得到如下结论：
1) 声发射参数变化从侧面较为准确地反映了混凝土单轴受压破坏过程，能量率变化规律与应力应变曲线变化规律较为吻合.
2) 通过综合分析裂隙体积应变的变化规律和声发射参数演化规律，建立了混凝土单轴压缩损伤本构模型，并验证了其合理性.
3) 对比分析理论应力应变曲线和试验应力应变曲线可以发现，混凝土单轴压缩过程各阶段吻合度较高，从侧面表述混凝土单轴加载过程中裂隙的萌生、发育、贯通的完整过程，说明可以通过损伤变量值量化判断混凝土损伤程度.
[1]周辉，孟凡震，卢景景，等.硬岩裂纹起裂强度和损伤强度取值方法探讨 [J].岩土力学，2014，35(4)：913-918.
(ZHOU Hui，MENG Fan-zhen，LU Jing-jing，et al.Discussion on methods for calculating crack initiation strength and crack damage strength for hard rock [J].Rock and Soil Mechanics，2014，35(4)：913-918.)
[2]纪洪广，卢翔.常规三轴压缩下花岗岩声发射特征及其主破裂前兆信息研究 [J].岩石力学与工程学报，2015，34(4)：694-702.
(JI Hong-guang，LU Xiang.Characteristics of acoustic emission and rock fracture precursors of granite under conventional triaxial compression [J].Chinese Journal of Rock Mechanics and Engineering，2015，34(4)：694-702.)
[3]吴贤振，刘建伟，刘祥鑫，等.岩石声发射振铃累计计数与损伤本构模型的耦合关系探究 [J].采矿与安全工程学报，2015，32(1)：28-34.
(WU Xian-zhen，LIU Jian-wei，LIU Xiang-xin，et al.Study on the coupled relationship between AE accumulative ring-down count and damage constitutive model of rock [J].Journal of Mining and Safety Engineering，2015，32(1)：28-34.)
[4]郭清露，荣冠，姚孟迪，等.大理岩热损伤声发射力学特性试验研究 [J].岩石力学与工程学报，2015，34(12)：2388-2400.
(GUO Qing-lu，RONG Guan，YAO Meng-di，et al.Experimental study on acoustic emission behaviors and mechanical properties of thermal damaged marbles [J].Chinese Journal of Rock Mechanics and Engineering，2015，34(12)：2388-2400.)
[5]曾正文，马瑾，吴秀泉，等.单节理岩体变形与破坏过程中声发射能量的特征及意义 [J].地震地质，1994，16(1)：71-77.
(ZENG Zheng-wen，MA Jin，WU Xiu-quan，et al.Characteristics and implications of acoustic emission energy in the process of deformation and failure of single-joint rockmass [J].Seismology and Geology，1994，16(1)：71-77.)
[6]Rusch H.Physical problems in the testing of concrete [J].Zement-Kalk-Gips，1959，12(1)：1-9.
[7]郭庆华，郤保平，李志伟，等.混凝土声发射信号频率特征与强度参数的相关性试验研究 [J].中南大学学报(自然科学版)，2015，46(4)：1482-1488.
(GUO Qing-hua，XI Bao-ping，LI Zhi-wei，et al.Experimental research on relationship between frequency characteristics of acoustic emission and strength parameter in concrete [J].Journal of Central South University (Science and Technology)，2015，46(4)：1482-1488.)
[8]赖于树，熊燕，程龙飞.受载混凝土破坏全过程声发射信号频带能量特征 [J].振动与冲击，2014，33(10)：177-182.
(LAI Yu-shu，XIONG Yan，CHENG Long-fei.Frequency band energy characteristics of acoustic emission signals in damage process of concrete under uniaxial compression [J].Journal of Vibration and Shock，2014，33(10)：177-182.)
[9]杨跃飞，刘京红，薛如政，等.混凝土材料分级加载过程的声发射特征分析 [J].河北农业大学学报，2018，41(1)：100-105.
(YANG Yue-fei，LIU Jing-hong，XUE Ru-zheng，et al.Acoustic emission characteristic analysis of concrete materials under step loads [J].Journal of Hebei Agricultural University，2018，41(1)：100-105.)
[10]中华人民共和国交通运输部.JTG-E41-2005公路工程岩石力学试验规范 [S].北京：人民交通出版社，2005.
(Ministry of Transport of the People′s Republic of China.JTG-E41-2005 Test methods of rock for highway engineering [S].Beijing：China Communications Press，2005.)
[11]沈为.损伤力学 [M].武汉：华中理工大学出版社，1995.
(SHEN Wei.Damage mechanics [M].Wuhan：Huazhong University of Science and Technology Press，1995.)
[12]刘保县，黄敬林，王泽云，等.单轴压缩煤岩损伤演化及声发射特性研究 [J].岩石力学与工程学报，2009，28(增刊1)：3234-3238.
(LIU Bao-xian，HUANG Jing-lin，WANG Ze-yun，et al.Study on damage evolution and acoustic emission character of coal rock under uniaxial compression [J].Chinese Journal of Rock Mechanics and Engineering，2009，28(Sup1)：3234-3238.)