抗滑桩作为滑坡治理工程的主要支挡措施被广泛采用,目前,抗滑桩内力计算已经较为成熟[1],抗滑桩结构设计计算的关键是桩身作用荷载的确定.
抗滑桩承受的外力主要是桩后滑坡推力和桩前土体抗力.各国在计算滑坡推力方法上差别不大[2-6],大都采用传递系数法,计算时将滑坡范围内滑动方向与滑动速度大体一致的部分滑体视为一个计算单元,并在其中选择一个或几个顺滑坡主轴方向的地质纵断面为代表,按滑动面坡度和地层性质的不同,把整个断面上的滑体适当划分成若干竖直条块,自后向前,依次计算各滑块边界上的剩余下滑力.但对于桩前土体抗力的研究多集中于抗力分布规律上,目前桩前土体抗力大小的求解一般通过滑坡推力曲线确定,并与桩前被动土压力作比较,取二者中较小值,若桩前土体不稳定或被挖走,则需要考虑折减或不计桩前抗力[7].利用滑坡推力曲线求解桩前土体抗力时无法考虑抗滑桩的变形因素,计算结果偏大;而被动土压力是土体处于极限状态的土压力,桩前土体抗力通常不会达到被动土压力.
本文在前人研究的基础上,基于地基系数法中的“K”法,推导出桩前土体抗力的计算公式,并结合实际工程,利用MIDAS GTS NX有限元软件论证分析了其合理性与正确性.
1 桩前土体抗力计算
在抗滑桩设计中,由于桩前土体抗力计算的复杂性与不确定性,大部分设计人员都不考虑桩前土体抗力,这虽然使设计偏于安全,但也造成了不必要的浪费,正确求解桩前土体抗力,能在保证安全的前提下降低工程造价.
本文基于地基系数法中的“K”法来求解桩前土体抗力,计算模型如图1所示.图1中,L为抗滑桩滑动面以上受荷段的长度,q为桩后滑坡推力.滑体是一种粘聚力较大的地层,滑坡推力分布图形可按矩形考虑,如果滑体是一种以内摩擦角为主要抗剪特性的堆积体,其推力分布图形可近似按三角形考虑,介于两者中间的可按梯形考虑.本文根据镇江地区土质特性假设滑坡推力为矩形分布,滑坡推力为三角形或梯形分布时亦可按本文方法推导.地基系数法是把整根桩当作弹性地基上的梁来计算,因此,用弹簧代替桩前土体与抗滑桩的相互作用.
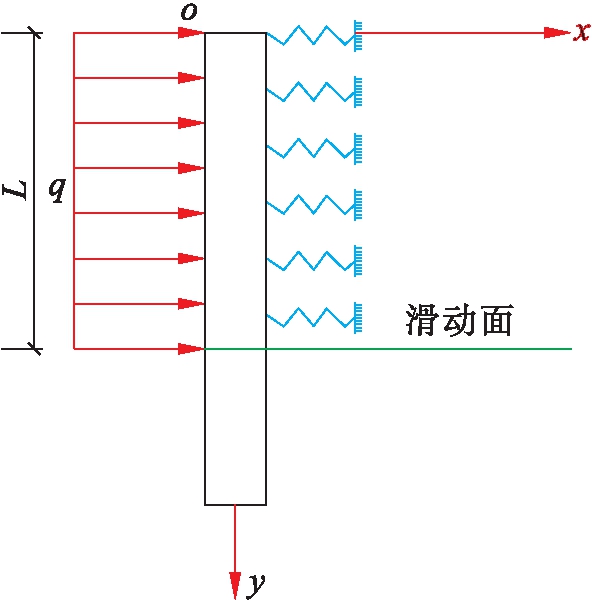
图1 抗滑桩桩前土体抗力计算简图
Fig.1 Calculation diagram of soil resistance before anti-slide pile
根据地基系数法中的“K”法,受荷段的挠曲微分方程为
(1)
式中:E为桩的弹性模量;I为桩的截面惯性矩;K为地基系数,或称弹性抗力系数;b为桩的实际宽度;Bp为桩的计算宽度,对于矩形桩,Bp=b+1,对于圆形桩,Bp=0.9(b+1);KxBp为桩前土体作用于桩上的水平抗力.引入变形系数![]() 即KBp=4EIβ4,则式(1)可写成
即KBp=4EIβ4,则式(1)可写成
(2)
解此方程,可得受荷段桩身变形计算公式[8]为
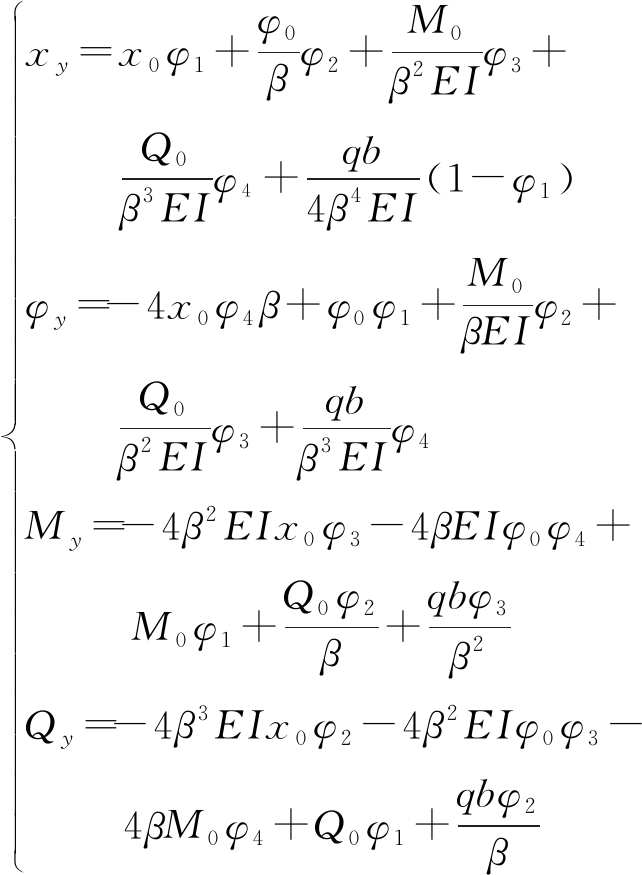
(3)
式中:xy、φy、My、Qy分别为抗滑桩受荷段桩身任一截面位移、转角、弯矩、剪力;x0、φ0、M0、Q0分别为抗滑桩桩顶的位移、转角、弯矩、剪力;φ1、φ2、φ3、φ4为“K”法的影响函数值,计算公式为
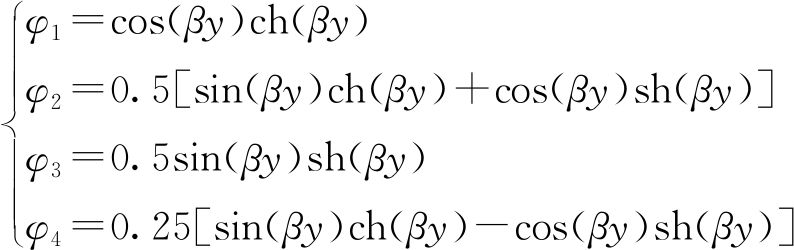
(4)
由文献[8]可知,滑坡的滑体与滑床的材料参数相差较大,导致强度与刚度差异巨大,根据嵌固段岩石的完整或破碎程度,滑面处的边界条件分为固定端、铰支端和自由端,自由端在实际工程中出现较少,本文不予考虑.
1) 当滑面按固定端考虑时,边界条件为:当y=L时,x=0,φ=0,且桩顶为自由端,则M0=0,Q0=0,将此条件代入式(3)中可联解得到桩顶变形为
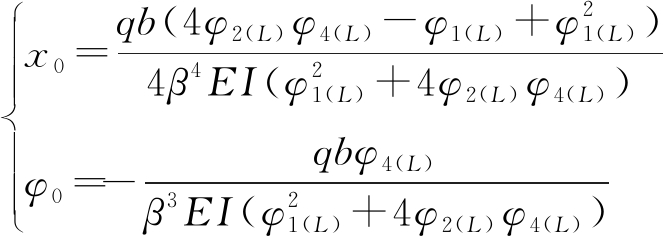
(5)
将式(5)中的桩顶位移和转角公式代入式(3),即可得到受荷段桩身变形计算公式,其中,受荷段桩身位移公式为
![]()
(6)
2) 当滑面按铰支端考虑时,边界条件为:当y=L时,x=0,M=0,且桩顶为自由端,则M0=0,Q0=0,将此条件代入式(3)中可联解得到桩顶变形为
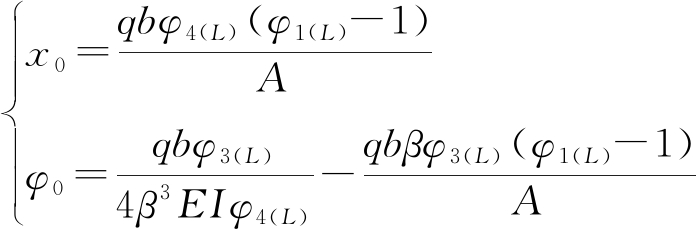
(7)
式中,A=qbφ2(L)φ3(L)+4β4EI(φ1(L)φ4(L)-φ2(L)φ3(L)).
将式(7)中的桩顶位移和转角公式代入式(3),即可得到受荷段桩身变形计算公式,其中,受荷段桩身位移公式为
(8)
求出受荷段桩身位移后,沿桩身按式(9)积分就可得到桩前土体总的抗力,即
R=Bp![]() Kxy/D
Kxy/D
(9)
式中:R为桩前土体抗力;D为抗滑桩的桩中心距.
同样可以根据“m”法的桩身挠曲微分方程及边界条件求得用“m”法计算时受荷段桩身位移公式,代入式(9)即可求得基于“m”法的桩前土体抗力计算公式,此处不再赘述.“K”法和“m”法各有其适用条件,可根据桩前岩、土体性质等选择使用.利用文本方法求解桩前土体抗力时,首先需根据现有方法(滑坡推力曲线法)确定桩前土体的剩余抗滑力,若根据计算无剩余抗滑力,说明桩前土体不稳定,可能滑走;有剩余抗滑力则说明桩前土体基本稳定,可按本文方法求解桩前土体抗力.本文方法所求桩前土体抗力应小于或等于桩前土体实际具有的剩余抗滑力,否则应改用换算地基系数重新计算.
2 有限元论证分析
随着计算技术的发展,近年来,数值模拟方法开始用于抗滑桩的受力分析,使用有限元强度折减法计算滑坡推力与桩前土体抗力时遵循桩![]() 土共同作用的原则,计算结果更符合实际情况.本文利用MIDAS GTS NX有限元软件结合工程实例论证分析所推导桩前土体抗力计算公式的适用性与正确性.
土共同作用的原则,计算结果更符合实际情况.本文利用MIDAS GTS NX有限元软件结合工程实例论证分析所推导桩前土体抗力计算公式的适用性与正确性.
2.1 强度折减法理论
强度折减法[9]的基本原理是获取边坡中某高斯点的应力状态.为了模拟土体的破坏状态,对土体强度参数进行规律性折减,计算公式为
(10)
式中:c为土体的粘聚力;φ为土体的内摩擦角;Fs为边坡的安全系数.
通过对c、φ值折减得到c′、φ′,使其接近莫尔圆,即将该点应力状态修正为土体的破坏状态.随着折减系数的增加,破坏点也将增加,边坡最终将发生整体破坏.
边坡稳定分析时安全系数定义为:边坡恰好处于临界破坏状态时的折减系数Fs,即该边坡的安全系数.对于其临界破坏的判断依据主要包括:1)非线性程序计算是否收敛;2)塑性区是否贯通,形成完整的塑性带;3)位移是否发生突变.
在MIDAS GTS NX软件中主要以非线性计算是否收敛(能量、位移、内力)为边坡失稳判断的主要依据,其具有无需提前假设滑动面位置和几何形状,能考虑边坡土体变形对稳定性的影响,可以较为准确地计算出滑动带和直接求出安全系数等优点.
2.2 计算模型
模型边坡为镇江市烈士陵园东北侧滑坡7-7剖面.镇江市烈士陵园位于京口区四牌楼街道,东吴路以南,第一楼街以东,属低山丘陵岗地地貌单元.经现场调查,镇江市烈士陵园东北侧滑坡分为东侧滑坡和北侧滑坡两段.东侧滑坡南北长约78 m,东西宽约45 m,坡顶标高27~29 m,坡底标高8~12 m,坡高约16~18 m,坡度60°~85°;北侧滑坡东西长约100 m,南北宽约35 m,坡顶标高27~29 m,坡底标高8~8.5 m,坡高约16~20 m,坡度60°~85°.土层依照其物理及力学性质特征自上而下划分为4层,通过勘查区钻探取样进行室内土工分析,确定本片区岩土体的主要物理力学性质指标.进入雨季后,山体多处发生滑坡,坡体整体稳定性差,为确保人民群众的生命财产安全,彻底消除地质灾害隐患,避免和减轻地质灾害造成的损失,故需对其进行综合治理以消除滑坡隐患.治理方案选用抗滑桩支护,抗滑桩尺寸为1.0 m×1.2 m,间距为2.0 m,桩长为18.0 m,治理剖面图如图2所示.
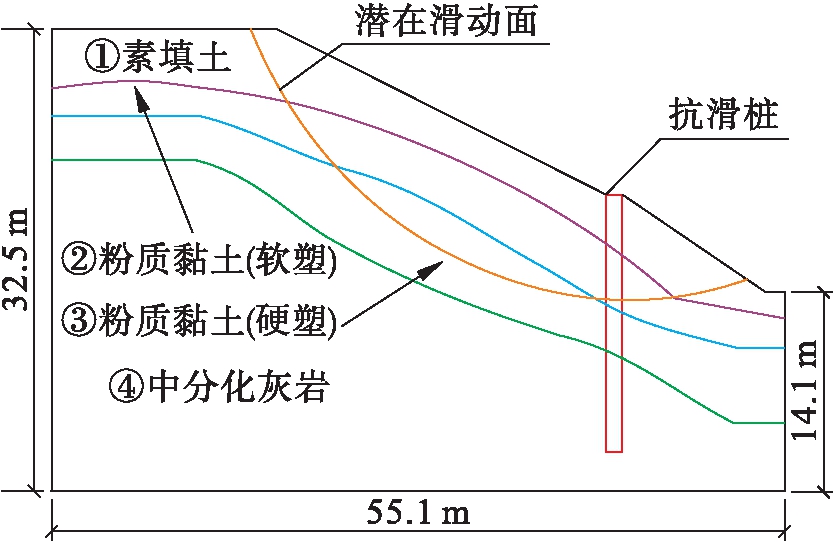
图2 边坡支护剖面图
Fig.2 Profile diagram of slope support
2.3 有限元模型分析
数值模拟采用MIDAS GTS NX有限元计算软件,边坡体采用Mohr-Coulomb弹塑性模型,抗滑桩采用弹性模型.模型参数如表1所示.
表1 各参数取值
Tab.1 Parameters values
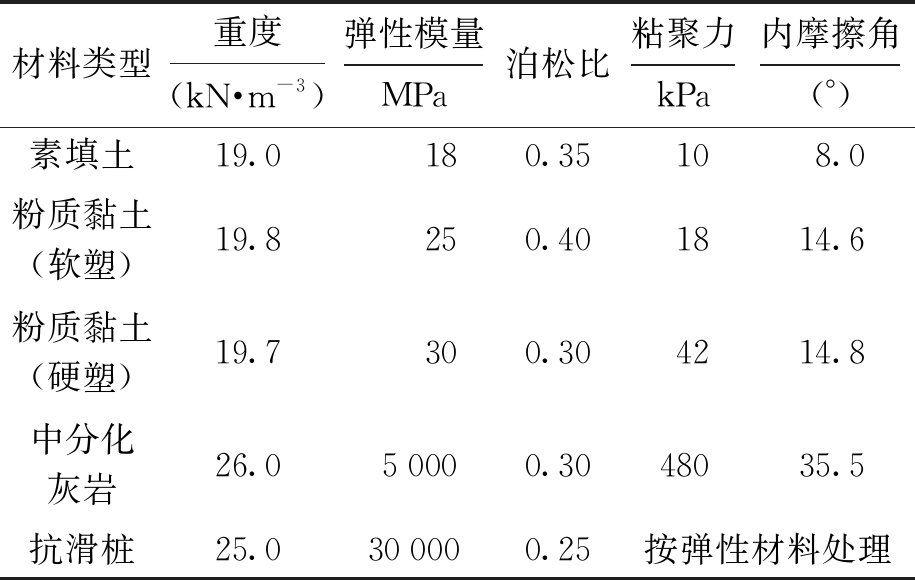
材料类型重度(kN·m-3)弹性模量MPa泊松比粘聚力kPa内摩擦角(°)素填土19.0 180.35108.0粉质黏土(软塑)19.8250.401814.6粉质黏土(硬塑)19.7300.304214.8中分化灰岩26.050000.3048035.5抗滑桩25.0300000.25按弹性材料处理
根据图2边坡模型剖面图以及表1的各参数取值建立三维边坡支护模型,如图3所示.图3中,四种颜色从上到下分别表示素填土、粉质黏土(软塑)、粉质黏土(硬塑)和中分化灰岩,黄色表示抗滑桩.
首先定义单元尺寸生成2D网格组,然后扩展为3D网格组,为每一网格组赋上相应土层材料属性后,对模型施加边界条件和荷载,采用有限元强度折减法对模型进行整体稳定性分析,得出塑性应变云图如图4所示.从图4中可以看出,设置抗滑桩后,有效阻止了原始滑动面的贯通与发展,新的滑动面在抗滑桩上部土体形成,边坡得到有效治理.通过有限元软件求解桩前土体抗力时,应选取原始滑动面以上的桩前每个实体单元应力乘以单元面积然后再求和,便可得到实际桩前土体抗力.

图3 抗滑桩支护边坡有限元模型图
Fig.3 Finite element model for slope supported by anti-slide pile
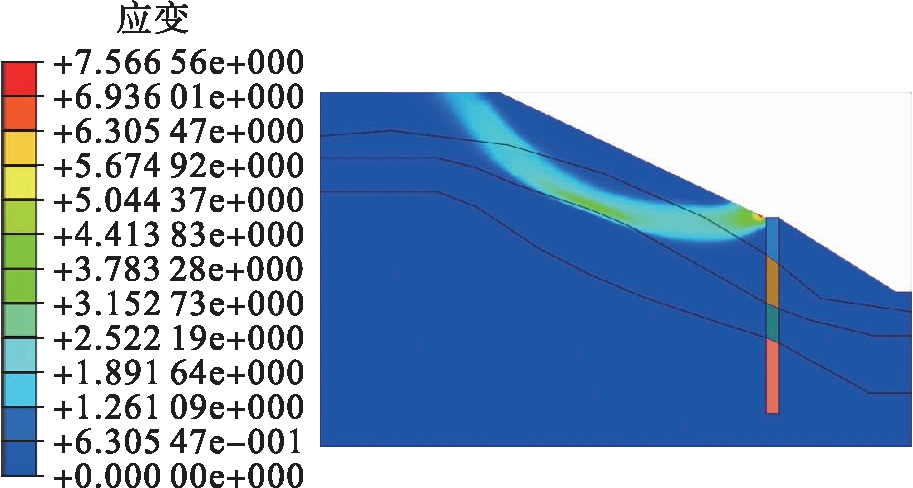
图4 塑性应变云图
Fig.4 Nephogram of plastic strain
2.4 计算结果及分析
通过有限元法可以得到比较接近实际情况的桩前土体抗力,将其与现有计算方法以及本文方法求解得到的桩前土体抗力进行对比,结果如表2所示.
表2 不同方法计算结果对比
Tab.2 Comparison of calculated results by different methods kN

有限元法滑坡推力曲线被动土压力法本文方法95.8216.4896.8102.6
由表2可以看出,被动土压力值过大,不符合实际情况,不宜采用;滑坡推力曲线所求桩前土体抗力因为无法考虑土体变形,比有限元法所求值大,适当折减方可使用,说明用现有方法求解的桩前土体抗力值偏大,使设计方案偏危险;而本文方法所求桩前土体抗力值与有限元法所求值较为接近,说明本文方法所求桩前土体抗力值较符合实际情况,可用于实际工程设计.
目前,大部分设计人员进行抗滑桩设计时,出于方便计算和安全考虑,忽略了桩前土体抗力的作用.本文算例就没有考虑桩前土体抗力的作用,导致内力和配筋计算结果偏大,将考虑桩前土体抗力情况下桩的内力和配筋计算结果与原设计相比较,对比结果如表3所示.
表3 桩身内力和配筋
Tab.3 Internal force and reinforcement of pile body

计算方法滑坡推力/kN桩前抗力/kN桩身最大剪力/kN桩身最大弯矩/(kN·m)配筋截面面积/mm2本文方法318.0102.6517.02544.36428实际情况318.00763.23756.29772
由表3可以看出,原设计方案中没有考虑桩前土体抗力,导致抗滑桩配筋过大,造成不必要的浪费,考虑本文方法计算所得桩前土体抗力,桩身内力会明显减少,配筋减少约34%,说明本文提出的桩前土体抗力计算方法在保证安全的前提下,可以大大降低工程造价.可以准确求解桩前土体抗力,帮助设计人员选择滑坡推力较小的位置设桩,更有利于降低工程造价[10].
3 结 论
基于地基系数法中的“K”法,推导了滑面为固定端和铰支端情况下的桩前土体抗力计算公式,并结合工程实例,采用有限元软件分析论证了该公式的合理性与正确性,得出如下结论:
1) 基于地基系数法中的“K”法所建立的模型能够较为准确地计算桩前土体抗力,计算结果的精确度取决于地基系数选取的准确性和桩上实际作用外力的分布形式.
2) 本文提出的桩前土体抗力计算公式具有实际应用价值.在实际工程中,准确求解桩前土体抗力,可以在保证安全的前提下大大降低工程造价,避免不必要的浪费,创造了巨大的社会经济效益.
3) 准确求解桩前土体抗力不仅能降低工程造价,并且能帮助选出更合适的抗滑桩设桩位置.
[1]刘晓燕.考虑桩前土体抗力的抗滑桩内力计算方法研究及工程应用 [D].西安:长安大学,2017.
(LIU Xiao-yan.Research and application of internal force calculation method of anti slide piles considering soil resistance before anti slide piles [D].Xi’an:Chang’an University,2017.)
[2]Mohamed A,Hamed A.Analysis of pile stabilized slopes based on soil-pile interaction [J].Computers and Geotechnics,2012,39:85-97.
[3]范志强,唐辉明,汪丁建,等.考虑土体应变软化特性的滑坡抗滑桩设计推力研究 [J].岩土力学,2016,37(增刊2):665-672.
(FAN Zhi-qiang,TANG Hui-ming,WANG Ding-jian,et al.A method for designed thrust of anti-slide pile considering strain softening properties of soil [J].Rock and Soil Mechanics,2016,37(Sup2):665-672.)
[4]赵尚毅,郑颖人,敖贵勇.考虑桩反作用力和设计安全系数的滑坡推力计算方法——传递系数隐式解法 [J].岩石力学与工程学报,2016,35(8):1668-1676.
(ZHAO Shang-yi,ZHENG Ying-ren,AO Gui-yong.Calculation method of landslide thrust considering the reaction force of piles and factor of safety-implicit solution using transfer coefficient [J].Chinese Journal of Rock Mechanics and Engineering,2016,35(8):1668-1676.)
[5]陈昌富,戴宇佳,梁冠亭,等.基于改进SW滑楔模型刚性抗滑桩极限滑坡推力智能优化计算方法 [J].水文地质工程地质,2014,41(6):38-43.
(CHEN Chang-fu,DAI Yu-jia,LIANG Guan-ting,et al.Intelligent optimum algorithms of ultimate thrust acting on the rigid anti-slide pile based on modified strain-wedge model [J].Hydrogeology & Engineering Geology,2014,41(6):38-43.)
[6]赵博,张翛,元天宇.边坡风险评价动态模型的构件及其应用 [J].沈阳工业大学学报,2018,40(2):229-234.
(ZHAO Bo,ZHANG Xiao,YUAN Tian-yu.Establishment and application of dynamic model for slope risk evaluation [J].Journal of Shenyang University of Technology,2018,40(2):229-234.)
[7]陆业奇,梁慧琛.抗滑桩桩前滑体抗力分布规律及工程应用研究 [J].人民长江,2011,42(22):38-41.
(LU Ye-qi,LIANG Hui-chen.Research and engineering application of resistant force distribution law of sliding body before anti-slide pile [J].Yangtze River,2011,42(22):38-41.)
[8]王玉刚.双排抗滑桩的稳定性分析与研究 [D].西安:西安工业大学,2017.
(WANG Yu-gang.Stability analysis and research of double-row anti-slide piles [D].Xi’an:Xi’an Technological University,2017.)
[9]王创业,刘伟,张琪,等.强度折减法在边坡稳定性中的对比分析 [J].矿业研究与开发,2018,38(1):67-70.
(WANG Chuang-ye,LIU Wei,ZHANG Qi,et al.Contrastive analysis of strength reduction method in slope stability [J].Mining Research and Development,2018,38(1):67-70.)
[10]方龙建.大排距双排抗滑桩在边坡加固中的作用机理及设计方法研究 [D].镇江:江苏科技大学,2018.
(FANG Long-jian.Study on the mechanism of double-row anti-slide piles with large row distance in slope engineering and the design method [D].Zhenjiang:Jiangsu University of Science and Technology,2018.)