传统悬索桥的加劲主梁一般支承于两主塔横梁上,为适应山区峡谷地形特点,可以设计主梁长度小于塔距,主梁支撑在峡谷两侧稳定岩层上(而非塔下横梁),将主梁与主塔完全分离,这样既能减少工程量降低成本,又能尽最大可能地保护原生环境,与自然和谐相融,湖南矮寨悬索桥是该桥型的首次应用.
崔剑峰等[1]对矮寨大桥进行了结构静力分析,验证了悬索桥主缆、吊索、斜拉扣、钢加劲梁与桥塔等结构均满足使用要求,介绍了地锚索、斜拉扣以及伸缩缝伸缩量的分析计算方法;马碧波等[2]详细叙述了悬索桥地锚索的设计与安装过程;刘榕等[3]对塔梁分离式悬索桥桥型结构与传统悬索桥结构进行了最大缆力、加劲梁最大位移、最大吊索力以及桥塔塔顶位移等对比分析,验证了在湘西特殊地形下选用塔梁分离式悬索桥方案的优越性;余崇[4]为得到悬索桥在地震动作用下各关键截面的应力、位移及损伤情况,模拟了地震动作用下湘西矮寨大桥损伤分析;张新[5]采用了增量分析方法,研究不同损伤指标对关键构件易损性的影响规律;王杰等[6]对不同纵向约束体系下悬索桥地震反应影响进行研究;董学智[7]对处于峡谷地区带地锚索的少塔悬索桥进行了地震动作用下结构响应研究;柳国环、蔡小瑾等[8-10]分析了跨越V形峡谷桥梁的抗震性能;Wang等[11]研究了地质条件对双塔悬索桥抗震性能的影响;刘长喜[12]对高震区悬索桥动力特性及抗震性能进行了研究;Apaydin等[13]分析了悬索桥在空间变化多支点地震激励下的响应;Bi等[14]研究了跨峡谷桥梁以减小地震对结构造成的二次效应,在桥面与桥墩之间需设置最小分隔距离;Jiao等[15]研究了随机地震动作用下大跨度三塔悬索桥的地震响应;Siringoringo等[16]通过对地震监测系统长期全面的观测与研究,得出了悬索桥在地震作用下的响应;Qi等[17]对处在深峡谷地区的矮寨桥进行了岩石基础稳定性研究;Sgambi等[18]对大跨度桥梁在空间变化地震动下的结构响应进行了分析;鲍文博等[19]等通过对减震控制效应进行弹塑性能量响应分析,研究结构的减震控制.
本文主要分析以下三方面内容:加劲主梁支承方式的改变会在多大程度上影响悬索桥的动力特性与地震响应;吊跨比的变化对结构动力特性以及抗震性能的影响;辅助地锚索的设置及设置数量对结构动力与抗震性能的影响.
1 工程概况
本文依托实际悬索桥工程——矮寨大桥,该桥跨越大峡谷地形,同时也是世界首例采用塔梁分离结构设计的悬索桥.矮寨桥总体布置如图1所示(单位:mm).主塔为由塔柱与横梁组成的双柱式门式框架结构,塔梁为分离式,主缆孔跨布置为242 m+1 176 m+116 m,垂跨比f/l为1/9.6,上下游主缆中心距为27.0 m,全桥设68对吊索(间距为14.5 m),3对地锚索,吉首岸(J岸)采用重力锚,茶洞岸(C岸)采用隧道锚.
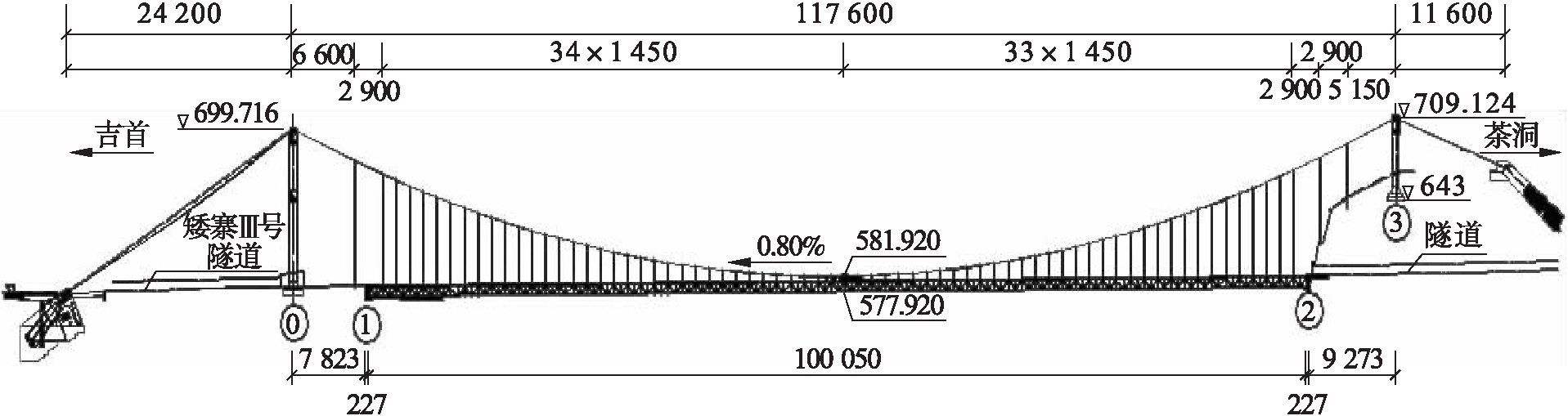
图1 矮寨大桥布置图
Fig.1 Layout of Aizhai bridge
2 模型建立及验证
本文采用Ansys有限元软件进行建模分析,主桁用Beam4梁单元模拟,放大钢材密度以考虑螺栓、节点板等附加质量影响;考虑主缆垂度效应和大变形等影响确定其初始平衡状态,采用Link10单元模拟;吊索用Link10单元模拟;考虑到主塔由自重引起的初应变效应,采用Beam4单元模拟;桥面及车辆活载的1/2简化为质量单元Mass21均布于主梁节点.边界条件的模拟情况包括:主塔塔底固端约束,主缆两端固端约束,塔顶位置主缆与塔自由度耦合,地锚索采用岩锚锚固于基岩,主梁设竖向及横桥向约束.图2为塔梁分离式悬索桥三维有限元模型.
对所建立的塔梁分离式悬索桥模型进行自重作用下的静力非线性分析,将其与文献[4]中模态频率进行对比,二者的最大相对误差为3.9%,差异极小,表明本文所建立的有限元模型是合理的.图3为本文有限元模型与文献[4]有限元模型模态对比图.

图2 塔梁分离式悬索桥三维有限元模型
Fig.2 Three-dimensional finite element model of suspensionbridge with separated girder and tower
3 塔梁分离式悬索桥动力特性分析
塔梁分离式悬索桥与传统悬索桥在结构上的差异必然导致其具有特殊的动力特征,本文研究了主梁支承条件、吊跨比以及地锚索三方面变化对塔梁分离式悬索桥动力特性的影响.
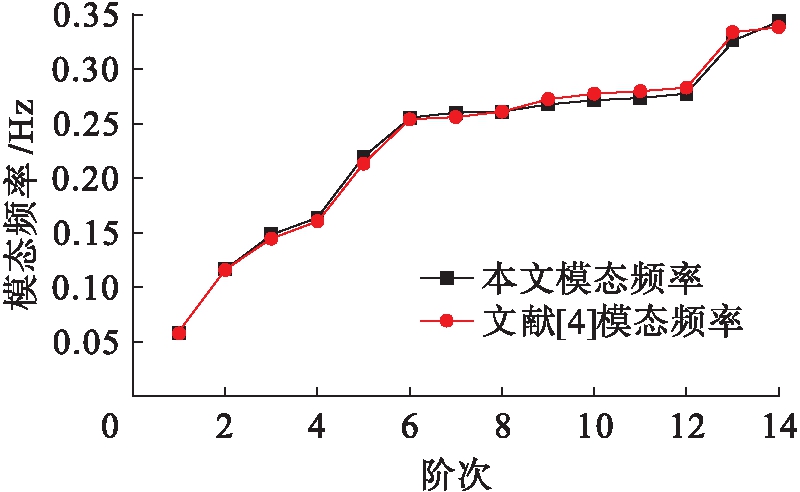
图3 有限元模型与文献[4]中矮寨桥模态对比
Fig.3 Mode comparison between finite element model and Aizhai bridge in literature [4]
3.1 主梁支撑条件对结构动力特性的影响
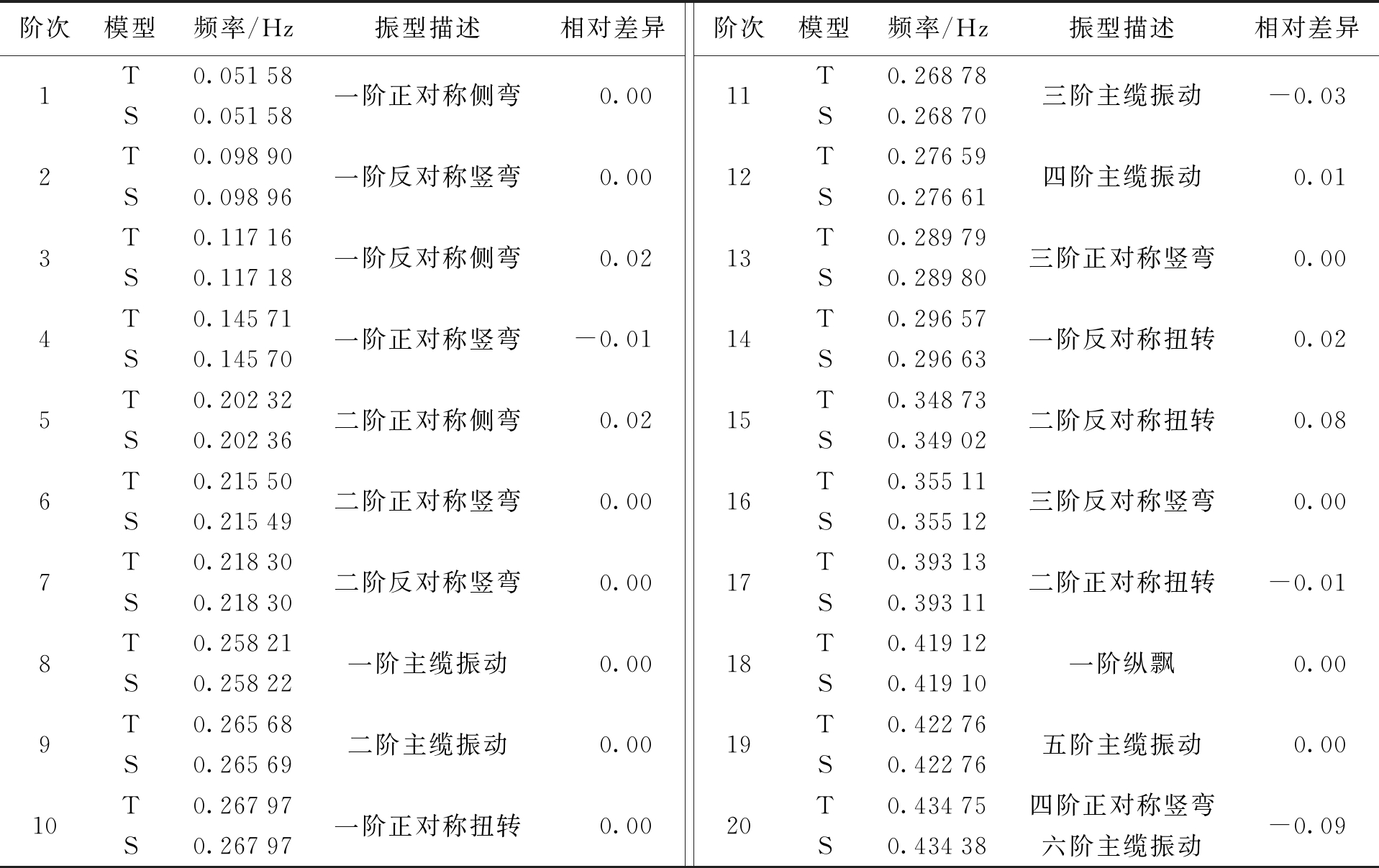
采用Block Lanczos求解塔梁分离式悬索桥和传统悬索桥的自振频率及对应阵型.表1为两种悬索桥前20阶自振情况,T代表传统悬索桥,S代表塔梁分离式悬索桥.
表1 传统悬索桥与塔梁分离式悬索桥前20阶自振特性对比
Tab.1 Comparison of first 20 order self-vibration characteristics between traditional suspension bridge and suspension bridge with separated grinder and tower
阶次模型频率/Hz振型描述相对差异12345678910T0.05158S0.05158T0.09890S0.09896T0.11716S0.11718T0.14571S0.14570T0.20232S0.20236T0.21550S0.21549T0.21830S0.21830T0.25821S0.25822T0.26568S0.26569T0.26797S0.26797一阶正对称侧弯 0.00一阶反对称竖弯0.00一阶反对称侧弯0.02一阶正对称竖弯-0.01二阶正对称侧弯0.02二阶正对称竖弯0.00二阶反对称竖弯0.00一阶主缆振动0.00二阶主缆振动0.00一阶正对称扭转0.00阶次模型频率/Hz振型描述相对差异11121314151617181920T0.26878S0.26870T0.27659S0.27661T0.28979S0.28980T0.29657S0.29663T0.34873S0.34902T0.35511S0.35512T0.39313S0.39311T0.41912S0.41910T0.42276S0.42276T0.43475S0.43438三阶主缆振动四阶主缆振动三阶正对称竖弯一阶反对称扭转二阶反对称扭转三阶反对称竖弯二阶正对称扭转一阶纵飘五阶主缆振动四阶正对称竖弯六阶主缆振动-0.030.010.000.020.080.00-0.010.000.00-0.09
由表1可知:1)两桥梁模型基频相同,且第一阶侧弯、竖弯、扭转、主缆振动、纵飘出现的频率也相同;2)前20阶自振特性中,两模型的自振频率相差均在0.1以内;3)各阶自振特性所对应的振型,仅在频率密集处出现前后交叉的现象,以主塔为主的振型一般出现较晚.
3.2 吊跨比对悬索桥动力特性的影响
将悬吊主梁两端部吊索间的距离与两桥塔之间距离的比值定义为吊跨比,是塔梁分离式悬索桥设计的一个重要参数.设置塔梁分离式悬索桥两桥塔之间的距离不变,仅改变桥长,同时按原间距加设吊索,设计出吊跨比由0.75增加至0.95的五种塔梁分离式悬索桥模型.图4为塔梁分离式悬索桥随吊跨比改变的动力特性图.
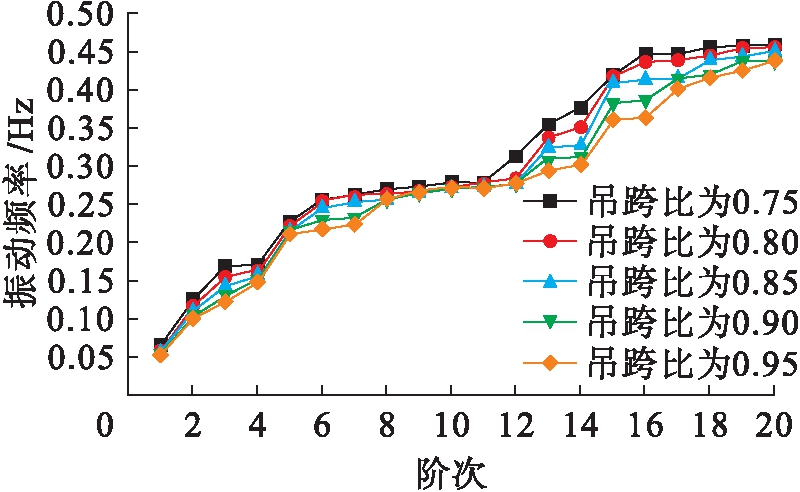
图4 五种吊跨比前20阶频率比较
Fig.4 Comparison of first 20 order frequency underfive ratios of suspension length to span
由图4可知:1)随着吊跨比的增加,各阶自振特性频率均有所减小,同时,在前20阶自振频率中,各阶振动频率的变化也不尽相同,频率之间的差异随着阶次的增加也在逐渐增大,说明吊跨比对悬索桥动力特性的影响会随着振动阶次的增加而被逐渐放大;2)随着吊跨比减小,侧弯(第1、3阶)与竖弯(第2、4阶)基频均表现出递增趋势,说明随着吊跨比减小,主梁长度缩短,直接导致主梁侧向与竖向抗弯刚度增加.
3.3 地锚索对悬索桥动力特性的影响
以吊跨比为0.75的塔梁分离式悬索桥模型为模型A;在主梁两侧各增设一对地锚索,使广义吊跨比(即两端地锚索之间的距离与两桥塔间距离的比值)为0.85,记为模型B;在主梁两侧各增设两对地锚索,使广义吊跨比为0.90,记为模型C.图5为增设地锚索的模型B及C前20阶自振频率相对于无地锚索模型A的增幅.
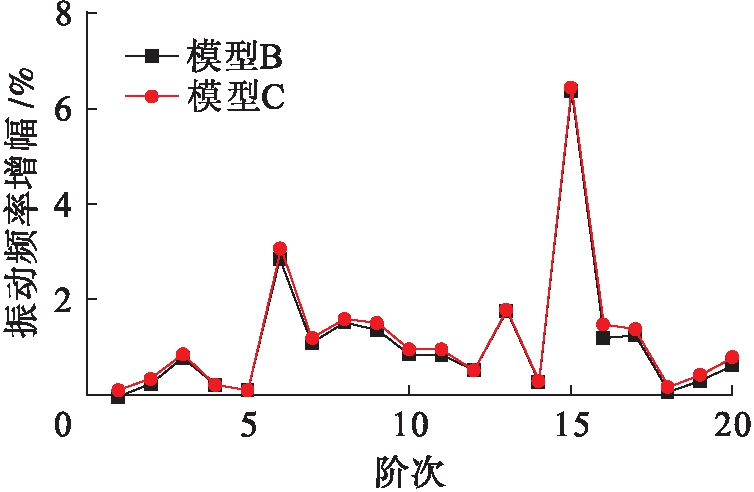
图5 增设地锚索模型振动频率增幅
Fig.5 Increase amplitude of vibration frequency with ground-anchored cable model
通过图5可知:1)设置地锚索使结构的各阶自振频率均有所增大,振动频率增幅最大值为7%,说明增设地锚索提高了悬索桥整体的刚度;2)地锚索设置数量增大,可以提高桥梁整体刚度,使自振频率增大,但增幅并不如有无地锚索的差异显著.
4 塔梁分离式悬索桥抗震性能分析
基于桥位地震分组及场地条件,依据规范谱选择两条天然波,并生成一条人工波,地震动时程如图6所示(峰值加速度调整为66 m/s2).
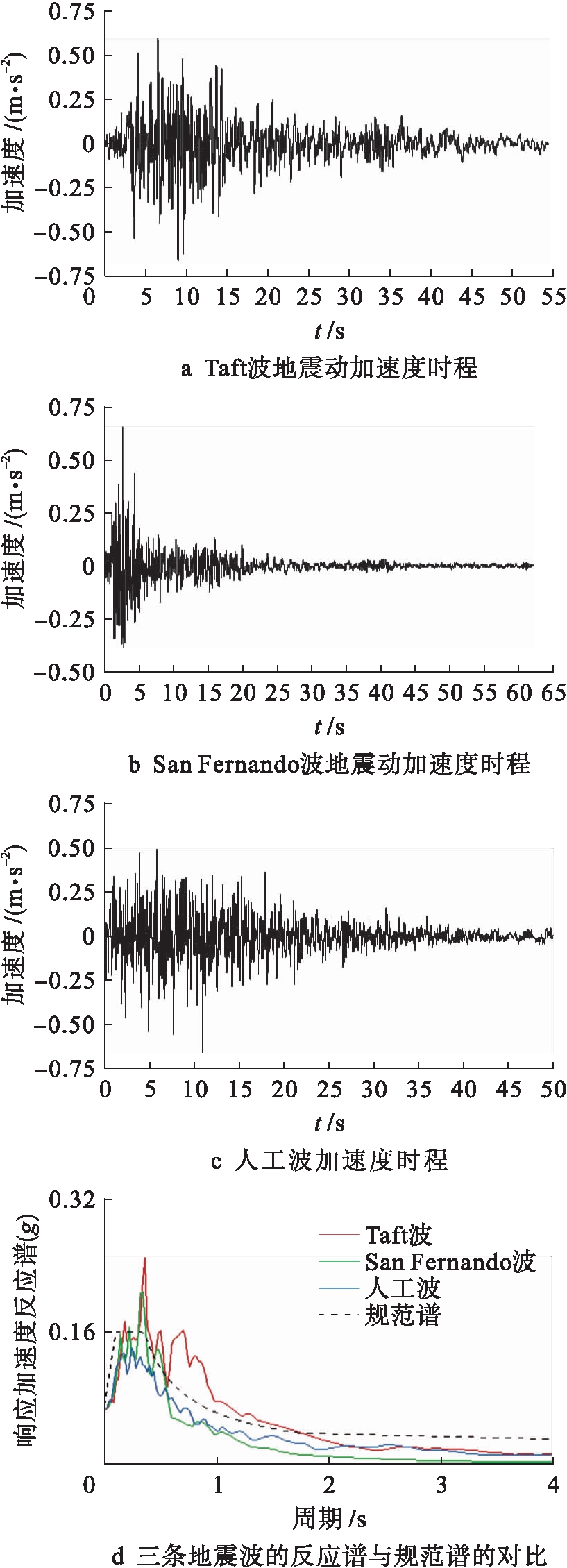
图6 地震动时程曲线
Fig.6 Curves of seismic time history
4.1 塔梁分离对悬索桥抗震性能的影响
虽然单纯的塔梁分离式悬索桥相较于传统的悬索桥在模态分析上的差异可以忽略,但由于地震动具有随机性和不确定性,需对塔梁分离式悬索桥与传统悬索桥进行地震动下的响应分析.表2~3分别为T(传统式)、S(塔梁分离式)悬索桥关键位置的结构响应,表3中应力幅是指在每次应力循环中最大拉应力值与最小拉应力或压应力(拉力为正,压力为负)的差值的一半.
表2 塔梁分离式悬索桥位移峰值
Tab.2 Peak displacement of suspension bridge with separated girder and tower mm
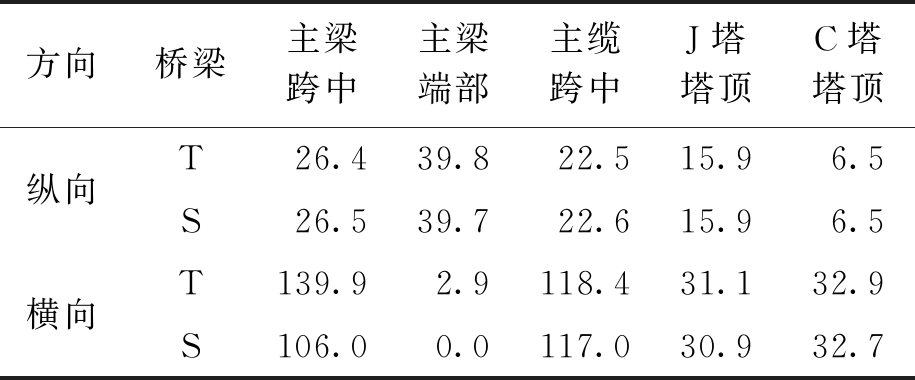
方向桥梁主梁跨中主梁端部主缆跨中J塔塔顶C塔塔顶纵向横向T26.439.822.515.96.5S26.539.722.615.96.5T139.92.9118.431.132.9S106.00.0117.030.932.7
表3 塔梁分离式悬索桥内力峰值
Tab.3 Peak internal force of suspension bridge with separated girder and tower
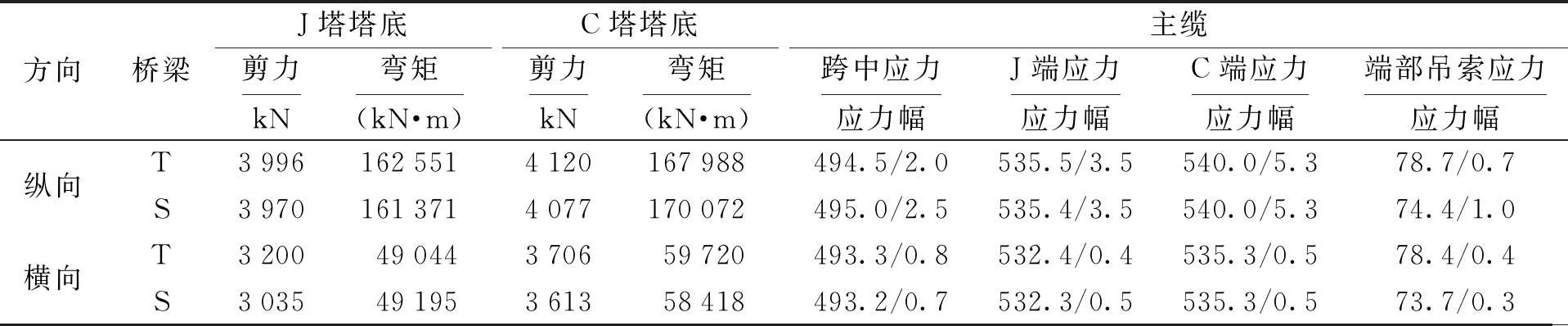
方向桥梁J塔塔底剪力kN弯矩(kN·m)C塔塔底剪力kN弯矩(kN·m)主缆跨中应力应力幅J端应力应力幅C端应力应力幅端部吊索应力应力幅纵向横向T39961625514120167988494.5/2.0535.5/3.5540.0/5.378.7/0.7S39701613714077170072495.0/2.5535.4/3.5540.0/5.374.4/1.0T320049044370659720493.3/0.8532.4/0.4535.3/0.578.4/0.4S303549195361358418493.2/0.7532.3/0.5535.3/0.573.7/0.3
注:应力和应力幅的单位均为MPa.
由表2~3可知:1)纵桥向地震输入下,塔梁分离式悬索桥与传统悬索桥的各部件纵向位移基本没有差异;2)纵桥向和横桥向地震作用下塔梁分离式悬索桥主塔内力略有轻微减小,对缆索内力基本没有影响.
4.2 吊跨比对塔梁分离式悬索桥抗震性能的影响
通过对上文建立的吊跨比从0.95至0.75的五个塔梁分离式悬索桥模型进行模态分析,可以看出吊跨比的减小使得桥面长度减小,继而使主梁抗弯,抗扭刚度明显增大.本文将对塔梁分离式悬索桥模型在五种不同吊跨比情况下进行抗震性能分析,结果如图7所示.
从分析结果可知:1)随着吊跨比增大,主塔刚度增大,振动随之减弱,纵桥向与横桥向位移响应与内力响应减小;主缆与吊索的应力响应整体上呈减小趋势,但变化并不十分明显.2)随着吊跨比增大,主梁刚度减小,主梁刚度的变化趋势与主缆、主塔相反,导致在纵桥向与横桥向地震作用下,主梁位移响应的变化规律不单调,出现交替;主缆位移响应也受其影响,表现与主梁类似,尤其是接近跨中位置.
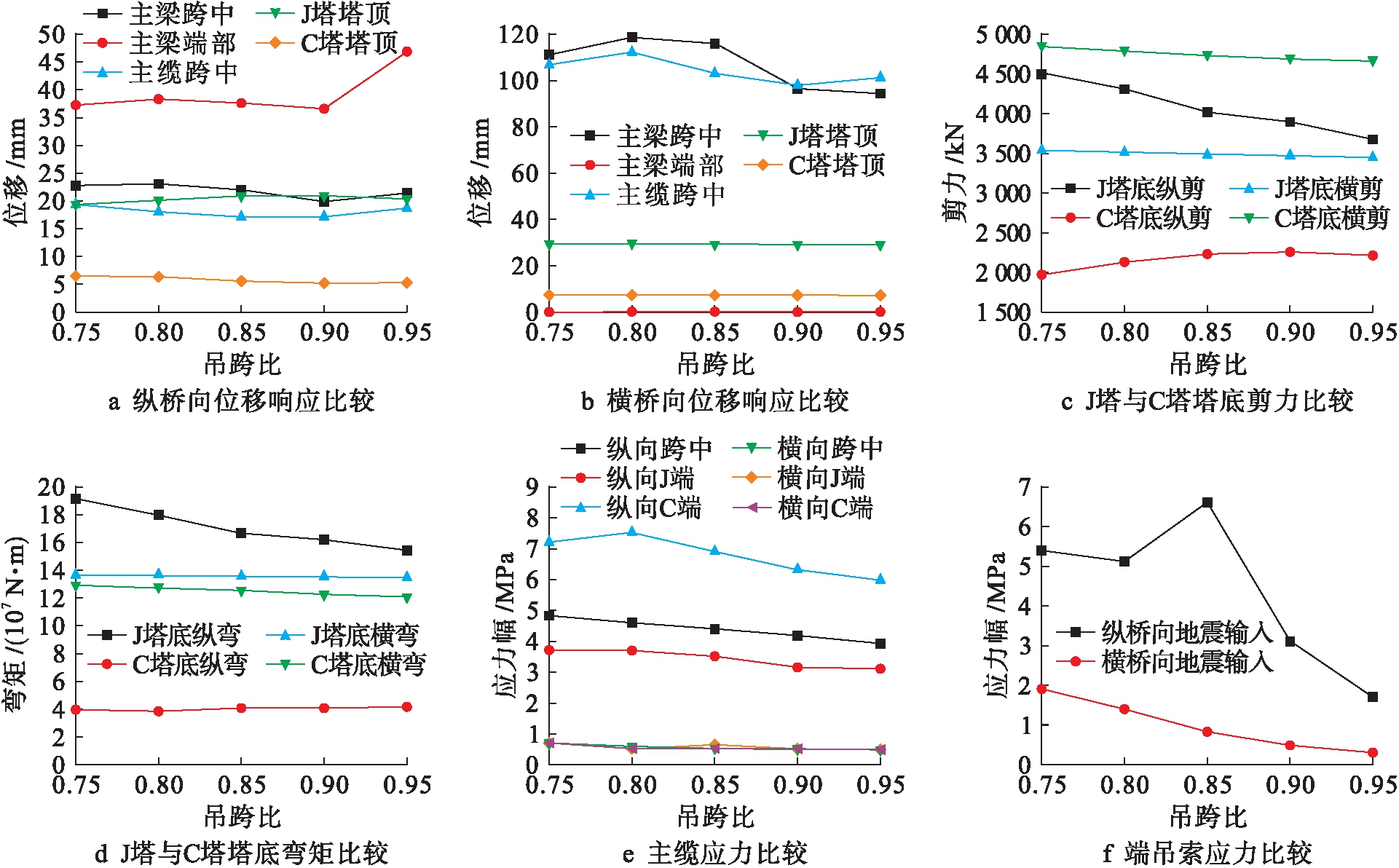
图7 吊跨比对结构响应的影响
Fig.7 Effect of ratio suspension length to span on structural response
4.3 地锚索设置对塔梁分离式悬索桥抗震性能的影响
通过对不同地锚索设置数量的塔梁分离式悬索桥进行模态分析得知,地锚索的设置能提高悬索桥的整体刚度,尤其是主缆刚度;而地锚索设置数量的增加对悬索桥整体刚度几乎无贡献.本文将对不同地锚索设置数量的悬索桥模型进行抗震性能分析,位移与内力响应分析结果如图8所示.
由图8可知:1)地锚索的设置能很大程度提高悬索桥的整体刚度;2)在横桥向地震作用下,除其周边区域的端部缆索外,设置地锚索对结构基本没有影响;3)地锚索主要影响纵桥向地震响应,设置地锚索减小了主塔位移与内力响应,幅度约为5%,同时降低了主缆与端部吊索的应力响应;4)增加地锚索数量对上述改变基本没有影响,有时还会削弱上述影响.
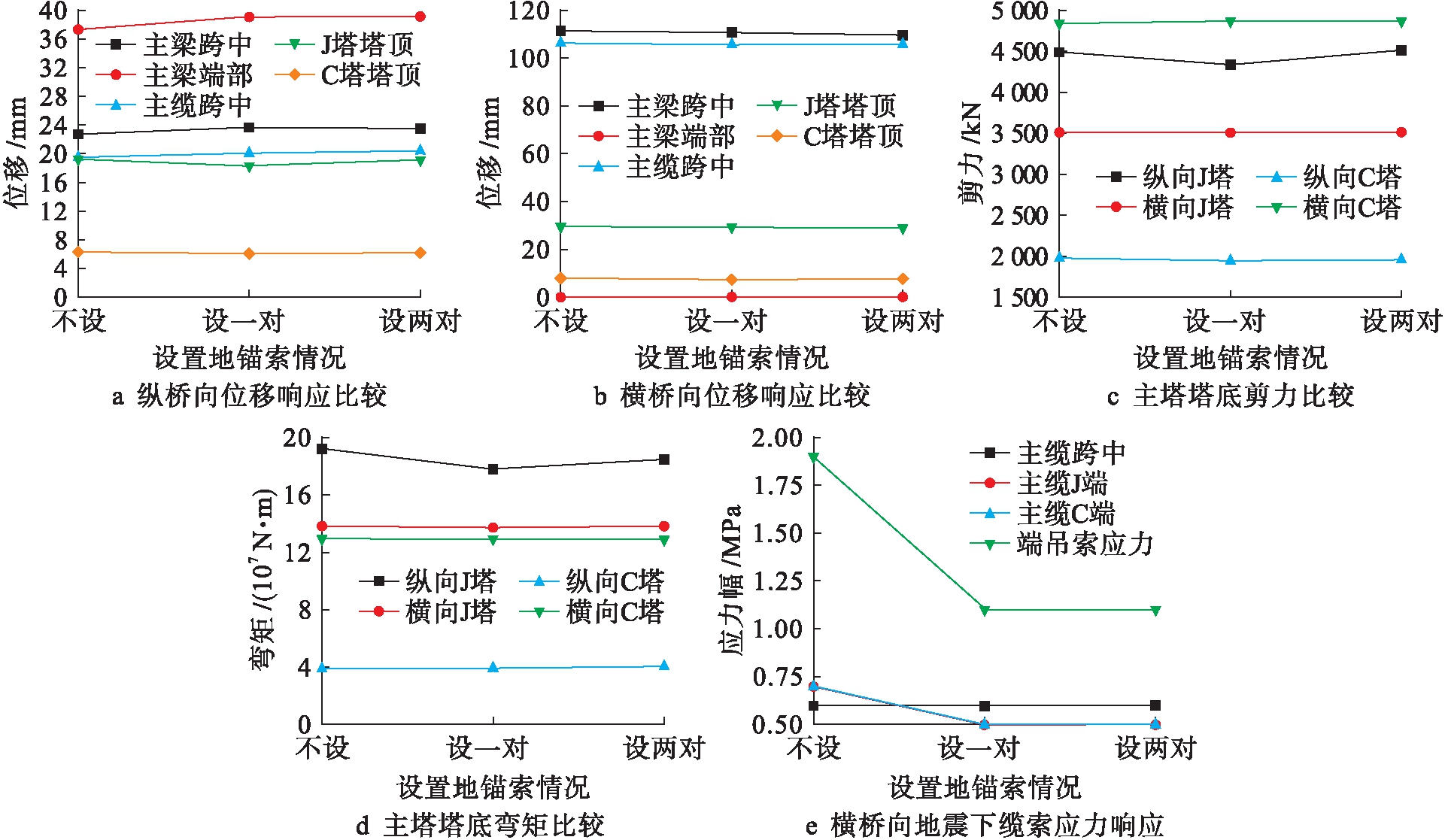
图8 地锚索对结构弹性抗震的影响
Fig.8 Influence of ground-anchored cable on structural elastic seismic behavior
5 结 论
本文在主梁的支承条件、吊跨比以及地锚索数量改变情况下,对塔梁分离式悬索桥抗震性能进行影响分析,得出以下结论:
1) 悬索桥支撑条件的改变几乎不影响自由振动模态.同时,塔梁分离式悬索桥的自振特性频率随着吊跨比的增加而逐渐减小;地锚索的设置能较大提高桥梁结构的整体刚度与自振频率,而增加地锚索的数量对模态影响较为微弱.
2) 在横桥向地震作用下,地锚索的设置能很大程度抑制主缆以及端部吊索的振动,而对主塔几乎不产生影响,同时,梁端杆件内力随着地锚索的设置也有所增大.在纵桥向地震作用下,地锚索的设置能大幅减小主塔位移与内力响应,减小幅度约为5%,能显著减小梁端杆件内力与端部吊索的振动,而对主缆几乎无影响.增加地锚索设置的数量对桥梁结构抗震性能影响不大.
[1]崔剑峰,胡建华,刘榕.矮寨大桥总体结构静力分析 [J].湖南交通科技,2008,34(2):75-78.
(CUI Jian-feng,HU Jian-hua,LIU Rong.Static analysis of overall structure of Aizhai bridge [J].Hunan Communication Science and Technology,2008,34(2):75-78.)
[2]马碧波,王良洪,沈锐利.矮寨特大悬索桥地锚索的设计、影响与安装过程分析 [J].中外公路,2010,30(6):136-139.
(MA Bi-bo,WANG Liang-hong,SHEN Rui-li.Ana-lysis of design,influence and installation of ground-anchored cables in Aizhai extra large suspension bridge [J].Journal of China & Foreign Highway,2010,30(6):136-139.)
[3]刘榕,胡建华,陈国平,等.湘西矮寨大桥塔![]() 梁分离式悬索桥桥型结构研究 [J].桥梁建设,2012,42(5):1-8.
梁分离式悬索桥桥型结构研究 [J].桥梁建设,2012,42(5):1-8.
(LIU Rong,HU Jian-hua,CHEN Guo-ping,et al.Study on bridge-structure of tower-girder separated suspension bridge of Aizhai bridge in West Hunan [J].Bridge Construction,2012,42(5):1-8.)
[4]余崇.矮寨大桥基于性能的地震易损性分析 [D].长沙:湖南大学,2013.
(YU Chong.Performance-based seismic fragility ana-lysis of Aizhai bridge [D].Changsha:Hunan University,2013.)
[5]张新.深切峡谷场地悬索桥地震易损性分析 [D].成都:西南交通大学,2018.
(ZHANG Xin.Analysis on seismic vulnerability of suspension bridge in deep cutting gorge area [D].Chengdu:Southwest Jiaotong University,2018.)
[6]王杰,李建中.不同纵向约束体系对三塔悬索桥地震反应影响研究 [J].石家庄铁道大学学报(自然科学版),2016,29(2):1-5.
(WANG Jie,LI Jian-zhong.Influence of different longitudinal constrain systems on seismic response of triple-tower suspension bridge [J].Journal of Shi-jiazhuang Tiedao University(Natural Science),2016,29(2):1-5.)
[7]董学智.峡谷地区带地锚索的少塔悬索桥地震响应研究 [D].成都:西南交通大学,2016.
(DONG Xue-zhi.Research on seismic response of suspension bridge which has rock anchor hangers and whose tower is omitted partly or wholly in the valley [D].Chengdu:Southwest Jiaotong University,2016.)
[8]柳国环,冯啸,江大来.跨越Ⅴ形峡谷桥梁多层介质效应的多点激励破坏模式 [J].中国公路学报,2019,32(8):101-113.
(LIU Guo-huan,FENG Xiao,JIANG Da-lai.Failure mode of bridges under multi-support excitation in a V-shaped canyon with multi-layer topography [J].China Journal of Highway and Transport,2019,32(8):101-113.)
[9]柳国环,冯啸.跨越V形峡谷的桥梁抗震分析:多水平成层非均匀介质V形场地多点地震动模拟 [J].中国公路学报,2017,30(12):150-158.
(LIU Guo-huan,FENG Xiao.Analysis of seismic response for bridges located on a V-shaped canyon:si-mulation of multi-support seismic motions in a V-shaped canyon with inhomogenenous multi-layer togography [J].China Journal of Highway and Transport,2017,30(12):150-158.)
[10]蔡小瑾.跨越山区V形山谷桥梁抗震性能分析 [J].工程与建设,2019,33(3):407-409.
(CAI Xiao-jin.Seismic performance analysis of V-shaped valley bridge across mountainous area [J].Engineering and Construction,2019,33(3):407-409.)
[11]Wang J,Hu S,Wei X.Effects of engineering geolo-gical condition on response of suspension bridges [J].Soil Dynamics & Earthquake Engineering,1999,18(4):297-304.
[12]刘长喜.高震区悬索桥动力特性及抗震性能研究 [J].工程抗震与加固改造,2015,37(1):32-39.
(LIU Chang-xi.Study on dynamic characteristics and seismic performance of suspension bridge in high seismic zones [J].Earthquake Resistant Engineering and Retrofitting,2015,37(1):32-39.)
[13]Apaydin N M,Bas S,Harmandar E.Response of the Fatih Sultan Mehmet Suspension bridge under spatially varying multi-point earthquake excitations [J].Soil Dynamics and Earthquake Engineering,2016,84:44-54.
[14]Bi K M,Hao H,Chouw N.Required separation distance between decks and at abutments of a bridge crossing a canyon site to avoid seismic pounding [J].Earthquake Engineering & Structural Dynamics,2010,39(3):303-323.
[15]Jiao C K,Dong X,Li A Q,et al.Seismic response of long-span triple-tower suspension bridge under random ground motion [J].Mathematical Problems in Engineering,2017(1):1-16.
[16]Siringoringo D M,Yozo F.Seismic response of a suspension bridge:insights from long-term full-scale seismic monitoring system [J].Structural Control and Health Monitoring,2018(10):1-25.
[17]Qi H Z,Yu J L,Yu M W,et al.Study of the rock foundation stability of the Aizhai suspension bridge over a deep canyon area in China [J].Engineering Geology,2015,198:65-77.
[18]Sgambi L,Garavaglia E,Basso N,et al.Monte Carlo simulation for seismic analysis of a long span suspension bridge [J].Engineering Structures,2014,78:100-111.
[19]鲍文博,于玄烨.消能减震框架结构减震控制 [J].沈阳工业大学学报,2018,40(3):340-344.
(BAO Wen-bo,YU Xuan-ye.Seismic control of energy dissipation frame structure [J].Journal of Shenyang University of Technology,2018,40(3):340-344.)