表面科学是物理学的一个重要分支，也是自然科学中发展最快的一个交叉学科.对表面性质具有重要影响的现象为集体激发效应，例如磁性薄膜中的自旋微扰可以引起表面自旋波的传播.关于磁性薄膜表面和界面磁性的研究对提高记录密度和改善许多磁性仪器的性能具有重要作用.沿磁性薄膜表面传播的表面自旋波具有大量显著特征，可以应用于自旋波电子学领域.磁性薄膜的动态特性和自旋波特性是自旋电子学的重要组成部分，且与纳米磁记忆器件、传感器和逻辑器件等新型自旋电子学器件的性能密切相关[1-2].磁性薄膜表现出的新特性引起了人们的极大兴趣.许多研究者利用自旋波共振、光散射等实验手段对磁性薄膜的结构、磁性等进行了探讨[3-4].相关线性理论[5]表明，对于表面自旋自由的纯交换耦合铁磁体而言，并不存在表面自旋波.人们从动力学观点出发，利用转移矩阵方法和相关函数理论等对磁性薄膜的动力学性质、自旋波谱和色散关系进行了研究[6-7].Mamica[5]研究表明，在磁性薄膜中传播的交换自旋波表现出一些动力学效应，即仅由波传播引起的效应主要集中在四个现象上：表面(和次表面)局部化、体能带缩为一个能级、自旋波谱中模序的反转以及薄膜动态分离为两个子系统.王焕等[8]研究了由铁磁与反铁磁材料构成的异质双层薄膜结构在界面耦合处的界面自旋波及其相关物理特性，得到界面自旋波的存在条件与色散关系.Flaviano等[9]采用绝热近似方法分析了W(110)表面的自旋波色散现象，并利用格林函数的第一原理电子结构分析了磁交换相互作用.张光富等[10]利用微磁学模拟方法研究了磁性纳米薄膜末端形状对自旋波模式特性的影响，结果表明，纳米膜的末端边缘形状对自旋波模式特性影响不大，但随着磁场的增大，自旋波频率呈现不同变化.本文试图从理论角度采用量子格林函数方法研究温度、外磁场、表面交换耦合和表面各向异性对铁磁性薄膜结构中表面自旋波频率的影响.
1 海森堡模型和哈密顿量
采用具有单格点各向异性的海森堡模型研究铁磁性薄膜中表面自旋波的频率.铁磁性薄膜中含有12个原子层并沿着z方向堆砌，其中，铁磁性薄膜的平面结构与表面布里渊区如图1所示.
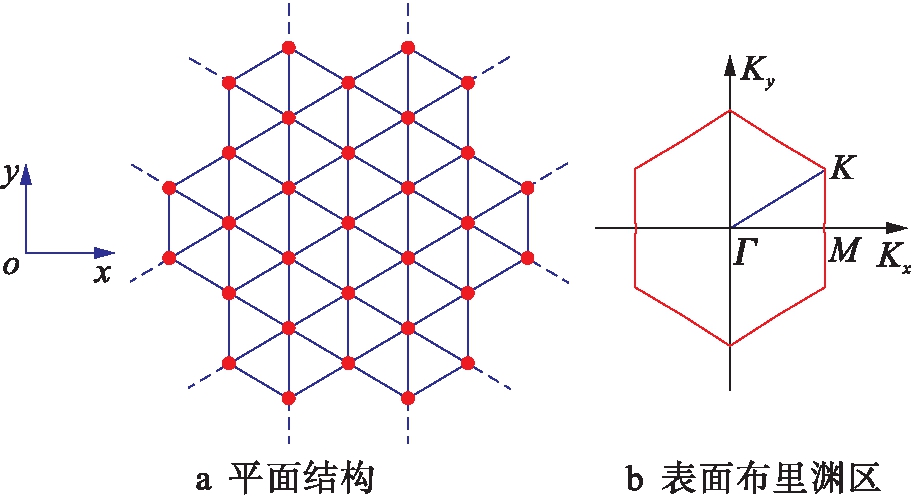
图1 铁磁性薄膜平面结构与表面布里渊区
Fig.1 Planar structure and surface Brillouin zone of ferromagnetic thin film
哈密顿量可以表示为
(1)
式中：l和l′为磁性离子的不同层数，而j和j′为磁性离子的不同平面位置；Slj为l层离子在j位置的自旋算符，而
为该自旋算符的z方向分量；Sl′j′为l′层离子在j′位置的自旋算符；Jljl′j′为l层离子j位置与l′层离子j′位置之间的交换耦合参数；Dl为l层离子的单格点各向异性参数；g为郎德因子；μB为玻尔磁子；B为外磁场磁感应强度.此外，式(1)第一项表示所有离子的最近邻耦合情况，第二项表示其各向异性能，第三项表示外磁场对自旋的作用能.每个格点上自旋初始方向与外磁场方向均为z轴正方向.每个格点上的最近邻自旋通过交换耦合方式进行铁磁性耦合.本文中12层铁磁性薄膜的上下表面离子交换耦合参数用Js表示，其他磁性离子的最近邻耦合参数用J表示，上下表面离子的各向异性参数用Ds表示，薄膜中间层的各向异性参数用D表示.为了分析磁性薄膜中的表面自旋波性质，根据文献[11]引入格林函数，即
(l=1，2，…，12；l′=1，2，…，12)
(2)
式中：S+和S-分别为自旋产生和湮灭算符；a为常数；ω为自旋波频率.
采用Tyablikov退耦近似方法处理交换耦合项，采用Anderson-Callen退耦近似方法处理单格点各向异性项.建立格林函数的运动方程，其中格林函数的奇异点对应自旋波谱的解，具体建立过程参见文献[12].在磁性薄膜表面自旋波频率的计算中，自旋量子数与薄膜中间磁性离子的最近邻交换耦合常数均取值为1，为了简化计算，其他物理量均取与交换耦合常数作比值后获得的约化数值(无量纲单位).
2 计算结果分析
图2为温度对铁磁性薄膜中表面自旋波频率的影响.在计算过程中相关参数取值为：B=0.15、Ds=0.05、D=1.在布里渊区表面自旋波存在的Γ-K区域选取k1=4.188 8、k2=3.708 6、k3=3.228 5的三个波矢进行分析.图2a中Js=0.75，此时薄膜中存在声学表面自旋波，而图2b中Js=2，此时薄膜中存在光学表面自旋波.此外，图2横坐标为约化温度且τ=T/Tc，本文中声学表面自旋波对应的Tc为系统参数S=1、Js=0.75、J=1、B=0.15、Ds=0.05、D=1时薄膜的居里温度，而光学表面自旋波对应的Tc为系统参数S=1、Js=2、B=0.15、Ds=0.05、D=1时薄膜的居里温度.
由图2可见，声学和光学表面自旋波频率均随着温度的增加而降低.文献[13]表明，当温度升高时会发生自旋波频率软化现象，这与本文结论一致.由图2a可见，在低温区波矢越大，声学表面自旋波频率越大；在高温区随着波矢的增大，自旋波频率增大幅度不明显.由图2b可见，在低温区随着波矢的增大，光学表面自旋波频率随之增大；而在高温区随着波矢的增大，自旋波频率增加幅度同样不明显.对比图2a、b可知，当约化温度为0.3～0.5时，光学表面自旋波频率随着温度的增加而急速降低.
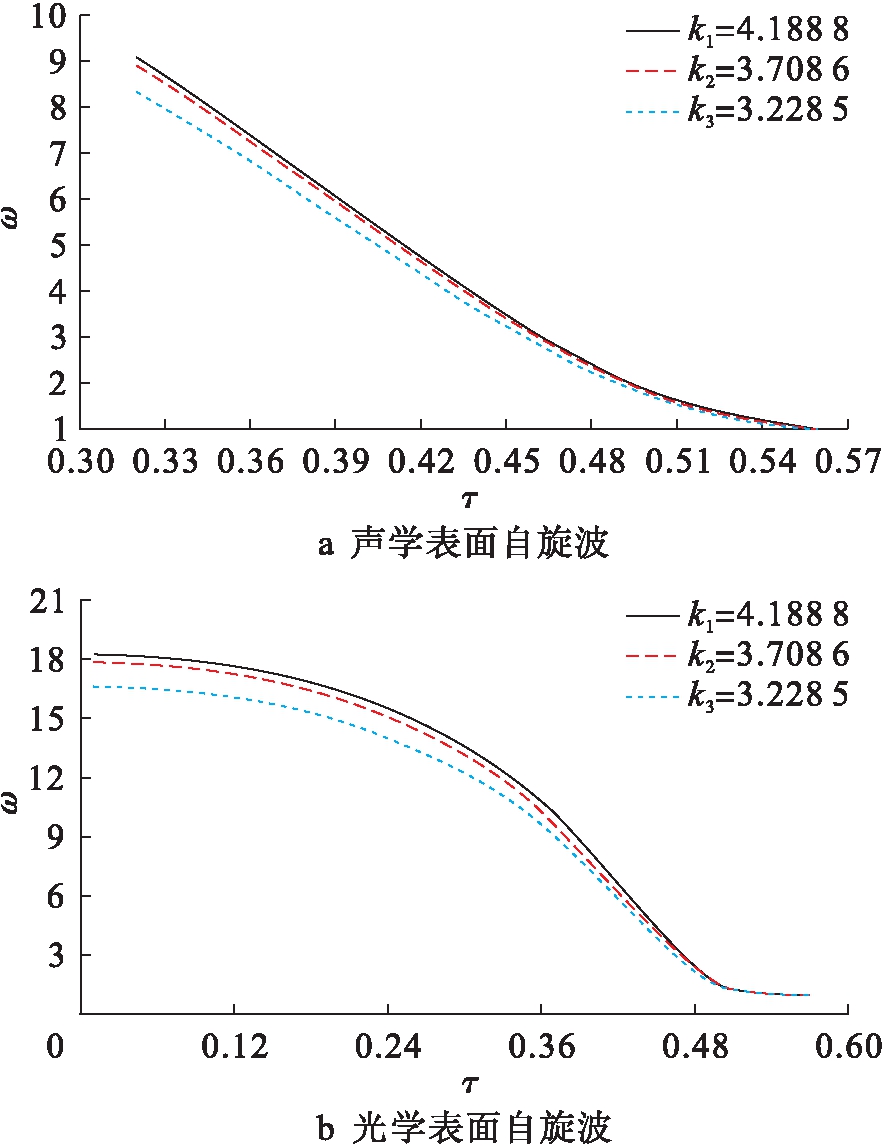
图2 表面自旋波频率随温度的变化
Fig.2 Change of frequency of surface spin waves with temperature
图3为外磁场磁感应强度对表面自旋波频率的影响，且Ds=0.05、D=1、τ=0.5.图3a中Js=0.75，而图3b中Js=2.由图3可见，声学和光学表面自旋波频率均随着外磁场磁感应强度的增加而增加.这是由于当磁场增强时，磁振子的能量增大.对比图3a、b可知，光学表面自旋波随着磁场加强而增大的幅度大于声学表面自旋波.当外磁场磁感应强度处于0.15～0.5区域时，随着波矢的变化，声学和光学表面自旋波频率的变化并不明显.当外磁场磁感应强度较大时，波矢对声学和光学表面自旋波频率的影响较大.这是由于当外磁场强度较大时，能谱较高，因而波矢的改变对能谱的影响较大.
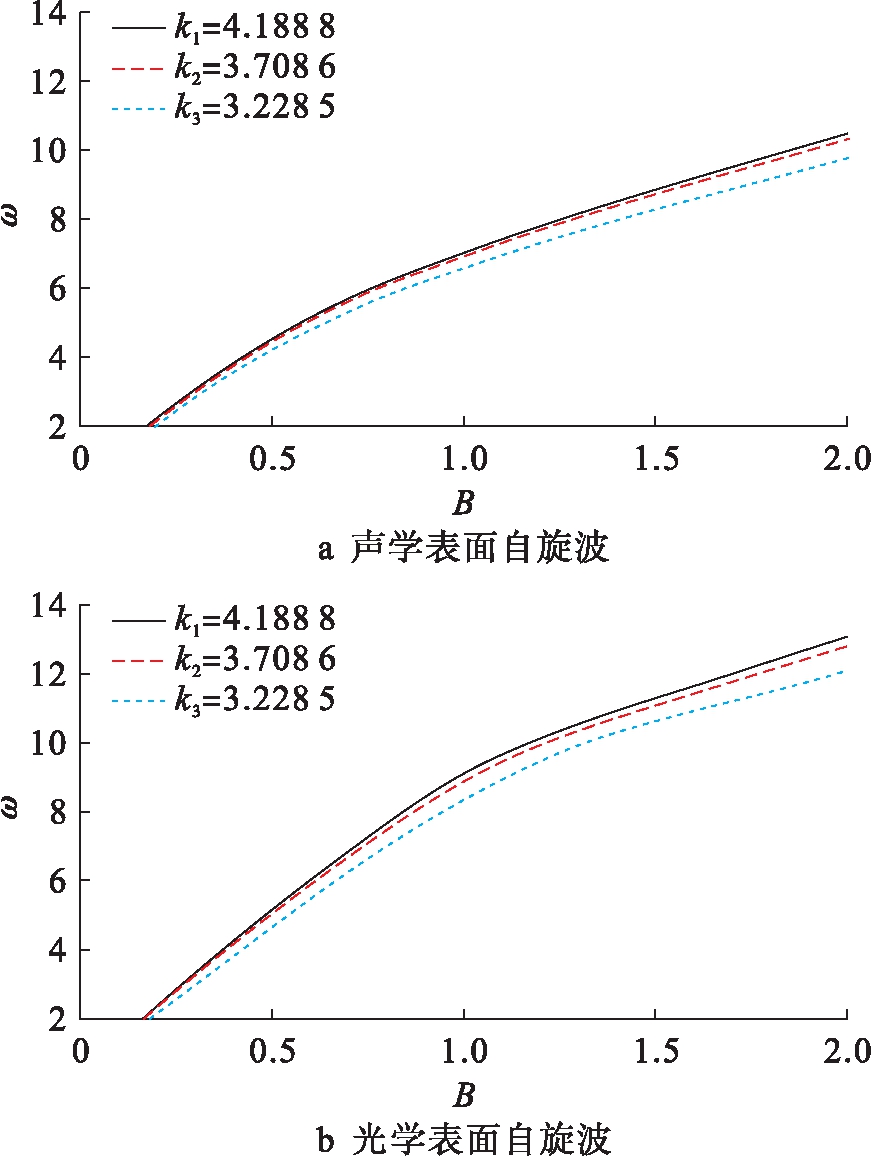
图3 表面自旋波频率随外磁场的变化
Fig.3 Change of frequency of surface spin waves with external magnetic field
图4为表面交换耦合参数对表面自旋波频率的影响，且B=0.15、Ds=0.05、D=1、τ=0.5、J=1.由图4可见，声学和光学表面自旋波频率均随着表面交换耦合参数的增加而增加.这是由于当表面交换耦合作用增强时，磁振子的能量增大.对比图4a、b可知，表面交换耦合对声学表面自旋波的影响较大.
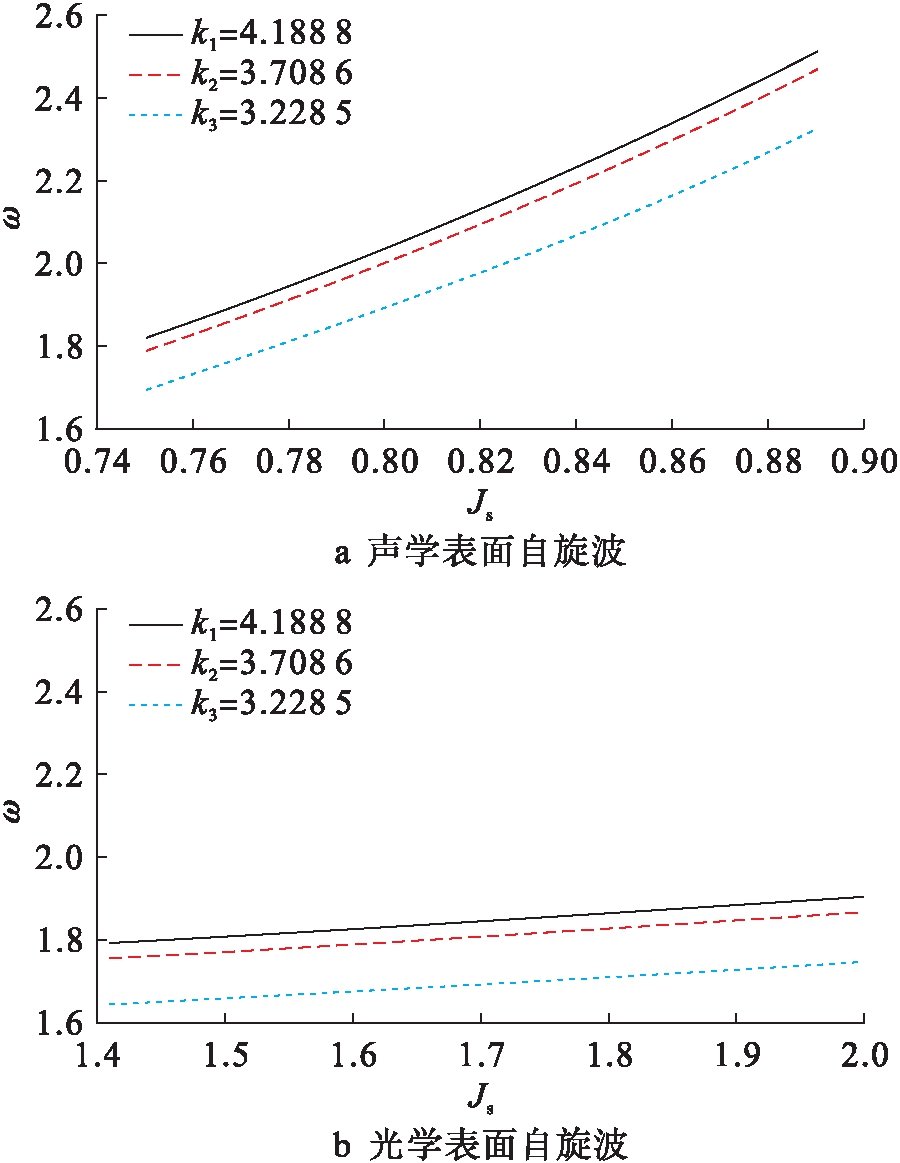
图4 表面自旋波频率随表面交换耦合的变化
Fig.4 Change of frequency of surface spin waves with surface exchange coupling
图5为表面各向异性参数对表面自旋波频率的影响，且τ=0.5、B=0.15、J=1.图5a、b中Js分别为0.75和2.由图5可见，声学和光学表面自旋波频率均随着表面各向异性参数的增加而增加.这是由于当表面各向异性参数增加时，磁振子能量增大.对比图5a、b可知，表面各向异性对声学表面自旋波频率的影响较大.
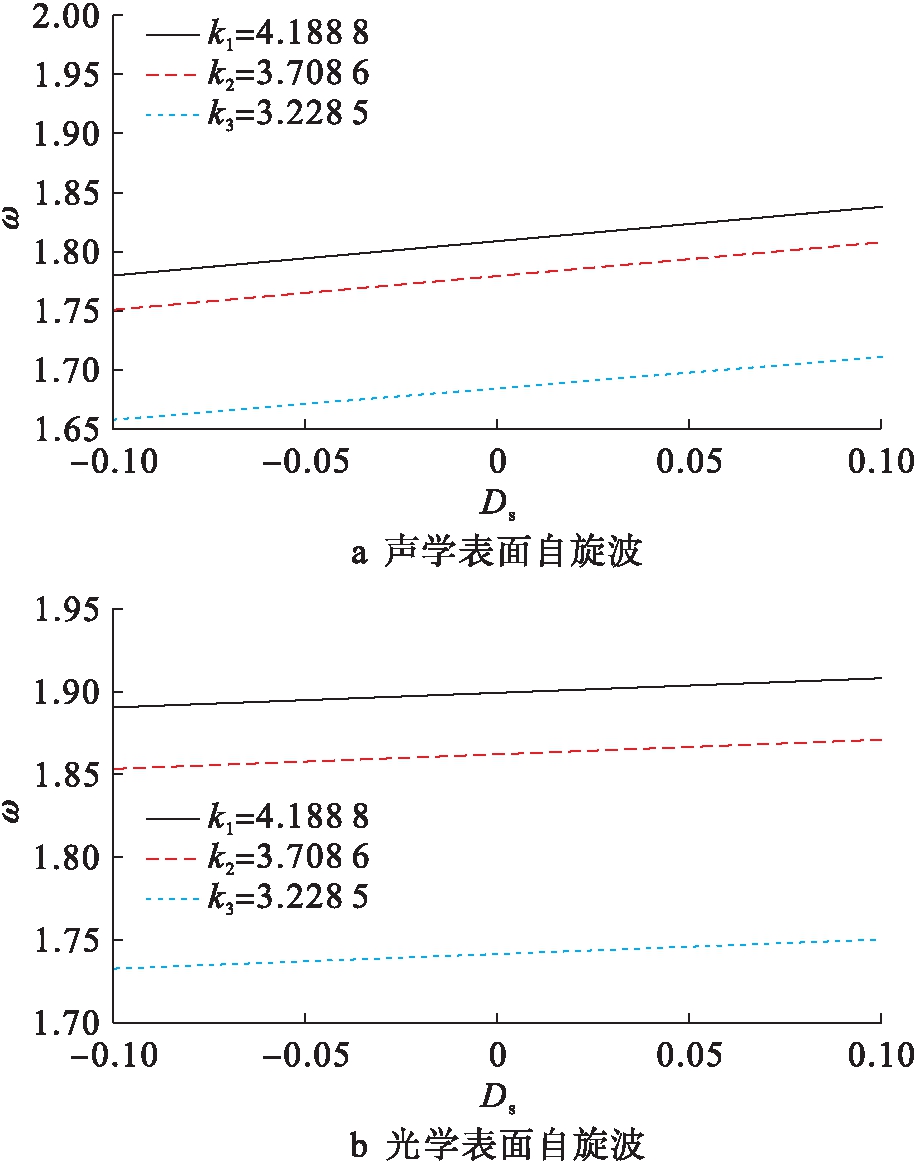
图5 表面自旋波频率随表面各向异性的变化
Fig.5 Change of frequency of surface spin waves with surface anisotropy
图6为在布里渊区Γ-M区域中薄膜厚度对声学和光学表面自旋波频率的影响.其中，B=0.15、J=1、τ=0.5.图6a、b中Js分别为0.75和2.在布里渊区Γ-M区域中，当波矢等于或大于临界波矢kc时，薄膜中出现表面自旋波.由图6a可见，当层数大于5后，声学表面自旋波频率随着薄膜厚度的增加而稍微增大.由图6b可见，当层数大于5时，光学表面自旋波频率随着薄膜厚度的增加而稍微减小.在布里渊区Γ-M区域中，光学表面自旋波频率大于声学表面自旋波频率.观察图6可以发现，不论是声学还是光学表面自旋波，4层与其他层具有明显区别，且本文结果与文献[14]一致，即表面自旋波频率实际上与5个原子层以上的薄膜厚度无关.
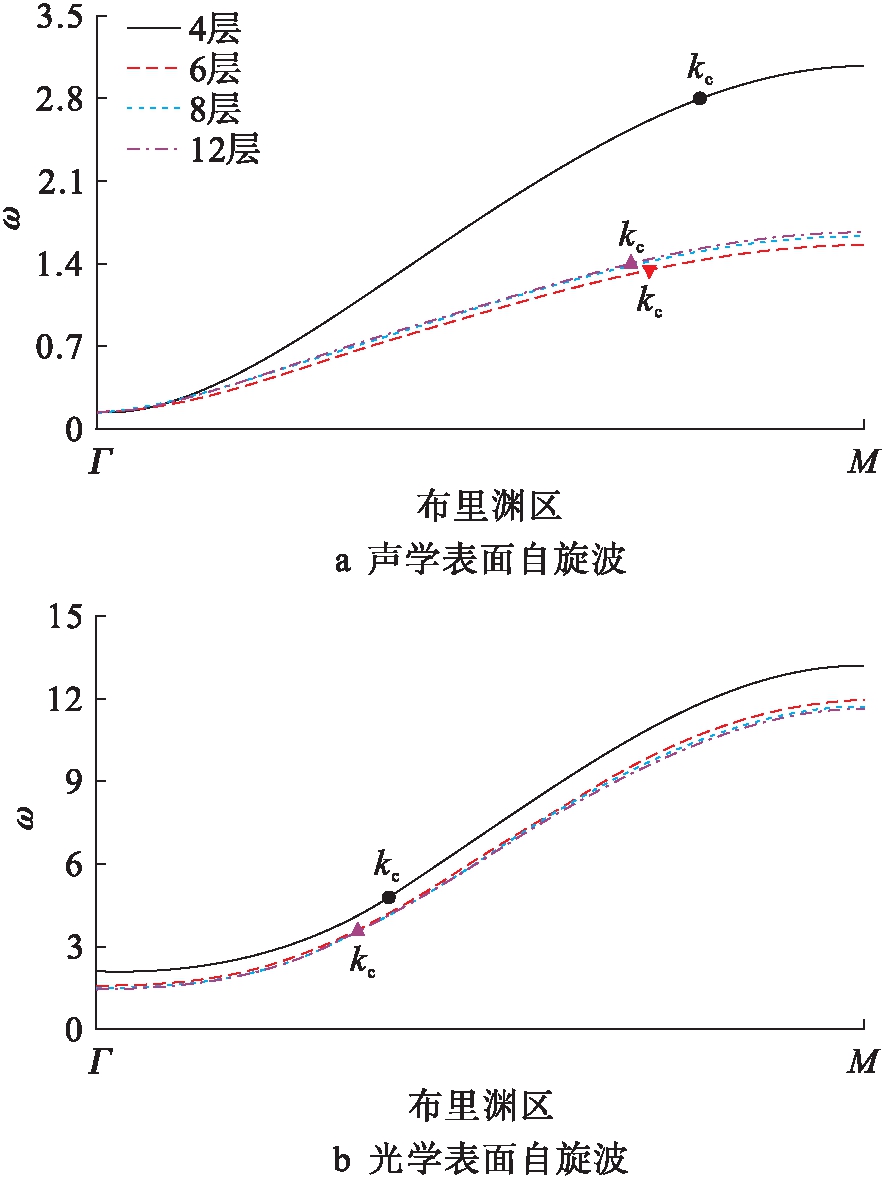
图6 表面自旋波频率随薄膜厚度的变化
Fig.6 Change of frequency of surface spin waves with thickness of thin film
本文中外磁场的增强使得表面自旋波的频率增大，这与文献[15-16]中有关共振频率的结论相符.文献[17]研究了磁性薄膜表面自旋波的色散关系，结果表明，表面自旋波频率随着表面交换耦合和表面各向异性的增强而增大，这与本文结果一致.文献[18]研究了薄膜层数对共振频率变化的影响，其结果亦与本文结论相符.
3 结 论
采用格林函数方法，讨论了铁磁性薄膜中温度、外磁场、表面交换耦合、表面各向异性和薄膜厚度对表面自旋波频率的影响.随着温度的增加，声学和光学表面自旋波频率减小，但在低温区声学表面自旋波的变化比光学表面自旋波的变化大，在高温区则相反.当外磁场磁感应强度增加时，声学和光学表面自旋波频率均增加，但外磁场对光学表面自旋波的影响较大.随着表面交换耦合作用的增加，声学和光学表面自旋波频率也随之明显升高，但表面交换耦合对声学表面自旋波的影响较大.随着表面各向异性的增大，声学和光学表面自旋波频率均增大，且表面各向异性对声学表面自旋波的影响较大.声学和光学表面自旋波频率随波矢的增大而增大.当薄膜原子层数大于5时，光学表面自旋波频率随着薄膜厚度的增加而稍微减小，而声学表面自旋波频率则随薄膜厚度的增加而稍微增大.
[1] 苏刚.磁性纳米结构中的自旋操控及其应用 [J].现代物理知识，2016，20(5)：45-49.
(SU Gang.Spin manipulation in magnetic nanostructures and its application [J].Modern Physics Knowle-dge，2016，20(5)：45-49.)
[2] Gowtham P G，Moriyama T，Ralph D C，et al.Traveling surface spin-wave resonance spectroscopy using surface acoustic waves [J].Journal of Applied Physics，2015，118(23)：233910-233915.
[3] Ei S，Yuichiro A，Sergey D，et al.Spin-wave-induced lateral temperature gradient in a YIG thin film/GGG system excited in an ESR cavity [J].Applied Physics Letters，2018，112(21)：1-5.
[4] Li X，Labanowski D，Salahuddin S，et al.Spin wave generation by surface acoustic waves [J].Journal of Applied Physics，2017，122(4)：1-8.
[5] Mamica S.Propagation effects in the spin-wave spectrum of the ferromagnetic thin film [J].Advances in Condensed Matter Physics，2015，56(10)：1-17.
[6] Landeros P，Mills D L.Spin waves in periodically perturbed films [J].Physical Review B，2012，85(5)：1-10.
[7] 涂宽.磁性纳米结构的微磁学模拟及其微波器件的研究 [D].成都：成都电子科技大学，2016.
(TU Kuan.Micromagnetic simulation of magnetic nanostructures and research of microwave devices [D].Chengdu：Chengdu University of Electronic Science and Technology，2016.)
[8] 王焕，么强.异质双层磁性薄膜中的界面自旋波 [J].内蒙古农业大学学报(自然科学版)，2015，36(1)：150-154.
(WANG Huan，YAO Qiang.Interfacial spin waves in heterogeneous bilayer magnetic films [J].Journal of Inner Mongolia Agricultural University (Natural Science Edition)，2015，36(1)：150-154.)
[9] Flaviano J D S，Manuel D S D，Samir L.First-principles investigation of spin wave dispersions in surface-reconstructed Co thin films on W(110) [J].Physical Review B，2016，95(13)：1-14.
[10] 张光富，张学军，蒋练军.末端形状对磁纳米薄膜自旋波模式特性的影响 [J].材料导报，2016，30(5)：148-151.
(ZHANG Guang-fu，ZHANG Xue-jun，JIANG Lian-jun.Effect of end shape on spin wave mode characteristics of magnetic nanofilms [J].Material Report，2016，30(5)：148-151.)
[11] Callen H B.Green function theory of ferromagnetism [J].Physics Review，1963，130：890-898.
[12] 邱荣科，郭非非，刘忠菊.三层软磁镍超晶格薄膜的共振频率 [J].沈阳工业大学学报，2016，38(1)：30-35.
(QIU Rong-ke，GUO Fei-fei，LIU Zhong-ju.Resonance frequency of three-layer soft magnetic nickel superlattice film [J].Journal of Shenyang University of Technology，2016，38(1)：30-35.)
[13] 李正中.固体理论(第二版) [M].北京：高等教育出版社，2002.
(LI Zheng-zhong.Solid state theory (2nd edition) [M].Beijing：Higher Education Press，2002.)
[14] Etzkorn M，Kumar P S A，Vollmer R，et al.Spin waves in ultrathin Co-films measured by spin polari-zed electron energy loss spectroscopy [J].Surface Science，2004，566(1)：241-245.
[15] Qiu R K，Ma F J，Zhang Z D.Spin-wave resonance frequency in a multi-layer film [J].Journal of Magnetism and Magnetic Materials，2015，394：454-462.
[16] de Sousa M A，Pelegrini F，Alayo W，et al.Parallel ferromagnetic resonance and spin-wave excitation in exchange-biased NiFe/IrMn bilayers [J].Physica B：Condensed Matter，2014，450：167-172.
[17] Wang Z J，Mitsudo S，Watanabe K，et al.Spin-wave resonance in ferromagnetic coupled Co/Cu multilayers [J].Journal of Magnetism and Magnetic Materials，1997，176(2/3)：127-133.
[18] Khivintsev Y V，Reisman L，Lovejoy J，et al.Spin wave resonance excitation in ferromagnetic films using planar waveguide structures [J].Journal of Applied Physics，2010，108(2)：1-6.