大跨度斜拉桥的调索，包括理想成桥状态和施工阶段索力的确定，需要较多的工程实践经验和较高的理论水平[1].目前的通用结构计算程序，往往缺少相应的调索模块，使用起来也有很多的局限性.设计人员在斜拉桥设计时，需要丰富的调索经验，否则很难得到合理的索力[2-3].
针对斜拉桥调索，研究人员提出了各种不同的方法.吴霄等[4]给出了索力优化的遗传算法；陈志军等[5]给出了基于粒子群算法的独塔斜拉桥成桥索力优化方法；苑仁安等[6]以及李国平等[7]针对斜拉索索力调整的无应力状态法进行了研究.以上研究方法均需要设计者具有较高的理论水平.本文结合佛山南海东平大道大桥的设计，针对大跨独塔公轨两用混合梁斜拉桥，提出实用简单的调索方法：理想成桥状态采用经验试算法；施工阶段采用两阶段调索方法.实用调索方法原理简单，容易掌握，调索快，主梁和主塔受力合理，达到了较好的效果.
1 工程介绍
佛山南海东平水道大桥为目前国内最宽的公轨同层独塔双索面混合梁斜拉桥.该桥主桥跨径为(35+260+51.5+66+62.5) m，全长475 m.为了减小主跨前端梁端转角值，主桥设置了跨径35 m的前伸跨，边跨侧设置两个辅助墩.全桥采用墩
塔梁固结体系，其桥型布置如图1所示(单位：mm).桥梁全宽46.5 m，包括双向六车道公路，双线轨道交通和双侧人行道.主跨采用分离式钢箱梁，边跨采用分离式混凝土箱梁.桥塔为A字形，塔高124.8 m，塔身位于公路和轨道交通之间，桥塔构造如图2所示(单位：mm).斜拉索扇形布置，拉索最大型号PES 7-253，最小型号PES 7-127.主跨钢梁拉索锚固间距为9.0 m，边跨混凝土梁高为6.0 m，主塔上锚固间距为2.0 m.全桥共52对拉索.
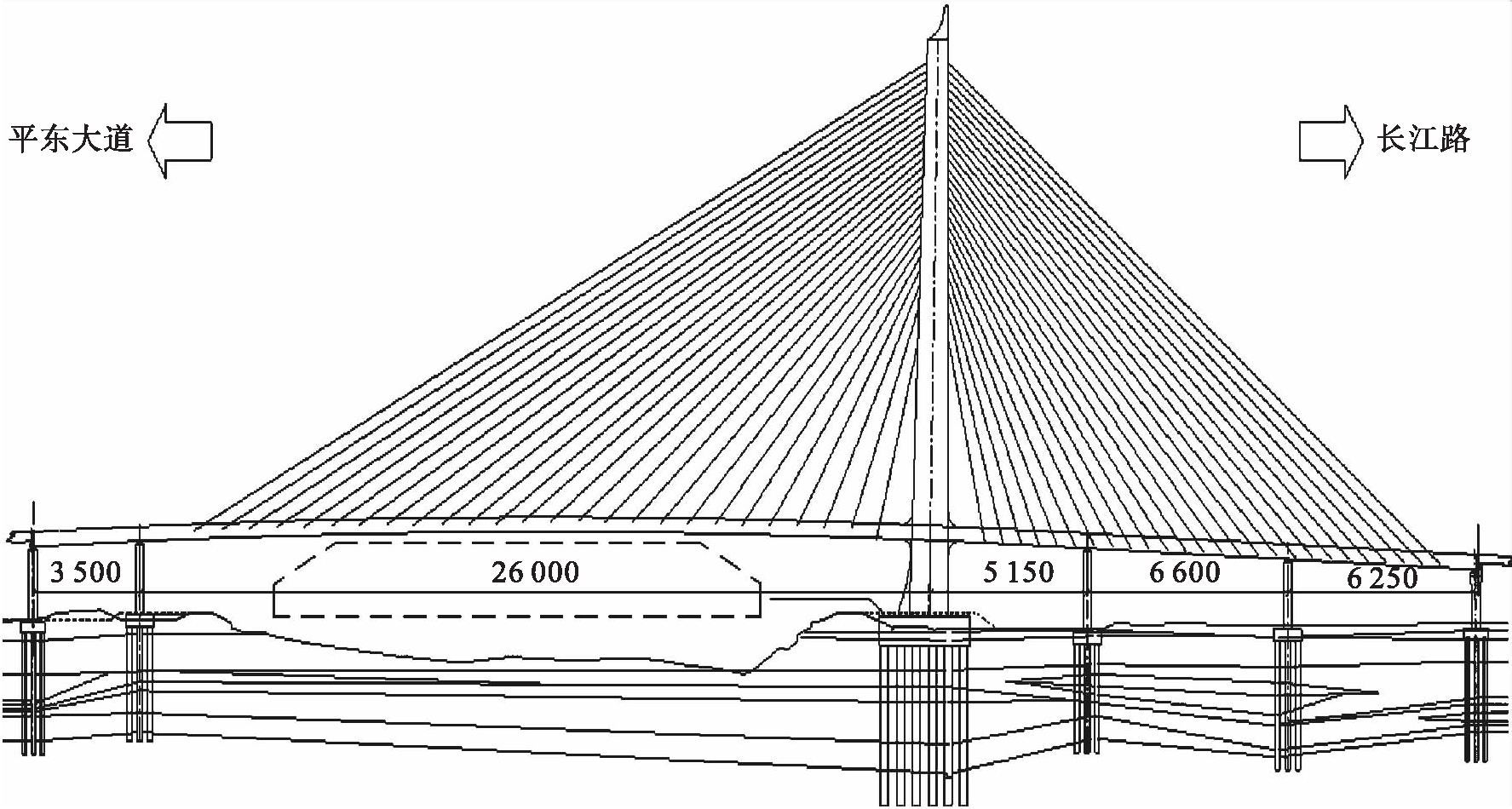
图1 东平桥桥型布置
Fig.1 Layout of Dongping Bridge
2 理想成桥索力确定
2.1 调索目标
斜拉桥成桥后，其内力状态和线形状态均应满足设计要求.通过施工过程设置预拱度，斜拉桥线形可以不断调整，以满足成桥的线形.因此，重点在于合理控制斜拉桥的成桥内力，使得结构受力满足要求.调索时应满足“塔直梁平”的基本准则.针对独塔公轨两用混合梁斜拉桥的受力特点，制定了相应的调索目标.
1) 桥塔.桥塔为压弯构件，由于轴向力的预加力效应，可承受较大的弯矩.调索时，应使恒载作用下两侧弯矩基本平衡.根据公轨两用斜拉桥活载占比相对较大的受力特点，考虑运营之后汽车和轨道交通荷载的共同作用，可借鉴主梁预拱度的原理，塔身向岸侧偏移，在一半活载效应的作用下，塔身基本保持竖直.
2) 主梁.对于主跨钢梁，应使成桥状态钢梁弯矩量值较小，同样由于公轨两用斜拉桥活载较大，调索时应为主梁预留一定的负弯矩，使得在活载包络下，正负弯矩量值基本相同.对于边跨混凝土梁，由于斜拉索的弹性支承作用以及辅助墩的设置，可通过配置预应力钢束使得其应力满足规范要求.由于钢混结合段主梁受力复杂，应保证合理成桥状态钢混结合段位置弯矩剪力较小，截面受力均匀.
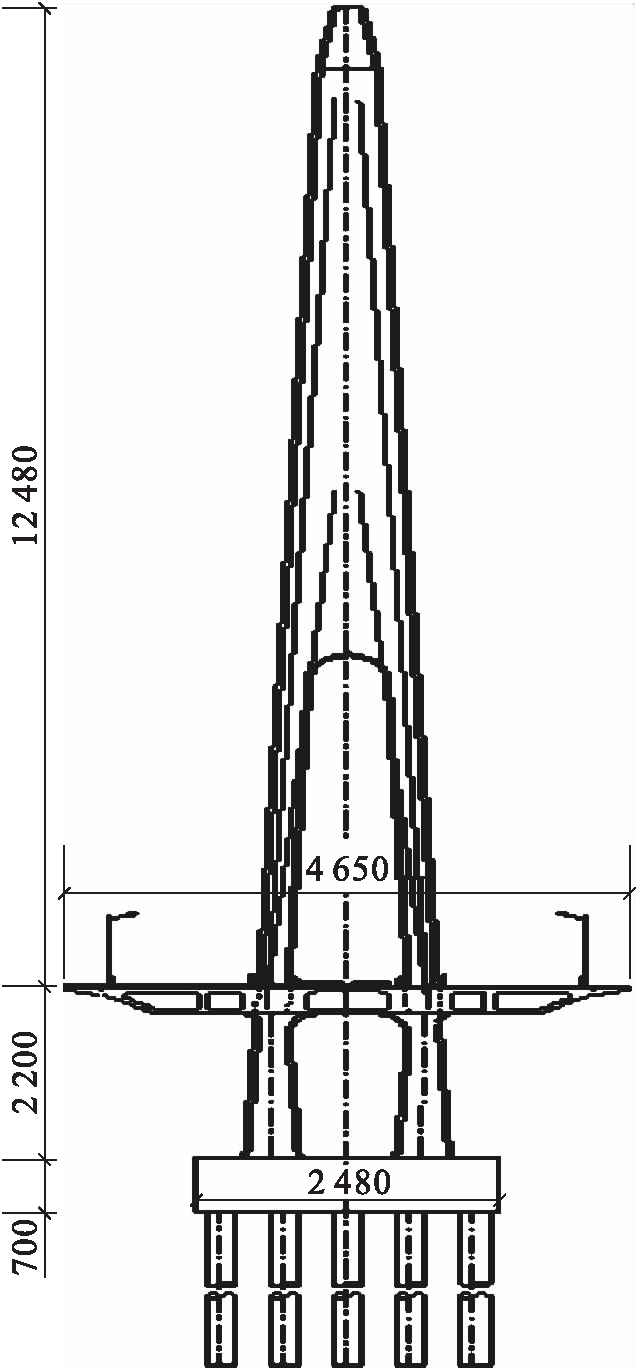
图2 桥塔构造
Fig.2 Structure of pylon
3) 拉索.索力分布均匀，一般从最外侧拉索往内索力逐渐减小.考虑到钢混结合段构造复杂，梁重较重，因此，其附近拉索索力可灵活掌握.
4) 锚墩和辅助墩.锚墩和辅助墩支座不出现负反力，或者通过压重即可消除负反力.这样就可以避免设置构造复杂，造价昂贵且容易产生疲劳问题的拉力支座.
2.2 索力求解方法
理想成桥索力的确定一般不用考虑施工阶段的影响，合理成桥状态确定后，可以通过某种施工方案或者施工工序的调整，实现给定的合理成桥状态.理想成桥索力求解时，初始索力的拟定非常关键.良好的初始索力值对后期调索可起到事半功倍的效果.类似于刚性支承连续梁法的求解原理，针对佛山南海东平水道混合梁斜拉桥，采用索力竖向分量平衡梁重，并乘以放大系数的经验试算法确定初始索力，该方法原理简单，通过几次试算即可满足要求，具体步骤如下：
1) 算出中跨混合梁钢梁部分各个梁段的重量，然后使相应斜拉索的竖向分量等于梁段重量，通过角度转换得到中跨侧索力，边跨索力通过与中跨索力水平分量相等求得.初始索力的拟定如图3所示.
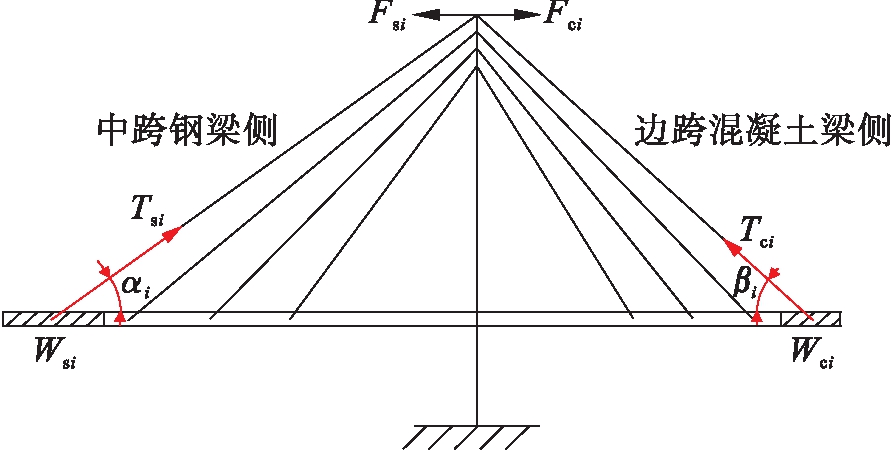
图3 初始索力拟定
Fig.3 Determination of initial cable force
忽略主梁抗弯刚度的影响，令Wsi为第i根索所支承的恒载重量，根据竖向力的平衡，可得
Tsi=Wsi/sin αi
(1)
中跨侧斜拉索引起的水平力为
Fsi=Tsicos αi=Wsi/tan αi
(2)
忽略桥塔抗弯刚度的影响，则主边跨索力的水平分量应相等，于是可求得边跨侧斜拉索初始索力，即
(3)
2) 上述初始索力计算中，未考虑活载的影响，根据活载所占结构总荷载的比例，对所求索力乘以一个放大系数，输入结构中进行计算.之后对局部拉索索力进行微调，调整原则是短索索力小，长索索力大，呈递增趋势，索力均匀以及主塔弯矩小等，就可得到较理想的成桥索力.
采用上述方法计算时，应注意桥塔在恒载作用下应向边跨侧有一定偏移.具体调索时，可通过对边、中跨调整放大系数来实现.该方法原理简单，操作方便，便于设计人员掌握.
3 施工阶段索力确定
大跨独塔混合梁斜拉桥施工时，斜拉索的张拉可采用一次张拉法或者多次张拉法.采用一次张拉法成桥后不再对拉索进行张拉，张拉次数少.但是施工过程索力需照顾到成桥索力的大小，该方法可能会造成斜拉桥施工过程中结构内力过大，对于二期恒载较大的斜拉桥，一次张拉法可能无法得到合理的成桥状态.
斜拉桥施工过程中，由于存在施工误差等因素，为了使斜拉桥受力达到理想状态，一般均会在成桥后进行一次调索.综合以上因素，斜拉索张拉建议采用二阶段调索法，其主要步骤如下：
1) 悬臂拼装阶段索力只是为了达到施工过程中的受力要求.因此，该索力主要用于平衡当前施工阶段的主梁自重以及施工过程中的荷载等.
2) 在成桥后对拉索进行二次调索，调索采用影响矩阵法[8-10]，通过迭代计算使其达到理想成桥状态的要求.
采用二阶段调索法，悬臂拼装阶段斜拉索初始拉力的确定只需满足施工过程中的安全性，保证主梁基本平直，重点在于第二次调索，通过成桥后第二次调索拟合合理的成桥状态.
3.1 索力优化方法
假定斜拉桥受力处于线弹性状态，则可建立如下线性方程组，即
AΔT=ΔR
(4)
式中：ΔT为索力调整量；ΔR为控制目标与理想成桥状态控制目标的差值；A为索力调整对控制目标的影响矩阵.
在式(4)控制目标中应加入各种可能引起控制作用的物理量，使得该方程组的方程个数大大超过调整索力数，从而成为一个矛盾方程组，可求其广义解(即最小二乘解).其原理为求ΔT，使得
(5)
为最小.式中，m、n分别为ΔT和ΔR的元素个数.根据极值原理，为了使得式(5)最小，则有
ATAΔT=ATΔR
(6)
根据上述计算公式，针对第二阶段的调索，利用影响矩阵法编制了基于MATLAB的斜拉桥调索程序，可方便得到拟合合理成桥状态的第二阶段拉索索力.影响矩阵可以采用大型有限元程序MIDAS直接求取.
3.2 控制目标和加权矩阵的选取
在结构布置确定的情况下，斜拉桥成桥合理状态仅与恒载分布、索力及支座反力(成桥状态三要素)有关，与结构刚度分布、结构非线性、施工过程无关.该定理可以从力的平衡条件推出，任何结构布置和恒载分布给定的斜拉桥，只要索力和支座反力已知，结构就成为静定体系，斜拉桥的内力状态可由索力和支座反力唯一确定.
因此，控制目标ΔR可以取各对斜拉索索力以及各个支承处反力的差值.只要上述控制指标接近目标值，则施工后成桥索力即接近于理想成桥索力.本桥斜拉索共52对，因此，索力调整向量ΔT为52×1的向量，ΔR取斜拉索索力加上各个支承处竖向反力，因此其为59×1的向量.
由于不同的控制量量纲、数值大小或者重要程度不同，在式(4)中引入正定对角加权矩阵ρ，则该方程变为
ρAΔT=ρΔR
(7)
求取式(7)的最小二乘解，可以得到
ATρ2AΔT=ATρ2ΔR
(8)
加权矩阵ρ的取值，可以根据其量纲和控制量的重要程度灵活选取，得到更优值.通过设置加权系数，可有效提高式(6)的求解速度和精度.
4 东平水道大桥调索结果
调索时应尽量采用简化计算模型，减少计算工作量.采用大型有限元程序MIDAS建立东平水道大桥单梁脊骨梁计算模型.主梁和桥塔均采用空间梁单元，斜拉索采用空间桁架单元，其中，钢混结合梁梁段采用双单元法进行模拟，塔底根部采用弹簧单元模拟桩基和承台等下部结构的作用.斜拉索边跨侧最外侧拉索为C26，由外向内变化至C1；中跨侧最外侧斜拉索编号为P26，由外向内变化至P1.全桥有限元模型如图4所示.
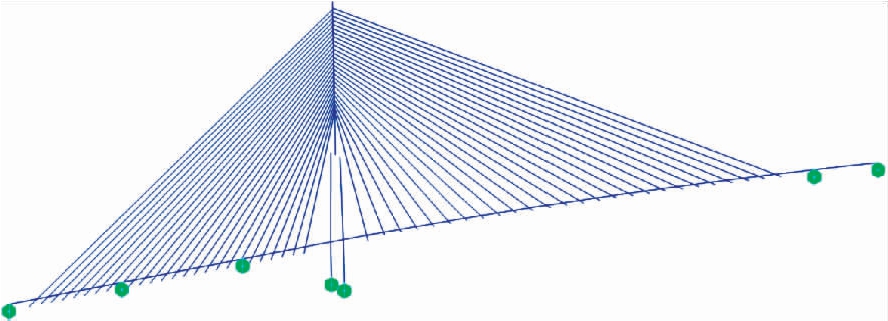
图4 东平桥有限元模型
Fig.4 Finite element model for Dongping Bridge
4.1 理想成桥索力
采用经验试算法进行理想成桥索力的求解.试算时调整桥塔两侧索力的比例系数，使得桥塔在恒载作用下人为往边跨侧产生一定程度的偏移.一般可参考常规主梁预拱度的设置方法，使得在1/2活载作用下，主塔基本保持竖直.
1) 主塔.恒载作用下，主塔塔顶往边跨侧偏移61 mm，活载满载后，桥塔向中跨偏移67 mm，桥塔塔身受力合理，基本处于全截面受压状态.
2) 索力.索力采用经验试算法进行，最终索力如图5所示.其中，P26拉索最大索力为5 235 kN.索力由边索向中间索由大到小均匀变化，桥塔根部由于有钢混结合段，索力大于附近拉索.
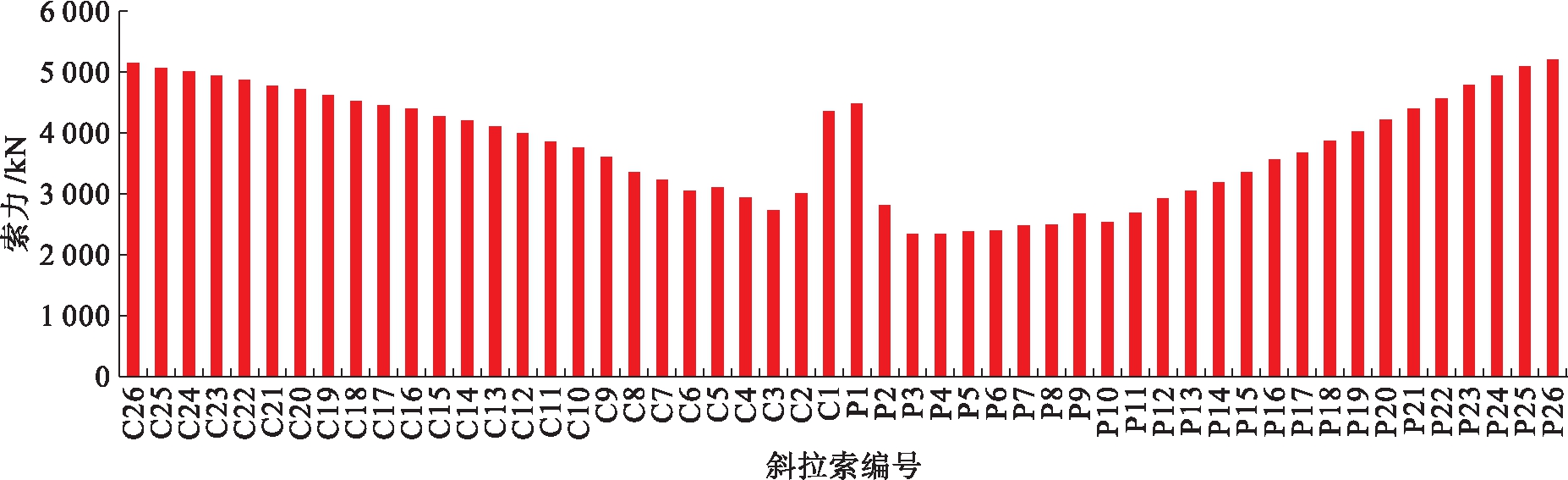
图5 理想成桥状态下斜拉索索力
Fig.5 Cable forces under ideally completed state
3) 主梁.主梁受力合理，恒载作用下，主跨钢梁侧向上预留一部分负弯矩，如图6所示(单位：kN·m).主力+附加力荷载组合下，钢梁弯矩包络图正负弯矩值分布均匀，受力合理，如图7所示(单位：kN·m).
图6 成桥状态弯矩图
Fig.6 Bending moment diagram under completed bridge state
图7 主+附弯矩包络图
Fig.7 Envelope diagram of bending moment under main and additional force
通过向上预留负弯矩，使得主梁在主力+附加力组合下，正负弯矩幅值相近，满足了主梁受力的要求.混凝土梁由于在边跨侧设置了两个辅助墩，跨径较小，且由于斜拉索多点弹性支承和预压作用，改善了主梁受力，通过配置适当的预应力钢束即可满足要求.
4) 锚墩、辅助墩支反力.表1给出了P2墩(前伸跨中墩)墩顶部设置压重后计算结果.如未设置压重，虽然P2墩顶支座均未出现负反力，但最小竖向力仅为361 kN，富裕量较小，考虑到后期超载的可能性等其他不确定性因素，设计时在P2墩顶适当设置一定的压重.设置压重长度为28 m，荷载集度为260 kN/m，总压重为7 280 kN.
表1 各墩(塔)支承处竖向反力
Tab.1 Vertical reaction force at each pier (pylon) support kN
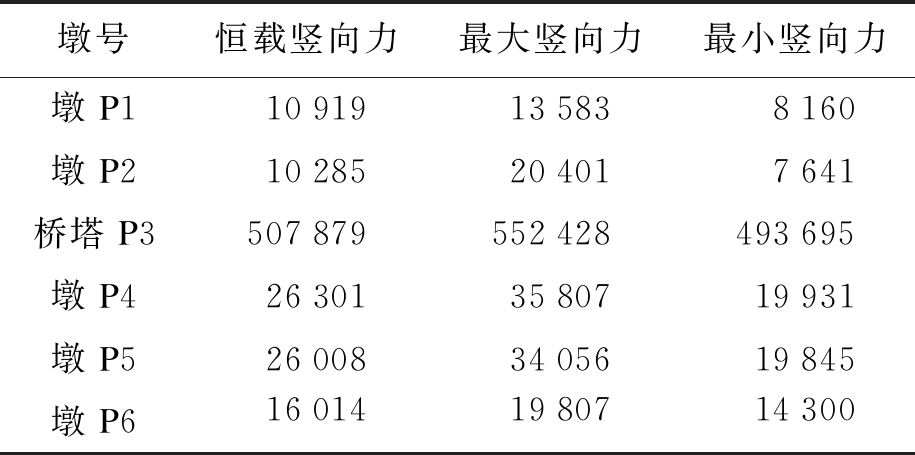
墩号恒载竖向力最大竖向力最小竖向力墩P11091913583 8160墩P210285204017641桥塔P3507879552428493695墩P4263013580719931墩P5260083405619845墩P6160141980714300
4.2 施工阶段索力
根据施工阶段索力确定的二阶段调索法原理，首先求得悬臂拼装阶段的索力.该阶段索力的确定方法类似于理想成桥状态下索力的确定方法，确定的原则是拉索索力的竖向分量平衡斜拉桥梁段的重量.第一次和第二次拉索张拉力如图8所示.
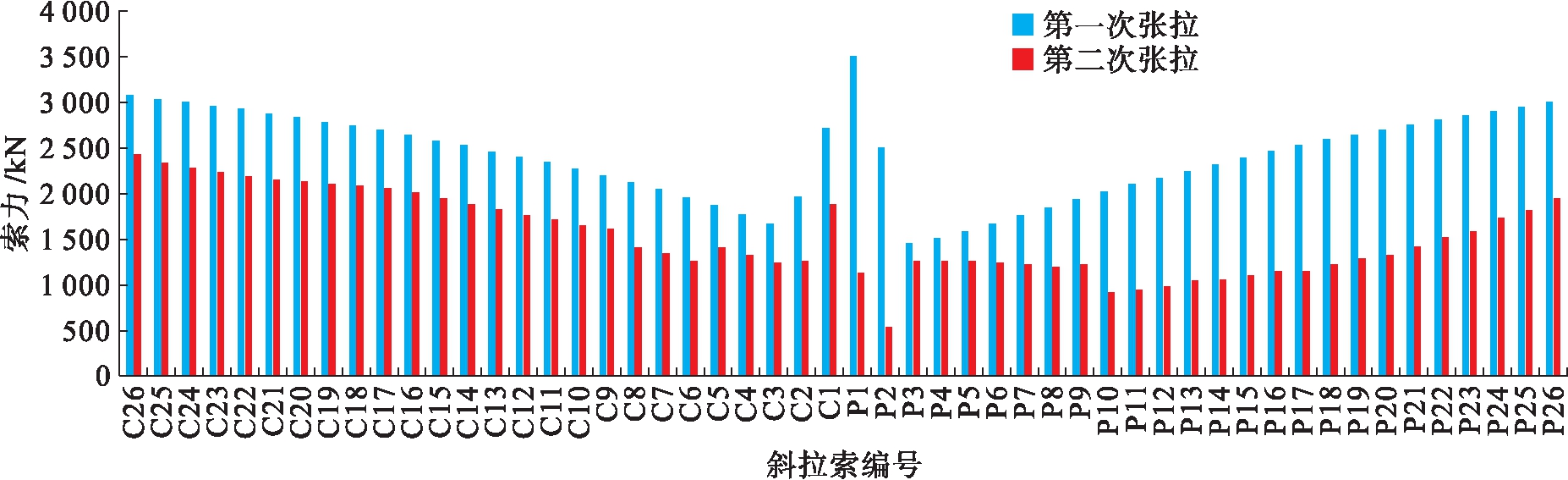
图8 第一次和第二次拉索张拉力
Fig.8 First and second cable tension force
斜拉桥成桥合龙上二期恒载之后，一般最好不再调整索力.如果调整将在桥面铺装层中产生附加内力.因此，桥梁合龙未上二期恒载之前，对全部斜拉索进行第二次张拉.影响矩阵A采用MIDAS程序求解，对各根斜拉索施加单位索力(一般取100 kN)，求取施加单位索力时，各根斜拉索索力的变化值以及各个支承处的支承反力值.本桥影响矩阵A的维数为59×52.加权矩阵ρ反应了结构控制量的量纲和重要程度，其维数为59×59，矩阵对角线上的数值可根据索力和支反力的量纲和重要程度进行试算.
通过优化求解后，重新模拟施工计算求得成桥内力，与确定的理想成桥状态对比，可通过修改这些控制参数的目标值或调整加权系数，将两者的不闭合程度降到最低.值得注意的是，结构最终形成的内力与其施工顺序有密切的关系，理想成桥状态只是作为一个理想目标值.通过迭代计算后，其最终成桥状态只能接近于理想成桥状态.最终提交设计文件的成桥索力等参数应该是考虑施工阶段后的成桥索力.
通过计算，最终成桥索力以及理想成桥索力的对比如图9所示，两者相差最大不超过1.9%.最终成桥阶段，斜拉桥各个构件的内力和变形情况均很好地满足了设计要求.
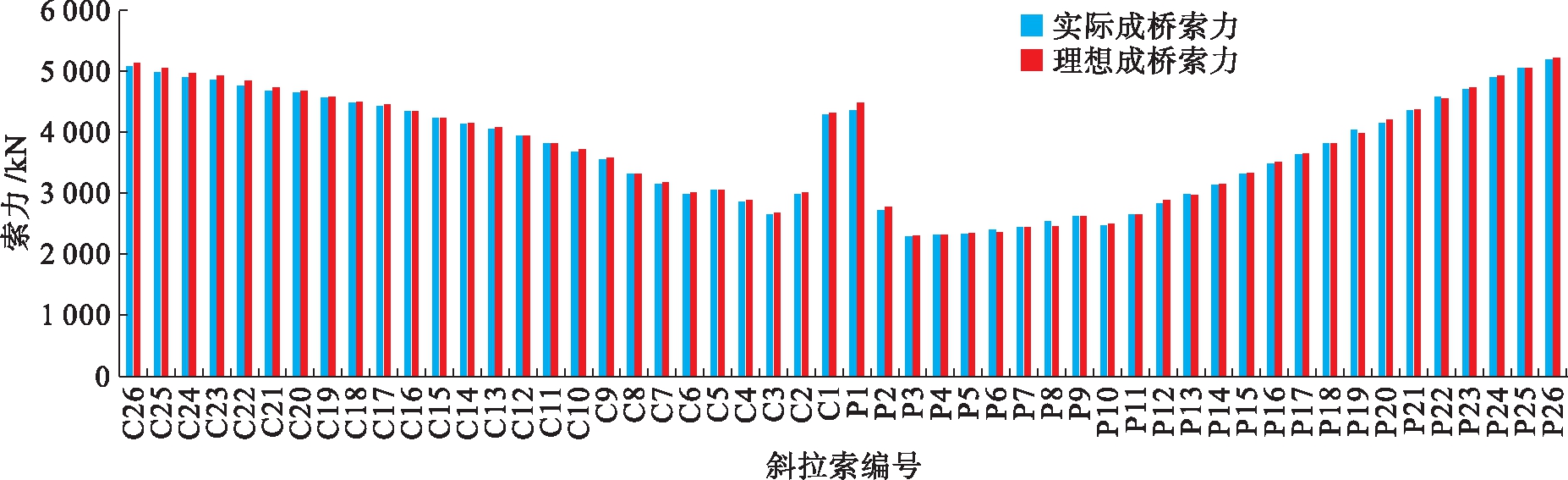
图9 实际成桥和理想成桥索力对比
Fig.9 Comparison of cable force between actually and ideally completed bridges
5 结 论
针对斜拉桥调索需要较高的理论水平，设计者较难掌握的现实，结合佛山南海东平水道大桥的调索，给出了确定其理想成桥索力和施工阶段索力的方法.目前，该斜拉桥已经顺利合龙，主梁主塔受力合理，调索取得了较好的效果.实用调索方法具有较好的推广应用价值.针对大跨独塔混合梁斜拉桥的调索，得出以下结论：
1) 公轨两用混合梁斜拉桥调索时，应合理制定成桥目标：考虑到公轨两用斜拉桥活载较大，应使桥塔成桥状态预先向边跨侧偏移，这样活载作用后，桥塔受力更合理；对于主梁，同样应预留一些负弯矩，使得考虑活载后，主梁受力更均衡.
2) 理想成桥状态采用索力竖向分量平衡梁重，并乘以放大系数的方法试算确定合理成桥索力，计算简单，容易掌握.
3) 施工阶段索力推荐采用二阶段调索方法：第一阶段仅需满足施工阶段受力需求，平衡相应梁段重量和施工阶段荷载即可；第二阶段在主梁合龙上二期前采用影响矩阵法对所有斜拉索进行二次调索.其中，影响矩阵可以通过MIDAS有限元程序求得，并采用基于MATLAB语言编制的影响矩阵法程序求取二次调索索力.该方法简单实用，容易掌握，调索速度快，很好地满足了设计要求.
[1] 王海军，王子山，刘红钊，等.基于温度循环迭代精确施加斜拉桥初始索力 [J].沈阳工业大学学报，2018，40(2)：224-228.
(WANG Hai-jun，WANG Zi-shan，LIU Hong-zhao，et al.Precisely imposed initial cable force for cable stayed bridge based on temperature cycle iteration [J].Journal of Shenyang Universtiy of Technology，2018，40(2)：224-228.)
[2] 康春霞，杜仕朝，邬晓光.斜拉桥合理施工状态计算方法对比分析研究 [J].铁道科学与工程学报，2017，14(1)：87-93.
(KANG Chun-xia，DU Shi-zhao，WU Xiao-guang.Discussion and comparative analysis on calculation method of reasonable construction state of cable stayed bridge [J].Journal of Railway Science and Engineering，2017，14(1)：87-93.)
[3] 李艳凤，梁力，罗威力.预应力混凝土斜拉桥箱梁剪力滞规律 [J].沈阳工业大学学报，2016，38(6)：710-714.
(LI Yan-feng，LIANG Li，LUO Wei-li.Law of shear lag effect in box girder of prestressed concrete cable-stayed bridge [J].Journal of Shenyang Universtiy of Technology，2016，38(6)：710-714.)
[4] 吴霄，肖汝诚.基于遗传算法的大跨度混合梁斜拉桥索力优化 [J].江苏大学学报，2014，35(6)：722-726.
(WU Xiao，XIAO Ru-cheng.Optimization of cable force for cable-stayed bridges with mixed stiffening girders based on genetic algorithm [J].Journal of Jiangsu University，2014，35(6)：722-726.)
[5] 陈志军，刘洋，杨立飞，等.基于粒子群优化算法的独塔斜拉桥成桥索力优化 [J].桥梁建设，2016，46(3)：40-44.
(CHEN Zhi-jun，LIU Yang，YANG Li-fei，et al.Opimization of stay cable tension of completed bridge of single-pylon cable-stayed bridge based on particle swarm optimization algorithm [J].Bridge Construction，2016，46(3)：40-44.)
[6] 苑仁安，秦顺全.无应力状态法在钢绞线斜拉索施工中的应用 [J].桥梁建设，2012，42(3)：75-79.
(YUAN Ren-an，QIN Shun-quan.Application of unstressed state method to construction of steel strand stay cable [J].Bridge Construction，2012，42(3)：75-79.)
[7] 李国平，黎金星.基于无应力长度目标的平行钢绞线斜拉索张拉方法 [J].中国公路学报，2017，30(2)：48-56.
(LI Guo-ping，LI Jin-xing.Tension strategy derived by non-stress length of parallel steel strand stay cables [J].China Journal of Highway Transportation，2017，30(2)：48-56.)
[8] 任志刚，刘为俊，杜小勇，等.斜拉桥施工阶段二次调索计算方法 [J].桥梁建设，2011，41(3)：56-60.
(REN Zhi-gang，LIU Wei-jun，DU Xiao-yong，et al.Calculation methods of two-time cable force adjustment for cable-stayed bridges at construction stage [J].Bridge Construction，2011，41(3)：56-60.)
[9] 白先梅.高速铁路斜拉桥二次调索计算分析 [J].高速铁路技术，2016，7(4)：46-49.
(BAI Xian-mei.Calculation and analysis of secondary adjustment of cable force of high-speed railway cable-stayed bridge [J].High Speed Railway Technology，2016，7(4)：46-49.)
[10] 武振国.独塔斜拉桥成桥索力优化方法的研究 [J].兰州工业学院学报，2016，23(5)：22-24.
(WU Zhen-guo.The study on cable force optimization on cable-stayed bridge [J].Journal of Lanzhou Institute of Technology，2016，23(5)：22-24.)