由于输变电工程的建设过程复杂、建设周期长、投资金额大，同时受环境等因素的影响较大，使得输变电工程造价的预测难度大大提高[1-2].对输变电工程造价的精准预测能够有效控制项目预算，从而可有效提升电力企业的效益、规范资金管控.因此，研究输变电工程造价的准确预测方法对于电力企业的运营具有重要意义[3-5].
Mann-Kendall(简称MK)法是目前时序数据分析领域的主流分析方法，其本质是对数据进行非参数检验，进而分析时序数据的变化趋势.目前MK法已经在国内外各领域得到了广泛应用，并取得了较好的效果[6].MK法的优势在于能够实现非参数检验，但仅能对变量在未来的变化趋势进行判断，而无法准确预测变量未来所处的范围阈值.此外，由于工程造价受市场材料价格变动的影响较大，因此，必须引入适用于基础数据波动较大的预测方法.指数平滑(exponential smoothing，ES)法是目前发展较为成熟的预测方法，在各领域的应用较为广泛，主要应用于数据的短期和中期预测[7-9].指数平滑法的实质是依据时间顺序利用平滑系数对以往数据进行加权运算，综合考虑了远近两个时期的数据进行预测.由于指数平滑法对于历史数据的要求较低，因此在基础数据波动较大的中短期数据预测方面均具有较大的优势.其中，由于三次指数平滑法(three exponential smoothing method，TESM)可以准确预测时序数据的变化趋势，能够得到波动较大的非线性数据变化规律，具有预测结果可靠、运算简便和数据周期需求量较低等优势，故应用范围更为广泛[10].
针对输变电工程造价预测精度较低的问题，本文提出一种基于MK-TESM法的输变电工程造价数据预测方法.该方法采用MK法对输变电工程造价的未来变化趋势进行预测，在此过程中结合三次指数平滑法建立输变电工程造价预测模型，预测未来工程造价实际值.将计算结果与实际结果进行对比可知：采用MK-TESM法预测电力系统输变电工程造价的结果较为准确，与实际结果的偏差较小.由此表明，本文提出的基于MK-TESM法的输变电工程造价数据预测方法可以满足工程造价精准预测的需要.
1 研究方法
1.1 Mann-Kendall趋势检验法
使用Mann-Kendall法对数据未来趋势进行分析判断时，假设H0所代表的时序数据样本(x1，x2，…，xn)为独立同分布，无相应的变化趋势；假设H0属于双边检验，那么对于全部i，j≤n，且i≠j，此时xi与xj分布不一致，检验统计量S的计算表达式为
(1)
检验统计量S的分布方式为正态分布，其平均值经计算后应为0，其方差表达式为
(2)
对统计量Z进行标准化得到
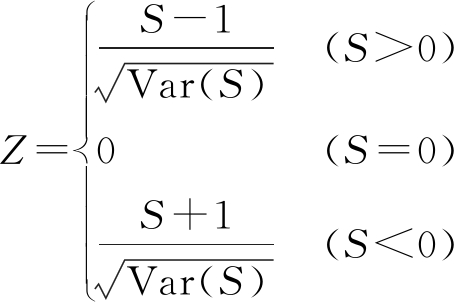
(3)
考虑应用双边趋势检验，则应当设定α置信水平满足
其中，
表示位于标准正态分布的
分位数，γ表示双边趋势检验的置信水平.统计量Z可以体现数据变化趋势，对于相应的统计量Z而言，Z>0表示时序数据具有升高趋势，Z<0表示时序数据具有降低趋势.若要通过置信度为90%、95%和99%的显著性检验，则需要Z的绝对值分别大于或等于对应的数值，这些数值分别为1.28，1.64和2.32.
1.2 三次指数平滑法
1.2.1 基于三次指数平滑法的造价预测模型
在预测数据时，如果数据变化趋势和与二次函数曲线变化趋势相近，则通常选用三次指数平滑法，该方法是在一次指数平滑法和二次指数平滑法基础上推导得出的.将第n年作为起始时序数据的期数，即选择输变电工程造价数据的期数.记Xt为第t年输变电工程造价数据的实际值(t=1，2，…，n)，用来预测未来年份的输变电工程造价数据.搭建基于三次指数平滑法的输变电工程造价预测模型[11]为
Yt+T=at+btT+ctT2
(4)
(5)
(6)
(7)
(8)
(9)
(10)
式中：Yt+T为当年输变电工程造价预测值；T为预测提前的年数；at、bt、ct分别为第t年的预测系数；
分别为第t年相应的一次、二次、三次指数平滑值；α为平滑系数，且
分别为一次、二次和三次指数平滑初始值.
1.2.2 预测模型求解流程
在对预测模型进行求解时，首先要确定模型的平滑初始值，然后通过运算选取合适的平滑系数，最后根据公式计算得到未来输变电工程造价预测值.具体流程如下：
1) 平滑初始值的确定.平滑初始值实质就是平滑计算过程中，开始运算时所需要的初始值
当获得了平滑初始值后才能利用式(8)～(10)求解得到下一年份的平滑值.通常情况下，当原始时序数据的年数t≥15时，可以忽略原始时序数据初始值对结果的影响，将原始时序数据第一年的实际数据值选定为平滑初始值；当原始时序数据的年数t<15时，将原始时序数据前三年的数据平均值选定为平滑初始值.
2) 平滑系数的选取.指数平滑法预测的准确程度通常是由选取的平滑系数所决定的[12].未来数据的预测值通常是由新历史数据与旧预测值的权重占比所决定的，两者关系主要由平滑进行表征.平滑系数越大，则预测值中新历史数据的权重越多，反之同理.确定平滑系数基本方法为：分析历史时序数据的变化特征，若时序数据相对较为稳定，波动较小，则平滑系数可以取较小值，通常取值为0.1～0.3；若时序数据短期有波动，但长远来看比较稳定，则通常取值为0.3～0.5；当时序数据波动较大且长远来看难以稳定，具有较为显著的快速升高或降低现象，则平滑系数通常选取较大值，一般取值为0.6～0.9.
3) 数据预测.将平滑初始值与平滑系数代入式(8)～(10)求解得到下一年份新的一次、二次、三次平滑时序数值，并根据式(5)～(7)计算每一年的预测系数；最后将平滑系数与第t年平滑值代入式(4)，选择适当的预测提前年数，从而预测得到未来的输变电工程造价数值.
2 工程造价预测
针对某地区110 kV输变电工程2014～2018年的工程造价进行统计，发现其造价数据满足MK趋势检验法的样本容量分析要求，因此，本文对该地区110 kV输变电工程在2014～2018年的造价数据进行研究并分析其变化趋势，进而验证本文所提出方法预测的准确性.
2.1 110 kV变电站造价趋势分析及预测
2.1.1 110 kV变电站造价趋势分析
为了对某地区110 kV变电站的造价趋势变化进行分析，选择以下几个数据作为评价指标[13]：单位容量造价、变压器造价及户内和户外GIS造价.表1给出了2014～2018年评价指标的相应数据.
表1 2014～2018年110 kV变电站造价评价指标
Tab.1 Cost evaluation indexes of 110 kV substation from 2014 to 2018
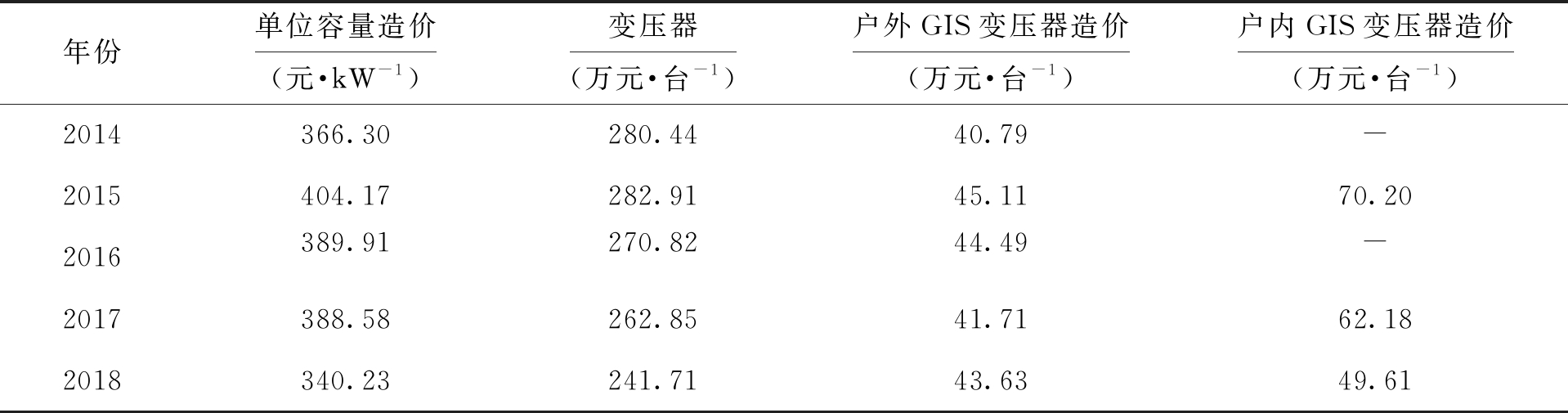
年份单位容量造价(元·kW-1)变压器(万元·台-1)户外GIS变压器造价(万元·台-1)户内GIS变压器造价(万元·台-1)2014366.30280.4440.79-2015404.17282.9145.1170.202016389.91270.8244.49-2017388.58262.8541.7162.182018340.23241.7143.6349.61
应用MK法对该变电站工程造价的变化趋势进行分析，将表1中数据代入式(1)～(3)进行计算，得到样本检验值如表2所示.
表2 变电站工程造价样本检验值
Tab.2 Sample test values of project cost of substation
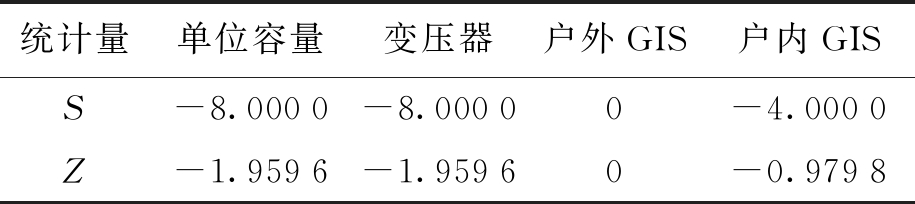
统计量单位容量变压器户外GIS户内GISS-8.0000-8.00000-4.0000Z-1.9596-1.95960-0.9798
由表2可以看出，在该地区110 kV变电站工程造价的单位容量和变压器这两个评价指标中，得到的统计量Z值均等于-1.959 6，此时Z<0且其绝对值大于1.64，则可判断这两个造价指标在未来有降低的趋势，其置信水平为95%；对户外GIS这一指标进行检验统计，得到的统计量Z=0，表明在检验水平为0.05的双边检验中接受原假设，即该指标在未来处于波动中；对户内GIS这一指标进行检验统计，得到的统计量Z=-0.979 8，此时Z<0且其绝对值小于1.28，表明在检验水平为0.05的双边检验中接受原假设，即该指标在未来处于波动中.
2.1.2 110 kV变电站造价预测
首先针对该地区110 kV变电站单位容量造价进行预测.根据表1中的指标数据，利用TESM法预测2019年变电站的单位容量造价，设定平滑系数取值范围为0.1～0.8，每次的调整幅度为0.1.利用程序进行自动调整，得到不同平滑系数对应的预测结果如图1所示.对预测结果进行误差分析，所得结果如表3所示.观察表3可看出，当平滑系数为0.1时，平均绝对误差率最小，仅为5.21%；相对标准差也最小，仅为26.81.由此表明，平滑系数为0.1时预测的结果为最优值，因此设定平滑系数为0.1，并对2019年的单位容量造价进行预测.预测结果表明，2019年的单位容量造价约为374.09元/kW，浮动值为26.81元/kW.
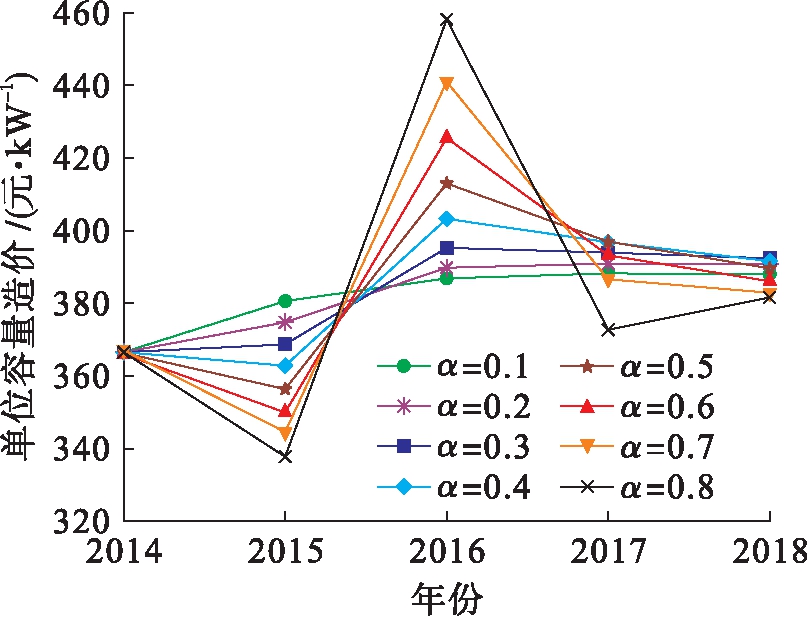
图1 2014～2018年单位容量造价预测结果
Fig.1 Prediction results of unit capacity cost from 2014 to 2018
表3 变电站单位容量造价预测值误差分析
Tab.3 Error analysis of predicted values for unit capacity cost of substation
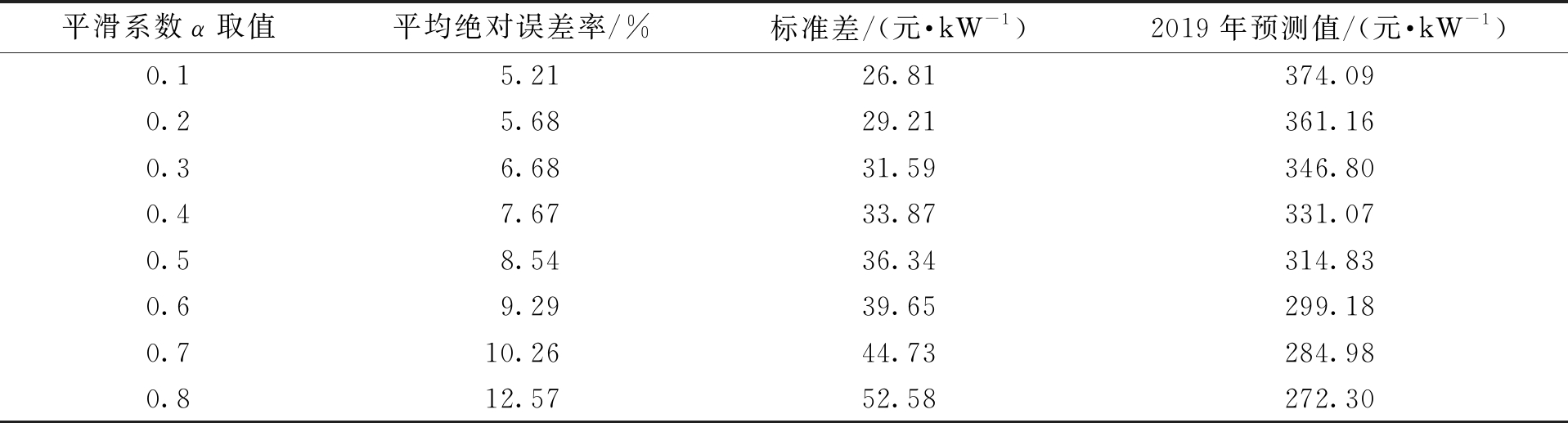
平滑系数α取值平均绝对误差率/%标准差/(元·kW-1)2019年预测值/(元·kW-1)0.15.2126.81374.090.25.6829.21361.160.36.6831.59346.800.47.6733.87331.070.58.5436.34314.830.69.2939.65299.180.710.2644.73284.980.812.5752.58272.30
接下来针对该地区110 kV变电站变压器造价进行预测.根据表1中2014～2018年变压器造价数据，采用TESM法预测2019年变电站的变压器造价，设定平滑系数取值范围为0.1～0.8，每次的调整幅度为0.1.利用程序进行自动调整，得到不同平滑系数对应的变压器造价预测结果如图2所示，表4给出了预测值误差分析结果.观察表4可以发现，当平滑系数取0.6时平均绝对误差率最小，仅为2.47%，相对标准差为8.93万元/台.预测变压器造价时平滑系数取0.6可以得到最优解，因此设定平滑系数为0.6，并对2019年的变压器造价进行预测.预测结果表明，2019年的变压器造价约为219.96万元/台，浮动值为8.93万元/台.
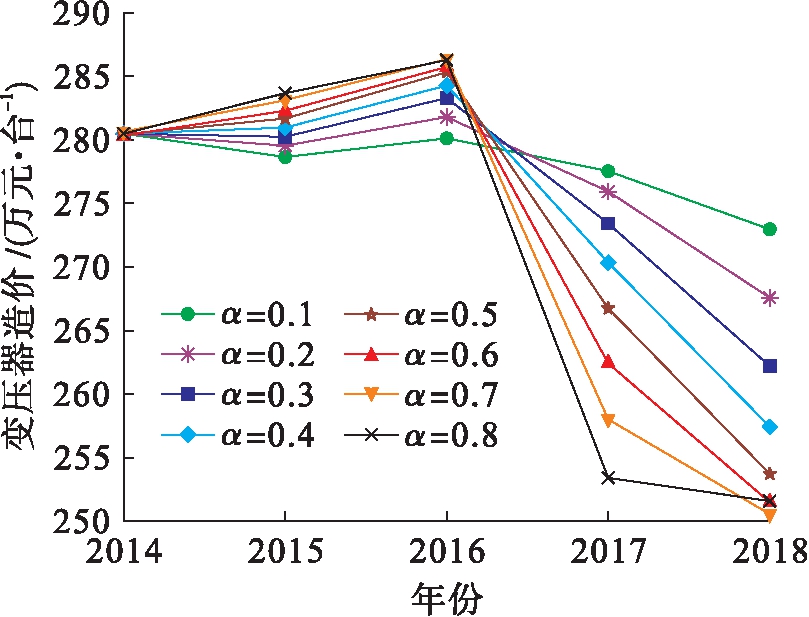
图2 2014～2018年变压器造价预测结果
Fig.2 Prediction results of transformer cost for substation from 2014 to 2018
表4 变电站变压器造价预测值误差分析
Tab.4 Error analysis of predicted values for substation transformer cost
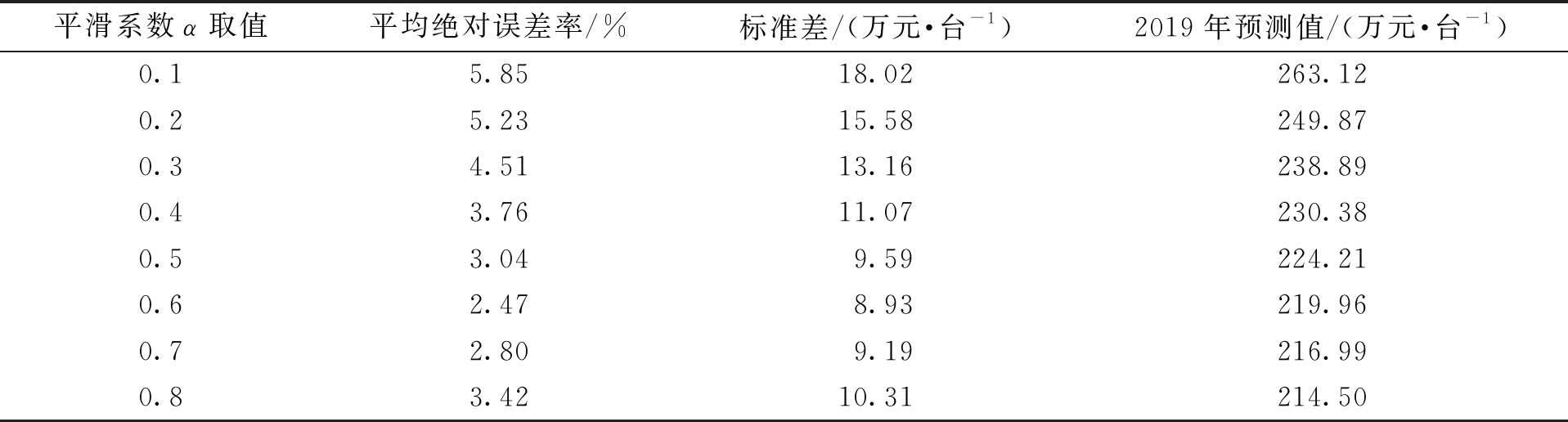
平滑系数α取值平均绝对误差率/%标准差/(万元·台-1)2019年预测值/(万元·台-1)0.15.8518.02263.120.25.2315.58249.870.34.5113.16238.890.43.7611.07230.380.53.049.59224.210.62.478.93219.960.72.809.19216.990.83.4210.31214.50
2.2 110 kV架空线路造价趋势分析及预测
2.2.1 110 kV架空线路造价趋势分析
表5给出了2014～2018年110 kV架空线路造价数据.采用MK法对其变化趋势进行分析，得到统计量结果如表6所示.
表5 2014～2018年110 kV架空线路造价评价指标
Tab.5 Evaluation indexes of 110 kV overhead line cost from 2014 to 2018
年份单位长度造价/(万元·km-1)单位容量长度造价/(元·(kW)-1·km-1)塔材/(元·t-1)线材/(元·t-1)201455.768.378369.6517505.63201559.038.318408.8715984.77201674.718.708357.4015612.18201788.889.947103.1114701.12201867.418.756388.6613372.61
表6 2014～2018年110 kV架空线路工程造价样本检验值
Tab.6 Sample test values of 110 kV overhead line project cost from 2014 to 2018
统计量单位长度造价单位容量长度造价塔材线材S5.00005.0000-8.0000-10.0000Z1.22471.2247-1.9596-2.4495
由表6可以看出，在该地区110 kV架空线路工程造价的评价指标中，对其单位长度造价与单位容量长度造价两个评价指标进行检验统计时，得到的统计量Z=1.224 7<1.28，可以初步判断这两个评价指标有升高趋势，其置信水平为90%.而塔材单价统计量Z=-1.959 6，此时Z<0且其绝对值大于1.64，则可判断塔材单价在未来有降低的趋势，其置信水平为95%.线材单价统计量Z=-2.449 5，此时Z<0且其绝对值大于2.32，则可判断线材单价在未来有降低的趋势，其置信水平为99%.
2.2.2 110 kV架空线路造价预测
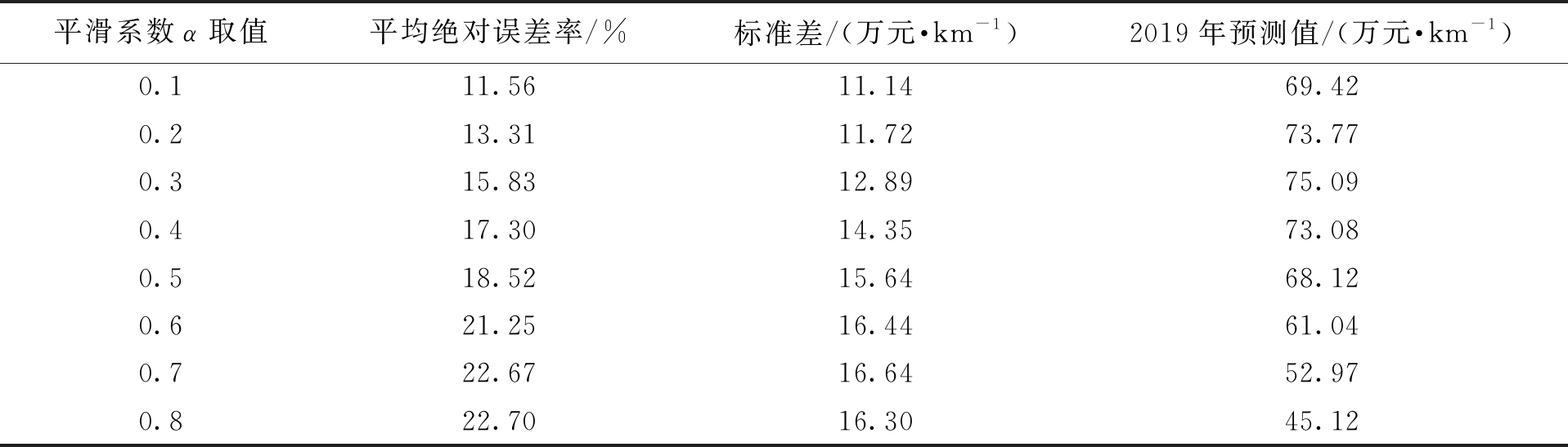
由于架空线路造价主要根据单位长度造价进行评估，因此利用TESM法对该指标进行预测分析.设定平滑系数取值范围为0.1～0.8，每次的调整幅度为0.1，利用程序进行自动调整，得到不同平滑系数对应的预测结果如图3所示.表7给出了预测值误差分析结果.观察表7可以发现，当平滑系数取0.1时平均绝对误差率最小，仅为11.56%，相对标准差为11.14万元/km.预测变压器造价时，平滑系数取0.1可以得到最优解.对2019年的单位长度造价进行预测，预测结果表明，2019年的单位长度造价约为69.42万元/km，浮动值为11.14万元/km.
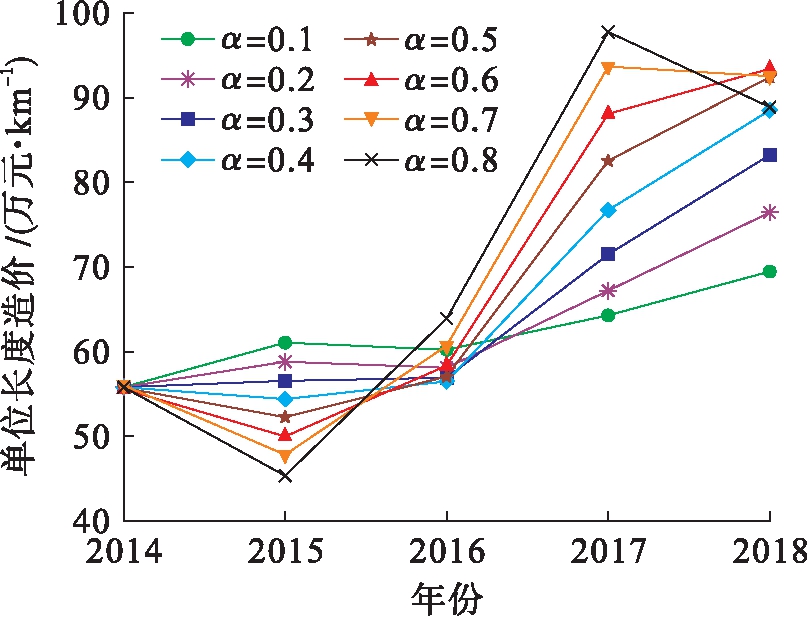
图3 2014～2018年架空线路单位长度造价预测结果
Fig.3 Prediction results of unit length cost of overhead line from 2014 to 2018
表7 输电线路单位长度造价预测值误差分析
Tab.7 Error analysis of predicted values for unit length cost of transmission lines
平滑系数α取值平均绝对误差率/%标准差/(万元·km-1)2019年预测值/(万元·km-1)0.111.5611.1469.420.213.3111.7273.770.315.8312.8975.090.417.3014.3573.080.518.5215.6468.120.621.2516.4461.040.722.6716.6452.970.822.7016.3045.12
3 结 论
本文以某地区110 kV输变电工程造价数据作为样本，利用MK法对工程造价的变化趋势进行分析，初步判断其未来的变化情况.然后采用三次指数平滑法对2019年的造价数据进行预测，研究结果表明：
1) 该地区110 kV变电站工程造价评价指标中，单位容量造价与变压器造价均呈降低趋势.其中，单位容量造价预估在2019年降低至(374.09±26.81)元/kW，变压器造价预估在2019年降低至(219.96±8.93)万元/台，而户外与户内的GIS造价位于波动状态，未来造价处于不稳定状态.
2) 该地区110 kV架空线路工程造价评价指标中，单位长度造价与单位容量造价均呈升高趋势.其中，单位长度造价作为核心造价评价指标预估在2019年升高至(69.42±11.14)万元/km.而塔材与线材的造价呈降低趋势，这可能是由材机调差系数变动造成的.
3) 本文针对该地区近5年的输变电工程造价数据进行预测分析.预测结果表明，本文所提出的输变电工程造价预测方法较为准确，能够为输变电工程造价评估提供有效的参考.在应用三次指数平滑法进行预测的过程中，确定平滑系数的主要方法是经验估算法与试算法，但这两种方法的效率仍有待提高.未来研究将着重研究最优平滑系数选取算法，提升指数平滑法效率.此外，由于样本容量的限制，未能进一步针对预测数据进行验证，未来研究时会考虑将研究范围扩展到其他电压等级输变电工程造价中.在未来分析预测数据与实际数据差异时，将考虑各类因素对工程造价的影响，以进一步完善本文所提出的预测方法，使预测结果更加准确.
[1] 周昊，钱亦雯，王闰瑶.基于工程量清单计价模式的输变电工程造价风险评估模型研究 [J].现代电子技术，2017，40(18)：23-25.
(ZHOU Hao，QIAN Yi-wen，WANG Run-yao.Research on cost risk assessment model of power transmission and transformation project based on bill of quantity valuation mode [J].Modern Electronics Technology，2017，40(18)：23-25.)
[2] 李万磊，陈天星，刘善邦，等.基于数据处理一体化的输变电工程标准测量系统构建 [J].电子设计工程，2018，26(20)：139-142.
(LI Wan-lei，CHEN Tian-xing，LIU Shan-bang，et al.Construction of standard measurement system for transmission and transformation engineering based on data processing integration [J].Electronic Design Engineering，2018，26(20)：139-142.)
[3] 陆宇烨，张健钊，徐岩哲，等.电力系统负荷预测方法综述 [J].电子科技，2013，26(11)：173-175.
(LU Yu-ye，ZHANG Jian-zhao，XU Yan-zhe，et al.Overview of load forecasting methods in power system [J].Electronic Science and Technology，2013，26(11)：173-175.)
[4] 耿云鹏，齐霞，尹冰冰，等.输变电工程基本预备费费率测算模式与方法研究 [J].陕西电力，2015，43(10)：58-61.
(GENG Yun-peng，QI Xia，YIN Bing-bing，et al.Research on new basic reserve fund rate calculation method for transformation and distributed project [J].Shaanxi Electric Power，2015，43(10)：58-61.)
[5] 郭新菊，邵永刚，李旭阳，等.基于BP神经网格的配电网工程造价预测模型建立与应用 [J].电子设计工程，2017，25(23)：63-68.
(GUO Xin-ju，SHAO Yong-gang，LI Xu-yang，et al.Establishment and application of cost prediction model for distribution network project based on BP neural network [J].Electronic Design Engineering，2017，25(23)：63-68.)
[6] Aziz O I A，Burn D H.Trends and variability in the hydrological regime of the Mackenzie River Basin [J].Journal of Hydrology，2006，319(1/2)：288-294.
[7] Steven R G.Bagging exponential smoothing methods using STL decomposition and Box-Cox transformation [J].International Journal of Forecasting，2016，32(2)：303-312.
[8] Tratar L F.Demand forecasting with four-parameter exponential smoothing [J].International Journal of Production Economics，2016，181(9)：162-173.
[9] 王洪德，曹英浩.道路交通事故的三次指数平滑预测法 [J].辽宁工程技术大学学报(自然科学版)，2014，33(1)：42-46.
(WANG Hong-de，CAO Ying-hao.Cubic exponential smooth method of road traffic accident forecasting [J].Journal of Liaoning Technical University (Natural Science Edition)，2014，33(1)：42-46.)
[10] 周金辉，徐琛，葛晓慧，等.基于模型预测控制的分布式热电联供系统优化调度 [J].浙江电力，2017(5)：23-28.
(ZHOU Jin-hui，XU Chen，GE Xiao-hui，et al.Optimal scheduling of distributed cogeneration system based on model predictive control [J].Zhejiang Electric Power，2017(5)：23-28.)
[11] 蒋艳辉.基于指数平滑法与马尔科夫链的道路交通事故预测研究 [D].哈尔滨：哈尔滨工业大学，2018
(JIANG Yan-hui.Research of road traffic accident prediction based on exponential smoothing method and Markov chain [D].Harbin：Harbin Institute of Technology，2018.)
[12] Lin H，Mu B L.Anempirical study on exponential smoothing and seasonal model [J].Applied Mechanics and Materials，2014，8(5)：599-601.
[13] 韩文军，余春生.面向输变电工程数据存储管理的分布式数据存储架构 [J].沈阳工业大学学报，2019，41(4)：366-371.
(HAN Wen-jun，YU Chun-sheng.Distributed data storage architecture for data storage management of power transmission and transformation engineering [J].Journal of Shenyang University of Technology，2019，41(4)：366-371.)