当前太阳能发电两大主流技术为光热发电和光伏发电[1].新兴的热声发电技术是新能源应用领域前沿研究方向之一，可广泛应用于太阳能、燃烧余热、工业废热及汽车尾气等分布式能源系统发电领域，特别是可以利用太阳能集热的低品质热源发电.热声发电技术作为一种新型的太阳能光热发电技术，在提高冷热电联产系统一次能源利用效率等方面优势明显，为可再生能源的利用提供新的方向，具有广泛的应用前景[2].
热声发电系统(TAEGS)是热声发电技术的功能载体，其核心部件由热声发动机和直线发电机组成[3].热声发动机捕获太阳能等低品质热源的热能，并根据热声效应原理将热能转换成声能；直线发电机镶嵌在热声发动机的声学流道内，在声功波动驱动下将热声发动机输出的机械能(声能)转换成电能[4-5]，因此提高直线发电机从热声发动机里捕获的声功是提高TAEGS声电转换效率和系统输出电功的重要条件[6-8].Wu等[9]优化设计TAEGS驻波谐振管提高了直线发电机捕获的声功，其采用锥形谐振管方法提高发电机捕获的声功，在TAEGS原输入端状态不变的条件下，发电机捕获的声功显著提高.但方法是在热声发动机声波环路里加入谐振管的方式实现声功补偿，减小了热声发动机声功功率.Yu等[10]采用声学调谐小桩方法提高了TAEGS直线发电机捕获的声功，但这种提高声功捕获的方法是从热声发动机的机械结构设计出发，没有对整个TAEGS进行耦合设计，只是将发电机看作热声发动机声学负载.刘玮等[11]给出了声功波动小振幅工作状态时，利用电路模拟TAEGS声学阻抗流源机理和声学特性的线性分析方法；何新等[12-13]通过声力电类比方法分析了TAEGS中声功波动频率、活塞直径、外接负载电阻和弹簧刚度系数间相互耦合的关系.
本文根据相似定理和TAEGS声学阻抗流源机理，采用类电路相量法给出TAEGS最大声功捕获的直线发电机弹簧刚度系数和外接负载电容参数匹配设计方法.与现有的提高声功捕获方法相比，根据系统参数设计的声学阻抗匹配优化设计方法简单易行且精确可控，可直接调整直线发电机子系统参数，匹配热声发动机子系统声学循环的声学阻抗，实现两机声学阻抗匹配运行，提高了TAEGS捕获的声功.
1 热声发电系统数学模型
TAEGS主要由行波热声发动机、永磁直线发电机和可控调谐电负载组成，如图1所示.
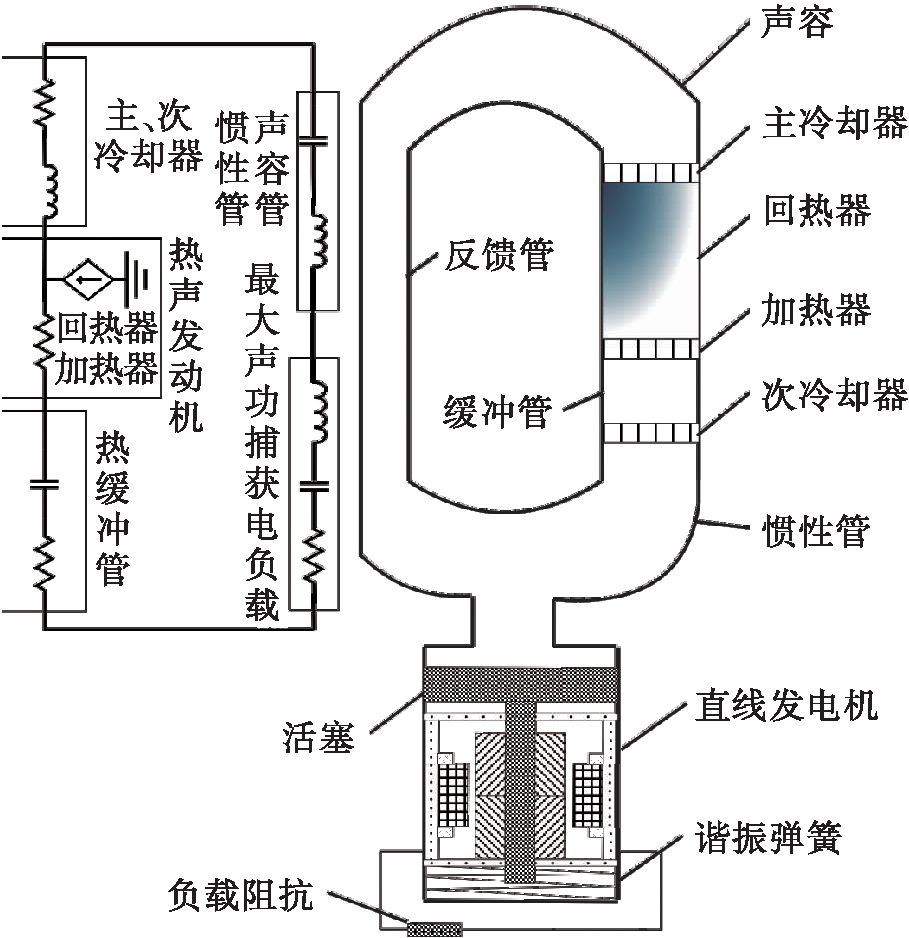
图1 TAEGS示意图
Fig.1 Schematic diagram of TAEGS
根据牛顿运动定律和KVL定律可得TAEGS控制方程为
(1)
E=kev=(R+r+jX)i
(2)
式中：M为系统运动部件总质量；B为等效机械阻尼系数；K为等效弹簧刚度系数；Fa为声功波动压力(声波驱动力与背腔压力的合力)；Fe为发电机电磁力；E为发电机感应电动势；v为次级速度；ke为机电常数；x为活塞位移；r为永磁直线发电机内阻；R为负载电阻；X为初级线圈绕组等效电抗，X=ωL-1/(ωC)；L为发电机初级线圈绕组电感；C为发电机谐振电容；ω为声功波动频率.
基于声学阻抗类比模型，联合式(1)、(2)可求得力电类比平衡方程为
(3)
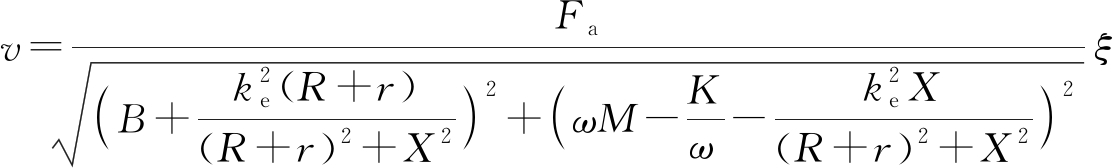
(4)
式中，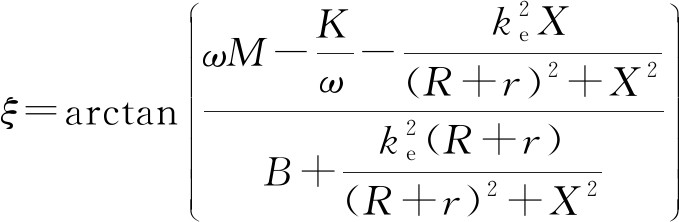
为发电机次级运行速度与声功波动的相位角.进一步可得直线发电机的输入声学阻抗为
(5)
TAEGS等效阻尼为
(6)
直线发电机的机械阻抗虚部为
(7)
直线发电机捕获的声功为
Wa=Re(Fav*)=Favcos ξ=
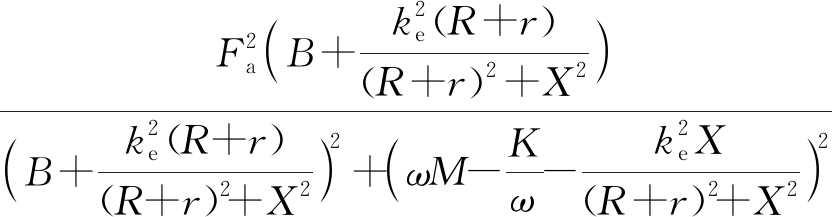
(8)
当声功波动压力Fa与次级速度v同相位时，TAEGS处于机械谐振状态，此时ξ=0，即
于是可推出直线发电机捕获的最大声功为
Wa=Re(Fav*)=Favcos ξ=
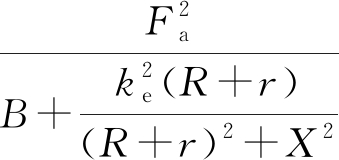
(9)
此时机械谐振弹簧刚度系数为
(10)
TAEGS处于机械谐振状态下，选择合适的机械谐振弹簧刚度系数和谐振电容参数可实现最大声功捕获.声功波动频率、系统运动部件总质量都会影响谐振弹簧刚度系数.
通过上述分析可知，选取合适刚度系数的谐振弹簧并匹配相应的电阻抗，对TAEGS进行阻抗匹配优化设计，可以有效减小声功波动与次级速度的相角，使TAEGS处于机械谐振状态，此时永磁直线发电机能够实现最大声功捕获的目标.
2 仿真分析
TAEGS包含多个可控制的输入参数和多个相互关联的输出参数[8].如图2所示，直线发电机电路谐振时，修正弹簧刚度系数使TAEGS处于机械谐振频域内，直线发电机捕获声功随负载电阻增大而增大.
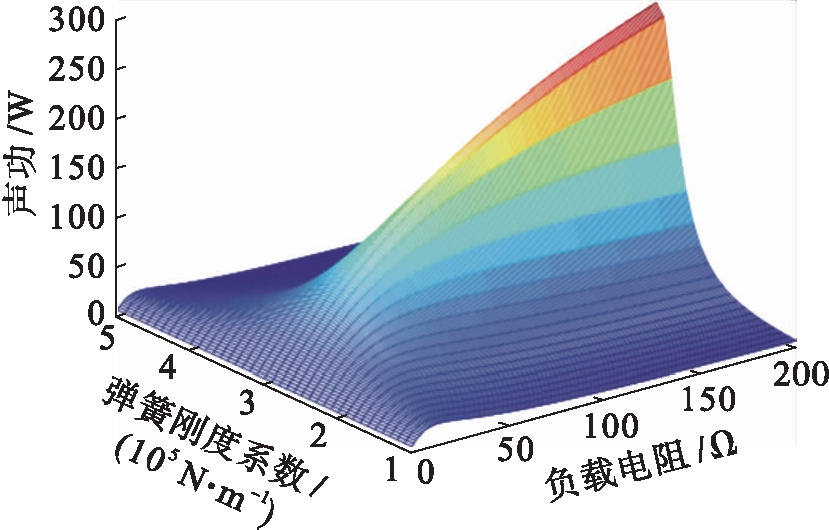
图2 电路谐振时负载电阻和弹簧刚度对声功捕获的影响
Fig.2 Effect of load resistance and spring stiffness on acoustic power capturing during circuit resonance
当TAEGS处在声学阻抗匹配运行状态时，电阻和弹簧刚度对声功捕获影响如图3所示，只有弹簧刚度系数位于使TAEGS机械谐振的频域内，发电机捕获的声功迅速增大；反之直线发电机捕获声功的能力大大减弱.如果弹簧刚度系数超出TAEGS机械谐振的频域时，负载电阻对直线发电机捕获声功不能有效调节.
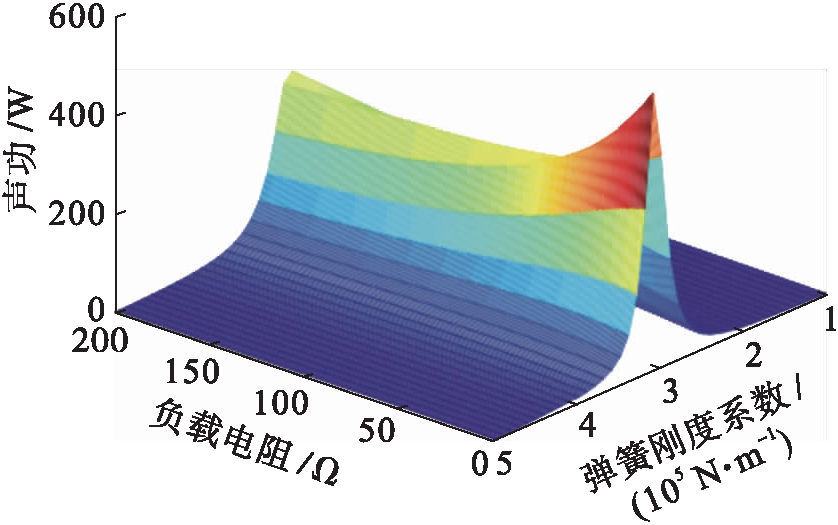
图3 声学阻抗匹配时负载电阻和弹簧刚度对声功捕获影响
Fig.3 Effect of load resistance and spring stiffness on acoustic power capturing under acoustic impedance matching
当TAEGS负载电阻值给定时，谐振电容和弹簧刚度对声功捕获的影响如图4所示，发电机捕获的声功频域很小，仅限于谐振电容范围内.如果谐振电容离开声学匹配频域，尽管弹簧刚度系数处在机械谐振频域内，直线发电机捕获的声功也很小.
当TAEGS处于机械谐振运行状态时，谐振电容和负载电阻对声功捕获的影响如图5所示，直线发电机捕获的声功受谐振电容参数影响比重更明显.即使直线发电机处于电路谐振运行状态时，直线发电机捕获的声功也很少.谐振电容只有在声学阻抗匹配频域内进行修正，才使发电机捕获的声功最大.
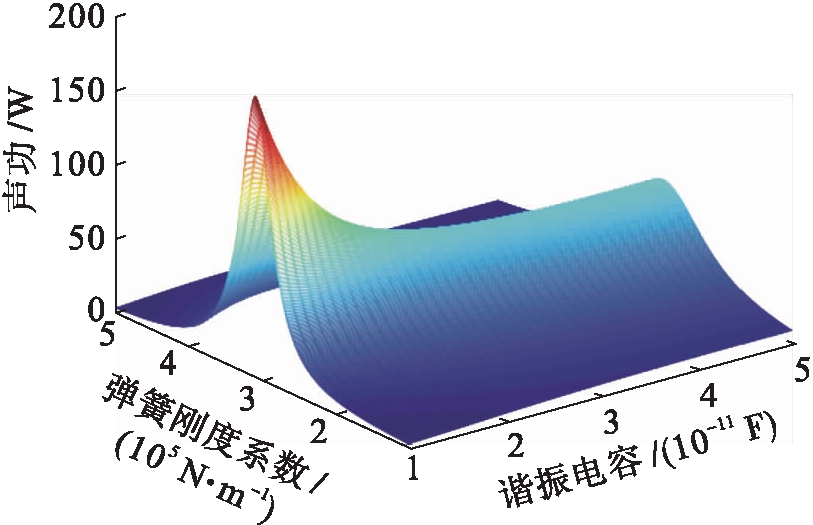
图4 谐振电容和弹簧刚度对声功捕获的影响
Fig.4 Effect of resonant capacitance and spring stiffness on acoustic power capturing
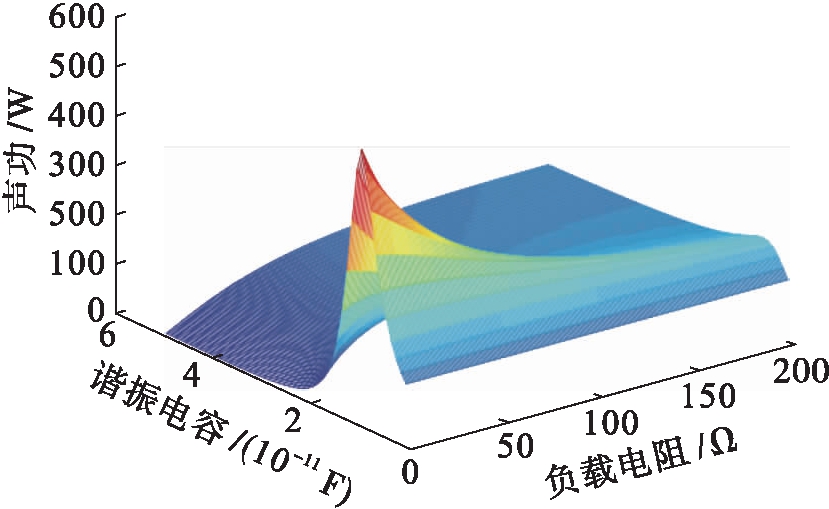
图5 谐振电容和负载电阻对声功捕获的影响
Fig.5 Effect of resonant capacitance and load resistance on acoustic power capturing
当热声发电系统与机械阻抗匹配时，谐振电容对声学相位角的影响如图6所示.通过修正TAEGS负载电阻和谐振电容参数减小声波压力和体积流率的声学相位角，使其趋近于零，提高发电机的声功捕获能力.当负载电阻为10 Ω、谐振电容为12.6 μF时，可以使声学阻抗角等于零，提高直线发电机捕获的声功；而负载电阻为50 Ω、谐振电容为18 μF时，仅能通过减小声学阻抗角提高声功的捕获能力；但当外接负载电阻为200 Ω时，谐振电容无法调节声学相位角，只有修正弹簧刚度系数才能减小声波压力和体积流率的声学阻抗角，提高发电机的声功捕获能力.
当直线发电机处于机械阻抗匹配状态时，谐振电容对声波体积流率的影响如图7所示.通过修正TAEGS负载电阻和谐振电容参数增大声波体积流率，增强发电机声功捕获的能力.当负载电阻为10 Ω、谐振电容为12.6 μF时，体积流率最大值为6.6×10-3 m3/s，直线发电机捕获最大声功；当负载电阻为50 Ω、谐振电容为8.6 μF时，体积流率最大值为4.9×10-3 m3/s；当负载电阻为200 Ω、谐振电容为4 μF时，体积流率最大值为3.9×10-3 m3/s，谐振电容调节声功波动体积流速的能力略有下降.
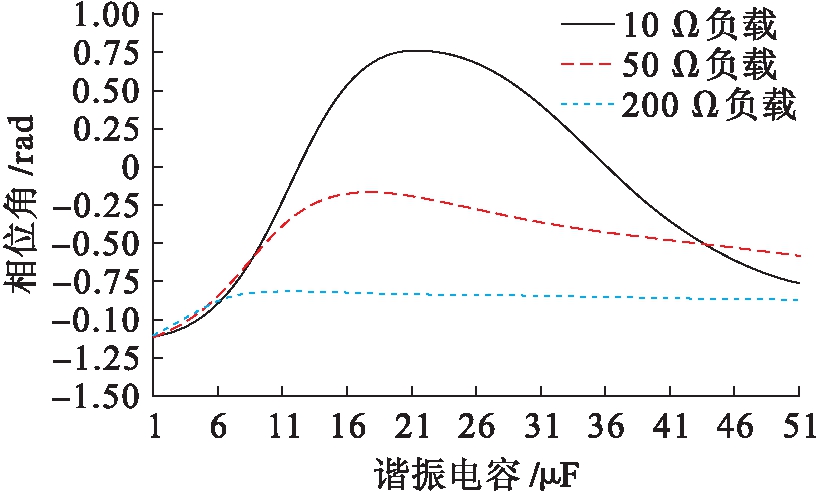
图6 谐振电容对声学相位角的影响
Fig.6 Effect of resonant capacitance on acoustic phase angle
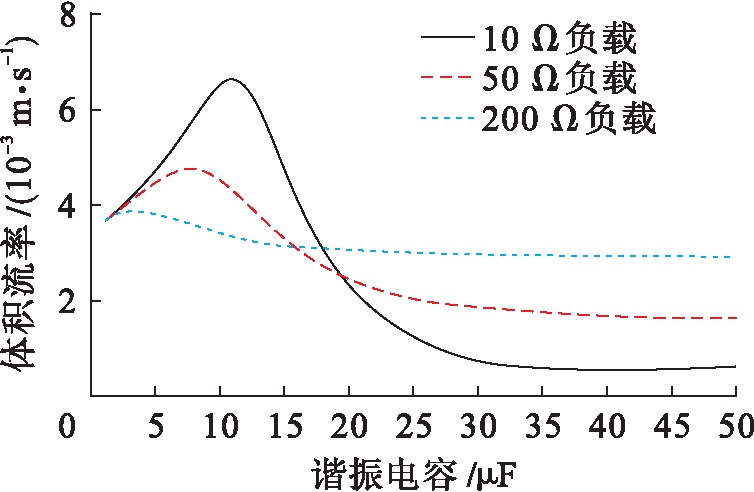
图7 谐振电容对声波体积流率的影响
Fig.7 Effect of resonant capacitance on acoustic volume flow rate
3 实验分析
TAEGS运行时呈直线往复振荡状态，因此借用等效弹簧刚度和等效摩擦系数模拟推动发电机次级运行的非线性驱动力.在此理论基础上，本文利用直线振荡装置作为TAEGS模拟实验平台，把热声直线发电机次级轴与等效弹簧相连，以此模拟声波压力驱动直线发电机；在直线导轨上滑块与等效弹簧相连，等效弹簧为直线发电机次级往复振荡提供足够刚度并有效控制其行程.表1给出了TAEGS的原始相关参数.
表1 TAEGS模拟参数
Tab.1 Simulation parameters for TAEGS
参数取值声功压力Fa154N绕组电感L60mH阻尼系数B20N·s/m运行频率f110Hz参数取值绕组内阻r2Ω机电常数ke65N/m运动质量M0.6kg
TAEGS工作时从外部热源中获得热能，热声发动机内气体工质不均衡与加热温度的不稳定会使TAEGS工作频率不断改变，进而影响发电机捕获声功的效果.分析TAEGS变频工作时，谐振电容对发电机声功捕获的影响如图8所示.
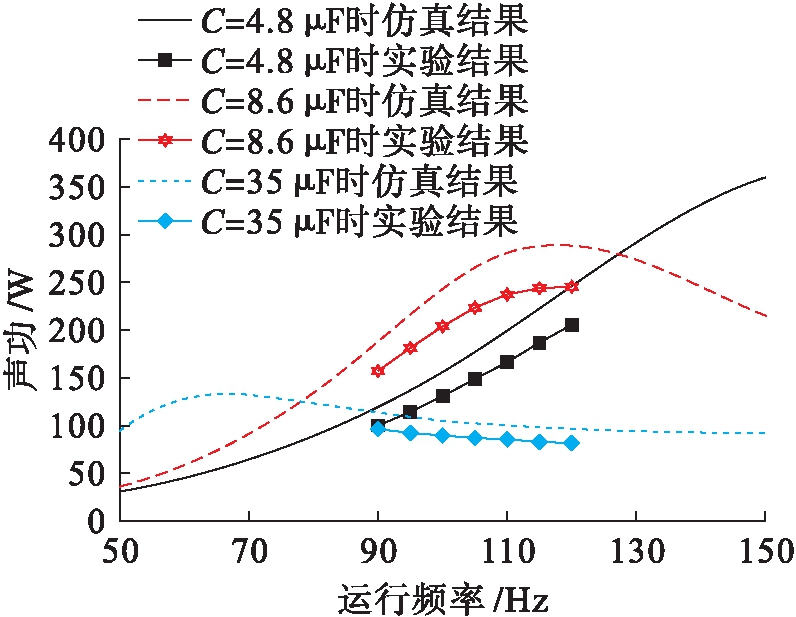
图8 TAEGS变频运行时谐振电容对声功捕获的影响
Fig.8 Effect of resonant capacitance on acoustic power capturing in operation at variable frequency of TAEGS
从图8对比结果可知，当外接负载电阻50 Ω，TAEGS变频工作在90～120 Hz，谐振电容为8.6 μF时，发电机捕获最大声功为150～241 W(仿真计算结果为168～276 W)；当谐振电容为4.8 μF时，发电机捕获最大声功为96～196 W(仿真计算结果为100～222 W).实验过程中，当负载电容为35 μF(发电机电路谐振)，系统运行频率在110 Hz时，发电机捕获的声功仅为90 W，而110 Hz运行频率外接8.6 μF电容时发电机捕获的声功已经达到241 W.当谐振电容参数偏离TAEGS声学阻抗匹配频域时，即使TAEGS工作在电路谐振状态，直线发电机捕获声功的能力也大幅下降；当TAEGS运行频率为60 Hz且TAEGS外接负载电容35 μF时，TAEGS处于电路谐振状态，直线发电机捕获的声功最大；当TAEGS运行频率超过120 Hz，谐振电容大于35 μF时，直线发电机捕获声功变化不大.
TAEGS稳定运行频率为110 Hz时，谐振电容对声功捕获的影响如图9所示，即热声直线发电机满足弹簧机械阻抗匹配的条件，此时弹簧刚度系数为286.4 kN/m，热声直线发电机捕获最大声功时的谐振电容值在9.6 μF附近.当TAEGS负载电阻为10 Ω时直线发电机捕获最大声功298 W，负载电阻为50 Ω时直线发电机捕获最大声功216 W，负载电阻为200 Ω时直线发电机捕获最大声功111 W.由此可见，TAEGS在额定频率运行时，直线发电机捕获最大声功的负载电容值与外接电阻负载值相关；TAEGS外接负载电阻越大，直线发电机捕获最大声功时需要的谐振电容值越小.
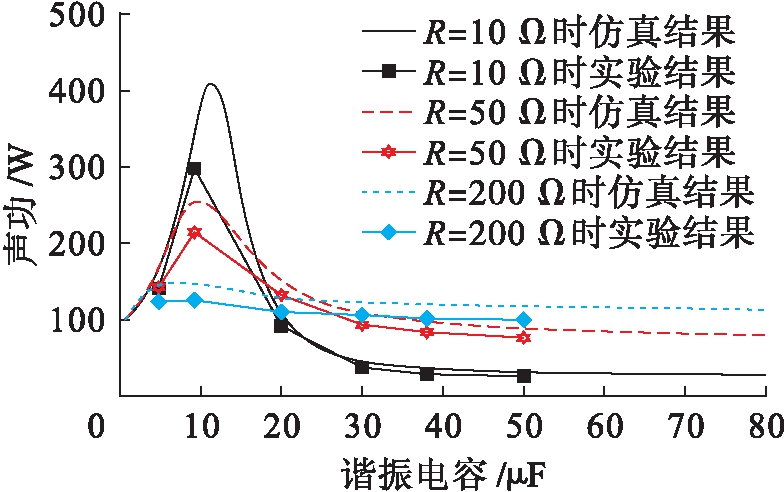
图9 TAEGS恒频运行时谐振电容对声功捕获的影响
Fig.9 Effect of resonant capacitance on acoustic power capturing in operation at constant frequency of TAEGS
实验中，调节负载电阻和谐振电容参数对发电机捕获声功的实验测量数据和数值计算数据进行对比.根据图8、9的对比可知，弹簧刚度系数和谐振电容参数对发电机声功捕获影响的变化趋势完全一致.只是通过数值计算的数据均大于实验测量的数据，二者存在误差的原因为：1)数值计算时忽略热声发动机的非线性因素，而建模基于理想运行条件；2)数值计算把气体工质的运行看作线性运动；3)实验过程中实验装置存在机械摩擦损耗；4)实验过程中存在测量误差.仿真和实验结果验证了TAEGS声功捕获数学模型和基于直线发电机声学阻抗优化设计方法的正确性和有效性.
4 结 论
本文在热声发电理论的基础上，证明了合理匹配热声直线发电机声学阻抗可以实现TAEGS最大声功捕获，并采用数值计算和实验平台进行验证.与热声发动机驻波型声学谐振管和声学调谐小桩的优化技术相比，基于直线发电机声学阻抗优化设计可通过设计弹簧机械阻抗和谐振电容容抗的参数值，实现最大声功捕获.设计方法灵活易操作，设计精度高.
实验平台所设计TAEGS稳定运行频率为110 Hz时，发电机弹簧刚度系数为286.4 kN/m，谐振电容参数为9.6 μF，在外接负载电阻10 Ω条件下，发电机捕获声功达到298 W.基于弹簧刚度系数和谐振电容参数的直线发电机声学阻抗优化设计对于深入研究TAEGS能量传输机理，指导系统设计具有实际意义.
[1] 金红光，隋军，徐聪，等.多能源互补的分布式冷热电联产系统理论与方法研究 [J].中国电机工程学报，2016，36(12)：3150-3160.
(JIN Hong-guang，SUI Jun，XU Cong，et al.Research on theory and method of muti-energy complementary distributed CCHP system [J].Proceedings of the CSEE，2016，36(12)：3150-3160.)
[2] 陈柏翰，冯伟，孙凯，等.冷热电联供系统多元储能及孤岛运行优化调度方法 [J].电工技术学报，2019，34(15)：3231-3243.
(CHEN Bo-han，FENG Wei，SUN Kai，et al.Multi-energy storage system and islanded optimal dispatch method of CCHP [J].Transactions of China Electrotechnical Society，2019，34(15)：3231-3243.)
[3] 吴正民，余国瑶，戴巍，等.5kW(e)级自由活塞斯特林发电机热电联产性能研究 [J].中国电机工程学报，2018，38(11)：3275-3280.
(WU Zheng-min，YU Guo-yao，DAI Wei，et al.Performance of the CHP system by using a 5kW(e) class free piston stirling generator [J].Proceedings of the CSEE，2018，38(11)：3275-3280.)
[4] 李潜葛，罗恩博，吴张华，等.太阳能热声发电技术研究进展 [J].中国电机工程学报，2016，36(12)：3242-3250.
(LI Qian-ge，LUO En-bo，WU Zhang-hua，et al.Re-search progress of solar power generation technology [J].Proceedings of the CSEE，2016，36(12)：3242-3250.)
[5] 章杰，孙大明，王凯，等.行波热声发电系统的阻抗匹配 [J].浙江大学学报(工学版)，2017，51(3)：494-499.
(ZHANG Jie，SUN Da-ming，WANG Kai，et al.Impedance matching of traveling-wave thermoacoustic electric generating system [J].Journal of Zhejiang University (Engineering Science)，2017，51(3)：494-499.)
[6] 徐静远，陈燕燕，罗二仓.行波热声发电系统自激振荡的非线性动力学研究 [J].低温工程，2016(4)：1-10.
(XU Jing-yuan，CHEN Yan-yan，LUO Er-cang.Investigation on nonlinear dynamics of self-excited oscillation of a traveling wave thermoacoustic generator [J].Cryogenics，2016(4)：1-10.)
[7] 夏加宽，李文瑞，何新，等.各向异性横向磁通永磁直线电机穿片漏磁分析 [J].电工技术学报，2015，30(14)：518-524.
(XIA Jia-kuan，LI Wen-rui，HE Xin，et al.Analysis of anisotropic permeate leakage flux on transverse flux permanent magnet linear machine [J].Transactions of China Electrotechnical Society，2015，30(14)：518-524.)
[8] 夏加宽，李文瑞，何新，等.热声发电系统最大电能输出阻抗匹配及机械谐振特性分析 [J].中国电机工程学报，2015，35(22)：5908-5914.
(XIA Jia-kuan，LI Wen-rui，HE Xin，et al.Analysis on impedance matching and mechanical resonance cha-racteristics of maximum electric power output for thermo-acoustic electric generation systems [J].Proceedings of the CSEE，2015，35(22)：5908-5914.)
[9] Wu Z H，Man M，Luo E C，et al.Experimental investigation of a 500W traveling-wave thermoacoustic electricity generator [J].Chinese Science Bulletin，2011，56(19)：1975-1977.
[10] Yu Z B，Jaworski A J，Backhaus S.Travelling-wave thermoacoustic electricity generator using an ultra-compliant alternator for utilization of low-grade thermal energy [J].Applied Energy，2012，99：135-145.
[11] 刘玮，李佳敏，马丽，等.热声驱动制冷与发电一体机的设计与优化 [J].中国电机工程学报，2016，36(12)：3192-3197.
(LIU Wei，LI Jia-min，MA Li，et al.Designing and optimizing an integral device of the thermoacoustic engine driven cooler and electric generator [J].Proceedings of the CSEE，2016，36(12)：3192-3197.)
[12] 何新，夏加宽，李文瑞，等.热声发电系统双功率优化运行阻抗匹配分析 [J].中国电机工程学报，2016，36(19)：5272-5278.
(HE Xin，XIA Jia-kuan，LI Wen-rui，et al.Analysis on impedance matching of optimal dual power for thermo-acoustic electric generation system [J].Proceedings of the CSEE，2016，36(19)：5272-5278.)
[13] 何新，夏加宽，苏浩，等.热声发电系统最大声电效率阻抗匹配分析 [J].电工技术学报，2017，32(9)：92-100.
(HE Xin，XIA Jia-kuan，SU Hao，et al.Analysis on impedance matching of thermoacoustic electric generation system for the maximum acoustic-to-electric efficiency [J].Transactions of China Electrotechnical Society，2017，32(9)：92-100.)