人工智能算法近年来得到了广泛的研究和应用,其中机器学习是应用最为广泛的算法类型.按照智能体与环境之间的交互关系,机器学习可分为监督学习、半监督学习和强化学习[1-2].强化学习凭借其不需要专家系统的内在特征,具备更强的适应性,已成为当前应用最广泛的机器学习类型.
宁剑等[3]系统介绍了基于控制响应函数的区域电网自动发电控制(automatic generation control,AGC)方法,该研究表明控制响应函数自身计算的复杂性是实际应用的重要瓶颈,为此利用强化学习等智能算法成为该领域研究的热点.张孝顺等[4-5]基于多智能体协同学习,提出了面向互联电网的区域AGC控制算法;Lin等[6]综合考虑AGC功率分配中安全、节能、经济等多方面调控目标,提出了基于Q学习算法的多目标AGC调节容量动态优化分配方法;余涛等[7]结合大规模互联电网中各区域电网协同控制的要求,提出了基于改进分层强化学习的多区域电网CPS指令动态优化分配算法.
当前强化学习在电网AGC控制方面的研究集中于大电网或微电网控制层面,对区域电网的控制方法研究仍相对较少.本文围绕区域电网AGC控制问题,介绍Q学习算法基本原理和算法流程.基于区域电网AGC控制需求,在信息物理系统体系下构建其控制框架,并提出其动作空间、回报函数、环境状态等3个关键特征量,基于某地区电网实际数据构造算例,验证本文所提出算法的有效性.
1 Q学习算法基本原理与算法流程
1.1 强化学习基本原理
强化学习是近年来发展较快的机器学习算法,其最大特点在于智能体通过与环境不断交互,实现策略的改进,因此,具有较强的适应性和鲁棒性.强化学习的基本框架如图1所示,其中,共涉及5个基本要素:状态空间、动作空间、转移函数、回报及动作策略[8],其实施策略可简述如下:
1) 学习智能体基于监测到的环境状态,按照自身策略在给定的动作空间中选择相应的动作执行;
2) 环境将因此发生状态改变,学习智能体据此对其动作优劣进行评价,计算该动作的回报;
3) 通过统计分析回报值的大小调整自身策略,直至取得最优策略.
按照强化学习框架中上述5个要素是否已知,可将强化学习分为有模型学习和免模型学习两类.有模型学习可根据模型关系直接推导得到学习智能体的最优策略,而对于免模型学习,则需要根据智能体与环境之间的交互,不断改进策略以获得最优策略.
1.2 Q学习算法实施流程
Q学习算法是以时序差分马尔科夫决策过程为基础的免模型强化学习算法,其基本思路是通过对动作![]() 状态值函数的迭代更新,实现智能体对环境的适应学习,获得最优策略.动作
状态值函数的迭代更新,实现智能体对环境的适应学习,获得最优策略.动作![]() 状态值函数在环境状态下按照策略选择动作所获得回报的期望值,可表示为
状态值函数在环境状态下按照策略选择动作所获得回报的期望值,可表示为
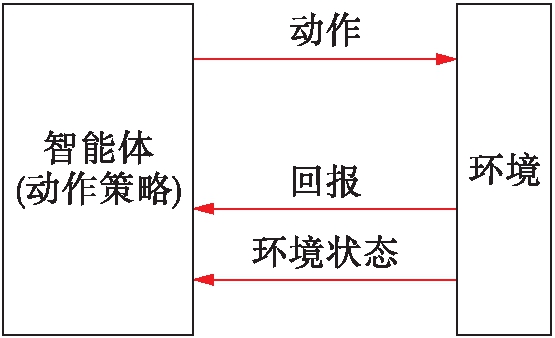
图1 强化学习基本框架
Fig.1 Basic framework of reinforced learning
(1)
式中:Q(x,a)为环境状态x下采取动作a的动作![]() 状态值函数;R(x,x′,a)为由环境状态x经过动作a作用转移到环境状态x′所获得的回报;P(x′|x,a)为转移概率;
状态值函数;R(x,x′,a)为由环境状态x经过动作a作用转移到环境状态x′所获得的回报;P(x′|x,a)为转移概率;![]() 为环境状态下所有动作可获得的最大动作
为环境状态下所有动作可获得的最大动作![]() 状态值函数;γ为人工给定的折扣因子.Q学习算法的执行流程如图2所示.
状态值函数;γ为人工给定的折扣因子.Q学习算法的执行流程如图2所示.
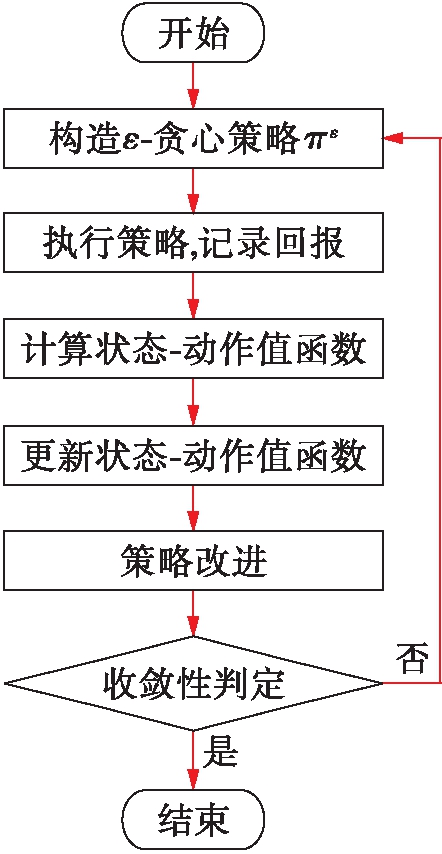
图2 Q学习算法实施流程
Fig.2 Implementation process of Q-learning algorithm
流程主要包括以下4个主要步骤:
1) 构造ε-贪心策略πε并执行.为避免原策略在动作选择上可能的“仅利用”倾向,Q学习算法将利用ε-贪心策略对原策略重构,所获得新策略可表示为
(2)
式中:π、πε分别为原策略和新构造的策略;πε(x)、π(x)为新策略和原策略在环境状态下所采取的动作;ΔA为均匀概率选择的动作;ε为人工给定的贪心系数.对于基于ε-贪心算法构造的新策略πε,将以概率1-ε采用原策略下的动作,并以总概率1-ε在动作空间中均匀选取任一动作执行.利用构造所得的ε-贪心策略作用于环境,并记录所获取的回报值.
2) 更新状态![]() 动作值函数.根据执行所得的回报值,更新状态
动作值函数.根据执行所得的回报值,更新状态![]() 动作值函数,更新公式可表示为
动作值函数,更新公式可表示为
Qk+1(xk,ak)=Qk(xk,ak)+α[R(xk,xk+1,ak)+
(3)
式中:Qk(xk,ak)、Qk+1(xk,ak)分别为第k次迭代前后所得的动作![]() 状态值函数;xk、xk+1分别为第k次迭代前后所得的环境状态;ak为第k次迭代所采用的动作;α为学习因子,用以控制迭代收敛速度;
状态值函数;xk、xk+1分别为第k次迭代前后所得的环境状态;ak为第k次迭代所采用的动作;α为学习因子,用以控制迭代收敛速度;![]() 为遍历所有可能的动作在环境状态xk+1下的最大状态
为遍历所有可能的动作在环境状态xk+1下的最大状态![]() 动作值函数.
动作值函数.
3) 策略改进.策略更新的目标在于获取最优的动作策略,保证在各环境状态下按照该策略执行所获得回报期望最高,策略改进公式可表示为
(4)
式中:π*(x)为环境状态x下的最优策略;![]() 为在该环境状态下所有动作中动作
为在该环境状态下所有动作中动作![]() 状态值函数最大的动作.
状态值函数最大的动作.
4) 收敛判定.当迭代满足策略改进后,策略改变量小于给定值时,则可判定收敛并输出结构,该判定关系可表示为
(5)
式中:π*k(x)、π*k+1(x)分别为第k次迭代前后的最优策略;δ为给定限值.
2 区域发电控制的Q学习建模实现
2.1 基于CPS的区域电网AGC控制架构
所谓信息物理系统(cyber-physical system,CPS)是指通过通信网络将物理系统与信息系统紧密联系的一体化控制系统,通过信息的高效采集、传输与计算,实现对物理系统的精准控制[9-10].
区域电网信息物理系统架构如图3所示,区域电网的信息物理系统架构包括:以电网、发电厂构成的一次物理系统和以采集量测装置、通信设备、运行控制中心构成的二次信息系统.其中根据电源的运行控制要求,可将其划分为传统电源和新能源两大类.新能源主要是指风电、光伏等可再生能源,相对运行控制要求而言,由于新能源出力主要受气象等因素影响,因此可控性较差;而水电、火电等传统电源出力可控性较高.为提升电网运行清洁化水平,一般要求优先通过调整传统电源出力,满足区域电网的调控要求.
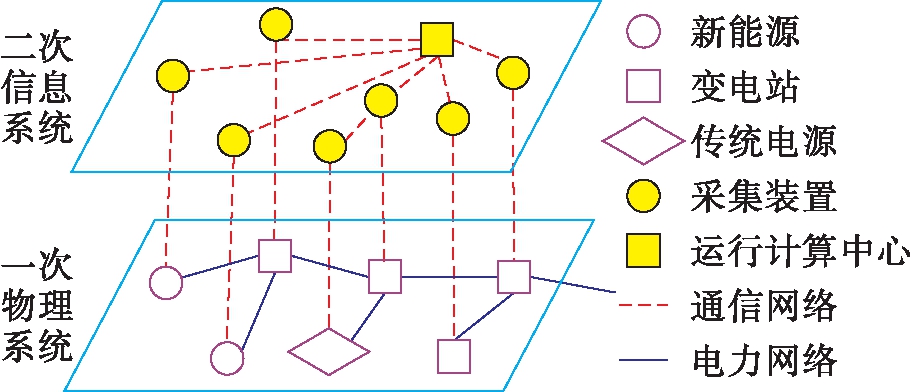
图3 区域电网信息物理系统架构
Fig.3 CPS architecture of regional power grid
2.2 环境状态
与大电网AGC控制不同,区域电网AGC控制不仅要考虑电网频率偏差的调控要求,还需要考虑区域电网断面送出潮流的调整要求[11].在Q学习算法框架下,其环境状态可表示为![]() 其中,
其中,![]() 依次为断面潮流离散化数值,
依次为断面潮流离散化数值,![]() 为电网频率偏差调整量离散化数值.
为电网频率偏差调整量离散化数值.
为得到上述离散化取值,首先需要对断面潮流和电网频率偏差调整量进行归一化,其计算公式为
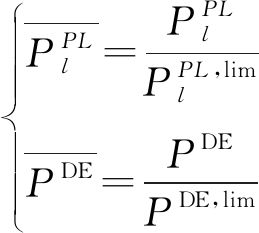
(6)
式中:![]() 分别为归一化前后所得的送电通道潮流;
分别为归一化前后所得的送电通道潮流;![]() 为该送电通道的功率传输限值;
为该送电通道的功率传输限值;![]() 分别为归一化前后所得的电网频率偏差调整量;
分别为归一化前后所得的电网频率偏差调整量;![]() 为调整量最大值.
为调整量最大值.
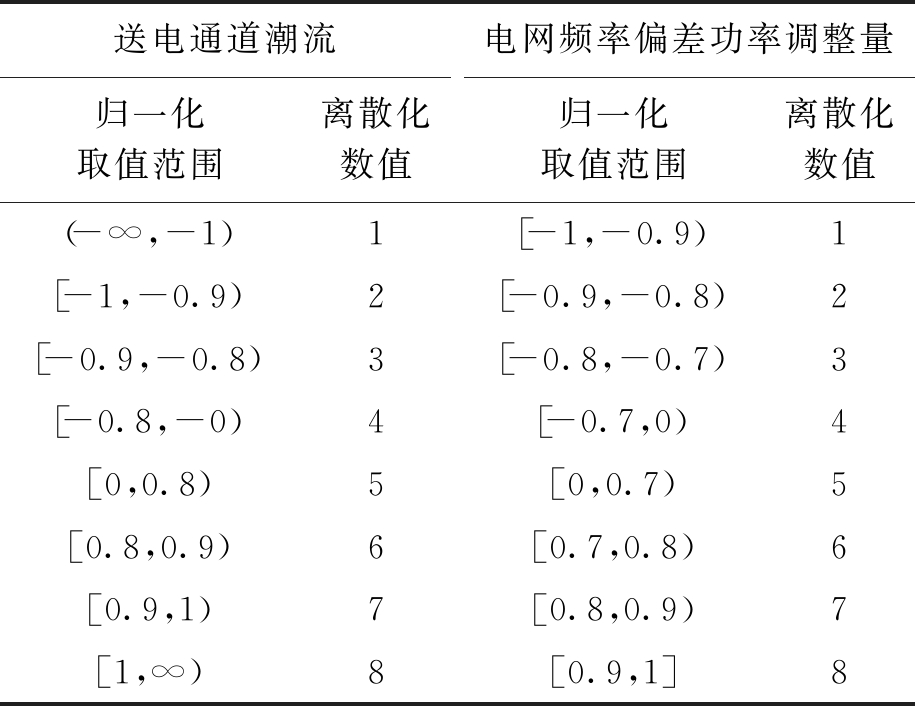
在得到上述归一化环境状态量后,还需要进一步对其进行离散化处理.考虑到送电通道潮流和电网频率偏差功率调整量存在的方向性要求,文中对多环境状态进行离散化处理,结果如表1所示.
2.3 动作空间
区域AGC控制的动作空间,即为区域火电机组及风电场功率的调节量,可表示为![]() 其中,
其中,![]() 依次为火电机组的调节量离散化数值;
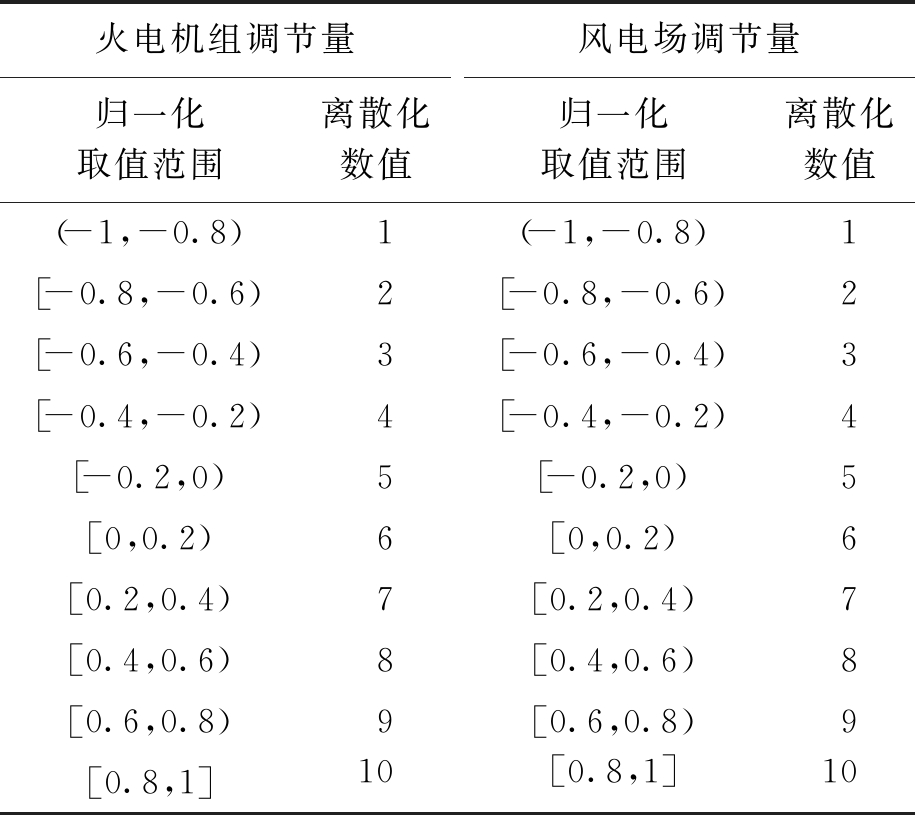
依次为火电机组的调节量离散化数值;![]() 依次为风电场调节量离散化数值;C、W分别为区域电网中火电机组数和风电场数.类似环境状态的处理方式,可根据最大调整量对动作空间进行归一化处理,结果如表2所示.
依次为风电场调节量离散化数值;C、W分别为区域电网中火电机组数和风电场数.类似环境状态的处理方式,可根据最大调整量对动作空间进行归一化处理,结果如表2所示.
表1 环境状态变量离散化结果
Tab.1 Discretization results for environmental state variables
送电通道潮流归一化取值范围离散化数值电网频率偏差功率调整量归一化取值范围离散化数值(-∞,-1)1[-1,-0.9)1[-1,-0.9)2[-0.9,-0.8)2[-0.9,-0.8)3[-0.8,-0.7)3[-0.8,-0)4[-0.7,0)4[0,0.8)5[0,0.7)5[0.8,0.9)6[0.7,0.8)6[0.9,1)7[0.8,0.9)7[1,∞)8[0.9,1]8
表2 动作空间变量离散化结果
Tab.2 Discretization results for action space variables
火电机组调节量归一化取值范围离散化数值风电场调节量归一化取值范围离散化数值(-1,-0.8)1(-1,-0.8)1[-0.8,-0.6)2[-0.8,-0.6)2[-0.6,-0.4)3[-0.6,-0.4)3[-0.4,-0.2)4[-0.4,-0.2)4[-0.2,0)5[-0.2,0)5[0,0.2)6[0,0.2)6[0.2,0.4)7[0.2,0.4)7[0.4,0.6)8[0.4,0.6)8[0.6,0.8)9[0.6,0.8)9[0.8,1]10[0.8,1]10
2.4 回报函数
“风火打捆”模式不同于传统模式,要求优先调整火电机组出力以保证区域送出功率,按照其给定计划曲线执行[12],并在断面潮流存在裕度的情况下,响应系统的频率偏差调控要求.根据上述运行要求,回报函数可表示为
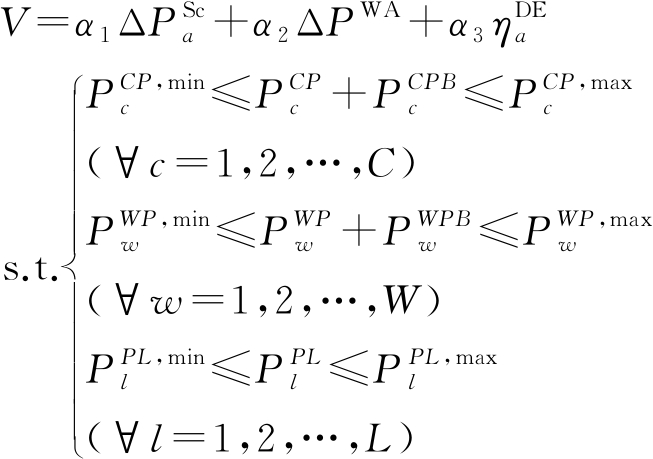
(7)
式中:![]() 分别为区域送出计划改进量、弃风电量与电网频率偏差调节贡献度;α1、α2、α3为对应的系数;
分别为区域送出计划改进量、弃风电量与电网频率偏差调节贡献度;α1、α2、α3为对应的系数;![]() 分别为火电机组的出力上下限;
分别为火电机组的出力上下限;![]() 为风电场的出力上下限;
为风电场的出力上下限;![]() 为断面潮流上下限;
为断面潮流上下限;![]() 分别为火电机组发电功率、风电场发电功率.
分别为火电机组发电功率、风电场发电功率.
3 算例分析
3.1 基础数据
本算例中将对IEEE-30节点系统进行改造,在原节点26与节点28处分别增加一条对外联络线,以模拟区域电网与主网相连的场景,验证本文所提算法的有效性.改造后所得的地区电网网架结构如图4所示.
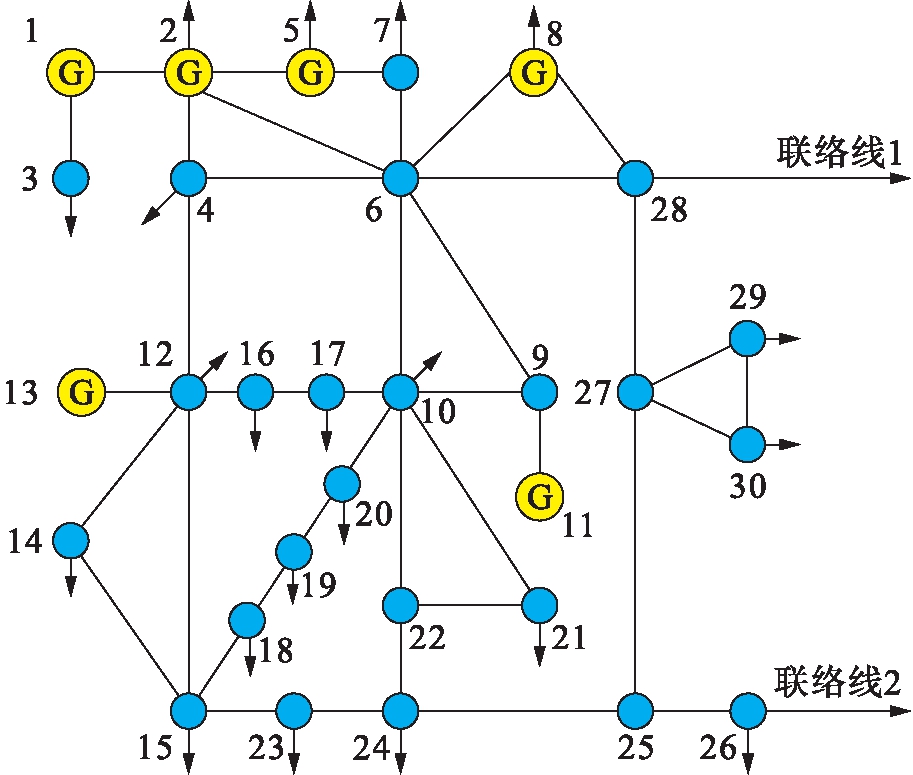
图4 区域电网网架
Fig.4 Framework of regional power grid
该区域电网的电源包括:火电厂3个,风电场3个,各电源的基本参数如表3所示.
表3 电源基本参数
Tab.3 Basic parameters for power sources
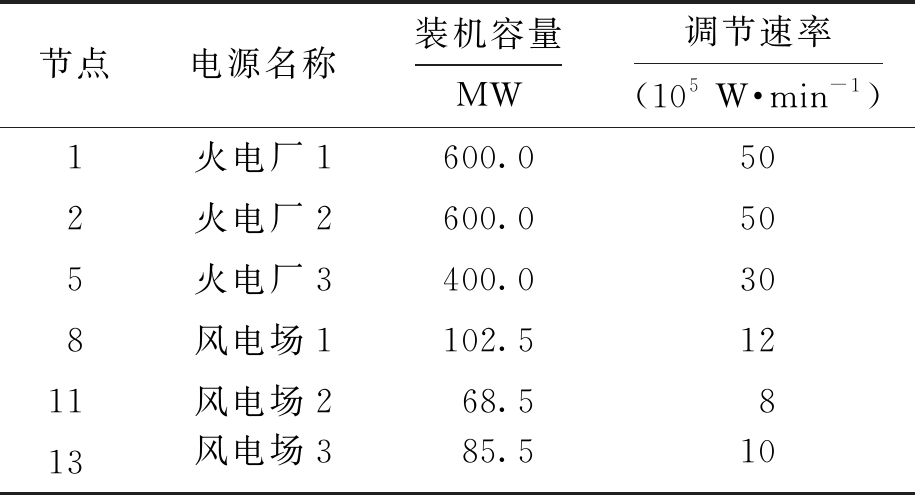
节点电源名称装机容量MW调节速率(105W·min-1)1火电厂1600.0502火电厂2600.0505火电厂3400.0308风电场1102.51211风电场268.5813风电场385.510
3.2 结果分析
算例中Q学习算法模型所用到的基础参数为α1=6,α2=3,α3=1.Q学习算法在实际应用生产控制智能体前,需要经过历史数据的学习.为此,利用宁剑等[3]所介绍的基于控制响应函数的AGC控制方法,逐一计算各运行场景下的电源出力调节要求,将其作为区域发电Q学习控制方法学习的基础数据.为验证该智能体在区域电网AGC控制中的实际效果,进一步设计了静态仿真和动态仿真两个场景.
1) 静态仿真.算例中的静态仿真不考虑智能体控制耗时和传统基于控制响应函数计算耗时,本文方法和文献[3]调控策略差异对比如图5所示.场景一中风电增加出力10 MW,为防止断面越限,传统方法控制策略共减少火电出力9.85 MW,而本文所提出方法减少火电出力9.8 MW;场景二中风电减少出力10 MW,传统方法控制策略共增加火电出力10.2 MW,而本文所提出方法增加火电出力10.0 MW.两个场景下,两种方法的控制策略偏差不超过2%,表明在静态控制中,两种方法具有相近的控制效果.
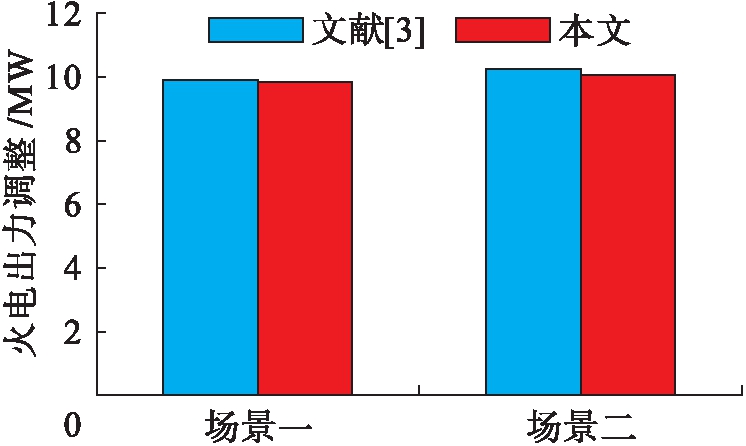
图5 静态调控效果对比
Fig.5 Comparison of static control effects
2) 动态仿真.本文所设计的风电出力变化曲线如图6所示,两种控制方法的火电调节控制变化和联络线交换功率变化分别如图7、8所示.在相同的风电出力变化动态过程中,传统方法由于计算控制响应函数耗时较长,导致火电机组出力变化滞后于本文所提出的方法,进而导致联络线交换功率变化的响应速度也相应滞后.该联络线交换功率控制值为815 MW,本文所提出方法的断面功率越限时间仅为5 min,而传统方法则超过8 min,表明本文所提出的方法具有更高的控制效果,对消除区域电网断面越限等具有显著效果.
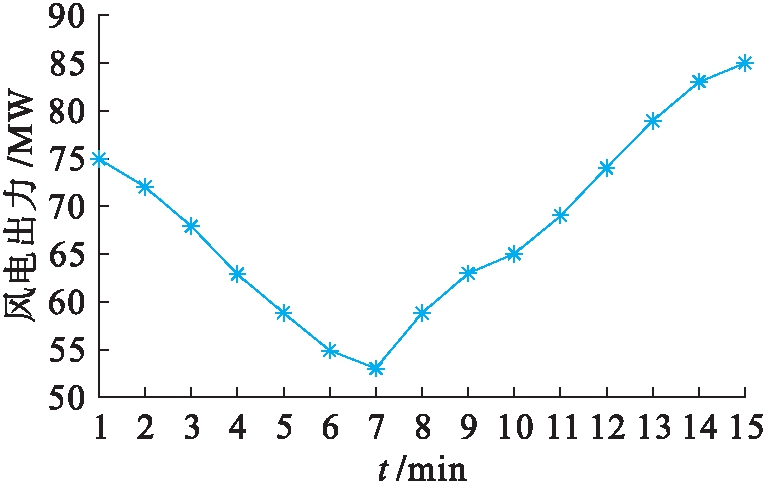
图6 风电场出力
Fig.6 Wind power generation
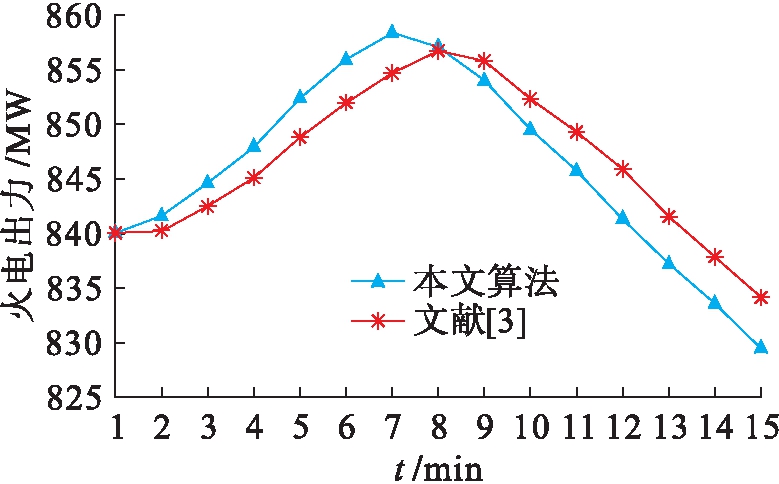
图7 火电出力
Fig.7 Coal power generation
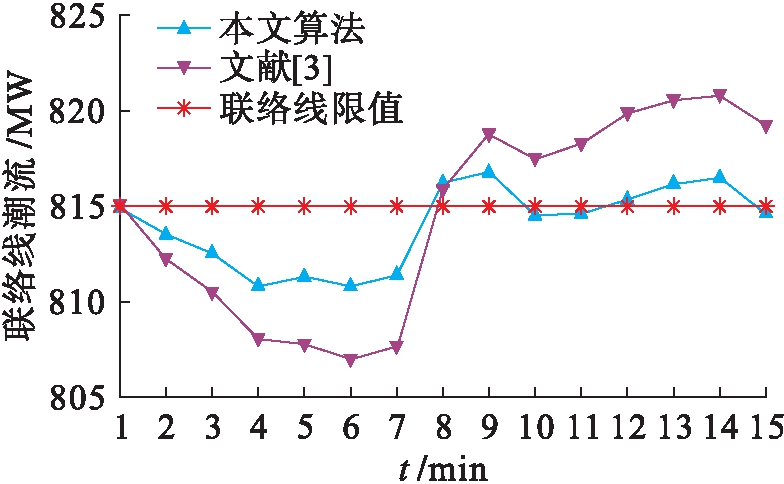
图8 联络线功率
Fig.8 Transmission wire power
4 结 论
本文研究了基于Q学习算法的区域电网AGC控制问题.与传统的大电网AGC控制相比,区域电网AGC控制在控制目标上不仅要考虑频率偏差调整,还需要考虑传输断面的运行控制要求;在控制对象上,需要区分传统电源和新能源在调节次序上的差别.传统的AGC控制策略难以适应上述控制要求,而以Q学习算法为核心的强化学习计算方法具有较强的适应性,能够较好地满足不同类型区域电网的运行控制要求.
[1] 孙秋野,杨凌霄,张化光.智慧能源——人工智能技术在电力系统中的应用与展望 [J].控制与决策,2018,33(5):938-949.
(SUN Qiu-ye,YANG Ling-xiao,ZHANG Hua-guang.Smart energy:applications and prospects of artificial intelligence technology in power system [J].Control and Decision,2018,33(5):938-949.)
[2] 刘颖,胡楠,杨壮观,等.基于深度学习的电网监控视频中工作人员检测与识别 [J].沈阳工业大学学报,2019,41(5):544-548.
(LIU Ying,HU Nan,YANG Zhuang-guan,et al.Detection and identification of staff in power grid monitoring video based on deep learning [J].Journal of Shenyang University of Technology,2019,41(5):544-548.)
[3] 宁剑,谈超,江长明,等.区域电网省级AGC控制区的灵活组合控制策略 [J].电力系统自动化,2019,43(10):171-179.
(NING Jian,TAN Chao,JIANG Chang-ming,et al.Flexible combination control strategy for control area of provincial AGC in regional power grid [J].Automation of Electric Power Systems,2019,43(10):171-179.)
[4] 张孝顺,李清,余涛,等.基于协同一致性迁移Q学习算法的虚拟发电部落AGC功率动态分配 [J].中国电机工程学报,2017,37(5):1455-1467.
(ZHANG Xiao-shun,LI Qing,YU Tao,et al.Collabo-rative consensus transfer Q-learning based dynamic generation dispatch of automatic generation control with virtual generation tribe [J].Proceedings of the CSEE,2017,37(5):1455-1467.)
[5] 张孝顺,余涛,唐捷.基于CEQ(λ)多智能体协同学习的互联电网性能标准控制指令动态分配优化算法 [J].电工技术学报,2016,31(8):125-133.
(ZHANG Xiao-shun,YU Tao,TANG Jie.Dynamic optimal allocation algorithm for control performance standard order of interconnected power grids using synergetic learning of multi-agent CEQ(λ) [J].Transactions of China Electrotechnical Society,2016,31(8):125-133.)
[6] Yin L,Yu T,Zhou L,et al.Artificial emotional reinforcement learning for automatic generation control of large-scale interconnected power grids [J].IET Gene-ration,Transmission & Distribution,2017,11(9):2305-2313.
[7] 余涛,王宇名,叶文加,等.基于改进分层强化学习的CPS指令多目标动态优化分配算法 [J].中国电机工程学报,2011,31(19):90-96.
(YU Tao,WANG Yu-ming,YE Wen-jia,et al.Multi-objective dynamic optimal dispatch method for CPS order of interconnected power grids using improved hierarchical reinforcement learning [J].Proceedings of the CSEE,2011,31(19):90-96.)
[8] 赵星宇,丁世飞.深度强化学习研究综述 [J].计算机科学,2018,45(7):1-6.
(ZHAO Xing-yu,DING Shi-fei.Research on deep reinforcement learning [J].Computer Science,2018,45(7):1-6.)
[9] 薛禹胜,李满礼,罗剑波,等.基于关联特性矩阵的电网信息物理系统耦合建模方法 [J].电力系统自动化,2018,42(2):11-19.
(XUE Yu-sheng,LI Man-li,LUO Jian-bo,et al.Mo-deling method for coupling relations in cyber physical power systems based on correlation characteristic matrix [J].Automation of Electric Power Systems,2018,42(2):11-19.)
[10] 刘林,张运洲,王雪,等.能源互联网目标下电力信息物理系统深度融合发展研究 [J].中国电力,2019,52(1):2-9.
(LIU Lin,ZHANG Yun-zhou,WANG Xue,et al.Research on deep integration of power cyber physical system under energy Internet goals [J].Electric Power,2019,52(1):2-9.)
[11] 冉莉莉,石繁荣.基于PEMFC延时特性的发电系统建模与控制 [J].电源技术,2017,41(10):1416-1419.
(RAN Li-li,SHI Fan-rong.Modeling and control strategy of generation system based on time delay characteristics of PEMFC [J].Chinese Journal of Power Sources,2017,41(10):1416-1419.)
[12] 葛维春,刘前卫,刘富家,等.高比例清洁能源电网灵活调节方法 [J].沈阳工业大学学报,2018,40(5):481-485.
(GE Wei-chun,LIU Qian-wei,LIU Fu-jia,et al.Flexi-ble adjustment method for power grid with high-proportion clean energy [J].Journal of Shenyang University of Technology,2018,40(5):481-485.)