Ti-6Al-4V双相钛合金在具备比强度高、综合力学性能好、焊接性能优良等特点的同时,还具有良好的超塑性,被广泛应用于国防武器装备、新能源汽车、医疗器械等领域复杂结构零件的成型制造[1-4].然而金属材料超塑性变形过程是一个多元非线性过程,其变形行为对温度、应变速率等参数十分敏感.通常情况下,流变应力的变化规律能够较好地反映材料的超塑性变形行为,也决定了材料施加载荷的大小和能量的耗散与再分配.因此,系统性地研究Ti-6Al-4V合金的超塑性变形工艺参数对流变应力的动态响应,对揭示该合金的超塑性变形行为以及优化变形工艺参数具有重要意义.目前,针对金属材料超塑性变形行为的研究,通常以超塑性拉伸试验数据为基础,对数据进行筛选与分析,通过多元线性回归方法获得合金超塑性变形的应力![]() 应变曲线.但上述研究方法存在如下的局限性:首先,超塑性变形行为研究涉及大量正交试验,成本较高;其次,现有Ti-6Al-4V合金超塑性流变应力理论模型有限,当变形工艺参数变化较大,尤其是出现典型的边界效应(高温低应变速率、低温高应变速率)时,对该合金超塑性流变应力的变化趋势无法进行较为准确的描述.
应变曲线.但上述研究方法存在如下的局限性:首先,超塑性变形行为研究涉及大量正交试验,成本较高;其次,现有Ti-6Al-4V合金超塑性流变应力理论模型有限,当变形工艺参数变化较大,尤其是出现典型的边界效应(高温低应变速率、低温高应变速率)时,对该合金超塑性流变应力的变化趋势无法进行较为准确的描述.
人工神经网络(artificial neutral network,ANN)是一种较为先进且实用的信息处理技术,能够通过输入、输出参数设定、算法选择、运算精度调节等,实现对数据分析过程的自学习、自训练.采用该方法进行数据分析时,既不需要特定的物理模型,也不需要假设与修正,就能够对数据进行自我深度学习,从而获得各参数之间的内在规律,有效解决传统模型构建与数据回归方法中无法解决的难题.因此,针对材料成型工艺参数变化较为复杂且呈现多维度正交变化趋势的研究领域,该方法具有广阔应用前景.为此,国内外学者及相关研究机构进行了如下研究工作:中国科学院金属研究所侯介山等[5]针对NiAl合金的超塑性变形过程,采用BP人工神经网络方法实现了对其在不同成分和不同工艺参数下的断裂伸长率的预测;张学敏等[6]对WSTi3515S阻燃钛合金的超塑性变形行为进行了预测;崔岩等[7]采用人工神经网络技术开展了材料基因工程方面的相关研究工作;刘雅芳等[8]采用RBF型人工神经网络研究了碳/陶瓷复合材料的化学成分对其硬度的影响;张建平等[9]采用人工神经网络算法对6061铝合金稳态应力进行了预测与精度分析;Lakshmi等[10]采用BP人工神经网络技术结合试验验证方法,研究了ASS304合金塑性区域的力学性能变化规律,获得了较好的预测精度;Kapoor等[11]采用人工神经网络技术对Zr-2.5Nb-0.5Cu合金的变形行为进行了系统研究.然而,目前文献报道中关于采用BP人工神经网络技术对Ti-6Al-4V合金超塑性变形行为的研究内容相对较少.
本文以Ti-6Al-4V双相钛合金的超塑性拉伸试验数据为基础构建三层网络模型,并充分考虑模型构建过程中的算法选择与预测精度,分别对该合金超塑性变形过程中的峰值流变应力和稳态流变应力进行预测,从而为该合金的超塑性变形行为提供新的研究方法与思路.
1 材料及方法
试验材料选用厚度为2 mm的Ti-6Al-4V双相钛合金板材,其合金成分如表1所示.
表1 Ti-6Al-4V合金的化学成分(w)
Tab.1 Chemical composition of Ti-6Al-4V alloy (w) %

TiAlVFeC>905.5~6.83.5~4.5≤0.3≤0.1
参照GB/T 228.2-2015标准,利用AG 250 KNE型电子拉伸试验机对合金进行超塑性拉伸试验,拉伸试样尺寸如图1所示(单位:mm).试验温度为670~820 ℃,保温时间为10 min,初始应变速率为5×10-3、1×10-3和5×10-4 s-1,保护气体为氩气.试样断裂后水淬至室温,从而保留高温变形组织.
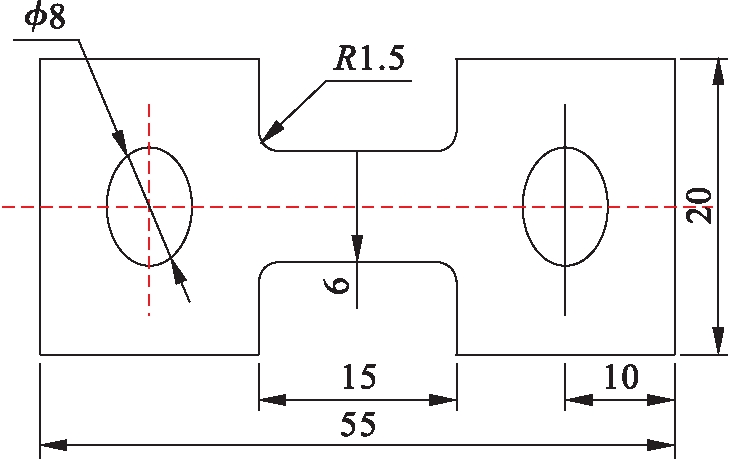
图1 超塑拉伸试样尺寸示意图
Fig.1 Schematic size of superplastic tensile specimen
采用OLYMPUS GX51金相显微镜观察试样超塑性拉伸后的光学显微组织.腐蚀第一阶段(晶界腐蚀):浸蚀剂为6 mL HNO3+100 mL H2O+3 mL HF;腐蚀第二阶段(区分β相):浸蚀剂为98 mL C2H2O4·2H2O+1 g Fe(NO3)3+2 mL HF.
2 结果与分析
2.1 BP人工神经网络模型预测的数据基础
金属材料的微观组织,尤其是晶粒尺寸对其超塑性变形性能起着重要影响作用.晶粒尺寸计算方法为
d=1.74L
(1)
式中,L为金相显微组织线截距.
图2为Ti-6Al-4V合金的初始显微组织.结合式(1)和图2,计算得出该合金的晶粒尺寸分别为5.68、6.98和7.95 μm,本文将其分别定义为Ⅰ类(5~6 μm)、Ⅱ类(6~7 μm)和Ⅲ类(7~8 μm).

图2 Ti-6Al-4V合金初始显微组织
Fig.2 Initial microstructures of Ti-6Al-4V alloy
选取Ti-6Al-4V合金(Ⅰ类)进行超塑性拉伸试验,获得该合金在不同应变速率下的峰值流变应力和稳态流变应力,结果如图3、4所示.由图3、4可见,随着超塑性变形温度的升高,该合金的峰值流变应力与稳态流变应力均呈现降低趋势.
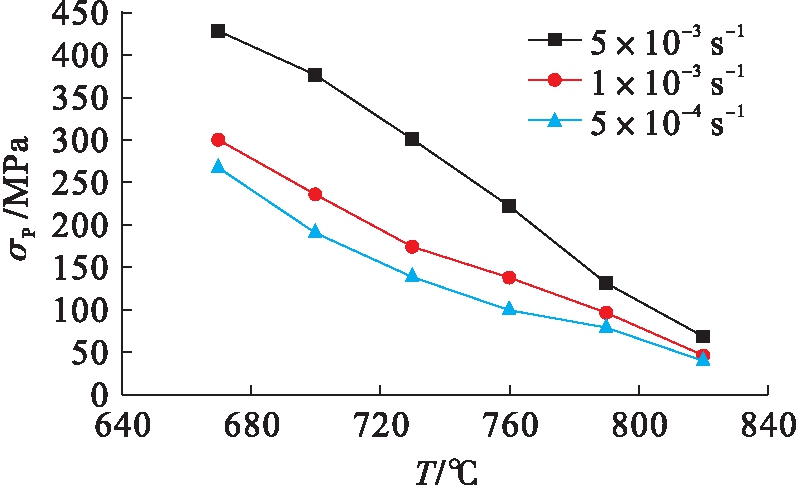
图3 Ti-6Al-4V合金的峰值流变应力变化曲线
Fig.3 Changing curves of peak flow stress of Ti-6Al-4V alloy
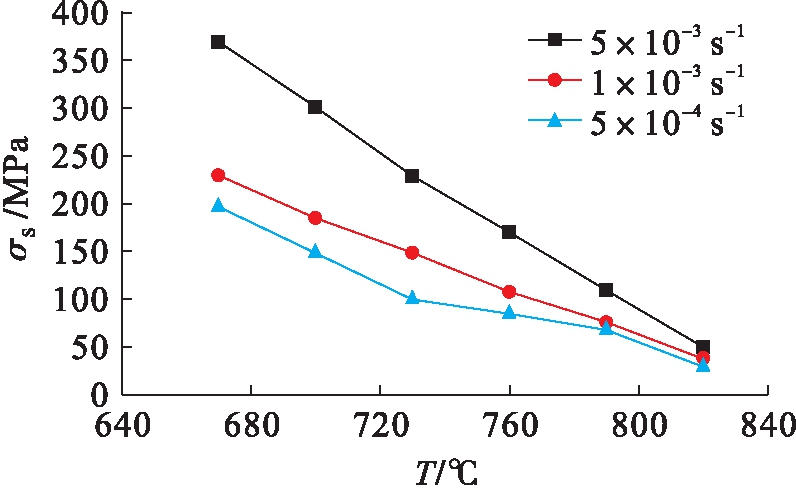
图4 Ti-6Al-4V合金的稳态流变应力变化曲线
Fig.4 Changing curves of steady flow stress of Ti-6Al-4V alloy
选取Ti-6Al-4V合金超塑性变形过程中的温度、应变速率和晶粒尺寸为BP人工神经网络模型的输入参数,而将峰值流变应力和稳态流变应力作为输出参数.在54组数据中随机抽取45组进行神经网络训练,剩余9组数据作为预测样本,具体测试样本数据如表2所示.由表2可见,输入、输出参数数值相差较大,且会产生数值“溢出”现象.
表2 Ti-6Al-4V合金测试样本数据
Tab.2 Data of test samples of Ti-6Al-4V alloy
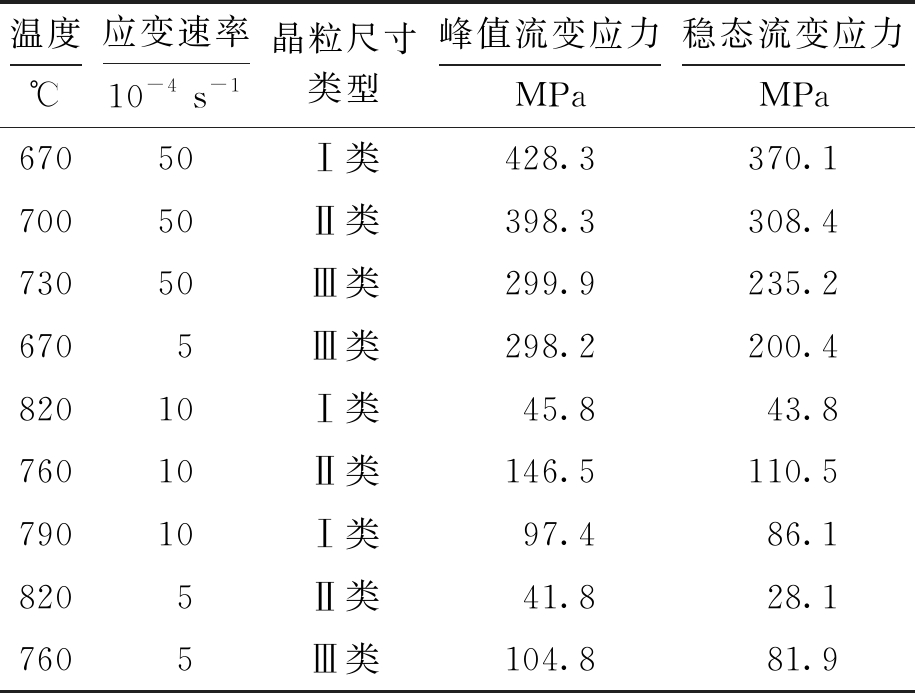
温度℃应变速率10-4s-1晶粒尺寸类型峰值流变应力MPa稳态流变应力MPa67050Ⅰ类428.3370.170050Ⅱ类398.3308.473050Ⅲ类299.9235.26705Ⅲ类298.2200.482010Ⅰ类45.843.876010Ⅱ类146.5110.579010Ⅰ类97.486.18205Ⅱ类41.828.17605Ⅲ类104.881.9
为了提高预测精度,对训练数据按照式(2)进行归一化处理[12],即
(2)
式中:Z为原始数据;Zmax、Zmin为原始数据的最大值和最小值;Z′为标准化后的数值.
采用MATLAB自带的BP人工神经网络软件,以试验数据为基础,确定输入、输出参数,利用神经元对输入、输出参数进行反复自学习与训练并对权值和阈值进行调节,直至满足预先设定的精度值后输出结果.本文所构建的BP人工神经网络模型结构如图5所示.当进行BP人工神经网络训练时,温度为670~820 ℃,应变速率为5×10-4~5×10-3 s-1,晶粒尺寸为5~8 μm.在三层网络模型中选用Trainlm函数,设定网络预测样本数为45,测试样本数为9,经过3 586次运算后多重相关系数为0.82,网络模型误差范围为2.02×10-4~4.85×10-4,此时得到峰值流变应力为41.8~428.3 MPa,稳态流变应力为28.1~370.1 MPa.
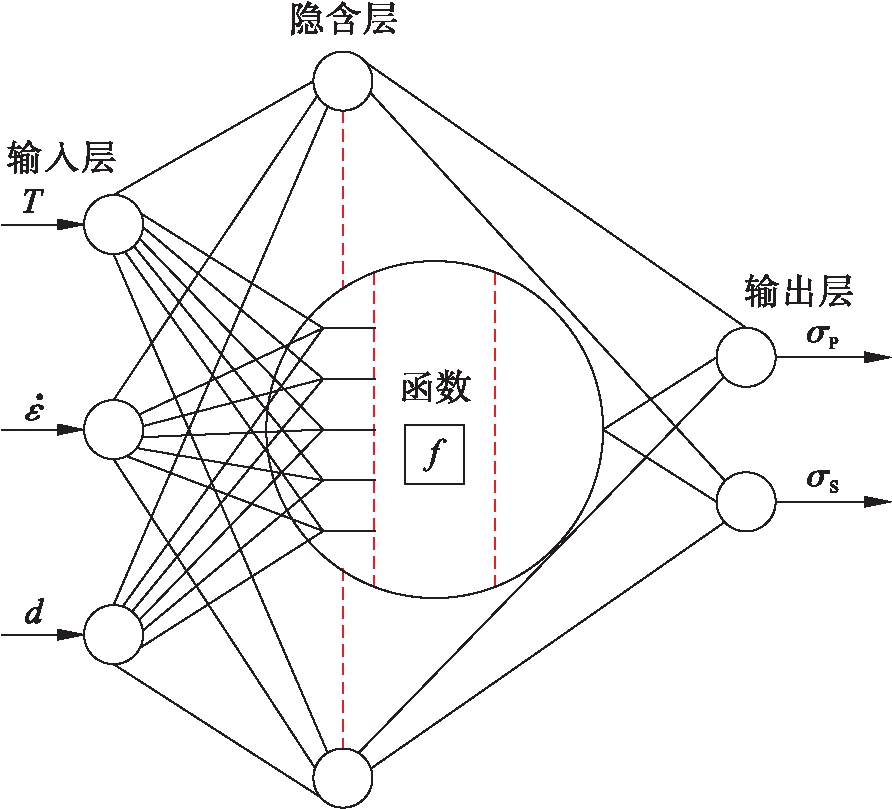
图5 人工神经网络结构和神经元示意图
Fig.5 Schematic diagram of artificial neural network configuration and neurons
2.2 BP人工神经网络的训练
BP人工神网络的训练与预测过程是在输入参数范围内选取一定的步长,通过权值、阈值的调节使得测试数据无限接近样本值(试验结果值),经过多次训练后,达到预先设定的精度要求.在网络模型构建过程中,需要充分考虑输入层![]() 隐含层权重、隐含层
隐含层权重、隐含层![]() 输出层权重、隐含层节点数(神经元个数)、算法选择等因素.图6为Ti-6Al-4V合金平均误差值与迭代次数、隐含层神经元个数(隐含层节点数)之间的关系.由图6a可见,当迭代次数处于500~2 000区间内时,平均误差显著下降;当迭代次数超过2 000时,平均误差较低且处于稳定状态,说明所构建的模型达到设定误差值时的迭代次数应大于2 000.由图6b可见,平均误差值随着隐含层神经元个数的增加呈现显著降低(神经元个数为5~8)、趋于平稳(神经元个数为8~11)、随后增加(神经元个数为11~19)的变化趋势,当神经元个数为8时,平均误差值最小,因而选定神经元个数为8.
输出层权重、隐含层节点数(神经元个数)、算法选择等因素.图6为Ti-6Al-4V合金平均误差值与迭代次数、隐含层神经元个数(隐含层节点数)之间的关系.由图6a可见,当迭代次数处于500~2 000区间内时,平均误差显著下降;当迭代次数超过2 000时,平均误差较低且处于稳定状态,说明所构建的模型达到设定误差值时的迭代次数应大于2 000.由图6b可见,平均误差值随着隐含层神经元个数的增加呈现显著降低(神经元个数为5~8)、趋于平稳(神经元个数为8~11)、随后增加(神经元个数为11~19)的变化趋势,当神经元个数为8时,平均误差值最小,因而选定神经元个数为8.
图7为分别选用动量LM算法(函数为Trainlm)、MOBP算法(函数为Traindm)、RPROP算法(函数为Trainrp)和SDBP算法(函数为Traingd)4种典型算法预测后的函数收敛曲线.由图7可见,在设定相同预测精度下,当选择LM算法时,最少运算次数函数曲线收敛,表明LM算法的运算效率最高,因此,本文选用该算法进行BP人工神经网络模型的训练与测试.
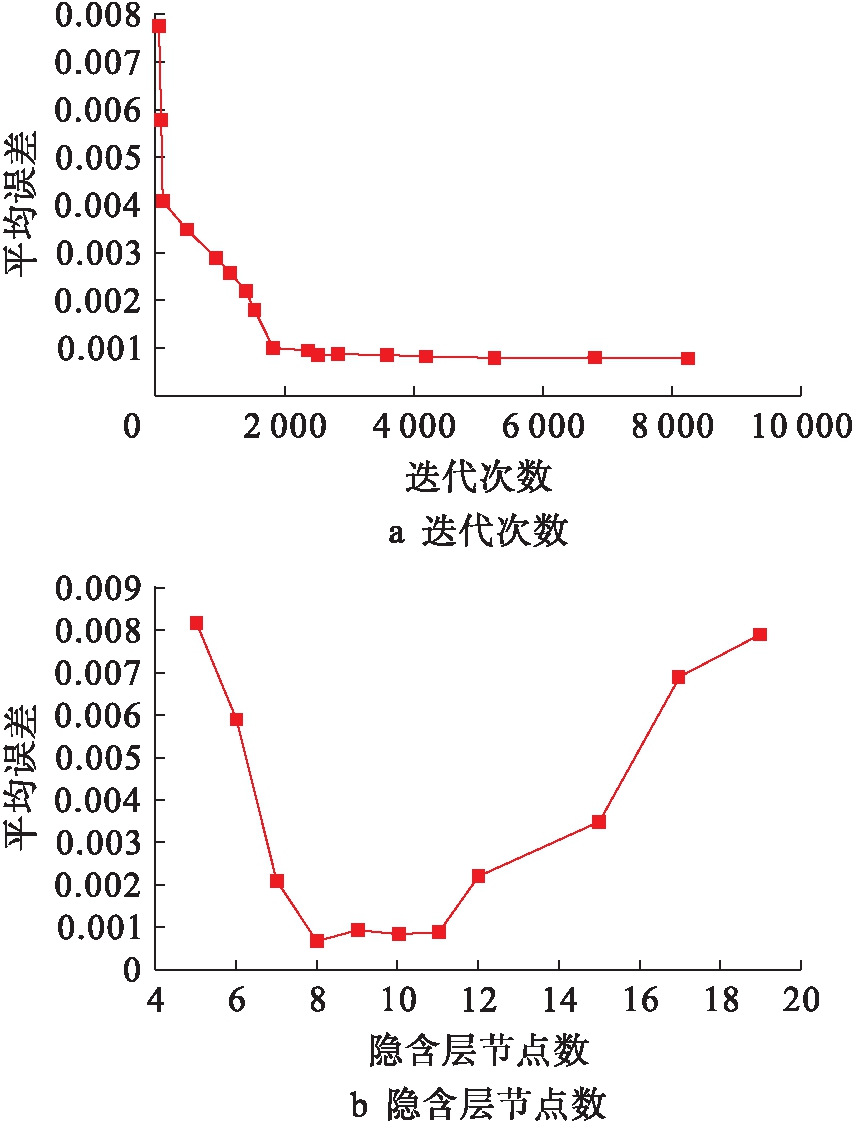
图6 Ti-6Al-4V合金平均误差与迭代次数和隐含层神经元个数的关系
Fig.6 Average error in relation with iteration times and neuron number in hidden layer of Ti-6Al-4V alloy
按照温度、应变速率、晶粒尺寸三维交叉均衡选取原则,随机选取BP人工神经网络模型训练后的流变应力值与试验值进行误差分析,结果如表3所示.由表3可见,Ti-6Al-4V合金的峰值流变应力、稳态流变应力的网络预测值与试验数据之间的最大相对误差为5.3%,表明网络预测值与试验值之间吻合度较高,因此,所建立的神经网络模型具有较高的训练精度.
2.3 Ti-6Al-4V合金超塑性流变应力预测
按照表3中的参数构建BP人工神经网络模型,并对Ti-6Al-4V合金超塑性变形过程中的峰值流变应力和稳态流变应力进行预测,结果如图8所示.由图8可见,随着应变速率的增大,峰值流变应力、稳态流变应力均升高;随着变形温度的升高,峰值流变应力和稳态流变应力均降低.当应变速率为5×10-4 s-1且温度大于790 ℃时,峰值流变应力和稳态流变应力较低(<60 MPa),说明当该合金在高温低应变速率下进行超塑性拉伸时,流变应力较低,即合金具有良好的超塑性变形性能.
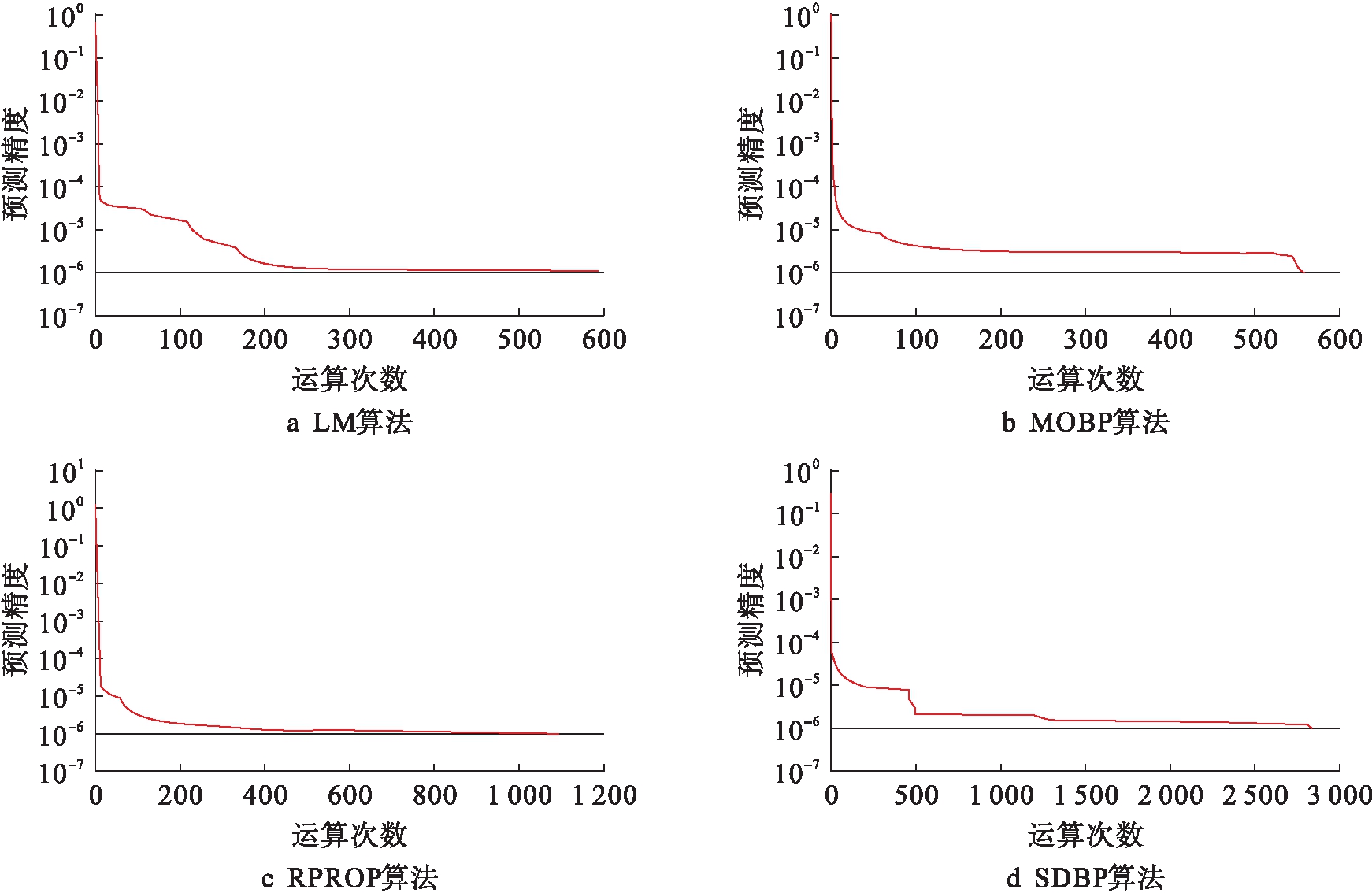
图7 不同训练算法下的函数收敛曲线
Fig.7 Function convergence curves under different training algorithms
表3 Ti-6Al-4V合金测试样本数据与网络预测值的比较
Tab.3 Comparison of sample test data with values predicted by network for Ti-6Al-4V alloy
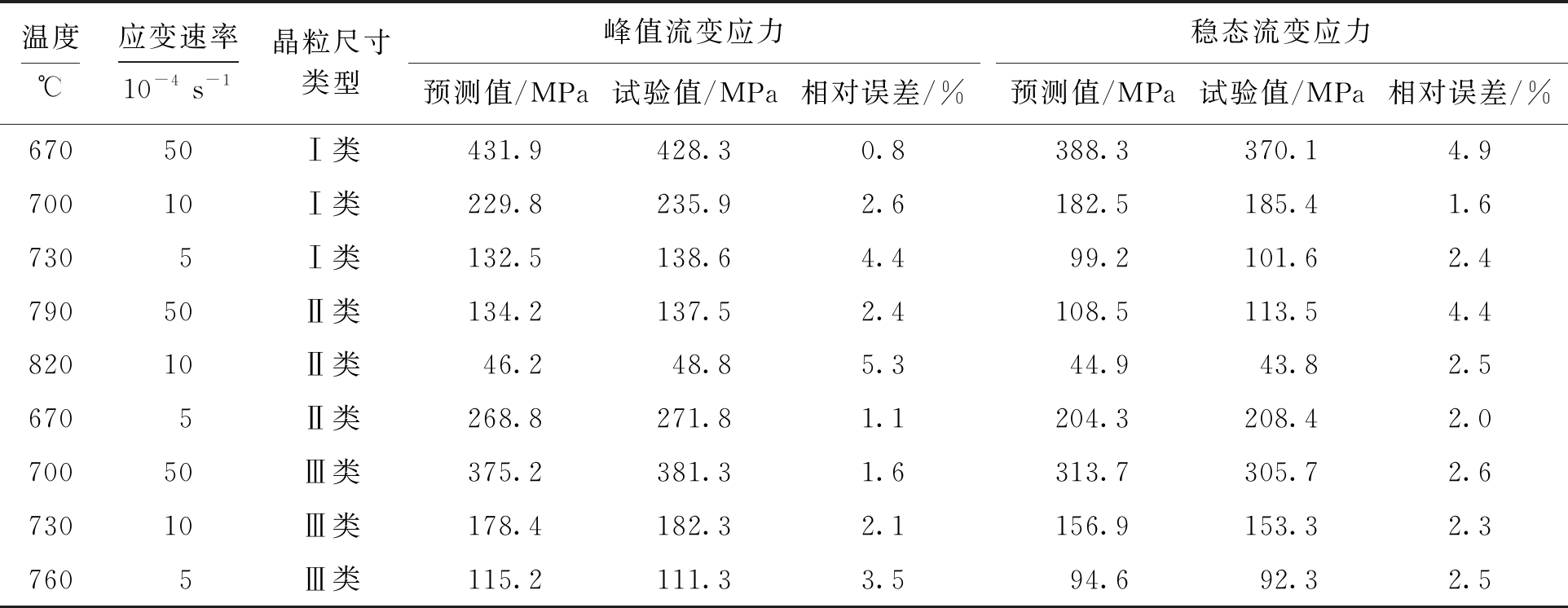
温度℃应变速率10-4s-1晶粒尺寸类型峰值流变应力预测值/MPa试验值/MPa相对误差/%稳态流变应力预测值/MPa试验值/MPa相对误差/%67050Ⅰ类431.9428.30.8388.3370.14.970010Ⅰ类229.8235.92.6182.5185.41.67305Ⅰ类132.5138.64.499.2101.62.479050Ⅱ类134.2137.52.4108.5113.54.482010Ⅱ类46.248.85.344.943.82.56705Ⅱ类268.8271.81.1204.3208.42.070050Ⅲ类375.2381.31.6313.7305.72.673010Ⅲ类178.4182.32.1156.9153.32.37605Ⅲ类115.2111.33.594.692.32.5
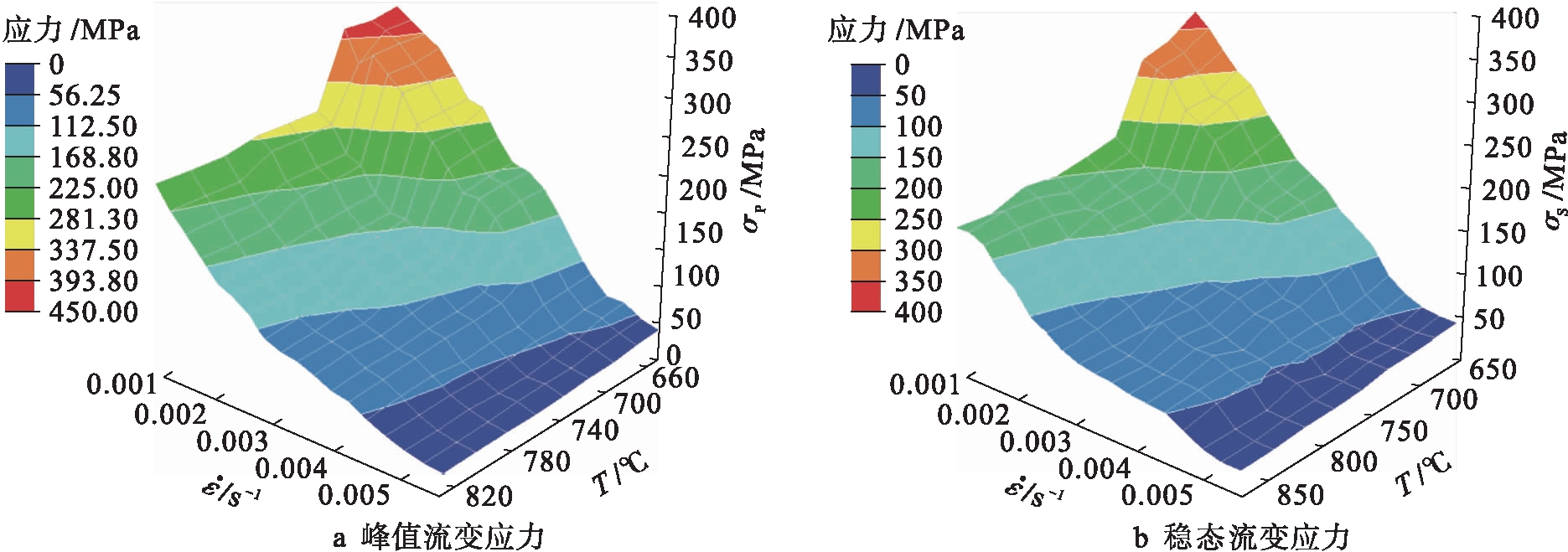
图8 Ti-6Al-4V合金的流变应力变化曲线
Fig.8 Changing curves of flow stress of Ti-6Al-4V alloy
3 结 论
采用BP人工神经网络技术建立了三层神经网络模型,对Ti-6Al-4V合金不同超塑性拉伸试验下的峰值流变应力和稳态流变应力进行了较为准确的预测.通过以上分析可以得出如下结论:
1) 当采用LM算法对Ti-6Al-4V合金超塑性变形行为进行BP人工神经网络测试时,运算效率较高且误差分析曲线收敛,具有良好的预测精度,最大误差仅为5.3%.
2) Ti-6Al-4V合金在高温低应变速率下进行超塑性变形时,稳态流变应力和峰值流变应力均低于60 MPa,表明合金具有良好的超塑变形性能.
[1] Vanderhasten M,Rabet L,Verlinden B.Deformation mechanisms of Ti-6Al-4V during tensile behavior at low strain rate [J].Journal of Materials Engineering and Performance,2007,16(2):208-212.
[2] Meng B,Fu M W,Shi S Q.Deformation behavior and microstructure evolution in thermal-aided meso-forming of titanium dental abutment [J].Materials & Design,2016,89:1283-1293.
[3] Li K,Fu X S,Chen G Q,et al.Mechanical properties of strengthened surface layer in Ti-6Al-4V alloy induced by wet peening treatment [J].Transactions of Nonferrous Metals Society of China,2016,26:2868-2873.
[4] Li Z Q,Han K,Hou H L,et al.Effect of hydrogen on diffusion bonding behavior and mechanism of Ti-6Al-4V alloy [J].Rare Metal Materials and Engineering,2014,43(2):306-310.
[5] 侯介山,周兰章,郭建亭,等.NiAl合金超塑性的人工神经网络预测 [J].金属学报,2013,49(11):1333-1338.
(HOU Jie-shan,ZHOU Lan-zhang,GUO Jian-ting,et al.Application of artificial network for prediction of superplastic behaviour in NiAl alloys [J].Acta Metallurgica Sinica,2013,49(11):1333-1338.)
[6] 张学敏,惠玉强,李咪,等.基于BP神经网络的WSTi3545S阻燃钛合金超塑性变形行为预测 [J].特种铸造及有色合金,2019,39(6):668-671.
(ZHANG Xue-min,HUI Yu-qiang,LI Mi,et al.Prediction of superplastic deformation behavior of WSTi3545S burn-resistant titanium alloy based on BP artificial neural network [J].Special Casting & Nonferrous Alloy,2019,39(6):668-671.)
[7] 崔岩,卢昀坤,曹雷刚,等.面向材料基因工程的人工神经网络研究 [J].热加工工艺,2018,47(12):13-16.
(CUI Yan,LU Yun-kun,CAO Lei-gang,et al.Research on artificial neural network for material genetic engineering [J].Hot Working Technology,2018,47(12):13-16.)
[8] 刘雅芳,董万鹏,由伟,等.基于RBF型人工神经网络的碳/陶瓷复合材料的化学成分对硬度的耦合影响分析 [J].材料导报,2015,29(6):153-157.
(LIU Ya-fang,DONG Wan-peng,YOU Wei,et al.Coupling effects of chemical compositions on the hardness of carbon/ceramic composite material by RBF artificial neural network [J].Material Review,2015,29(6):153-157.)
[9] 张建平,李斌,方芳.6061铝合金稳态应力预测与精度分析 [J].热加工工艺,2016,45(21):138-141.
(ZHANG Jian-ping,LI Bin,FANG Fang.Prediction and precision analysis of steady state stress of 6061 aluminum alloy [J].Hot Working Technology,2016,45(21):138-141.)
[10] Lakshmi A A,Rao C S,Srikanth M,et al.Prediction of mechanical properties of ASS 304 in superplastic region using artificial neural networks [J].Materials Today:Proceedings,2018,5(2):3704-3712.
[11] Kapoor R,Pal D,Chakravartty J K.Use of artificial neural networks to predict the deformation behavior of Zr-2.5Nb-0.5Cu [J].Journal of Materials Processing Technology,2005,169(2):199-205.
[12] 于雪梅,周舸,刘波,等.应用人工神经网络模型构造TC21 合金加工图 [J].塑性工程学报,2018,25(6):250-256.
(YU Xue-mei,ZHOU Ge,LIU Bo,et al.Processing map of TC21alloy established on artificial neural network model [J].Journal of Plasticity Engineering,2018,25(6):250-256.)