人们对无线通信的需求随着网络科技的飞速进步呈现出多样化特征,而位置服务[1-3]就是这些需求中最为关键的一项,然而位置服务会受到无线定位技术的限制.无线定位技术以地理位置为前提能够进行室内和室外定位[4-5].通常情况下能够经过北斗和GPS等卫星导航系统加以A-GPS辅助完成室外定位,且具有定位精度良好且效率高等特点.然而卫星信号穿透能力非常微弱,与此同时建筑物的墙壁也会对其产生阻挠作用,这在很大程度上使得卫星信号不能为室内设备提供定位服务.另外室内无线信号环境又非常繁杂,建筑物墙体和房间布局等很多因素都能致使无线信号产生多径效应.
随着智能手机等内部配置无线接入仪器的迅速发展,Wi-Fi信号已运用至大部分室内环境,同时以Wi-Fi技术为基础的位置指纹定位可以利用无线接入点在建筑内相异坐标的信号强度值,构建位置坐标和离线信号强度的指纹数据库,并将其作为在线定位的基础[6-7].通常情况下此方式的定位精度和效率会受到离线指纹数据库的有效性和位置相互匹配算法扰动的影响,因而本文提出了一种基于Wi-Fi指纹离散程度的WKNN定位算法(DD-WKNN算法).
1 离线位置指纹数据聚类
1.1 构建初始位置指纹数据库
设构建某个定位区域离线位置指纹数据库需有D个指纹信息采集点数据,同时其二维空间位置坐标为Li=(xi,yi),i=1,2,…,D.各采样点可得到N个无线接入点的信号强度值,即
Ri=(ri1,ri2,…,riN)
(1)
各组指纹信息的数据结构可以表示为
Fi=(Li,Ri)=(xi,yi,ri1,ri2,…,riN)
(2)
将采样获得的数据运用行方式完成保存,进而获得其所有离线位置的数据库,即
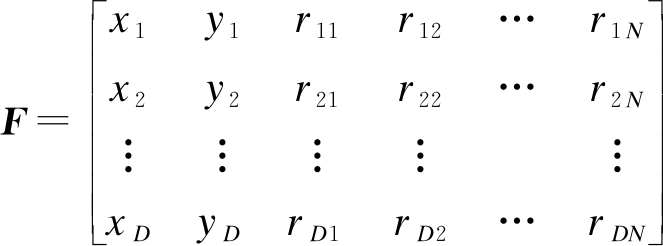
(3)
式中,xD和yD分别为D指纹信息采集点的横坐标和纵坐标.
1.2 基于K-means算法的数据聚类
第一步:从D个指纹信息中随意择取K个指纹作为初始聚类中心集合C,且C=(C1,C2,…,CK),Ci的数值与随意择取的位置指纹数据Ri(i=1,2,…,K)相等,即
C=(R1,R2,…,RK)
(4)
第二步:运算剩余的D-K个指纹和C中每个聚类中心Ci的欧氏距离,从而获得与此指纹相对最为逼近的聚类中心Ci,随之将其归至此聚类中,进而获得包括D个指纹信息的K个聚类,将各聚类中指纹信息个数定义为nCi(i=1,2,…,K).
第三步:重新运算K个聚类各自的聚类中心,随后用其替换原有的聚类中心,即
(5)
式中,Rm为第i个聚类中第m个位置的指纹数据.
第四步:以此循环往复第二、第三步直至运算获得的聚类中心值等于上个步骤的数值,换言之就是其收敛至极值,进而获得最终离线位置指纹信息聚类[8-9].
2 DD-WKNN位置指纹定位算法
在基于参考位置指纹离散程度的WKNN定位算法中,需要在上述所得数据内择取和在线实测RSSI值欧氏距离相对最为逼近的指纹数据,然后依照其离散程度设置位置估算参考权重的权值,令k个位置指纹的变异系数代表离散程度,随之完成归一化加权求和,其具体算法流程如下:
1) 在待定位位置实测各Wi-Fi无线接入点的RSSI采样值,记为RL,其表达式为
RL=(rL1,rL2,…,rLn)
(6)
式中,rLn为第n个Wi-Fi无线接入点在此待定位位置的信号强度RSSI采集值.
2) 依照RSSI采集值搜索与之对应的离线位置指纹数据库,利用式(7)择取k个和RSSI采样值欧氏距离最小的离线位置指纹数据库Fk,即
(7)

(8)
3) 针对k个位置的指纹,通过运算获得各离线位置指纹数据内每个RSSI值的平均数![]() 和标准差si(i=1,2,…,k),随之获得变异系数vi进而完成其离散程度的表示,通常情况下位置指纹的vi越小表示其能够参考的信任度越大,相关参数表达式为
和标准差si(i=1,2,…,k),随之获得变异系数vi进而完成其离散程度的表示,通常情况下位置指纹的vi越小表示其能够参考的信任度越大,相关参数表达式为
(9)
(10)
(11)
4) 将vi归一化后转化为权重系数wi,且二者关系为
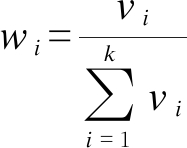
(12)
5) 依照获得的权重系数完成对每个参考点的加权求和运算以估算其位置坐标,即
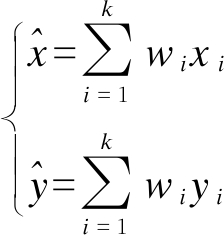
(13)
最终估测出的待定位位置坐标为![]() 此时即可完成定位.
此时即可完成定位.
DD-WKNN算法具体实现流程如图1所示.

图1 DD-WKNN算法流程图
Fig.1 Flow chart of DD-WKNN algorithm
3 结果分析
择取实验地点为某大学能够感知多个Wi-Fi无线接入点RSSI值的办公区楼道,其Wi-Fi型号为AP6476,然后择取一块20 m×2 m的条形区域,此楼道区间能够同时得到大于等于8个未知位置传输出来的接入点信号,同时可测得其RSSI值.择取(0 m,1 m)~(20 m,1 m)作为待定位位置实际坐标区间,按照1 m间隔距离设定17个待定位位置,每间隔3 s完成一次各接入点信号的RSSI采样值记录,1 min后运算其平均值作为最终RSSI采样值.待定位位置具体布置如图2所示.
由于存在于所选区间房间内的Wi-Fi型号相同,同时每个房间都包含书桌、电脑和书柜等很多物体,且各房间门均为防盗门,因而所选区域Wi-Fi无线接入点的RSSI值可以认为是均匀分布的.在此区域内利用智能手机装置Wi-Fi检视仪获取周围Wi-Fi无线接入点的RSSI值[10].离线位置指纹数据的采样点择取楼道两边房间门所处的两条直线上,在(0 m,0 m)~(20 m,0 m)和(0 m,2 m)~(20 m,2 m)坐标范围内,每间隔1.5 m设定一个待测位置,且待定位位置总数为28,完成对8个Wi-Fi无线接入点RSSI值的采集后,取其平均值保存至指纹数据库,设K-means算法的聚类数目为3,最终获得的数据如表1所示.
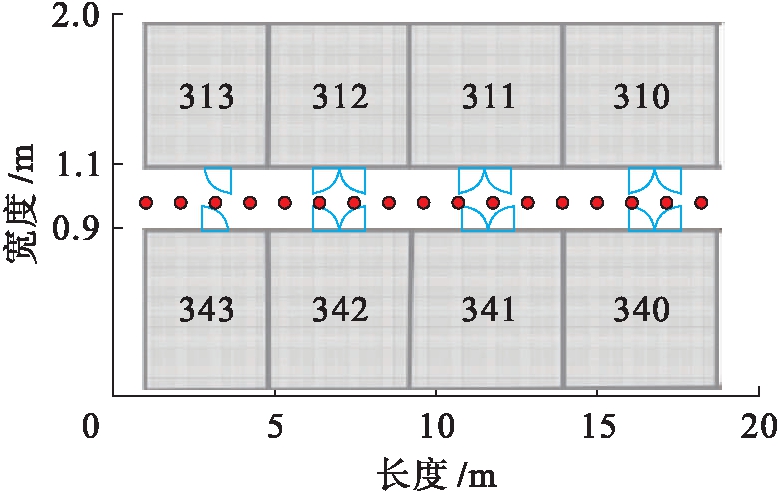
图2 待定位位置布置
Fig.2 Layout and positions to be located
表1 指纹数据库中的采样点位置数据
Tab.1 Sample point location data in fingerprint database

编号采集点位置坐标m接入点RSSI值/dBm①②③④⑤⑥⑦⑧1(0,0)-80-94-89-74-74-78-87-922(0,2)-80-73-67-68-74-74-85-723(1.5,0)-79-80-69-75-59-77-85-604(1.5,2)-80-79-71-73-68-71-83-755(3,0)-94-78-65-73-66-70-86-706(3,2)-78-74-64-63-57-69-85-877(4.5,0)-84-76-75-78-59-79-81-758(4.5,2)-75-75-71-70-63-72-89-799(6,0)-80-75-76-75-60-72-71-8510(6,2)-69-71-80-75-64-73-74-7211(7.5,0)-78-69-74-65-58-80-74-7312(7.5,2)-75-59-64-74-70-65-72-7313(9,0)-74-68-72-85-67-70-74-7814(9,2)-73-80-71-75-64-70-80-7515(10.5,0)-74-78-75-68-74-76-77-7316(10.5,2)-65-64-80-75-68-70-73-7117(12,0)-65-74-85-74-69-75-69-7818(12,2)-75-69-78-74-80-68-85-8019(13.5,0)-67-80-75-89-70-75-74-7320(13.5,2)-74-75-79-85-70-69-74-7521(15,0)-80-75-74-93-68-64-75-7322(15,2)-75-77-74-66-89-80-75-7123(16.5,0)-67-85-74-71-78-67-84-8024(16.5,2)-70-81-68-75-74-85-87-7425(18,0)-64-70-78-75-83-80-70-6826(18,2)-65-69-75-84-79-80-69-8427(19.5,0)-76-69-75-80-70-65-78-6528(19.5,2)-65-69-75-74-76-69-70-76
为了检验从各位置采集到的Wi-Fi无线接入点数目对算法定位误差的扰动程度,从Wi-Fi无线接入点中择取4~8个点与最近邻NN算法进行对比分析,两种算法的定位误差分布如图3所示.
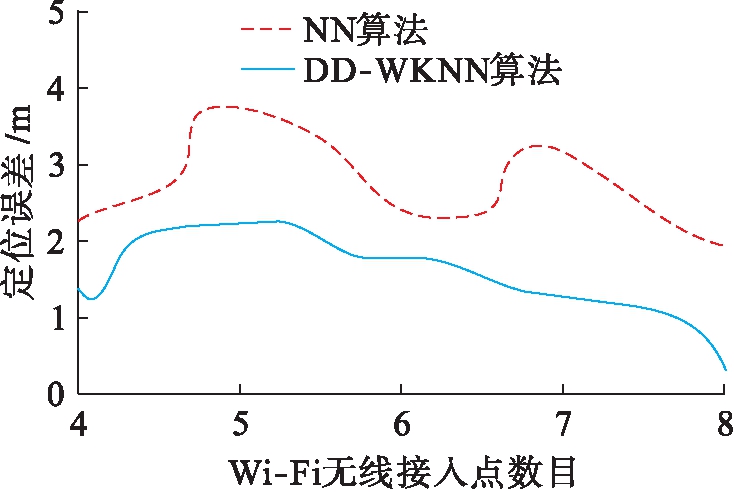
图3 无线接入点数目的扰动箱线图
Fig.3 Perturbation boxplots of number of wireless access points
由图3可见,当参考Wi-Fi无线接入点数目从4扩增至8时,最近邻NN算法[11]定位误差中值约从3.4 m缩减至3 m以下,而DD-WKNN算法则约从2.5 m缩减至0.5 m,可见,参考Wi-Fi无线接入点数目对位置指纹定位具有一定扰动,同时表现出正相关关系,即随着Wi-Fi无线接入点数目的不断扩大,最近邻NN算法和DD-WKNN算法的定位精度都有所改善.另外,在择取一致的Wi-Fi无线接入点数目情况下,DD-WKNN算法定位精度高于NN算法,同时其误差波动情况相对更小.
将本文算法、最近邻NN算法和基于欧氏距离的传统WKNN算法进行定位精度对比分析.分别在实验区域的(0 m,0.5 m)~(20 m,0.5 m)和(0 m,1.5 m)~(20 m,1.5 m)坐标范围内每距离1 m完成对待定位位置的RSSI值采集,且待定位位置总数为42.各采样点每间隔1 min完成对各无线接入点RSSI值的10次采样,同时择取其平均值作为实际测量值,分别运用三种算法完成对待定位位置坐标的估算,各算法的误差累积概率分布如图4所示.
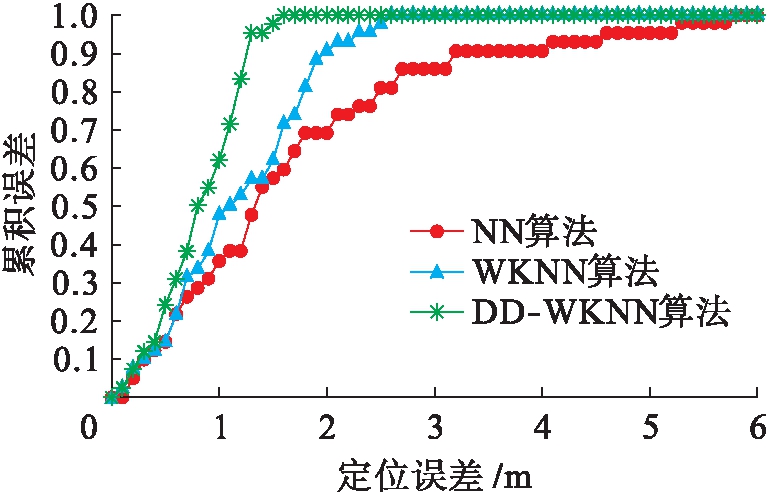
图4 三种算法的实测性能对比
Fig.4 Comparison of actual performance of three algorithms
由图4可知,最近邻NN算法定位误差具有较高的数值,误差累积函数收敛速度相对最为缓慢,同时还具有相对较高的最大误差值.基于欧氏距离的传统WKNN算法的定位精度相比NN算法具有较大的优势,其最大误差值约为2.5 m.DD-WKNN算法的定位精度表现更加良好,其误差累积函数具有很快的收敛速度,同时其最大定位误差值约为1.6 m.综上所述,DD-WKNN算法在很大程度上提高了定位精度,同时具有相对更小的误差波动区间.
4 结 论
DD-WKNN算法将k个和待定位位置实际测量RSSI值欧氏距离相对最为逼近的指纹数据作为位置估计参照点,同时以其离散度作为权重系数的基础,对k个位置指纹数据进行加权求和运算以完成位置估计.依照位置指纹离散度权重信息将离散度相对较小的位置指纹数据赋予相对较高的权重,这能够在很大程度上防止Wi-Fi无线接入点由于室内布局导致RSSI值出现较大改变而引发的定位误差问题.实验分析结果表明:DD-WKNN算法的定位精度高于以欧氏距离作为权重系数的传统WKNN算法和最近邻NN算法,且DD-WKNN算法具有更小的误差波动.
[1] 李东静,李博涵,张潮,等.不确定移动对象的概率反向最远邻查询算法 [J].小型微型计算机系统,2017,38(2):282-286.
(LI Dong-jing,LI Bo-han,ZHANG Chao,et al.Proba-bilistic reverse furthest neighbor queries on uncertain moving object [J].Journal of Chinese Computer Systems,2017,38(2):282-286.)
[2] 林国勇.关于无线网络移动通信信息定位优化研究 [J].计算机仿真,2017,34(2):410-413.
(LIN Guo-yong.Research on location optimization of mobile communication in wireless network [J].Computer Simulation,2017,34(2):410-413.)
[3] 何国玺,林默涵,李岩松,等.基于无线通信基站的室内三维定位问题 [J].数学的实践与认识,2017,47(14):162-172.
(HE Guo-xi,LIN Mo-han,LI Yan-song,et al.Indoor three-dimensional location problem based on wireless communication base station [J].Mathematics in Practice and Theory,2017,47(14):162-172.)
[4] 王开锋,张琦,李辉,等.适用于高速铁路地震预警系统的列车无线指纹定位方法 [J].中国铁道科学,2018,39(4):131-138.
(WANG Kai-feng,ZHANG Qi,LI Hui,et al.Wireless fingerprint positioning method for train in earthquake early warning system of high speed railway [J].China Railway Science,2018,39(4):131-138.)
[5] 彭凤英,焦键.基于移动锚节点的无线传感网络节点定位算法 [J].现代电子技术,2019,42(3):26-30.
(PENG Feng-ying,JIAO Jian.Gauss-Markov-based mobile anchor-localization algorithm in WSNs [J].Modern Electronics Technique,2019,42(3):26-30.)
[6] 李方敏,张韬,刘凯,等.基于距离测量和位置指纹的室内定位方法研究 [J].计算机学报,2019,42(2):111-122.
(LI Fang-min,ZHANG Tao,LIU Kai,et al.An indoor positioning method based on range measuring and location fingerprinting [J].Chinese Journal of Computers,2019,42(2):111-122.)
[7] 王培良,张婷,肖英杰.改进指纹库精度下的室内定位算法研究 [J].电子技术应用,2018,44(10):103-107.
(WANG Pei-liang,ZHANG Ting,XIAO Ying-jie.Research on indoor positioning algorithm based on improved fingerprint library accuracy [J].Application of Electronic Technique,2018,44(10):103-107.)
[8] 金纯,邱灿,王腾,等.基于半监督仿射传播聚类和KLDA的室内定位算法 [J].计算机应用研究,2018,35(9):105-108.
(JIN Chun,QIU Can,WANG Teng,et al.Indoor localization algorithm based on semi-supervised affinity propagation clustering and KLDA [J].Application Research of Computers,2018,35(9):105-108.)
[9] 王玙璠,艾浩军,涂卫平.Wi-Fi指纹聚类在室内感兴趣区域定位中的应用 [J].计算机应用,2016,36(2):488-491.
(WANG Yu-fan,AI Hao-jun,Tu Wei-ping.Application of Wi-Fi fingerprint clustering in indoor interest region localization [J].Computer Applications,2016,36(2):488-491.)
[10] 毕京学,甄杰,汪云甲,等.高斯函数定权的改进KNN室内定位方法 [J].测绘通报,2017(6):13-16.
(BI Jing-xue,ZHEN Jie,WANG Yun-jia,et al.The method of enhanced Gaussian function weighted KNN indoor positioning [J].Bulletin of Surveying and Mapping,2017(6):13-16.)
[11] 董艳侠,张红英,陈姣.基于Wi-Fi室内定位的位置指纹算法 [J].工业控制计算机,2015,28(1):72-74.
(DONG Yan-xia,ZHANG Hong-ying,CHEN Jiao.Location fingerprinting algorithm based on Wi-Fi indoor positioning [J].Industrial Control Computer,2015,28(1):72-74.)