对于桥梁结构，在不同强度地震作用下，如何能够明确地给出桥墩的抗震性能水平，是一项比较有意义的研究方向.而近年来发展起来的Pushover分析方法[1]在确定结构的地震响应方面有较好的效果，该方法最早在1988年由Fajfar与Fischinger在第九届世界地震工程大会中提出，2017年，我国学者林君[2]在国外研究基础上提出了一个计算简单且概念明了的改进方法；2006年，谢礼立等[3]使用Pushover方法对不同模态下的结构进行了分析；2012年，唐玉等[4]对Pushover分析水平力在扭转不规则构件时的分布模式进行了系统分析.该方法具备了一些其他地震分析方法所不具有的优点，比如实用性强、简单易操作等，因而逐渐成为结构基于性能抗震设计方法的主体内容.本文参照沈阳市某大桥桥墩采用有限元软件Midas Civil对其进行建模，采用Pushover分析方法[5]对双柱框架桥墩进行抗震分析，并对其抗震性能进行综合评估.
1 Pushover分析介绍
1.1 Pushover分析概述
Pushover分析最早是将结构的多自由度体系用单自由度体系来表达，是将结构的静力弹塑性分析[6]转换成高阶振型作用在结构上，其主要内容由两方面组成：1)通过对模型的计算求得能力曲线；2)求出结构控制点的目标位移，根据结果对结构的抗震性能进行评价.
通过对建立的有限元模型进行第一阶段分析后可以得出构件的荷载
位移曲线，但不能把结构上选取的控制点作为代表构件抗震性能的目标位移，这需要与规范给定的限值进行比较，从而确定构件的抗震性能是否达到了规范要求.
1.2 Pushover分析过程
根据材料的本构关系，一般情况下构件在荷载作用的初始阶段处于弹性状态，而当作用在构件上的水平荷载超出一定值时，结构就会出现开裂甚至是屈服，而在这时结构的阻尼系数和刚度都会出现变化，结构的荷载跟位移将显示出非线性[7].图1为内力和位移的关系.构件最初处于弹性范围内，而A点即为弹性和塑性的临界点，称A点为弹性极限，在A点之后构件的位移将随着荷载的增加而呈现大幅增加的现象，而构件的状态到达B点后结构只需较小的力，构件将会产生巨大的位移，而到达C点后即使不给结构外力，构件的位移也会显著增加，这时就称C点为极限承载能力点.
C点是对结构求解荷载增量后计算出的极限点，而对于C点以后的曲线只能采用位移进行控制，即位移控制法[8].因为在结构出现裂缝和屈服时构件的刚度会发生变化，而在进行Pushover分析时会产生不平衡力，这种不平衡力为残余力，为了抵消这种不平衡现象的出现，Midas Civil采用了迭代计算[9]，双柱和多柱墩塑形铰区域截面顺桥向超强弯矩可按单柱墩塑性铰区域超强弯矩[10]计算得出.
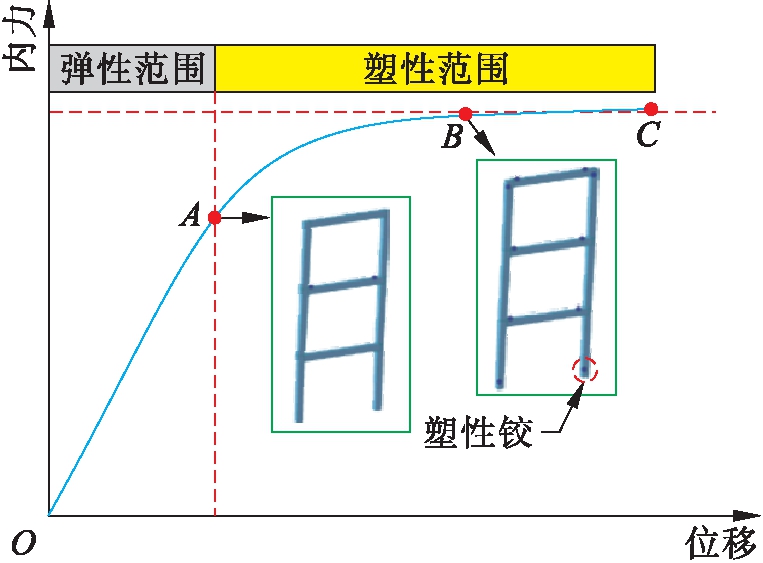
图1 内力和位移的关系
Fig.1 Relationship between internal force and displacement
2 双柱框架桥墩设计及荷载计算
2.1 桥墩尺寸设计及配筋
本文研究了现浇桥墩构件在地震力作用下的抗震性能，构件的基本尺寸是由某实际桥梁进行1∶4比例缩尺而来.构件包括一个盖梁、一个承台和两个等高的普通钢筋混凝土桥墩，墩柱为矩形实心截面.其中盖梁、桥墩、承台的混凝土分别采用C50、C40和C30，桥墩主筋采用8根HRB400级普通钢筋，箍筋间距为120 mm，在节点区进行加密，箍筋直径为80 mm，盖梁及承台配筋只要满足构件不发生破坏即可，具体的尺寸设计与配筋如图2～3所示(单位：mm).
采用Midas Civil软件对构件建立有限元模型，模型中桥墩混凝土强度按照C40进行建模，桥墩与盖梁及桥墩与承台的边界条件采用刚性连接，承台采用一般支承，限制各个方向的自由度，桥墩模型如图4所示.
2.2 静力荷载计算
根据《城市桥梁抗震设计规范》(GJJ 166-2011)[11]中7.3.7条对双柱墩横桥向的要求，由于很难根据弹塑性铰转动能力直接给出墩顶容许位移的计算公式，建议采用推倒分析方法计算墩顶容许位移.而墩顶位移的计算需要先求出容许转角，而容许转角需要依据横桥向弯矩的计算，本试验模型横桥向超强弯矩具体计算过程如下：
1) 假设墩柱轴力为横载轴力，通过建立有限元模型，结果得出上部荷载的力为670.1 kN，本文采用了两点加载，即在两个桥墩的墩顶施加335 kN的竖向力.
2) 按截面实配钢筋定义材料的本构模型[12]，材料强度的数值采用强度标准值，通过弯矩曲率曲线计算出各墩柱塑性铰区域截面超强弯矩.本文对构件的材料本构模型进行了定义，如图5所示，黄色部分为非约束混凝土，红色部分为约束混凝土.
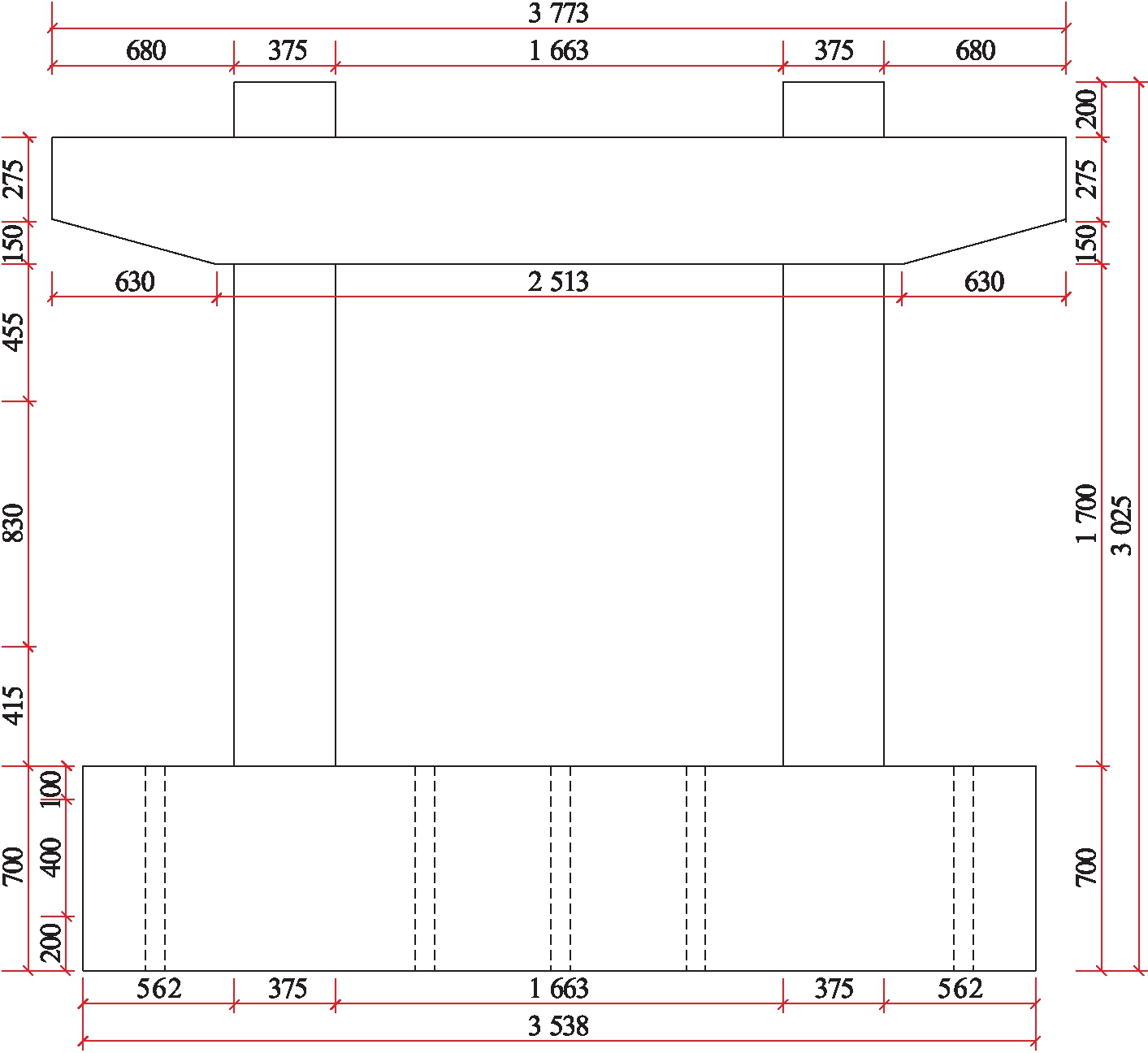
图2 桥墩设计尺寸
Fig.2 Design drawings of piers
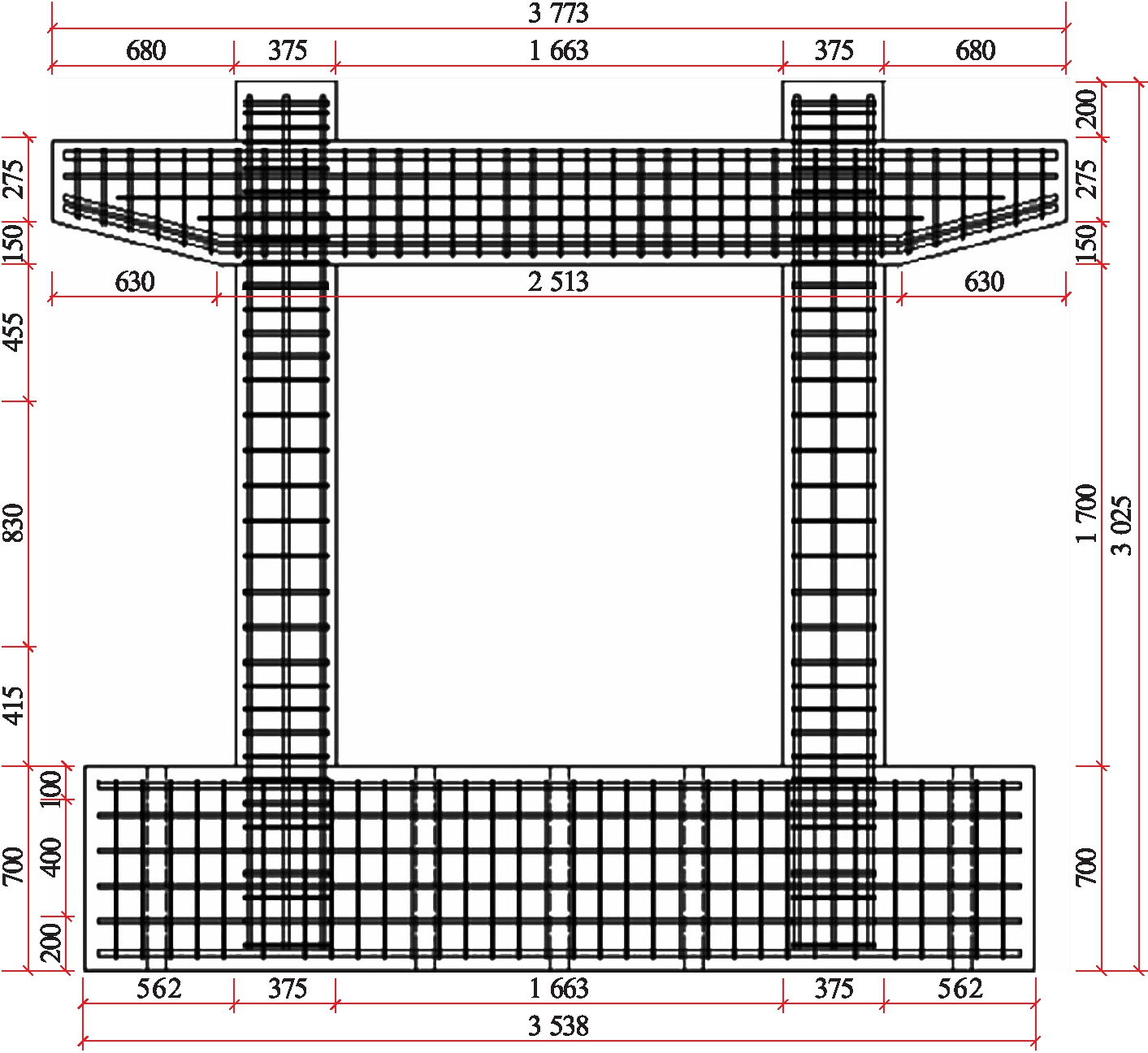
图3 桥墩配筋图
Fig.3 Reinforcement bars of piers
钢筋的滞后模型[13]采用了双折线模型，骨架曲线中钢筋抗拉强度fy=400 N/mm2，弹性模量E1=200 000 N/mm2，E1/E2=0.001，其中，E2为约束混凝土弹性模量.混凝土分为约束混凝土和无约束混凝土，其滞后模型都采用了Mander模型，Mander模型给出的混凝土极限压应变的保守估计[14]为
所以国内混凝土构件需要在原来强度的基础上乘以0.85的折减系数.约束混凝土的极限压应变可由横向约束钢筋达到最大应力时所释放的总应变能与混凝土由于横向钢筋的约束作用而吸收的能量相等的条件进行推导.混凝土的类型需要选用保护层混凝土，对于约束混凝土，截面和约束钢筋类型需要选择矩形.根据上述弹塑性材料的本构模型，可以计算出桥墩截面的弯矩曲率曲线，如图6所示.
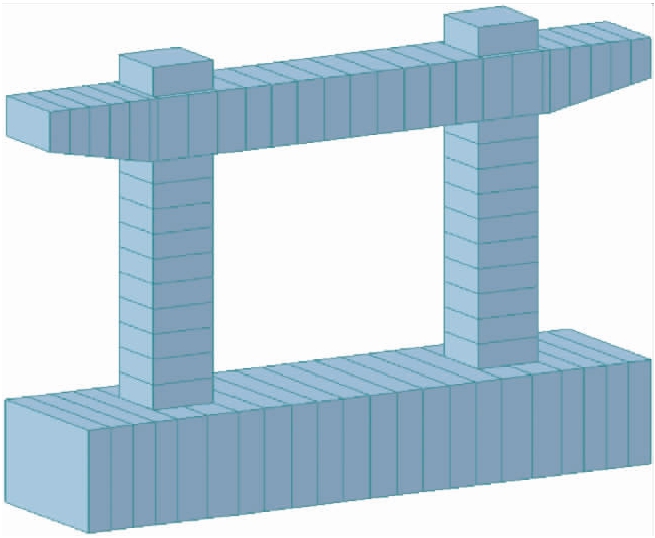
图4 现浇桥墩有限元模型
Fig.4 Finite element model for cast-in-site pier
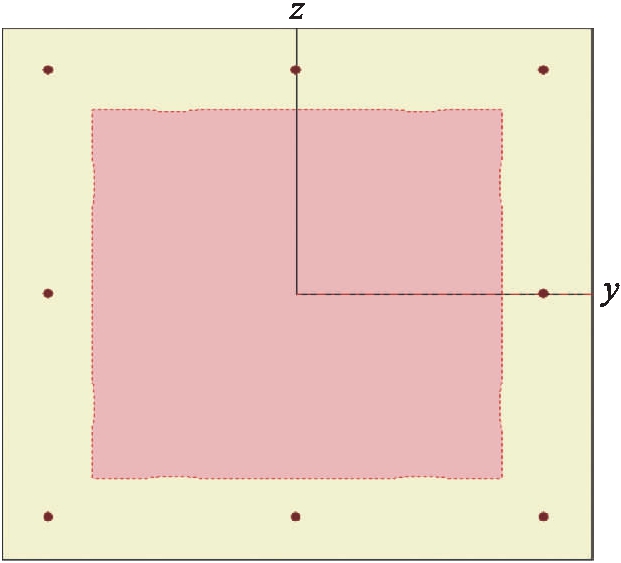
图5 塑性铰截面示意图
Fig.5 Schematic section of plastic hinge
图6中，C点以前的结构为弹性阶段，C点为混凝土开始开裂的点；C点到Y0点代表结构开始进行弹塑性阶段，Y0点代表构件中钢筋开始发生屈服；Y0点到Y点代表构件开始屈服，Y点则代表构件进入完全屈服；Y点到U点代表构件进入塑性阶段，U点代表结构达到极限破坏.求得各阶段弯矩曲率如表1所示.
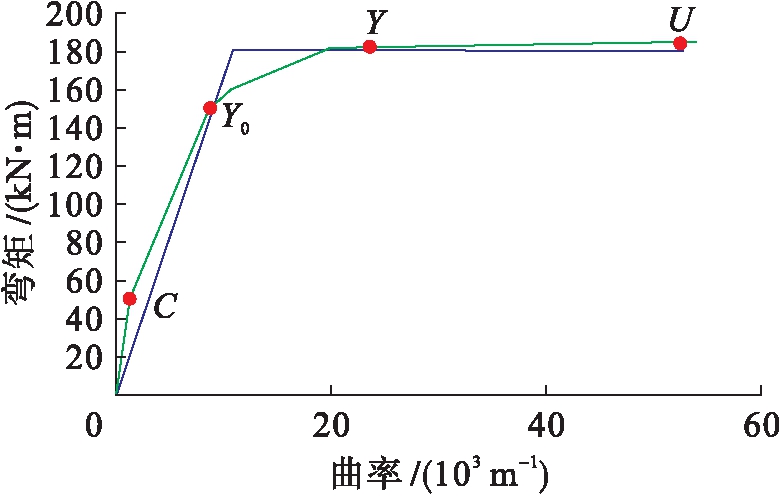
图6 弯矩曲率曲线
Fig.6 Moment-curvature curves
表1 弯矩曲率数据
Tab.1 Moment-curvature data
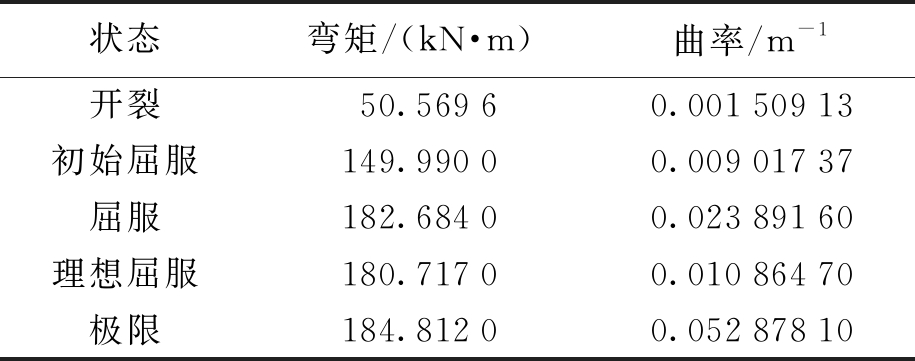
状态弯矩/(kN·m)曲率/m-1开裂50.56960.00150913初始屈服149.99000.00901737屈服182.68400.02389160理想屈服180.71700.01086470极限184.81200.05287810
3) 根据弯矩曲率曲线求得理想化情况下的弯矩，《公路桥梁抗震设计细则》(JTG/T B02-01-2008)[15]中6.8.2条延性桥墩沿顺桥向和横桥向的剪力计算值为Vc0=
计算出左墩相应于其超强弯矩的剪力值为197.9 kN，右墩相应于其超强弯矩的剪力值为300.5 kN，求各墩柱剪力值之和为498.4 kN.
4) 将各剪力值之和按正负号分别施加于盖梁质心处，计算出左墩柱所产生的轴力为52.5 kN，右墩柱所产生的轴力为640.1 kN.
5) 将合剪力产生的轴力与横载轴力组合后，经Midas Civil计算后可以得到最不利荷载组合下的轴力，重复步骤2)和4)进行迭代计算，经过计算得出相邻两次的剪力和相差3.1%，满足规范要求的相邻两次计算各墩柱剪力和相差在10%以内.迭代具体数值如表2所示.
表2 桥墩迭代过程
Tab.2 Iteration process of piers
桥墩墩底轴力kN等效弯矩(kN·m)墩高m单墩等效剪力kN作用盖梁质心力kN较前次迭代差异%左墩52.5140.19161.7197.9176498.3443-3.1右墩640.1212.80231.7300.4268498.3443-3.1
通过Midas Civil建立有限元模型，根据最不利荷载组合(水平计算推力的重力二重效应和上部荷载产生的轴力还有桥墩的自重)对有限元模型进行分析，可以得出左墩的墩底轴力为52.5 kN，右墩的墩底轴力为640.1 kN，计算结果如图7所示.
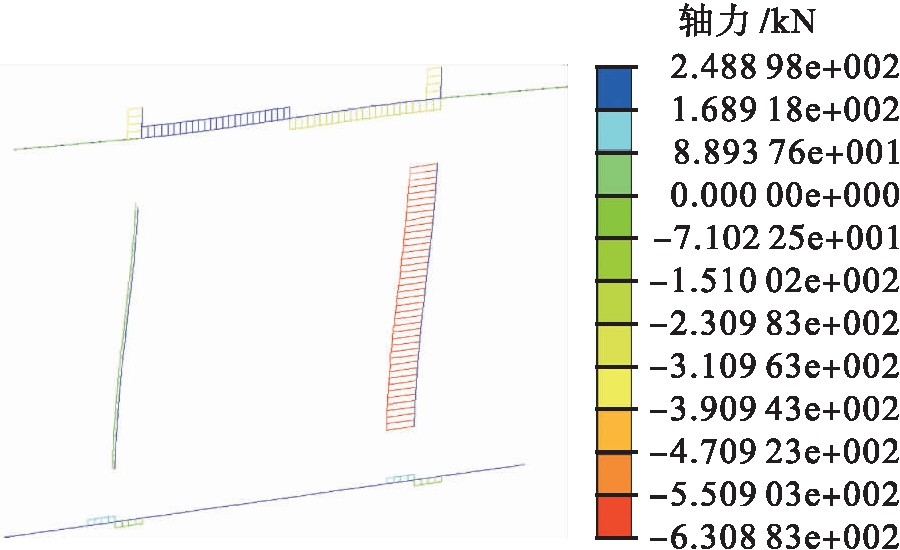
图7 墩底轴力
Fig.7 Shaft force at pier bottom
3 Pushover分析
本文在整体控制中把上部荷载和结构自重加载到静力荷载计算，相当于在开始就加载了荷载的初始力.之后进行荷载工况的控制，计算步数为400步，采用位移控制，主控节点设置在盖梁的中心点处，且在计算中考虑P-Delta效应[16-17]，即当单元同时受重力和横向荷载作用下，单元上将产生附加内力和附加变形，即重力加剧弯曲变形，产生所谓的重力二阶效应.
铰特性定义如下，单元类型选取柱单元，骨架类型选取三折线类型[18].根据弯矩曲率曲线计算可以先计算出初始刚度、第二刚度和第三刚度，根据计算出的刚度值可以得出左墩的刚度折减系数为α1=0.059 962，α2=0.001 806，同理可以求出右墩的刚度折减系数为α1=0.152 453，α2=0.064 049，结合弯矩曲率曲线就可以完成对三折线的自定义.
将定义好的铰特性分配给墩单元，根据弯矩曲率曲线可以求得规范规定的极限容许曲率为0.025 26.表3为铰单元达到极限曲率步骤.
表3 铰单元达到极限曲率步骤
Tab.3 Steps of hinge units reaching curvature limit
铰单元号29单元38单元39单元48单元加载步316216953
水平力作用在盖梁的中心处，试验控制水平方向的位移，通过不同加载步得出不同的试验现象，而Midas Civil通过计算钢筋混凝土的本构模型，可以得出桥墩在混凝土开裂、初始屈服、屈服、极限状态的临界数据，这些数据结合Pushover的计算结果可以得出表3中不同铰单元的极限容许加载步，通过比较可以得出桥墩在第31步被推覆，通过查看Midas Civil位移等值线可以得出桥墩不同单元的水平方向位移，结果如图8所示.
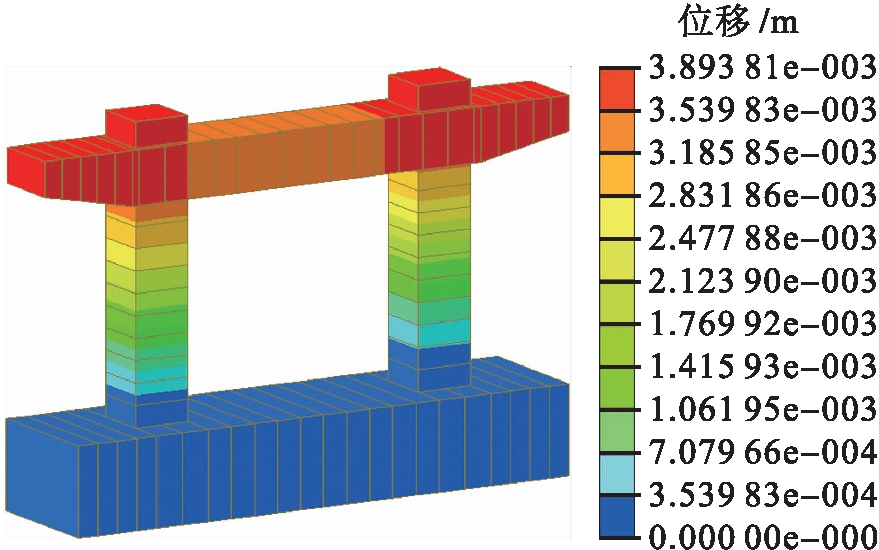
图8 桥墩推覆时极限容许位移
Fig.8 Allowable displacement limit during Pushover analysis of piers
从图8的位移等值线可以得出，现浇桥墩在达到规范规定的极限转角时位移为7.8 cm，该位移表示盖梁桥梁下部结构中各个节点的水平方向最大位移，该位移是根据表3中不同铰状态的加载步和再推覆的步数计算出最小的极限破坏位移.作用在盖梁上水平力的大小，通过查看Midas Civil的计算结果，可以得出桥墩达到极限容许转角时作用在盖梁中心处的水平力为351.7 kN，结果如图9所示.
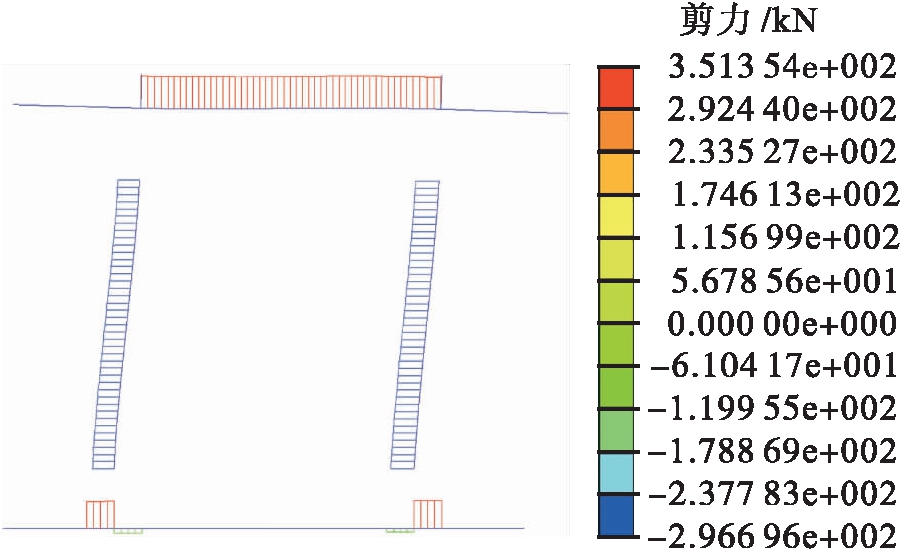
图9 桥墩横桥向水平力
Fig.9 Horizontal force in transverse direction of piers
根据计算模型同样可以求得构件在达到极限容许位移时，构件所受到的弯矩，该弯矩大小会受到作用在盖梁上水平力的影响，结果与结构本构关系模型求出的数值有一定差别，但是可以用来验证通过弯矩曲率曲线求得的数值.由图9可以看出，右桥墩下部铰理论上会先达到极限破坏状态，使桥墩失去承载能力，具体计算结果如图10所示.
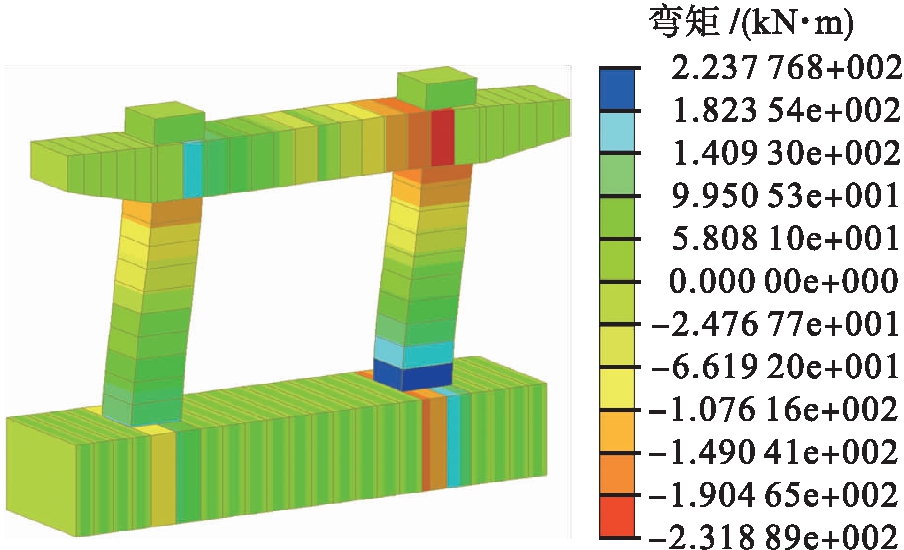
图10 塑性铰破坏状态
Fig.10 Damage state of plastic hinge
根据建立的Midas Civil模型可以查看塑性铰[19]的状态，塑性铰的确定无论在实际工程中还是在科学研究中都具有重要的指导意义，可以根据结构的塑性铰变形来确定试验方案中应变片的位置，设计时，在保证强剪弱弯的前提下可以加强铰的长度，而实际中铰长度的计算采用了规范给出的公式，该公式计算比较偏于保守.本文根据有限元模型进行精确计算，结果为塑性铰长度约为30 cm，与通过规范计算的结果接近.Midas Civil计算结果如图11所示.
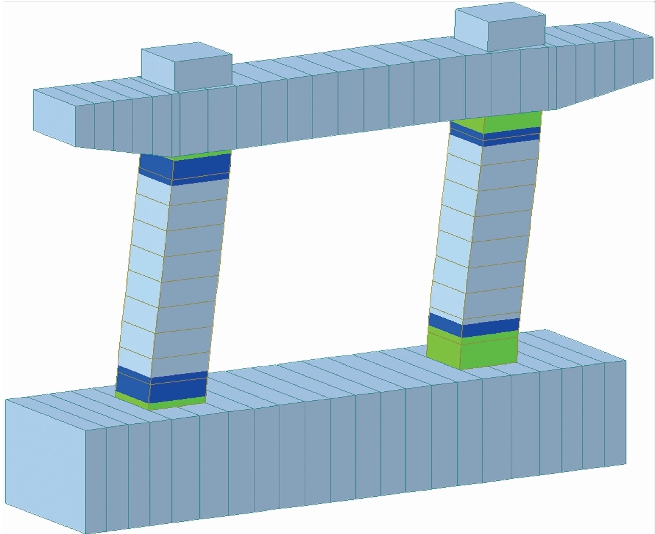
图11 塑性铰长度
Fig.11 Length of plastic hinge
本文对现浇桥墩结构进行了系统的有限元分析，得出现浇桥墩在水平力作用下的位移和该位移所对应的水平力.结果对实际工程具有指导意义，根据建立的有限元模型可以得出Pushover曲线，从Pushover曲线中可以提取出位移谱、加速度谱、基底剪力等数据，如表4所示.
4 结 论
本文通过使用Midas Civil有限元分析软件对装配式桥墩抗震性能进行验证可知，桥墩推覆时出现的最大水平力为351.7 kN.从该结构的整体位移图中可以看出，盖梁处产生的位移最大，桥墩的最大水平位移为78 mm，承台与桥墩之间刚性连接，不受荷载作用，表面基本无变形.根据有限元模型计算出桥墩塑性铰长度为30 cm，在实际工程中塑性铰长度的计算多采用规范给出的公式，该公式的计算比较偏于保守，基于Pushover分析方法计算双柱墩塑性铰位置及长度较规范给出的计算方法精度更高，对双柱框架桥墩抗震性能的研究有重要参考意义.
表4 Pushover曲线特征数据
Fig.4 Characteristic data of Pushover curves
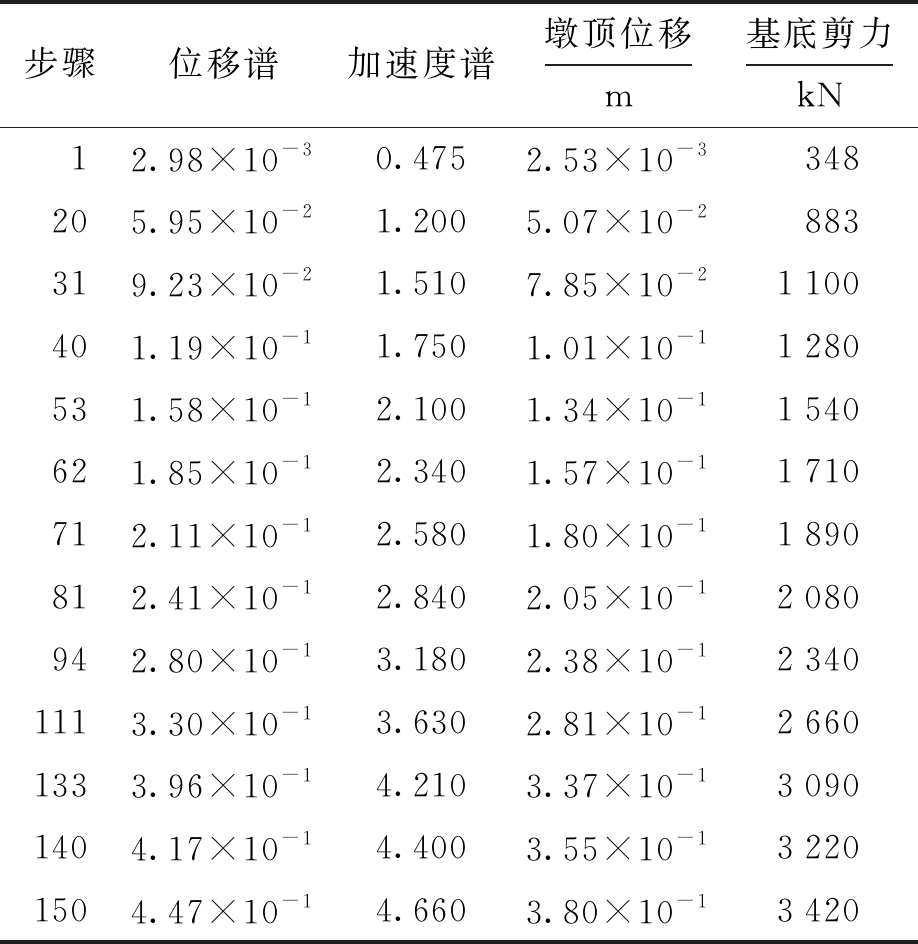
步骤位移谱加速度谱墩顶位移m基底剪力kN 12.98×10-30.4752.53×10-3348205.95×10-21.2005.07×10-2883319.23×10-21.5107.85×10-21100401.19×10-11.7501.01×10-11280531.58×10-12.1001.34×10-11540621.85×10-12.3401.57×10-11710712.11×10-12.5801.80×10-11890812.41×10-12.8402.05×10-12080942.80×10-13.1802.38×10-123401113.30×10-13.6302.81×10-126601333.96×10-14.2103.37×10-130901404.17×10-14.4003.55×10-132201504.47×10-14.6603.80×10-13420
[1] 彭俊.三维Pushover方法在空间不规则结构抗震分析中的应用研究 [D].南京：东南大学，2011.
(PENG Jun.Studies on 3-D Pushover analysis procedure applied to seismic analysis of spatial-irregular structures [D].Nanjing：Southeastern University，2011.)
[2] 林君.既有钢筋混凝土框架结构的Pushover分析——基于不同施工质量状况 [J].福建建筑，2017(1)：50-54.
(LIN Jun.Pushover analysis of existing reinforced concrete frame structure-based on different construction qualities [J].Fujian Architecture & Construction，2017(1)：50-54.)
[3] 毛建猛，谢礼立，翟长海.模态pushover分析方法的研究和改进 [J].地震工程与工程振动，2006，26(6)：50-55.
(MAO Jian-meng，XIE Li-li，ZHAI Chang-hai.Studies on and improvements in modal pushover analysis [J].Earthquake Engineering and Engineering Vibration，2006，26(6)：50-55.)
[4] 唐玉，郑七振，楼梦麟.扭转不规则结构水平侧向力分布模式与pushover分析 [J].地震工程与工程振动，2012，32(3)：67-72.
(TANG Yu，ZHENG Qi-zhen，LOU Meng-lin.A modified lateral-load pattern for pushover analysis of torsion-irregular structures [J].Earthquake Engineering and Engineering Vibration，2012，32(3)：67-72.)
[5] 高依强.基于Pushover分析的桥梁抗震研究 [D].西安：西安建筑科技大学，2013.
(GAO Yi-qiang.The Pushover analysis of double-column piers [D].Xi’an：Xi’an University of Architec-ture and Technology，2013.)
[6] 陈相.公路隧道结构性能化抗震设计方法研究 [D].重庆：重庆交通大学，2017.
(CHEN Xiang.Study on performance-based seismic design method for highway tunnel structure [D].Chongqing：Chongqing Jiaotong University，2017.)
[7] 王景荣.Pushover法评估山地建筑掉层结构的抗震性能 [D].重庆：重庆大学，2015.
(WANG Jing-rong.Evalution of seismic performance of step-terrace structure by Pushover method [D].Chongqing：Chongqing University，2015.)
[8] 李云飞，陈朝晖，杨永斌，等.基于刚体准则和广义位移控制法的拱结构屈曲与后屈曲分析 [J].土木工程学报，2017(12)：37-45.
(LI Yun-fei，CHEN Zhao-hui，YANG Yong-bin，et al.Buckling & post-buckling analysis of arches based on rigid body rule and GDC method [J].China Civil Engineering Journal，2017(12)：37-45.)
[9] Soleimani S，Aziminejad A，Moghadam A S.Extending the concept of energy-based pushover analysis to assess seismic demands of asymmetric-plan buildings [J].Soil Dynamics and Earthquake Engineering，2017，93：29-41.
[10] Louzai A，Abed A.Evaluation of the seismic behavior factor of reinforced concrete frame structures based on comparative analysis between non-linear static pushover and incremental dynamic analyses [J].Bulletin of Earthquake Engineering，2015，13(6)：1773-1793.
[11] 中华人民共和国住房和城乡建设部.CJJ 166-2011城市桥梁抗震设计规范 [S].北京：中国建筑工业出版社，2011.
(Ministry of Housing and Urban-Rural Development of the People’s Republic of China.CJJ 166-2011 Code for seismic design of urban bridges [S].Beijing：China Construction Industry Press，2011.)
[12] 徐仲卿，袁泉，杨振坤，等.早龄期混凝土力学性能试验及其单轴本构模型 [J].沈阳工业大学学报，2015，37(1)：92-96.
(XU Zhong-qing，YUAN Quan，YANG Zhen-kun，et al.Mechanical property experiment and uniaxial constitutive model for concrete at early age [J].Journal of Shenyang University of Technology，2015，37(1)：92-96.)
[13] 周长东，李慧，曾绪朗，等.预应力碳纤维条带加固混凝土圆柱滞回性能有限元分析 [J].应用基础与工程科学学报，2015，23(3)：586-595.
(ZHOU Chang-dong，LI Hui，ZENG Xu-lang，et al.Finite element analysis of hysteretic behavior for circular reinforced concrete columns strengthened with prestressed CFRP strips [J].Journal of Basic Science and Engineering，2015，23(3)：586-595.)
[14] 赵金钢，杜斌，占玉林.OpenSees中Mander模型用于模拟钢筋混凝土柱滞回性能的适用性 [J].兰州理工大学学报，2017，43(5)：127-133.
(ZHAO Jin-gang，DU Bin，ZHAN Yu-lin.Applicability of Mander model in OpenSees for simulation of hysteretic behavior of reinforced concrete column [J].Journal of Lanzhou University of Technology，2017，43(5)：127-133.)
[15] 重庆交通科研设计院.JTG/T B02-01-2008公路桥梁抗震设计细则 [S].北京：人民交通出版社，2008.
(Chongqing Traffic Research and Design Institute.JTG/T B02-01-2008 Guidelines for seismic design of highway bridge [S].Beijing：People’s Transportation Press，2008.)
[16] Tsantaki S，Adam C，Ibarra L F.Intensity measures that reduce collapse capacity dispersion of P-Delta vulnerable simple systems [J].Bulletin of Earthquake Engineering，2016，15(3)：1-25.
[17] López S E，Ayala A G，Adam C.A novel displacement based seismic design method for framed structures considering P-Delta induced dynamic instability [J].Bulletin of Earthquake Engineering，2015，13(4)：1227-1247.
[18] 梁仁杰，吴京，王春林.P-Δ效应下滞回特征对结构抗倒塌能力的影响 [J].东南大学学报(自然科学版)，2013，43(1)：188-194.
(LIANG Ren-jie，WU Jing，WANG Chun-lin.Influence of hysteretic characteristic on collapse resistance capacity ofstructure with P-Δ effect [J].Journal of Southeast University (Natural Science)，2013，43(1)：188-194.)
[19] Yuan F，Wu Y F.Effect of load cycling on plastic hinge length in RC columns [J].Engineering Structures，2017，147：90-102.