冷链物流是在冷冻工艺学的基础上,采用制冷技术手段实现低温配送运输的过程,通过恒定低温配送,保证产品的质量.对应各类产品所需的不同储藏温度,可采用多温共配方式实现配送过程中的复杂温度需求[1].冷链物流配送车辆的路径选择与优化问题是冷链物流行业的重要研究内容之一,选取恰当的冷链物流配送车辆行驶路径,能够实现冷链物流配送过程中对客户需求的快速响应,提高配送服务的时效与质量,减少成本支出,提升客户满意度[2].多客户配送路径的确定是一种比较复杂的运算过程,路径优化的目标是在短时间内规划出运输成本最低的配送方案,根据业务的实际配送情况形成对应的约束条件,最终产生最优的配送计划[3].现有方法取得一些成果,王力锋等[4]提出物流配送车辆最优网络路径选取仿真,建立以物流配送成本最低为最优目标的车辆调度数学模型,将改进后的蚁群算法应用到模型中,获取物流配送车辆的最优网络路径.该方法的单车装载率较高,但日均转载率较低,优化效果不理想.陈立伟等[5]提出基于Memetic算法的两级车辆路径优化方法.利用最优分割法获得一级配送路径,确定中转站配送数量,求解二级配送路径,依次递推实现路径优化.该方法的日均转载率较高,但单车装载率较低.
本文在上述方法的基础上,融合量子计算与蚁群算法,提出多温共配冷链物流车辆配送路径优化方法.
1 配送路径优化的干扰因素分析
在多温共配冷链物流车辆配送过程中,路径的合理选择能够有效降低多温冷链物流的配送成本,节约冷链物流的配送时间,减少多温冷链物流的配送风险,将产品安全、快速地送达配送终点,送至客户手中.通过相关资料的学习研究,得到多温共配冷链物流车辆配送路径优化的主要干扰因素,其包括:多温冷链物流配送时间、成本及风险,属于多目标优化决策问题[6].
1) 多温冷链物流配送时间.多温冷链物流配送时间可划分为中转节点间的冷链物流配送车辆行驶时间、中转节点的换装时间及等待发车时间三部分.冷链物流配送时间是产品运输的关键评测指标,受到产品运输温度控制和保质时间的双重影响,配送时间需根据用户需求控制在一定范围内.
2) 多温冷链物流配送成本.多温冷链物流配送成本是指将产品从发货地点运输至终点,交付到客户手中所花费的全部费用,主要包括节点间的运输费用和中转节点换装费用.多温冷链物流配送成本主要取决于运输路径与方式,以及换装质量与技术等.
3) 多温冷链物流配送风险.多温冷链物流配送风险主要是指产品运输及换装过程中,受到产品本身特性、冷链物流运输路况、交通运输及换装工具等因素的影响,导致产品受到损伤的可能性.可通过完善交通运输及换装工具,提高驾驶人员等相关技术工作人员的技术水平,从而降低部分风险,并在计算过程中添加抵消因子进行调节[7-8].
2 多温冷链物流配送路径优化模型
通过上述分析,假设多温共配冷链物流车辆配送运输网络节点的集合为V,网络节点为i,j=1,2,…,n,节点i、j(i≠j)之间的路段为eij,多温共配冷链物流配送运输网络内各节点间的路段集合为E,冷链物流配送车辆集合为W,则可得到冷链物流车辆配送运输网络为G=(V,E,W).车辆编号a∈W,该车辆在运输网络节点i、j间的货运量为![]() 单位冷链物流配送运输成本为
单位冷链物流配送运输成本为![]() 车辆行驶距离为
车辆行驶距离为![]() 冷链物流配送时间为
冷链物流配送时间为![]() 发生产品损伤及运输事故的概率为
发生产品损伤及运输事故的概率为![]() 取值区间为[0,1].多温共配冷链物流车辆配送运输过程中,在中转节点i处由车辆a转换为b的货运量为
取值区间为[0,1].多温共配冷链物流车辆配送运输过程中,在中转节点i处由车辆a转换为b的货运量为![]() 单位换装花费及事故发生概率分别为
单位换装花费及事故发生概率分别为![]() 和
和![]() 取值范围为[0,1].在冷链物流配送运输网络节点j处由车辆a转换为b的过程消耗的时间为
取值范围为[0,1].在冷链物流配送运输网络节点j处由车辆a转换为b的过程消耗的时间为![]() 冷链物流配送运输车辆换装结束时刻为
冷链物流配送运输车辆换装结束时刻为![]() 车辆b向节点k的最早出发时刻为
车辆b向节点k的最早出发时刻为![]() 配送产品通过车辆b从节点j运输至k的过程中,θ类产品的易损值为fθ∈[0,100].
配送产品通过车辆b从节点j运输至k的过程中,θ类产品的易损值为fθ∈[0,100].![]() 代表风险抵消因子,m=1,2,3分别代表驾驶员技能、运输工具性能及路况对应的运输风险抵消因子;
代表风险抵消因子,m=1,2,3分别代表驾驶员技能、运输工具性能及路况对应的运输风险抵消因子;![]() 代表产品换装过程中的风险抵消因子[9],l=1,2,3分别代表换装技术人员、工具性能及换装管理产生的抵消因子.
代表产品换装过程中的风险抵消因子[9],l=1,2,3分别代表换装技术人员、工具性能及换装管理产生的抵消因子.
多温共配冷链物流车辆配送运输网络节点的内、外邻节点集合分别为φ(i)={vi|eij∈E}、φ(i)={vi|eji∈E},设在冷链物流配送运输路段eij是否采用车辆a进行运输的决策变量为![]() 如果是,则
如果是,则![]() 反之
反之![]() 冷链物流配送过程中,是否在邻节点vi将运输车辆类型由a转换为b的决策变量为
冷链物流配送过程中,是否在邻节点vi将运输车辆类型由a转换为b的决策变量为![]() 如果是,则
如果是,则![]() 反之
反之![]()
综上,以多温共配冷链物流配送总成本、时间及风险为目标,构建多温共配冷链物流配送路径优化模型.多温共配冷链物流配送总成本、时间及风险目标函数分别为D1、D2和D3,且由于共有3辆配送车辆,因此车辆编号a和b的最大值为3,表达式分别为
(1)
(2)
(3)
上述模型需要满足的约束条件为:![]() 且有
且有
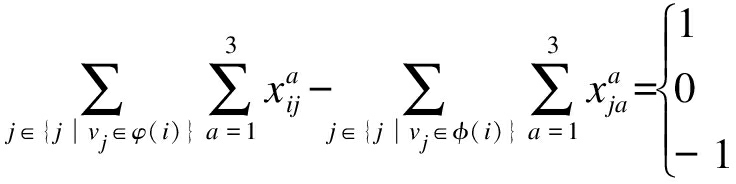
(4)
式中:值为1表明vi为起点;值为0表明vi非起点或终点;值为-1表明vi为终点.
多温共配冷链物流配送路径优化为多目标优化问题,针对该类问题,利用线性加权方法进行转化,将多目标优化问题简化为单目标优化问题来求解,从而提高路径优化的效率[10-11].为便于计算,需要通过下述处理将各类目标的量值进行归一化,之后再进行统一运算[12].假设冷链物流配送路径优化问题的可行性方案数量为M,第η个路径优化方案的第ξ目标方案函数值为Dξη,其中,η=1,2,…,M,ξ=1,2,3.将Dξη处理为量纲为1的目标值dξη,对应的计算公式为
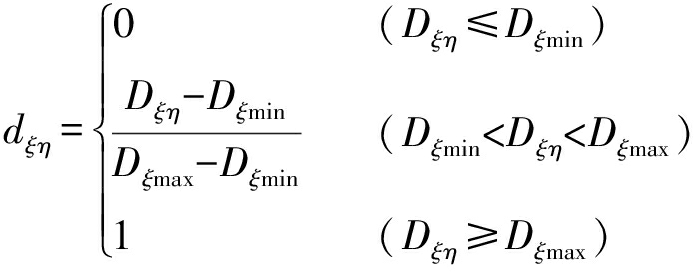
(5)
式中:Dξmax为目标函数最大值;Dξmin为目标函数最小值.由于ξ=1,2,3,则将第ξ目标函数量纲化处理后得到的函数分别记作r1、r2和r3,综合考虑用户需求及决策选择,各目标函数的权重分别为ω1、ω2和ω3,将多温共配冷链物流车辆配送路径优化的多目标问题转换成单目标优化问题,得到综合函数rω,构造综合优化模型为
min rω=ω1r1+ω2r2+ω3r3
(6)
3 基于优化模型的多温共配冷链物流路径优化求解
根据上述构建的路径优化模型,利用量子比特[13]描述配送路径的相关信息,结合蚁群算法对优化模型进行最优路径求解运算,实现路径优化.其中,蚁群算法是一种生物行为进化算法,它通过模拟蚂蚁觅食过程中发现路径的行为而实现[14].
利用量子比特描述多温共配冷链物流车辆配送路径的相关信息,对应的双态系统中,含有n个量子位的个体概率幅为
(7)
式中,单位量子描述因子αi、βi需要满足
![]() =1
=1
(8)
一般情况下,单位量子描述因子αi、βi均取值为1.
对应的量子个体可描述任一量子叠加态,并用于表示各冷链物流配送路径所含信息素.得到序号为k′的蚂蚁在各条冷链物流运输路径上的信息素编码为
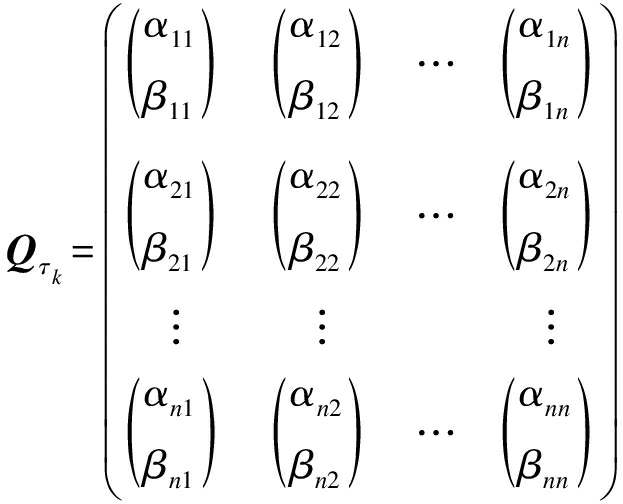
(9)
式中,![]() 为路径节点i与j之间的信息素概率幅,满足约束条件为
为路径节点i与j之间的信息素概率幅,满足约束条件为
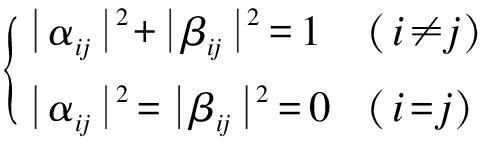
(10)
当有蚂蚁经过某一路径时,对应的信息素会随之增强,否则路径信息素会挥发减少[15].当蚁群内全部蚂蚁的觅食路径构建完成后,对各路径的信息素进行更新.信息素挥发过程对应的计算公式为
τ′ij=(1-ρ)τij
(11)
式中,ρ为各路径上的信息素挥发率.每只蚂蚁经过对应路径时,会在路径上留下信息素,对应的计算公式为
(12)
式中,![]() 为蚂蚁k′释放在通过路径的信息素量.
为蚂蚁k′释放在通过路径的信息素量.
设蚁群内蚂蚁数量为m′,矩阵R代表多温共配冷链物流车辆配送路径方案设计系统求解得到配送起点至所有配送终点路径对应的解,R[i,j]=1(i≠j)代表R内包含从节点i到j的路径.利用矩阵Rk′(k′=1,2,…,m′)记录序号为k′的蚂蚁所得到的路径选择方案,利用Rb代表得到的当前最优解.在此基础上调整量子信息概率幅,采用多温共配冷链物流配送路径优化模型,再次对路径信息素进行更新,若此时得到的最优解满足预设条件,将对应的最优解输出,否则重新迭代上述过程.求导更新后每一次迭代输出的最优解表达式为
(13)
式中:![]() 为第t次迭代过程中i到j之间冷链物流配送路径所包含的信息素概率幅;γ为量子位的转动角度,利用该参数可调节算法求解的收敛速率.
为第t次迭代过程中i到j之间冷链物流配送路径所包含的信息素概率幅;γ为量子位的转动角度,利用该参数可调节算法求解的收敛速率.
至此能够根据路径优化目标构建配送路径优化模型,采用优化模型求解出多温共配冷链物流配送的优化路径.
4 实验结果与分析
为检验所提出的多温共配冷链物流车辆配送路径优化方法的综合有效性,在CPU为双核2.73 GHz,内存为4 GB,操作系统为Windows 7的实验平台上,利用Matlab 2012软件实现仿真实验.设置单位量子描述因子αi=1,βi=1.
实验数据来自于某企业的多温冷链物流配送中心数据库,该企业的多温冷链物流配送中心数量为3个,多温冷链物流配送中心A、B的坐标分别为(15,75)和(45,65),所管理的配送车辆均为3辆,多温冷链物流配送中心C的坐标为(18,30),所管理的冷链物流配送车辆数量为2辆;配送目标的数量为16个,各目标点与配送中心的相对位置如图1所示,其中A、B、C三个配送中心之间的距离在图1中用虚线表示.
采用所提路径优化方法(M1)与文献[4]提出的物流配送车辆最优网络路径选取仿真方法(M2),以及文献[5]提出的基于Memetic算法的两级车辆路径优化方法(M3)进行实验,对比各方法的综合性能,其中对比项分别为最优值的优化迭代次数、最优路径方案的平均距离、最优路径方案策划时间.根据式(13)能够求出每一次迭代输出的最优解,因此,M1、M2和M3方法的最优值优化迭代次数即是三种方法分别得到最优值所需的实验次数.而三种不同方法的最优路径方案平均距离和最优路径方案策划时间分别是多次实验后得到的平均值.对比项的数值,即三种路径优化方法的综合性能比较结果如表1所示,各方法的优化效果如图2所示.
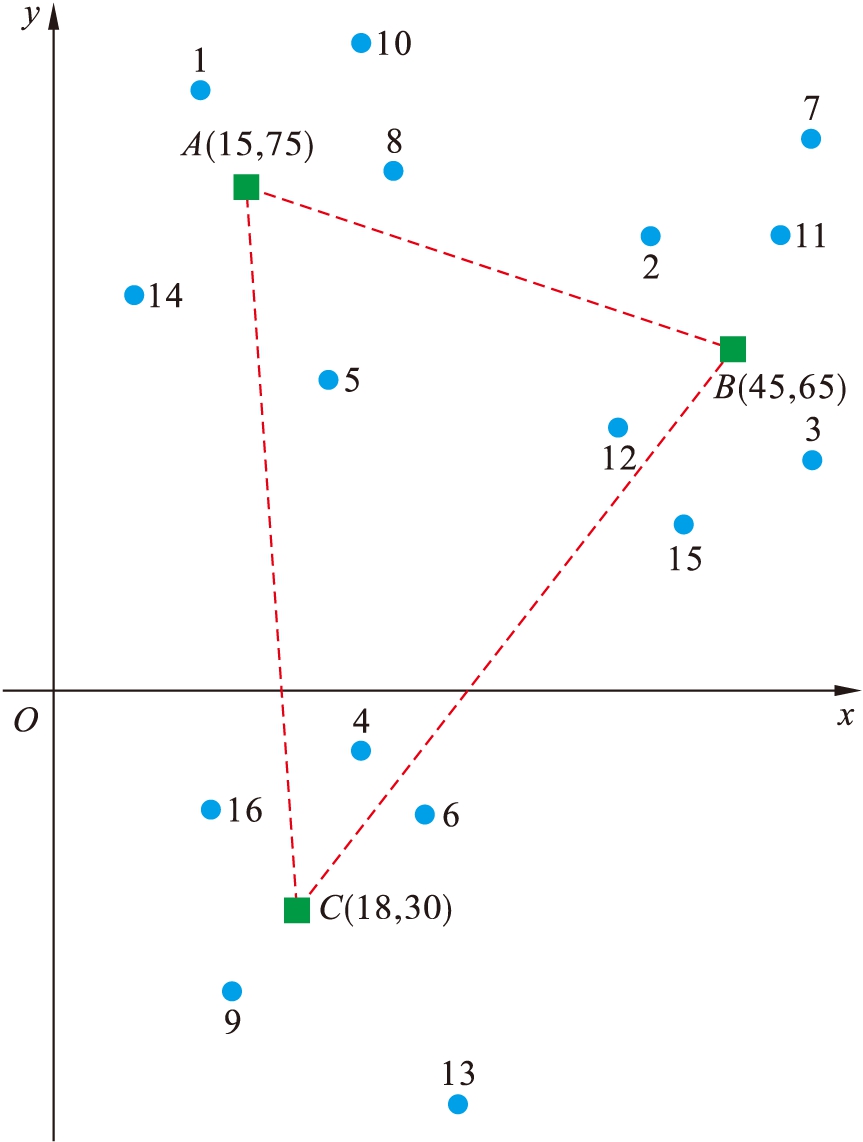
图1 配送中心与各目标的相对位置
Fig.1 Locations of distribution center relative to each target
表1 三种路径优化方法的综合性能比较
Tab.1 Comparison of comprehensive performance for three path optimization methods
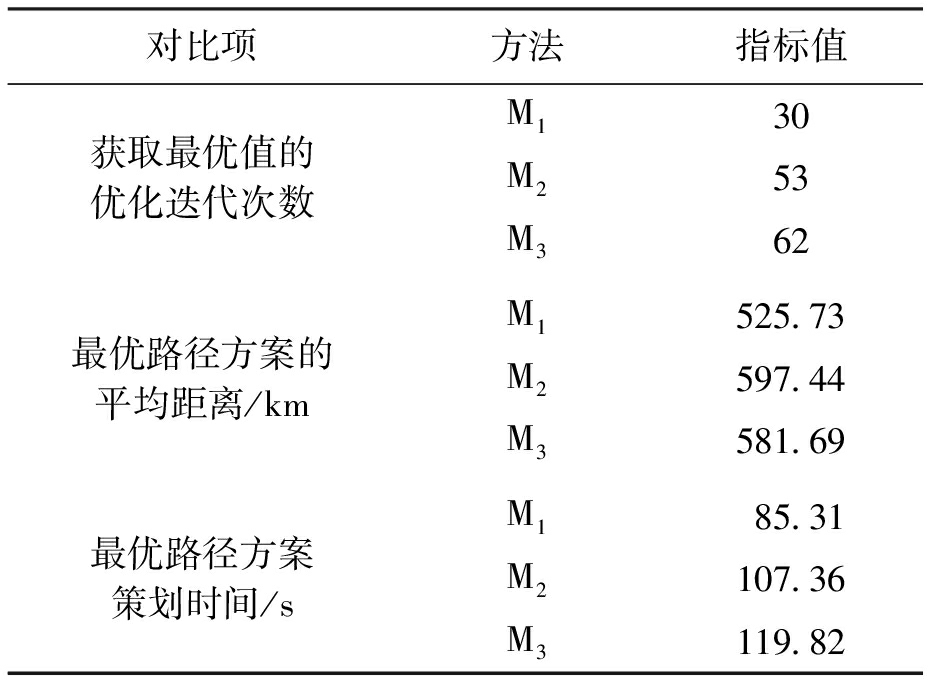
对比项方法指标值获取最优值的优化迭代次数最优路径方案的平均距离/km最优路径方案策划时间/sM130M253M362M1525.73M2597.44M3581.69M185.31M2107.36M3119.82
分析表1中数据可知,所提方法获取最优值所需的优化迭代次数较少,检验了量子信息概率幅调整最优路径求解收敛速度的效果,且最优路径方案策划过程消耗的时间明显缩短,增强了冷链物流配送路径规划的时效性.对比各方法获取的最优路径方案的平均距离可知,本次研究实验中,所提方法路径优化方案的平均距离比另外两种方法分别减少了71.71 km和55.96 km,节约了配送时间与成本.综合图2进行分析,采用本文所提方法优化后,能够有效降低运输过程的成本支出,其优化性能优于实验对比方法.
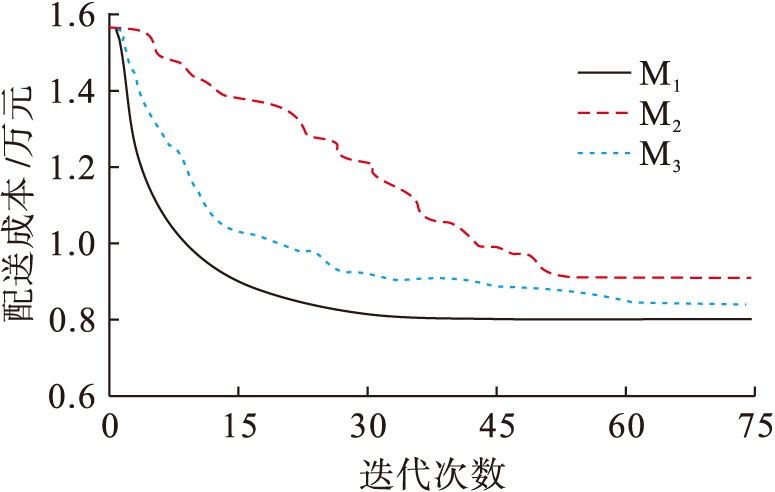
图2 各方法的优化效果及收敛速度比较
Fig.2 Comparison of optimization effects and convergence speed for each method
采用所提方法进行路径优化后,记录冷链物流配送过程中的单车装载率及中转效率,统计后得到实验结果如表2所示.其中,单车装载率的计算式为
(14)
中转单车日均配送量的计算式为
(15)
中转单车日均转载率的计算式为
(16)
表2 路径优化前后的指标内容比较
Tab.2 Comparison of indicators before and after path optimization
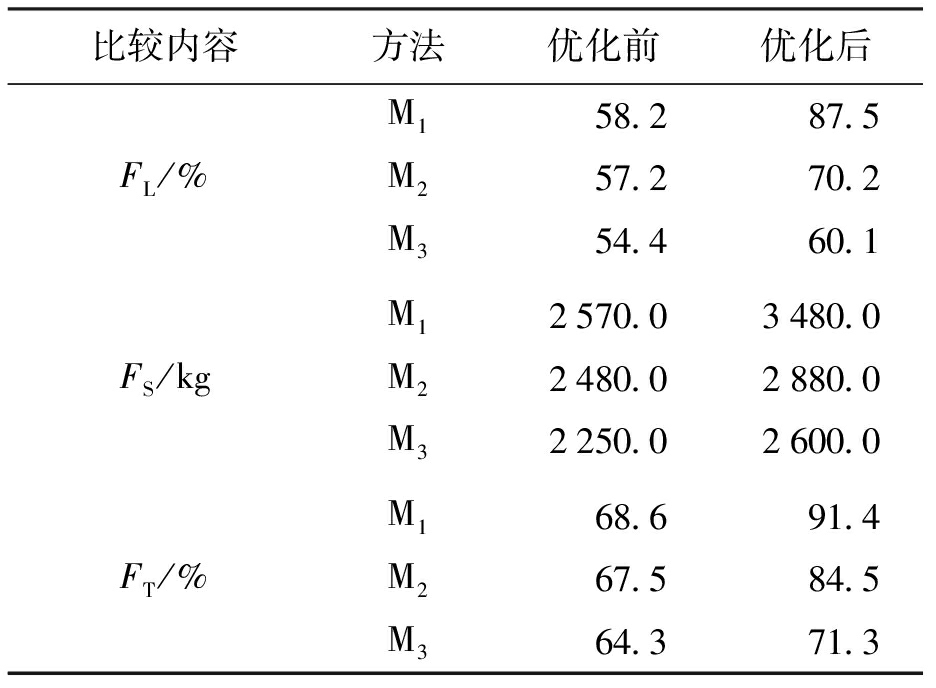
比较内容方法优化前优化后FL/%FS/kgFT/%M1 58.2 87.5M257.270.2M354.460.1M12570.03480.0M22480.02880.0M32250.02600.0M168.691.4M267.584.5M364.371.3
分析表2数据可知,采用M2方法进行冷链物流配送车辆路径优化后,单车装载率提高了13%,中转单车的日均配送量增加了400 kg,且日均转载率提升了17%;采用M3方法进行冷链物流配送车辆路径优化后,单车装载率提高了5.7%,中转单车的日均配送量增加了350 kg,且日均转载率提升了7%;采用所提方法进行冷链物流配送车辆路径优化后,单车装载率提高了29.3%,中转单车的日均配送量增加了910 kg,且日均转载率由68.6%提升到了91.4%.对比三种不同方法的实验结果,充分说明本文所提方法在对物流配送路径进行优化后,能够大幅度提高多温共配冷链物流的配送中转效率,验证出配送路径的最优性,以及该方法的有效性和可行性.
5 结 论
多温共配冷链物流配送的方法与运输线路是否科学、合理,直接影响到冷链物流配送的速度、成本及企业效益,为满足日益提升的市场需求,提高客户满意度,提出多温共配冷链物流配送车辆路径优化方法,并通过仿真实验与当前方法进行对比.通过以上实验过程及结果分析,得出如下结论:
1) 综合考虑各类影响因素,通过将冷链物流配送中的成本、时间及风险多目标优化问题转化为单目标问题,构建对应的多温共配冷链物流优化模型,实现各优化目标均衡的同时,降低了计算复杂度.
2) 蚁群算法本质上是一种自组织并行运算,能够及时进行正反馈,具有良好的鲁棒性.采用量子计算与蚁群算法相结合的方式进行优化求解计算,提高了求解过程的收敛效率,有效降低了迭代次数,缩短了优化运算时间.
3) 通过仿真实验与当前方法进行对比,所提方法能够有效完成冷链物流配送车辆路径优化,且效率较高.
[1]王维军,罗伟.基于改进智能水滴算法的冷链物流配送路径优化问题研究 [J].工业工程,2017,20(2):38-43.
(WANG Wei-jun,LUO Wei.A research of cold-chain logistic distribution path optimization based on the improved intelligent water drop algorithm [J].Industrial Engineering Journal,2017,20(2):38-43.)
[2]范立南,董冬艳,李佳洋,等.基于生鲜农产品的冷链物流配送路径优化 [J].沈阳大学学报(自然科学版),2017,29(2):125-131.
(FAN Li-nan,DONG Dong-yan,LI Jia-yang,et al.Route optimization of cold chain logistics based on fresh agricultural products [J].Journal of Shenyang University(Natural Science),2017,29(2):125-131.)
[3]张立毅,王迎,费腾,等.混沌扰动模拟退火蚁群算法低碳物流路径优化 [J].计算机工程与应用,2017,53(1):63-68.
(ZHANG Li-yi,WANG Ying,FEI Teng,et al.Research on low carbon logistics routing optimization based on chaotic-simulated annealing ant colony algorithm [J].Computer Engineering and Applications,2017,53(1):63-68.)
[4]王力锋,杨华玲.物流配送车辆最优网络路径选取仿真 [J].计算机仿真,2018,35(5):162-165.
(WANG Li-feng,YANG Hua-ling.Logistics distribution vehicle optimal network path selection simulation [J].Computer Simulation,2018,35(5):162-165.)
[5]陈立伟,唐权华.基于Memetic算法的两级车辆路径优化 [J].重庆大学学报,2017,40(3):95-104.
(CHEN Li-wei,TANG Quan-hua.Two-echelon ve-hicle path optimization based on Memetic algorithm [J].Journal of Chongqing University,2017,40(3):95-104.)
[6]杨光,郭生练,陈柯兵,等.基于决策因子选择的梯级水库多目标优化调度规则研究 [J].水利学报,2017,48(8):914-923.
(YANG Guang,GUO Sheng-lian,CHEN Ke-bing,et al.Multi-objective cascade reservoir optimal operation rules based on decision factor selection [J].Journal of Hydraulic Engineering,2017,48(8):914-923.)
[7]魏利鹏,王辉,孙学珊.生鲜电商众包物流模式风险评价指标体系构建研究 [J].物流科技,2017,40(2):38-40.
(WEI Li-peng,WANG Hui,SUN Xue-shan.Research on risk evaluation index system of fresh electricity crowd sourcing logistics model [J].Logistics Sci-Tech,2017,40(2):38-40.)
[8]王顺林,陈一芳.“互联网+”物流信息安全管理的用户行为路径优化研究 [J].科技管理研究,2018,38(16):183-189.
(WANG Shun-lin,CHEN Yi-fang.Research on user behavior path optimization of Internet+logistics information security management [J].Science and Technology Management Research,2018,38(16):183-189.)
[9]叶威惠,张飞舟.真实路况下的快递配送路径优化研究 [J].计算机工程与科学,2017,39(8):1530-1537.
(YE Wei-hui,ZHANG Fei-zhou.Express distribution route optimization under real-time road condition [J].Computer Engineering and Science,2017,39(8):1530-1537.)
[10]张晶蓉,曾小红,王振肖,等.基于多目标优化的高校智能快递柜网点布局研究 [J].物流科技,2018,41(5):65-68.
(ZHANG Jing-rong,ZENG Xiao-hong,WANG Zhen-xiao,et al.Research on network layout of intelligent express cabinet on university based on multi-objective optimization [J].Logistics Sci-Tech,2018,41(5):65-68.)
[11]张新.改进差分进化算法在物流配送中的多目标优化研究 [J].自动化仪表,2018,39(4):18-21.
(ZHANG Xin.Research on multi-objective optimization of logistics distribution based on improved diffe-rential evolution algorithm [J].Process Automation Instrumentation,2018,39(4):18-21.)
[12]王璐,张小宁,隋杨,等.机场物流中加油车服务调度双目标优化研究 [J].航空计算技术,2017,47(5):10-13.
(WANG Lu,ZHANG Xiao-ning,SUI Yang,et al.Bi-objective optimization of scheduling fuelling vehicle in airport logistics [J].Aeronautical Computing Technique,2017,47(5):10-13.)
[13]黄江.弱测量对四个量子比特量子态的保护 [J].物理学报,2017,66(1):25-32.
(HUANG Jiang.The protection of qudit states by weak measurement [J].Acta Physica Sinica,2017,66(1):25-32.)
[14]李杰,赵旭东,王玉霞.面向电商终端物流配送路径优化的改进蚁群算法 [J].制造业自动化,2017,39(10):90-94.
(LI Jie,ZHAO Xu-dong,WANG Yu-xia.An improved ant colony algorithm for terminal logistics distribution routing optimization in e-commerce [J].Manufacturing Automation,2017,39(10):90-94.)
[15]肖超,张立毅,费腾.冷链低碳物流配送路径优化的细菌觅食——蚁群算法研究 [J].数学的实践与认识,2017,47(21):98-107.
(XIAO Chao,ZHANG Li-yi,FEI Teng.Research on bacteria foraging ant colony optimization algorithm for cold chain low carbon logistics distribution routing optimization [J].Mathematics in Practice and Theory,2017,47(21):98-107.)