随着海上船舶朝着高速化、自动化方向的发展，船舶的自动舵控制系统受到研究人员的广泛关注.自动舵是船舶的操纵控制装置，可以根据航向偏差计算船舶所需的舵角，实现航向保持或者跟踪控制.1911年Sperry采用陀螺罗经测量船舶的实际航向，通过反馈控制设计出第一台自动舵控制装置.随后，Nicholas Minorsky将PID控制算法应用到船舶航向控制系统[1].Banazadeh等[2]采用频域辨识技术识别巡逻船的模型参数，设计了一种PID船舶航向控制器.以上船舶航向控制器的设计均采用线性Nomoto模型，而实际在海上行驶的船舶具有非线性、大惯性等特点，线性Nomoto模型可以描述船舶在直线行驶情况下的运动特性，但是当船舶处于转向状态时，则需要采用非线性操纵模型来描述船舶的运动.针对船舶的非线性操纵特性，Perera等[3]利用输入输出线性化技术，将船舶运动系统分为线性动态和内部动态，基于Lyapunov和Hurwitz分析方法设计船舶航向控制器.Wang等[4]采用不连续控制策略实现了船舶航向控制系统有限时间稳定，提出了一种全局有限时间控制律，该控制律对于船舶航向控制问题具有较快的收敛能力.Perera和Wang等[3-4]均未考虑船舶模型中的不确定特性，船舶运动受到本身的负载、航速以及外界时变的环境影响，这些影响会导致船舶操纵模型中存在不确定项.随着控制理论的发展，许多智能控制方法被应用到船舶运动控制系统设计中.针对存在不确定项的船舶操纵问题，Rigatos等[5]利用模糊逻辑系统估计船舶模型中的不确定项，设计出自适应模糊控制律.杨迪等[6]应用神经网络逼近船舶模型中的不确定项，设计出欠驱动船舶路径跟踪控制律.针对存在外界环境干扰的情况，Liu[7]采用非线性干扰观测器估计外界环境扰动，设计了自适应航向保持控制律.
本文同时考虑船舶模型中存在不确定项和外界环境干扰的情况，构造RBF神经网络逼近船舶模型中的不确定项，利用扰动观测器估计未知的外界环境干扰，设计了一种基于扰动观测器的自适应神经网络控制律，应用Lyapunov函数证明了船舶航向跟踪闭环系统的误差信号一致最终有界.仿真结果表明，所设计的控制律可以克服外界环境扰动，迫使船舶跟踪期望的航向，具有较强的鲁棒性.
1 问题描述
1.1 船舶操纵运动非线性数学模型
考虑模型中存在非线性、不确定项以及外界干扰等因素，采用Norribin非线性模型描述船舶的操纵特性[8]，即
(1)
式中：ψ和δ分别为船舶的航向角和舵角；
为模型中的不确定项；δw为由于外界环境扰动导致的等效舵角；K和T分别为增益常数和时间常数；α为Norribin系数.
为了书写方便，定义状态变量x1=ψ和
船舶航向非线性数学模型可以表示成如式(2)的状态空间形式，即
(2)
式中：θ1=-1/T；θ2=-α/T；θ3=K/T；u=δ；f(x1，x2)=
1.2 外界环境干扰模型
在海上行驶的船舶会受到风、浪、流等外界环境干扰，由外界扰动引起的等效舵角可以表示为
δw=δA+δB
(3)
式中：δB为由波浪干扰引起的等效舵角；δA为其他综合干扰的等效舵角，以恒值或正弦信号实现.
根据文献[9]，描述波浪作用的传递函数为
(4)
式中：yB(s)为波浪运动；ω(s)为零均值高斯白噪声；b由下式确定，即
(5)
其中，Hs为有效波高，g为重力加速度，U为船舶的航速，χ为遭遇角.波浪对船舶施加的转舵力矩MB表达式为
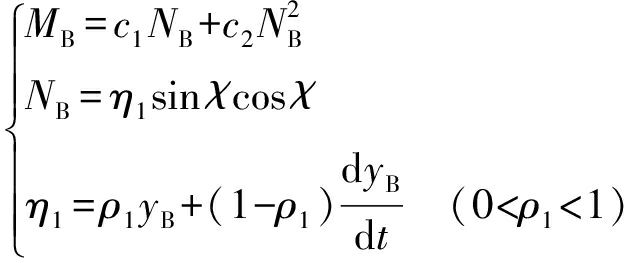
(6)
式中：ρ1为波浪系数；c1、c2为待设计参数.由波浪引起的等效舵角为
(7)
式中，KB为关于船舶大小和载重的比例系数.考虑到船舶操纵运动模型中存在不确定项以及外界环境干扰的情况，设计船舶航向自适应神经网络控制律，使得船舶的实际航向ψ跟踪期望航向ψd，并保证船舶航向跟踪闭环系统的误差信号一致最终有界.
2 控制律设计
本文将利用反步设计法、神经网络逼近技术、非线性扰动观测器、Lyapunov稳定理论实现船舶航向跟踪控制律的设计，控制律的设计可由两步骤组成.
1) 定义如下误差变量
(8)
式中：α1为虚拟控制律，用于镇定z1子系统；ψd为期望航向角.对z1取时间导数，可得
(9)
设计虚拟控制律α1为
(10)
式中，c1>0为待设计参数.将式(10)代入式(9)可得
(11)
2) 对式(8)中z2取时间导数，可得
(12)
由于f(x1，x2)是未知函数，可采用神经网络估计技术处理，为了设计方便，利用RBF神经网络估计未知函数f(x1，x2)，可得
f(x1，x2)=θ-1WTσ(x1，x2)+θ-1ε
(13)
式中：θ>0为扰动观测器的设计参数；(x1，x2)为网络的输入信号；W=(w1，w2，…，wh)T为理想的权值系数；σ=(σ1，σ2，…，σh)T为高斯函数，有h个隐层节点；ε为神经网络的估计误差.未知项f(x1，x2)的估计表示为
将式(13)代入式(12)可得
θ-1WTσ(x1，x2)+θ3u+ξ
(14)
式中，ξ=θ-1ε+w为复合扰动.根据神经网络的逼近理论，
是有界的.实际中的船舶受到外界环境干扰有限，故假定
是有界的，因此，复合扰动
是一个正数.根据式(14)可设计神经网络自适应律、扰动观测器以及控制律分别为
(15)
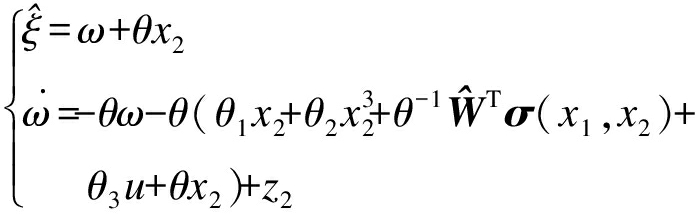
(16)
(17)
式中：
和
分别为W和ξ的估计值；F>0、η>0和c2>0为待设计参数；ω为观测器的辅助变量.定义估计误差为
3 稳定性分析
定理1 针对式(2)描述的船舶航向非线性操纵系统，设计的控制律(17)、神经网络自适应律(15)和扰动观测器(16)能够保证闭环系统的所有误差信号
一致最终有界，从而实现船舶航向跟踪控制.
证明 对整个闭环系统选取Lyapunov函数V，即
(18)
对V取时间导数并考虑式(11)、(14)得
(19)
将式(15)、(17)代入式(19)得
(20)
根据式(16)和式(2)中第二个方程可得
θ-1WTσ(x1，x2)+θ3u+ξ)+z2)=
(21)
考虑到神经网络的高斯函数是有界的，即
ħ，ħ>0，根据杨氏不等式得
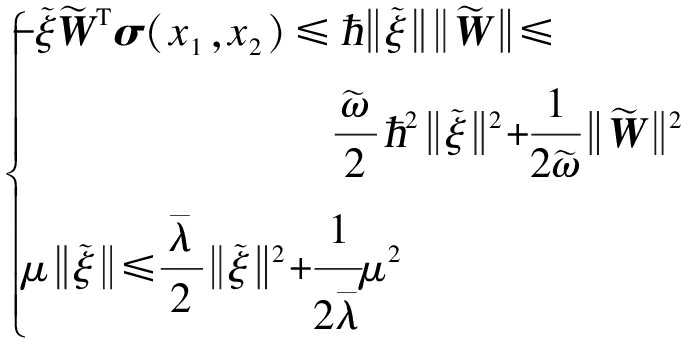
(22)
式中：
根据神经网络的权值特性有
(23)
将式(21)～(23)代入式(20)得
-lV+M
(24)
式中，
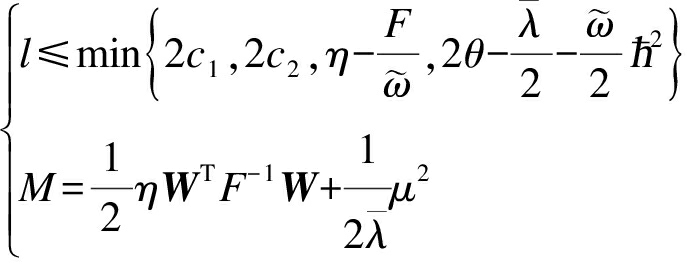
(25)
为了保证闭环系统的稳定，设计参数范围应该选择
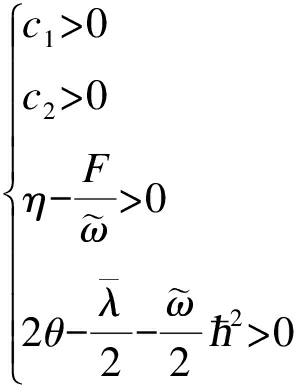
(26)
令
β=M/l
(27)
由式(24)得
V≤β+(V(0)-β)e-lt
(28)
可知闭环系统的所有误差信号一致最终有界，可以通过调节l决定界的大小进行控制，l越大，β越小，也就是说闭环系统的所有误差信号越小，定理1得证.
4 实验结果与分析
为验证所设计的船舶航向神经网络控制律的有效性，本文利用Matlab对其进行数值模拟，并与传统PID控制律的性能进行比较.采用文献[10]介绍的船舶作为被控对象进行仿真研究，该船的增益常数和时间常数分别为K=0.5 s-1和T=31 s，Norribin系数α=0.4 s2，这些参数的值都是船舶在航速U=5 m/s的情况下通过辨识得到的.在仿真中考虑船舶舵角的幅值限制，最大的舵角幅值为δmax=30°.采用文献[11]中的外界环境干扰模型参数g=9.8 m/s2，χ=π/6，ρ1=0.9，c1=5.6×103，c2=90，KB=3 500，其他综合干扰的等效舵角为δA=16°+2°sin(0.2t)+5°cos(0.5t).
在船舶航向控制系统中，可以采用模型参考技术[8]产生期望的航向角ψd，模型参考的传递函数为
(29)
式中：ψr为航向改变的设定信号；ξψ和ωn为闭环系统的响应特性.参考模型(29)是设定信号ψr的预滤波，其响应特性应与船舶的响应特性相匹配，当设定信号ψr发生改变时，参考模型(29)可以产生光滑且有界的期望航向角ψd.本文参考模型中ξψ=0.8，ωn=0.05，船舶设定信号ψr为
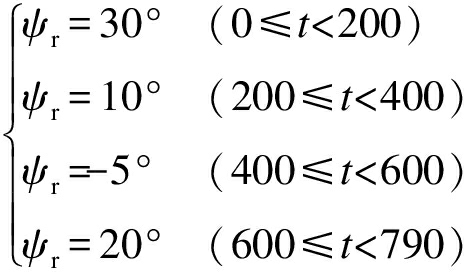
(30)
为验证所设计的船舶航向神经网络控制律的鲁棒性，分别进行标称模型下的仿真和考虑模型不确定项和外界干扰的仿真.船舶的初始状态(x1(0)，x2(0))=(-1.5°，0 (°)/s)，船舶模型中的不确定项
控制律参数选择为c1=0.01，c2=5，θ=20，F=0.003，η=0.2，神经网络采用h=13个隐层节点，网络的输入为
进行对比分析的传统PID数学表达式为
(31)
式中：kp=50；ki=0.01；kd=200.这些参数都是经过多次调整得来的.
4.1 标称模型下的仿真
船舶操纵模型完全已知，不存在不确定项以及外界干扰.仿真结果如图1～3所示，图1、2分别为航向跟踪曲线和航向跟踪误差曲线，在本文所设计控制律的作用下，可以迫使船舶实际的航向ψ跟踪期望的航向ψd，并且具有满意的控制性能.由图2可知，船舶在PID控制律作用下，航向偏差出现了小幅度的震荡.图3为控制舵角的响应曲线，PID的控制舵角在45 s时出现了1°的震荡，而本文的控制律未发生震荡的情况.因此，船舶在标称模型情况下，本文控制律比PID控制律的控制效果稍好.
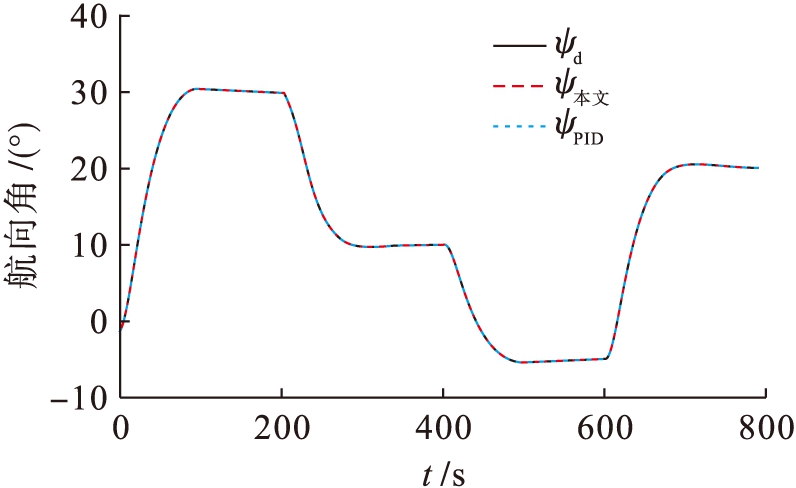
图1 标称模型情况下的航向跟踪曲线
Fig.1 Course tracking curves under nominal model
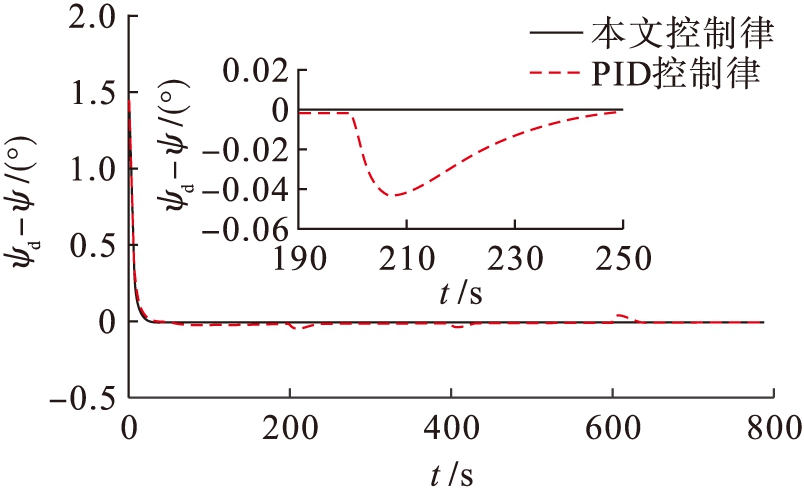
图2 标称模型情况下的航向跟踪误差曲线
Fig.2 Course tracking error curves under nominal model
4.2 考虑模型不确定项和外界干扰
船舶操纵模型中存在不确定项以及外界干扰，在两种控制律参数不进行调整的情况下进行仿真研究，仿真结果如图4～8所示.
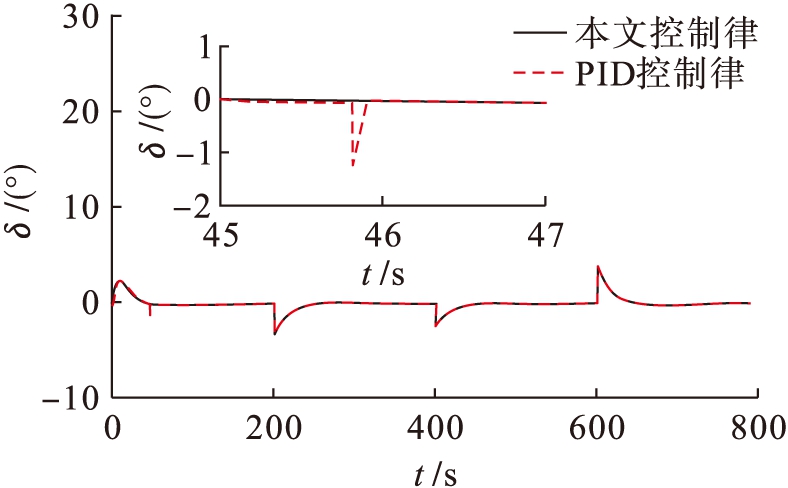
图3 标称模型情况下的控制舵角曲线
Fig.3 Control rudder curves under nominal model
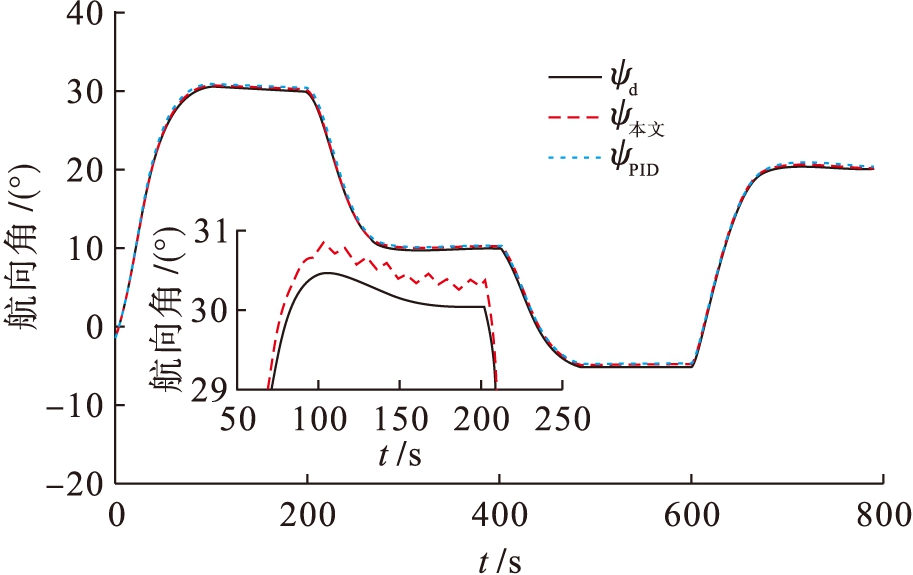
图4 航向跟踪曲线
Fig.4 Course tracking curves
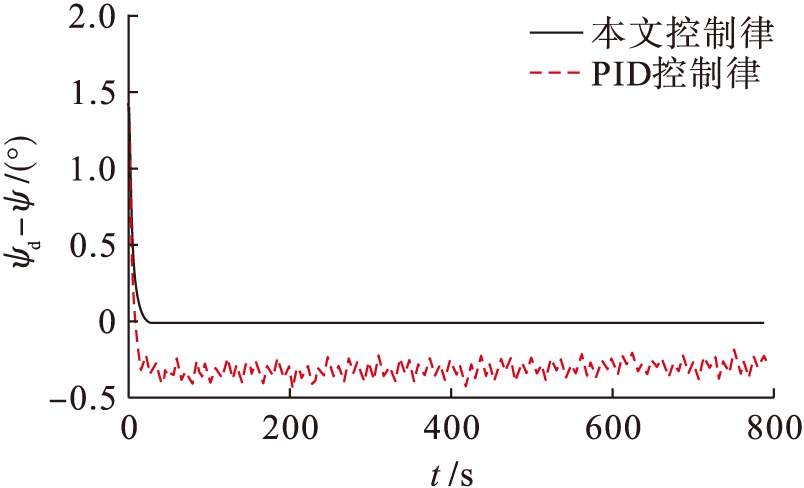
图5 航向跟踪误差曲线
Fig.5 Course tracking error curves
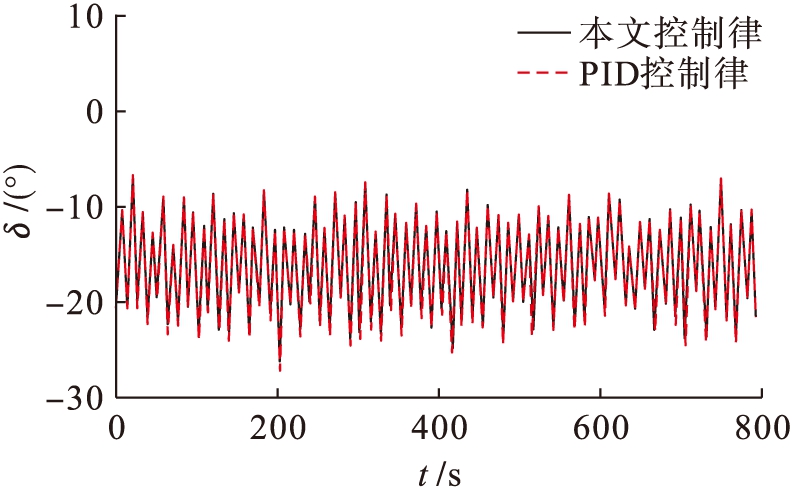
图6 控制舵角曲线
Fig.6 Control rudder curves
图6为控制舵角的响应曲线，本文控制律与PID控制律舵角曲线相差不大.图7为不确定项及其神经网络的逼近曲线，神经网络可在60 s左右实现不确定项的逼近.图8为扰动项及其估计曲线，由图8可知本文所设计的扰动观测器可在8 s左右实现干扰的估计.即使模型中存在不确定项以及外界干扰，本文所设计的自适应神经网络控制律可以使得船舶跟踪期望航向，验证了控制律的鲁棒性，而在控制参数不进行调整的情况下，PID控制律的航向误差曲线发生了波动，并存在稳态误差，进而说明了本文控制律的优越性.
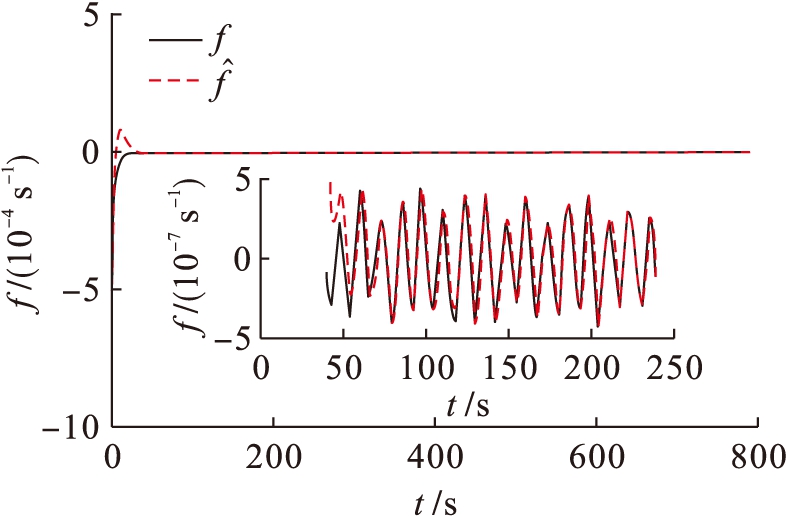
图7 不确定项及其神经网络逼近值
Fig.7 Uncertain items and its neural network approximation value
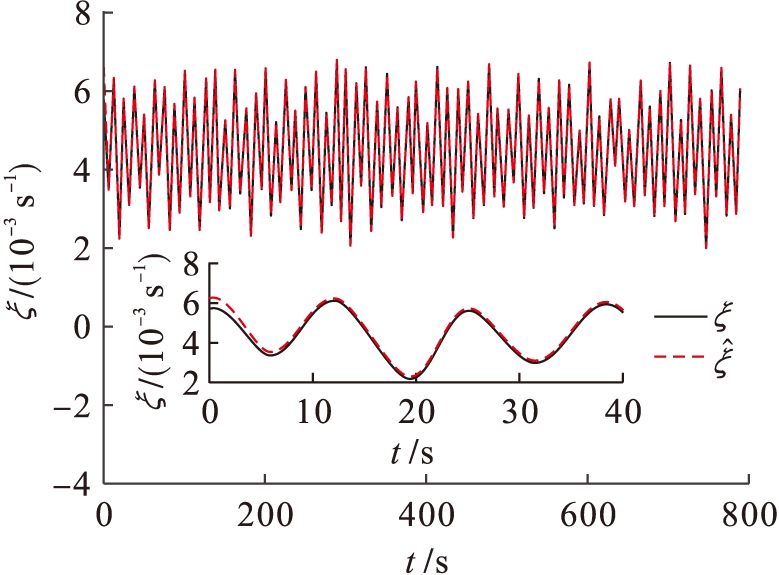
图8 扰动项及其估计值
Fig.8 Disturbance items and its estimation value
5 结 论
本文针对船舶航向跟踪问题，提出了一种自适应神经网络控制律.利用神经网络估计船舶模型中的建模不确定项，构造扰动观测器估计未知的外界环境干扰，并对控制量前馈补偿，提高控制系统的鲁棒性，应用Lyapunov函数证明了闭环系统的误差信号一致最终有界.通过对比仿真实验，验证了所设计控制律的优越性，本文控制律的设计对船舶运动控制领域中的自动舵装置研制具有重要的现实意义.
[1]Fossen T I.Handbook of marine craft hydrodynamics and motion control [M].West Sussex：Wiley，2011.
[2]Banazadeh A，Ghorbani M T.Frequency domain identification of Nomoto model to facilitate Kalman filter estimation and PID heading control of a patrol vessel [J].Ocean Engineering，2013，72：344-355.
[3]Perera L P，Soares C G.Lyapunov and Hurwitz based controls for input-output linearization applied to nonlinear vessel steering [J].Ocean Engineering，2013，66：58-68.
[4]Wang N，Lü S L，Liu Z Z.Global finite-time heading control of surface vehicles [J].Neurocomputing，2016，175：662-666.
[5]Rigatos G，Tzafestas S.Adaptive fuzzy control for the ship steering problem [J].Machatronics，2006，16(8)：479-489.
[6]杨迪，郭晨，朱玉华，等.欠驱动船舶神经网络自适应路径跟踪控制 [J].智能系统学报，2018，13(2)：254-260.
(YANG Di，GUO Chen，ZHU Yu-hua，et al.Neural network adaptive path tracking control for underactua-ted ships [J].CAAI Transactions on Intelligent Systems，2018，13(2)：254-260.)
[7]Liu Z Q.Ship adaptive course keeping control with nonlinear disturbance observer [J].IEEE Access，2017，5：17567-17575.
[8]Wang S S，Fu M Y，Wang Y H.Robust adaptive steering control for unmanned surface vehicle with unknown control direction and input saturation [J].International Journal of Adaptive Control and Signal，2019，33(7)：1212-1224.
[9]李勇，刘文魁，陈永冰，等.基于航向自动舵实船环境模拟的海浪扰动模型研究 [J].海军工程大学学报，2002，14(5)：60-63.
(LI Yong，LIU Wen-kui，CHEN Yong-bing，et al.Wave disturbance model based on the simulation of autopilot’s navigation environment [J].Journal of Naval University of Engineering，2002，14(5)：60-63.)
[10]Fossen T I，Paulsen M J.Adaptive feedback linearization applied to steering of ships [C]//Proceedings of 1st IEEE Conference on Control Applications.Dayton，USA，1992：1088-1093.
[11]Du J L，Hu X，Sun Y Q.Adaptive robust nonlinear control design for course tracking of ships subject to external disturbances and input saturation [J].IEEE Transactions on Systems，Man and Cybernetics：Systems，2017，99：1-10.