在防屈曲钢板剪力墙结构体系中,约束板是直接与主要耗能构件内嵌板产生面外接触的唯一构件.约束板侧向刚度的大小将直接影响内嵌板的屈曲抑制程度,而约束板的厚度则是其侧向刚度大小的直接体现.清华大学郭彦林等[1]对约束板最小厚度进行了研究;台湾大学蔡克铨等[2]对约束板厚度进行了对比试验.同样,笔者提出的全钢防屈曲钢板剪力墙结构体系中,约束板厚度对抑制内嵌板屈曲也有重要的作用.
随着钢板剪力墙的发展,研究目标已不再局限于在工程中得到应用的薄钢板墙和加劲钢板墙,在两者基础上提出的其他类型钢板剪力墙也得到了充分的关注,包括为改善结构破坏形式而提出的开缝钢板剪力墙[3];以避免或削弱拉力场对边柱的不利作用为出发点而提出的侧向承载系统与主立柱分离钢板剪力墙[4];采用薄钢板作为墙体覆面板,增强耐火性能及抗震性能的薄钢板覆面冷弯薄壁型钢墙[5];钢板与现浇混凝土协同工作的组合钢板剪力墙[6-9]以及通过用螺栓拉结两侧混凝土盖板实现约束钢板屈曲的防屈曲钢板剪力墙[10-11]等.基于此,本文进行了全钢防屈曲钢板剪力墙抗震性能影响的试验研究.
本次试验设计制作了以约束板厚度为变量的3组试件,进行低周往复荷载试验.分析总结了约束板厚度变量组试件的破坏形态,得到试件的滞回曲线和骨架曲线,并通过数据处理得到了本组试件的承载力关键点、刚度退化、承载力退化系数和能量耗散系数等重要指标,得出约束板厚度对全钢防屈曲钢板剪力墙结构体系抗震性能的影响.
1 试验概况
1.1 试件设计
全钢防屈曲钢板剪力墙由外框架、内嵌钢板、约束板、加劲肋组成,所有构件均采用Q235b钢材.框架梁由两块20#槽钢组成,框架柱由两块18#槽钢及两块9 mm钢垫板组成.梁腹板由两排间距为100 mm的M16螺栓连接,柱腹板由两排间距为80 mm的M16螺栓连接,梁柱腹板内同一排螺栓间距为200 mm.在梁柱连接的位置,将梁柱节点处梁的翼缘割除,腹板插入柱内对应位置,梁腹板所带来的缝隙由钢垫板找平,每个节点通过四个M16螺栓和一个φ30带开口孔销轴将框架柱和框架梁连接.内嵌钢板由约束板和加劲肋夹在中间,采用M18螺栓固定,且两侧加劲肋布置方向互相垂直.板面预留孔洞直径为30 mm,加劲肋为20a#工字钢沿腹板中心线方向剖开所得T型钢.
试件框架详图及加载装置如图1所示(单位:mm).试件总高1 600 mm,框架柱中心距离1 420 mm,底梁两边各外伸500 mm.本次试验共设计了3组试件,试件1~3的约束板厚度分别为1.5、2、3 mm.
1.2 试验方法
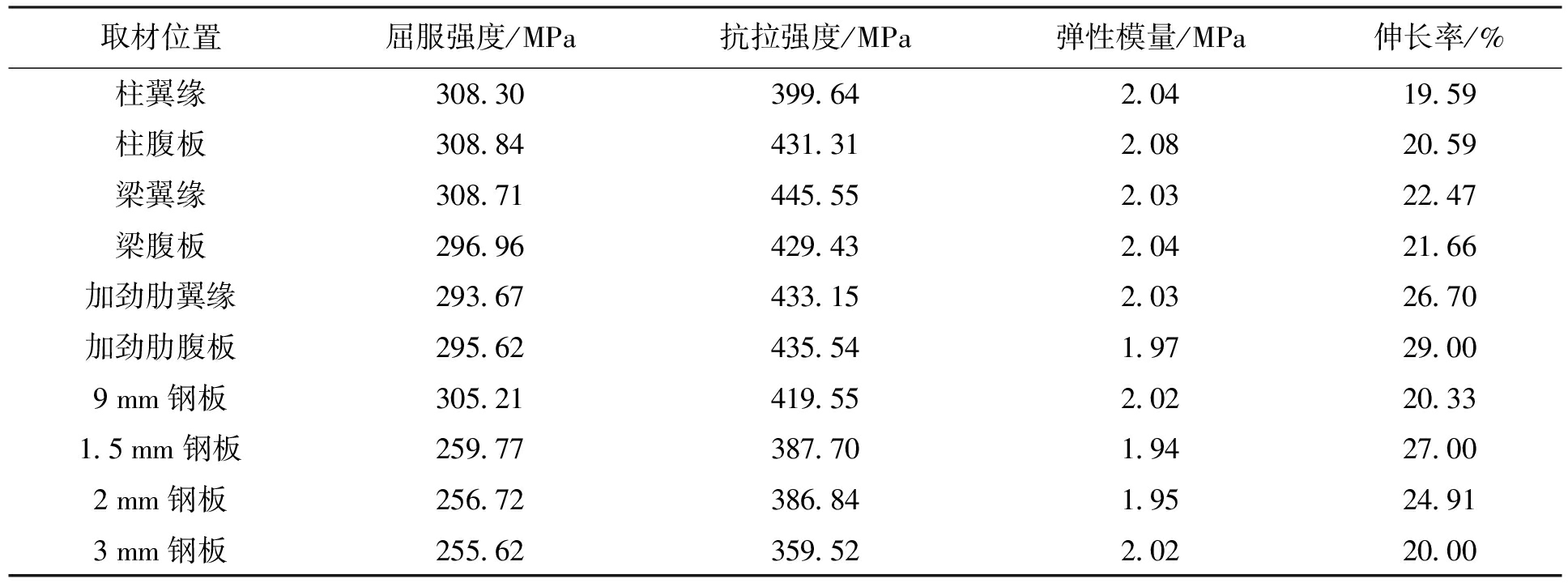
钢材材性试验为单向拉伸试验,在沈阳建筑大学材料力学实验室进行,主要测量钢材的弹性模量、屈服强度、抗拉强度及伸长率,为分析试验结果和理论计算提供相关依据.材性试验结果如表1所示.
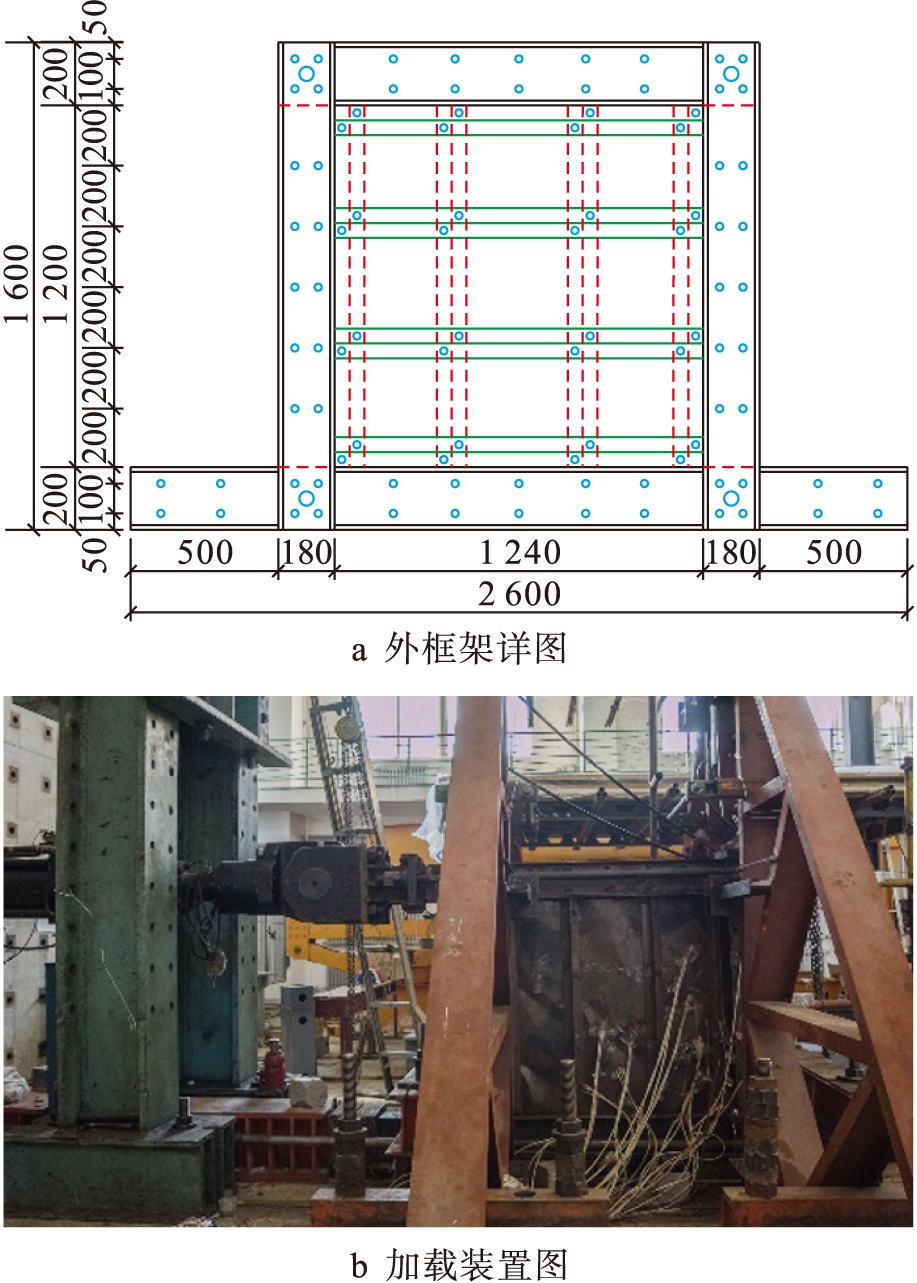
图1 外框架及加载装置图
Fig.1 External frame and loading device
低周往复荷载试验在沈阳建筑大学结构实验室进行,加载装置实物如图1b所示.为模拟地震作用下剪力墙的受力状态,根据《建筑抗震试验规程》(JGJ/T 101-2015)的相关规定,采用固定在反力墙上的150 t MTS电液伺服作动器进行水平加载,加载点位于顶梁中心点.竖直方向上,采用两个固定在竖向反力架上的60 t顶推式千斤顶提供竖向荷载,千斤顶通过加载连接端板和锚杆固定在竖向反力架上.根据构件对轴压比的计算,首先施加200 kN的竖向力.水平方向加载采用力和位移联合控制,在试件屈服之前采用荷载控制,根据试件本身的承载力推测,设定初始荷载为100 kN,随后以50 kN为基数进行加载.试件在整体屈服之后采用变形控制,变形加载阶段采用的控制位移按照屈服位移的1、1.5、2、2.5倍数递增,每级循环两次,直到水平荷载下降至峰值荷载的85%时停止加载,具体加载制度可以根据试验的实际情况进行调整.具体测量方案如下:
1) 框架柱腹板及内嵌板应变采用三向直角应变花进行测量,应变花具体布置如图2所示(单位:mm).框架柱腹板应变花沿柱高布置,每根柱三个测点,测点编号为J~O;内嵌板应变花沿水平、竖直及斜向布置,测点编号分别为A~I.
表1 材性试验结果
Tab.1 Test results of mechanical properties of materials
取材位置屈服强度/MPa抗拉强度/MPa弹性模量/MPa伸长率/%柱翼缘308.30399.642.0419.59柱腹板308.84431.312.0820.59梁翼缘308.71445.552.0322.47梁腹板296.96429.432.0421.66加劲肋翼缘293.67433.152.0326.70加劲肋腹板295.62435.541.9729.009mm钢板305.21419.552.0220.331.5mm钢板259.77387.701.9427.002mm钢板256.72386.841.9524.913mm钢板255.62359.522.0220.00
2) 框架柱翼缘应变由单向应变片测量,应变片沿纵向粘贴于翼缘内侧距离边缘20 mm处,其布设点高度与柱腹板应变花布设点高度相同.
3) 柱顶及柱中位移分别通过位移计进行测量,编号分别为w1和w2,w1位置设在试件的顶梁中心点,即与水平加载作动器高度相同处,w2设置在柱高二分之一处.
4) 水平荷载由压力传感器通过数据采集装置进行采集.
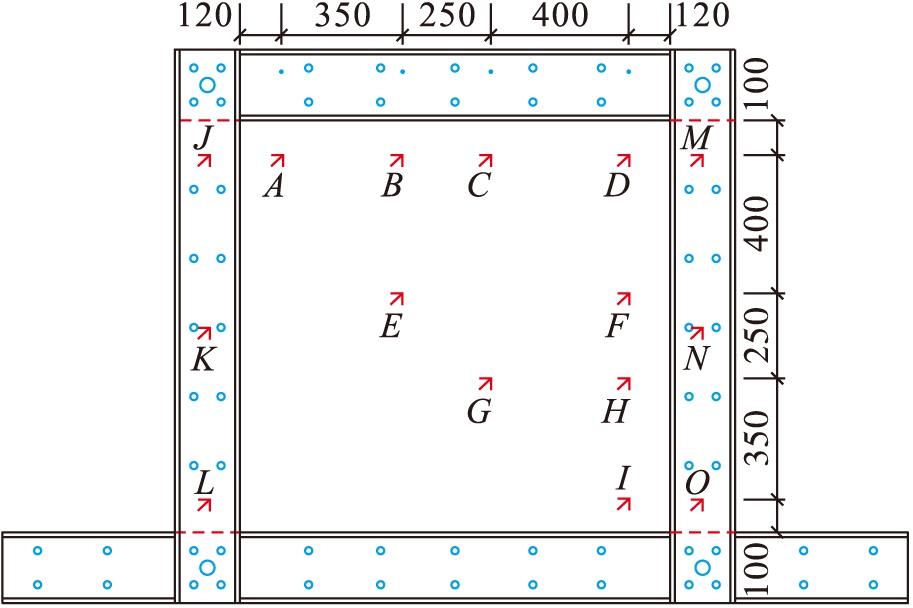
图2 应变花布置图
Fig.2 Arrangement of strain rosettes
应变片及应变花生产厂家为河北邢台金力传感元件厂,规格为5 mm×3 mm,型号分别为BX120-3AA及BX120-3CA.柱顶位移计量程为200 mm,柱中位移计量程为100 mm.
2 结果与分析
2.1 试验过程与现象
2.1.1 试件1试验过程与破坏形态
图3为试件1破坏形态图.在前几级加载过程中,试件出现了轻微的金属摩擦声音,在推向200 kN加载级内出现了金属挤压声,在拉向加载到300 kN时,出现类似金属断裂的“砰砰”声,约束板出现了轻微的鼓曲,荷载![]() 位移曲线斜率已经降低,试件屈服,屈服位移δy为13 mm;在4.5δy加载级过程中,一侧面外支撑的滚珠滑道支撑头掉落;5δy加载级过程中,由于侧向支撑参与受力,故可认为试验结束,如图3a所示,约束板上也出现了许多斜向接近贯通的明显屈曲褶皱.
位移曲线斜率已经降低,试件屈服,屈服位移δy为13 mm;在4.5δy加载级过程中,一侧面外支撑的滚珠滑道支撑头掉落;5δy加载级过程中,由于侧向支撑参与受力,故可认为试验结束,如图3a所示,约束板上也出现了许多斜向接近贯通的明显屈曲褶皱.

图3 试件1破坏形态图
Fig.3 Failure morphologies of specimen 1
2.1.2 试件2试验过程与破坏形态
图4为试件2破坏形态图.拉向250 kN加载级出现了金属挤压声,试件未屈服,加载推向350 kN时出现金属断裂声,拉向加载到450 kN时,约束板角部出现鼓曲,在卸荷后鼓曲消失.加载到拉向550 kN时,三种声音基本都维持在音量较大且频率比较稳定的状态,观察荷载![]() 位移曲线斜率已经出现下降,试件屈服,屈服位移δy为40 mm.约束板仅角部及中部出现四条明显屈曲褶皱,其余变形均为沿着加劲肋方向发生的鼓曲,变形形态与内嵌板不同,比试件1约束板平整,如图4b所示.
位移曲线斜率已经出现下降,试件屈服,屈服位移δy为40 mm.约束板仅角部及中部出现四条明显屈曲褶皱,其余变形均为沿着加劲肋方向发生的鼓曲,变形形态与内嵌板不同,比试件1约束板平整,如图4b所示.
2.1.3 试件3试验过程与破坏形态
图5为试件3破坏形态图.推向300 kN加载级出现金属挤压声音,试件未屈服,金属摩擦声与

图4 试件2破坏形态图
Fig.4 Failure morphologies of specimen 2
挤压声保持连续.加载到推向600 kN时,约束板角部出现轻微鼓曲,且偶有几次金属断裂声音出现.加载到700 kN时,出现多次音量较大的金属断裂声.加载到800 kN时,金属断裂声持续不断,荷载![]() 位移曲线斜率出现下降,试件屈服,屈服位移δy为60 mm.约束板左上角出现明显褶皱,褶皱的区域与内嵌板褶皱的区域相同,其余部分基本保持平整,试件3的平整度优于试件2及试件1的平整度,如图5b所示.
位移曲线斜率出现下降,试件屈服,屈服位移δy为60 mm.约束板左上角出现明显褶皱,褶皱的区域与内嵌板褶皱的区域相同,其余部分基本保持平整,试件3的平整度优于试件2及试件1的平整度,如图5b所示.

图5 试件3破坏形态图
Fig.5 Failure morphologies of specimen 3
2.2 承载力分析
在周期反复循环加载过程中,结构的损伤会不断累积和加剧,从而导致结构出现强度退化的现象.结构或构件的强度退化采用承载力退化系数λi进行衡量,其表达式为
(1)
式中:![]() 为j倍屈服位移加载时,第i+1次循环峰点荷载值;
为j倍屈服位移加载时,第i+1次循环峰点荷载值;![]() 为j倍屈服位移加载时,第i次循环峰点荷载值.
为j倍屈服位移加载时,第i次循环峰点荷载值.
图6为试件受力性能对比图.图6a中,三个试件的极限荷载明显不对称,拉向的极限荷载均大于推向的极限荷载,其原因是试验先推后拉的加载顺序所致,增加约束板厚度明显提高了试件的极限荷载.三个试件的拉向屈服荷载强于推向屈服荷载,试件2的屈服荷载大于试件1、3的屈服荷载,原因仍与试件2在加载过程中出现的滑移有关,如图6b所示.
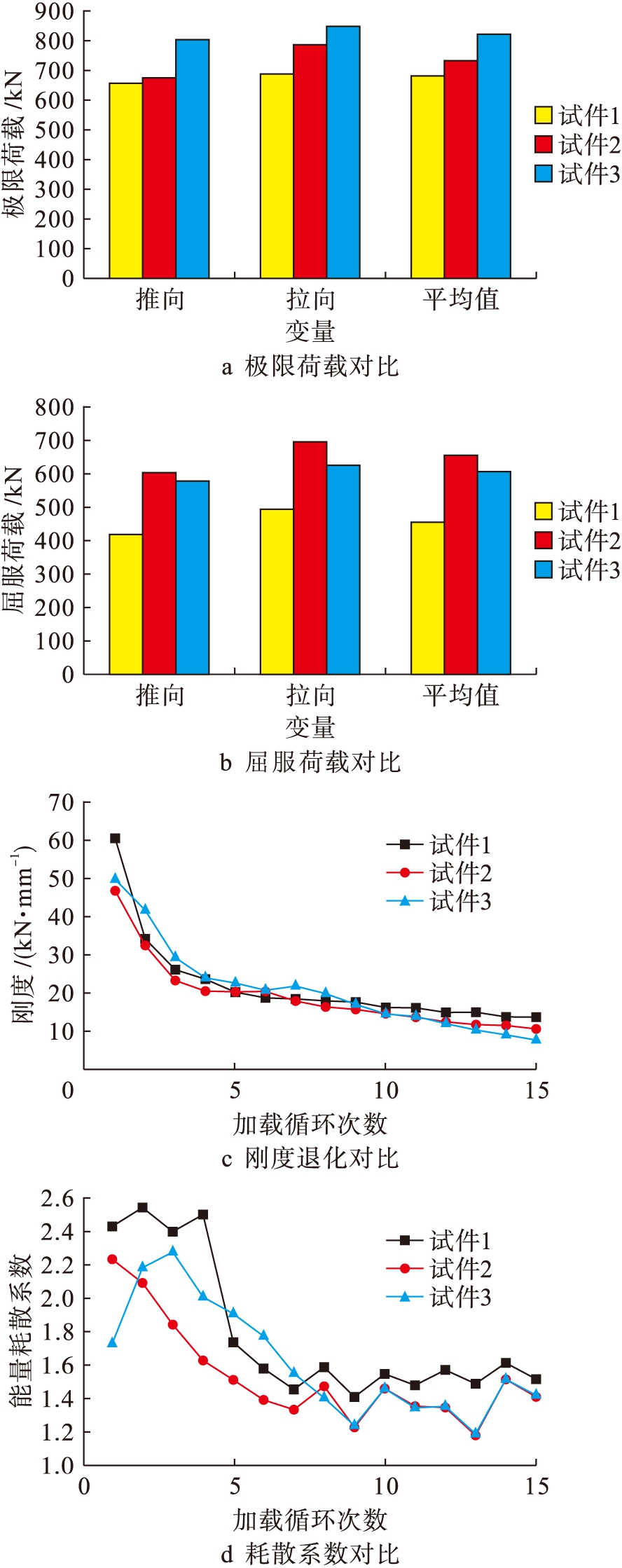
图6 试件受力性能对比图
Fig.6 Comparison of mechanical properties of specimens
2.3 刚度退化
由图6c可知,在加载初期,试件2的刚度小于试件1、3的刚度,随着加载的进行,滑移相对于位移的影响越来越小,试件2的刚度退化趋势开始向试件1、3接近;试件1、3的初始刚度较大,加载初期退化较快,且试件1的退化速度大于试件3的退化速度,在加载中后期,试件3的退化速度与试件1相比较大;试验结束时,试件1的刚度高于试件2、3的刚度,通过对比每个试件的刚度退化值,可知增加约束板厚度延缓了加载初期试件刚度退化的速度,使试件刚度以较为平稳的趋势下降.
2.4 强度退化
试件1的承载力退化系数始终保持在较高水平,几乎都大于0.97,说明整个加载过程中,试件1的强度退化并不明显,能够保持稳定的承载力.试件2承载力退化系数总体小于试件1的承载力退化系数,保持在0.89以上,在整个加载过程中,试件2有一定的强度退化.试件3的承载力退化系数最小,但也大于0.8,试件3有一定的强度退化.比较三个试件的承载力退化系数,全钢防屈曲钢板墙具有较高的承载力稳定性,不会突然发生强度破坏,但随着约束板厚度的增加,承载力的退化加快.
2.5 耗能能力
试件的耗能能力主要与其耗能机理有关,钢板剪力墙主要通过内嵌钢板的几何和材料非线性进行耗能.耗能能力可以由能量耗散系数E来表征,其表达式为
(2)
式中:s1为各级滞回环所包围的面积;s2为峰值荷载点与x轴围成三角形的面积.
图6d为能量耗散系数随加载循环次数变化的曲线,可见三个试件的能量耗散系数均为前期较高,中后期一直保持平稳.三个试件的能量耗散系数变化规律是相近的,说明全钢防屈曲钢板剪力墙具有稳定的耗能能力.
2.6 试件滞回曲线与骨架曲线
根据试验数据,分析整理后得到的3组试件的滞回曲线和骨架曲线如图7所示.从滞回曲线可以看出,滞回曲线形状介于梭型与反S型之间,有不同程度的“捏缩”现象.试件3具有最高的极限承载力和最大的极限位移,试件1最小.试件2在最后几个加载循环和试件3在80 mm加载级中,均出现了拉向卸荷阶段有明显的位移波动,原因是试件在拉向加载过程中带动了压梁或者侧向支撑,在卸荷过程中,压梁或者侧向支撑由于失去了试件的带动而回归原位,产生了试件滞回曲线的波动.试件2、3在拉方向的极限承载力大于推方向的极限承载力.
从骨架曲线上看,试件1的推拉方向基本对称,其承载力一直处于上升阶段,试件仍有继续承载的可能性;试件2的拉向较推向强,达到极限荷载之前其骨架曲线接近于直线,看不出明显屈服阶段;试件3的拉向极限承载力大于推向极限承
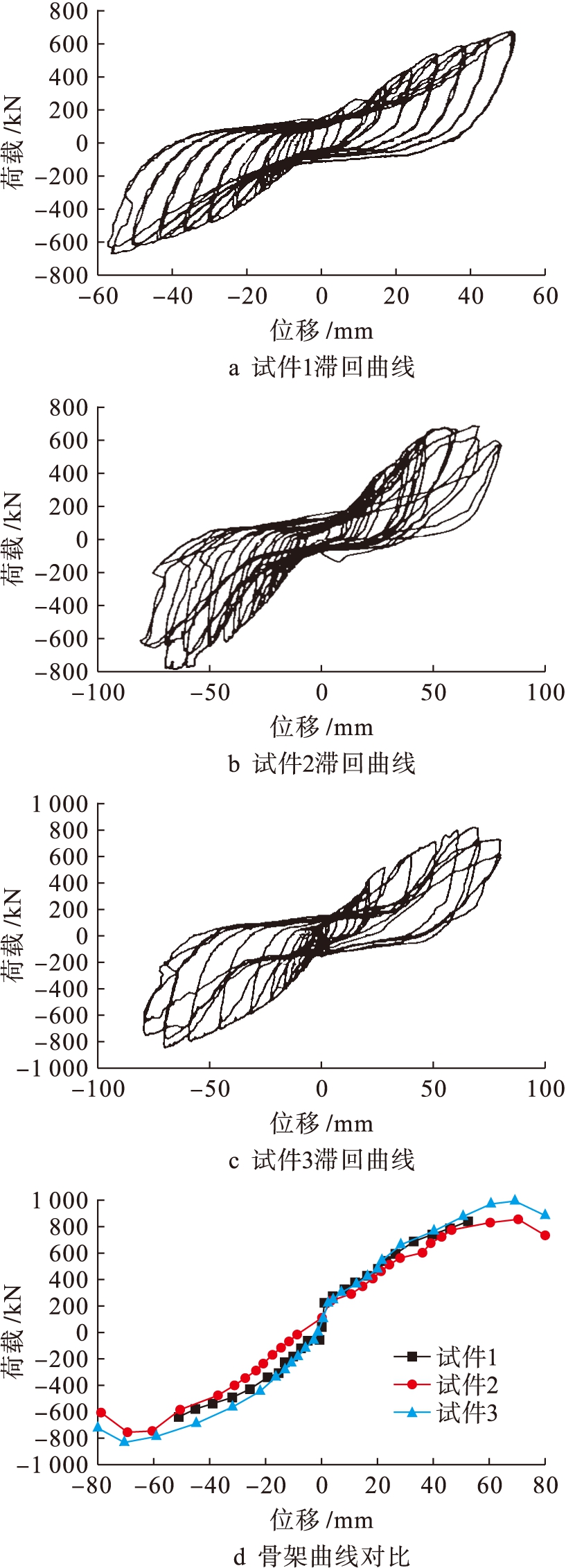
图7 试件滞回曲线及骨架曲线
Fig.7 Hysteretic and skeleton curves of specimens
载力,但试件3极限承载力高于试件2的极限承载力.
3 结 论
本文通过分析得出以下结论:
1) 约束钢板对内嵌板具有一定屈曲抑制作用,刚度退化速度较为平稳;
2) 在加载后期,承载力退化加速,且加快了承载力在推拉方向上退化的不对称性;
3) 随着约束板厚度的增加,局部贯通的褶皱明显减少,屈服荷载和极限荷载均显著提高.
[1]郭彦林,周明.钢板剪力墙的分类及性能 [J].建筑科学与工程学报,2009,26(3):1-13.
(GUO Yan-lin,ZHOU Ming.Classification and performance of steel plate shear wall [J].Journal of Ar-chitecture and Civil Engineering,2009,26(3):1-13.)
[2]蔡克铨,林盈成,林志翰.钢板剪力墙抗震行为与设计 [J].建筑钢结构进展,2007,9(5):19-25.
(CAI Ke-quan,LIN Ying-cheng,LIN Zhi-han.Seismic behavior and design of steel plate shear wall [J].Progress in Steel Building Structure,2007,9(5):19-25.)
[3]白杨,王卫华,张伟,等.开缝钢板剪力墙滞回性能研究 [J].建筑钢结构进展,2018,20(2):28-35.
(BAI Yang,WANG Wei-hua,ZHANG Wei,et al.Study on hysteretic behavior of shear wall with slotted steel plate [J].Progress in Steel Building Structure,2018,20(2):28-35.)
[4]Shekastehband B,Azaraxsh A,Showkati H.Experimental and numerical study on seismic behavior of LYS and HYS steel plate shear walls connected to frame beams only [J].Archives of Civil & Mechanical Engineering,2017,17(1):154-168.
[5]徐敬文.薄钢板覆面冷弯薄壁型钢墙体抗剪性能研究 [D].沈阳:沈阳工业大学,2017.
(XU Jing-wen.Study on shearing properties of cold-formed thin-walled steel walls [D].Shenyang:Shen-yang University of Technology,2017.)
[6]汤序霖,丁昌银,陈庆军,等.带加劲肋多腔双层钢板![]() 混凝土组合剪力墙的抗震性能试验 [J].工程力学,2017,34(12):150-161.
混凝土组合剪力墙的抗震性能试验 [J].工程力学,2017,34(12):150-161.
(TANG Xu-lin,DING Chang-yin,CHEN Qing-jun,et al.Experimental study on seismic behavior of composite shear walls with stiffened multi-cavity and double-wall plates [J].Engineering Mechanics,2017,34(12):150-161.)
[7]陈丽华,夏登荣,刘文武,等.双钢板![]() 混凝土组合剪力墙抗震性能试验研究 [J].土木工程学报,2017,50(8):10-19.
混凝土组合剪力墙抗震性能试验研究 [J].土木工程学报,2017,50(8):10-19.
(CHEN Li-hua,XIA Deng-rong,LIU Wen-wu,et al.Experimental study on seismic behavior of double steel plate-concrete composite shear walls [J].China Civil Engineering Journal,2017,50(8):10-19.)
[8]Rassouli B,Shafaei S,Ayazi A,et al.Experimental and numerical study on steel-concrete composite shear wall using light-weight concrete [J].Journal of Constructional Steel Research,2016,126:117-128.
[9]Shafaei S,Ayazi A,Farahbod F.The effect of concrete panel thickness upon composite steel plate shear walls [J].Journal of Constructional Steel Research,2016,117:81-90.
[10]Zhao Q,Astaneh-Asl A.Cyclic behavior of traditional and innovative composite shear walls [J].Journal of Structural Engineering,2004,130(2):271-284.
[11]Dong Q L,Guo Y L.Ultimate shear capacity of buckling-restrained steel plate shear walls [C]//Proceeding of Eighth Pacific Structural Steel Conference:Steel Structures in Natural Hazards.Wairakei,New Zealand,2007:335-340.