构件受压时GFRP管对核心混凝土具有较好的约束作用[1-3]，而对于GFRP管钢骨混凝土受弯构件来讲，GFRP管对核心混凝土的约束效果相对较差，但实际工程中GFRP混凝土组合构件承受弯矩作用却较为常见，如大偏心受压构件、小偏心受压构件和拉弯构件除承受轴力作用外也会受到弯矩的作用[4-5].受风荷载或地震荷载作用的多层、高层建筑的承重柱，受水平荷载作用的桩基础等均承受弯矩作用，因此，研究GFRP管混凝土构件的受弯力学性能是十分必要的[6-7].
现阶段国内对GFRP管约束钢骨混凝土受弯构件的研究较少.周乐[8]进行了三组试验构件分析管壁厚度和纤维缠绕角度对组合构件受弯承载力的影响，由于试验构件有限，不能详细分析各因素对受弯承载力的影响.本文通过有限元软件ABAQUS建立数值计算模型，在数值模拟结果与试验结果吻合良好的前提下，进一步研究GFRP管的纤维缠绕角度、剪跨比、GFRP管管壁厚度等因素对GFRP管约束混凝土组合构件受弯力学性能的影响.
1 有限元分析
1.1 混凝土本构关系
目前，国内外关于GFRP约束混凝土的本构模型研究较多[9-11].钱稼茹和刘明学通过大量的试验研究，考虑到FRP管本身的结构、纤维铺层缠绕以及构件的加载方式等主要因素的影响，提出了适用于FRP管混凝土的σ-ε计算模型[12]，即
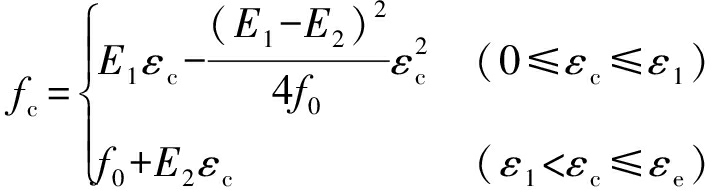
(1)
式中：f0为直线段在应力轴上的值，f0=(1+0.303fy/f ′co)f ′co；εc为混凝土受约束状态下峰值应变；E1为约束混凝土的弹性模量，全截面加载FRP管约束混凝土时，E1=(Ec+pEGFRP)/(1+p)；p为FRP管与混凝土截面面积的比值，
为直线段的斜率，
1.2 GFRP管本构模型
本文采用ABAQUS中单层板模型模拟GFRP管的弹性段力学性能，复合材料的损伤演化过程则采用Hashin破坏准则进行模拟[13]，而单层板的相关材料参数采用文献[14]中数据(见表1)，并利用复合材料细观力学中的计算方法进行计算，同时利用ABAQUS中composite layup模块对GFRP管进行铺层设计来实现不同管壁厚度和纤维缠绕角度的模拟.铺层设计以6 mm厚、纤维缠绕角度为30°的GFRP管为例，铺层情况如表2所示，铺层方式如图1所示.
表1 单层板材料参数
Tab.1 Material parameters of single layer plate
Xt/MPaXc/MPaYt/MPaYc/MPaE11/MPaE22/MPaG12/MPaSL/MPaV123501501405012680843022870400.3
表2 GFRP管铺层情况
Tab.2 Laying situation of GFRP tube
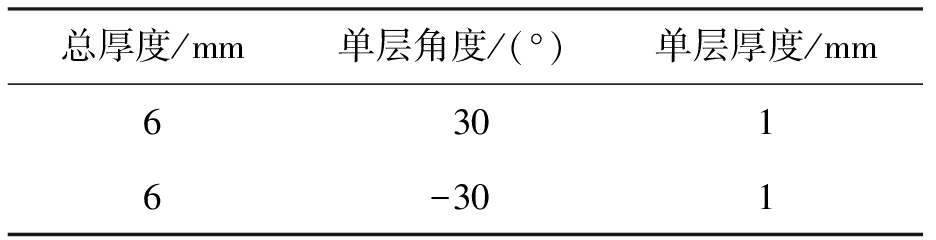
总厚度/mm单层角度/(°)单层厚度/mm6 3016-301
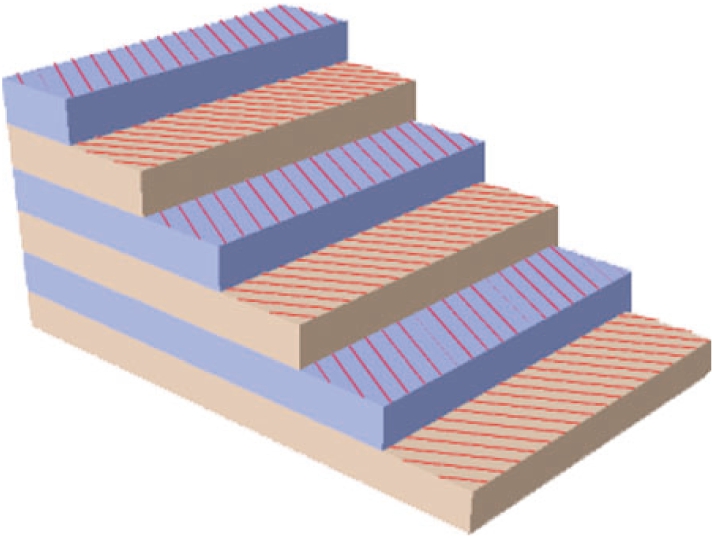
图1 GFRP管铺层方式
Fig.1 Laying pattern of GFRP tube
1.3 有限元模型建立
混凝土和GFRP管之间的接触在切向部分采用ABAQUS中自带的库伦摩擦模型，GFRP管与核心混凝土通过粘结作用使得它们之间的相对运动为零，GFRP管与端板接触采用shell to solid coupling命令，钢骨采用embed命令嵌入混凝土.为提高数值计算效率，简化计算模型，取1/2模型进行计算分析，跨中施加关于Z轴对称约束，并施加竖向荷载，端板处施加X向约束，混凝土和垫块采用C3D8R单元，型钢和GFRP管采用壳单元S4R进行模拟，厚度方向上均采用3个积分点的Poisson积分，各部分的有限元模型及边界条件如图2所示.
2 试验验证
为验证数值模型的准确性，本文采用文献[8]中试验数据与数值模拟的荷载
挠度(N-U)曲线进行对比，试验进行的三组详细数据以及计算承载力与试验承载力对比如表3所示，数值模拟数据与试验数据的对比结果如图3所示.
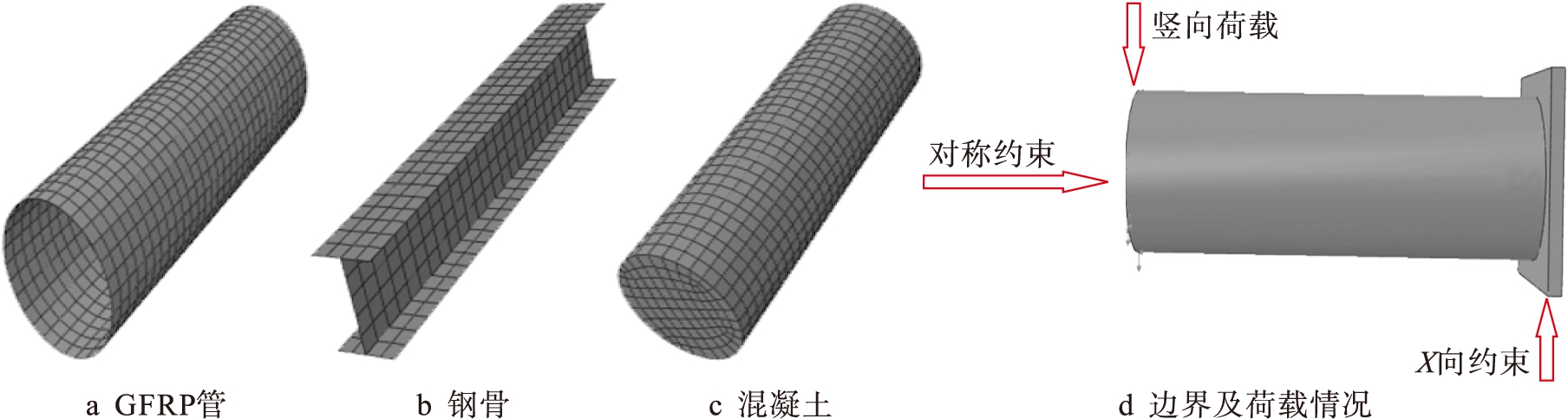
图2 各部分构件模型边界及网格划分情况
Fig.2 Boundary and meshing condition for each member modelling
表3 构件试验数据
Tab.3 Test data of members
试件编号t/mmL/mmD/mmfc/MPa纤维缠绕角度/(°)Nexp/kNNcal/kNNexp/NcalWGSC15120020048.6801771870.95WGSC25120020048.6601962030.97WGSC33120020048.6601801761.02
注：t为管壁厚度；L为梁的计算跨度；D为梁的外径；fc为混凝土圆柱体抗压强度；Nexp为试验承载力；Ncal为计算承载力.
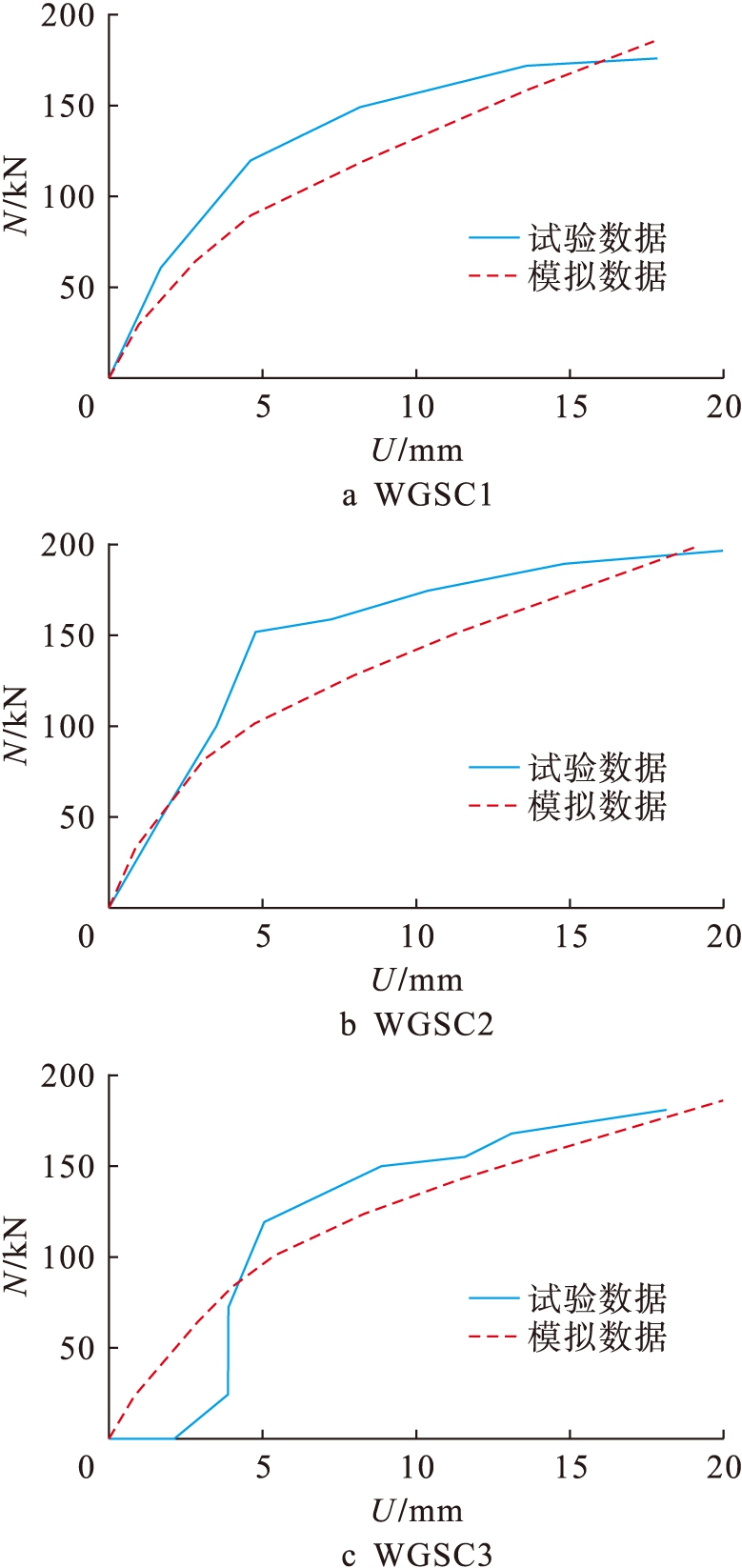
图3 试验曲线与模拟曲线对比
Fig.3 Comparison of experiment and simulation curves
由试验与数值模拟N-U曲线对比可见，模拟数据与试验数据在构件的弹性阶段吻合较好.但是随着挠度进一步增加，模拟数据和试验数据出现一定偏差，这是由于随着挠度增加，纤维断裂，GFRP管对混凝土约束作用下降，而有限元模拟时假定GFRP管和混凝土之间的作用不改变，并忽略两者之间的相对滑动，但从总体来看，试验曲线与模拟曲线较为接近.由表3可知，计算承载力与试验承载力计算结果比值平均值为0.98，均方差为0.03，承载力计算结果较为准确，因此，模型准确性得到验证.
3 M-U曲线影响因素分析
影响GFRP管约束混凝土组合构件受弯力学性能的主要因素有：GFRP管纤维缠绕角度、剪跨比和GFRP管管壁厚度等.图4为纤维缠绕角度影响曲线.由图4a可知，纤维缠绕角度对弯矩挠度(M-U)曲线的影响在荷载作用初期较小，因为荷载作用初期混凝土的侧向膨胀比较小，GFRP管对混凝土的约束作用不明显，构件挠度相似；随着荷载继续增大，混凝土受拉开裂，钢骨和GFRP管的约束效果开始显现，构件挠度增长变缓；当挠度达到30 mm时，纤维缠绕角度为60°和80°构件的受弯承载力分别比角度为30°的构件提升了47%和66%.可见纤维缠绕角度越大，构件受弯能力越强，这是由于混凝土裂纹与玻璃纤维之间夹角越大，其对混凝土在弯矩荷载作用下竖向挠度起到约束作用越强.受弯承载力随着纤维缠绕角度的增加基本呈线性增长，如图4b所示.
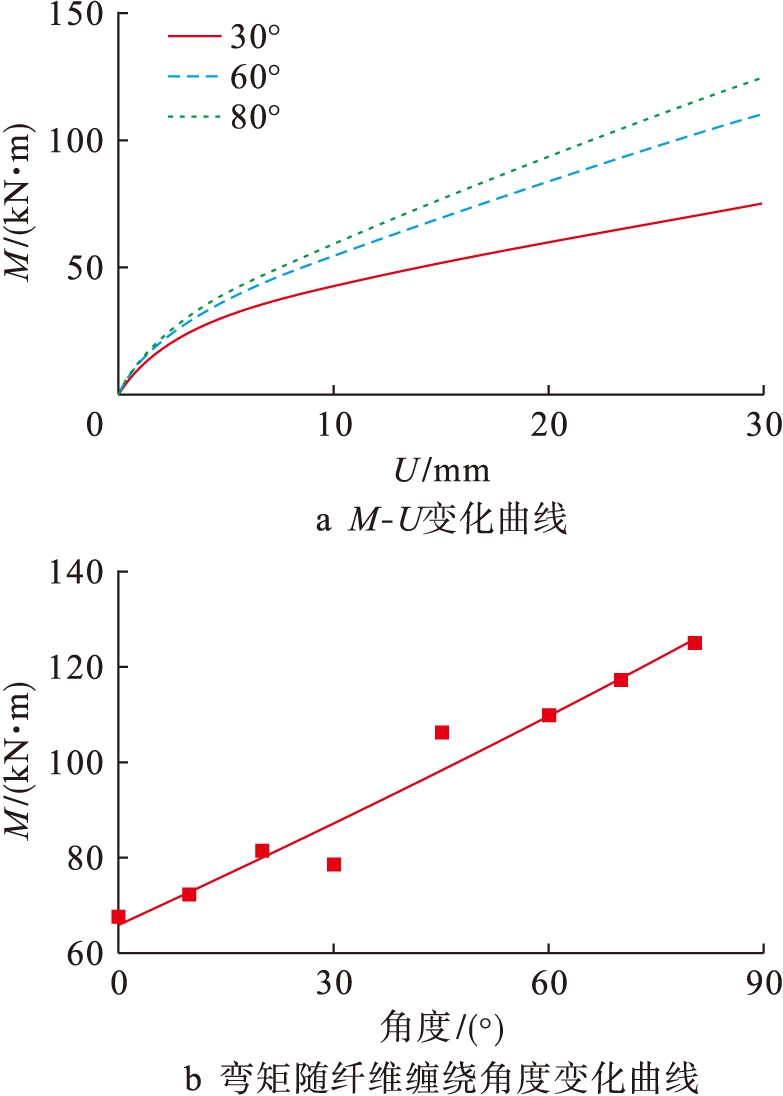
图4 纤维缠绕角度对M-U影响曲线
Fig.4 Effect of fiber winding angle on M-U curve
图5为钢骨型号影响曲线.由图5a可知，随着钢骨型号改变，钢骨截面积增大，钢骨的存在提高了组合结构的初始刚度，M-U曲线弹性段增大，弹性段M-U曲线斜率较大，构件受弯承载力大大提升.钢骨型号I14和I16对应的弯矩比I12.6提高了10%和25%，弯矩随钢骨型号改变呈抛物线型增长，如图5b所示.
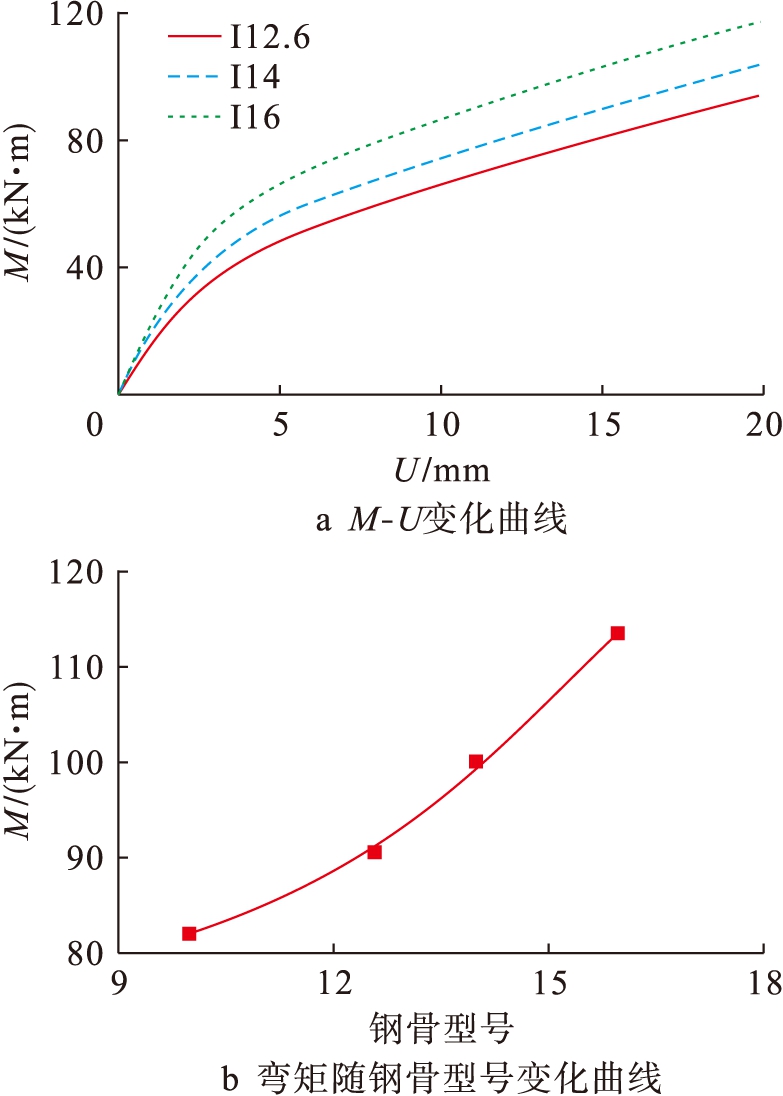
图5 钢骨型号对M-U影响曲线
Fig.5 Effect of steel type on M-U curve
图6为混凝土强度等级影响曲线.由图6a可知，由于混凝土为脆性材料，弹性阶段时混凝土受垂直于截面的荷载作用，很快达到抗拉强度极限，此时挠度增长较小，在荷载作用下，混凝土受拉区退出工作，因此，混凝土强度等级对组合构件的受弯承载力影响不大.由图6b可知，受弯承载力随混凝土强度等级的提高基本呈线性增长，但增幅较小.
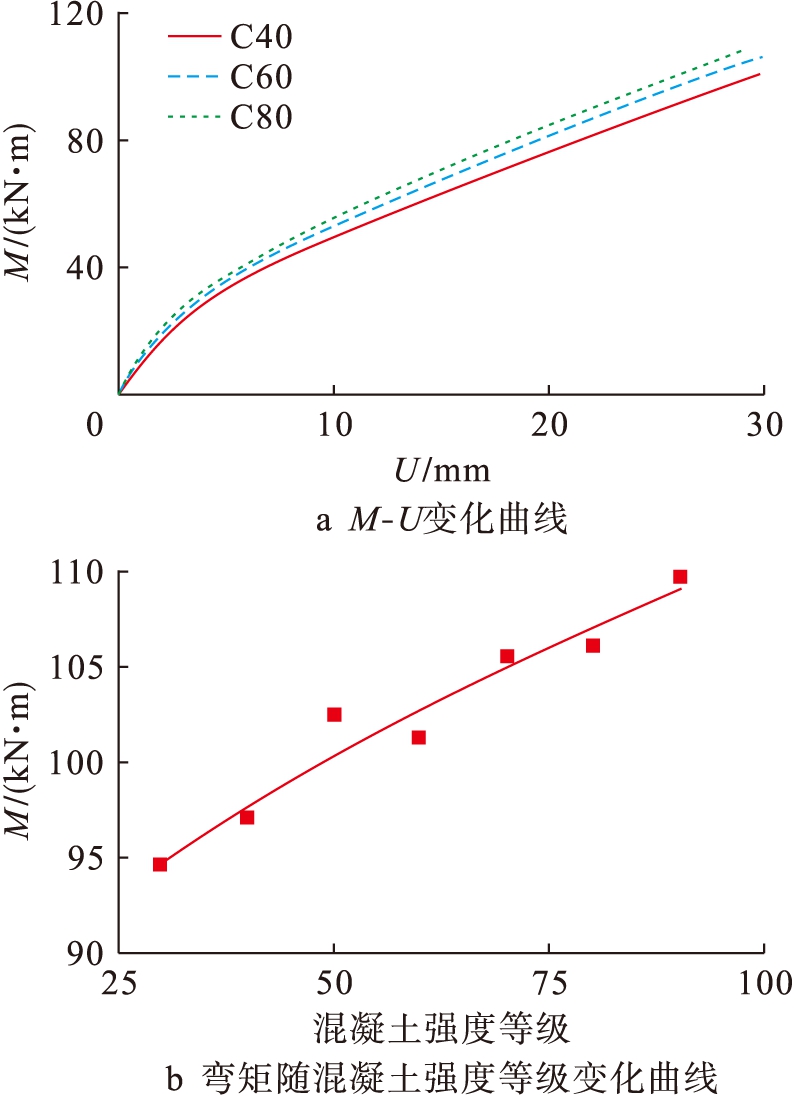
图6 混凝土强度等级对M-U影响曲线
Fig.6 Effect of concrete strength grade on M-U curve
图7为钢骨强度影响曲线.在受力初期，核心混凝土、钢骨在粘结滑移的作用下协同工作，可看成一个整体，高强度的钢骨使得混凝土和钢骨的组合初始刚度变大，弹性段延长.由图7a可知，钢骨强度为Q300和Q400构件的受弯承载力比钢骨强度为Q235构件的承载力分别提高7%和18%.随着钢骨屈服强度增加，受弯承载力也基本呈线性增长.
图8为剪跨比影响曲线.剪跨比对组合柱的M-U曲线具有显著影响，随着剪跨比的增大，试件在承担相同荷载作用下还要承担自身重力，自身重力引起的跨中弯矩与长度呈二次函数关系；剪跨比由3增加至3.75和5时，其对应的受弯承载力分别下降了28.8%和57.8%.承载力随跨度的增加基本呈二次函数下降趋势.
图9为管壁厚度影响曲线.弹性阶段组合构件的受弯能力主要由受拉混凝土提供，侧向膨胀小，GFRP管不参与工作，此时M-U曲线基本重合；随着荷载增加，混凝土受拉裂纹增多，GFRP管约束作用进一步提高，较厚的GFRP管纤维缠绕层数多，其能很好地抑制侧向裂纹的扩展，对核心混凝土起到较强的约束作用；管壁厚度为6 mm和7 mm时构件的受弯承载力比4 mm的构件提升了13%和26%.构件承载力随管壁厚度的增加呈线性增长.
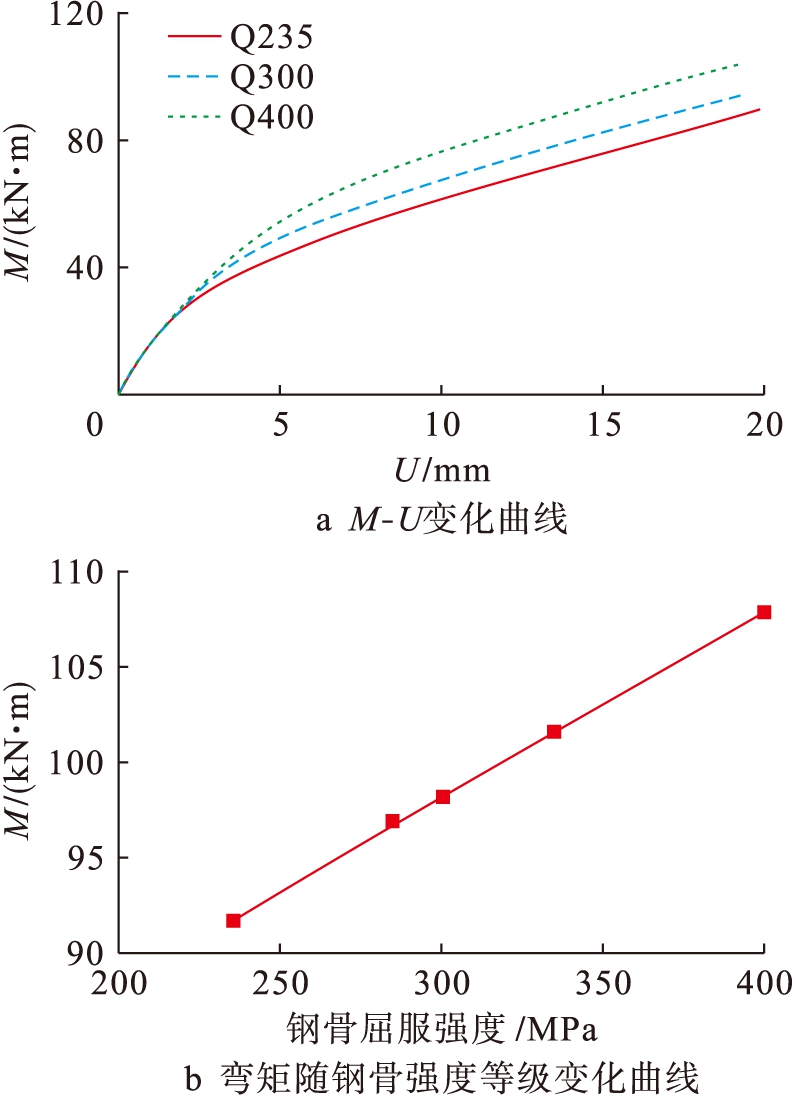
图7 钢骨强度对M-U影响曲线
Fig.7 Effect of steel strength on M-U curve
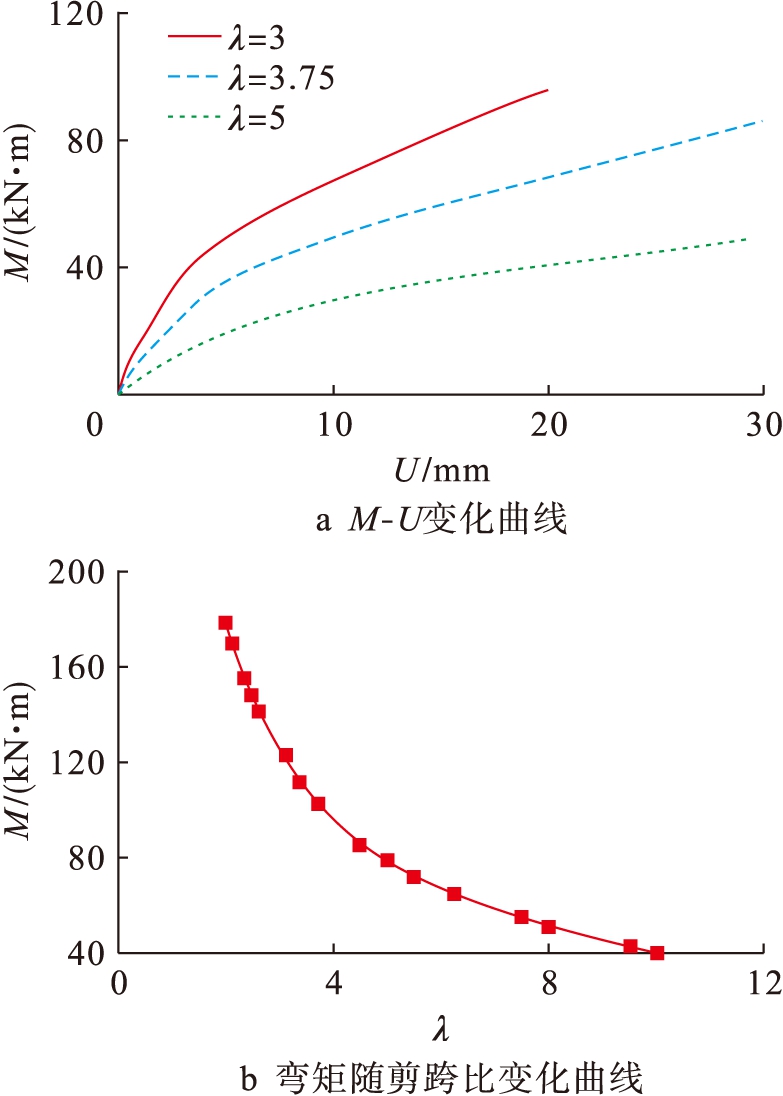
图8 剪跨比对M-U影响曲线
Fig.8 Effect of shear span ratio on M-U curve
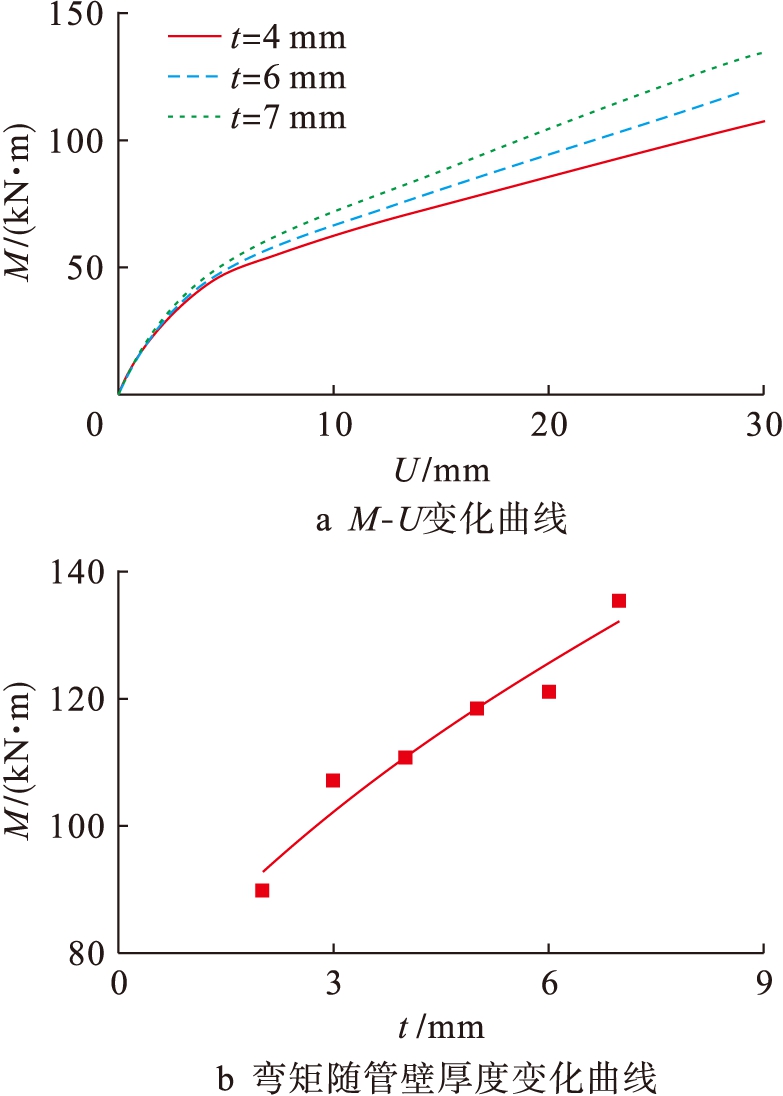
图9 GFRP管管壁厚度对M-U影响曲线
Fig.9 Effect of wall thickness of GFRP tube on M-U curve
将受弯承载力影响因素简化为套箍系数θ(θ=
为GFRP管的环向抗拉强度，Af为GFRP管的截面积)与配骨指标
为钢骨的屈服强度，As为钢骨截面积).
图10为套箍系数与配骨指标对承载力的影响曲线.由图10a可知，随着套箍系数的增大，GFRP管有效面积增大，当构件受跨中荷载作用时，跨中侧向挠度增长较快，有效面积较大的GFRP管对核心混凝土的约束作用较强，约束混凝土在三向受压下保持较高的刚度，即GFRP管组合构件的承载力随着套箍系数的增加而增加，呈线性变化趋势.
对于配骨指标的影响，由图10b所示，在核心混凝土一定的情况下，型钢与混凝土粘结在一起形成统一整体，型钢截面积增大时，型钢翼缘和腹板对混凝土的约束也随之增强，这都能使得组合构件的初始刚度得到提升，从而使得承载力显著提升，承载力的增长与配骨指标也基本呈直线关系.
4 承载力公式简化计算
基于钢管混凝土的统一理论，文献[8]给出了GFRP管混凝土组合构件受弯的承载力计算公式，但未考虑剪跨比引起的构件承载力衰减问题.
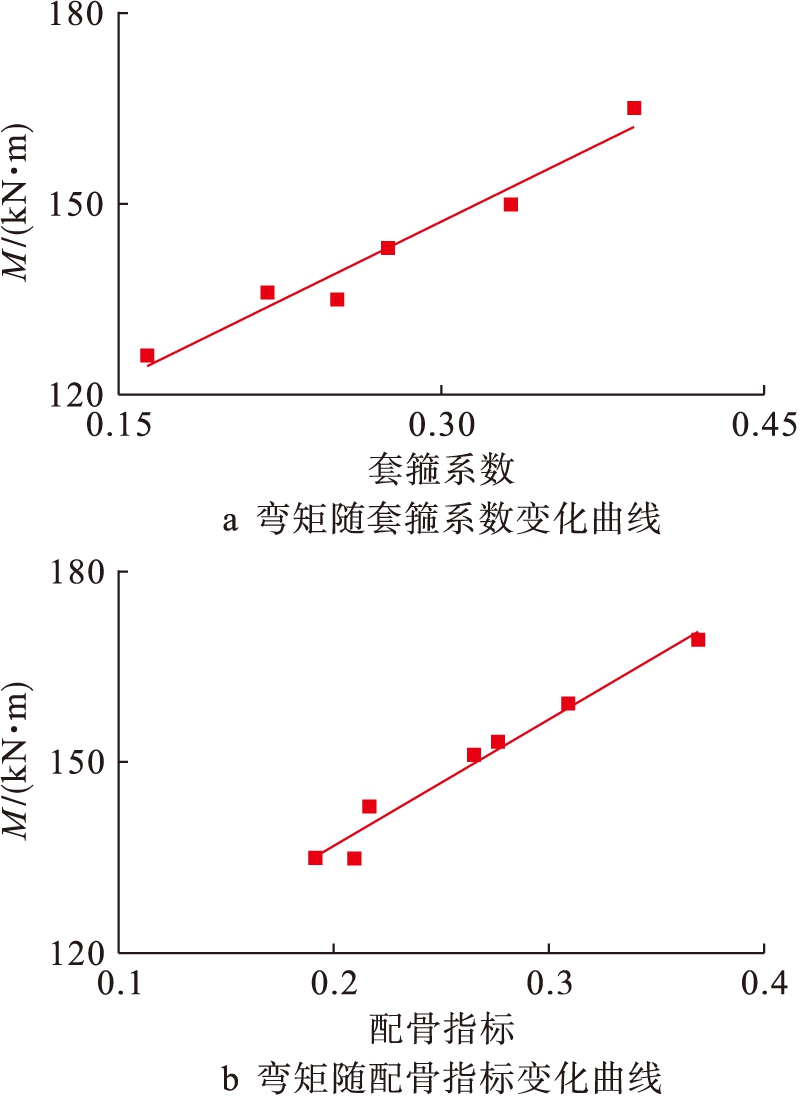
图10 套箍系数与配骨指标对承载力的影响曲线
Fig.10 Effect of hoop coefficient and steel index on flexural capacity curve
本文通过对ABAQUS计算结果和已有试验结果进行回归分析，对已有受弯承载力公式进行简化计算，即
M=φ0.282 1r(0.894 37+1.000 1θ+
0.992 7ρs)Ac fc
(2)
式中：φ为稳定系数，
为剪跨比折减系数；r为构件截面外半径.
剪跨比折减系数的推导通过改变试件剪跨比进行数值分析.梁跨中的弯矩随剪跨比的增加而减小，对计算结果和试验数据进行回归，得到梁承载力随剪跨比的折减系数计算公式，即
(3)
为了验证本文建立的承载力计算公式的适用性和精确程度，将文献[8]和计算的试验数据代入式(2)进行计算，计算结果如表4所示.由表4可知，计算结果与试验结果吻合较好，Mcal/Mexp的平均值为1.057，均方差为0.046，因此，该承载力公式符合要求，但是由于试验数据不足，无法全面反映组合构件实际受弯时的复杂性，该公式的应用具有一定局限性，其准确度需进一步进行验证.
表4 计算值与试验值对比
Tab.4 Comparison of calculated and experimental values
试件编号λθρsMexpMcalMcal/MexpSW12.20.75580.364665.4070.821.08SW22.60.65390.2239103.33105.760.98WGSC23.01.00770.364672.3679.681.10SW33.30.62290.364661.8066.141.07
注：Mexp为试验弯矩值；Mcal为计算弯矩值.
5 结 论
通过采用ABAQUS对GFRP管混凝土组合构件的受弯力学性能影响因素进行系统数值模拟，对比分析其弯矩挠度曲线，可得出以下结论：
1) 所采用模型的数值模拟计算结果与已有文献试验结果较为吻合，证明本文所采用方法及模型的正确性.
2) 管壁厚度、剪跨比、纤维缠绕角度对承载力影响较大，其中管壁厚度为6和7 mm时构件的受弯承载力比4 mm的构件提升了13%和26%；剪跨比由3增加至3.75和5时，其对应的受弯承载力分别下降了28.8%和57.8%；缠绕角度为60°和80°构件的受弯承载力分别比角度为30°的构件提升了47%和66%.而混凝土强度等级对承载力影响较小.GFRP组合构件的受弯承载力与管壁厚度、纤维缠绕角度、混凝土强度等级、钢骨强度、套箍指标呈线性关系，随着钢骨截面面积的增加呈抛物线型增长，随剪跨比跨度的增加基本呈二次函数下降趋势.
3) 基于试验、数值模拟结果和钢管混凝土统一理论，在考虑剪跨比的影响下对受弯承载力公式进行修正，公式的计算结果与试验结果吻合较好，对GFRP约束混凝土构件受弯承载力研究有一定参考意义.
[1]曹朋朋.FRP管约束钢骨混凝土中长柱偏压力学性能研究 [D].沈阳：沈阳建筑大学，2013.
(CAO Peng-peng.Mechanical behavior of steel-encased concrete filled FRP tube column under unidirec-tional eccentric compression [D].Shenyang：Shen-yang Jianzhu University，2013.)
[2]夏玉民.GFRP管钢筋混凝土组合构件偏心受压的力学性能研究 [D].沈阳：沈阳建筑大学，2011.
(XIA Yu-min.Mechanical behavior study on GFRP tube filled with reinforced concrete members under eccentric compression [D].Shenyang：Shenyang Jianzhu University，2011.)
[3]宋志刚，樊成，宋力.GFRP管混凝土轴压短柱承载力研究 [J].水利与建筑工程学报，2017，15(2)：71-75.
(SONG Zhi-gang，FAN Cheng，SONG Li.Bearing capacity of the GFRP tube filled with concrete under the axial compression [J].Journal of Water Resources and Architectural Engineering，2017，15(2)：71-75.)
[4]李文，杨思雨，那昱.GFRP管混凝土钢管组合柱轴压性能 [J].沈阳工业大学学报，2017，39(3)：346-351.
(LI Wen，YANG Si-yu，NA Yu.Axial compression performance of GFRP-concrete-steel tubular composite column [J].Journal of Shenyang University of Technology，2017，39(3)：346-351.)
[5]李文，孟瑞，那昱.轴压下GFRP管混凝土钢管组合柱的尺寸效应 [J].沈阳工业大学学报，2017，39(4)：464-468.
(LI Wen，MENG Rui，NA YU.Size effect of GFRP-concrete-steel tubular composite columns under axial compression [J].Journal of Shenyang University of Technology，2017，39(4)：464-468.)
[6]李阳.GFRP管钢筋混凝土梁受力性能分析 [D].大庆：东北石油大学，2013.
(LI Yang.Research on mechanical properties of the reinforced concrete filled GFRP tube beams [D].Daqing：Northeast Petroleum University，2013.)
[7]张霓，王连广.GFRP管混凝土钢管受弯构件非线性分析 [J].钢结构，2014(12)：8-12.
(ZHANG Ni，WANG Lian-guang.Nonlinear analysis of flexural menbers of GFRP-concrete-steel double-skin tubular [J].Steel Construction，2014(12)：8-12.)
[8]周乐.GFRP管钢骨高强混凝土组合构件力学性能研究 [D].沈阳：东北大学，2009.
(ZHOU Le.Mechanical behaviors study of GFRP tube filled with steel-reinforced high-strength concrete composite members [D].Shenyang：Northeastern University，2009.)
[9]Lam L，Teng J G.Design-oriented stress-strain model for FRP-confined concrete [J].Construction and Building Materials，2003，17(6/7)：471-489.
[10]Toutanji H，Saafi M.Durability studies on concrete columns encased in PVC-FRP composite tubes [J].Composite Structures，2001，54(1)：27-35.
[11]吴刚，吕志涛.FRP约束混凝土圆柱无软化段时的应力应变关系研究 [J].建筑结构学报，2003，24(5)：1-9.
(WU Gang，LÜ Zhi-tao.Study on the stress-strain relationship of FRP-confined concrete circular column without a strain-softening response [J].Journal of Building Structures，2003，24(5)：1-9.)
[12]刘明学，钱稼茹.FRP约束圆柱混凝土受压应力应变关系模型 [J].土木工程学报，2006，39(11)：1-6.
(LIU Ming-xue，QIAN Jia-ru.Compressive stress-strain model for concrete of FRP confined cylinders [J].China Civil Engineering Journal，2006，39(11)：1-6.)
[13]Hashin Z.Failure criteria for unidirectional fiber composites [J].Journal of Applied Mechanics，1980，47(2)：329-334.
[14]秦国鹏.GFRP管钢筋混凝土构件力学性能研究 [D].沈阳：东北大学，2010.
(QIN Guo-peng.Mechanical behaviors study on GFRP tube filled with reinforced concrete members [D].Shenyang：Northeastern University，2010.)