目前,大功率兆瓦级风力机的空气动力学和结构特性优化设计已经成为了研究重点.而风轮作为风力机的主要组成部分,其成本占到整个风力机的20%左右,同时风轮也是风力机捕获风能的关键部分,因此,国内外学者从不同的方面,对于风力机叶片进行优化设计研究,以获取良好的气动特性和结构特性.研究者们提出在保持风轮直径不变或增加较少的前提下,将叶片适当后掠的概念,也称为几何自适应[1].研究表明:作为一种自适应的气动降载布局设计,后掠型叶片在相同结构载荷下,可增加风轮直径,从而增大捕风面积,增加发电量,降低度电成本;在保证相同发电量下,可有效减少结构载荷,降低风轮与相关零部件的制造成本,提高结构可靠性,降低维护成本,因此,这种叶片具备较好的使用价值和应用前景[2].
后掠叶片在气动载荷作用下发生沿顺桨方向的扭转,虽然降低了叶片上的气动力,但是也可能降低叶片的功率输出,因此,在设计后掠自适应叶片时,进行一体化设计优化是必需的[3],这其中就包括各运行风况下,后掠叶片桨距角的优化设计.丁勇钢等[4]通过对风机控制系统的优化,实现发电量的最大化和叶片轴向推力的最小化.
后掠叶片在结构和空气动力学方面表现出较强非线性,需要采用恰当的非线性气弹耦合模型表达空气动力与叶片弹性变形以及振动时的相互作用.为此,本文通过将柔性叶片离散为由运动副和力元联接的多体系统[5-6],应用计算多体系统动力学理论建立叶片非线性气弹耦合方程[7].在叶片气动载荷分析方面,后掠叶片表现出显著的三维流动,螺旋尾涡升力线模型将叶片用环量连续变化的升力线代替,具有较好的三维流场分析能力[8].
采用“超级单元”方法[9]将后掠叶片离散成若干个由运动副和力元联接的刚体,应用Roberson-Wittenburg递推建模方法,结合螺旋尾涡升力线模型建立叶片非线性气弹耦合方程.以变桨角为优化设计变量,最大年发电量作为目标函数,将风力机额定功率、最大叶尖挥舞位移和最大轴向推力设为约束条件,对变桨角进行寻优并对结果进行对比分析.
1 后掠叶片非线性气弹耦合模型
后掠叶片具有与直叶片不同的气弹特性,有必要建立恰当的后掠叶片气弹耦合模型.本文在后掠叶片结构非线性模型的基础上,结合升力线理论建立叶片气弹耦合模型.
1.1 后掠叶片结构非线性模型
为了准确描述叶片的结构变形,采用“超级单元”建立叶片模型.其中,每个超级单元由4个刚体(B1~B4)组成,各刚体通过运动副、弹簧和阻尼器连接[5-6],用来描述叶片的挥舞、摆振和扭转变形,其模型如图1所示.
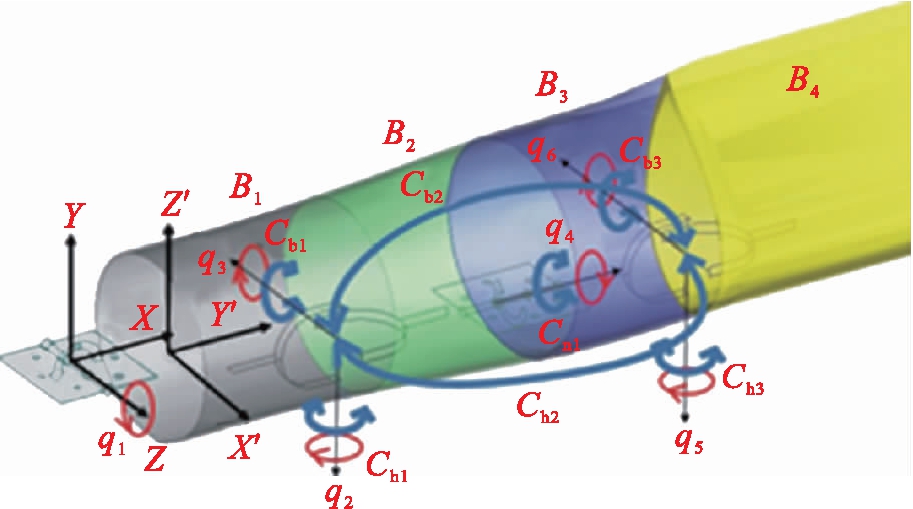
图1 超级单元模型
Fig.1 Super-element model
应用多体系统动力学中的R-W方法,取各铰的转动方向为广义坐标,则从柔性叶片的拓扑构形可得其广义坐标阵为
q(t)=(q1(t),q2(t),…,qs(t))
(1)
式中:q(t)对时间的一阶和二阶导数![]() 分别为广义速度和广义加速度;s为系统自由度,本文s为21.Ch、Cb、Cn分别表示挥舞、摆振、扭转方向的刚度系数.叶片带拉格朗日乘子的多体系统动力学方程表示为
分别为广义速度和广义加速度;s为系统自由度,本文s为21.Ch、Cb、Cn分别表示挥舞、摆振、扭转方向的刚度系数.叶片带拉格朗日乘子的多体系统动力学方程表示为
(2)
式中:Z为广义质量阵;Z′为广义力阵;Φq为约束方程的雅克比矩阵;λ为拉格朗日乘子阵;![]() 为拉格朗日乘子项,表示刚体间所有理想约束力的贡献[10].
为拉格朗日乘子项,表示刚体间所有理想约束力的贡献[10].
1.2 基于升力线理论的后掠叶片气动载荷计算
由于后掠叶片具有显著的展向流动和积叠线弯曲特点,采用升力线模型模拟后掠叶片流场的三维流动.
升力线模型的核心思想是将风力机叶片三维流场中的涡量分布简化为一根涡量沿叶片展向变化的线涡,表示叶片与流场之间的相互作用.该线涡代表了叶片三维流场中的环量分布,因而该线涡也称作附着涡.由Helmholtz第二定理可知,在无粘流体环境中,涡量并不能在流体内部终止,而只能延伸至流体边界或构成封闭区间,附着涡沿叶展方向变化的涡量会从附着涡上脱落形成尾涡,涡方法模型如图2所示.
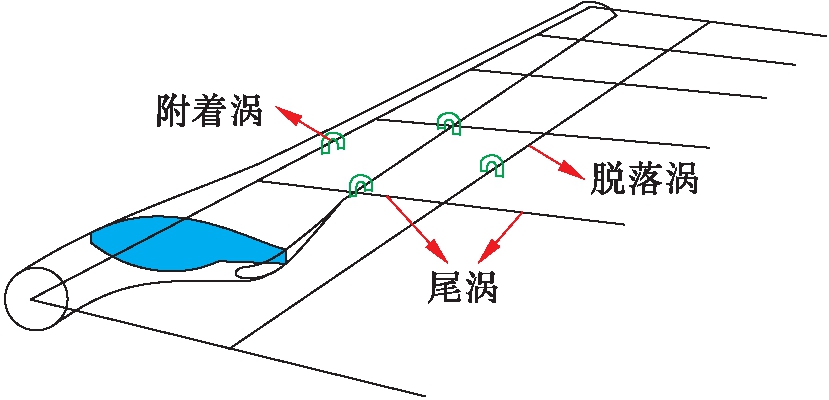
图2 涡方法模型示意图
Fig.2 Schematic model diagram of vortex method
从附着涡上脱落的螺旋尾涡流向叶片下游无限远处,形成诱导速度场,本文采用刚性尾涡模型,尾涡坐标系如图3所示.
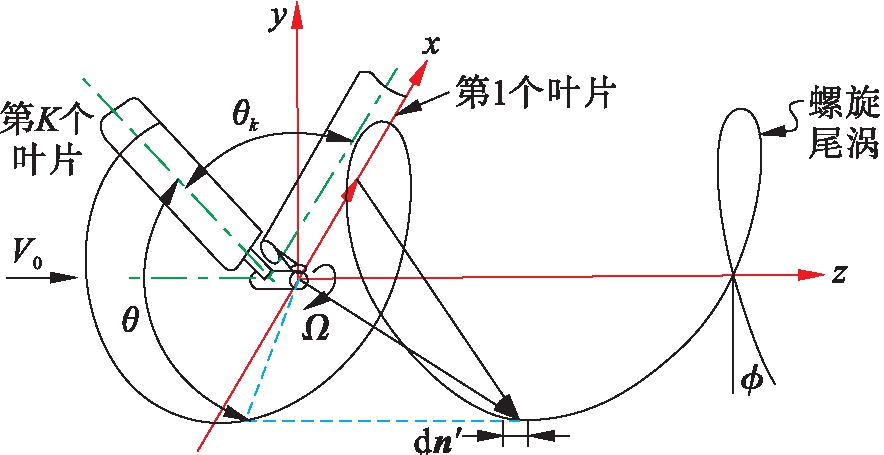
图3 刚性尾涡及其坐标系示意图
Fig.3 Schematic diagram of rigid wake vortex and its coordinate system
文献[10]指出,诱导速度Wn垂直于未受扰动的相对风速W′,并给出了附着涡任意位置e′(已知惯性坐标(x′,y′,z′))处由所有尾涡引起的诱导速度,即
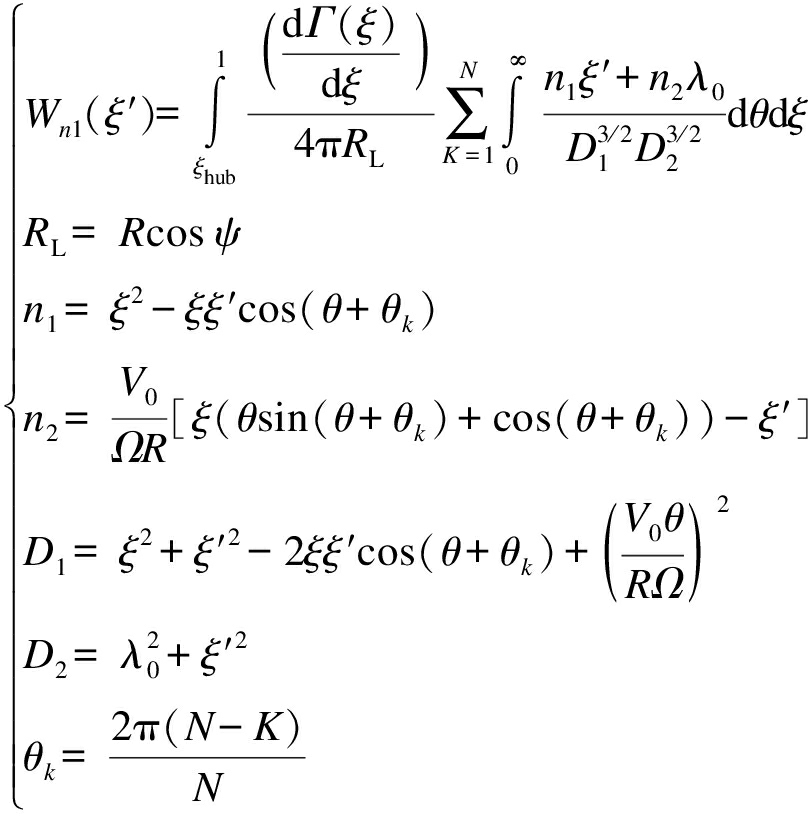
(3)
式中:Γ(ξ)为螺旋尾涡的环量;R为风轮半径;ξ、ξ′为叶展方向无量纲位置参数;ξhub为叶展方向轮毂位置处的无量纲参数;λ0=V0/(RΩcos Λ);V0为来流风速;Λ为当地后掠角;Ω为风轮转速;ψ为风轮锥角;θ为螺旋尾涡的方位角;θk为控制点所在的叶片与发出尾涡的叶片之间的夹角;N为叶片数;K为控制点所在叶片序号.
附着涡线为空间曲线,涡量从轮毂沿着叶片径向流向叶尖,形成诱导速度场,附着涡坐标系如图4所示.
叶片展向位置处受到附着涡上某一直线涡量微段dn′的诱导速度为
(4)
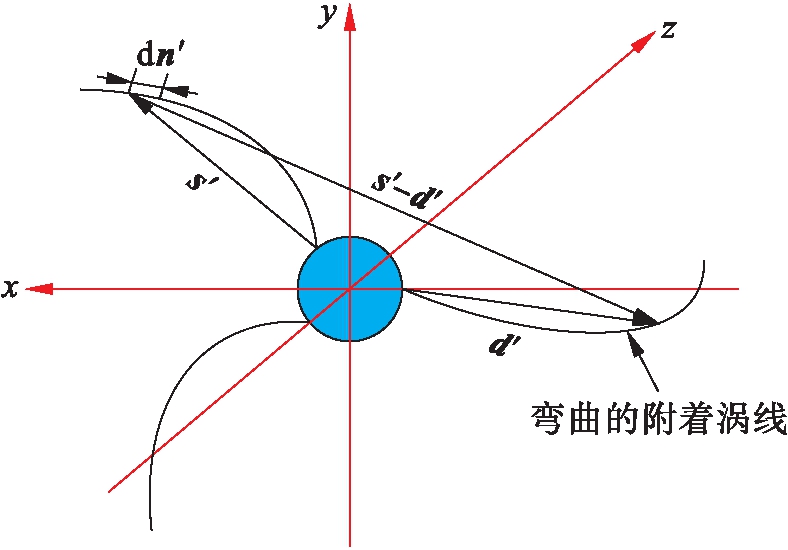
图4 附着涡线及其坐标系示意图
Fig.4 Schematic diagram of attached vortex line and its coordinate system
式中:dWi2为附着涡诱导速度;dwx2、dwy2、dwz2分别为dWi2在x、y、z轴的分量;dn′为附着涡上的微段向量;s′为轮毂中心指向微段dn′的向量;dn′和s′与积叠线形状有关.附着涡诱导速度垂直于相对风速,经过叶片积分得到所有叶片附着涡对控制点的诱导速度为
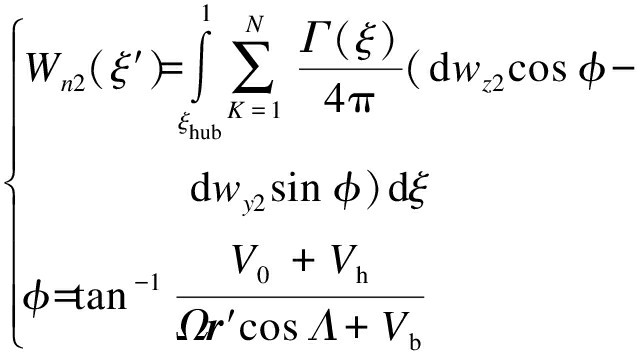
(5)
式中:φ为入流角;Vh和Vb分别为叶片的挥舞、摆振速度.当N=K时,即|s′-e′|=0,式(4)中分子和分母均为0,这不符合物理实际.实际上,由于粘性的作用会使得靠近涡线的中心速度趋于有限值,形成所谓的粘性涡核[8].基于粘性涡核模型建立修正的Biot-Savart公式,在计算诱导速度时引入粘性修正因子,即
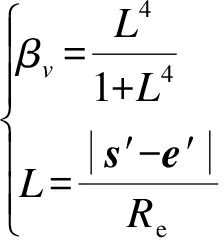
(6)
式中,Re为涡核的有效半径.修正的Biot-Savart公式为
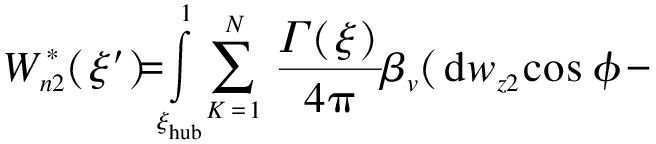
dwy2sin φ)dξ
(7)
控制点上总的诱导速度为
Wn=Wn1+Wn2
(8)
诱导速度表达式(3)和(7)中环量项Γ(ξ)未知.假设附着涡的环量分布为Fourier级数,并且满足边界条件Γ(ξhub)=Γ(1)=0,设环量分布函数为
(9)
一般m取9即可[10].根据Kutta-Joukovski定理可知,环量与升力系数之间的关系为
Γ=0.5cWCL
(10)
式中:c为对应翼型的弦长;CL为升力系数;W为截面位置受扰动的相对风速.
联立式(3)和(7)~(10),代入m个控制点的已知数据,即可得到m个方程,方程组中只有Am未知,求解该方程组可得到Am的初值,利用迭代法[10]可以得到数值精度更高的有效攻角αe.迭代结束得到有效攻角αe和诱导攻角αi,通过二维翼型数据表线性插值得到升力系数CL和阻力系数CD后,沿着叶片径向积分求得轴向推力F和转动功率P,即
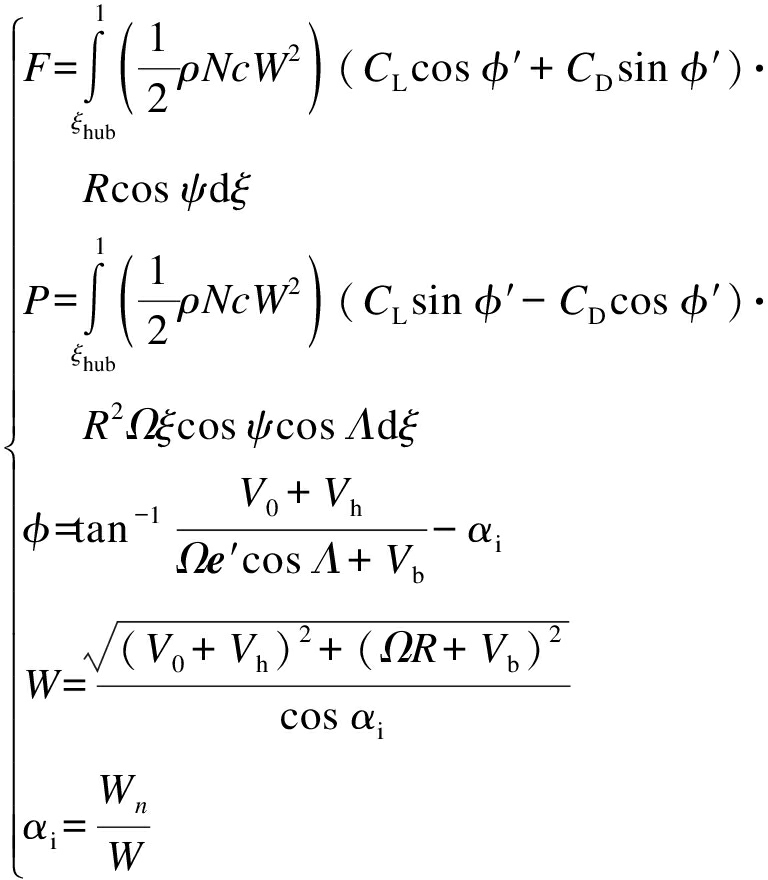
(11)
式中:ρ为空气密度;φ′为实际入流角.
1.3 后掠叶片气弹耦合模型验证算例
为验证后掠叶片非线性气弹耦合模型的准确性和可行性,选用NREL实验室的5 MW风力机直叶片数据[11]和后掠4 m叶片数据[12]进行模型验证.
采用本文建立的气弹耦合模型分别分析了直叶片和后掠叶片风轮在5~25 m/s风速下的气动性能与结构响应,并与文献[12]采用叶素动量理论(BEM)气动模型的分析结果进行对比,结果如图5所示.
从图5可以看出,无论直、后掠叶片,应用本文所建立的气弹耦合模型能够比较准确地进行气动性能计算,结果与文献[12]的结果基本一致.两种分析模型结果随风速增大相差更大一些,这主要是因为对于大型柔性叶片,存在着沿叶片展向的流动,后掠叶片这种流动更为显著一些,使用叶素动量理论计算气动性能时,忽略了气流在叶片展向的流动影响,之后可通过叶根和叶尖损失等经验修正模型进行弥补.而升力线模型考虑了叶片的展向流动与尾流对整个叶片的影响,无需引入经验修正模型,考虑的影响因素和分析效率更高.在结构上由于本文所建立的“超级单元”模型和文献[12]铁木辛柯梁的模型差异,带来计算模拟结果的误差.
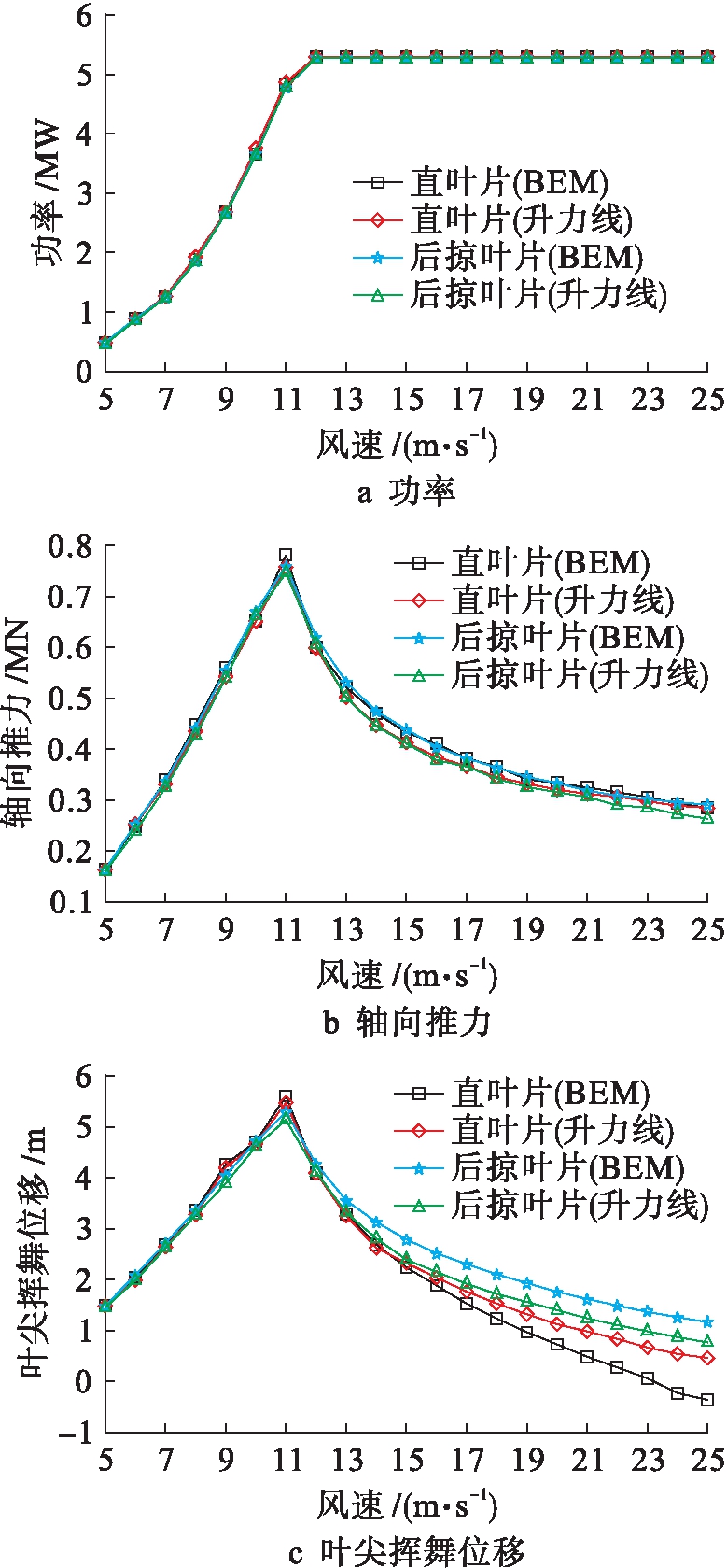
图5 升力线理论和叶素动量理论的稳态计算结果
Fig.5 Steady-state calculation results for lift line and blade element momentum theories
算例验证结果表明,相较于叶素动量理论,基于升力线所建立的气弹耦合模型具有更好的三维流场分析能力,验证了该方法的有效性与准确性.
2 优化设计模型
2.1 后掠叶片外形设计与运行条件
文献[12]后掠叶片积叠线形状计算表达式为
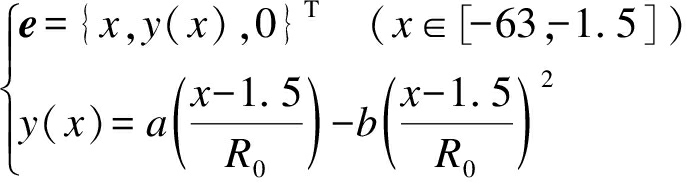
(12)
此处分别取a=8,b=12,即叶尖后掠4 m,R0为叶片长度,R0=61.5 m,则根据式(12)积叠线形状为
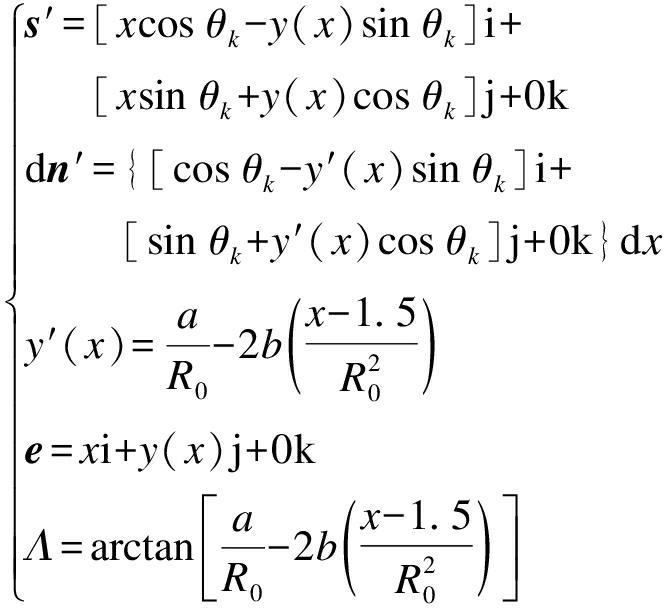
(13)
根据文献[12]取后掠叶片的切入风速为5 m/s、切出风速为25 m/s.在较低风速时叶片保持尖速比8.7运行,随着风速的增加,叶片转速从6 r/min开始增大,当转速提高到12.1 r/min时不再保持额定尖速比,在额定风速达到11.4 m/s后,风轮转速保持为12.1 r/min.
2.2 目标函数
年发电量(AEP)与风场风速的威布尔分布有关[13],理论年发电量的计算公式为
(14)
式中:H为年小时,此处取8 766 h;vi和vi+1为风速;P(vi)和P(vi+1)为风速vi和vi+1对应的功率;B和u分别为风速威布尔分布的尺度因子和形状因子.本文中计算AEP时u取2,B取7.334 5.
2.3 约束条件
为了确保传递到发电机的轴功率不超过其最大容量,需要约束风力机风轮在各风速下的转动功率不能超过额定功率5.3 MW[11],即
Pmax≤5.3 MW
(15)
为保证叶片不会因为挥舞方向变形过大引起结构破坏,变桨角优化后的风机叶片最大叶尖挥舞位移小于NREL 5 MW直叶片的最大叶尖挥舞位移[12],即
δmax≤5.6 m
(16)
风力机风轮的工作寿命、结构强度均与最大轴向推力有关.变桨角优化后的风机叶片最大轴向推力小于NREL 5 MW直叶片的最大轴向推力[12],即
Fmax≤0.779 MN
(17)
2.4 优化变量与优化方法
采用一维搜索优化方法,以变桨角为优化变量,寻求各个风速下,变桨角与功率的拟合函数关系,并求出拟合函数最大功率所对应的变桨角,计算气动性能和结构响应.
3 优化结果分析
按照前面所建立的优化设计方法,对后掠量为4 m的风机叶片在各个风速下的变桨角进行优化,分析中采用升力线模型.图6为优化的后掠叶片与直叶片、后掠叶片[12]在5~25 m/s风速范围内气动性能和结构响应的结果对比(仿真环境为匀流风,不考虑塔影效应和重力影响,设计尖速比为8.7,转速范围为6~12.1 r/min,优化变量为变桨角).
表1为直叶片、后掠叶片与变桨角优化的后掠叶片在风速11 m/s时最大叶尖挥舞位移、最大轴向推力.变桨角优化的后掠叶片与原后掠叶片最大叶尖挥舞位移小于5.6 m,最大轴向推力小于0.779 MN,保证了叶片不会因为挥舞方向变形过大引起结构破坏且不会对风轮的工作寿命和结构强度产生较大影响.
图6a结果表明,在6~11 m/s风速下,变桨角优化的后掠叶片输出功率显著提升;在12~25 m/s风速下,各叶片的输出功率已经达到额定功率5.3 MW,功率不再增加.通过式(14)计算变桨角优化的后掠叶片、原后掠叶片和直叶片的年发电量,其值分别为14 393 942、13 257 036、13 378 251 kW·h,变桨角优化的后掠叶片年发电量相较于其余叶片的年发电量有明显提高,与原后掠叶片相比提高约8.58%、与直叶片相比提高约7.59%.
图6b、c结果表明,在6~11 m/s风速下,后掠叶片的轴向推力、叶尖挥舞位移有所增加;在12~25 m/s风速下,轴向推力、叶尖挥舞位移显著减少.通过优化后掠叶片的变桨角,使叶片在高风速下维持5.3 MW的同时,减少了对风轮和塔架的载荷,提高结构可靠性.
图6d结果表明,原后掠叶片在5~11 m/s风速下变桨角一直减小,这是由于叶片积叠线后掠,在相同条件下后掠叶片切向力要乘上后掠角余弦值,使功率(转动力矩)比直叶片要小;要让后掠叶片获得与直叶片相近的功率(转动力矩)则需要增大气动载荷,所以后掠叶片变桨距角比直叶片小,在11 m/s风速下取得最小值.在12~25 m/s风速下变桨角一直增大,使得功率维持在5.3 MW附近,变桨角优化的后掠叶片在7~11 m/s风速下,变桨角进一步减小,增大了有效攻角,提高了升力系数CL,从而提高了功率,增大轴向推力和叶尖挥舞位移.
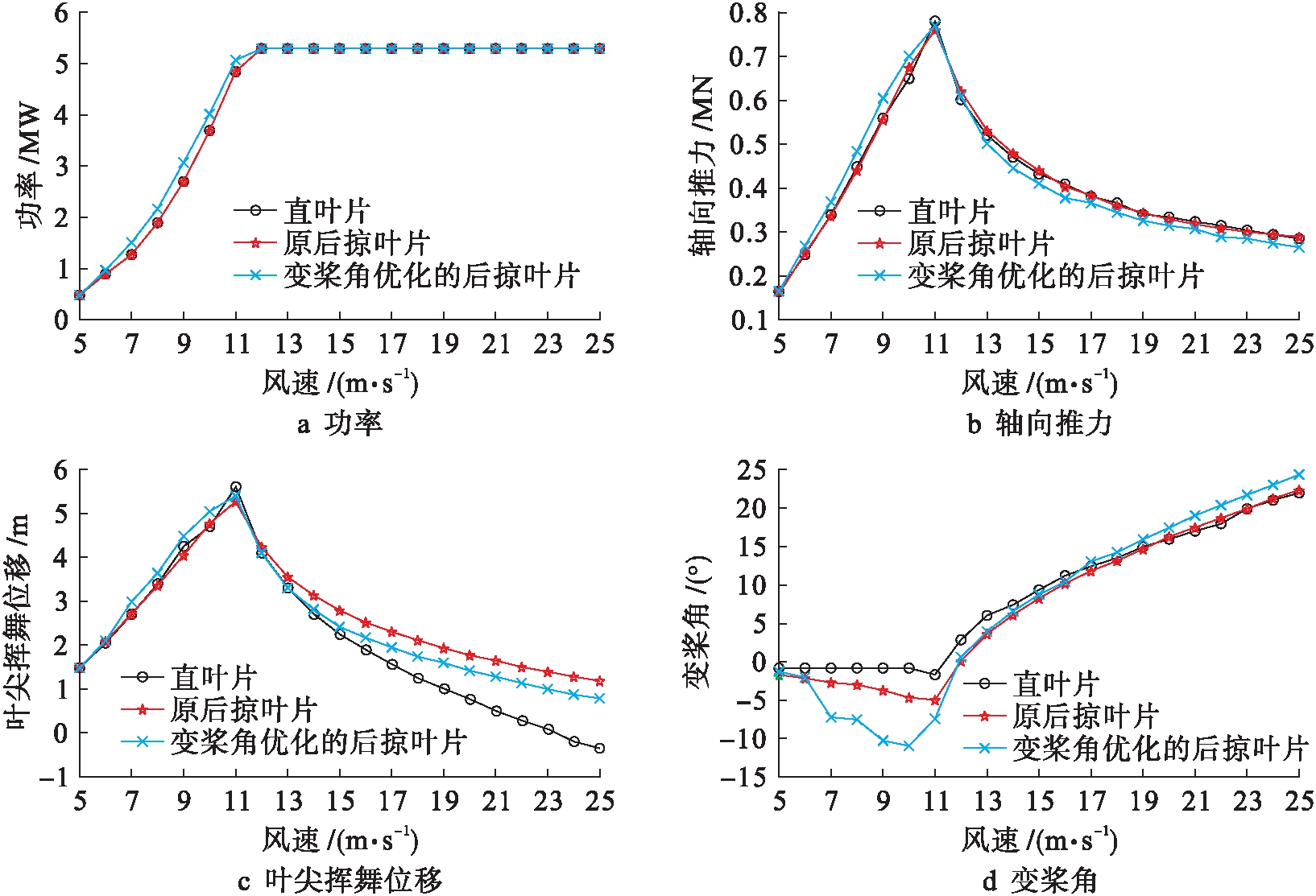
图6 气动性能和结构响应计算结果
Fig.6 Calculation results for aerodynamic performance and structural response
表1 11 m/s风速下最大叶尖挥舞位移、最大轴向推力
Tab.1 Maximum flapwise tip deflection and axial thrust at wind speed of 11 m/s
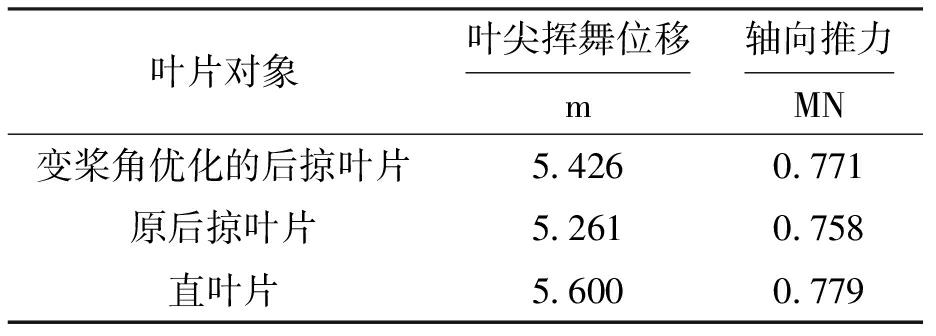
叶片对象叶尖挥舞位移m轴向推力MN变桨角优化的后掠叶片5.4260.771原后掠叶片5.2610.758直叶片5.6000.779
4 结 论
本文建立叶片非线性气弹耦合方程,并验证模型的有效性和准确性.以5 MW后掠4 m叶片为原型,变桨角为优化变量,年发电量作为目标函数,将风力机额定功率、最大轴向推力、最大叶尖挥舞位移设为约束条件,通过后掠叶片非线性气弹耦合程序,计算叶片的气动性能和结构响应,得到结论如下:
1) 利用基于升力线的叶片非线性气弹耦合程序,计算后掠叶片的气动性能和结构响应具有较高的效率和精度,为风力机的优化设计提供理论依据.
2) 对变桨角进行优化,所得到的桨距角随风速变化曲线可以作为风机运行时桨距角变化的实际控制运行规律曲线.
3) 通过该优化模型,变桨角优化的后掠叶片相较于原后掠叶片和直叶片,在年发电量上分别提高了8.58%、7.59%;该优化模型也为风力机叶片的优化设计提供了参考.
[1]Zuteck M.Adaptive blade concept assessment:curved planform induced twist investigation [R].Albuquerque:Sandia National Laboratories,2002.
[2]康传明,张卫民.利用掠![]() 扭耦合效应降低风电机组叶片载荷的研究 [J].风能,2010(10):58-60.
扭耦合效应降低风电机组叶片载荷的研究 [J].风能,2010(10):58-60.
(KANG Chuan-ming,ZHANG Wei-min.Research on using sweep-torsion coupling effect to reduce load of wind turbine blade [J].Wind Energy,2010(10):58-60.)
[3]李书兴.后掠式叶片气动外形设计及流场数值模拟 [D].北京:华北电力大学,2014.
(LI Shu-xing.Aft-swept blade aerodynamic shape design and numerical simulation of flow field [D].Beijing:North China Electric Power University,2014.)
[4]丁勇钢,张兴,李美之.变速变桨控制水平轴风力机桨距角优化 [J].工程热物理学报,2016,37(10):2130-2135.
(DING Yong-gang,ZHANG Xing,LI Mei-zhi.Pitch angle optimization of varible speed pitch control HAWTs [J].Journal of Engineering Thermophysics,2016,37(10):2130-2135.)
[5]Zhao X,Maisser P,Wu J.A new multibody modelling methodology for wind turbine structures using a cardanic joint beam element [J].Renewable Energy,2007,32(3):532-546.
[6]李德源,汪显能,莫文威,等.动态气动载荷和构件振动对风力机气弹特性的影响分析 [J].机械工程学报,2016,52(14):165-173.
(LI De-yuan,WANG Xian-neng,MO Wen-wei,et al.Analysis on the influence of dynamic aerodynamic loads and component vibration of a wind turbine on aeroelastic loads [J].Journal of Mechanical Engineering,2016,52(14):165-173.)
[7]Khair A S M,Meyer N.Flexible multibody dynamic modeling of a floating wind turbine [J].International Journal of Mechanical Sciences,2018,142/143:518-529.
[8]王强.水平轴风力机三维空气动力学计算模型研究 [D].北京:中国科学院工程热物理研究所,2014.
(WANG Qiang.Study on 3d aerodynamic computational models of HAWT [D].Beijing:Institute of Engineering Thermophysics,Chinese Academy of Sciences,2014.)
[9]Shabana A A.Dynamics of multibody systems [M].New York:Cambridge University Press,2005.
[10]Jeng D R,Keith T G,Aliakbarkhanafjeh A.Aerodynamic performance prediction of horizontal axis wind turbines [C]//Proceedings of the DOE/NASA Wind Turbine Dynamics Conference.Cleveland,USA,1981:9-18.
[11]Jonkman J,Butterfield S,Musial W,et al.Definition of a 5-MW reference wind turbine for offshore system development [R].New York:National Renewable Energy Laboratory,2009.
[12]Hansen M.Aeroelastic properties of backward swept blades [C]//49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum & Aerospace Exposition.Orlando,USA,2011:3475-3493.
[13]丁勇钢,张兴,宋梦譞,等.水平轴风力机后掠式叶片设计方法研究 [J].工程热物理学报,2015,36(11):2481-2486.
(DING Yong-gang,ZHANG Xing,SONG Meng-xuan,et al.Design method of backward sweep blade of HAWT [J].Journal of Engineering Thermophysics,2015,36(11):2481-2486.)