水资源既是重要的基础性自然资源和战略性经济资源,也是生态环境发展的支撑性要素,具有不可替代性[1-2].随着社会发展和科技的进步,水资源的污染和缺失问题日益严重,由此增加了各国对水资源的保护压力[3-4].为了促进水资源的保护工作,加强对水资源利用区域的管理,我国相继出台了《全国重要江河湖泊水功能区划》(2011~2030)、《水功能区监督管理办法》等政策,为全国水资源利用区划和保护提供了支撑[5-6].
但目前的区划方法着重于定性分析,具有较强的主观性及随意性.随着产业结构不断调整,城市布局发生了显著变化,导致区划覆盖面积不全面、功能定位不准确等问题.因此,本文通过分析我国水资源量、功能区划选取原则、区划体系及结果,总结了我国在水资源区划管理中遇到的问题与不足,并提出其水资源优化布局方案.基于优化布局的要求及规范,挖掘影响水资源系统特征搭建指标体系,降维后进行K-means聚类分析.采用Python工具建立聚类模型,通过大渡河流域的水资源功能区划结果来验证所提方法的可行性与科学性.
1 水资源功能区划现状分析
根据2019年中国水资源公报,全国水资源总量为29 041亿m2,比近年来的平均值增长了4.8%.但人均水资源总量远低于全世界人均总量,全国接近70%的省市存在缺水问题,总缺口量已达到60亿m2.水资源功能区划[7-9]目的是为水资源的开发利用和保护管理提供科学依据,以实现水资源的可持续发展及利用.全国水资源功能区划为两级,如图1所示.一级水资源功能区包括:保护区、保留区、开发利用区、缓冲区;二级水资源功能区在开发利用区上进一步划分为:工业用水区、渔业用水区、农业用水区、饮用水源区、过渡区、景观娱乐用水区、排污控制区.
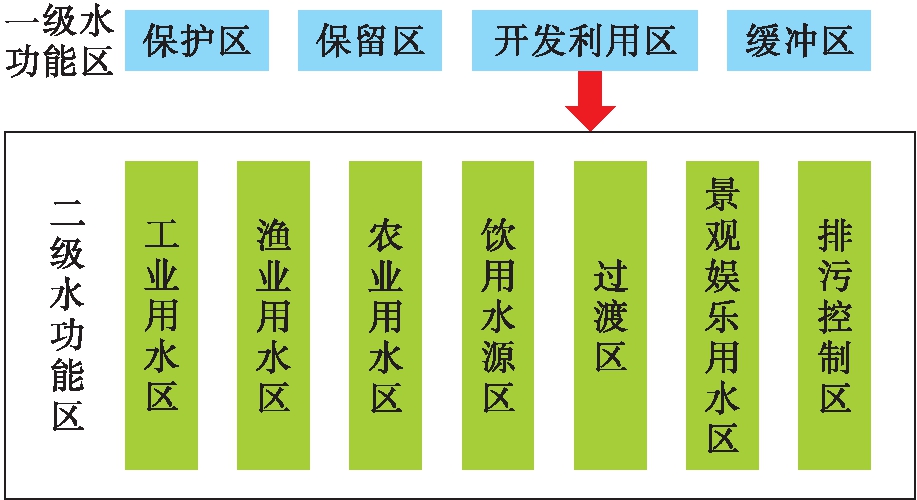
图1 水资源功能区划体系
Fig.1 Functional regionalization system of water resources
全国重要江河湖泊一级水资源功能区划结果(2011~2030年)共有2 888个,区划河长177 977 km,区划湖库面积43 333 km2.实际区划过程中,主要采用定性判断法,根据技术人员的经验和主观判断分析能力来划分水功能区.同一水域由不同技术人员划分所得到的结果可能不同,因此具有较强的不确定性和随意性.随着社会经济的快速发展,部分水功能区划已不能满足当前区域水资源开发利用形式,例如,部分农业用水区随着城市化发展正逐渐演变为工业用水区.因此,水资源系统具有非平衡性、多变性、自组织性、自相似性、随机性等特性,是极其复杂的非线性系统,需要通过定量的分析方式建立具有科学性、及时性、合理性、规范性的聚类模型进行水功能区划.
2 水资源功能区划指标体系
指标体系构建[10-11]是聚类分析过程中的基础环节,有助于对非线性复杂系统特征进行分析,且关系到水资源功能区划结果的科学性与规范性.影响水资源系统的因子较多,区划考虑的因子越多,区划则越复杂;区域内的差异越大,区划也越困难.合理的指标体系有利于设计和重构复杂的系统,使区域特征能够客观、规范、合理地进行描述和展示.
指标体系的核心在于以研究目的为基本前提进行构建.水资源功能区划以实现水资源的可持续开发利用为目的,建设指标体系应充分考虑自然环境与人类活动的供需平衡关系.社会经济现状和用水需求规划影响水资源的利用状态,反映了区域水资源的需求水平.因此,水域基本属性、区域自然情况、社会经济现状、用水需求规划四个层面的指标考虑了水资源供、用、耗、需的循环过程,涵盖了自然生态、社会经济和人类活动的矛盾关系.
在具体的指标筛选中,根据层面指标结构,统计出现频率较高的指标作为参考指标,结合专家咨询和理论分析以及考虑数据的可收集性,建立了水资源功能区划指标体系,如图2所示.
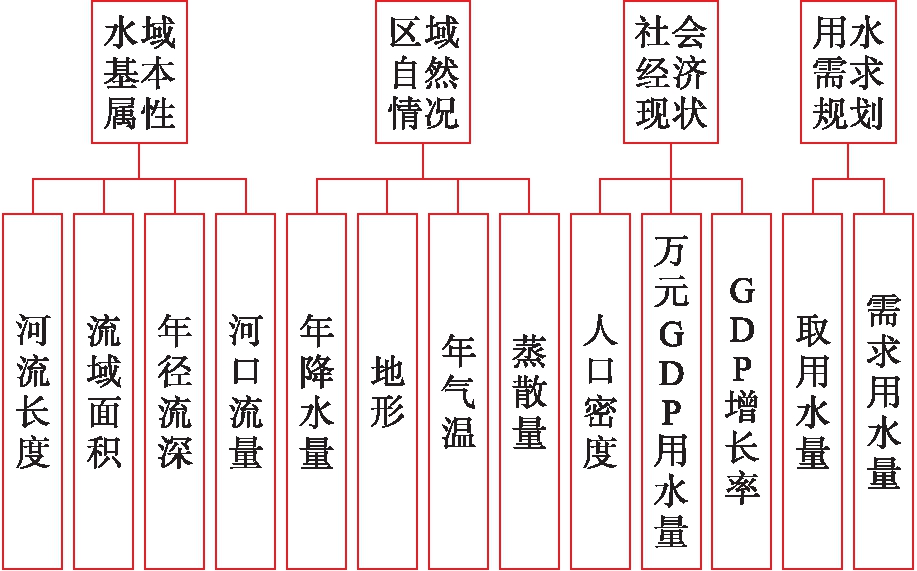
图2 水资源功能区划指标体系
Fig.2 Index system of functional regionalization of water resources
3 水资源功能区划聚类模型
3.1 主成分分析
在水资源功能区划的研究及应用中,本文收集了大量的数据进行分析,多维度、多特征的大样本虽然为水资源区划提供了丰富的信息,但一定程度上也增加了系统复杂度,且众多特征之间存在相关性,即信息上的重叠.主成分分析[12-14]是将各特征之间相互关联的复杂关系进行简化处理的方法.在信息数据损失最少的原则下,将多个特征转化为少数几个能够反映原先特征信息的综合指标,且各个指标保持相互独立,减少信息的重叠,即对高维空间进行降维处理.
1) 标准化处理.为了消除数据量级与量纲的影响,需要对数据进行标准化处理.假设原始数据Y有n个样本,m个特征,即
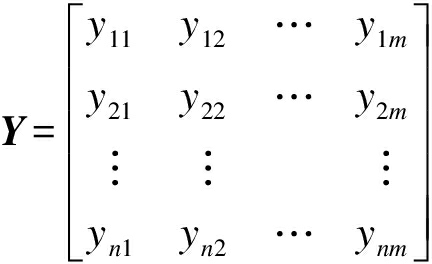
其中,yij为第i个样本的第j个特征值,将各特征值yij进行标准化处理,即
(1)
式中:![]() 为指标化后的特征值;
为指标化后的特征值;![]() 与σj分别为第j个特征的样本平均值和标准差,其表达式分别为
与σj分别为第j个特征的样本平均值和标准差,其表达式分别为
(2)
(3)
2) 计算相关系数矩阵R.计算标准化后数据矩阵各特征之间的相关系数矩阵,即
R=(rpq)m×m=
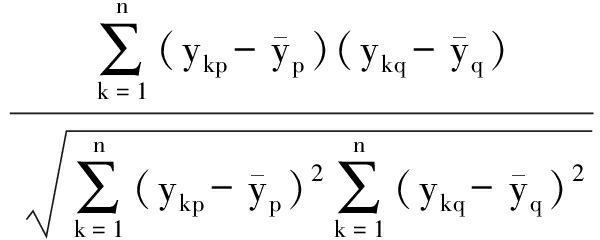
(4)
式中:rpq为特征变量yp和yq的相关系数;![]() 与
与![]() 分别为第p个特征和第q个特征的平均值.
分别为第p个特征和第q个特征的平均值.
3) 计算特征值和特征向量.求解|λI-R|=0,其中I为单位矩阵,计算相关系数矩阵R的特征值λj(j=1,2,…,m),并按从大到小的顺序进行排序.计算对应的特征向量μ1,μ2,…,μm,其中μj=(μ1j,μ2j,…,μnj)T,由特征向量组成m个新的指标,即
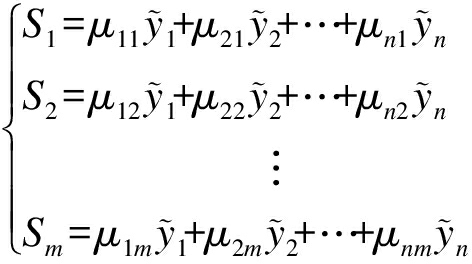
(5)
式中:Sm为第m个主成分;![]() 为指标化后的特征值.
为指标化后的特征值.
4) 计算特征值贡献率.选择一个主成分计算特征值的信息贡献率bj和累计贡献率al,其表达式分别为
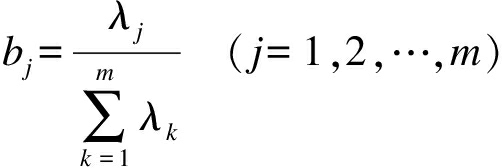
(6)
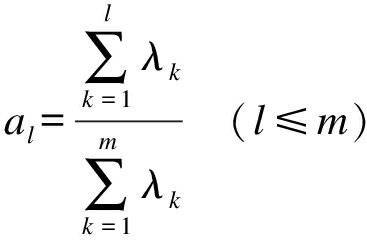
(7)
当al接近于1(一般al≥0.85)时,选择前1个指标S1,S2,…,Sl作为一个主成分,取代原先的m个特征.
3.2 K-means聚类算法
K-means是一种典型的无监督聚类算法,主要用于将相似的样本自动归为一类,适用于水资源区划场景[15-16].其中心思想是首先确定常数K,K表示最终的聚类类别数;然后随机选定K个样本点为质心,并计算每一个样本与K个质心之间的相似度,将样本归到最相似质心所属的类中.相似度采用欧式距离进行计算,其表达式为
(8)
式中,dist(x,c)为样本x到质心c的欧式距离;xt与ct分别为样本x和质心c的第t个主成分.所有样本归类后重新计算每个类的均值作为新的质心,重复以上过程直到满足收敛要求,即质心不再改变或已达到规定的收敛次数,最终确定出每个样本所属的类别及每个类的质心.K-means算法流程图如图3所示.
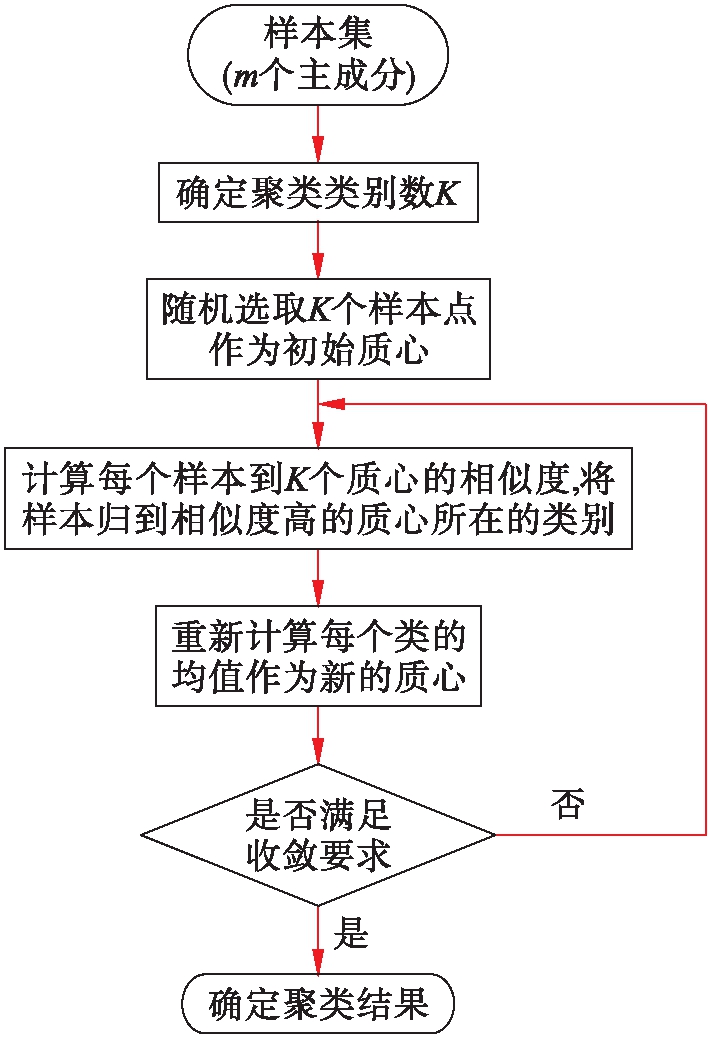
图3 K-means聚类算法流程图
Fig.3 Flow chart of K-means clustering algorithm
4 实验结果分析
以大渡河流域为例进行一级水资源功能区划.大渡河全长1 062 km,流域面积7.77万km2,共有47个单元河段.按照水资源功能区划体系收集水域基本属性、区域自然情况、社会经济现状、用水需求规划四个层面共13个指标数据.通过Python 3.8实现对各指标的主成分分析及K-means聚类分析.
为了消除数据量级与量纲的影响,按照式(1)对指标数据进行标准化处理,处理后的数据如表1所示.
表1 大渡河流域指标数据
Tab.1 Index data of Dadu River Basin
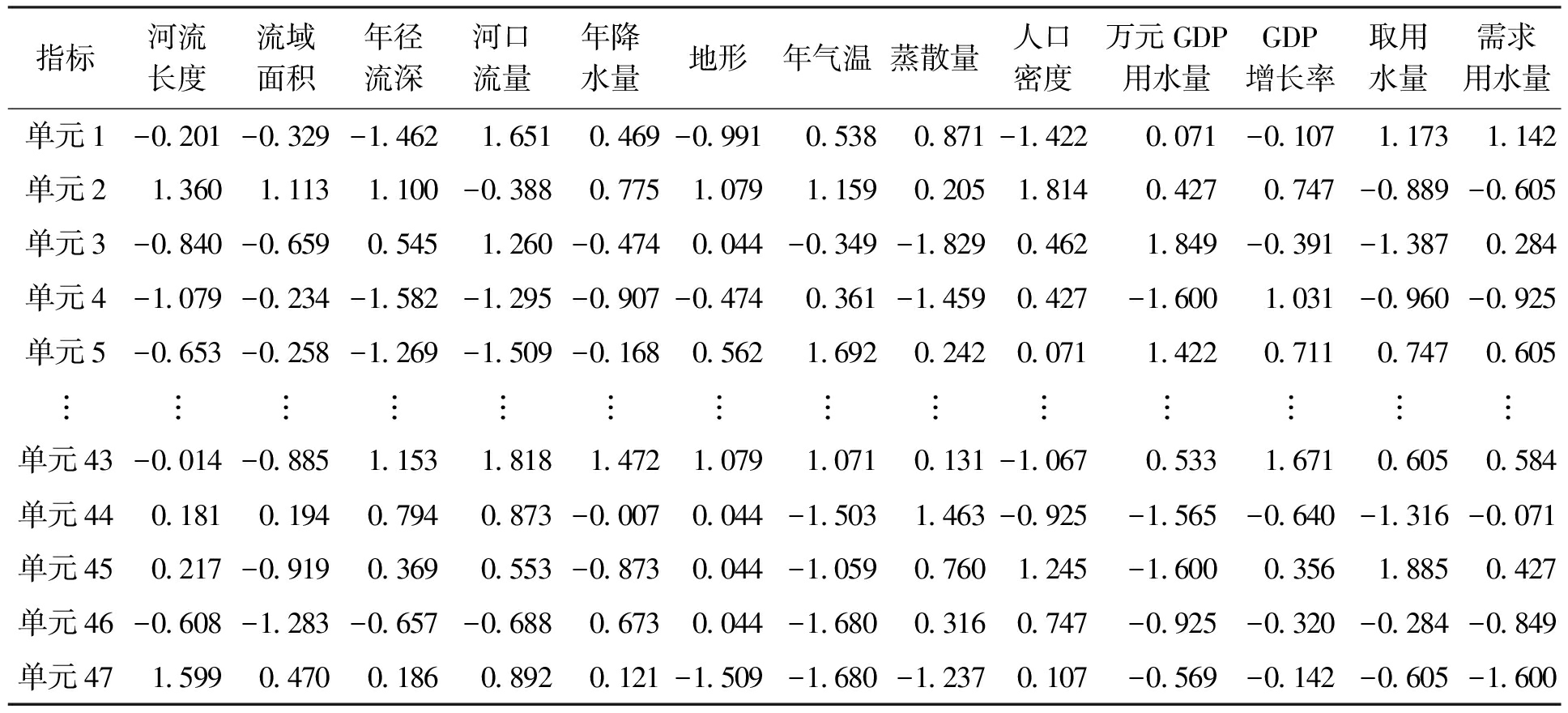
指标河流长度流域面积年径流深河口流量年降水量地形年气温蒸散量人口密度万元GDP用水量GDP增长率取用水量需求用水量单元1-0.201-0.329-1.462 1.651 0.469-0.991 0.538 0.871-1.422 0.071-0.107 1.173 1.142单元21.3601.1131.100-0.3880.7751.0791.1590.2051.8140.4270.747-0.889-0.605单元3-0.840-0.6590.5451.260-0.4740.044-0.349-1.8290.4621.849-0.391-1.3870.284单元4-1.079-0.234-1.582-1.295-0.907-0.4740.361-1.4590.427-1.6001.031-0.960-0.925单元5-0.653-0.258-1.269-1.509-0.1680.5621.6920.2420.0711.4220.7110.7470.605︙︙︙︙︙︙︙︙︙︙︙︙︙︙单元43-0.014-0.8851.1531.8181.4721.0791.0710.131-1.0670.5331.6710.6050.584单元440.1810.1940.7940.873-0.0070.044-1.5031.463-0.925-1.565-0.640-1.316-0.071单元450.217-0.9190.3690.553-0.8730.044-1.0590.7601.245-1.6000.3561.8850.427单元46-0.608-1.283-0.657-0.6880.6730.044-1.6800.3160.747-0.925-0.320-0.284-0.849单元471.5990.4700.1860.8920.121-1.509-1.680-1.2370.107-0.569-0.142-0.605-1.600
通过式(2)~(7)计算得到主成分分析结果,如表2所示.根据各指标的特征值和累计方差贡献率,前6个主成分的方差累计贡献率已达到85.604 4%,且从第7个主成分开始特征值合计小于1,因此,选择提取前6个主成分作为聚类的特征值.
表2 主成分分析结果
Tab.2 Results of principal component analysis
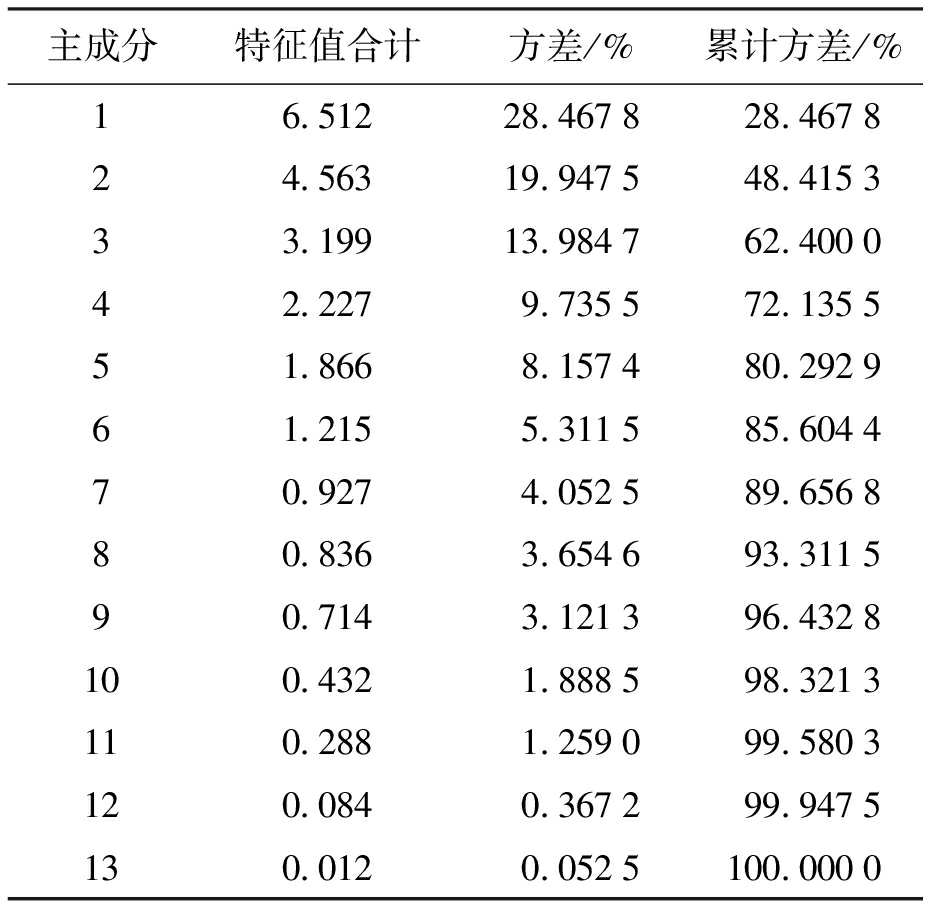
主成分特征值合计方差/%累计方差/%16.51228.467828.467824.56319.947548.415333.19913.984762.400042.2279.735572.135551.8668.157480.292961.2155.311585.604470.9274.052589.656880.8363.654693.311590.7143.121396.4328100.4321.888598.3213110.2881.259099.5803120.0840.367299.9475130.0120.0525100.0000
各指标在6个主成分中的相关系数如表3所示.相关系数取值范围为[-1,1],大于0表示正相关,小于0表示负相关,相关系数绝对值越接近1表示指标在主成分中影响度越大.因此,主成分1反映了水域基本属性,受河流长度、流域面积、年径流深等指标的影响;主成分2主要包括河口流量、年降水量、取用水量等指标;主成分3受人口密度、地形、需求用水量等指标的影响较大;主成分4反映社会经济现状,主要包括万元GDP用水量、GDP增长率指标;主成分5反映用水需求关系,主要包括取用水量、需求用水量指标;主成分6反映区域自然情况,主要受地形、年降水量、年气温、蒸散量指标的影响.
一级水功能区划包括:保护区、保留区、开发利用区、缓冲区4个类别,因此K=4.随机选取4个单元河段样本s1(0.512,-0.701,-0.452,-0.784,-0.873,-0.86),s2(0.592,-0.833,-0.461,0.910,0.360,-0.501),s3(0.321,-0.105,0.637,-0.092,0.598,-0.764),s4(0.839,-0.156,0.576,0.712,0.722,0.526)作为初始质心进行K-means聚类,聚类结果为:保护区{4,7,9,11,15,17,19,23,25,27,29,31,33,35,37,39,41,43,45};保留区{2,5,8,10,12,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,47};开发利用区{3,14,21,46};缓冲区{1,6,13}.与政府部门的区划类型结果《水功能区划分标准》(GB/T50594-2010)进行对比,结果如表4所示.47个河段单元有4个不同类别,分析原因是由于政府部门区划时间为2010年,距离现在周期较长,河段单元的属性和特征发生了变化.
表3 指标的主成分相关系数
Tab.3 Principal component correlation coefficients of indexes
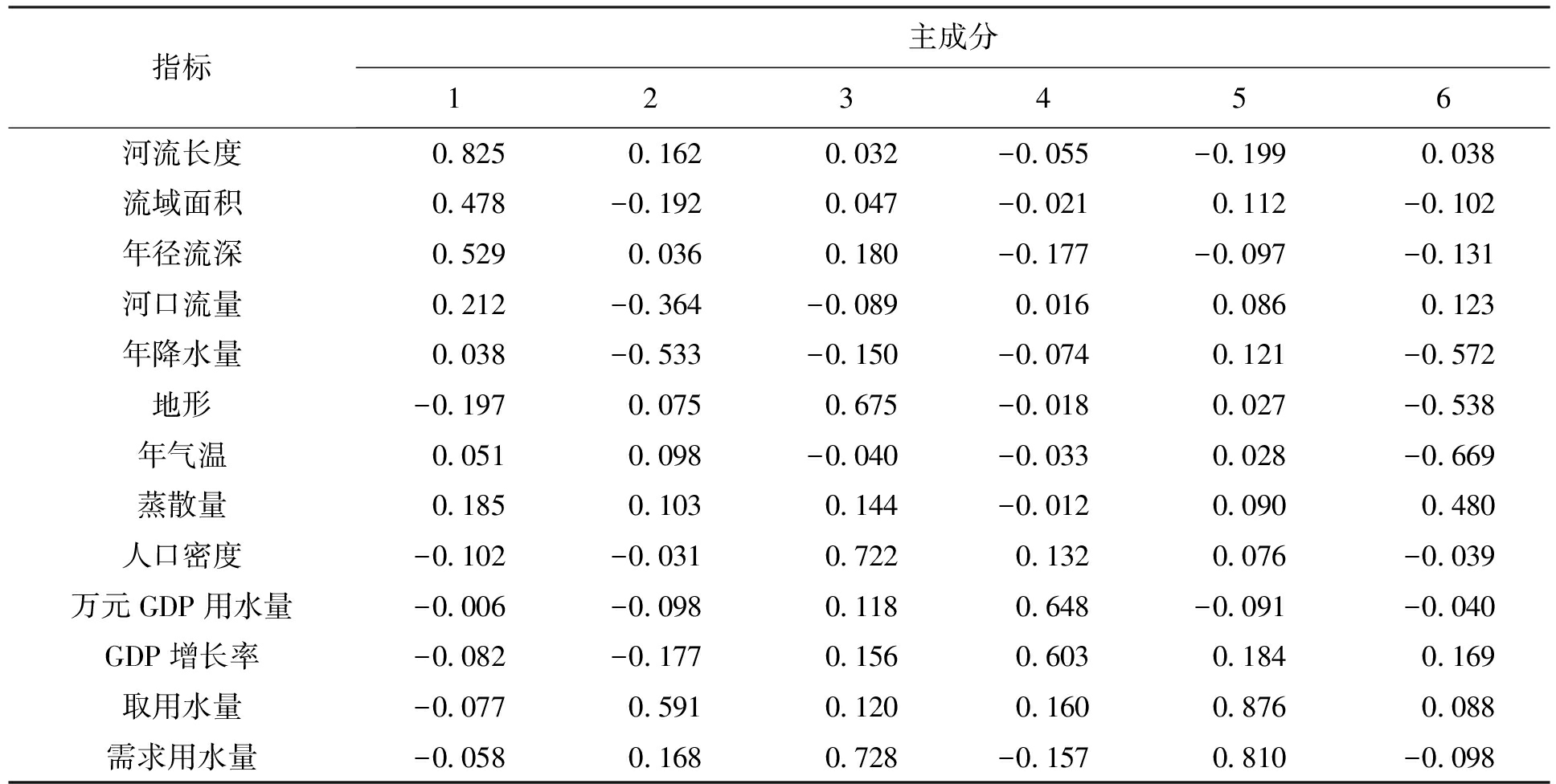
指标主成分123456河流长度 0.825 0.162 0.032-0.055-0.199 0.038流域面积0.478-0.1920.047-0.0210.112-0.102年径流深0.5290.0360.180-0.177-0.097-0.131河口流量0.212-0.364-0.0890.0160.0860.123年降水量0.038-0.533-0.150-0.0740.121-0.572地形-0.1970.0750.675-0.0180.027-0.538年气温0.0510.098-0.040-0.0330.028-0.669蒸散量0.1850.1030.144-0.0120.0900.480人口密度-0.102-0.0310.7220.1320.076-0.039万元GDP用水量-0.006-0.0980.1180.648-0.091-0.040GDP增长率-0.082-0.1770.1560.6030.1840.169取用水量-0.0770.5910.1200.1600.8760.088需求用水量-0.0580.1680.728-0.1570.810-0.098
表4 大渡河流域区划结果
Tab.4 Regionalization results of Dadu River Basin
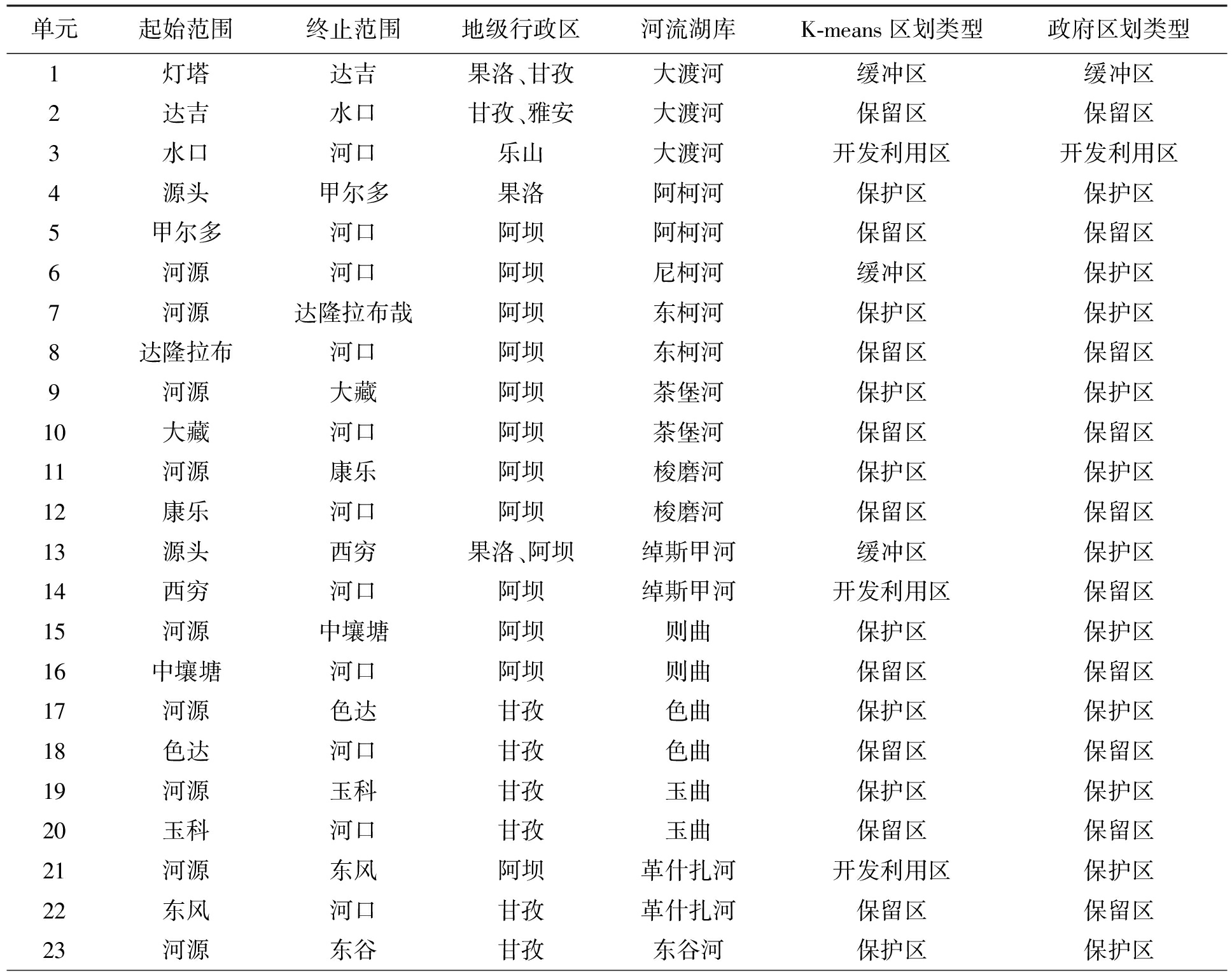
单元起始范围终止范围地级行政区河流湖库K-means区划类型政府区划类型1灯塔达吉果洛、甘孜大渡河缓冲区缓冲区2达吉水口甘孜、雅安大渡河保留区保留区3水口河口乐山大渡河开发利用区开发利用区4源头甲尔多果洛阿柯河保护区保护区5甲尔多河口阿坝阿柯河保留区保留区6河源河口阿坝尼柯河缓冲区保护区7河源达隆拉布哉阿坝东柯河保护区保护区8达隆拉布河口阿坝东柯河保留区保留区9河源大藏阿坝茶堡河保护区保护区10大藏河口阿坝茶堡河保留区保留区11河源康乐阿坝梭磨河保护区保护区12康乐河口阿坝梭磨河保留区保留区13源头西穷果洛、阿坝绰斯甲河缓冲区保护区14西穷河口阿坝绰斯甲河开发利用区保留区15河源中壤塘阿坝则曲保护区保护区16中壤塘河口阿坝则曲保留区保留区17河源色达甘孜色曲保护区保护区18色达河口甘孜色曲保留区保留区19河源玉科甘孜玉曲保护区保护区20玉科河口甘孜玉曲保留区保留区21河源东风阿坝革什扎河开发利用区保护区22东风河口甘孜革什扎河保留区保留区23河源东谷甘孜东谷河保护区保护区
表4(续)
Tab.4 (Continued)
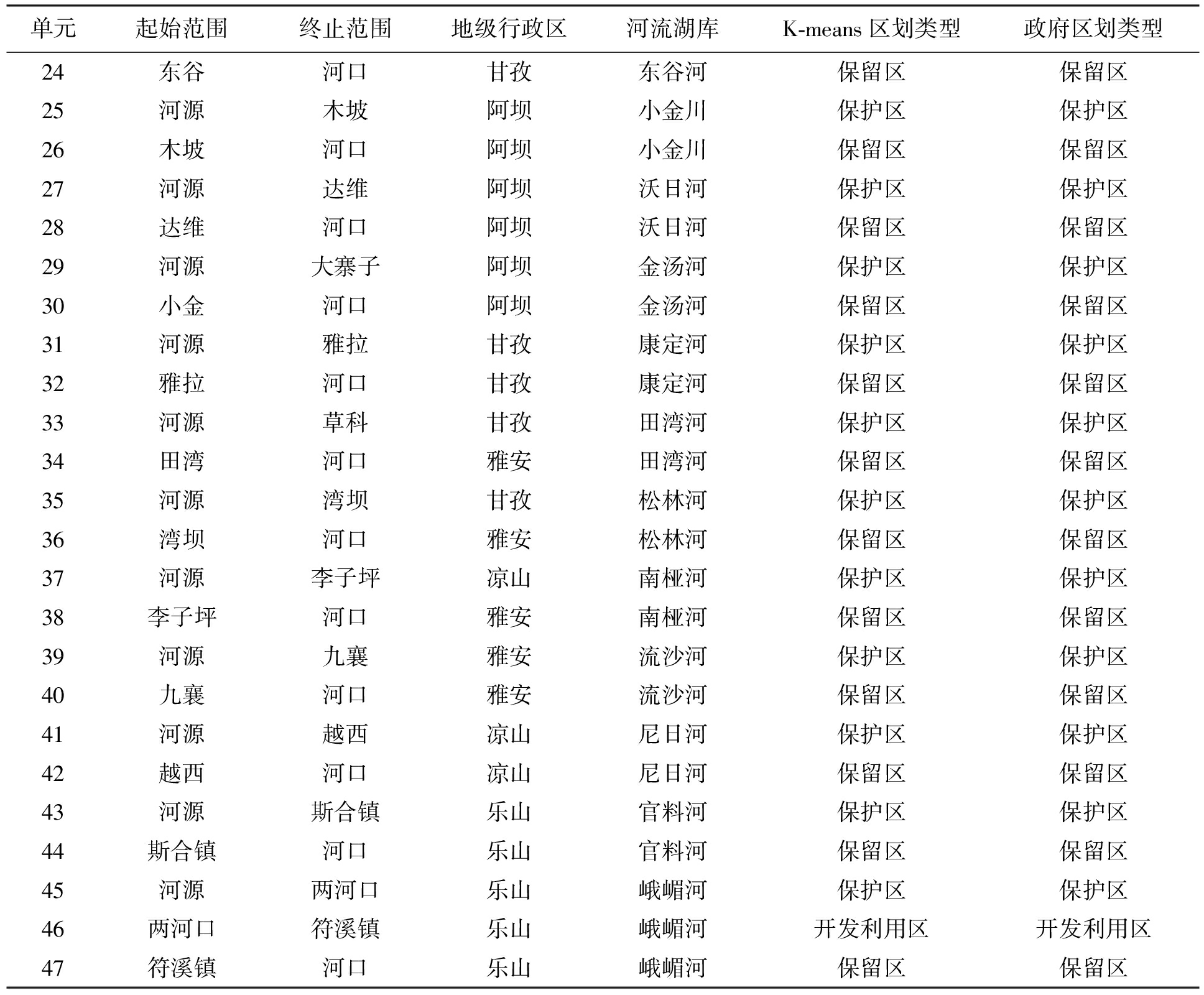
单元起始范围终止范围地级行政区河流湖库K-means区划类型政府区划类型24东谷河口甘孜东谷河保留区保留区25河源木坡阿坝小金川保护区保护区26木坡河口阿坝小金川保留区保留区27河源达维阿坝沃日河保护区保护区28达维河口阿坝沃日河保留区保留区29河源大寨子阿坝金汤河保护区保护区30小金河口阿坝金汤河保留区保留区31河源雅拉甘孜康定河保护区保护区32雅拉河口甘孜康定河保留区保留区33河源草科甘孜田湾河保护区保护区34田湾河口雅安田湾河保留区保留区35河源湾坝甘孜松林河保护区保护区36湾坝河口雅安松林河保留区保留区37河源李子坪凉山南桠河保护区保护区38李子坪河口雅安南桠河保留区保留区39河源九襄雅安流沙河保护区保护区40九襄河口雅安流沙河保留区保留区41河源越西凉山尼日河保护区保护区42越西河口凉山尼日河保留区保留区43河源斯合镇乐山官料河保护区保护区44斯合镇河口乐山官料河保留区保留区45河源两河口乐山峨嵋河保护区保护区46两河口符溪镇乐山峨嵋河开发利用区开发利用区47符溪镇河口乐山峨嵋河保留区保留区
5 结 论
水资源功能区的合理区划是对水资源保护的有效支撑.本文通过对水资源功能区划现状进行研究,分析了目前功能区划方法的不足,从而提出了优化布局方案.建立指标体系对水资源系统的特征进行描述,采用主成分分析方法在数据信息损失最小的情况下,将多指标高空间进行降维处理,提升系统的鲁棒性.基于欧氏距离的K-means聚类算法实现水资源功能区划,以大渡河流域为例进行实验,以此验证所提方法的可行性.后续将进行人工现场复核,对所提方法进行优化,从而进一步提升其科学性.
[1]张根宝,李开明.基于GPRS网络的水资源管理远程监控系统的设计 [J].工业控制计算机,2017,30(10):65-66.
(ZHANG Gen-bao,LI Kai-ming.Design of remote monitoring system of water resources management based on GPRS [J].Industrial Control Computer,2017,30(10):65-66.)
[2]严栋飞,姜仁贵,解建仓,等.基于数字地球的渭河流域水资源监控系统研究 [J].计算机工程,2019,45(4):49-55.
(YAN Dong-fei,JIANG Ren-gui,XIE Jian-cang,et al.Research on water resources monitoring system of Weihe river basin based on digital globe [J].Computer Engineering,2019,45(4):49-55.)
[3]郭亮.基于大数据的区域水资源可持续承载力预测系统设计 [J].现代电子技术,2020,43(9):117-121.
(GUO Liang.Design of regional water resource sustainable carrying capacity prediction system based on big data [J].Modern Electronics Technique,2020,43(9):117-121.)
[4]Cheng K,Fu Q,Meng J,et al.Analysis of the spatial variation and identification of factors affecting the water resources carrying capacity based on the cloud model [J].Water Resources Management,2018,32(8):2767-2781.
[5]中华人民共和国水利部.水资源[2017]101号 水功能区监督管理办法 [S].北京:中华人民共和国水利部,2017.
(Ministry of Water Resources of the People Republic of China.Water Resources [2017] No.101 The mea-sures for the supervision and administration of water function zones [S].Beijing:Ministry of Water Resources of the People Republic of China,2017.)
[6]任玉芬,方文颖,王雅晴,等.我国城市水资源利用效率分析 [J].环境科学学报,2020,40(4):1507-1516.
(REN Yu-fen,FANG Wen-ying,WANG Ya-qing,et al.Analysis of urban water resources use efficiency in China [J].Acta Scientiae Circumstantiae,2020,40(4):1507-1516.)
[7]王金哲,张光辉,崔浩浩,等.适宜西北内陆区地下水功能区划的体系指标属性与应用 [J].水利学报,2020,51(7):796-804.
(WANG Jin-zhe,ZHANG Guang-hui,CUI Hao-hao,et al.System index attribute and application of groundwater function zoning in northwest inland area of China [J].Journal of Hydraulic Engineering,2020,51(7):796-804.)
[8]魏辰.水功能区优化布局研究:以淮河流域沙颍河为例 [D].西安:西北大学,2019.
(WEI Chen.Study on optimum layout of water function areas:taking Shaying river of Huaihe river basin as an example [D].Xi’an:Northwest University,2019.)
[9]郭书海,吴波.水生态功能区划流程:双关系树框架与概念模型 [J].应用生态学报,2017,28(12):4051-4056.
(GUO Shu-hai,WU Bo.A process of aquatic ecological function regionalization:the dual tree framework and conceptual model [J].Chinese Journal of Applied Ecology,2017,28(12):4051-4056.)
[10]陆可,邹启鸣,李鸣,等.基于R型聚类![]() 因子分析的指标体系简化方法 [J].计算机系统应用,2016,25(5):118-123.
因子分析的指标体系简化方法 [J].计算机系统应用,2016,25(5):118-123.
(LU Ke,ZOU Qi-ming,LI Ming,et al.Simplification method of index system based on R cluster analysis and factor analysis [J].Computer Systems & Applications,2016,25(5):118-123.)
[11]Bockstaller C,Girardin P,van der Werf H M G.Use of agro-ecological indicators for the evaluation of farming systems [J].Developments in Crop Science,1997,25:329-338.
[12]李竹婷,陈秀宏,孙慧强.基于分位函数的直方图符号数据非负主成分分析法 [J].计算机应用研究,2019,36(8):2415-2420.
(LI Zhu-ting,CHEN Xiu-hong,SUN Hui-qiang.Principal component analysis of histogram data with non-negative coefficients based on quantile function [J].Application Research of Computers,2019,36(8):2415-2420.)
[13]张素智,陈小妮,杨芮,等.基于类内和类间距离的主成分分析算法 [J].计算机工程与设计,2020,41(8):2177-2183.
(ZHANG Su-zhi,CHEN Xiao-ni,YANG Rui,et al.Method of principal component analysis based on intra-class distance and inter-class distance [J].Computer Engineering and Design,2020,41(8):2177-2183.)
[14]李志农,杨晓飞,陈长征.基于VMD-PARAFAC的轴承故障欠定盲源分离 [J].沈阳工业大学学报,2020,42(1):63-68.
(LI Zhi-nong,YANG Xiao-fei,CHEN Chang-zheng.Underdetermined blind source separation of bearing faults based on VMD-PARAFAC [J].Journal of Shen-yang University of Technology,2020,42(1):63-68.)
[15]毛秀,冒纯丽,丁岳伟.基于密度和聚类指数改进的K-means算法 [J].电子科技,2015,28(11):47-50.
(MAO Xiu,MAO Chun-li,DING Yue-wei.Improved K-means algorithm based on density and clustering index [J].Electronic Science and Technology,2015,28(11):47-50.)
[16]王丰斌.基于AHLO与K均值聚类的图像分割算法 [J].沈阳工业大学学报,2019,41(4):427-432.
(WANG Feng-bin.Image segmentation algorithm based on AHLO and K-means clustering [J].Journal of Shenyang University of Technology,2019,41(4):427-432.)