随着无人机技术的不断发展,在无人机上增加抓取装置以实现抓取和运输功能已成为行业趋势,其抓取末端有多种夹取方式,但是数量的增加并没有完全解决抓取稳定性与可靠性等问题.稳定牢固地抓取物体除了与控制机构相关,也与其结构密不可分,合理的抓取装置结构有助于减小空气阻力,提升结构强度与刚度.
国内外学者在此领域做了很多研究,如Doyle等[1]仿鸟类爪子进行设计抓取装置;Mellinger等[2]仿人类手指设计抓取装置;权龙哲等[3]仿蜻蜓设计蜓爪式末端,上述文献均是结合仿生学原理,采用工程技术进行仿生机械抓取装置的设计.有一些学者通过研究生物局部的非规则曲面形貌对结构特性的影响进行仿生设计,如张锐等[4]通过研究鸵鸟足底非规则曲面形貌设计仿生火星巡视器车轮;张伏等[5]通过研究山羊底部非规则曲面形貌设计仿生农业四足行走机器人;周宏根等[6]通过研究河鲀背部形貌曲面设计仿生减阻构件.
鳄鱼是现存与恐龙同时代的一种爬行动物,头部细长且扁平,具有强大的咬合力.它可以在水中潜伏慢慢靠近猎物而不被发现,捕猎时头骨可多次承受巨大的反作用力,这些均与其头部的特殊结构有关,同时上颚曲面形貌的不同对其结构本身的性能也具有一定的影响.因此,研究鳄鱼上颚曲面形貌对研究鳄鱼吻部的力学特性及其仿生设计有一定的意义.由于鳄鱼上颚的曲面较为复杂,直接应用于工程仿生难度较大,因此需将其转化为数学模型,再将其数学模型应用于仿生设计.
1 鳄鱼上颚模型重构
生物体结构较复杂,重构模型较困难,不能直接画出,因此需要对模型进行扫描得到点云数据,再利用逆向工程技术进行三维模型重构.离散点云数据三维重建方法有B-Spline(贝塞尔)、Bezier(B样条)、NURBS(有理非均匀有理B样条)拟合技术等.基于NURBS技术对处理变化幅度较大的数据效果较好,误差较小[7].它与描述自由型曲线曲面的B样条方法统一,但又能精确表示曲线曲面的数学方法,其控制参数较少又能控制曲线连续、平滑,可用于复杂曲线曲面的加工[8].NURBS曲面比B样条曲面灵活性强、效率高,能精确地解析自由曲面,同时具有强大的局部调控性与优良的光滑曲面拟合能力,因此被广泛应用,本模型基于NURBS曲面进行三维重构.
1.1 模型获取
菲律宾鳄头骨较为珍贵,不能对实物进行分析实验.本次研究对象的断层扫描数据由巴塞罗那自治大学克鲁萨芳古生物研究所博物馆的Josep教授与德国汉堡大学的Jordi教授提供.因鳄鱼上颚需要托盘承载进行扫描,所以扫描的三维点云数据中除了研究对象还会出现很多噪声点需要进一步手动分离,同时鳄鱼头骨的上颚较为复杂,扫描后的点云数据会有重叠、缺失等情况,因此需要使用逆向工程软件Geomagic Studio对模型进行修复.
1.2 模型重构
本文选用Avizo软件对断层扫描得到的数据进行重建.通过观察Ortho slice(矫正片)、Inosurface(等值面)、Orthoviews(正交视图)3个视图中的图像数据,分离研究对象与杂质,并删去由于扫描精度不高造成的重叠部分以及承载鳄鱼头骨上颚的载物托盘,减轻后期修复工作,避免影响分析.通过调整阈值,使用最佳阈值使呈现的上颚三视图更加清晰平滑,最后生成三维立体模型.
2 鳄鱼上颚模型修复
使用逆向工程技术可以提高模型的质量,现在应用比较成熟的软件有Imageware,Geomagic Studio和Rapidform等,Geomagic Studio对模型重构可以简化工作流程,使曲面重构的难度降低、偏差较小,同时还具有高效率、质量高等特点[9-10],在使用Geomagic Studio对模型进行修复时,要针对其个别问题以恰当的修补方法进行处理,才可以生成最优化的曲面与最佳拟合的曲面外形[11].
2.1 原始模型修复
修复过程主要分为两部分,由点转化为面,再由面转化为体.由于原模型数据量较大,首先进行适当简化,减小封装后三角形的数量;接着对简化后的模型进行降噪处理,再进行局部手动补偿,使其平滑无杂质;通过不断手动修复与网格医生辅助检测,直至各种缺陷均为0,最后进行精确曲面、自动曲面化、拟合曲面等操作.
由于鳄鱼头骨较复杂、数据较大,直接使用网格医生自动修复会造成电脑运算量过大且修复效果不好,因此先将模型整体简化70%,再进行修复.修复过程中通过移动点来补偿扫描仪的错误,使其点的排列更加均匀,从而实现降噪.由于内部杂质较多,直接进行网格医生修复会造成模型的缺失,因此进行手动补偿.修复前的整体与局部图如图1所示,原始三角形数为7 048 981,计算机处理数据难度较大,因此在不改变曲面形貌的前提下降低数据数量,减少计算机运算时间.
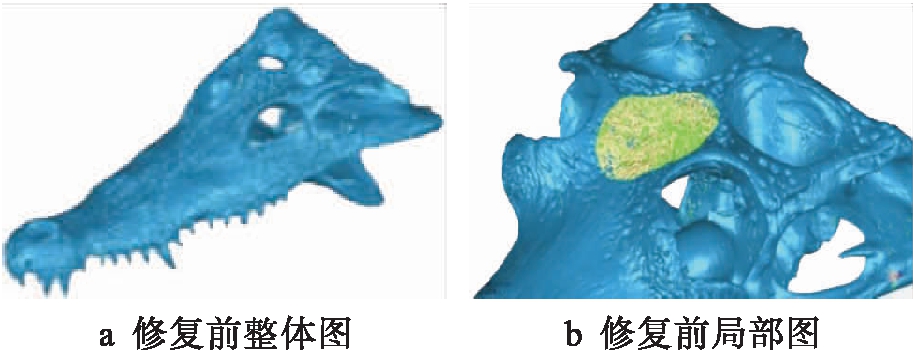
图1 修复前整体图与局部图
Fig.1 Overall and local images before repair
通过不断手动修复消除杂质,使内部光滑,再调节多边形网格与单个多边形之间的角度,减少误差和人为噪声,最后再使用网格医生功能对手动修复后的模型进行检查,使非流形边、自相交、高度折射边等都减为0,达到零缺陷.修复后的模型整体图与局部图如图2所示.
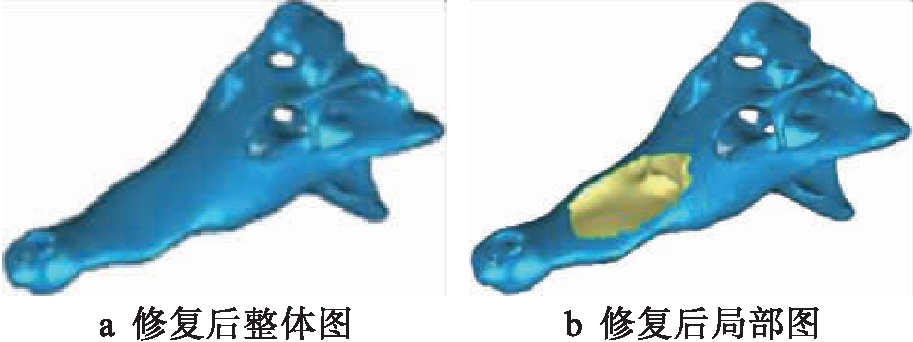
图2 修复后整体图与局部图
Fig.2 Overall and local images after repair
2.2 特征模型修复
由于原始模型有较多孔洞,不利于实际分析,现将修复后的鳄鱼头骨模型保留其眶前骨、鼻骨、纵向支撑脊等结构,填补孔洞生成特征模型.由于Geomagic Studio中的标准偏差即是拟合残差计算中的误差,因此将特征模型与修复后的原始模型进行偏差分析[12].通过分析计算结果可以得出,偏差主要在填补的孔洞部分,其余位置均未发生较大偏差,其特征模型的标准偏差为0.016 4 mm,平均偏差为-0.006 4/0.000 7 mm,3D偏差的最大范围是-0.118 4/3.227 1 mm,满足工程设计上的允许误差范围±5%[13],因此其特征模型可用于后续分析.
3 鳄鱼上颚曲面模型的建立
为探究其曲面形貌对其结构性能的影响,并能够将其应用于仿生设计,因此保留特征模型的上表面进行特征参数提取及分析.但其曲面为非规则曲面,直接转换为三维数学模型阶数较高且拟合不够精确,因此需对提取的曲面进行划分.
3.1 曲面模型提取
根据鳄鱼抓取特点选择其眼眶前骨到鼻部区域进行曲面形貌分析,首先运用Geomagic Studio软件中的裁剪功能提取特征模型的上表面,观察其表面的曲面形貌,可将其曲面划分为三部分,如图3所示.图3b中鼻部前端呈凸起状,类似于一个椭球面,其曲率变化明显,将此部分曲面命名为第Ⅰ曲面;中间部分曲面呈凹陷状,凹陷曲率较小趋于平缓,将此部分曲面命名为第Ⅱ曲面,如图3c所示;图3d中这部分呈上升的缓曲面命名为第Ⅲ曲面.
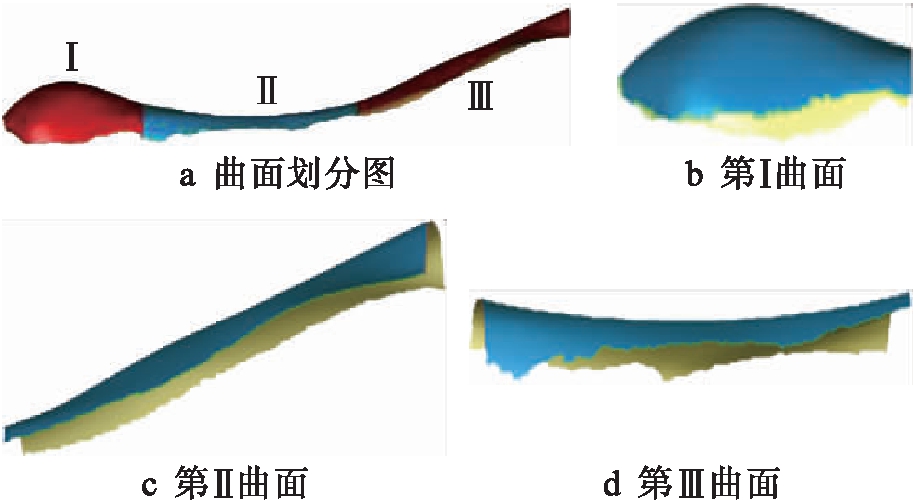
图3 鳄鱼上颚表面图
Fig.3 Upper jaw surface of crocodile
3.2 曲面点云处理
将划分的三个曲面模型转化为点云模型,由于其点云数据较多,影响曲面拟合的运算速度,因此需要对点云数据进行过滤处理.将点云导入Imageware进行过滤处理,有助于创建较高精度的曲面[14].本文采用距离采样方法,对点云数据进行过滤处理,操作前3个典型曲面的点数量分别为3 151、4 357、5 653,将距离公差设置为1.5,过滤后点数量分别为901、1 229、1 584,经过滤后点数据大量减少,但并未改变其曲面的曲率与形貌.
4 鳄鱼上颚数学模型的建立
鳄鱼上颚表面的3个曲面从外观上看不符合某个固定的数学模型,因此需要采用多项式拟合的方法对其分别进行拟合.MATLAB 2017B工具箱中的曲面拟合功能可以对三个曲面的点云数据分别进行多项式拟合.
4.1 第Ⅰ曲面数学模型
将x、y设置为自变量,z设置为因变量,选择多项式方法拟合该曲面特征点云,通过调整x、y的次幂数,观察拟合后的曲面与决定系数R2确定拟合的最终方程.由于建立的数学模型后续应用于仿生设计,所以拟合曲面时不仅精度要达到要求,还要考虑其复杂程度;既要保留原有形貌特征,又要使其加工成本降低,符合经济效益.综合考虑两方面因素,x、y不同指数的拟合结果如表1所示.
表1 不同指数自变量曲面Ⅰ的拟合结果
Tab.1 Fitting results of independent surface Ⅰ with different indexes
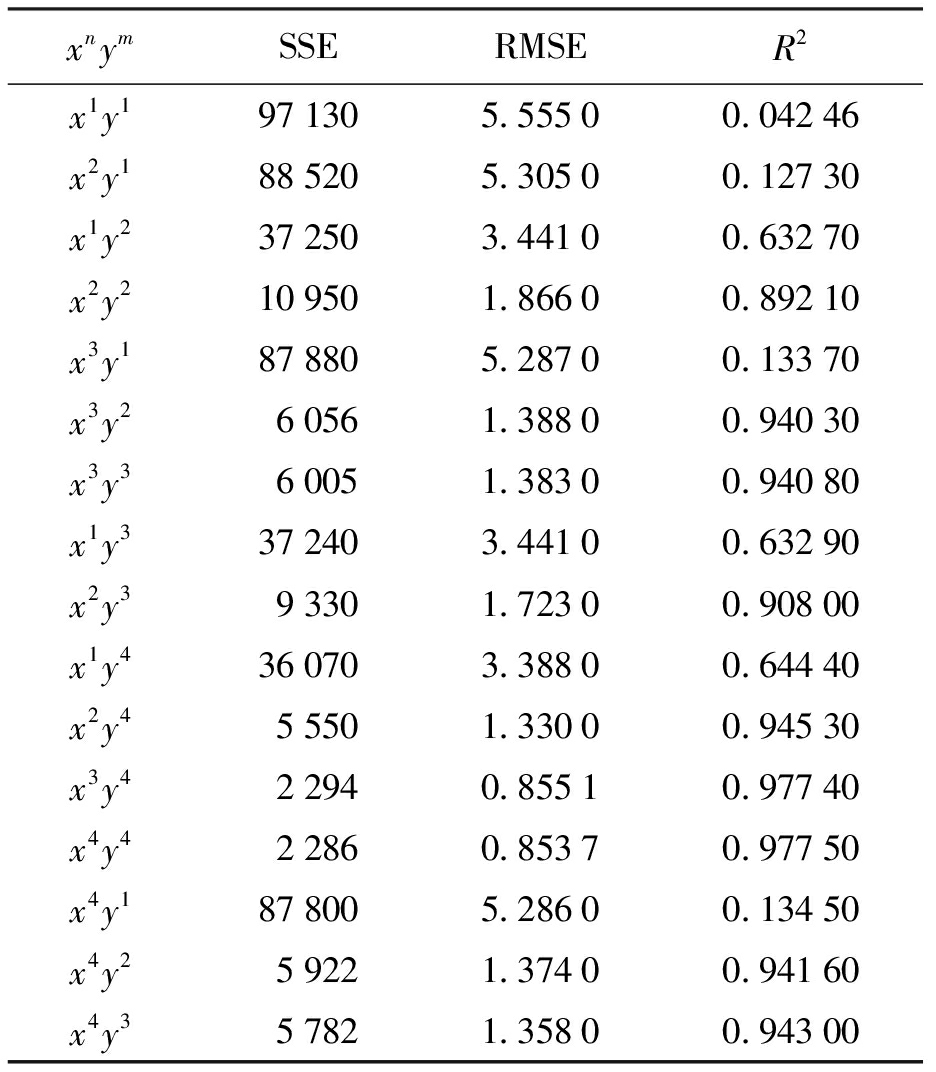
xnymSSERMSER2x1y1971305.55500.04246x2y1885205.30500.12730x1y2372503.44100.63270x2y2109501.86600.89210x3y1878805.28700.13370x3y260561.38800.94030x3y360051.38300.94080x1y3372403.44100.63290x2y393301.72300.90800x1y4360703.38800.64440x2y455501.33000.94530x3y422940.85510.97740x4y422860.85370.97750x4y1878005.28600.13450x4y259221.37400.94160x4y357821.35800.94300
注:xnym表示该拟合方程中x的指数最大为n,y的指数最大为m;SSE表示残差平方和;RMSE表示均方差;R2表示决定系数.
通过观察分析表1可以发现,随着x、y指数的不断增加,决定系数R2的值越来越大,这说明随着x、y指数的增加,其曲面拟合的精度逐渐变高,更加接近实际的曲面形貌.当x、y的指数由x3y3增加到x3y4时,残差平方和SSE由6 005减小到2 294,均方差RMSE由1.383减小到0.855 1,决定系数由0.940 8增加到0.977 4.继续增加次幂数,结果参数变化会更小,但曲面会更加复杂.综上所述,选取自变量x的指数为3,自变量y的指数为4,残差平方和SSE=2 294,均方差RMSE=0.855 1,决定系数R2=0.977 4,因此可得曲面Ⅰ的拟合方程为z1=f(x,y)=-77.22-5.008x-1.557y-0.080 14x2-0.078 2xy-0.067 06y2-0.000 399x3-0.001 29x2y-0.001 752xy2-0.000 680 3y3-6.859×10-6x3y-1.138×105x2y2-7.763×10-6xy3-3.058×10-5y4,鳄鱼上颚表面第Ⅰ曲面MATLAB拟合曲面如图4所示.
4.2 第Ⅱ曲面数学模型
以同种方法对鳄鱼上颚表面第Ⅱ曲面点云进行曲面拟合,同样考虑精度与实际加工难易程度后,x、y不同指数的拟合结果如表2所示.
通过分析表2可知,随着x、y指数的不断增加,当x的指数选取3,y的指数选取4时,残差平方和SSE=1 001,均方差RMSE=0.480 2,决定系数R2=0.955 4,因此曲面Ⅱ的拟合方程为z2=f(x,y)=32.35+0.083 8x-1.612y-0.002 963x2-0.040 58xy-0.082 27y2-1.71×10-5x3-0.000 326 4x2y-0.001 227xy2-0.000 339y3-8.416×10-7x3y-4.155×10-6x2y2-2.111×10-6xy3-1.055×10-5y4,鳄鱼上颚表面第Ⅱ曲面MATLAB拟合曲面如图5所示.
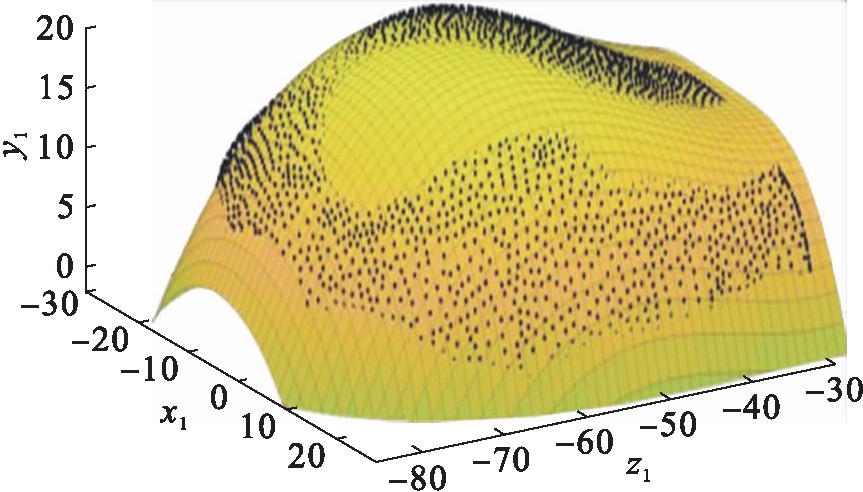
图4 上颚表面第Ⅰ部分拟合曲面图
Fig.4 Fitted surface of part Ⅰ of upper jaw surface
表2 不同指数自变量曲面Ⅱ的拟合结果
Tab.2 Fitting results of independent surface Ⅱ with different indexes
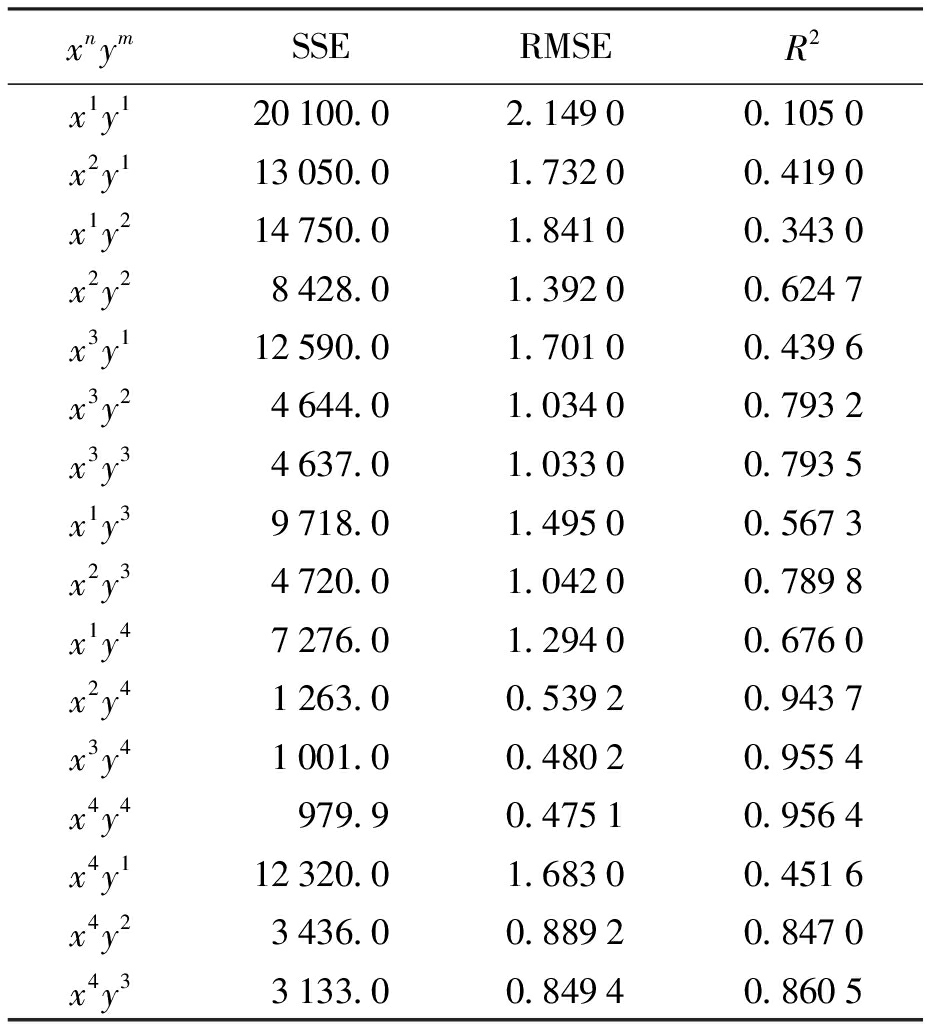
xnymSSERMSER2x1y120100.02.14900.1050x2y113050.01.73200.4190x1y214750.01.84100.3430x2y28428.01.39200.6247x3y112590.01.70100.4396x3y24644.01.03400.7932x3y34637.01.03300.7935x1y39718.01.49500.5673x2y34720.01.04200.7898x1y47276.01.29400.6760x2y41263.00.53920.9437x3y41001.00.48020.9554x4y4979.90.47510.9564x4y112320.01.68300.4516x4y23436.00.88920.8470x4y33133.00.84940.8605
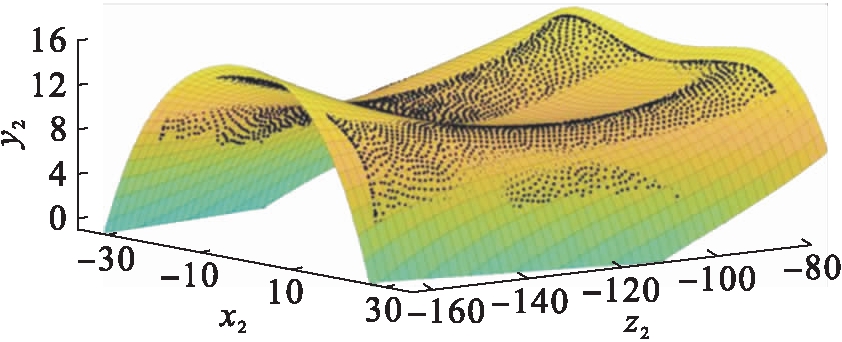
图5 上颚表面第Ⅱ部分拟合曲面图
Fig.5 Fitted surface of part Ⅱ of upper jaw surface
4.3 第Ⅲ曲面数学模型
以同种方法在MATLAB软件中对菲律宾鳄鱼上颚表面第Ⅲ曲面点云进行曲面拟合,同样考虑精度与实际加工难易程度后,x、y不同指数的拟合结果如表3所示.
表3 不同指数自变量曲面Ⅲ的拟合结果
Tab.3 Fitting results of independent surface Ⅲ with different indexes
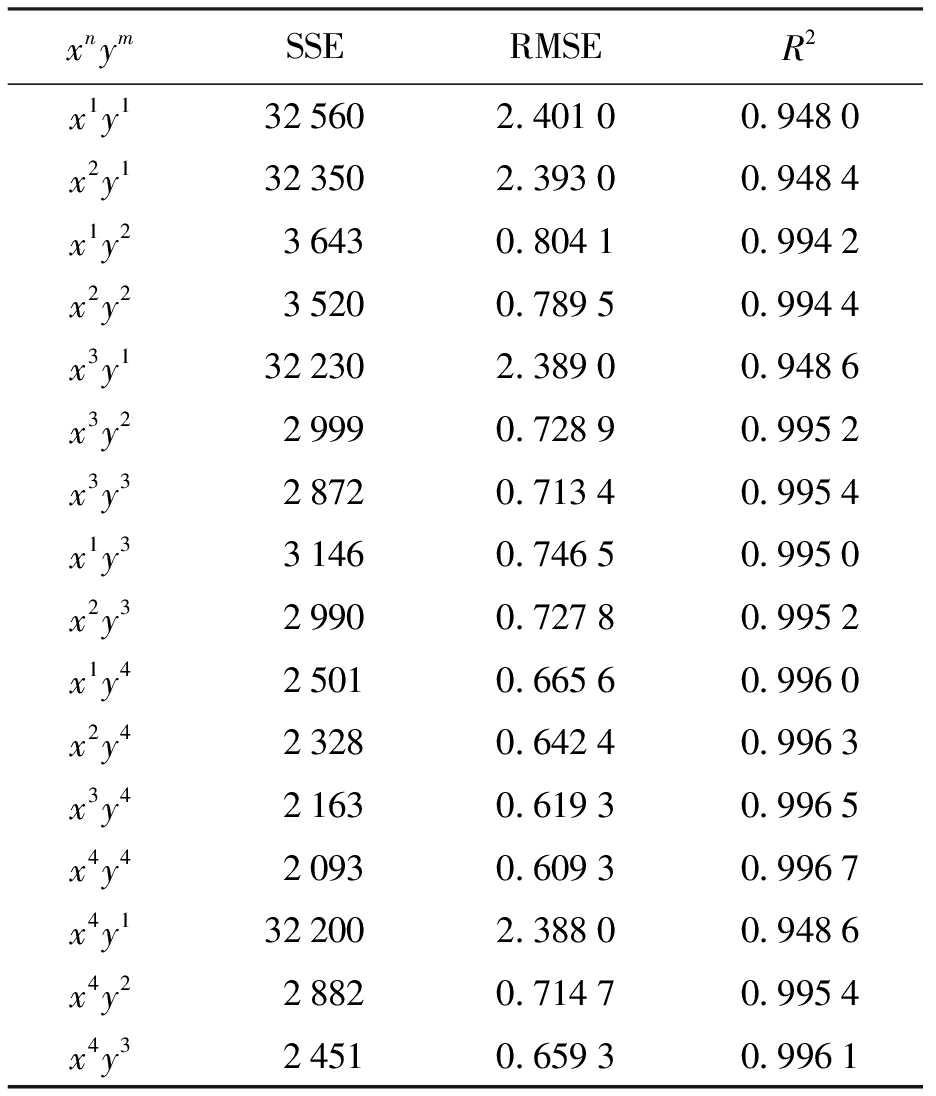
xnymSSERMSER2x1y1325602.40100.9480x2y1323502.39300.9484x1y236430.80410.9942x2y235200.78950.9944x3y1322302.38900.9486x3y229990.72890.9952x3y328720.71340.9954x1y331460.74650.9950x2y329900.72780.9952x1y425010.66560.9960x2y423280.64240.9963x3y421630.61930.9965x4y420930.60930.9967x4y1322002.38800.9486x4y228820.71470.9954x4y324510.65930.9961
通过分析表3可知,随着x、y指数的不断增加,当自变量x、y的指数均选取3时,残差平方和SSE=2 872,均方差RMSE=0.713 4,决定系数R2=0.995 4,因此曲面Ⅲ的拟合方程为z3=f(x,y)=39.18+1.058x-0.462 9y-0.007 816x2-0.004 383xy-0.000 625 4y2+1.341×10-5x3-1.095×105x2y+2.756×10-5xy2+2.422×10-5y3,鳄鱼上颚表面第Ⅲ曲面MATLAB拟合曲面如图6所示.
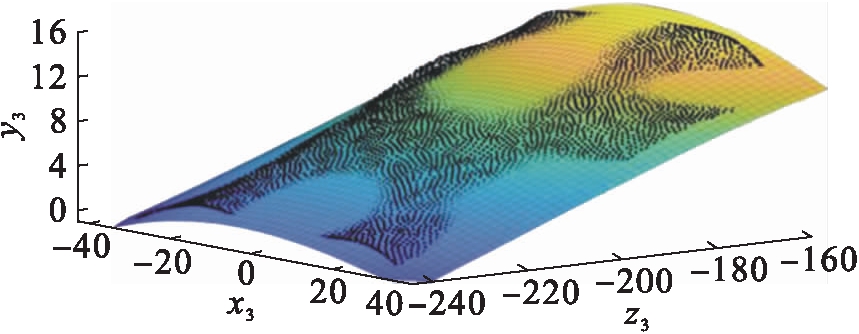
图6 上颚表面第Ⅲ部分拟合曲面图
Fig.6 Fitted surface of part Ⅲ of upper jaw surface
5 曲面合成
提取拟合后3个数学模型的数据,将其在Imageware中滤后合成,再将合成的点云数据在Geomagic Studio软件中进行封装,经平滑、降噪等处理后,得到的合并曲面如图7所示.将拟合后的模型与原模型进行偏差对比分析,结果表明:数字曲面模型的标准偏差为0.581 3 mm,平均偏差为-0.478 4/0.435 4 mm,拟合后的数字曲面模型较原生物曲面形貌相近,满足工程设计上的允许误差,可用于后续分析及其仿生设计.

图7 数学模型合并曲面图
Fig.7 Merged surface by mathematical model
6 结 论
通过上述分析,可以得到如下结论:
1) 通过将逆向工程技术与计算机技术结合,完成了对原始模型与特征模型的重构及修复.为校验特征较原始模型的改变,将两个模型进行偏差分析,结果表示,最大偏差在孔洞填补位置,标准偏差为0.016 4 mm,满足工程设计上的允许误差,因此特征模型可用于后续分析.
2) 运用多项式拟合的方法分别建立按照生物形貌特征划分3个曲面的数学模型,综合考虑拟合精度与后续仿生设计等方面因素,最终得到3个拟合后数学模型的方程表达式,且它们的决定系数R2均接近于1.
3) 将3个数学模型的数据进行合并,得到完整的曲面模型,并将其与原生物曲面进行偏差对比分析,其结果表明,拟合后的曲面模型较原生物曲面形貌相近,标准偏差为0.581 3 mm,满足工程设计要求.
[1]Doyle C E,Bird J J,Isom T A,et al.An avian-inspired passive mechanism for quadrotor perching [J].IEEE/ASME Transactions on Mechatronics,2013,18(2):506-517.
[2]Mellinger D,Lindsey Q,Shomin M,et al.Design,modeling,estimation and control for aerial grasping and manipulation [C]//IEEE/RSJ International Conference on Intelligent Robots & Systems.San Francisco,USA,2011:25-30.
[3]权龙哲,赵琳,李星辉,等.多功能蜓爪式仿生末端执行器设计与试验 [J].农业机械学报,2017,48(8):33-42.
(QUAN Long-zhe,ZHAO Lin,LI Xing-hui,et al.Design and test of multifunctional dragonfly claws form bio-mimetic end effector [J].Transactions of the Chinese Society for Agricultural Machinery,2017,48(8):33-42.)
[4]张锐,杨明明,潘润铎,等.鸵鸟足底非规则曲面形貌数学模型构建 [J].农业工程学报,2015,31(增刊1):71-78.
(ZHANG Rui,YANG Ming-ming,PAN Run-duo,et al.Mathematical model construction of the irregular surface morphology of ostrich plantar [J].Transac-tions of the Chinese Society of Agricultural Engineering,2015,31(Sup1):71-78.)
[5]张伏,王亚飞,马田乐,等.山羊蹄底部非规则曲面仿生形貌数学模型构建及验证 [J].农业工程学报,2018,34(15):30-36.
(ZHANG Fu,WANG Ya-fei,MA Tian-le,et al.Mathematical model construction and verification of bionic morphology of irregular curved surface at the foot of goat’s foot [J].Transactions of the Chinese Society of Agricultural Engineering,2018,34(15):30-36.)
[6]周宏根,崔杰,田桂中,等.河鲀背部形貌曲面拟合及数学建模 [J].吉林大学学报(工学版),2020,50(3):1131-1137.
(ZHOU Hong-gen,CUI Jie,TIAN Gui-zhong,et al.Surface fitting and mathematical modeling of puffer fish back morphology [J].Journal of Jilin University (Engineering and Technology Edition),2020,50(3):1131-1137.)
[7]于明旭.离散点云数据三维重建原理与误差分析 [J].科学技术创新,2019(5):21-23.
(YU Ming-xu.Principle and error analysis of 3D reconstruction of discrete point cloud data [J].Scienti-fic and Technological Innovation,2019(5):21-23.)
[8]马常丽,李庆斌,黄格格,等.基于非均匀有理B样条的压电陶瓷非线性校正 [J].沈阳工业大学学报,2017,39(2):183-187.
(MA Chang-li,LI Qing-bin,HUANG Ge-ge,et al.Non-linear correction of piezoelectric ceramics based on non-uniform rational B-spline [J].Journal of Shen-yang University of Technology,2017,39(2):183-187.)
[9]刘同海,滕光辉,张盛南,等.基于点云数据的猪体曲面三维重建与应用 [J].农业机械学报,2014,45(6):291-295.
(LIU Tong-hai,TENG Guang-hui,ZHANG Sheng-nan,et al.3D reconstruction and application of pig surface based on point cloud data [J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(6):291-295.)
[10]李涛,刘冲,李经民.动物头骨的三维实体模型重构 [J].机械设计与制造,2015(1):94-96.
(LI Tao,LIU Chong,LI Jing-min.Reconstruct the three-dimensional solid model of animal skulls [J].Machinery Design & Manufacture,2015(1):94-96.)
[11]杨洪斌.基于Geomagic Studio的残缺点云面片数据修复研究:以某型汽车配件为例 [J].装备制造技术,2016(11):28-31.
(YANG Hong-bin.Study on data repair of detect cloud based on Geomagic Studio:take an automobile fitting as an example [J].Equipment Manufacturing Technology,2016(11):28-31.)
[12]郭培闪,杜黎明.运用Geomagic Studio实现点云数据的曲面重建及误差分析 [J].地理信息世界,2015,22(1):57-60.
(GUO Pei-shan,DU Li-ming.Realized the surface reconstruction of point clouds and error analysis by using the Geomagic Studio [J].Geomatics World,2015,22(1):57-60.)
[13]张锐,乔钰,吉巧丽,等.驯鹿足底非规则特征形貌数学模型构建及验证 [J].农业工程学报,2017,33(8):56-61.
(ZHANG Rui,QIAO Yu,JI Qiao-li,et al.Mathematical model construction and verification of the irregular feature morphology of reindeer feet [J].Transactions of the Chinese Society of Agricultural Engineering,2017,33(8):56-61.)
[14]曾波,刘佩森,曾凤,等.基于Imageware涡轮叶片的逆向设计 [J].机械设计,2019,36(增刊1):180-182.
(ZENG Bo,LIU Pei-sen,ZENG Feng,et al.Reverse design of turbine blades based on Imageware [J].Journal of Machine Design,2019,36(Sup1):180-182.)
 de Paleontologia Miquel Crusafont, Universitat Autònoma de Barcelona, Barcelona 75005, Spain; 3. Center of Natural History, University of Hamburg, Hamburg 20146, Germany)
de Paleontologia Miquel Crusafont, Universitat Autònoma de Barcelona, Barcelona 75005, Spain; 3. Center of Natural History, University of Hamburg, Hamburg 20146, Germany)