现代控制理论的不断进步及控制方法多样化使得多关节机械手广泛应用于国民经济的各个领域，如生产线的装配机械臂、农业生产中的水果采摘机械手和智能机器人手臂等，在恶劣的工业生产环境中，多关节机械手已经取代人工操作，成为工业生产中必不可少的组成部分[1-3].由于多关节机械手系统存在各种不确定性和各关节间的非线性耦合，使得传统基于精确数学模型而设计的机械手控制器应用受限[4-5].
目前，国内外应用于不确定系统较为先进的控制策略主要有自适应控制、鲁棒控制、神经网络控制和迭代学习控制等.唐庆顺等[6]设计了一种自适应的二阶终端滑模控制器，通过实时修正控制参数来适应受控对象和外部干扰动态改变，使系统始终保持在最优或次优状态.但该方法对于含非参数不确定性因素的系统难以保证稳定性.刘益标等[7]引入了径向基函数神经网络算法跟踪双关节机械臂的运动轨迹，表现出了非线性逼近映射特性，对于处理控制系统中各种不确定性和非线性问题具有显著的优势.但是该方法对系统模型的精度要求较高，在实际应用中存在一定的局限性.考虑到模糊控制系统不依赖于系统模型的精确度，且能够有效抑制控制系统抖振特性，提出一种基于自适应模糊反演算法的双关节机械手控制系统.首先将复杂系统分解成若干简单系统，然后通过在虚拟控制中引入模糊系统，在不需要建立系统数学模型的情况下，实现了对双关节机械手系统自适应模糊反演控制，不仅保证了系统控制的稳定性，还有效提升了动态跟踪精度.
1 反演控制及问题描述
1.1 反演控制算法
反演控制算法通过引入静态补偿，将复杂的非线性系统分解为若干低阶次的简单子系统，然后分别对每个子系统设计相应的控制律，再组合子系统控制律完成对整个系统的设计[8-9].自适应反演控制算法已被用于解决各种高低速飞行器和无人机系统的姿态控制，解决复杂系统中的各种不确定性和非线性问题.Vaidyanathan等[10]将自适应反演控制用于处理复杂的混沌动力学系统，获得了表现出色的控制器.此外，反演控制算法还被普遍用于对输入量化不确定非线性系统、未知时滞不确定非线性系统、未知负载及外部干扰悬浮系统和未知结构参数及驱动故障系统，通过对反演控制算法中间虚拟控制量的设计，可衍生出具有不同特性的反演控制算法.如采用微分阻尼虚拟控制量的反演控制可有效提高系统的动态性能，而采用切换函数虚拟控制量的反演控制则具有与滑模控制算法相似的优点[11-12].这些研究成果均表明反演算法对于不确定非线性系统控制具有非常理想的可行性及高效性.
1.2 问题描述
双关节机械手在精确数学建模的过程中存在诸多不确定性：1)参数不确定性，包括各个结构部件质量和尺寸等物理参数的未知或部分已知；2)非参数不确定性，包括高频或低频未建模动态等；3)由工作环境引入的干扰、驱动器饱和、采样时滞及关节耦合等问题.这些诸多不确定性或非线性因素都会导致机械手控制系统发生质的改变，严重时甚至可能造成控制系统丧失稳定性.在虚拟控制中引入模糊系统，可演化为无需精确数学模型的自适应模糊反演控制，能够有效提高上述双关节机械手系统的控制精度.
2 双关节机械手动力学建模
在建模过程中对某些不确定性因素进行了合理的忽略，以达到简化机器人数学模型的目的.双关节刚性机械手结构简图如图1所示.
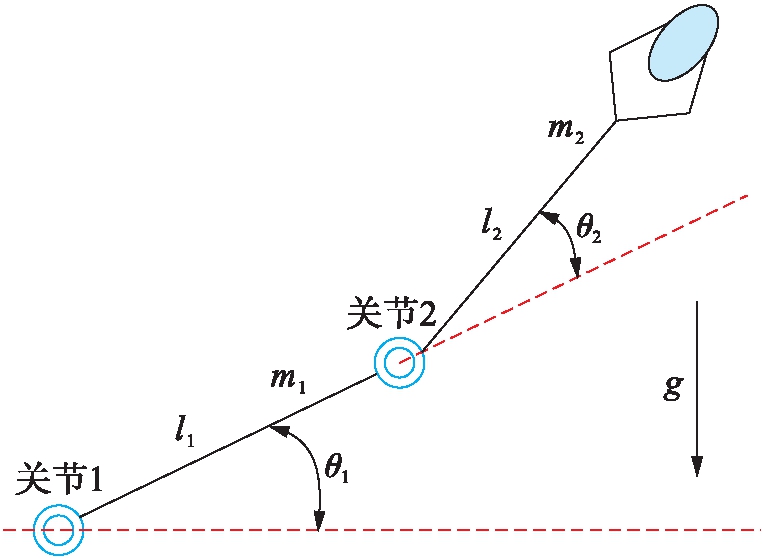
图1 双关节机械手结构简图
Fig.1 Structural sketch of two-joint manipulator
图1中，m1和m2为机械手两个关节的质量；l1和l2为两个关节的长度；θ1和θ2为这两个关节的转动角度；g为重力加速度.动态性能可由二阶非线性微分方程描述为
M(x1)x3+C(x1，x2)x2+G(x1)+F(x2)+d=τ
(1)
式中：x1=[θ1，θ2]为机器人的关节角位移量；x2和x3分别为机械手的角速度和角加速度；M(x1)为双关节机械手的惯性矩阵；C(x1，x2)为哥氏力；G(x1)为重力项；F(x2)为摩擦力矩；τ为控制力矩；d为外加扰动[13].一般来说，需要将双关节机械手系统参数假设为未知但有界的参数，并且该系统还应具有以下性质：1)惯性矩阵M(x1)为正定对称矩阵，且M(x1)有界；2)惯性矩阵
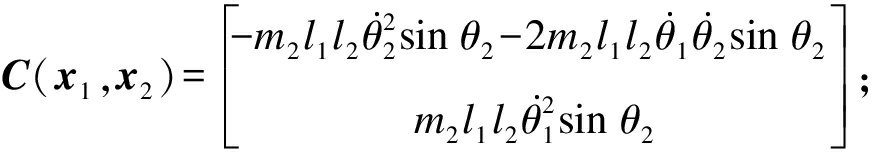
τ=[τ1，τ2]T.
3 反演控制器设计
反演控制算法通过逐步递推，利用后一个子系统来虚拟控制前一个子系统，最终使整个系统趋于正定稳定，特别适合于设计不确定非线性系统的控制器.通过与李雅普诺夫型自适应模糊规律的结合运用，可使整个被控系统获得所需的动静态性能指标[14].针对本文的双关节机械手系统，利用反演控制的基本思想将其分解为两个子系统，再分别为每一个子系统设计李雅普诺夫函数和中间虚拟控制项，最后来完成整个系统控制律的设计.
3.1 自适应模糊反演控制律的设计
设x0为双关节机械手系统理想的输出转角，且x0具有二阶导数，则系统的跟踪误差可定义为e1=x1-x0.同理，定义速度误差e2=x2-α1，若选择合适的虚拟控制量α1让e2趋于0，则有
(4)
根据式(4)，中间虚拟控制项可表示为
(5)
式中，λ1为控制系数.若定义李雅普诺夫函数
则有
(6)
显然，式(6)中的
则
对应的子系统稳定[15-16].但当
时，需要进一步设计，又因为
(7)
故取控制律τ=-λ2e2-e1-φ，定义李雅普诺夫函数为
则有
(8)
令
将τ代入式(7)可得
(9)
考虑到式(9)中的f包含双关节机械手系统的建模信息，因此，需要采用模糊系统逼近f以实现无需模型信息的反演控制.
3.2 自适应模糊控制律的设计
若定义φ为用于逼近非线性函数f的模糊系统，则可运用单值模糊化或重心平均反模糊化等方法对其进行模糊处理[17].设模糊系统由N个模糊规则组成，第i个规则表示为
Ri：IF x1 is 
and … xn is 
y is Bi.
其中，
为xj(j=1，2，…，n)的隶属度函数，则其对应的模糊系统的输出可表示为
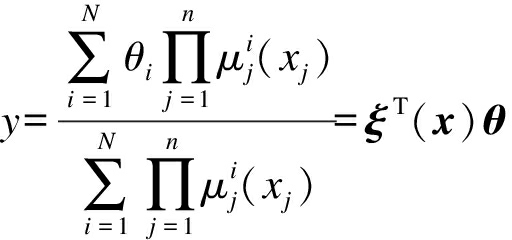
(10)
式中：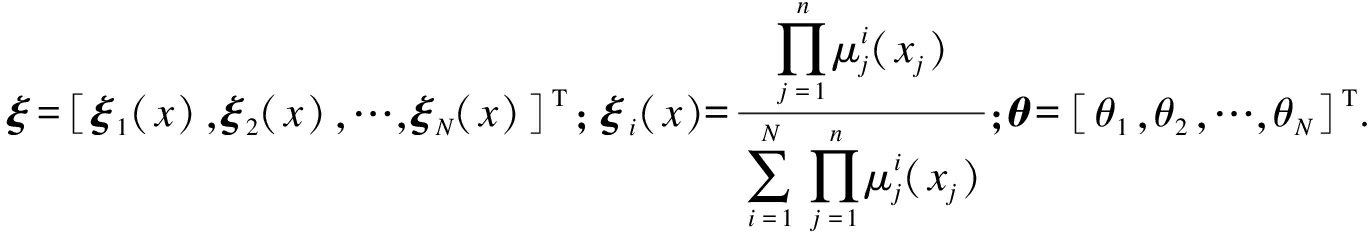
关于f的模糊逼近，利用分别逼近f(1)和f(2)的形式，则模糊系统可设计为
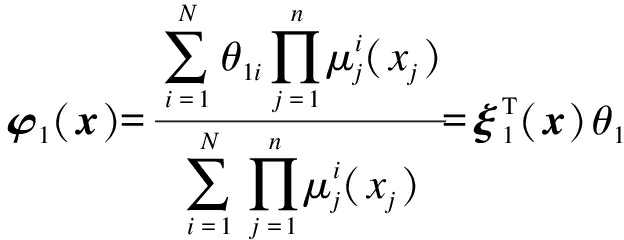
(11)
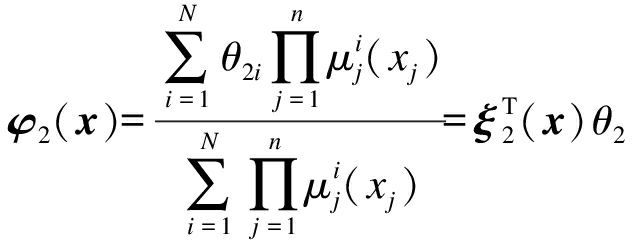
(12)
令
如果定义θ*为最优逼近常量，则存在任意给定的无穷小常量ε(ε>0)满足不等式
则本文所设计的自适应模糊控制律可表示为
(13)
式中，γ和κ为控制系数，且γ>0.
4 仿真实验与分析
在双关节机械手动力学建模基础上，针对动力学模型设计了反演控制器，通过对机械手的反演控制使其能够在工业生产现场操作中实现精确的位移轨迹跟踪.为了验证设计的反演自适应模糊控制器的性能，对双关节机械手连杆1和连杆2的位置跟踪轨迹及跟踪误差进行仿真实验.
双关节机械手系统的参数选取：m1=m2=1.0，l1=l2=0.5；双关节机械手系统的初始状态设定为x(0)=[1，0]T，系统输出的理想轨迹为y=sin(2πt)，采用高斯函数作为控制器的隶属度函数，数学定义可表示为
(i=1，2，3，4；j=1，2，3)
(14)
式中：均值cj分别选为-1.5、0和1.5；方差σj取为0.5.获得的控制器隶属度函数如图2所示.
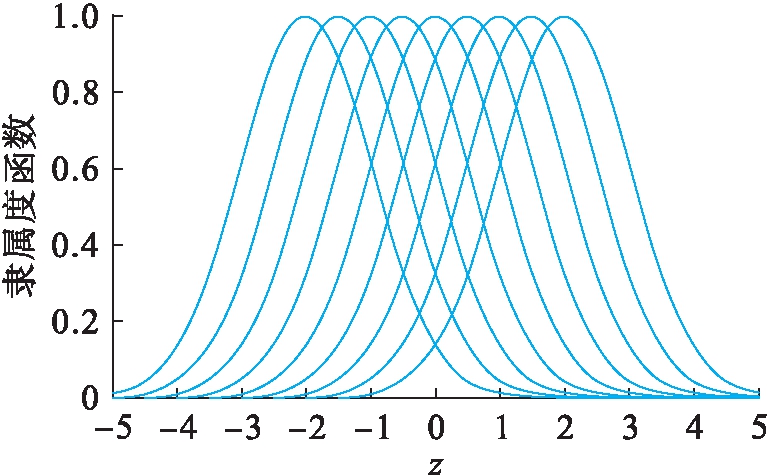
图2 模糊系统隶属度函数
Fig.2 Membership function of fuzzy system
为了对设计的自适应模糊反演控制器进行模拟仿真，将控制器的控制系数分别设为：λ1=8，λ2=12，γ=1.5，κ=2.5和λ1=2，λ2=2.5，γ=1.5，κ=2.5.为了更好地与实际情况进行匹配，同时也能对控制系统的有效性进行验证，系统设定外部干扰d=[0.25sin t，0.25cos t]为随机干扰量；采样周期取Ts=0.005 s.利用MATLAB Simulink模块仿真得到双关节机械手连杆1和连杆2的位置跟踪轨迹及跟踪误差的仿真结果如图3～4所示.
由图3～4的仿真结果可知，设计的控制器能够保证双关节机械手的两个连杆都具有较高的跟踪精度，其跟踪误差均小于0.87%，完全能够满足该控制器的设计性能要求.在连杆初始运动阶段，存在较大的跟踪误差，但当机械手处于稳定运动阶段后其连杆的运动轨迹与预期理想轨迹基本重合，从而很好地验证了自适应模糊反演算法对于双关节机械手控制的有效性和可行性.此外，通过对连杆1和连杆2跟踪误差的对比分析可知，连杆2在稳定状态的最大跟踪误差要小于连杆1的跟踪误差.
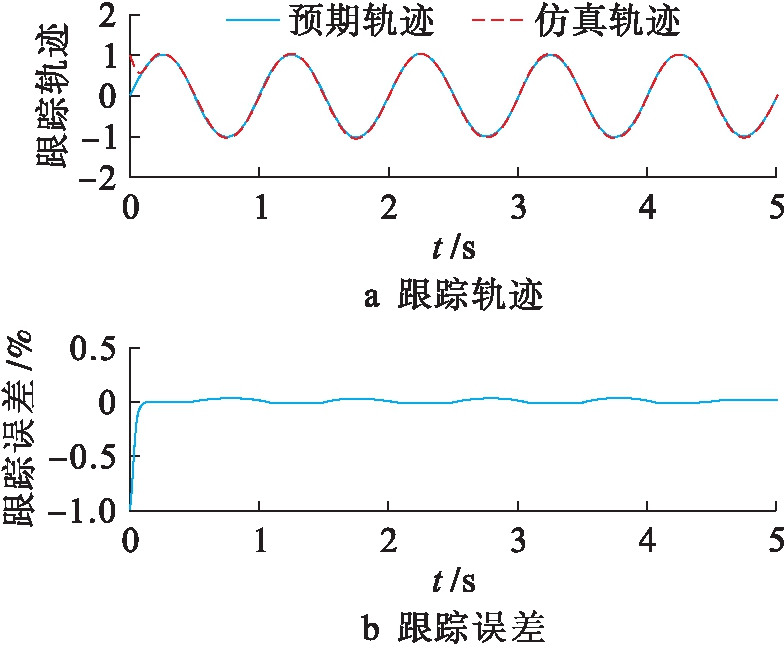
图3 连杆1位置跟踪轨迹及跟踪误差
Fig.3 Location tracking trajectory and tracking error of connecting rod 1
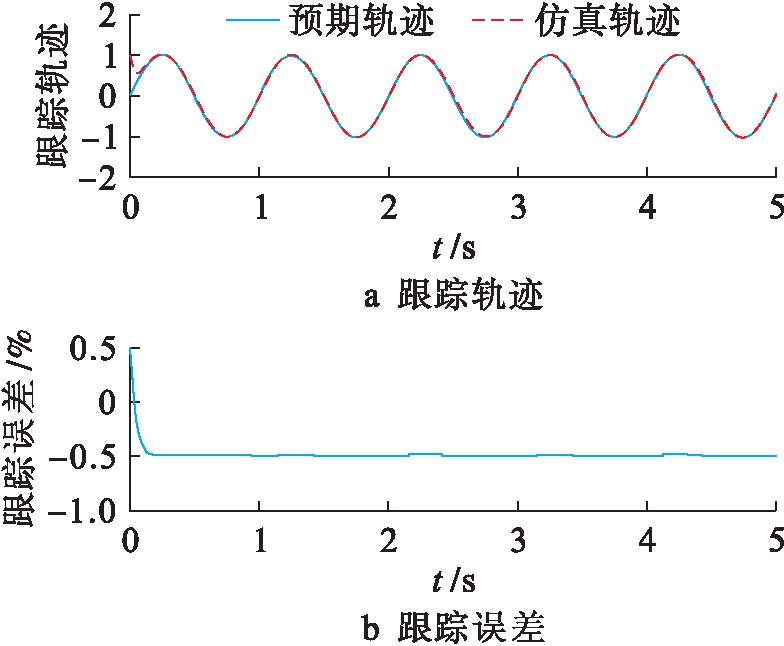
图4 连杆2位置跟踪轨迹及跟踪误差
Fig.4 Location tracking trajectory and tracking error of connecting rod 2
综上所述，将设计的自适应模糊反演算法用于双关节机械手的跟踪控制，无需对被控对象建立精确数学模型，可以消除非线性系统中不确定性因素的影响，最终实现对机械手的高精度跟踪控制.
5 结 论
由于双关节机械手系统中的不确定性和非线性，使其精确数学模型难以获得.本文提出了自适应模糊反演控制算法，设计了高精度反演控制器，并对两个关节的动态轨迹进行跟踪，通过Simulink对建立的模型和控制算法进行了仿真分析.结果表明：提出的自适应模糊反演控制算法能够在很大程度上提高双关节机械手位置轨迹跟踪的暂态性能，且其对应的跟踪误差均小于0.87%，保证了位置跟踪控制过程的稳定性及准确性.自适应模糊反演控制能够保证控制精度，同时简化了建模过程以及控制参数选择问题，从而使本文提出的自适应模糊反演控制应用领域更加广阔.
[1]韩冬，崔艳，杨培林，等.空间双臂机器人机械臂最优轨迹规划仿真 [J].计算机仿真，2018，35(10)：333-339.
(HAN Dong，CUI Yan，YANG Pei-lin，et al.Simulation of trajectory planning for minimizing base reaction and manipulators jerk of dual-arm space robot [J].Computer Simulation，2018，35(10)：333-339.)
[2]王丽梅，蔺威威.三轴运动平台改进型交叉耦合轮廓控制 [J].沈阳工业大学学报，2016，38(4)：361-366.
(WANG Li-mei，LIN Wei-wei.Improved cross-coupled contour control for three axis motion table [J].Journal of Shenyang University of Technology，2016，38(4)：361-366.)
[3]范曙远，王海波，吴小笛，等.工业装配外骨骼机械臂承重性能研究 [J].工程设计学报，2018，25(6)：697-702.
(FAN Shu-yuan，WANG Hai-bo，WU Xiao-di，et al.Research on load-bearing performance of industrial assembly exoskeleton manipulator [J].Journal of Engineering Design，2018，25(6)：697-702.)
[4]许洋洋，王莹，薛东彬.机械臂神经网络控制优化与仿真 [J].中国工程机械学报，2018，16(5)：416-420.
(XU Yang-yang，WANG Ying，XUE Dong-bin.Neural network control optimization and simulation of robot arm [J].Chinese Journal of Construction Machi-nery，2018，16(5)：416-420.)
[5]冯朝，凌杰，明敏，等.融合迭代学习与干扰观测器的压电微动平台精密运动控制 [J].机器人，2018，40(6)：825-834.
(FENG Chao，LING Jie，MING Min，et al.Precision motion control for a piezoelectric micro-positioning stage via integrating iterative learning and disturbance observer [J].Robot，2018，40(6)：825-834.)
[6]唐庆顺，金璐，李国栋，等.基于自适应终端滑模控制器的机械手跟踪控制 [J].山东大学学报(工学版)，2016，46(5)：45-53.
(TANG Qing-shun，JIN Lu，LI Guo-dong，et al.Robotic manipulators tracking control based on adaptive terminal sliding mode controller [J].Journal of Shan-dong University of Technology (Engineering Science)，2016，46(5)：45-53.)
[7]刘益标，陈均.基于径向基函数神经网络控制的机械臂轨迹误差研究 [J].机床与液压，2018，46(15)：105-108.
(LIU Yi-biao，CHEN Jun.Research on trajectory error of mechanical arm based on radial basis function neural network control [J].Machine Tool & Hydraulics，2018，46(15)：105-108.)
[8]邹思凡，吴国庆，茅靖峰，等.改进非线性干扰观测器的机械臂自适应反演滑模控制 [J].计算机应用，2018，38(10)：2827-2832.
(ZOU Si-fan，WU Guo-qing，MAO Jing-feng，et al.Adaptive backstepping sliding mode control for robotic manipulator with the improved nonlinear disturbance observer [J].Journal of Computer Applications，2018，38(10)：2827-2832.)
[9]罗连杰，佃松宜，蒲明.一类非线性不确定系统的滑模反演控制 [J].电光与控制，2017，24(12)：27-30.
(LUO Lian-jie，DIAN Song-yi，PU Ming.Backstepping sliding-mode control for an uncertain nonlinear system [J].Electronics Optics & Control，2017，24(12)：27-30.)
[10]Vaidyanathan S，Volos C K，Rajagopal K，et al.Adaptive backstepping controller design for the anti-synchronization of identical WINDMI chaotic systems with unknown parameters and its SPICE implementation [J].Journal of Engineering Science and Techno-logy Review，2015，8(2)：74-82.
[11]陶洪峰，沈建强，陈刚，等.非线性时滞系统的未知方向自适应学习控制 [J].控制工程，2017，24(6)：1170-1174.
(TAO Hong-feng，SHEN Jian-qiang，CHEN Gang，et al.Unknown direction adaptive learning control for nonlinear time-delay systems [J].Control Engineering of China，2017，24(6)：1170-1174.)
[12]张天平，葛继伟，夏晓南.具有输入未建模动态的纯反馈非线性系统自适应控制 [J].控制理论与应用，2017，34(12)：1637-1647.
(ZHANG Tian-ping，GE Ji-wei，XIA Xiao-nan.Adaptive control of pure-feedback nonlinear systems with input unmodeled dynamics [J].Control Theory & App-lications，2017，34(12)：1637-1647.)
[13]杨航，刘凌，倪骏康，等.双关节刚性机器人自适应BP神经网络算法 [J].西安交通大学学报，2018，52(1)：129-135.
(YANG Hang，LIU Ling，NI Jun-kang，et al.An adaptive BP neural network algorithm for 2-joint rigid robots [J].Journal of Xi’an Jiaotong University，2018，52(1)：129-135.)
[14]刘慧博，刘尚磊.基于干扰补偿和微分器的转台反演滑模控制 [J].系统仿真学报，2018，30(4)：1593-1600.
(LIU Hui-bo，LIU Shang-lei.Sliding backstepping mode control for flight simulator servo based on disturbance compensation and differentiator [J].Journal of System Simulation，2018，30(4)：1593-1600.)
[15]杨立本，章卫国，黄得刚，等.欠驱动四旋翼飞行器反演模糊自适应控制 [J].西北工业大学学报，2015，33(3)：495-499.
(YANG Li-ben，ZHANG Wei-guo，HUANG De-gang，et al.Adaptive fuzzy backstepping control for underactuated quadrotor UAV [J].Journal of Northwestern Polytechnical University，2015，33(3)：495-499.)
[16]孙平，刘博，杨德国.全方向康复步行训练机器人的跟踪控制 [J].沈阳工业大学学报，2017，39(1)：88-93.
(SUN Ping，LIU Bo，YANG De-guo.Tracking control of omnidirectional rehabilitative training walker [J].Journal of Shenyang University of Technology，2017，39(1)：88-93.)
[17]陈龙胜，王琦.MIMO纯反馈受限系统无模型非线性比例反演控制 [J].控制与决策，2018，33(4)：731-740.
(CHEN Long-sheng，WANG Qi.Nonlinear proportional back-stepping controlfor un-modeled MIMO pure feedback constrained systems [J].Control and Decision，2018，33(4)：731-740.)