乳化沥青厂拌冷再生是一种充分利用回收沥青路面材料，能够常温施工的路面再生技术，该技术可以充分利用废旧资源，减少环境污染[1].乳化沥青冷再生混合料不同养生条件对其各项性能均有较大的影响，在原材料指标准确控制下，研究其养生方式与性能之间的非线性相关关系对于提高乳化沥青冷再生混合料性能具有重要意义.王宏等[2]采用宏观力学试验以及工业CT无损检测试验研究了不同养生方式下乳化沥青冷再生混合料含水率、劈裂强度、抗压回弹模量的发展规律，并与路面芯样进行对比，揭示了不同的养生方式对乳化沥青冷再生混合料细观与微观的空隙分布特征的影响机理.李志刚等[3]采用力学试验对全封闭养生、开放养生、半封闭养生3种养生条件下泡沫沥青冷再生混合料的含水率、劈裂强度、无侧限抗压强度及抗剪参数的发展规律进行研究，利用工业CT无损检测试验对泡沫沥青冷再生混合料内部空隙结构进行研究.研究表明，在不同养生方式下，混合料内部水分迁移路径和散失速率不一致，导致混合料养生过程中含水率及强度发展规律不一.曹俊武等[4]对试件的养生采取在不同温度和不同龄期的组合条件下进行，测试了基质沥青混合料和改性沥青混合料马歇尔稳定度和车辙动稳定度，得出对于基质沥青混合料，养生条件对其稳定度不产生影响，而改性沥青混合料的马歇尔稳定度和车辙动稳定度随养生龄期的延长或养生温度的升高而提高，并逐渐趋于稳定值，相比于养生温度、养生龄期的影响要更加重要.童申家等[5]基于Verhulst模型建立针对沥青混合料低温劈裂强度、动稳定度进行准确预测的非线性方程，并进行准确性分析.谭忆秋等[6]基于神经网络理论构建沥青混合料低温弯拉应变预测模型，分析了层底弯拉应变的影响因素，并进行了敏感性排序.张尚龙[7]分析了试验温度、加载频率、加载应力、混合料级配及体积指标等对混合料动态模量和相位角的影响规律，根据时间
温度等效原理，拟合确定不同温度间的移位因子，确定动态模量主曲线方程，运用麦夸特法优化算法得到沥青混合料动态模量预估模型，并进行了验证.谭忆秋等[8]建立了适用于冻融条件下沥青混合料损伤的普适模型，通过快速冻融作用下混合料的各性能试验结果对该模型进行了验证，提出了模型应用于混合料冻融损伤后寿命预估模型.董雨明等[9]采用两种硬质沥青胶结料和粗、细两个级配设计了4种硬质沥青混合料，研究了其高温、低温和水稳定性，采用7个温度条件动态模量试验研究了硬质沥青混合料的动态黏弹特性，确定了基于反曲函数的黏弹模型，建立了动态模量主曲线，研究结果显示，硬质沥青混合料高温性能优异，低温性能和水稳定性均可满足现行规范的要求.
以往关于养生条件对沥青混合料的研究多是分析了养生条件对性能的影响，没有进行预测分析，而针对沥青混合料的预测模型研究多是针对性能研究，并没有在养生条件和性能之间建立预测模型.本文建立的支持向量机预测模型，以养生条件作为输入参数，分别对混合料40 ℃马歇尔稳定度和15 ℃劈裂强度进行预测研究，同时采用构建的BP神经网络模型进行预测分析，并对各个模型的结果进行对比分析.支持向量机作为一种泛化能力强、收敛速度较快且具有全局优化能力的小样本回归预测模型，已广泛应用于各个领域的预测研究[10-12].本文研究能够很好地揭示养生因素与40 ℃马歇尔稳定度和15 ℃劈裂强度的非线性相关关系.
1 试验设计及方法
1.1 原材料选择
试验采用旧料来自于辽宁省某高速公路的铣刨料，为了使乳化沥青冷再生混合料试件在早期能够达到良好的强度和水稳定性，以及优化原有级配使其满足级配要求，故在试验中加入42.5#普通硅酸盐水泥、粒径为10～20 mm的粗集料和石屑，材料的试验级配为RAP：10～20 mm集料∶石屑∶水泥=73.5∶8∶17∶1.5.所用的乳化沥青的各项基本参数指标为：乳化剂1.4%，稳定剂0.05%，水38.55%，基质沥青62%.成型试件拌和所采用的水为可饮用水，试验中外掺水用量和乳化沥青用量为4.3%和3.0%.
1.2 养生试验
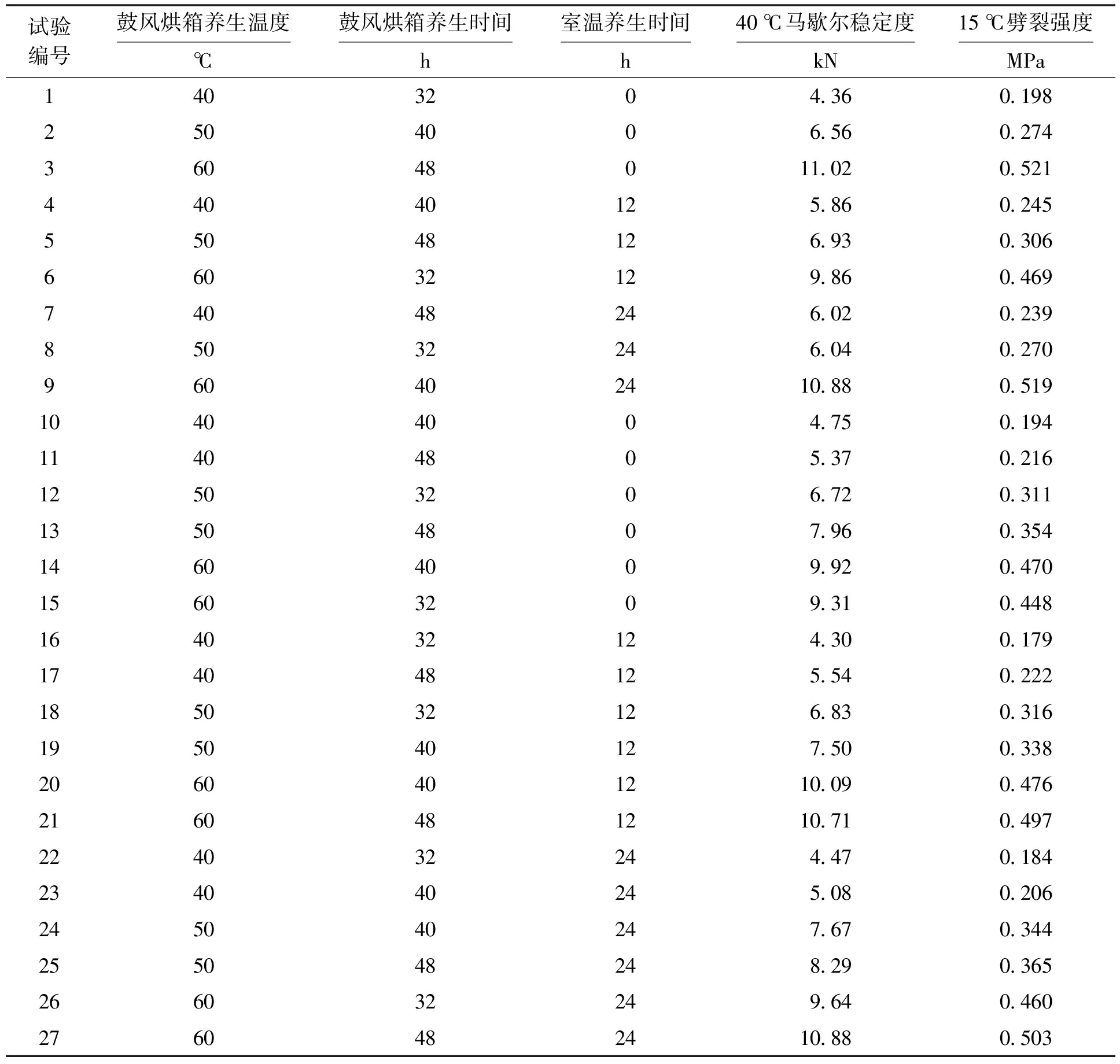
试验级配为73.5%RAP+8%(10～20 mm)集料+17%石屑+1.5%水泥，为了使样本数量充足，每组试验设置相同条件的平行试件，并取均值作为代表值，数据如表1所示.
2 模型介绍
支持向量机是一种基于统计分析理论发展而来较为先进的智能算法，已经在许多领域得到成功应用[13-14].支持向量机理论首先以学习有限个样本数据为基本脉络，再建立能够反映自变量与因变量非线性函数的关系，最后构造回归估计函数进行预测[15-17].利用Mapminmax函数进行试验数据的归一化处理，采用K-CV法优化惩罚参数c和径向基核参数g，从而搜寻到网络性能最佳时的c和g数值，借助最佳参数c和g训练支持向量机预测模型，实现对数据的预测.
遗传算法是由Holland教授创立的，其理论依据是“优胜劣汰，适者生存”.通过设置种群数量进行不断地种群选择、交叉和变异，不断提升种群的质量[17].
BP神经网络是一种通过误差逆向传递进行不断训练的多层前馈神经网络.借助遗传算法的全局搜寻最优解的能力来对神经网络进行优化，能够有效增大BP神经网络预测精度，其网络拓扑结构如图1所示.
表1 试验数据
Tab.1 Test data
试验编号鼓风烘箱养生温度℃鼓风烘箱养生时间h室温养生时间h40℃马歇尔稳定度kN15℃劈裂强度MPa1403204.360.1982504006.560.27436048011.020.52144040125.860.24555048126.930.30666032129.860.46974048246.020.23985032246.040.270960402410.880.51910404004.750.19411404805.370.21612503206.720.31113504807.960.35414604009.920.47015603209.310.448164032124.300.179174048125.540.222185032126.830.316195040127.500.3382060401210.090.4762160481210.710.497224032244.470.184234040245.080.206245040247.670.344255048248.290.365266032249.640.4602760482410.880.503
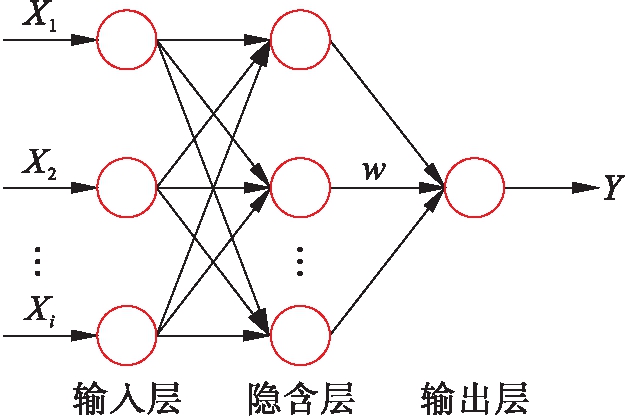
图1 BP神经网络拓扑结构
Fig.1 Topological structure of BP neural network
图1中，Xi为输入值，Y为输出值，w为网络权值.BP神经网络分为训练和预测两个部分，首先输入样本进行训练学习，当经过大量的学习之后，该网络对信息的挖掘识别能力会变得更为准确，进而对未知样本的预测就更为准确[18].遗传优化BP神经网络流程如图2所示.
3 模型建立与求解
3.1 K-CV优化支持向量机预测模型建立
选取试验鼓风烘箱养生温度、鼓风烘箱养生时间和室温养生时间作为输入参数，分别选取40 ℃马歇尔稳定度和15 ℃劈裂强度作为输出参数.利用上述Mapminmax函数，采用K-CV优化支持向量机模型输出结果，即相关性(R)、均方误差(MSE)和误差率来评价模型准确性，算法流程如图3所示.
针对40 ℃马歇尔稳定度的K-CV法参数选择结果等高线图如图4所示，参数选择结果3D视图如图5所示，预测结果如图6所示，误差率(预测值和真实值之差除以真实值)如图7所示.
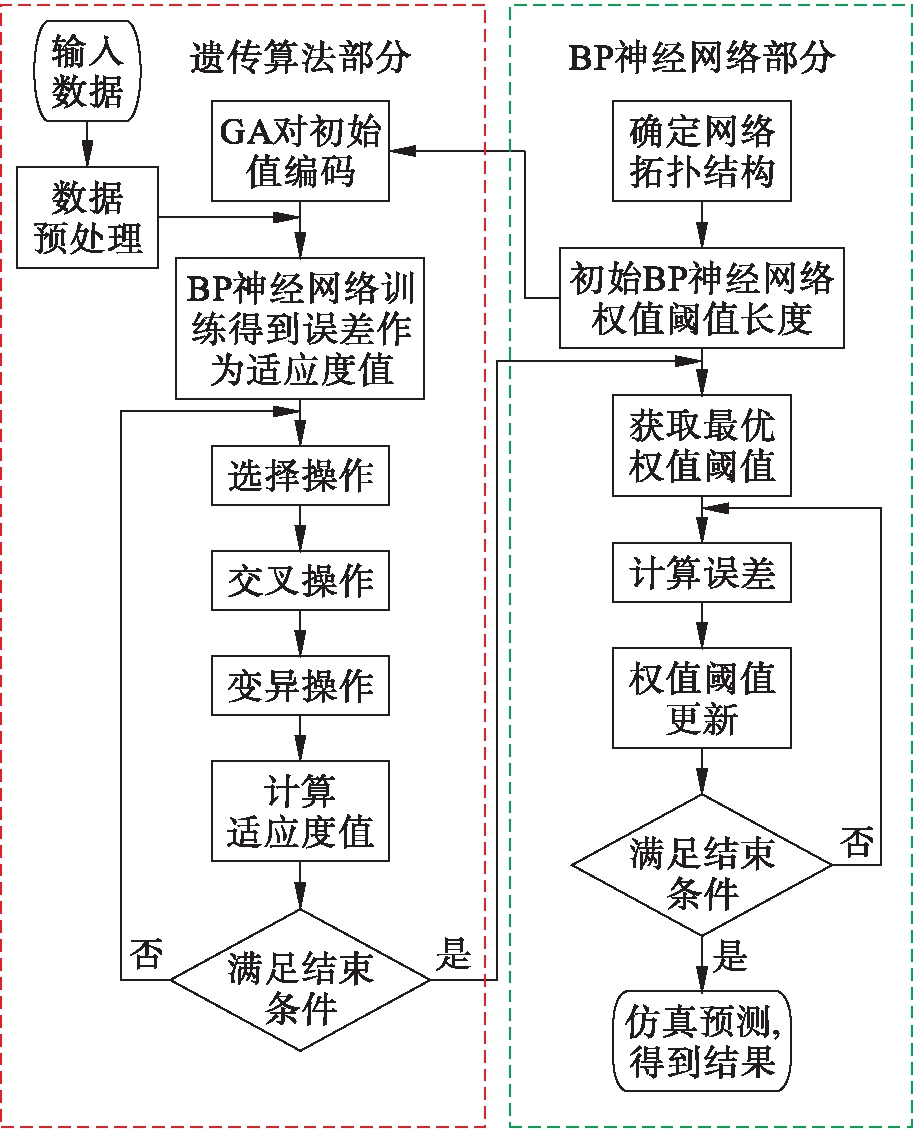
图2 优化流程
Fig.2 Flow chart of optimization
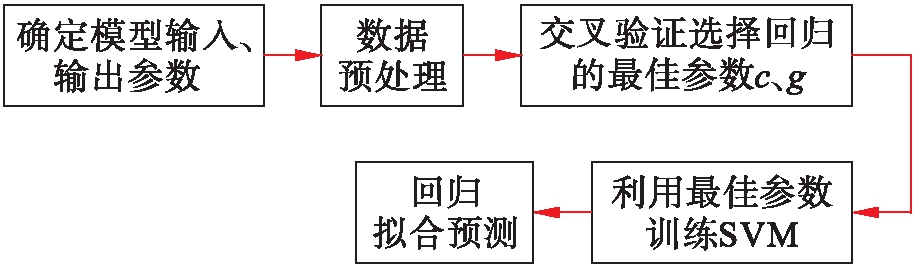
图3 算法流程
Fig.3 Flow chart of algorithm
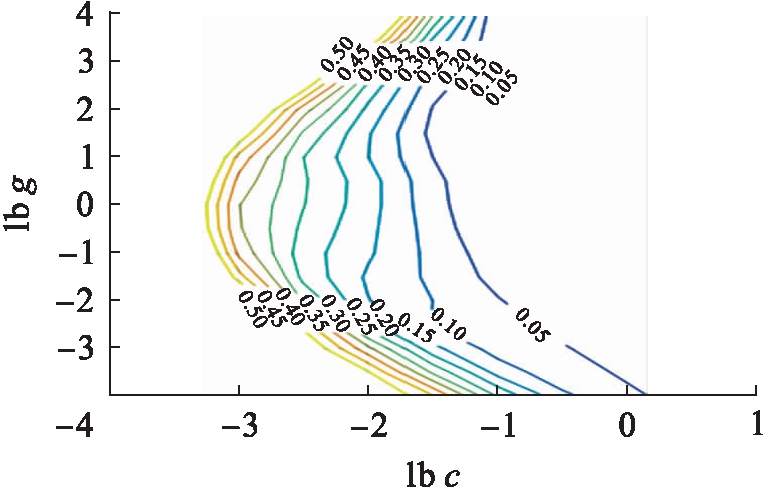
图4 40 ℃马歇尔稳定度参数选择等高线图
Fig.4 Contour of parameter selection with 40 ℃ Marshall stability
由图4～5可知，得到的最优参数为c=5.656 9，g=0.062 5.通过图6～7分析得出，40 ℃马歇尔稳定度预测值与真实值拟合效果良好，最大误差率小于6%，误差率集中在2%以内，表明回归预测结果准确.其中均方误差MSE=0.000 300 222，相关系数R=99.730 9%，表明该模型具有较好的数据拟合效果，并且预测误差小.
针对15 ℃劈裂强度的K-CV法参数选择结果等高线图如图8所示，参数选择结果3D视图如图9所示，预测结果如图10所示，误差率如图11所示.
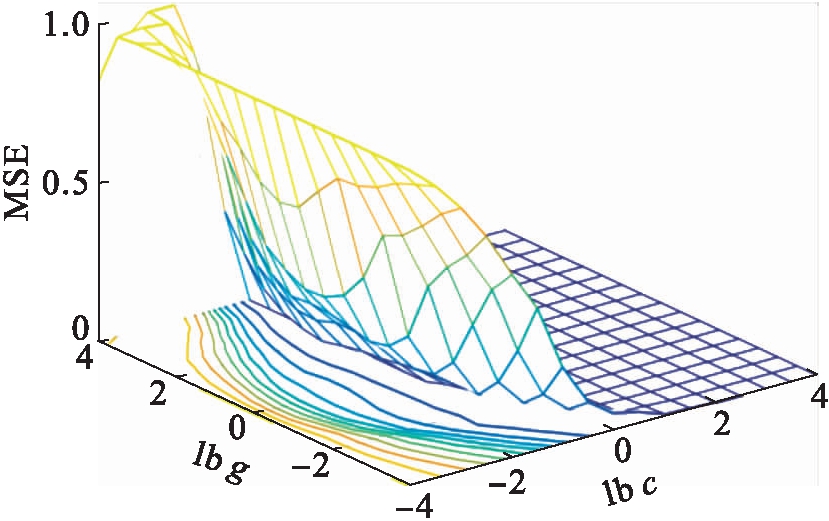
图5 40 ℃马歇尔稳定度参数选择结果3D视图
Fig.5 3D view diagram of parameter selection results with 40 ℃ Marshall stability
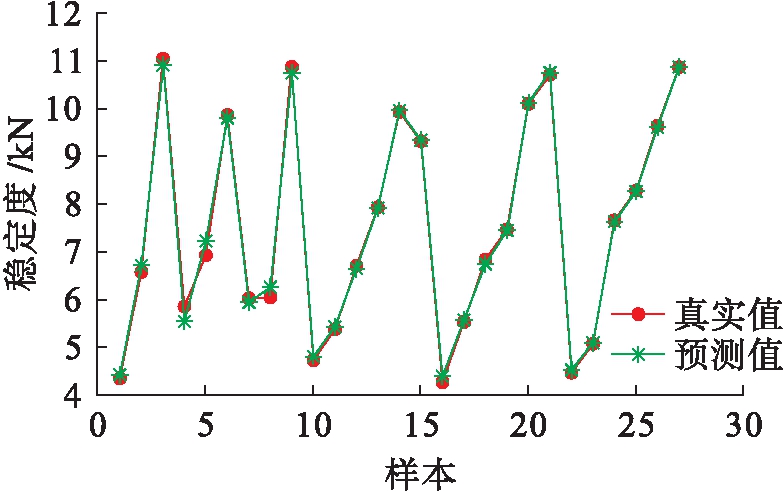
图6 SVM 40 ℃马歇尔稳定度预测结果
Fig.6 Prediction results of SVM with 40 ℃ Marshall stability
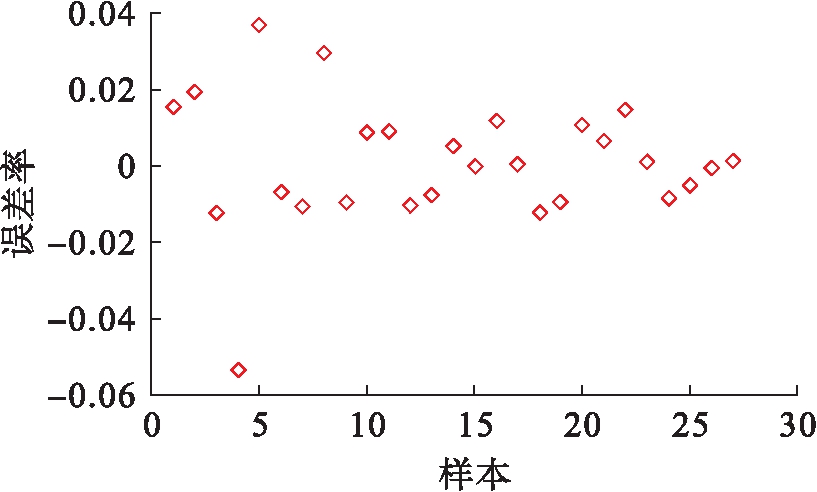
图7 SVM 40 ℃马歇尔稳定度误差率
Fig.7 Error rate of SVM with 40 ℃ Marshall stability
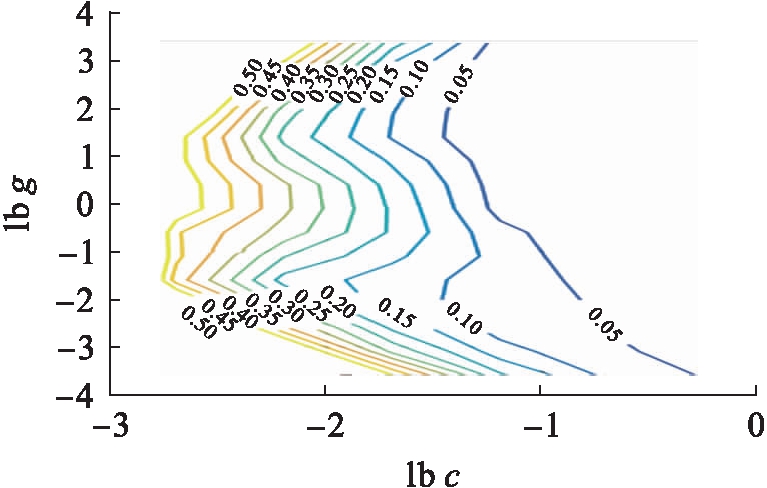
图8 15 ℃劈裂强度参数选择等高线图
Fig.8 Contour of parameter selection with 15 ℃ splitting strength
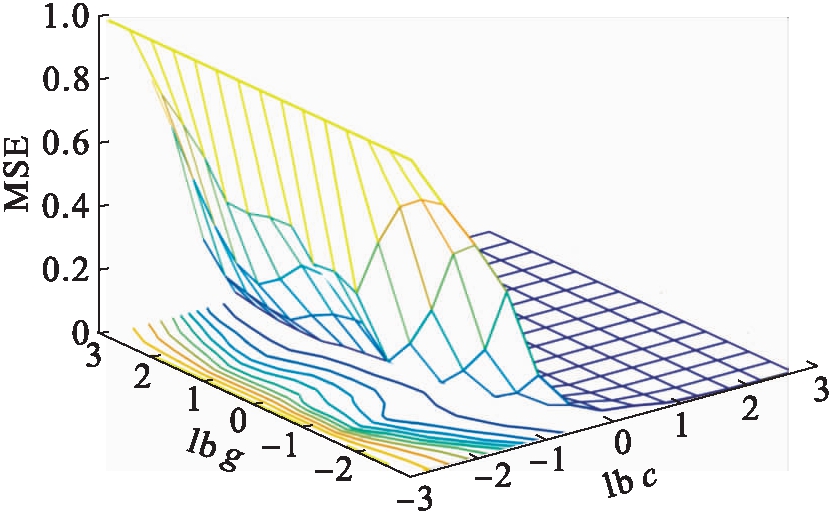
图9 15 ℃劈裂强度参数选择结果3D视图
Fig.9 3D view diagram of parameter selection results with 15 ℃ splitting strength
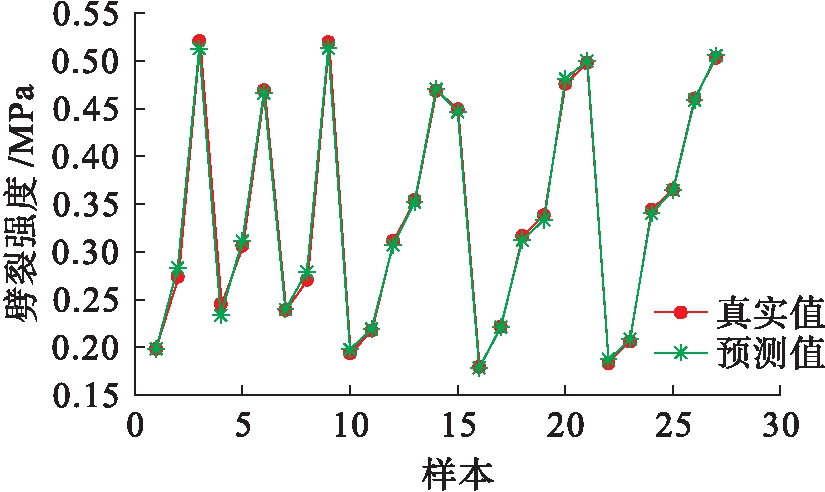
图10 SVM 15 ℃劈裂强度预测结果
Fig.10 Prediction results of SVM with 15 ℃ splitting strength
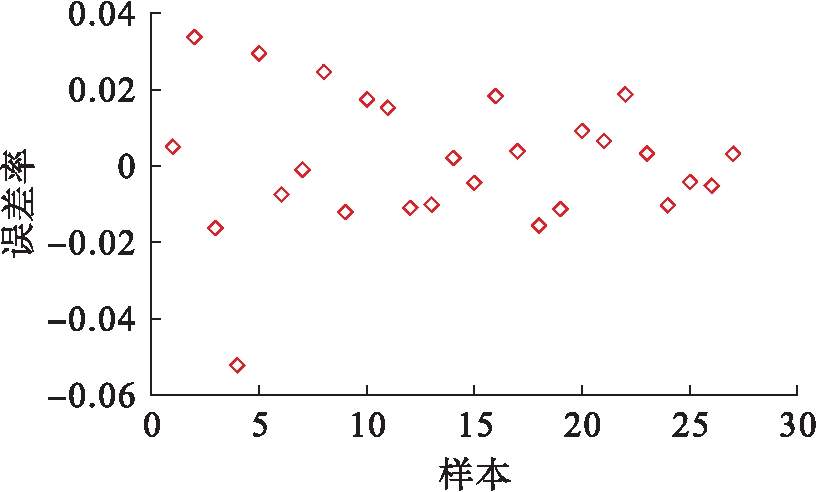
图11 SVM 15 ℃劈裂强度误差率
Fig.11 Error rate of SVM with 15 ℃ splitting strength
由图8～9可知，得到的最优参数为c=4.924 6，g=0.082 469.通过图10～11分析得出，15 ℃劈裂强度预测值与真实值拟合效果良好，最大误差率小于6%，误差率集中在2%以内，回归预测结果准确，其中均方误差MSE=0.000 210 547，相关系数R=99.828 1%，表明该模型具有较好的数据拟合效果，并且预测误差小.
3.2 GA优化BP神经网络预测模型建立
确定输入参数为试验鼓风烘箱养生温度、鼓风烘箱养生时间和室温养生时间，选取40 ℃马歇尔稳定度作为输出参数.根据图2优化神经网络流程图，首先采用遗传算法对权值阈值进行优化，其中种群规模为10，进化代数为100次，交叉和变异概率分别为0.4和0.2，其优化的适应度曲线变化如图12所示.
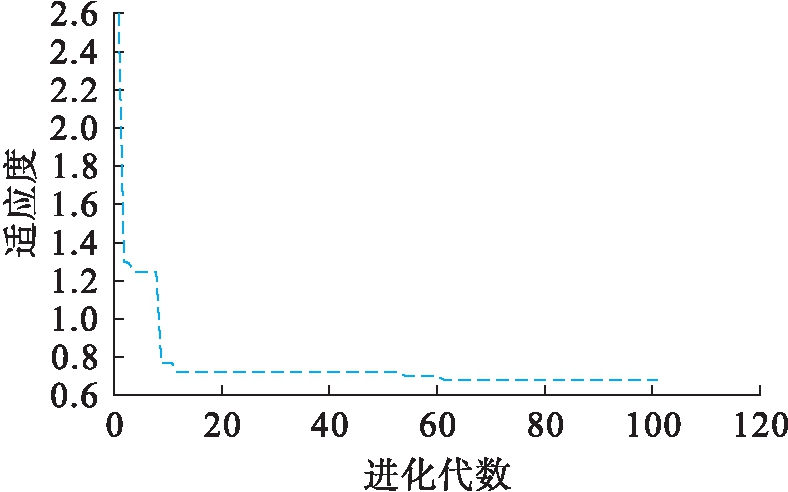
图12 40 ℃马歇尔稳定度适应度曲线
Fig.12 Fitness curve with 40 ℃ Marshall stability
由图12可知，经过15次迭代后，个体适应度基本稳定，表明该模型的稳定性较高，对于40 ℃马歇尔稳定度的预测结果如图13所示，预测误差如图14所示，模型的拟合优度图如图15所示.
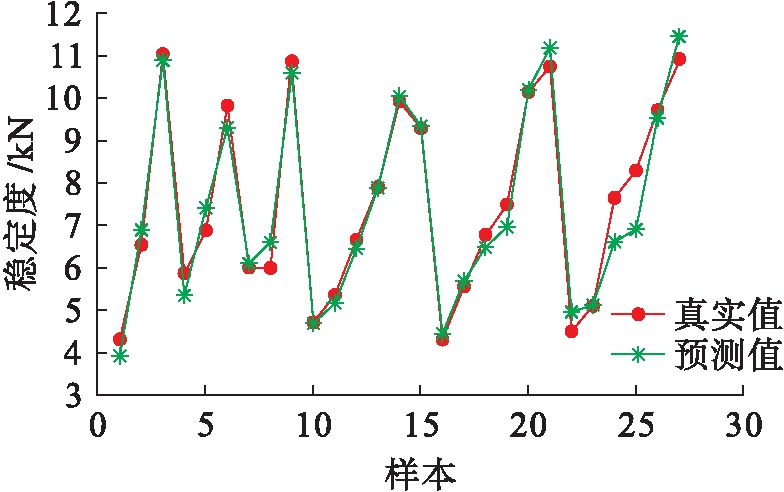
图13 40 ℃马歇尔稳定度预测结果
Fig.13 Prediction results with 40 ℃ Marshall stability
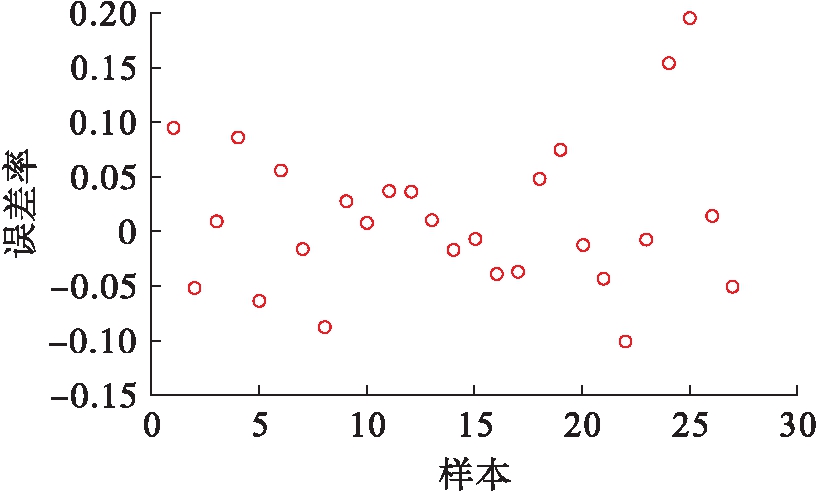
图14 40 ℃马歇尔稳定度误差率
Fig.14 Error rate with 40 ℃ Marshall stability
通过对图13～14的分析可知，该模型的预测误差率集中在0～5%之间，最大误差率小于20%，该模型的预测较为准确.
通过对图15进行分析，该模型的总体拟合优度R=0.979 08，拟合效果良好，模型的适用性较强.确定输入参数为试验鼓风烘箱养生温度、鼓风烘箱养生时间和室温养生时间，选取15 ℃劈裂强度作为输出参数，其优化的适应度曲线变化如图16所示.
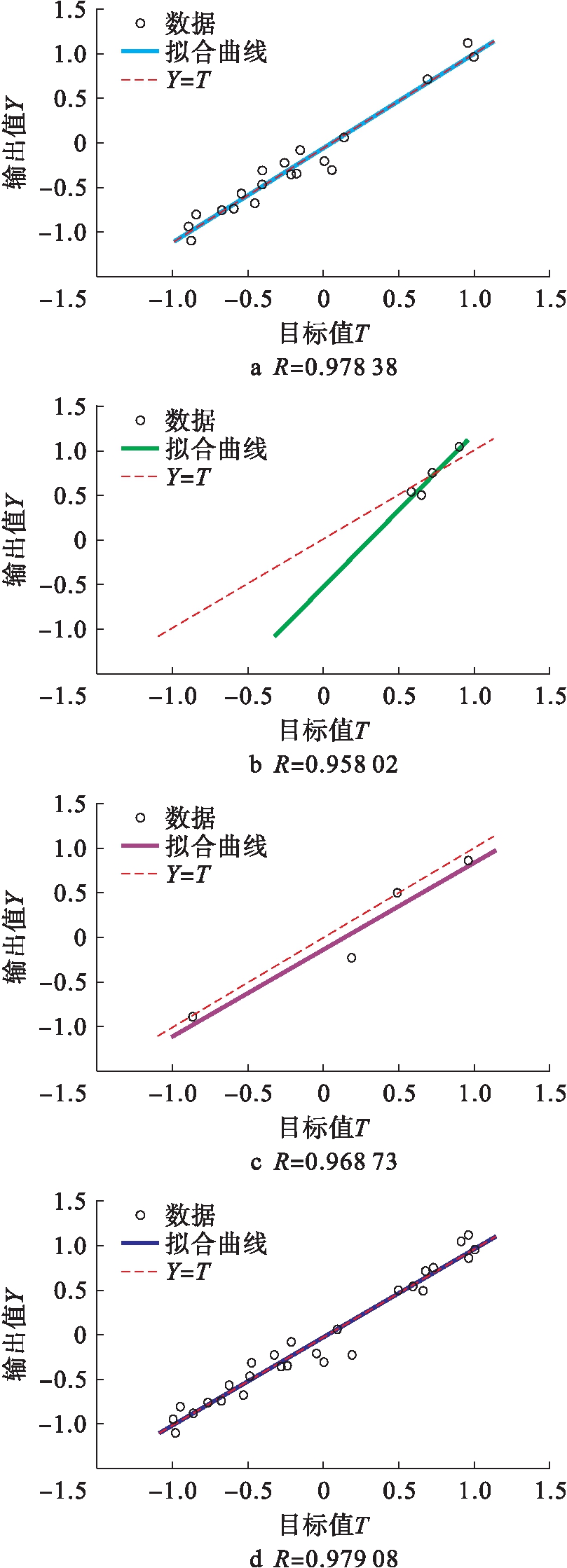
图15 40 ℃马歇尔稳定度拟合优度图
Fig.15 Fitted goodness with 40 ℃ Marshall stability
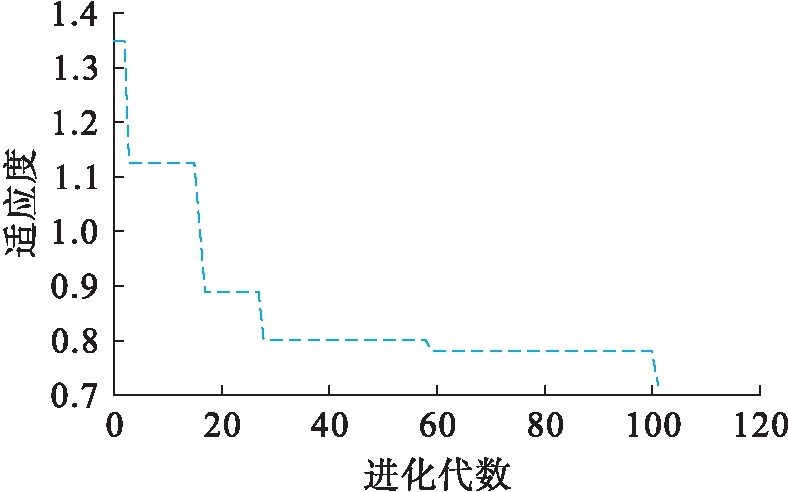
图16 15 ℃劈裂强度适应度曲线
Fig.16 Fitness curve with 15 ℃ splitting strength
通过对图16分析得出，在经过约25次迭代后，个体适应度逐渐趋于平稳，表明该模型的稳定性较高，对15 ℃劈裂强度的预测结果如图17所示，预测误差如图18所示，模型的拟合优度图如图19所示.
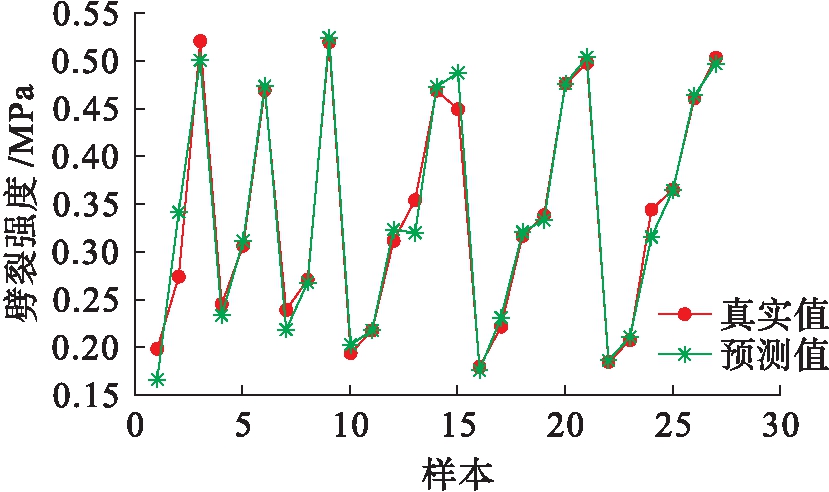
图17 15 ℃劈裂强度预测结果
Fig.17 Prediction results with 15 ℃ splitting strength
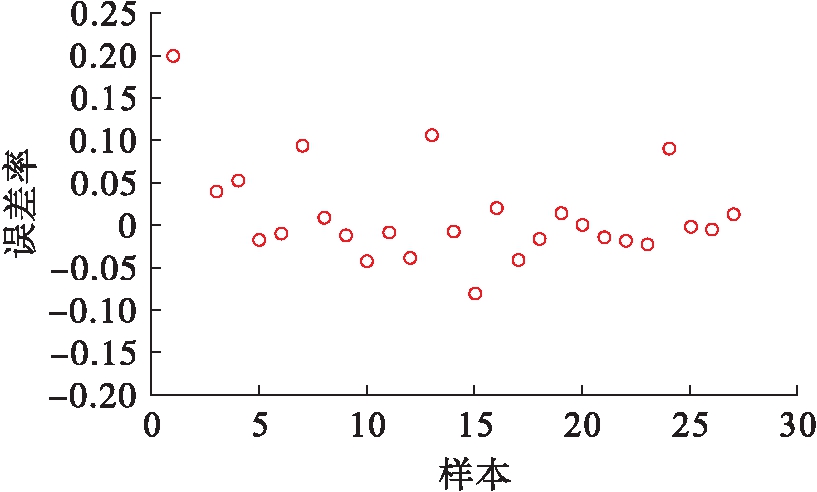
图18 15 ℃劈裂强度误差率
Fig.18 Error rate with 15 ℃ splitting strength
通过对图17～18进行分析可知，该模型的预测误差率集中在0～5%之间，最大误差率集中在20%以内，该模型的预测较为准确.
通过对图19分析可知，该模型的总体拟合优度R=0.986 04，拟合效果良好，模型的适用性较强.
4 结 论
本文通过分析得出以下结论：
1) 基于不同养生条件下40 ℃马歇尔稳定度和15 ℃劈裂强度的相关试验数据，构建的支持向量机模型能够准确预测40 ℃马歇尔稳定度，其均方误差MSE=0.000 300 222，拟合优度R=99.730 9%，最大误差率小于6%.对15 ℃劈裂强度也能进行准确预测，其均方误差MSE=0.000 210 547，拟合优度R=99.828 1%，最大误差率小于6%，该模型具有较好的数据拟合效果，并且预测误差小.
2) 构建的BP神经网络模型能够较为准确地预测40 ℃马歇尔稳定度，其预测误差多数在0～5%之间，总体拟合优度达到0.979 08.对15 ℃劈裂强度也能进行较为准确地预测，预测误差多数在0～5%之间，总体拟合优度达到0.986 04，模型具有较好的数据拟合效果，神经网络模型的预测误差总体大于支持向量机模型的预测误差，但也能进行较为准确地预测.
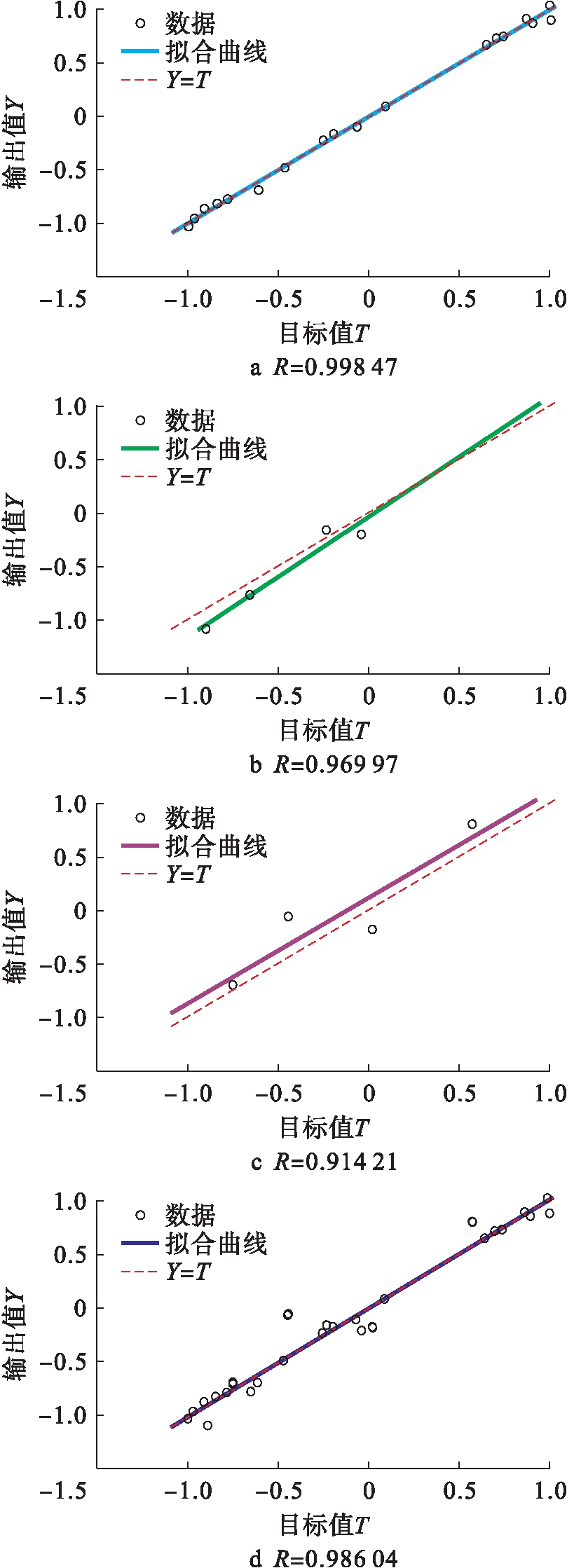
图19 15 ℃劈裂强度拟合优度图
Fig.19 Fitted goodness with 15 ℃ splitting strength
3) 相较两种模型，支持向量机的预测效果更能进行准确地预测，更适用于本文研究.
[1]Yongjoo K，David L H.Performance evaluation of cold in-place recycling mixtures using emulsified asphalt based on dynamic modulus，flow number，flow time，and raveling loss [J].Journal of Civil Engineering，2012，16(4)：586-593.
[2]王宏，刘锋，余建荣，等.乳化沥青冷再生混合料养生方式研究 [J].武汉理工大学学报(交通科学与工程版)，2015，39(3)：641-646.
(WANG Hong，LIU Feng，YU Jian-rong，et al.Research on curing methods of emulsified asphalt cold recycled mixture [J].Journal of Wuhan University of Technology(Transportation Science & Engineering)，2015，39(3)：641-646.)
[3]李志刚，郝培文.养生方法对泡沫沥青冷再生混合料性能的影响 [J].北京工业大学学报，2016，42(10)：1519-1525.
(LI Zhi-gang，HAO Pei-wen.Effect of curing procedure to foamed asphalt cold recycled mixture properties [J].Journal of Beijing University of Technology，2016，42(10)：1519-1525.)
[4]曹俊武，延喜乐，延西利.养生条件对温拌沥青混合料稳定度的影响 [J].公路，2018，63(1)：26-30.
(CAO Jun-wu，YAN Xi-le，YAN Xi-li.Influence of curing condition on stability of warm mixture asphalt [J].Highway，2018，63(1)：26-30.)
[5]童申家，谢祥兵，赵大勇，等，紫外光老化后沥青混合料路用性能非线性预测 [J].建筑材料学报，2016，19(1)：105-110.
(TONG Shen-jia，XIE Xiang-bing，ZHAO Da-yong，et al.Nonlinear asphalt prediction of road performance of mixture after ultraviolet aging [J].Journal of Building Materials，2016，19(1)：105-110.)
[6]谭忆秋，公维强，徐慧宁.基于BP神经网络沥青混合料低温弯拉应变预测模型 [J].沈阳建筑大学学报(自然科学版)，2009，25(2)：224-229.
(TAN Yi-qiu，GONG Wei-qiang，XU Hui-ning.Research on the application of neural network in the model for limiting flexural strain of asphalt mixture at low temperature [J].Journal of Shenyang Jianzhu University (Natural Science)，2009，25(2)：224-229.)
[7]张尚龙.基于动态模量的沥青混合料车辙预估模型研究 [D].西安：西安建筑科技大学，2014.
(ZHANG Shang-long.Research of asphalt mixture rutting prediction model based on dynamic modulus [D].Xi’an：Xi’an University of Architecture and Technology，2014.)
[8]谭忆秋，赵立东，蓝碧武，等.沥青混合料冻融损伤模型及寿命预估研究 [J].公路交通科技，2011，28(6)：1-7.
(TAN Yi-qiu，ZHAO Li-dong，LAN Bi-wu，et al.Research on freeze-thaw damage model and life prediction of asphalt mixture [J].Journal of Highway and Transportation Research and Development，2011，28(6)：1-7.)
[9]董雨明，谭忆秋.硬质沥青混合料的动态黏弹特性 [J].公路交通科技，2015，32(6)：18-24.
(DONG Yu-ming，TAN Yi-qiu.Dynamic viscoelastic property of hard grade asphalt mixture [J].Journal of Highway and Transportation Research and Development，2015，32(6)：18-24.)
[10]张倩，李泽，温志广，等.冻融受荷协同作用下沥青混合料损伤模型研究 [J].西安建筑科技大学学报(自然科学版)，2016，48(2)：188-194.
(ZHANG Qian，LI Ze，WEN Zhi-guang，et al.Research on the damage model of asphalt mixture under synergy action of freeze-thaw and loading [J].Journal of Xi’an University of Architecture and Technology，2016，48(2)：188-194.)
[11]黄发明，殷坤龙，蒋水华，等.基于聚类分析和支持向量机的滑坡易发性评价 [J].岩石力学与工程学报，2018，37(1)：156-167.
(HUANG Fa-ming，YIN Kun-long，JIANG Shui-hua，et al.Landslide susceptibility assessment based on clustering analysis and support vector machine [J].Chinese Journal of Rock Mechanics and Engineering，2018，37(1)：156-167.)
[12]吴忠强，康晓华，于丹琦.基于小波消噪和优化支持向量机的板形模式识别 [J].中国机械工程，2018，29(1)：95-103.
(WU Zhong-qiang，KANG Xiao-hua，YU Dan-qi.Flatness pattern recognition based on wavelet denoising and optimized SVM [J].China Mechanical Engineering，2018，29(1)：95-103.)
[13]王宁，谢敏，邓佳梁，等.基于支持向量机回归组合模型的中长期降温负荷预测 [J].电力系统保护与控制，2016，44(3)：92-97.
(WANG Ning，XIE Min，DENG Jia-liang，et al.Mid-long term temperature-lowering load forecasting based on combination of support vector machine and multiple regression [J].Power System Protection and Control，2016，44(3)：92-97.)
[14]Moghaddam T B，Soltani M，Shahraki H S.The use of SVM-FFA in estimating fatigue life of polyethylene terephthalate modified asphalt mixtures [J].Measurement，2016，90：526-533.
[15]Zhang G，Wang S，Wang Y，et al.LS-SVM approxi-mate solution for affine nonlinear systems with partially unknown functions [J].Journal of Industrial & Management Optimization，2017，10(2)：621-636.
[16]王彤彤，翟军海，何欢，等.BP神经网络和SVM模型对施加生物炭土壤水分预测的适用性 [J].水土保持研究，2017，24(3)：86-91.
(WANG Tong-tong，ZHAI Jun-hai，HE Huan，et al.Applicability of BP neural network model and SVM model to predicting soil moisture under incorporation of biochar into soils [J].Research of Soil and Water Conservation，2017，24(3)：86-91.)
[17]Moghaddam T B，Soltani M，Shahraki H S.The use of SVM-FFA in estimating fatigue life of polyethylene terephthalate modified asphalt mixtures [J].Measurement，2016，90：526-533.
[18]He W，Chen Y，Yin Z.Adaptive neural network control of an uncertain robot with full-state constraints [J].IEEE Transactions on Cybernetics，2016，46(3)：620-629.