钢纤维可阻滞基体混凝土裂缝的开展，使得钢纤维混凝土(SFRC)的抗弯、抗拉、抗剪强度等性能较普通混凝土有显著提高，其抗冲击、抗疲劳、裂后韧性和耐久性也有较大改善.目前，SFRC在桥梁和建筑等工程领域使用仍十分有限[1]，究其原因主要是SFRC材料在实际应用中，相关规范关于钢纤维规定仍存在着部分空白，同时，SFRC结构的数值分析方法，也主要停留在将SFRC作为一种宏观的材料进行分析.SFRC作为一种混凝土与钢纤维共同组成的材料，进行SFRC细观尺度数值分析具有一定的意义.对于纤维混凝土，其多相非均匀性显得尤为突出.无论是单一材料还是复合材料，材料细观尺度上的结构将直接影响其宏观尺度上的性能.细观尺度数值模型从细观尺度出发，能更好地揭示混凝土材料中裂缝的形成、发展和失稳过程，并能为混凝土材料细观结构优化设计提供指导.
一些学者开展了将骨料和钢纤维建立于基体中的细观尺度数值模拟方面的研究.苑坤兴[2]将聚丙烯纤维混凝土看成是由骨料、水泥砂浆、聚丙烯纤维及粘结界面层所组成的多相复合材料，建立了纤维
砂浆界面层的细观力学数值模型，并在此基础上探讨了聚丙烯纤维混凝土宏观尺度和细观尺度上的联系，但该模型在二维平面状态下，仅将聚丙烯纤维看成是小圆点，而忽略了在聚丙烯纤维长度方向的影响.李琳[3]从细观角度建立了普通混杂、层布式混杂以及不同几何尺寸的混杂纤维混凝土数值计算模型，并对其进行了力学性能模拟，但该细观模型未对纤维的形状进行考虑，同时试件中纤维的分布与受力方向大致垂直，与纤维随机分布的情形不符.Xu等[4]建立了弯钩型钢纤维圆形骨料混凝土和螺旋型钢纤维圆形骨料混凝土二维细观数值模型，并进行了抗压冲击荷载模拟及动力拉伸试验模拟.徐彬[5]总结并改进了传统的二维混凝土骨料生成算法，实现了二维全级配圆形、椭圆形及凸多边形混凝土骨料的随机生成与投放.
上述SFRC结构的数值分析，主要研究二维纤维与骨料的随机投放几何建模、单元划分及分析，SFRC结构的三维细观尺度数值方面的分析研究较少.王林[6]进行了基于Ansys的钢纤维随机分布建模与试验对比分析，其成果未详述三维钢纤维随机建模方法及与混凝土结构的耦合途径，且未进行钢纤维的细观力学行为分析；舒刚[7]通过自行编写Matlab随机序列程序和Python脚本文件，实现钢纤维在UHPC基体中的大批量随机乱向均匀分布建模.
建立于各种数值计算理论(如有限单元法FEM、有限差分法FDM、离散元法DEM等)之上的多尺度性能分析为细观尺度数值模拟提供了扎实的计算基础.但纤维混凝土梁进行细观尺度数值分析，仍存在以下问题：1)缺乏快速有效的建模方法.钢纤维在基体中呈随机分布，而且是按照一定数量，在限定空间内生成，如何快速、有效生成上述特性基体中的钢纤维，且该模型作为后期细观尺度数值模拟的基础模型；2)在细观尺度数值模型生成后，如何有效考虑纤维与基体之间力的传递和恰当的本构关系选择；3)如何从细观角度去评价其受力行为，提取关键技术指标.
本文通过Ansys二次开发，得到在指定空间生成三维随机分布钢纤维程序，作为SFRC几何模型建立的前处理工具；然后将三维随机分布钢纤维导入到Midas/FEA中进行非线性计算分析，并通过与既有抗折试验进行对比分析，试图得到SFRC三维细观尺度的数值分析方法，为SFRC三维细观尺度的数值提供参考.
1 SFRC抗折试验概况
Dinh[8]进行的钢纤维混凝土梁抗折试验共包含12根C40尺寸为15.24 cm×15.24 cm×50.8 cm试件，其钢纤维体积含量Vf均为0.75%.12根试件分为3组，每组构件4根，分别对应三种端钩型纤维：组Ⅰ，RC80/60BN，长lf=60 mm，直径df=0.75 mm，强度fsft=1 050 MPa；组Ⅱ，RC80/30BP，长lf=30 mm，直径df=0.38 mm，强度fsft=2 300 MPa；组Ⅲ，ZP305，长lf=30 mm，直径df=0.55 mm，强度fsft=1 100 MPa.其中，ZP305和RC80/60BN为常规强度纤维，常用于传统的SFRC中.RC80/30BP纤维具有2 300 MPa强度，适用于高强度混凝土中.ZP305纤维的长径比(lf/df=55)小于RC80/60BN和RC80/30BP纤维的长径比(lf/df=80)，具体尺寸形式如图1所示(单位：mm).
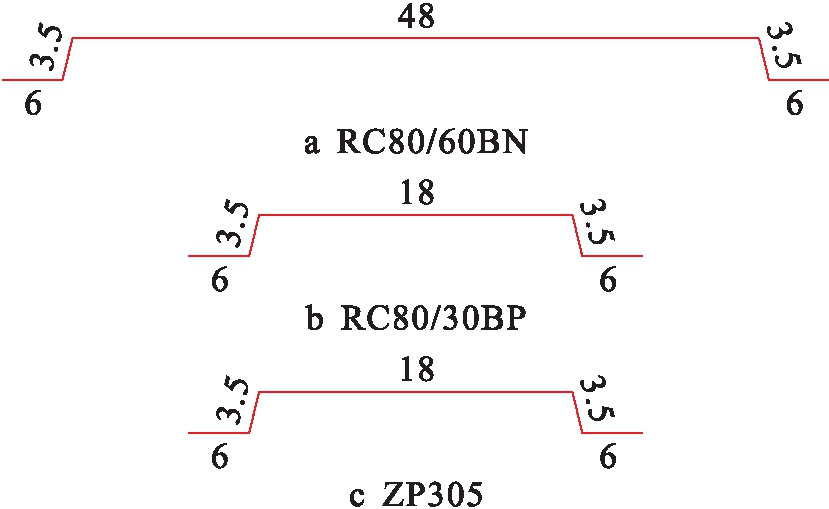
图1 钢纤维参数及尺寸
Fig.1 Parameters and size of steel fiber samples
试验采用四点弯曲测试装置，两点加载，加载速率为0.127 mm/s，最后加载到跨中挠度为3.048 mm时终止.对每组单根构件的试验结果加权平均绘制荷载位移曲线，如图2所示.
素混凝土抗折试验的破坏形式为脆性断裂.混凝土基体掺入上述三种钢纤维后，抗折试件最大破坏荷载为55.9 kN，提高了65.4%，且构件表现出良好的延性.SFRC梁到达其承载力峰值后，随着竖向位移的进一步施加，受掺入钢纤维形式不同的影响，表现出不同的延性特征.组Ⅰ掺入的钢纤维为RC80/60BN，其直径df=0.75 mm，更有利于抵抗纤维混凝土之间的粘结失效破坏，因此，相较短纤维(组Ⅱ、组Ⅲ)具有更好的延性.
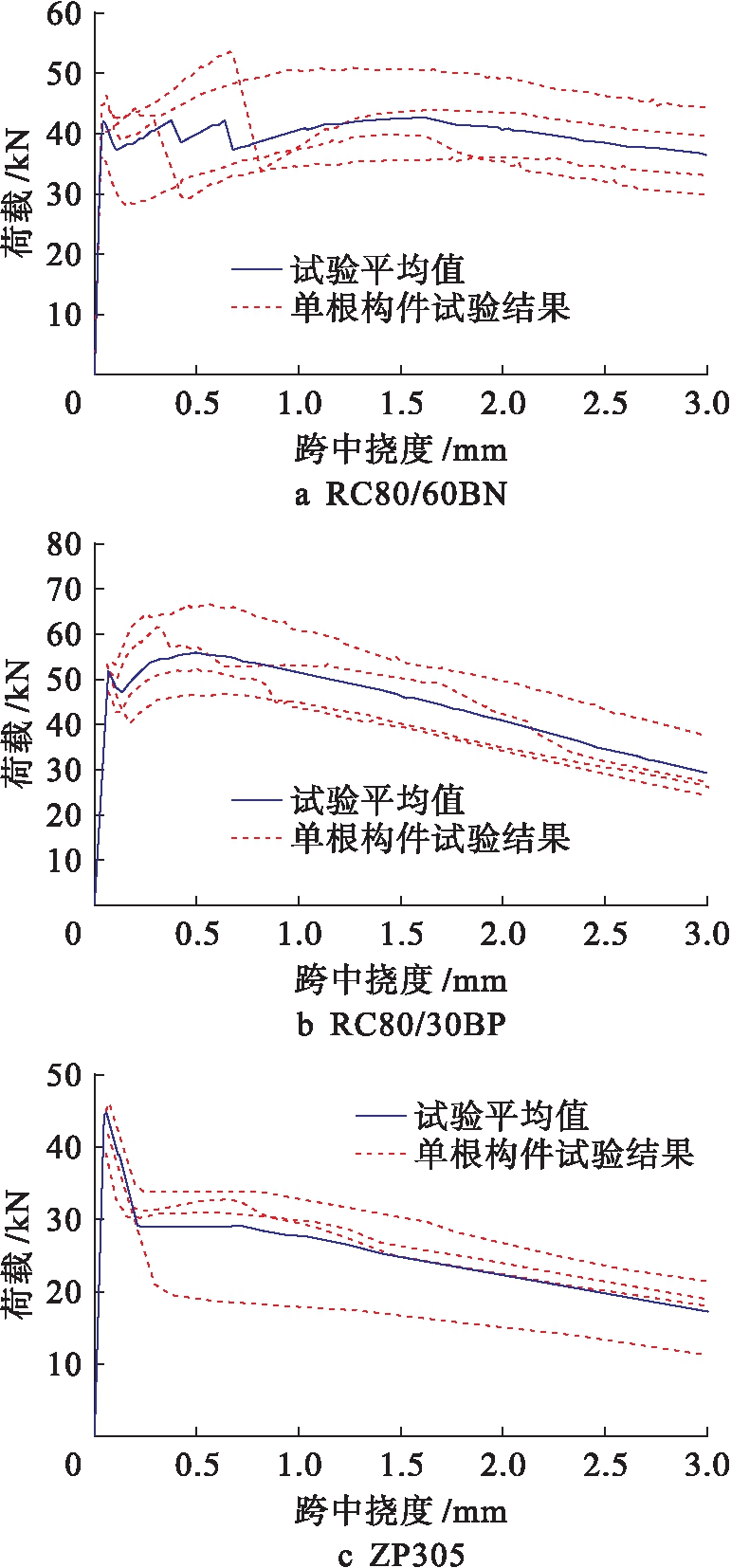
图2 SFRC抗折试验荷载位移曲线
Fig.2 Load and displacement curves of flexural test of SFRC
2 SFRC三维细观尺度数值模型建立与分析
2.1 随机分布钢纤维的生成
SFRC细观尺度数值分析模型，其钢纤维在混凝土基体中呈随机分布状态.本文基于Ansys中的APDL，开发了钢纤维在指定立方体中生成N根直线型钢纤维的参数化程序，可快速有效得到在指定立方体中随机分布钢纤维的几何模型.程序基本的建模思路如下：
1) 在指定空间范围{0，X0；0，Y0；0，Z0}内，采用RAND随机函数在指定空间中首先生成一个随机关键点Ki，作为该条钢纤维的起点，如图3a所示，其中，(Xi，Yi，Zi)为采用随机函数RAND生成的随机数，随机数Xi、Yi、Zi的生成区间分别为0≤Xi≤X0、0≤Yi≤Y0、0≤Zi≤Z0.
2) 在该起点建立以该点为坐标原点的局部坐标系，该局部坐标系为球坐标系；对该局部坐标系的X、Y、Z轴分别随机旋转一个随机角度RAND(0，360°)，如图3b所示.
3) 在坐标轴随机旋转后的局部坐标系下，在其X′轴上、距离Xi为lf的位置上生成钢纤维的终点Kj；提取该点坐标，如果该点坐标超出区间，则删除该点，返回第2)步，重新旋转局部坐标系，生成新的Kj点，直至Kj点满足0≤Xj≤X0，0≤Yj≤Y0，0≤Zj≤Z0为止，如图3c所示.
4) 采用线Line，连接Ki及Kj，得到一条随机分布的钢纤维.
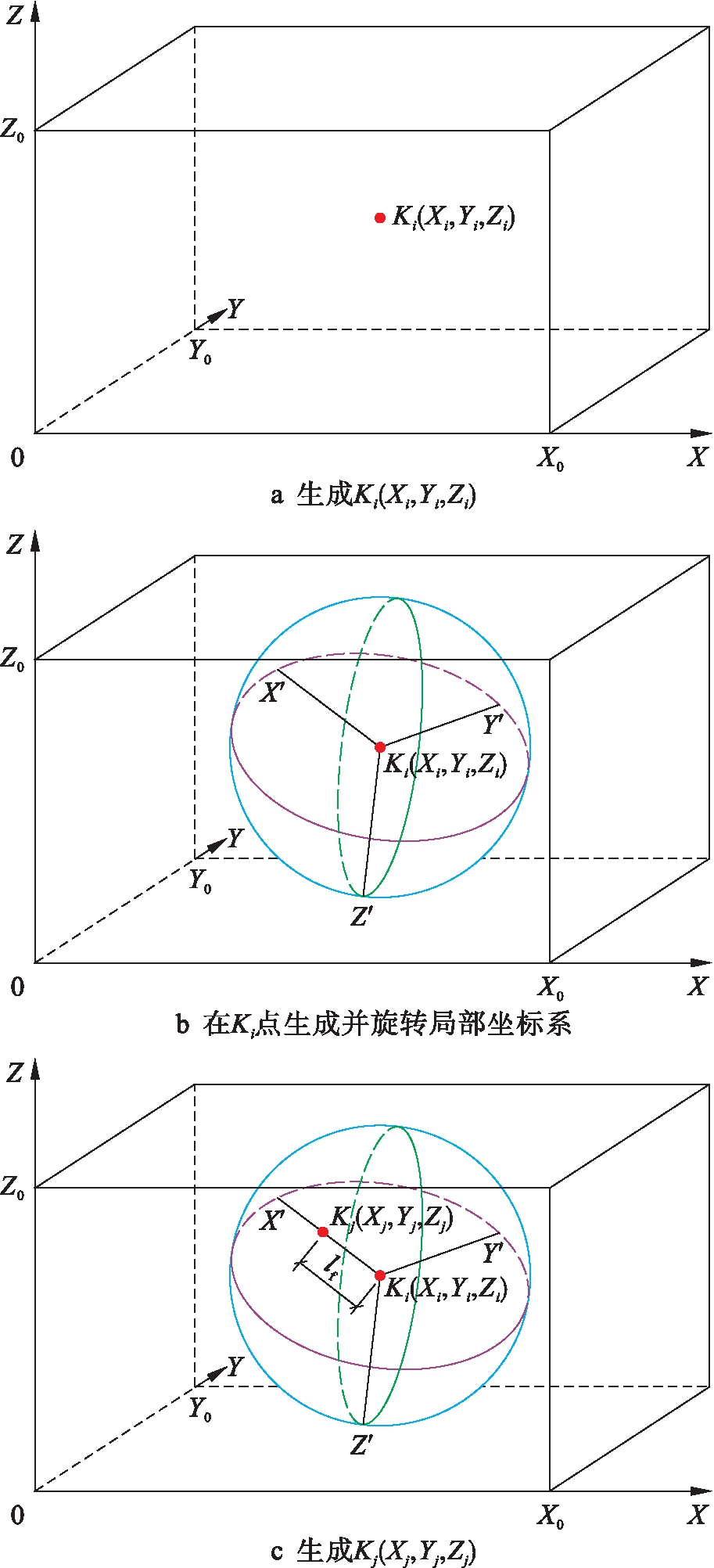
图3 随机分布钢纤维过程示意图
Fig.3 Schematic diagram of randomly distributed steel fibers
按照上述生成单根钢纤维的方法，循环N次，得到N根钢纤维.图4为单根钢纤维生成流程图.
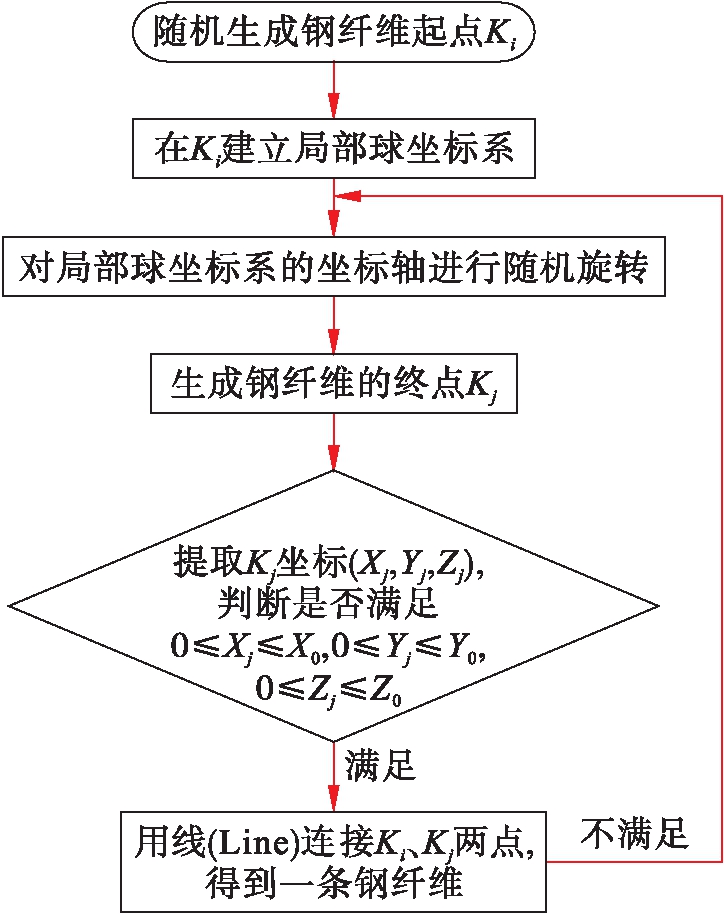
图4 单根钢纤维生成流程
Fig.4 Flow chart of generation of single steel fiber
图5为采用该程序在基体尺寸为15.24 cm×15.24 cm×50.8 cm的混凝土试件中生成体积含量为0.75%的RC80/60BN型的3 338根钢纤维(lf=60 mm).从钢纤维生成的结果来看，达到了钢纤维在基体随机生成的目的，整体分布情况良好.
图5 二次开发Ansys生成随机分布钢纤维
Fig.5 Randomly distributed steel fibers generated by secondary development of Ansys
2.2 钢纤维混凝土模型的建立
采用Ansys的APDL进行二次开发得到在指定空间内生成随机分布的钢纤维几何模型后，将几何模型输出为iges格式导出.在Midas/FEA中导入Ansys输出的iges格式的钢纤维几何模型，采用宏观混凝土与微观钢纤维相结合的方法建立SFRC三维细观尺度数值分析模型.在分析模型中，将每根钢纤维作为单根钢筋进行考虑，程序可实现钢筋与混凝土结构的自动耦合，从而建立三维细观尺度数值分析模型.图6为Midas/FEA中SFRC的三维细观尺度数值分析模型，支座处和位移加载处为防止局部应力集中，增设了弹性垫块.
图6 Midas/FEA中SFRC三维细观尺度数值分析模型
Fig.6 Numerical analysis model for SFRC in 3D meso-scale in Midas/FEA
混凝土的本构模型采用混凝土总应变裂缝模型.其中，受压本构模型采用在进行混凝土裂缝模拟中常用的抛物线模型.抛物线模型[9]是由Feenstra基于断裂能理论推导出的模型，如图7所示.该模型由抗压强度fc、抗压断裂能Gc、特征单元长度h三个特性值决定.
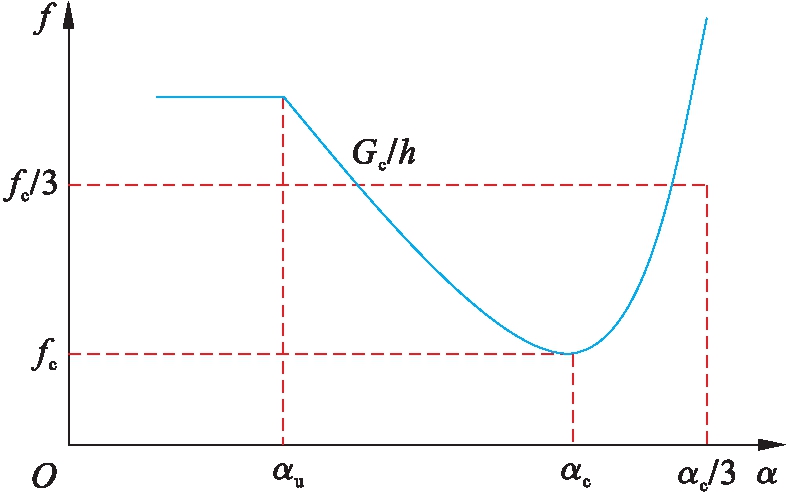
图7 抛物线型压缩曲线
Fig.7 Parabolic compression curve
对于总应变裂缝模型中混凝土的受拉模型，在Midas/FEA中提供了常量模型、弹性模型、脆性模型、线性模型、指数模型、Hordijk模型、多线性模型等.本文采用多线性模型进行数值模拟，超过抗拉强度时按照用户定义的折线发生软化[9]，如图8所示.最多可以输入30个点的坐标，第一个坐标必须是(0，0).
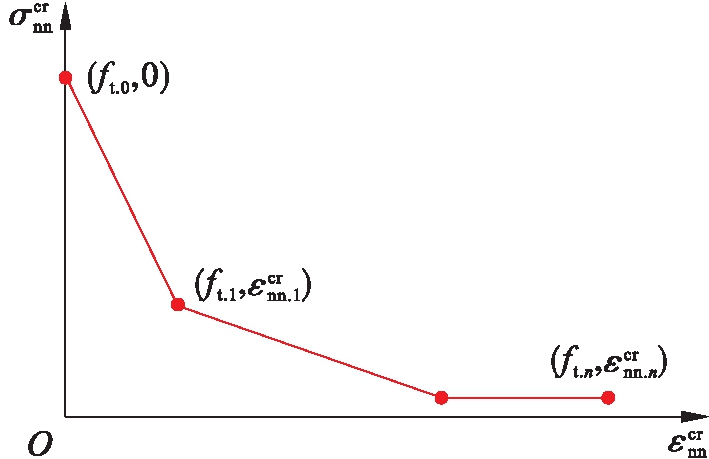
图8 多线性受拉曲线
Fig.8 Multi-linear tension curve
因钢纤维的初始屈服强度较大，且大量研究表明钢纤维主要以拔出形式发生破坏，因此，钢纤维本构模型选取在金属材料分析中广泛使用的Von Mises模型.
在进行模型分析计算时，由于钢纤维的数量较多，将钢纤维划分为钢筋网格时受计算机处理能力的影响，很多情况下不能一次将全部钢纤维划分为钢筋网格，需要对钢纤维逐步划分完成，整个划分钢纤维为钢筋网格的过程比较耗时.针对第三组模型，钢纤维共26 008根(体积含量为0.75%)，实际钢筋网格划分时，分为26次，每次划分1 000根，每次1 000根耗时约15 min.分析计算时，钢纤维数量越多，分析计算耗时越长.对于第三组模型分析计算时划分钢筋单元大约需要120 min，分析计算大约需要60 min.随着计算机处理性能及软件处理能力的提升，SFRC三维细观尺度数值模拟的效率会得到大幅提升.
3 数值模拟结果
模拟结果主要对比分析三组钢纤维混凝土梁的抗折试验，探寻有效的SFRC三维细观尺度的数值分析方法.计算模型中混凝土的拉压本构分别采用总应变裂缝模型中的抛物线模型和多线性模型，钢纤维采用Von Mises模型，采用宏观混凝土与细观钢纤维相结合的SFRC三维细观尺度数值模拟方法，采用位移加载(竖向3 mm)模式进行加载.由于钢纤维主要以拔出形式发生破坏[10-11]，也就是说钢纤维在未到达其屈服强度时，就以拔出形式发生了破坏.然而，在实际分析中，难以有效实现该类破坏形式.本文基于钢纤维在未到达其屈服强度时发生破坏的特点，提出了采用钢纤维强度折减替代钢纤维拔出破坏的方法.通过多次试算得到，影响钢纤维强度折减系数最主要的影响因素是纤维的长度，纤维长度长的，折减系数偏大，如RC80/60BN型钢纤维，lf=60 mm，强度折减系数η=0.714；纤维长度短的，折减系数偏小，如RC80/30BP、ZP305型钢纤维，lf=30 mm，强度折减系数分别为η=0.326、η=0.364.这也证明了钢纤维主要以拔出形式发生破坏的论断.钢纤维强度折减参数如表1所示.
3.1 极限承载力与延性分析
图9为各型钢纤维混凝土梁试验结果与模拟结果对照.由图9可以看出，三维细观尺度的数值结果与钢纤维混凝土梁试验均值结果吻合较好，三维细观尺度数值分析能较好地反映混凝土基体在加入钢纤维后其强度的提升，如组Ⅰ(RC80/60BN型钢纤维混凝土梁)所示，试验测得极限承载力Pu=42.4 kN，三维细观尺度的数值分析所得Pu=42.1 kN.
表1 钢纤维强度折减参数
Tab.1 Strength reduction of steel fibers
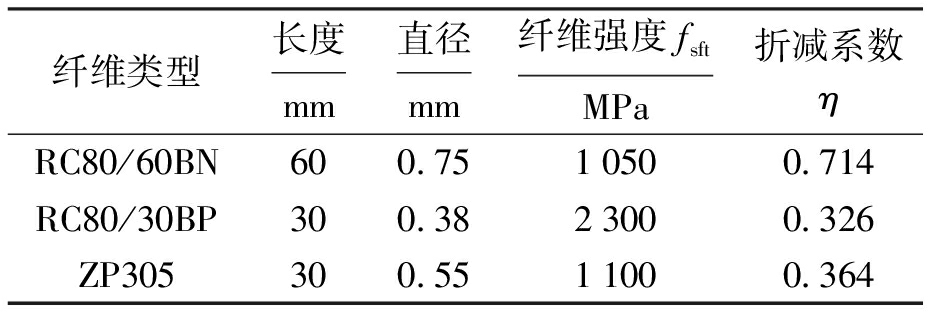
纤维类型长度mm直径mm纤维强度fsftMPa折减系数ηRC80/60BN600.7510500.714RC80/30BP300.3823000.326ZP305300.5511000.364
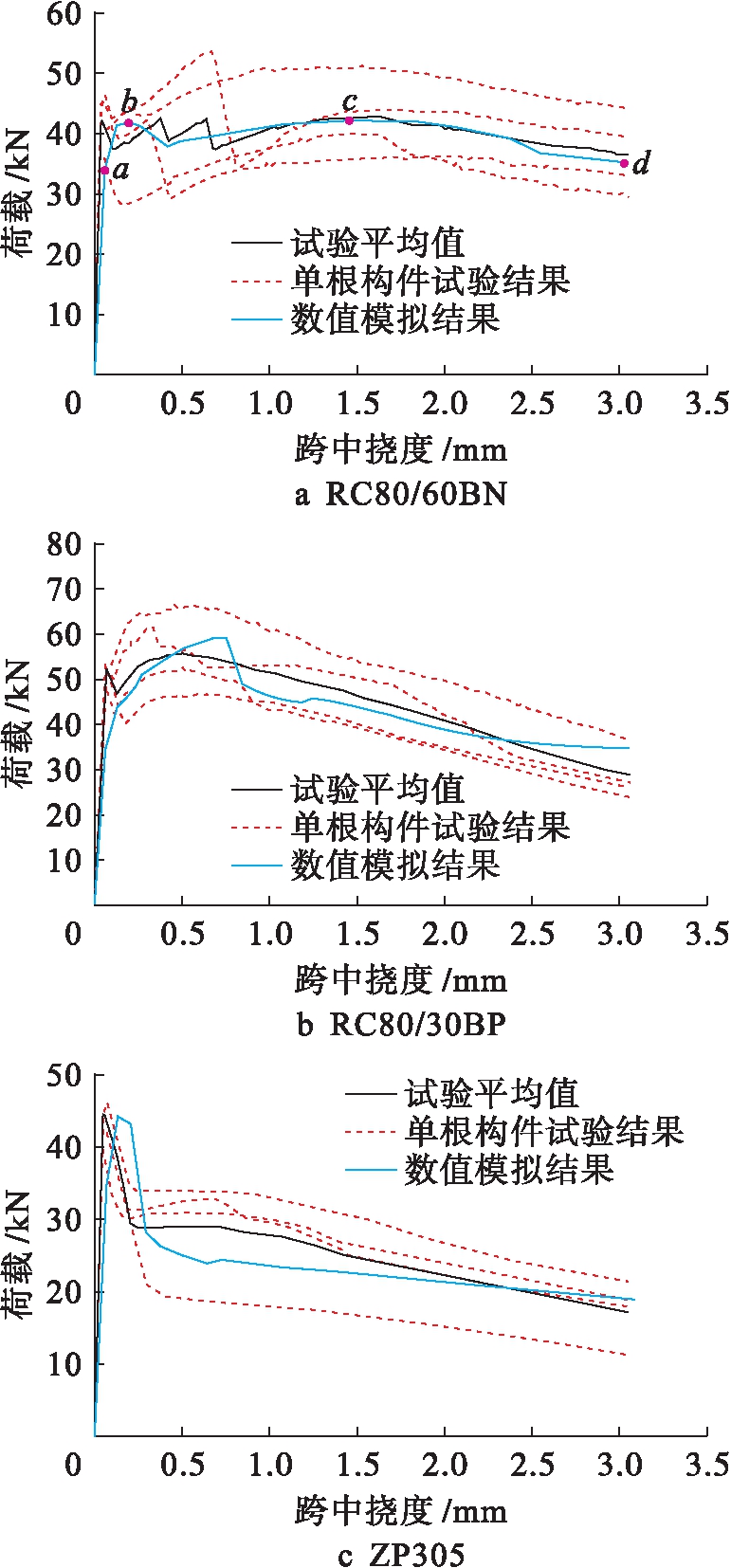
图9 各型钢纤维混凝土梁试验结果与模拟结果对照
Fig.9 Comparison between test and simulation results for various types of steel fiber concrete beams
抗折试验采用3组进行试验，每组4个构件，其破坏特征分别为：组Ⅰ的RC80/60BN型钢纤维长度较大(lf=60 mm)，相对而言，混凝土的粘结效果更好，因此，构件到达极限承载力后保持了三组中最好的延性.但构件钢纤维的掺入量是按照相同体积含量掺入钢纤维的，RC80/60BN型钢纤维长度较大，因而掺入钢纤维数量最少(组Ⅰ：3 338根、组Ⅱ：12 415根、组Ⅲ：26 008根)，因而其极限承载力提高最小.本文采用宏观混凝土与细观钢纤维相结合的SFRC三维细观尺度数值模拟方法，按照实际根数进行随机投放，得到的极限承载力与延性特征与试验值均值吻合较好.
组Ⅱ、组Ⅲ采用30 mm纤维，掺入的钢纤维根数多，强度相较组Ⅰ提高更大.但由于纤维长度相对较短，更容易发生纤维与基体的粘结失效破坏，所以到达承载力峰值后，强度下降迅速，后期下降段更陡.
3.2 细观尺度数值结果
SFRC三维细观尺度的数值模拟由于采用宏观混凝土与细观钢纤维相结合的SFRC三维细观尺度数值模拟方法，因而，其计算结果可直观分析得到钢纤维在整个受力中发挥作用的过程.本文重点以组Ⅰ：RC80/60BN型钢纤维混凝土梁进行说明，如图9a所示，共选取4个特征点用来观察钢纤维应力变化的过程.具体如下：1)a点，0.8Pu点(其中，Pu为SFRC梁极限承载力)；2)b点，1.0Pu点，该点为SFRC梁极限承载力所在的点；3)c点，加载至挠度为1.5 mm；4)d点：加载至挠度为 3 mm.
a点时混凝土内形成的微裂缝开始扩展，混凝土表现出一定的塑性，由图10a可知，该时刻对应的竖向荷载值约为33.9 kN，已达到素混凝土梁的最大承载力(约33.8 kN)，但由于钢纤维的参与受力，提高了试件的承载力，此时钢纤维最大拉应力为39.4 MPa(底部)，最大压应力为44.2 MPa(顶部)，钢纤维的应力强度较低；当到达极限承载力b点时，如图10b所示，钢纤维应力迅速增大，此时钢纤维最大拉应力约为750.5 MPa，最大压应力约为109.3 MPa，尤其是受拉区钢纤维的应力增长迅速，此时受压区混凝土的压应力为17.0 MPa，其破坏形式以受拉区混凝土退出工作，受拉区钢纤维到达ηfsft后，构件宣告破坏.随着荷载的进一步增大，更多、更大范围的钢纤维参与受力，尤其是两个加载点下形成的两道主裂缝处的钢纤维参与受力，使得构件表现出良好的延性，如图10c、d所示.通过分析可见，利用宏观混凝土与细观钢纤维相结合的SFRC三维细观尺度数值模拟方法，整个SFRC梁中钢纤维的受力过程得到了清晰展现，可得到受力过程中各个阶段及各个位置钢纤维应力情况.
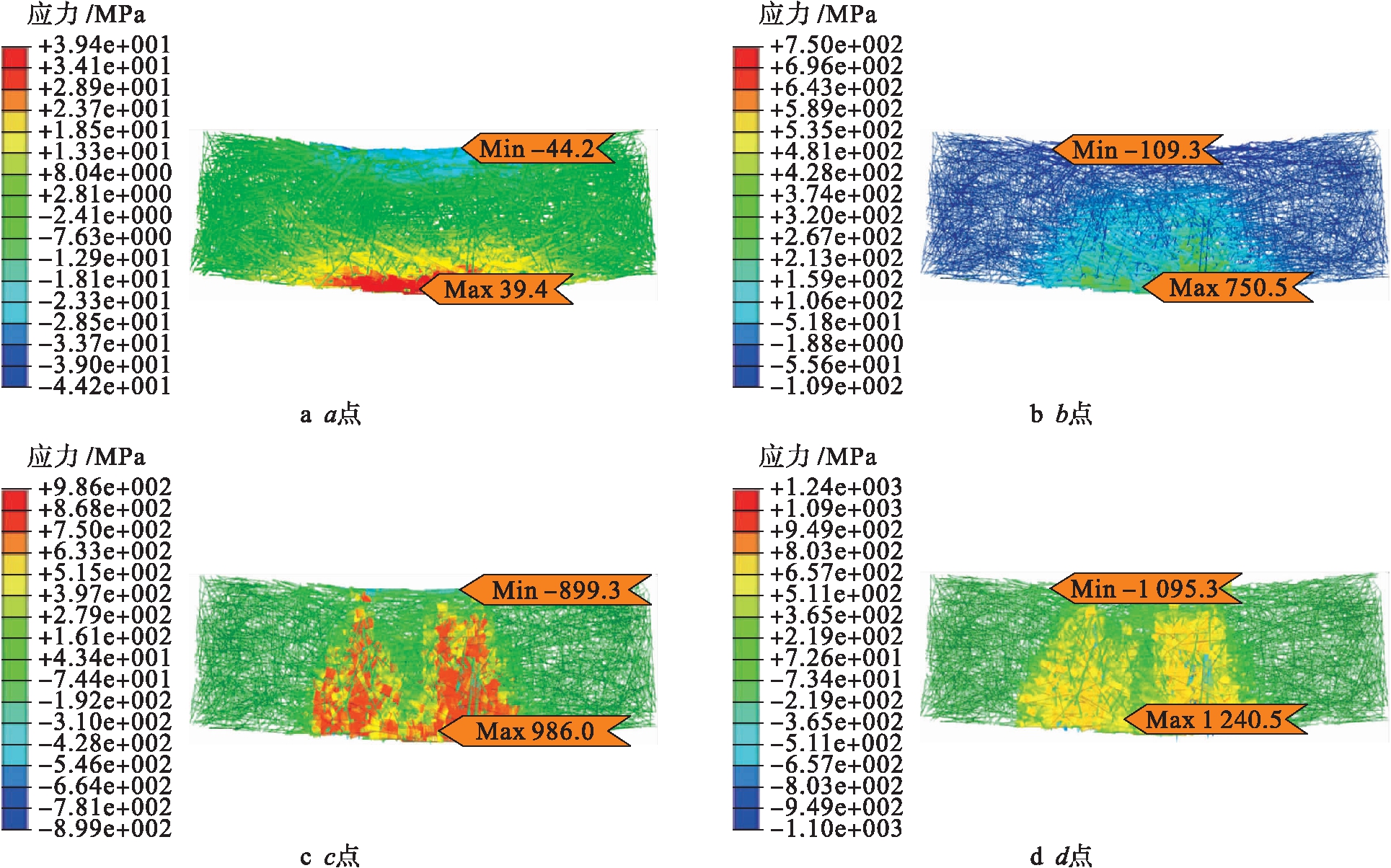
图10 加载过程钢纤维应力
Fig.10 Stress of steel fiber during loading process
宏观混凝土与细观钢纤维相结合的SFRC三维细观尺度数值模拟方法，在应用混凝土的总应变裂缝模型后，同样也能较好地反映结构裂缝发生及发展过程.图11为b点时梁体裂缝发展图.由分析结果得到，梁体的最大裂缝宽度为0.024 mm.
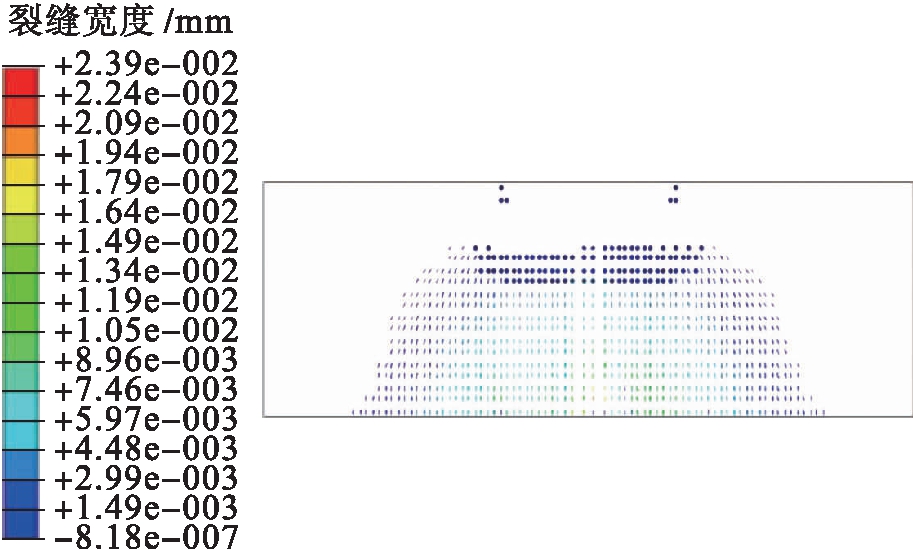
图11 组Ⅰ1.0 Pu梁体裂缝
Fig.11 Beam crack of 1.0 Pu point in groupⅠ
4 结 论
本文采用Ansys的APDL进行二次开发得到在指定空间内生成随机分布的钢纤维几何模型后，将几何模型输出为iges格式导出.在Midas/FEA中导入Ansys输出的iges格式的钢纤维几何模型，采用宏观混凝土与微观钢纤维相结合的方法建立SFRC三维细观尺度数值分析模型，进行非线性计算分析.得出如下结论：
1) 采用Ansys的APDL进行二次开发得到在指定空间内生成钢纤维几何模型，能较好地反映钢纤维随机分布的特征，且二次开发程序生成几何模型效率较高；
2) 采用强度折减方法分析纤维与混凝土的粘结滑移特性，方法可行，思路清晰；
3) 采用本文方法得到三组试件的强度与延性试验结果、数值分析结果拟合较好，能较好地反映结构的强度、延性等特征；
4) 本文方法能反映在构件受力过程中构件内钢纤维受力的变化过程，据此可进一步解释该类构件破坏发生的机理.
总体来说，本文提出的SFRC三维细观尺度数值分析模型模拟分析方法是可行的，但在纤维与基体粘结滑移方面，仍需要进一步研究.
[1]鲁丽华，罗丰，刘文胜，等.尾矿砂钢纤维喷射混凝土在铁矿巷道中的应用 [J].沈阳工业大学学报，2018，40(1)：109-113.
(LU Li-hua，LUO Feng，LIU Wen-sheng，et al.Application of tailing sand steel fiber sprayed concrete in iron mine tunnel [J].Journal of Shenyang University of Technology，2018，40(1)：109-113.)
[2]苑坤兴.聚丙烯纤维混凝土力学性能及细观结构的数值模拟 [D].青岛：中国石油大学(华东)，2011.
(YUAN Kun-xing.Numerical simulation of mechanical properties and microscopic structure of the polypropylene fiber concrete [D].Qingdao：China University of Petroleum，2011.)
[3]李琳.混杂纤维混凝土抗弯性能的细观力学分析 [D].广州：广州大学，2011.
(LI Lin.Meso-level mechanics analysis on bending resistance properties of hybrid fiber reinforced concrete [D].Guangzhou：Guangzhou University，2011.)
[4]Xu Z，Hao H，Li H N.Mesoscale modelling of fibre reinforced concrete material under compressive impact loading [J].Construction & Building Materials，2012，26(1)：274-288.
[5]徐彬.混杂纤维混凝土二维随机建模方法研究 [D].武汉：武汉理工大学，2014.
(XU Bin.Research on two-dimensional stochastic modeling methods of hybrid fiber reinforced concrete [D].Wuhan：Wuhan University of Technology，2014.)
[6]王林.基于ANSYS的钢纤维钢筋混凝土梁的弯曲静载与疲劳性能分析 [D].成都：成都理工大学，2017.
(WANG Lin.Finite element analysis of steel fiber reinforced concrete beams [D].Chengdu：Chengdu University of Technology，2017.)
[7]舒刚.超高性能混凝土中钢纤维锈蚀的细观力学分析 [J].西南交通大学学报，2019，54(6)：1268-1276.
(SHU Gang.Micromechanical analysis of steel fiber corrosion in ultra-high performance concrete [J].Journal of Southwest Jiaotong University，2019，54(6)：1268-1276.)
[8]Dinh H H.Shear behavior of steel fiber reinforced concrete beams without stirrup reinforcement [J].ACI Structural Journal，2010，107(5)：597-606.
[9]樊俊江，於林锋，韩建军，等.不同种类粗纤维混凝土基本力学性能及弯曲韧性试验研究 [J].施工技术，2018，47(20)：1-5.
(FAN Jun-jiang，YU Lin-feng，HAN Jian-jun，et al.Research on basic mechanical properties and flexural toughness of concrete with different kinds of coarse fibers [J].Construction Technology，2018，47(20)：1-5.)
[10]徐礼华，梅国栋，黄乐，等.钢聚丙烯混杂纤维混凝土轴心受拉应力应变关系研究 [J].土木工程学报，2014，47(7)：35-45.
(XU Li-hua，MEI Guo-dong，HUANG Le，et al.Study on uniaxial tensile stress-strain relationship of steel-polypropylene hybrid fiber reinforced concrete [J].China Civil Engineering Journal，2014，47(7)：35-45.)
[11]徐佳宇，刘筱玲，杜义祥，等.长径比对 SFRC 抗压性能的细观数值模拟 [J].混凝土与水泥制品，2018，8(8)：56-59.
(XU Jia-yu，LIU Xiao-ling，DU Yi-xiang，et al.Meso-scale simulation of aspect ratio on compressive properties of SFRC [J].China Concrete and Cement Pro-ducts，2018，8(8)：56-59.)