粘贴钢板加固钢筋混凝土桥梁(RC构件)主要目的是提高构件抗弯承载力，同时改善构件刚度，二者可以形成共同受力的整体，改善原RC构件应力状态，达到补强效果，在实际工程加固已得到广泛的应用和发展[1-3].
目前，国内外学者对钢板加固RC梁已有很多研究.郭文龙等[4]发现加固梁中性轴高度和抗弯刚度随荷载增加均呈非线性变化，且实际计算模型应考虑桥梁损伤的现实状态；张维真[5]对锈蚀RC梁进行加固，发现梁承载力提高明显，但屈服挠度变化不明显；Alam等[6]发现用钢板和粘接剂修复严重剪切损坏的钢板钢筋，可以完全恢复梁的原始剪切能力.
但大多数研究人员只停留在考虑一次受力状态，而忽略桥梁二次受力的影响.一般情况下，RC构件加固是在初始荷载存在时，构件加固前处于一次受力或不完全卸荷状态.为更加贴近实际RC构件加固工程，本文针对二次受力下钢板加固钢筋混凝土梁进行抗弯性能研究.采用数值模拟软件ABAQUS对二次受力下钢板加固RC梁进行模拟，并将得出的模拟数据与试验结果进行对比，分析钢板层数、配筋率和预载量等因素对钢板加固RC梁效果的影响，评估其可靠度和实用性，为修复实际RC桥梁加固工程提供理论基础.
1 试验与有限元分析
1.1 试 验
RC梁为适筋梁，梁长为1 700 mm，截面尺寸为b×h=120 mm×200 mm，纵向受拉、压钢筋分别为HRB400的2φ8、2φ12，配筋率为0.59%，混凝土保护层厚度为30 mm，箍筋型号为HPB300，箍筋配置为φ6@150 mm，混凝土强度等级为C30.单层钢板厚度为2 mm，宽度为120 mm，弹性模量为192 GPa，屈服强度为300 GPa，极限抗拉强度为610 GPa.图1为RC梁试验加载装置，采用三分点加载方式，RC梁试验加载方案如表1所示.
图1 RC梁试验加载装置
Fig.1 Loading device for RC beam test
1.2 有限元模型建立
采用ABAQUS软件对表1中各梁进行模拟，梁和钢板采用分离式模型[7-8]，假定钢板、钢筋为理想线弹性和理想弹塑性材料，不考虑二者与混凝土之间的粘结滑移.混凝土采用C3D8R单元，钢筋采用T3D2单元，钢板采用S4R单元.混凝土结构受拉、压本构模型采用文献[9-12]中提供的关系.图2～3分别为RC单轴应力
应变曲线、钢材和环氧树脂胶应力应变关系曲线，相关参数含义参见文献[9-12].钢筋embedded region嵌入混凝土，钢板取tie约束至混凝土.梁支座及加载点处均设置钢垫块，支座处钢垫块底部中线处添加铰接约束，分别约束5个方向自由度和4个方向自由度.
表1 RC梁试验加载方案
Tab.1 Loading schemes for RC beam test
梁试件编号加载方式钢板厚度mmML-1无,对比梁0ML-2无,直接加固2ML-3无,直接加固4ML-4加载至20%PML-1时持续加载2ML-5加载至50%PML-1时持续加载2ML-6加载至70%PML-1时持续加载2ML-7加载至90%PML-1时持续加载2
注：PML-1为对比梁ML-1实测极限荷载，加固梁粘贴钢板后加载至破坏.
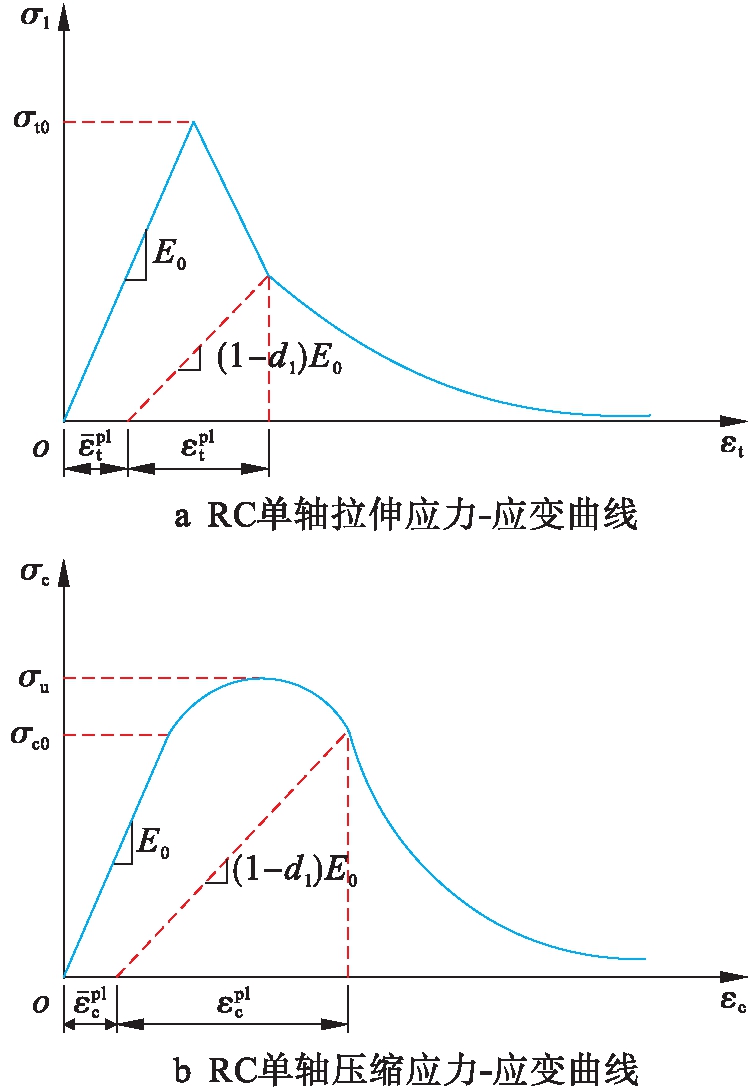
图2 RC单轴拉、压应力应变曲线
Fig.2 Stress-strain curve of RC under uniaxial tension and compression tests
根据上述条件建立有限元模型，如图4a所示.根据文献[13]，混凝土梁网格划分为30 mm，且种子按边布种.网格划分以及种子布置结果如图4b所示.
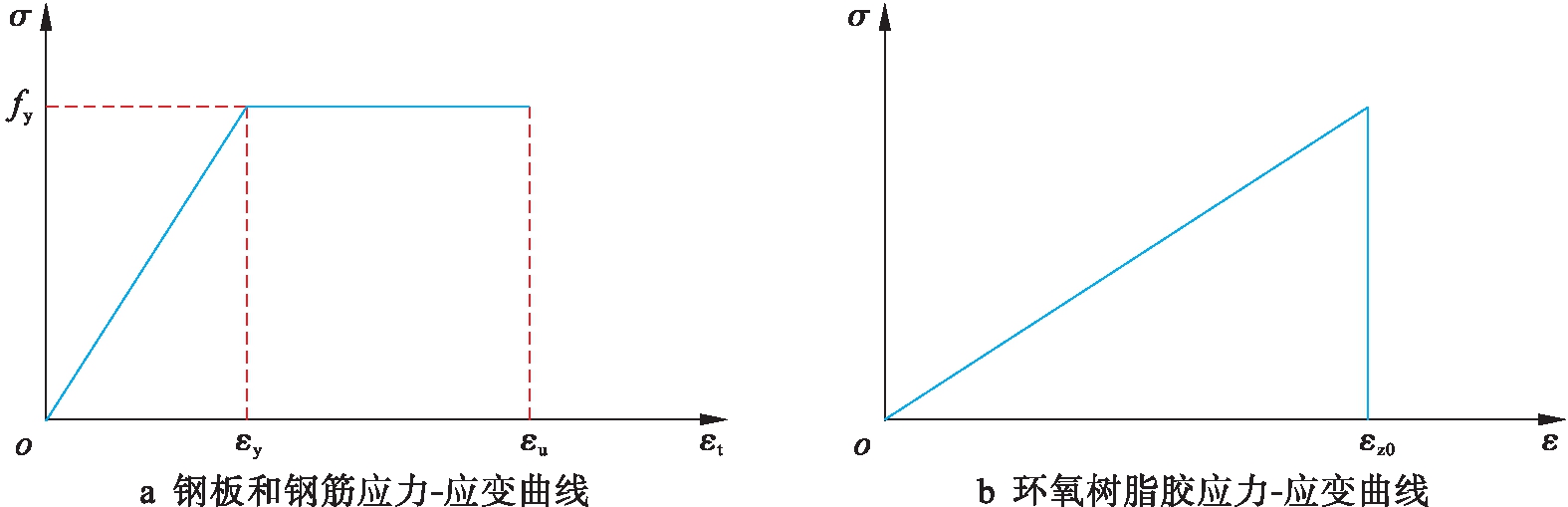
图3 钢材和环氧树脂胶应力应变曲线
Fig.3 Stress-strain curve of steel and epoxy adhesives
图4 梁模型有限元建立和网格划分、种子布置
Fig.4 Finite element establishment，meshing and seed placement of beam model
2 有限元结果与试验结果对比
将模拟得到的各个梁荷载位移曲线与相应试验结果进行对比分析，结果如图5所示.试验梁开裂荷载、屈服荷载、极限荷载、跨中挠度结果对比如表2所示.
由图5和表2可知，梁在各种模型下的荷载位移曲线与试验结果基本吻合.证明所建立的RC梁加固模型符合要求.有限元结果与试验结果误差均在8%以内，表明所建立的有限元模型是正确可靠的.
表2 有限元结果与试验结果对比
Tab.2 Comparison between finite element simulation and test results
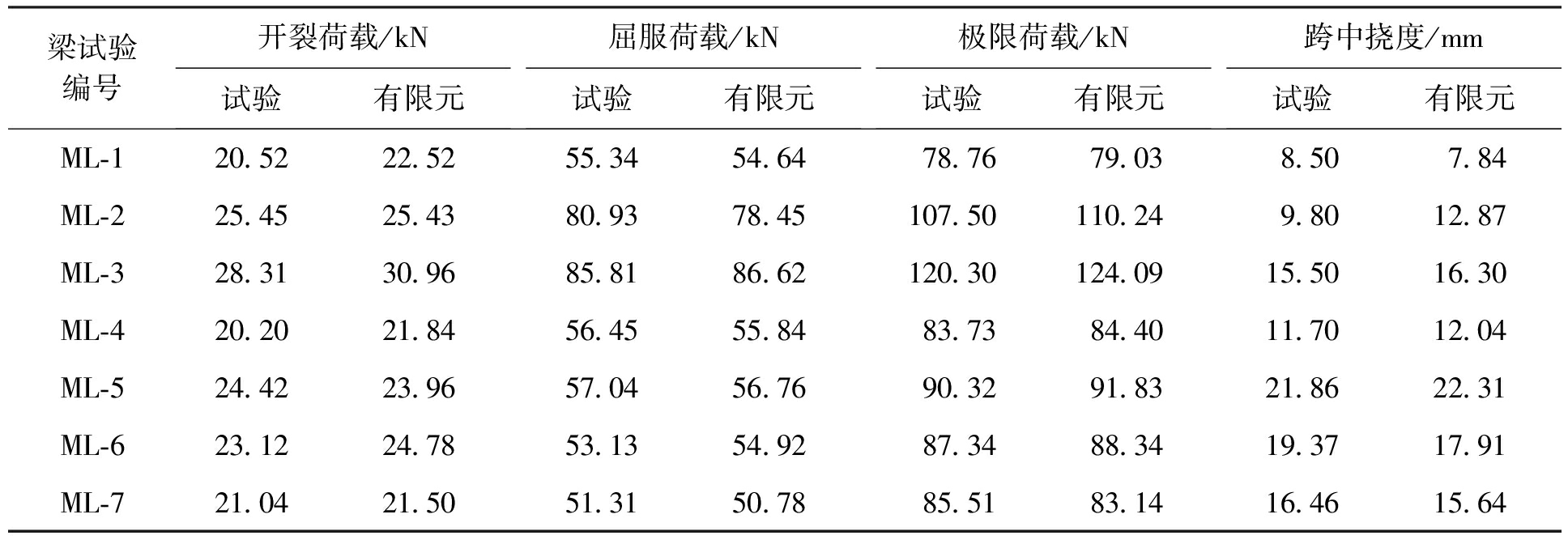
梁试验编号开裂荷载/kN试验有限元屈服荷载/kN试验有限元极限荷载/kN试验有限元跨中挠度/mm试验有限元ML-120.5222.5255.3454.6478.7679.038.507.84ML-225.4525.4380.9378.45107.50110.249.8012.87ML-328.3130.9685.8186.62120.30124.0915.5016.30ML-420.2021.8456.4555.8483.7384.4011.7012.04ML-524.4223.9657.0456.7690.3291.8321.8622.31ML-623.1224.7853.1354.9287.3488.3419.3717.91ML-721.0421.5051.3150.7885.5183.1416.4615.64
3 加固效果影响因素分析
3.1 钢板厚度因素
选取N、O两组数据结合对比梁ML-1进行分析，比较方案如表3所示，有限元模拟结果如图6所示，图7为钢板厚度对梁极限承载力影响柱状图.由图6、7可知：1)无论RC梁是否有加载历程，RC梁极限抗弯承载力都随着钢板厚度的增加而提高；2)当加载历程相同时，钢板厚度对RC梁极限抗弯承载力影响较为明显，且随钢板厚度增加而增大；3)对比NL-4和OL-4发现，无加载历程时，钢板厚度对RC梁的抗弯承载力提高更为明显(NL-1，2，3和OL-1，2，3结论相同)；4)无加载历程时，NL-4和NL-3相对于NL-2和NL-1对提高RC梁的抗弯承载力更大.
3.2 钢板长度因素
表4为钢板长度比较方案.图8为模拟结果.由图8可知，钢板长度为1 300 mm时对RC梁极限荷载提高幅度减弱或不是很明显；钢板长度对挠度影响很小.
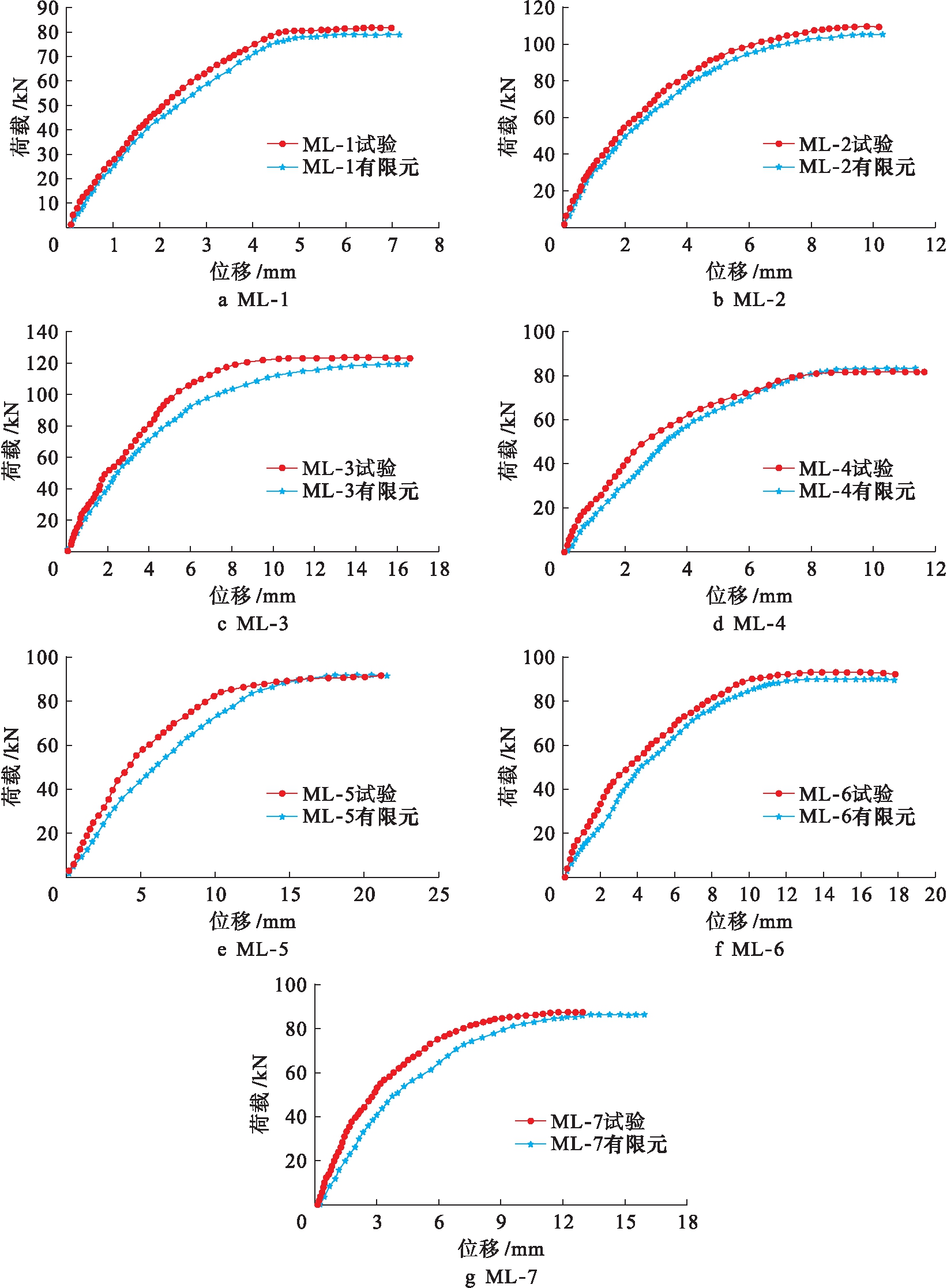
图5 有限元结果与试验结果荷载位移曲线对比
Fig.5 Comparison of load-displacement curves between finite element simulation and test results
表3 不同钢板厚度方案比较
Fig.3 Scheme comparison with various steel plate thickness
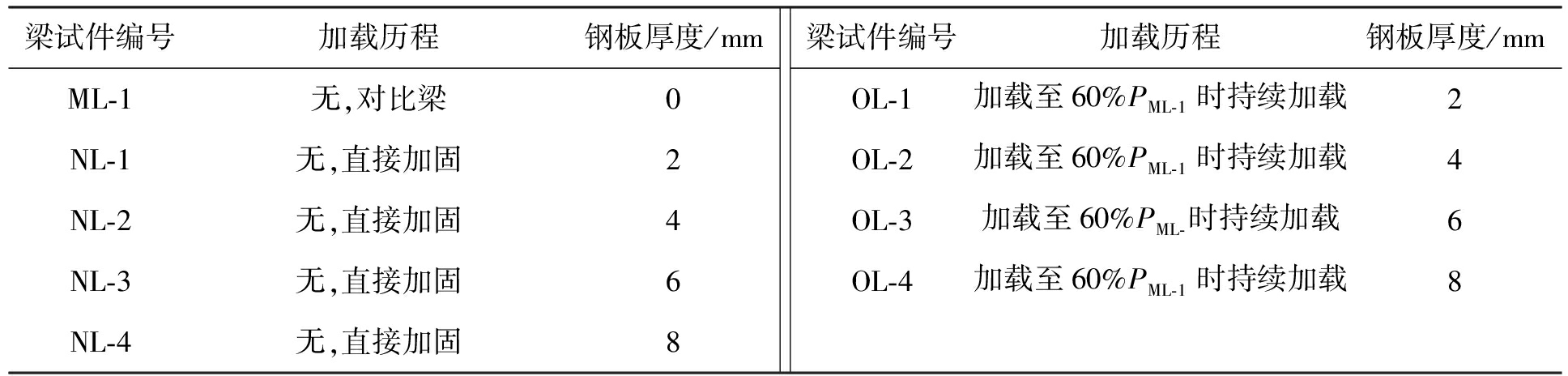
梁试件编号加载历程钢板厚度/mmML-1无,对比梁0NL-1无,直接加固2NL-2无,直接加固4NL-3无,直接加固6NL-4无,直接加固8梁试件编号加载历程钢板厚度/mmOL-1加载至60%PML-1时持续加载2OL-2加载至60%PML-1时持续加载4OL-3加载至60%PML-时持续加载6OL-4加载至60%PML-1时持续加载8
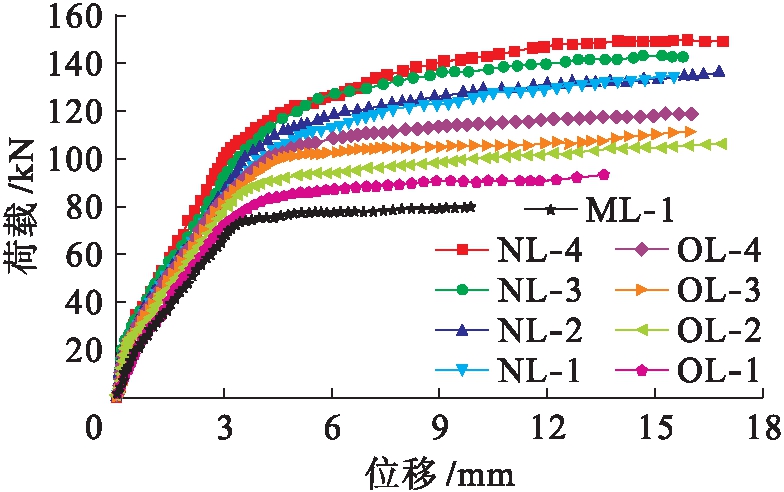
图6 钢板厚度和预载量对加固梁荷载位移曲线的影响
Fig.6 Effect of steel plate thickness and preload amount on load-displacement curves of reinforced beams
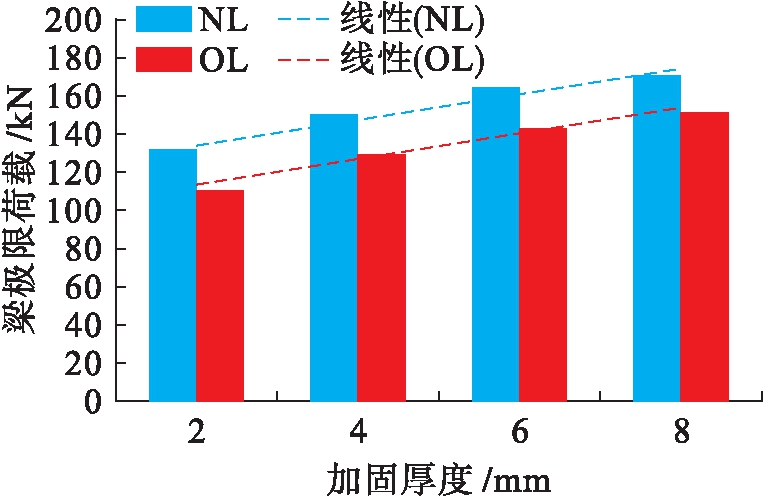
图7 加固厚度与梁极限抗弯承载力关系
Fig.7 Relationship between reinforcement thickness and ultimate bending capacity of beams
表4 钢板长度比较方案
Tab.4 Scheme comparison for various steel plate lengths
mm
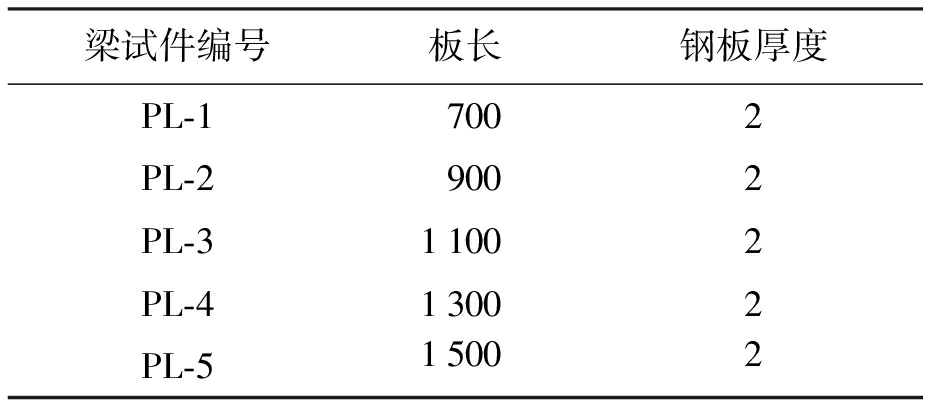
梁试件编号板长钢板厚度PL-17002PL-29002PL-311002PL-413002PL-515002
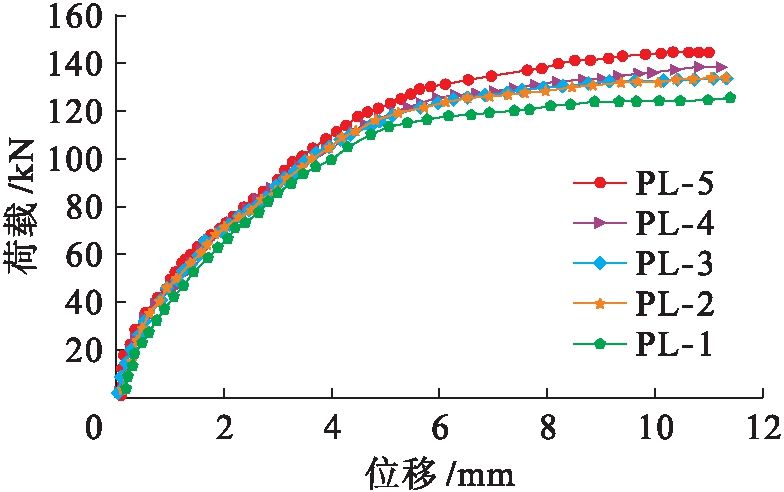
图8 不同钢板长度效果
Fig.8 Influence of various steel plate lengths
3.3 配筋率因素
表5为不同配筋率比较方案.图9为有限元结果.由图9可知：1)相同配筋率下，加固梁TL-3(TL-2和TL-1)相对于未加固梁SL-3(SL-2和SL-1)其极限荷载承载力提高45.30%(41.36%和37.94%)；2)钢板厚度相同情况下，RC梁抗弯承载力随配筋率增加而增大，但不明显；3)RC梁最大挠度值减小程度TL组大于SL组，即RC梁更快达到其抗弯承载力.
表5 不同配筋率对比方案
Tab.5 Scheme comparison for different reinforcement ratios
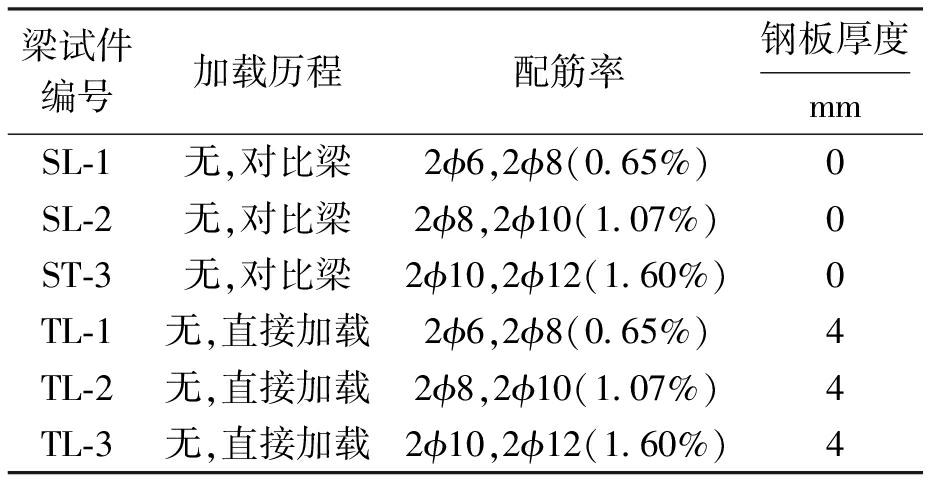
梁试件编号加载历程配筋率钢板厚度mmSL-1无,对比梁2ϕ6,2ϕ8(0.65%)0SL-2无,对比梁2ϕ8,2ϕ10(1.07%)0ST-3无,对比梁2ϕ10,2ϕ12(1.60%)0TL-1无,直接加载2ϕ6,2ϕ8(0.65%)4TL-2无,直接加载2ϕ8,2ϕ10(1.07%)4TL-3无,直接加载2ϕ10,2ϕ12(1.60%)4
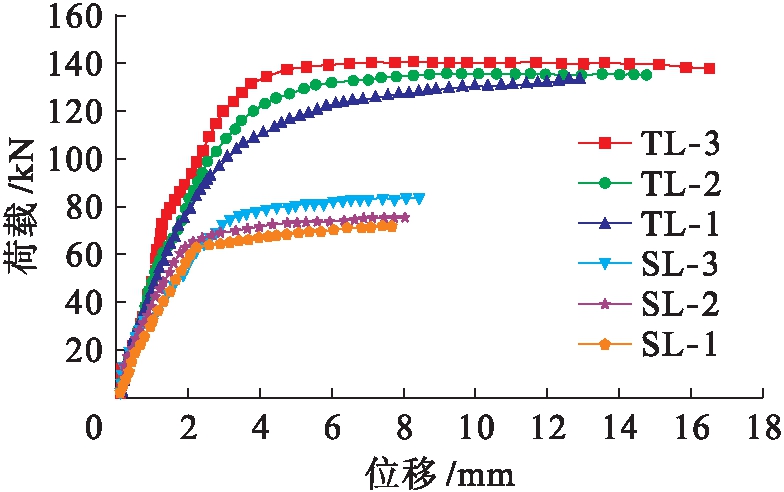
图9 不同配筋率影响结果
Fig.9 Influence of different reinforcement ratios
4 结 论
本文通过分析得出以下结论：
1) 当二次受力下RC梁配筋率较高时，使用钢板加固RC梁其极限承载力提高明显，即加固效果更好；相对于对比梁而言，增加配筋率对RC梁极限抗弯承载力影响较大.
2) 对二次受力下钢板RC梁加固时，梁抗弯承载力随钢板厚度增加而增大；当预载程度为60%且钢板厚度为6和8 mm时，其抗弯承载力增加很明显，分别为23.00%、25.80%，且钢板长度对挠度影响不大.
3) 存在最佳配板率，使得二次受力下钢板加固RC梁极限承载力提高不再明显或基本不提高.本文中钢板长度为1 300 mm时最好，占总长的86.70%，故实际工程应考虑合理的加固方案以节省钢板原材料.
[1]周良肖.关于粘贴钢板法在琅口桥加固工程中的应用 [J].低碳世界，2018(7)：288-289.
(ZHOU Liang-xiao.Application of paste plate method in the reinforcement project of Langkou Bridge [J].Low-carbon World，2018(7)：288-289.)
[2]王秀丽.粘钢加固法在隧道衬砌裂损快速修补中的应用研究 [J].施工技术，2018，47(10)：61-65.
(WANG Xiu-li.Research of bonded steel strengthening method in quick repair of tunnel lining cracking [J].Construction Technology，2018，47(10)：61-65.)
[3]柯美智.粘钢和碳纤维布技术在闸墩补强加固中的应用 [J].水利水电技术，2014，45(12)：25-29.
(KE Mei-zhi.Application of steel-bonded and carbon fiber cloth technology to reinforcement of gate pier [J].Water Resources and Hydropower Engineering，2014，45(12)：25-29.)
[4]郭文龙，韩之江，刘志华，等.PC梁加固前后使用性态差异性试验研究 [J].铁道学报，2017，39(11)：116-123.
(GUO Wen-long，HAN Zhi-jiang，LIU Zhi-hua，et al.Experimental study on performance and status diffe-rence of PC beams before and after reinforcement [J].Journal of the China Railway Society，2017，39(11)：116-123.)
[5]张维真.基于ABAQUS的粘贴钢板法加固钢筋混凝土梁力学性能分析 [J].吉林建筑大学学报，2017，34(5)：17-20.
(ZHANG Wei-zhen.Fea analysis of mechanical performance of RC beams strengthened with bonded steel plate based on ABAQUS software [J].Journal of Jilin Jianzhu University，2017，34(5)：17-20.)
[6]Alam M A，Jabbar A S A，Jumaat M Z，et al.Effective method of repairing RC beam using externally bonded steel plate [J].Applied Mechanics and Materials，2014，567：399-404.
[7]杜青，蔡美峰，李晓会.粘贴钢板加固钢筋混凝土梁的分离式有限元模型 [J].工程力学，2007，24(3)：154-158.
(DU Qing，CAI Mei-feng，LI Xiao-hui，et al.Separate finite element modeling of reinforced concrete beams bonded with steel plates [J].Engineering Mechanics，2007，24(3)：154-158.)
[8]杜青，蔡美峰，张献民.CFRP板加固钢筋混凝土梁的分离式有限元模型 [J].土木工程学报，2005，38(7)：11-14.
(DU Qing，CAI Mei-feng，ZHANG Xian-min.Separate finite element modeling of RC beams with exter-nally bonded CFRP plates [J].China Civil Engineering Journal，2005，38(7)：11-14.)
[9]王强，常凯，侯康康，等.用于ABAQUS梁单元的混凝土单轴本构模型 [J].建筑科学与工程学报，2018，35(5)：194-202.
(WANG Qiang，CHANG Kai，HOU Kang-kang，et al.Uniaxial concrete constitutive model for ABAQUS beam element [J].Journal of Architecture and Civil Engineering，2018，35(5)：194-202.)
[10]杨璐，石旭武.钢筋混凝土梁塑性损伤模型的数值模拟 [J].沈阳工业大学学报，2016，38(1)：97-101.
(YANG Lu，SHI Xu-wu.Numerical simulation of plastic damage model for reinforced concrete beam [J].Journal of Shenyang University of Technology，2016，38(1)：97-101.)
[11]秦浩，赵宪忠.ABAQUS混凝土损伤因子取值方法研究 [J].结构工程师，2013，29(6)：27-32.
(QIN Hao，ZHAO Xian-zhong.Study on the ABAQUS damage parameter in the concrete damage plasticity model [J].Structural Engineers，2013，29(6)：27-32.)
[12]舒兴旺，张影.环氧树脂/橡胶混凝土的应力应变曲线试验 [J].武汉理工大学学报(交通科学与工程版)，2016，40(1)：110-113.
(SHU Xing-wang，ZHANG Ying.Experiment on stress-strain curve of epoxy-rubber concrete [J].Journal of Wuhan University of Technology(Transportation Science & Engineering)，2016，40(1)：110-113.)
[13]宋力，王文源，樊成.BFRP布加固RC梁抗弯性能研究 [J].四川建筑科学研究，2018，44(3)：1-5.
(SONG Li，WANG Wen-yuan，FAN Cheng.Study on bending resistance properties of RC beams streng-thened with BFRP [J].Sichuan Building Science，2018，44(3)：1-5.)