园区自备储能系统为增量配电网园区拥有的多个设施中的可再生能源系统,通常使用分布式发电和存储单元来提供全部或部分终端用户的能源需求[1].自备储能系统根据用户的响应需求连接到用户子网终端,因此其目标包括降低运行成本、提高能源效率、平衡供需、减少碳排放等[2].未来随着国内实时电力市场的成熟,市场竞争将导致价格波动频繁.对于大客户可以采用自备储能系统来防止价格高峰[3],即在电价低谷期购电并在高峰期将储存的电力释放到子网中,因此,需要设计一种更有效的基于短期价格预测的自备储能系统调度策略以最优化经济效益.
电价预测和分类有利于自备储能系统的调度和竞价策略的制定,在竞争激烈的电力市场中具有重要意义.与短期负荷序列相比,电价序列具有更高的不确定性,在序列中反映出较大的非线性特性[4].
事实上,单独使用电价数据不能实现对自备储能系统操作的最优化调度.通过使用统计和机器学习模型,自备储能系统被赋予了更强的检测价格尖峰能力.Amjady等[5]利用概率神经网络和混合神经进化系统预测引擎,提供了一种新的特征选择过程和闭环预测机制.Christensen等[6]将价格峰值作为离散时间点,并使用自回归条件风险模型的非线性变量来建立澳大利亚电力市场的价格模型.陈杰尧等[7]提出了一种基于数据挖掘的方法,为价格峰值的产生提供了可靠预测.然而简单模型无法较好地处理价格波动中复杂的非线性关系,相比之下,深度学习技术[8]在非线性时间分析中体现出了显著的优势,并已被应用到电力负荷预测领域[9],这可以借鉴到短期价格预测过程中.
在价格预测领域已出现了一些基于卷积神经网络的研究成果,并反映出了一定的应用潜力[10-11],这也为优化调度自备储能系统提供了更多的选择.本文研究提出了一个基于多尺度卷积神经网络的5 min级周期多步电价预测模型,在未有额外计算开销的情况下可以提供更为理想的预测性能.
随后高分辨率的电价数据集被引入到电价预测中,并取得了显著的效果.Maciejowska等[12]在不同分辨率的数据集上分别评估了短期预测模型,认为高分辨率数据能够有效地加强电价预测的准确性.
对于传统的日前园区自备储能系统操作策略而言,一旦完成对第二天的预测,其时间表在整个调度周期内均是固定的且不会发生任何变化.但由于实时电价波动较大,导致电价估计误差大、调度成本增大.对抗变化的常见解决方案是在每一步中更新价格预测和操作计划,例如提前1 h调度,即滚动时域(RH)模型.目前,这一方法已成功地应用于微电网能量管理系统和时间相关设施[13]的调度中.RH模型每小时更新一次电价预测,并判断下一小时的电价是否为当天剩余时间的峰值.Chitsaz等[14]提出了滚动时域调度,电价的不确定性可被即时捕捉并用于实时预测,但其充放电策略局限于整小时,且精度受超参数影响较大.
本文主要以经济效益为导向,对削峰填谷的充放电策略进行优化,提出了一种基于高分辨率数据的自备储能系统滚动周期调度策略.鉴于调度策略高度依赖于模型的价格预测精确性,提出了一种基于深度学习的长短周期比较多尺度卷积神经网络模型进行价格预测,可以增强对价格变化中的非线性关系的学习能力并提供更优秀的性能.价格预测模型和优化策略的结合为储能系统提供了更强的峰值检测能力,因此可以做出更有效的充放电决策,使经济效益最大化.
1 方法论
1.1 自备储能系统的滚动周期调度
拥有自备储能系统的大型企业可以在电价谷值时段储能,并在电价峰值时段内释放,补充相应的耗电,以达到收益最大化.本文假设储能系统相对于整体市场来说足够小,因此其不会影响市场清算价格,且释放的能源可以完全被子网所利用.自备储能系统调度的经济目标可以表示为
(1)
式中:C为最大化利润;T为自备储能系统调度的单位周期,应用于日前调度,T=24 h;l为t时刻向增量配电网放电供销售的负荷量(lt>0),或向电网收费供购买的负荷量(lt<0);pt为t时刻的价格预测值.自备储能系统的优化目标受一系列条件φ约束,包括剩余容量、充电和放电速率、紧急安全电量、最大充电/放电率、每天最大数量充放电周期等.此次要解决的优化问题是调度自备储能系统中的lt部分运行能量,因此当每一步得到pt时,操作优化问题即可用线性回归等机器学习算法来解决.得到pt后,可根据式(1)计算C.
本文提出一种新的自备储能系统操作框架,其称为跨小时滚动时域,并引入包含5 min级市场清算价格的高分辨率数据集来提供更多的信息,以增强自备储能系统的预测和优化调度,操作原理图如图1所示.图1中h是当前一天的小时数,每小时包含12个细粒度的时间步,用s=0到s=11表示.O是应用到h中的调度操作决策.
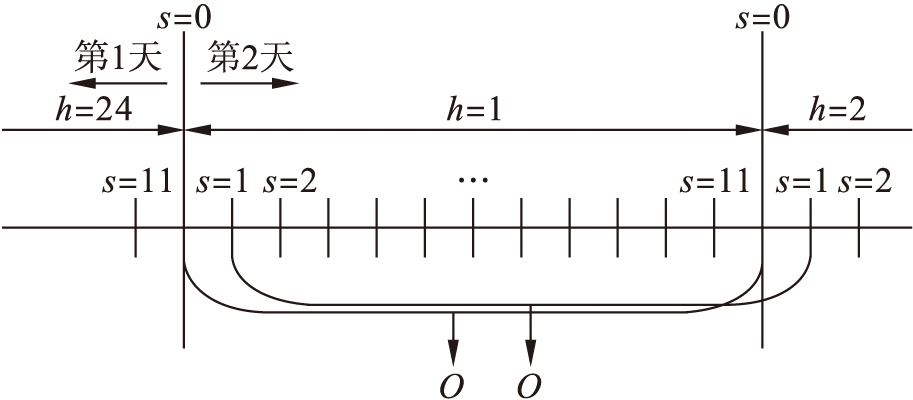
图1 跨小时滚动时域策略原理图
Fig.1 Schematic principle of hourly rolling horizon strategy
区别于IRH算法,引入每小时的前γ个5 min对当前小时做调度预测,跨小时滚动时域策略不再局限于整小时,而是小时之间的60 min跨度.每个时间步都对接下来的60 min进行操作预测,推导出尖峰、低谷和常态3种分类的概率,同时,本文取消了超参数γ的设置且增加了充放电调度的机会.
跨小时滚动时域算法应用一个单步和多步预测结合的模型,采用每5 min时间点前24 h的历史价格和影响因素作为输入.每一个时间步s对接下来60 min的平均电价值进行单步预测,并在每一个小时的开始对当天所有剩余时间进行小时级的多步预测.若当前单步预测值高于当天所有剩余小时的小时级多步预测值,则模型认为当前时间点达到峰值,并调度园区自备储能系统进行放电.若模型不认为时间步s后的60 min会产生峰值,则其继续将s+1时间步的价格加入更新预测中,并进行下一步预测.该预测与判断过程每5 min重复一次以更新预测,直到当天结束或峰值被捕获.
在本研究中假设自备储能系统充电或放电的影响范围是60 min,该策略考虑了更重要的实时价格信息,大幅度地提高了目标的预测精度和突变波形的检测精度.同时,其打破了整小时评估价格的传统观念,体现了更大的灵活性并有着扩大经济利润的潜力.
1.2 电价预测模型
由于预测策略高度依赖于单步和多步电价预测的精确度,因此需要对预测模型进行优化.在电价预测中,深度学习技术逐渐被广泛应用,并在实践中已验证了其有效性和精确性[15],这是因为深度学习在非线性时间分析中具有更好的识别特征和探索不确定性的能力.这些模型通常是长短期记忆(LSTM)神经网络的变体,但其受到梯度消失和特征提取能力相对较弱等问题的限制.借鉴以往的电力负荷预测研究,本文提出了一种用于跨小时、多步电价预测的多尺度空洞深度卷积神经网络.传统的卷积操作只在邻域提取特征,这限制了神经元之间的关系,而空洞卷积运算在不增加参数的情况下可扩大卷积核的感受野并提取多个尺度的特征,图2为一个典型的多尺度卷积块.
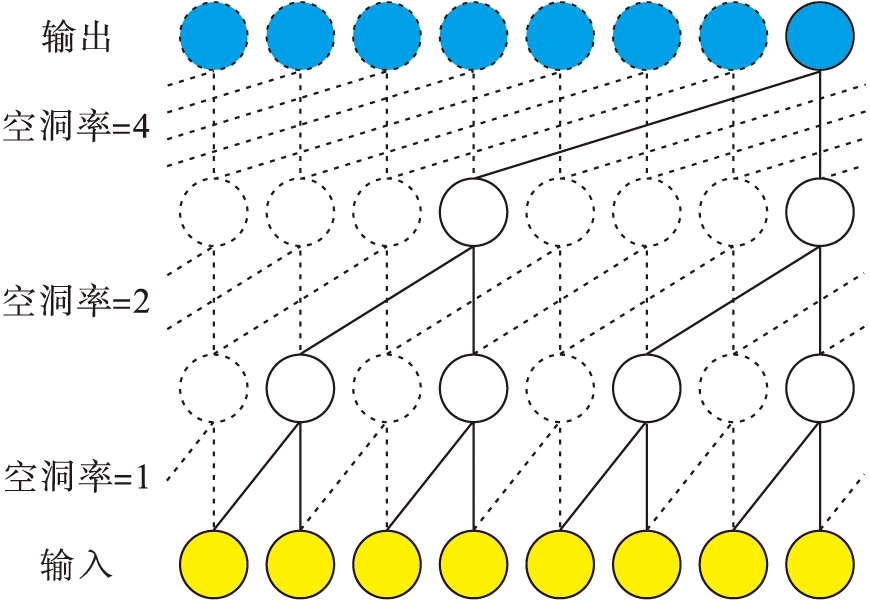
图2 包含3层空洞卷积层的卷积块
Fig.2 Convolution block with three dilated convolutional layers
文中提出的网络架构模型如图3所示.输入序列m×n表示m个n维向量,包括价格、负荷、需求、发电量、总流量、历史价格和时间编码信息.经过初始卷积层后,3个空洞卷积块连接到整个网络的基线中.块体中每一层采用不同的空洞率,在本文的网络中设置为1、2、4、8.从第3个卷积块引出的左分支负责单步价格预测,类似结构的右分支则关注未来24 h的多步预测.在实验中,为了达到效率和效果的平衡,文中选择了9个分位数进行预测,其可以在实际应用中增加分位数的数量,以进一步提高性能.
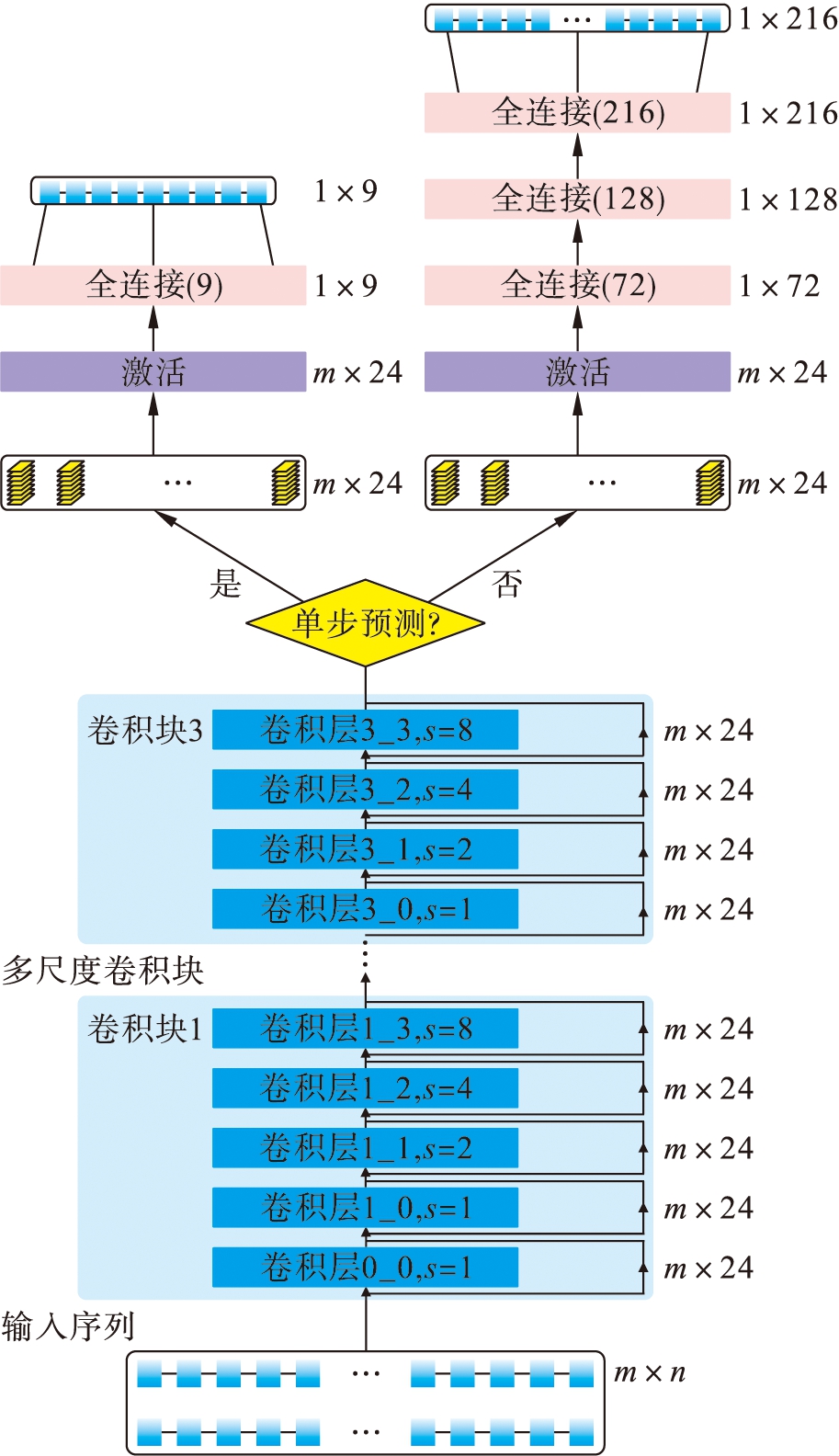
图3 基于深度学习的长短周期比较多步价格预测模型
Fig.3 Multi-step electricity price forecast model with long-short term comparison based on deep learning
本文的预测策略旨在捕获尽可能多的峰值和低谷价格,以优化自备储能系统操作.单步子网使用5 min级的高分辨率数据来探究即时价格波动.每小时的低分辨率市场数据在长期更有竞争力,因而其被馈入多步子网.融合两个分支,应用其提出的跨小时滚动时域策略,为自备储能系统的调度操作提供了更有效的峰值预测手段.
2 算例分析
本文在加拿大安大略省的市场电价数据集上验证提出模型的有效性和经济效益,并对模型的稳定性进行分析.
2.1 安大略电力市场价格数据集
安大略的电力市场是一个实时调度的市场,市场运营者通过特定的定价技术和程序进行清算投标,其中统一的市场清算价由所有市场参与者决定[16].位于安大略省电力市场中心的是独立电力系统运营商(如下简称运营商),其连接发电设备、电力供应商和消费者.市场清算后,价格每5 min记录一次,每小时的安大略电价ph在每小时的第一个5 min发布.同时,运营商还发布了提前调度价格pd.pd可看作是运营商计算出的价格预测值,接下来3 h的pd每小时发布一次,然而,发布的pd与ph之间却有着明显的偏差,计算表达式为
(2)
根据式(2)计算,2015年两种价格间的偏差约为38.49%.但若为了实现经济效益的最优化,直接使用pd数据调度则可能会错过价格的峰值.
2.2 统计分析
本节将从统计角度对所提出的预测模型准确性进行分析.使用2015年安大略省电价数据进行测试,同时使用2012~2014年的数据进行训练和验证.评估使用平均绝对误差(MAE)作为误差度量,月度平均绝对误差eMAE如图4所示.在0.1~0.9共9个分位数中,第5个分位数的eMAE总和是最小的,而几乎所有的9个分位数预测均能获得比pd更优的表现.虽然0.9分位数在11月和12月比pd差,但其平均值的表现较为理想.
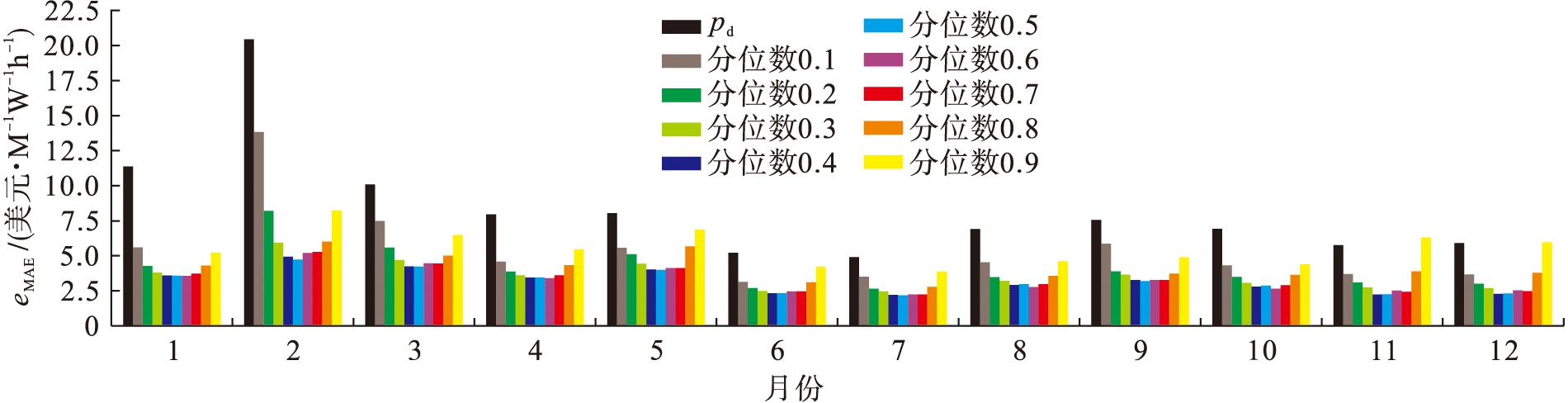
图4 月度平均eMAE
Fig.4 Monthly averaged eMAE
图5为2015年5月20日安大略省电力市场的实际价格和预测价格,结果表明,模型的预测结果能够较好地拟合实际电价的波动.尤其是本文模型不仅提供了合适的峰值位置,且提供了较为准确的数值预测.联合模型总体表现出了一定的跟随效应,其更倾向于接近前一时刻的价格.将全跟随模型与文中模型的预测值进行对比的结果显示,在经济效益分析中本文所提模型取得了更优的效果.
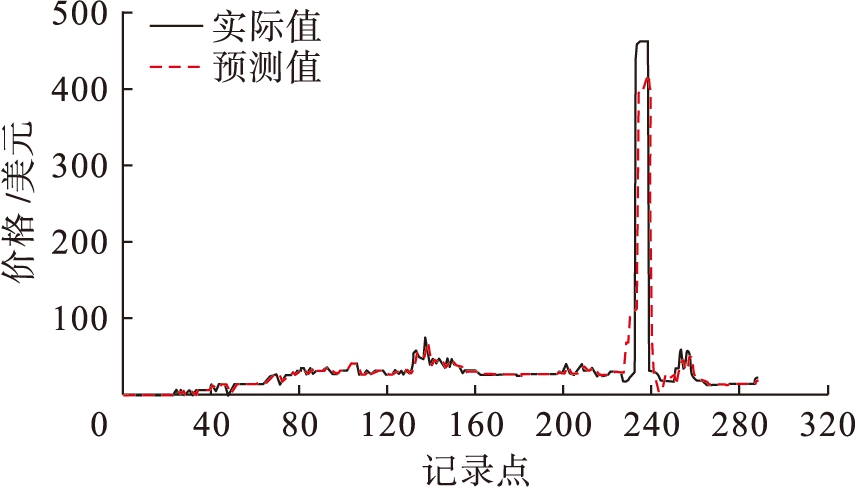
图5 单步子网预测结果与实际结果比较折线图
Fig.5 Line chart of single-step subnetwork forecast result in comparison with true data
图6为2015年5月8日模型输出的操作结果,每5 min后下一小时的平均价格用红色折线表示,而蓝色柱形则表示模型建议的放电时间(1为放电,0为不变).电池每天只能充放电一次,而充放电次数对经济效益影响较小,因此第一个蓝色柱的位置较为重要.在图6中,本文模型有效地捕捉了一天中第237个5 min的峰值.
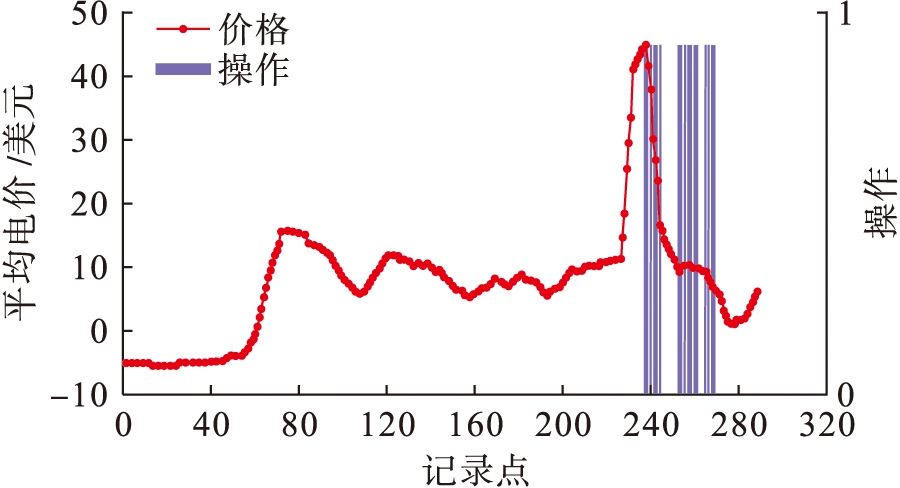
图6 电价折线图与模型预测操作
Fig.6 Line chart of electricity price and model forecasting operation
2.3 经济效益分析
本节从经济的角度来评估模型性能.模型被应用到安大略省增量配电网中的一个模拟自备储能系统上(容量为500 kW),以模拟其运行.电池部分容量必须预留以备紧急使用,其余容量可用于充放电套利.在模拟过程中,紧急负载为150 kW,电池放电深度为70%,因此剩余可用容量为200 kW.将电池运营套利利润作为评价指标,应用跨小时滚动时域策略对每5 min的操作进行预测.假设充放电的持续时间为1 h.
基于开放获取的运营商电价数据集,建立了6个不同的模型进行经济效益比较:
1)联合模型.在本文提出的联合模型中,多步分支主要关注小时水平的变化,而单步分支更关注每5 min当前时间步的变化.这两个分支的结合为自备储能系统的调度操作提供了必要的基础.在模型中,采用24个大小为8的卷积核,数据批次大小为128,采用均方误差作为损失函数并采用ADAM算法进行梯度下降优化,初始学习率为0.01.
2)ARX模型[14].采用带有外生变量的自回归模型(ARX)实现小时级多步电价预测,同时采用阈值策略来检测价格波动中可能出现的峰值.对于每个时间步,ARX采用300个小时级价格的历史数据序列重训练.
3)全跟随模型.使用前一时刻的值作为当前点的预测值,通过与全跟随模型的比较可以验证本文模型的时效性和对跟随效应的抵抗性.
4)预调度模型.使用开源的pd数据集作为预测值,采用pd数据的调度操作只能精确到小时级.
5)经验模型1.该模型计算2003~2014年按月的平均价格,本文选择平均价格最高的小时作为放电时间,反之谷值亦然.
6)经验模型2.充放电时间基于前一天价格的峰谷值经验确认.
在本实验中,计算了上述6种模型的月潜在利润,如图7所示.2015年的最大潜在利润合计约为5 532美元,应用本文的联合模型可捕获61.23%的潜在利润(合计3 387美元),相比于ARX模型提升了9.1%.ARX模型最终节省的价格是2 884美元,因为ARX的精度较低,阈值策略也有所影响.文中所提出的模型结果优于全跟随模型的结果(合计2 422美元),证明其有效克服了跟随效应.预调度模型是一种小时粒度模型,其结果并不理想(共679美元).与使用5 min粒度数据的模型相比,小时级预调度模型的利润率较低,这体现了使用细粒度数据的有效性.两种经验模型的总利润分别为1 787美元和1 229美元.
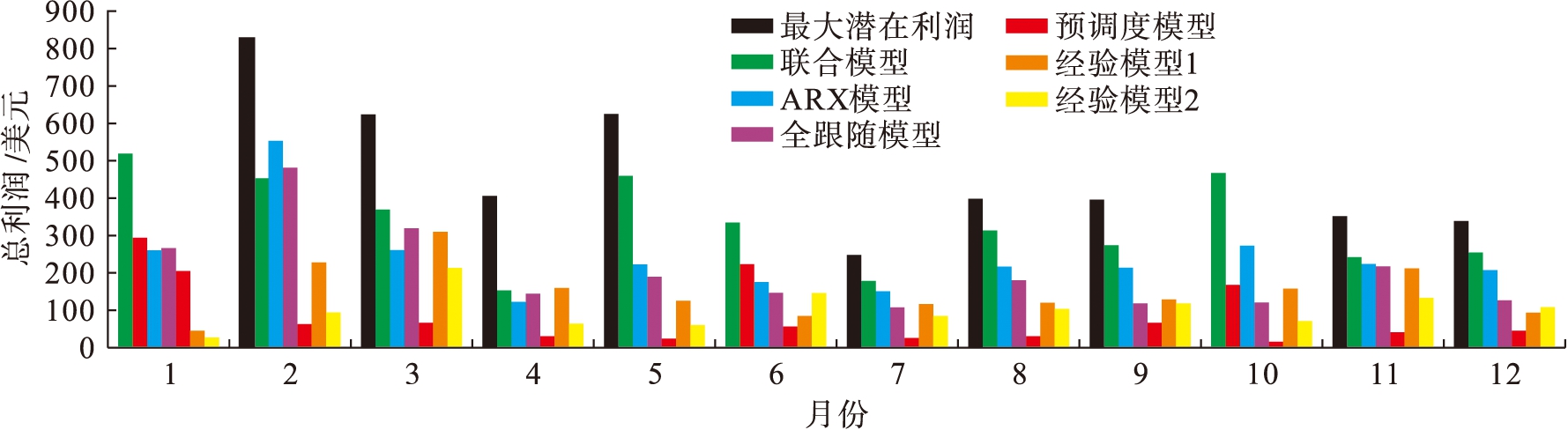
图7 不同模型的经济效益比较
Fig.7 Economic benefit comparation among different models
2.4 鲁棒性和效率分析
2.4.1 鲁棒性
通过对比实验验证了联合模型的稳定性,结果如表1所示,在两个对照实验中,测试集的5%和10%被随机置为0.经过相同的训练和预测步骤,计算并比较每月的经济效益.引入5%的噪声后,联合模型的精度未受明显影响,这些噪声甚至有助于其模型在价格数据波动较大的10月份获得更优的结果,且最终的利润为3 467美元.当引入10%的噪音数据时,联合模型的经济效益仍为2 862美元,接近无噪音的ARX模型,说明该模型具有较强的鲁棒性.
表1 引入5%和10%噪声后模型的月度利润
Tab.1 Monthly profits of model after importing 5% and 10 % noise 美元

工况1月2月3月4月5月6月7月8月9月10月11月12月正常294.2454.1369.4152.9460.3224.5178.3313.7274.2167.4243.5254.65%噪声255.8371.5384.5158.8439.6221.1177.0289.2285.4369.1253.1262.510%噪声280.4298.4362.1210.4174.9166.0168.9263.7259.3198.6244.9234.5
2.4.2 效率
由于电价具有较强的波动性,因此调整园区自备储能系统行为的时效性尤为重要.传统模型具有计算速度快的优点,但性能较差.同时,传统模型仍需对每个预测步骤和整个模型进行再训练,以获得更为准确的输出.然而,深度神经网络模型可在正式部署之前进行预训练,然后再按每周或每月的频率进行重训练.在这种情况下,神经网络模型的预测在实际应用中几乎不需要花费时间.此外,深度神经网络采用GPU并行运算来降低时间开销.因此相对于传统模型,深度神经网络模型的时效性更优、效率更高.在每一点处,本文使用和深度学习模型相同的前24 h信息重新训练ARX模型,并给出对接下来24 h的预测.据统计,ARX模型在每点处需要约6.42 s进行重训练和预测,而本文提出的深度模型对全年数据(共105 120条)做出预测,时间仅需7.03 s.在波动剧烈的电价市场中,预测时间的延后会造成较大的经济损失.
3 结 论
本文提出了一种跨小时滚动时域调度策略来运行自备储能系统,与传统方法相比,所提出的策略充电/放电操作不局限于一个完整的小时,这提供了更多的灵活性和潜在的利润.在电价预测中引入深度学习技术,能够增强对非线性关系的辨识能力.为了有效检测价格峰值,设计了一个应用长短周期比较模式的深度空洞卷积神经网络.该模型能够自动捕捉价格功能中的较大不确定性,突破了传统阈值法对外部因素敏感的局限性.通过充分的案例研究,证明了所提出模型在经济方面的有效性.
未来工作包括优化电价预测和使用深度学习技能的峰值检测,此外,基于实际应用场景的自学习充放电操作策略也是一个有价值的研究方向.
[1]焦永斌,秦会斌,华咏竹,等.电池储能系统参与配电网电压调节的策略研究 [J].电子技术应用,2020,46(9):123-126.
(JIAO Yong-bin,QIN Hui-bin,HUA Yong-zhu,et al.Battery energy storage systems participates in the stra-tegy research of voltage regulation of distribution network [J].Application of Electronic Technique,2020,46(9):123-126.)
[2]Tidemann C,Engerer N,Franklin E,et al.Promoting behind-the-meter battery storage:options for more effective government support and regulation [J].International Journal of Technology Intelligence and Planning,2018,12(1):77-98.
[3]Wu D,Kintner-Meyer M,Yang T,et al.Economic analysis and optimal sizing for behind-the-meter battery storage[C]//IEEE Power and Energy Society General Meeting (PESGM).Boston,USA,2016:1-5.
[4]黄靖茵,黄康乾,向德军,等.基于电力交易平台大数据的多区域电价预测研究 [J].电气应用,2020,39(9):36-41.
(HUANG Jing-yin,HUANG Kang-qian,XIANG De-jun,et al.Multi region electricity price prediction based on big data of electric power trading platform [J].Electrotechnical Application,2020,39(9):36-41.)
[5]Amjady N,Keynia F.A new prediction strategy for price spike forecasting of day-ahead electricity markets [J].Applied Soft Computing,2011,11(6):4246-4256.
[6]Christensen T M,Hurn A S,Lindsay K A.Forecasting spikes in electricity prices [J].International Journal of Forecast,2012,28(2):400-411.
[7]陈杰尧,陶春华,马光文,等.基于数据挖掘与支持向量机的现货市场出清价预测方法 [J].电网与清洁能源,2020,36(10):14-19.
(CHEN Jie-yao,TAO Chun-hua,MA Guang-wen,et al.Forecasting method of spot market clearing price based on data mining and support vector machine [J].Power System and Clean Energy,2020,36(10):14-19.)
[8]Deng Z,Wang B,Xu Y,et al.Multi-scale convolutional neural network with time-cognition for multi-step short-term load forecasting [J].IEEE Access,2019,7:88058-88071.
[9]许言路,武志锴,朱赫炎,等.基于多尺度卷积神经网络的短期电力负荷预测 [J].沈阳工业大学学报,2020,42(6):618-623.
(XU Yan-lu,WU Zhi-kai,ZHU He-yan,et al.Short-term load forecasting based on multi-scale convolutional neural network [J].Journal of Shenyang University of Technology,2020,42(6):618-623.)
[10] 缪冉,李菲菲,陈虬.基于卷积神经网络与多尺度空间编码的场景识别方法 [J].电子科技,2020,33(12):54-58.
(MIAO Ran,LI Fei-fei,CHEN Qiu.Scene recognition algorithm based on convolutional neural networks and multi-scale space encoding [J].Electronic Science and Technology,2020,33(12):54-58.)
[11] Afrasiabi M,Mohammadi M,Rastegar M,et al.Probabilistic deep neural network price forecasting based on residential load and wind speed predictions [J].IET Renew Power Gener,2019,13(11):1840-1848.
[12] Maciejowska K,Weron R.Shortand mid-term fore-casting of base load electricity prices in the UK:the impact of intra-day price relationships and market fundamentals [J].IEEE Transactions on Power System,2015,31(2):994-1005.
[13] 董鹤楠,苑舜,李闯,等.基于改进型P/Q控制的多源微电网功率脉动抑制 [J].沈阳工业大学学报,2020,42(1):7-11.
(DONG He-nan,YUAN Shun,LI Chuang,et al.Power pulsation suppression of multi-source microgrid based on improved P/Q control [J].Journal of Shenyang University of Technology,2020,42(1):7-11.)
[14] Chitsaz H,Zamani-Dehkordi P,Zareipour H,et al.Electricity price forecasting for operational scheduling of behind-the-meter storage systems [J].IEEE Transac-tions on Smart Grid,2017,10:19-30.
[15] Ugurlu U,Oksuz I,Tas O.Electricity price forecasting using recurrent neural networks [J].Energies,2018,11(5):1255-1267.
[16] 聂涌泉,顾慧杰,彭超逸,等.激励性含风电竞标日前市场出清电价机制的建模 [J].电力系统保护与控制,2020,48(19):25-34.
(NIE Yong-quan,GU Hui-jie,PENG Chao-yi,et al.Research on modeling the incentive electricity pricing mechanism in day-ahead electricity market clearing containing wind power bidding [J].Power System Protection and Control,2020,48(19):25-34.)