桥梁是公路交通系统的“咽喉”，在国家交通运输体系中占据重要位置[1].自20世纪以来，预应力混凝土梁以其结构简单、制作方便、造价经济等优点，在公路桥梁中广泛应用。据调查，我国通车公路里程中，预应力混凝土桥梁约占桥梁总数的90%.目前大规模在役期的预应力混凝土桥梁在车辆往复荷载作用下疲劳损伤累积显著，疲劳破坏成为桥梁事故的重要原因之一，因此，预测预应力混凝土桥梁疲劳寿命具有重要意义.
现阶段对于预应力混凝土桥梁的疲劳性能研究一般采用试验方法，但试验方法耗时且费力[2]，而能量方法在求解疲劳这类复杂的力学问题时有着其独特的便利性和准确性.目前，国内外学者利用能量耗散方法对桥梁动态响应和钢筋混凝土桥梁疲劳寿命预测[3]已取得一定研究成果，而对预应力混凝土梁疲劳寿命预测尚待深入研究.在相关钢筋混凝土梁疲劳寿命研究基础上[4]，本文引入动态预应力度指标，利用ANSYS软件对预应力混凝土梁进行疲劳模拟分析，研究不同动态预应力度指标下预应力混凝土梁耗散能密度变化规律，从而预测其疲劳寿命.
1 梁的能量耗散密度
由连续损伤理论可知，对于一个等温无穷小变形过程，材料的局部熵产生不等式[5]为
σijεij-φ≥0
(1)
式中：σij为Cauchy应力；εij为无穷小应变张量；φ为单位体积的Helmholtz比自由能.
假设材料在损伤过程中是各向同性的，φ与损伤变量D关系可表示为
φ=φ(εij，D)
(2)
假设材料初始状态为σij=εij=0，损伤变量D=0，根据内变量的正交流动法则[6-7]，推导得出φ=φ(εij，D)的级数展开式在εij的2阶项与D的N阶项截断表达式为
(3)
式中，C、B、A为n阶系数.由于材料经过加载后产生一定程度损伤后完全卸载，卸载后σij=εij=0，D取(0，1]某一值，代入式(3)可得
(4)
对于受弯弯矩为M的矩形截面(梁长为l、梁高为h、梁宽为b)纯弯梁，利用材料力学[7]中纯弯梁横截面上正应力分析推导公式可得
(5)
式中：ρ为弯矩作用下中性层曲率；θ为扭转角.由此可知
(6)
由于
等于纯弯梁的弯曲应变能，即可定义承受集中荷载的简支梁在循环过程中每次循环消耗的不可逆塑性功，即循环的耗散能密度为
w=∮Pdγ
(7)
式中：P为耗散能；γ为滞回路径.在挠度
荷载坐标系下，单个循环的滞回曲线所包夹面积即为耗散能密度.
在疲劳过程中，每次荷载循环都会有耗散能的累积，当荷载循环到n次时，累积的耗散能之和即为总耗散能.当疲劳循环次数达到N次，试件疲劳破坏时，总耗散能达到试件疲劳破坏时的临界耗散能.
2 模型设计
2.1 材料本构关系
2.1.1 混凝土本构关系
在预应力混凝土梁的疲劳过程中，梁的正截面下边缘处混凝土会处于波动的拉压状态，文献[8]中疲劳加载形式与本文相近，故混凝土疲劳剩余强度模型选择了该文献中的混凝土疲劳剩余强度模型来定义混凝土的疲劳性质，混凝土受压疲劳剩余强度表示为
αr(n)=αr(0)-[αr(0)-αmax](n/N)v
(8)
式中：αr(n)为疲劳加载到n次时混凝土疲劳剩余强度；αmax为疲劳荷载最大应力；N为疲劳寿命；v为与疲劳应力水平相关常数.混凝土受拉疲劳剩余强度表示为
ft，N=ftβt=ft(alg N+b)
(9)
式中：βt为混凝土受拉剩余强度修正强度；a、b为试验常数，由试验拟合得a=-0.091 3、b=1.
2.1.2 钢筋本构模型选择
文献[9]中模型梁钢筋和混凝土强度与本文模拟量相似，所以钢筋本构模型选择该文献的S-N曲线来定义钢筋的疲劳性质，其表达式为
lg N=12.904 7-3.240 2lg ΔF
(11)
式中，ΔF为钢筋的疲劳应力幅.
2.2 模型参数
试件模型采用预应力T型截面，模型梁总长3.3 m，支座中心距离3 m.模型梁混凝土强度等级为C50；为了使模型梁机构设计更加合理，结合文献[10]采用预应力1 860级7股钢绞线；普通钢筋采用HRB335普通钢筋.在模型梁加载点纯弯区段内，箍筋布置间距为200 mm，在支座至梁端150 mm内，箍筋间距为50 mm，其余区段间距100 mm.梁截面及加载方式如图1所示(单位：mm).
2.3 钢筋混凝土梁有限元模型建立
本仿真模拟采用三维实体单元建模，在梁体支座处和两个三分点处加垫块，并选取分离模式.预应力模拟采用初应变法进行预应力施加.混凝土构件单元选择为：混凝土采用SOLD65单元及CONCRETE材料，钢筋采用Link180单元，垫块`采用SOLD45.混凝土单轴受压的应力应变关系采用MISO模型；钢筋屈服准则选用BKIN模型.本模型采用边长为50 mm的六边形网格，仿真模拟采用了收敛性较好的面荷载施加方式[11].
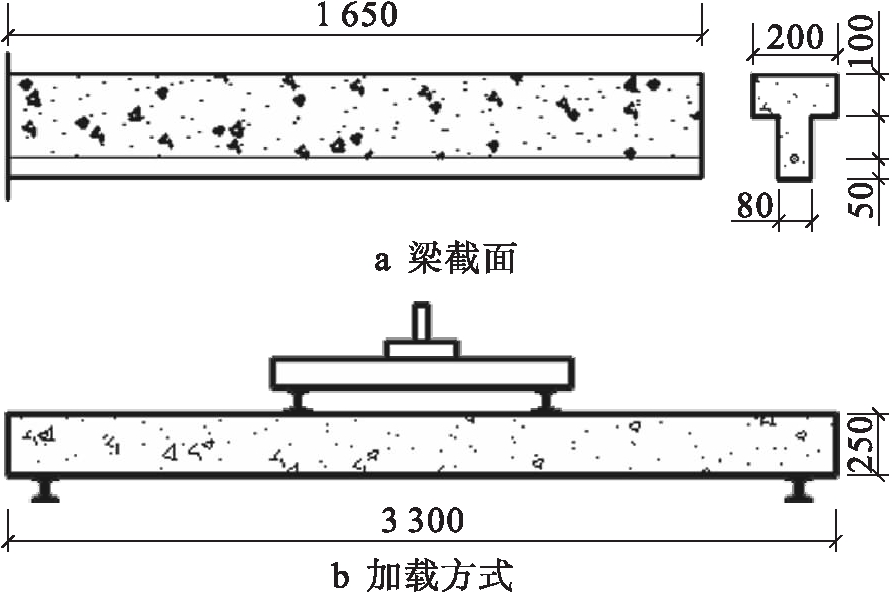
图1 梁截面及加载方式
Fig.1 Beam section and loading method
3 数值模拟及结果分析
3.1 加载及求解
静载模拟采用位移加载，疲劳荷载采用等幅阶跃荷载，在ANSYS的FATIGUE子模块对简支梁模型进行求解及计算.疲劳分析在时间历程处理器POST26中进行，计算完毕后，导出荷载及跨中挠度文件，在MATLAB中利用线性插值法，利用积分算出滞回曲线所围成的面积.
3.2 仿真算例
本文建立了6根预应力钢筋混凝土梁有限元模型，编号为L-1、L-2、L-3、L-4、L-5、L-6.L-1梁静载破坏，其余5根梁均采用等幅加载至疲劳破坏，等幅荷载最大荷载值均选取预应力钢筋控制张拉应力为标准值时的预应力梁静载λ=1的荷载值，并且将消压弯矩与循环荷载在单个周期内产生的最大弯矩比值定义为动态预应力度λd，模型工况如表1所示.每根模型梁除预应力钢筋张拉控制应力不同以外，其余模型设置均相同.当外部荷载相同时，改变消压弯矩即预应力钢筋控制张拉应力即可改变动态预应力度.
表1 模型工况
Tab.1 Model conditions
梁编号加载方式加载说明λdL-1静载破坏位移加载至破坏-L-2等幅疲劳0～24kN阶跃荷载0L-3等幅疲劳0～24kN阶跃荷载0.30L-4等幅疲劳0～24kN阶跃荷载0.50L-5等幅疲劳0～24kN阶跃荷载0.75L-6等幅疲劳0～24kN阶跃荷载1.00
3.2.1 静载仿真模拟
静载仿真模拟采用两步加载，第1步施加自重及预应力，第2步施加位移加载，得出力位移曲线模拟计算结果如图2所示.
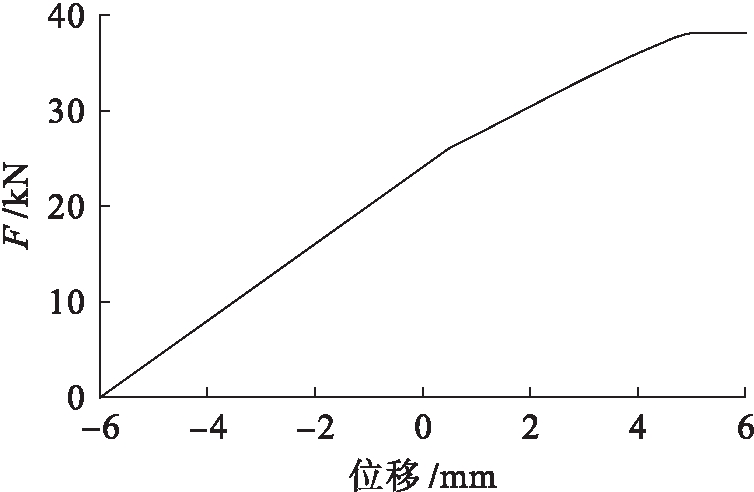
图2 L-1静载力位移曲线
Fig.2 L-1 static load-displacement curve
由图2可见，模型梁从加载到破坏，力位移曲线分为3个阶段，其规律与T梁静载破坏试验得出规律相同[12].由图2可知，梁施加自重及预应力后，反拱度为6 mm；当荷载施加到24 kN时，跨中位移为0 mm，此时消压弯矩等于外荷载产生弯矩，预应力度λ=1；当荷载施加到38 kN时，达到极限荷载，梁体破坏.
3.2.2 疲劳模拟
对L-2～L-6进行疲劳荷载模拟，各模型梁疲劳寿命如表2所示.图3为L-5模型梁第100次循环时的力位移曲线(滞回曲线).由图3可知，滞回曲线由前半周期加压过程的上升段和后半周期泄压过程下降段两部分组成，两段曲线包夹的面积即为梁的耗散能密度.将疲劳模拟算出的荷载、位移数据导出，在MATLAB中利用插值法求出两条曲线所包夹的面积.
表2 L-2～L-6疲劳寿命
Tab.2 L-2 to L-6 fatigue life
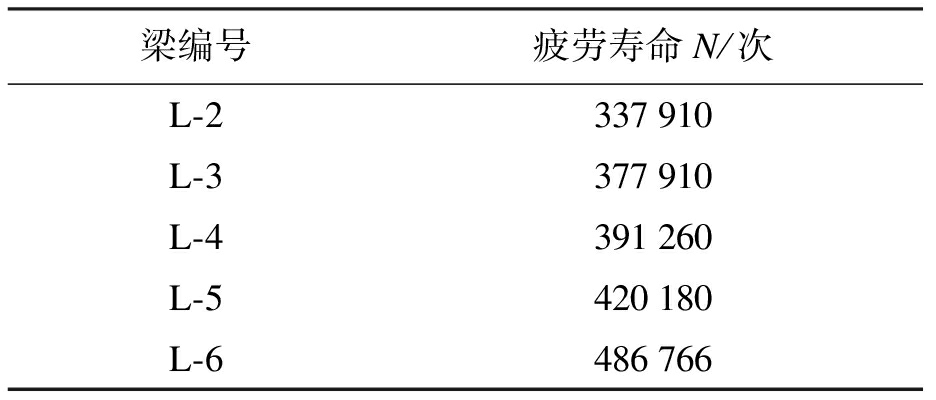
梁编号疲劳寿命N/次L-2337910L-3377910L-4391260L-5420180L-6486766
利用上述方法求得L-5模型梁不同循环次数的耗散能密度，如表3所示，并且将数据点拟合后得到折线如图4所示.由图4可知，该模型梁在疲劳过程总耗散能密度很明显分为3个阶段：耗散能密度较大并快速衰减的疲劳开始阶段；耗散能稳定的疲劳稳定发展阶段；耗散能极具增大至破坏的疲劳破坏阶段，其规律与针对钢筋混凝土简支梁疲劳试验测得的疲劳耗散能密度变化规律[5]保持一致.
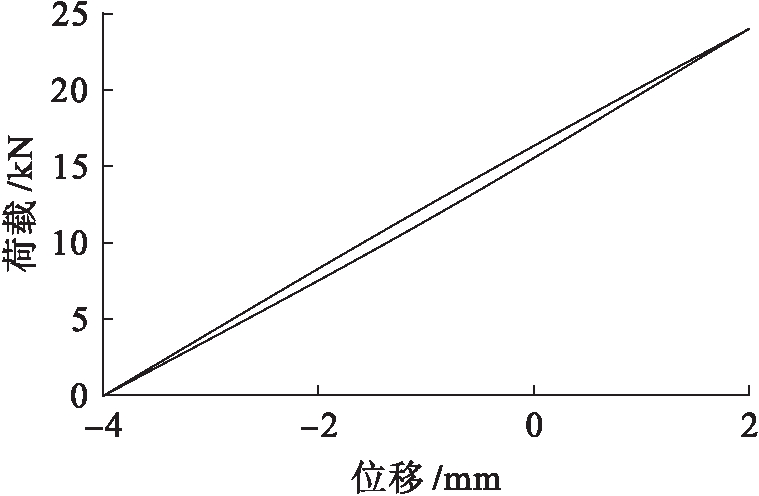
图3 L-5模型梁第100次循环时的滞回曲线
Fig.3 Hysteresis curve of L-5 model beam at 100th cycle
表3 L-5耗散能密度
Tab.3 L-5 dissipated energy density
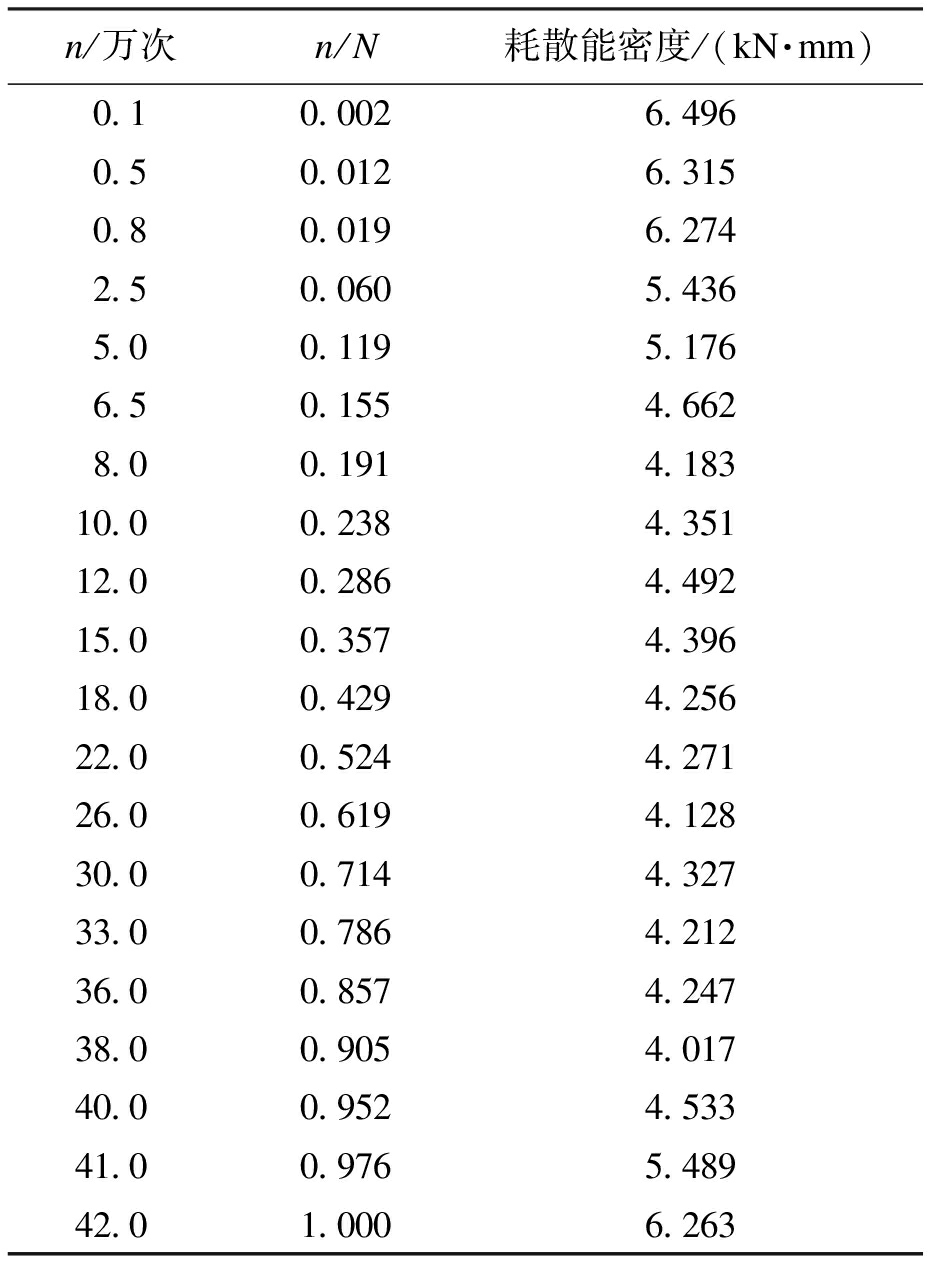
n/万次n/N耗散能密度/(kN·mm)0.10.0026.4960.50.0126.3150.80.0196.2742.50.0605.4365.00.1195.1766.50.1554.6628.00.1914.18310.00.2384.35112.00.2864.49215.00.3574.39618.00.4294.25622.00.5244.27126.00.6194.12830.00.7144.32733.00.7864.21236.00.8574.24738.00.9054.01740.00.9524.53341.00.9765.48942.01.0006.263
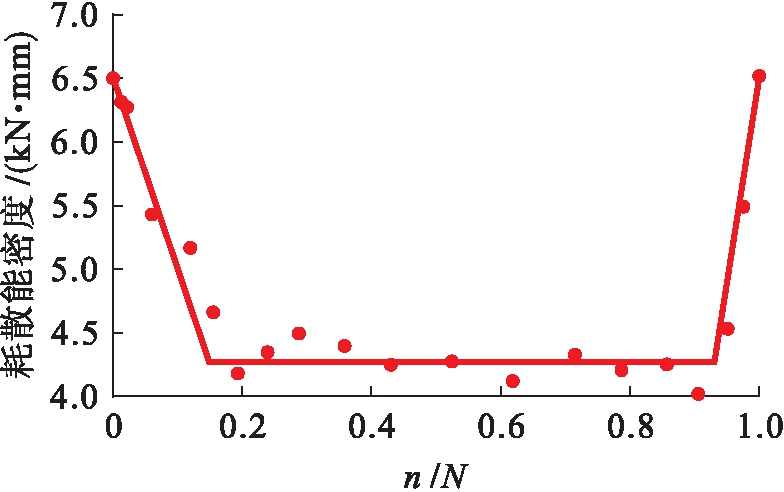
图4 L-5耗散能密度变化折线
Fig.4 Polyline showing changes of L-5 dissipated energy density
利用上述方法将各模型梁耗散能密度变化折线绘出，如图5所示.根据图5可知，不同动态预应力度模型梁在疲劳荷载作用下的能量耗散密度变化均呈现“三阶段”变化规律：动态预应力度低的模型梁在疲劳开始阶段耗散能衰减更加迅速且更快到达疲劳稳定阶段；当疲劳荷载相同时不同动态预应力度的模型梁在疲劳稳定阶段能量耗散密度相差不大，且几乎同时到达疲劳破坏阶段.
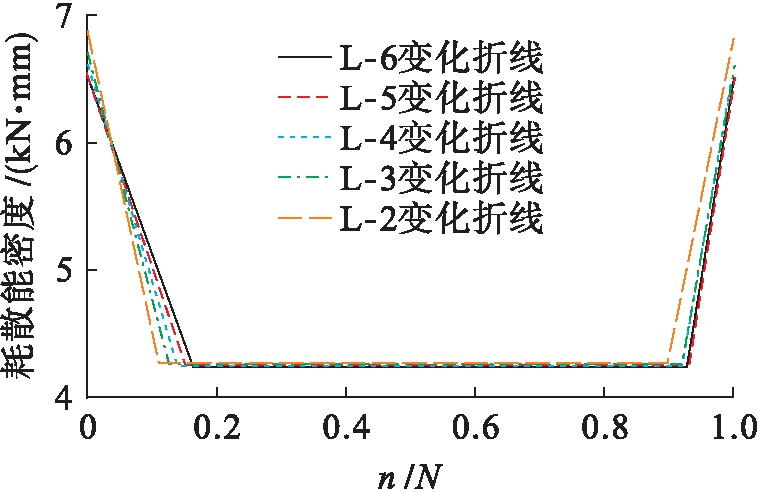
图5 各梁耗散能密度变化折线
Fig.5 Polyline showing changes of dissipated denergy density of each beam
4 结 论
根据上述分析，可以得到结论如下：
1) 混凝土梁在疲劳荷载的循环作用下存在着能量的耗散，能量的耗散与疲劳损伤存在着内在联系，当能量耗散总和达到临界耗散值时，梁体结构即发生疲劳破坏.
2) 通过疲劳仿真模拟，预应力梁的耗散能密度变化规律呈现非常明显的“三阶段”变化规律.动态预应力度低的梁，在疲劳开始阶段耗散能密度衰减更加迅速且更快到达疲劳稳定阶段，且疲劳稳定阶段持续时间更长.
3) 通过仿真结果数据分析可知，本算法可用于改进梁在疲劳稳定阶段的耗散能密度和荷载幅，实现利用线刚度预测构件疲劳寿命的目的.
[1]范立础.桥梁工程 [M].北京：人民交通出版社，2014.
(FAN Li-chu.Bridge engineering [M].Beijing：China Communications Press，2014.)
[2]王春生，周江，吴全有，等.既有混凝土桥梁疲劳寿命与使用安全评估 [J].中国公路学报，2012，25(6)：101-107.
(WANG Chun-sheng，ZHOU Jiang，WU Quan-you，et al.Fatigue life and safety assessment of existing concrete bridges [J].China Highway Journal，2012，25(6)：101-107.)
[3]朱红兵.公路钢筋混凝土简支梁桥疲劳试验与剩余寿命预测方法研究 [D].长沙：中南大学，2011.
(ZHU Hong-bing.Study on fatigue test and residual life prediction of highway reinforced concrete simply supported beam bridge [D].Changsha：Central South University，2011.)
[4]雷兵，宋玉普.基于ANSYS的部分预应力混凝土梁疲劳性能模拟 [J].工业建筑，2013，43(9)：71-76.
(LEI Bing，SONG Yu-pu.Fatigue performance simulation of partially prestressed concrete beams based on ANSYS [J].Industrial Building，2013，43(9)：71-76.)
[5]唐雪松，郑健龙，蒋持平.连续损伤理论与应用 [M].北京：人民交通出版社，2006.
(TANG Xue-song，ZHENG Jian-long，JIANG Chi-ping.The theory and application of continuous damage [M].Beijing：China Communications Press，2006.)
[6]Rice J R.Inelastic constitutive relations for solids：an internal-variable theory and its application to metal plasticity [J].Journal of the Mechanics & Physics of Solids，1971，19(6)：433-455.
[7]孙训方.材料力学 [M].北京：高等教育出版社，2002.
(SUN Xun-fang.Material mechanics [M].Beijing：Higher Education Press，2002.)
[8]朱劲松，朱先存.钢筋混凝土桥梁疲劳累积损伤失效过程简化分析方法 [J].工程力学，2012，29(5)：107-114.
(ZHU Jin-song，ZHU Xian-cun.Simplified analysis of failure process of fatigue cumulative damage on reinforced concrete bridges [J].Journal of Engineering Mechanics，2012，29(5)：107-114.)
[9]冯秀峰.混合配筋部分预应力混凝土梁疲劳性能研究 [D].大连：大连理工大学，2006.
(FENG Xiu-feng.Study on fatigue behavior of partially prestressed concrete beams with hybrid reinforcement [D].Dalian：Dalian University of Techno-logy，2006.)
[10]李艳凤，梁力，罗威力.预应力混凝土斜拉桥箱梁剪力滞规律 [J].沈阳工业大学学报，2016，38(6)：710-714.
(LI Yan-feng，LIANG Li，LUO Wei-li.Shear lag of box girders of prestressed concrete cable-stayed bridges [J].Journal of Shenyang University of Technology，2016，38(6)：710-714.)
[11]赵更歧，李可，张龙.高铁用HRBF500钢筋混凝土梁疲劳性能的数值分析 [J].郑州大学学报(工学版)，2010，31(6)：10-13.
(ZHAO Geng-qi，LI Ke，ZHANG Long.Experiment research on HRBF500 high strength RC beams for high speed railway under fatigue loading [J].Journal of Zhengzhou University (Engineering Science)，2010，31(6)：10-13.)
[12]张子璐，余小华，余华丽，等.折线配筋预应力混凝土T梁破坏试验受力性能研究 [J].中外公路，2017(3)：69-72.
(ZHANG Zi-lu，YU Xiao-hua，YU Hua-li，et al.Study on mechanical behavior of destructive test of prestressed concrete T-girder with broken-beam [J].Journal of China & Foreign Highway，2017(3)：69-72.)