时分复用系统主要用于视频会议、光纤传输、卫星电视等长距离高速传输线路.由于传输线较少，需要使用时分复用来解决线路拥挤的问题，同时长距离传输需要编解码算法保证数据正确性.低密度奇偶校验码(LDPC)算法已广泛应用于信道编码领域，在引入伽罗华域后，可以降低数据重复率从而进一步提高纠错效率.近年来国内外针对LDPC算法的研究主要集中在新算法开发和新硬件结构开发两个方面[1-2].
在新算法开发方面，Mateusz等[3]设计了一个正向纠错(FEC)编码系统；刘华军[4]提出了一种简单混合投影策略的 ADMM 译码算法，极大提升了译码性能和译码效率；邓熠[5]描写了基于高斯消去，基于上三角、下三角分解和基于近似下三角的编码方法，在译码方面提出了改进的标准化置信传播译码算法；Wang 等[6]进行了非二进制LDPC代码编码与FPGA实现研究.研究主要围绕硬判决和软判决算法进行创新，硬判决算法纠错能力较低，软判决算法又过于占用资源，因此本设计使用了增强型硬判决算法，保证足够多的纠错位数的同时也限制了硬件面积，对于单次传输的512 bit数据，最高可纠错7位.
在新硬件结构开发方面，Cheng 等[7]提出了地址解码器的平行循环移位结构；王梦[8]设计了一种流水线结构的LDPC-CC译码器；杨涛宇[9]从多码长和多码率方面研究了8种模式的LDPC多模式兼容结构；Yann 等[10]设计了一种基于模型的LDPC译码器.优化硬件结构通常是为了提高数据吞吐率，参考文献吞吐率基本在600 Mb/s以内，码率通常为0.5；本设计的码率高达0.812 5，吞吐率可达731.4 Mb/s.最后本文以文献[11]至文献[14]的设计参数作为对比以证明本设计的优势.
1 基于伽罗华域的LDPC编解码原理
伽罗华域(GF)定义了2n个符号的运算规则，特征是任何两个符号做加法和乘法运算后的结果仍然是这个符号集合中的符号，没有进位.GF(2n)域的加法为对应二进制表示的按位异或运算，乘除法通过查表得到.乘法表的推导方式为：先按多项式相乘，再用本元多项式解决溢出问题.
GF(16)定义了16个抽象符号，按二进制对应0000～1111.GF(16)域的本原多项式为
P(x)=x4+x+1
(1)
式中，x为伽罗华域中的元素，在GF(16)域中可以代表0～15共16个数据.
使用伽罗华域可以降低数据重复率，减小四环出现概率，使生成的校验矩阵无四环.本次设计的LDPC算法相关参数如表1所示.在本次设计中，为了平衡时分复用系统的并行传输和串行传输效率，同时保证电路具有较高的工作频率和吞吐率，最终确定了512 bit的码长.
将128 bit×24 bit规模的矩阵分为16×3个循环子矩阵，每个子矩阵为8 bit×8 bit的对角阵，由此确定行重为16，列重为3.保持右上角的子矩阵不动，同时随机循环右移其他子矩阵，最终构成无四环的近似下三角矩阵.编码矩阵构造如图1所示.
将图1参数化后可得到图2所示的下三角矩阵，矩阵H中n为矩阵H的列数，m为矩阵H的行数，g为可变参数.A、B、C、D、E分别是(m-g)(n-m)、(m-g)g、g(n-m)、gg、g(m-g)阶矩阵，T是(m-g)(m-g)阶下三角矩阵，即T的对角线上是非零GF(16)符号，对角线以外的元素都为0，进而可以进行LDPC编码.
表1 LDPC算法相关参数
Tab.1 Related parameters of LDPC algorithm
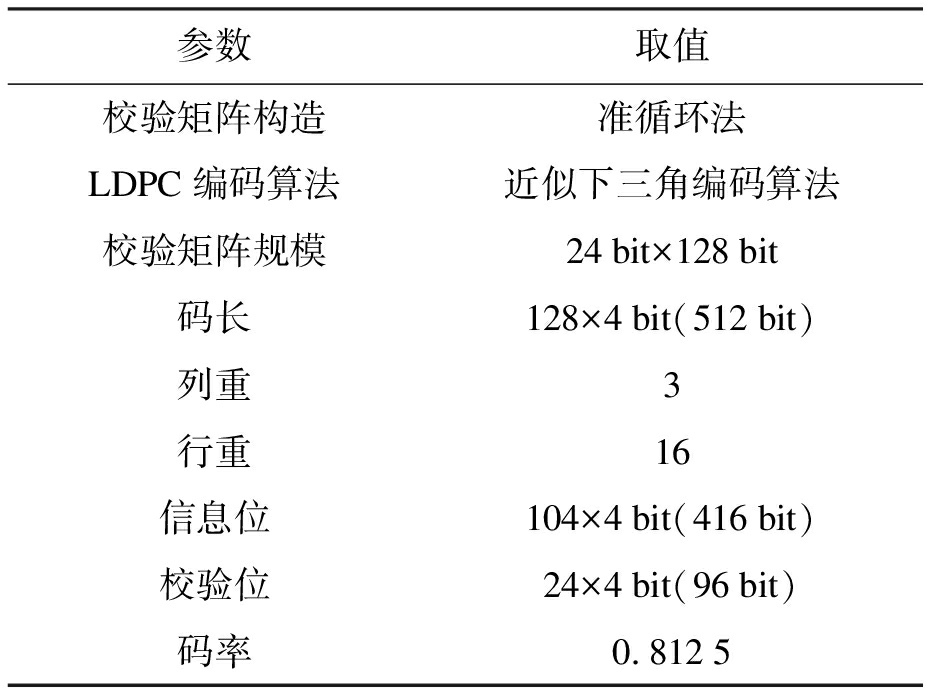
参数取值校验矩阵构造准循环法LDPC编码算法近似下三角编码算法校验矩阵规模24bit×128bit码长128×4bit(512bit)列重3行重16信息位104×4bit(416bit)校验位24×4bit(96bit)码率0.8125
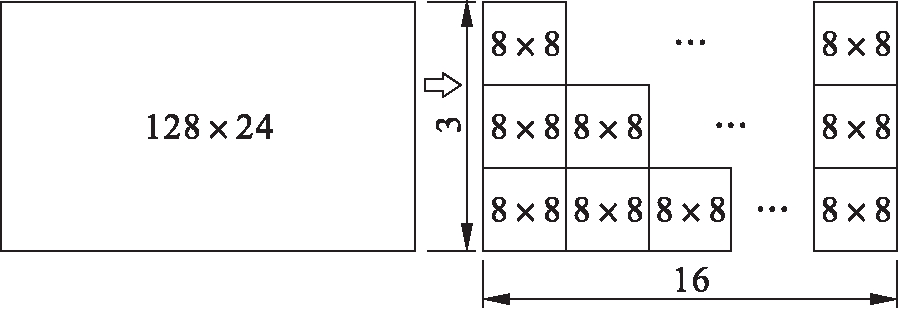
图1 编码矩阵构造
Fig.1 Construction of coding matrix
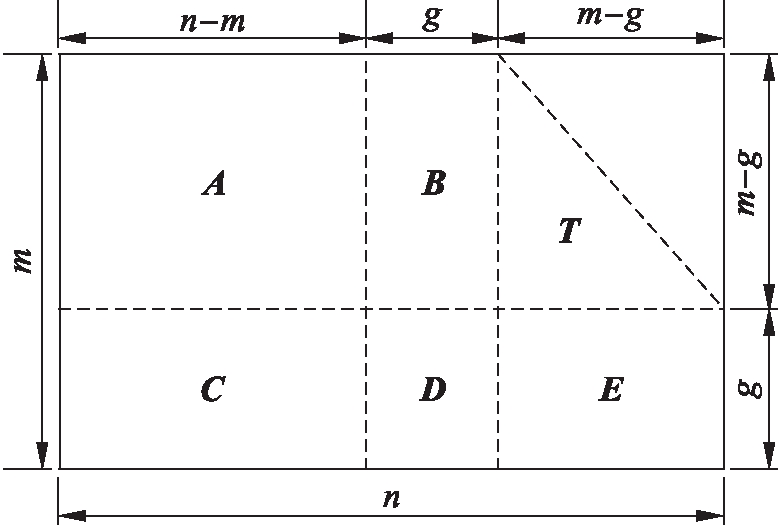
图2 下三角矩阵
Fig.2 Lower triangular matrix
LDPC编码由以下三部分组成
C=[s，p1，p2]
(2)
式中：s为信息位；p1、p2为校验位.令
φ=D-ET-1B
(3)
由CHT=0得到校验位公式为
(4)
将式(4)中的常量提取后，可以得到
(5)
式中，X、L、M为由软件生成的常数矩阵，其表达式分别为
X=(D-ET-1B)(ET-1A-C)
(6)
L=T-1A
(7)
M=T-1B
(8)
编码顶层架构如图3所示，蓝色线为数据通路，黑色线为控制信号.code_cntrl模块、code_p1模块以及code_p2模块为时序逻辑，分别负责产生编码过程的控制信号，进行p1和p2矩阵的编码.其他4个模块为组合逻辑，其中3个rom模块负责存储X、L、M矩阵的参数，code_multi模块负责将输入数据与对应矩阵参数进行GF(16)乘法.采用流水线设计，一次可以处理32 bit数据，每个周期进行累加，在最后一个数据传输完毕后一个周期即可完成编码并输出，具有较高的处理效率.
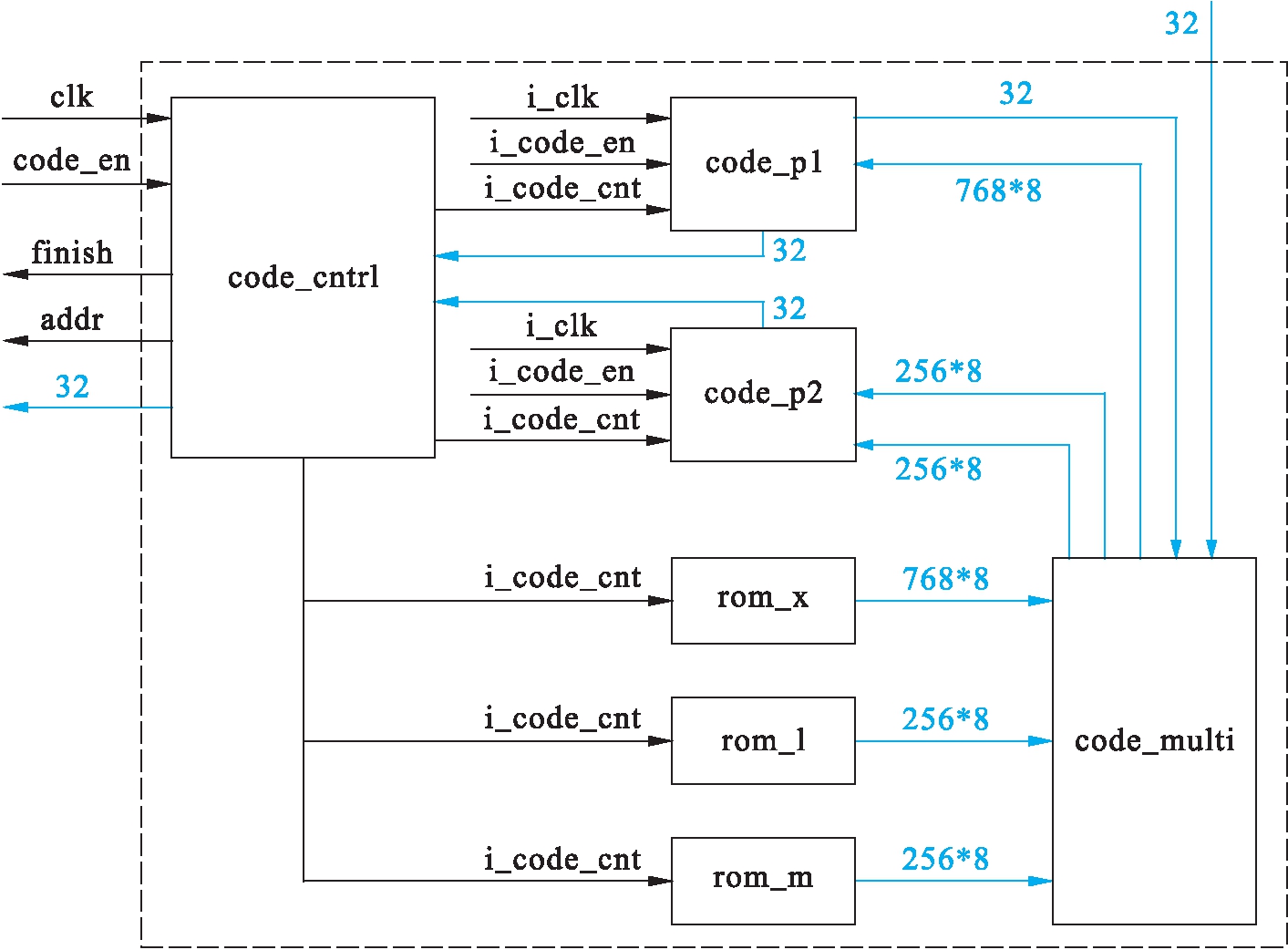
图3 编码模块顶层架构
Fig.3 Top-level architecture of encoding module
解码顶层架构如图4所示，采用流水线架构，decode_vn模块处理变量节点数据，decode_cn处理校验节点数据，decode_check模块校验输入数据，decode_check_ite模块校验迭代数据，以上模块由decode_cntrl模块产生控制信号进行流水线工作，每周期处理32 bit数据.其他模块用于存储GF(16)乘除法的查找表和用于迭代的概率表，为组合逻辑.
解码模块的核心是变量节点.将增强型硬判决算法生成的两种变量节点数据分别进行迭代和校验，相较于传统硬判决算法的优势在于将校验节点、后验信息以及输入数据都作为参数参与运算，用4个校验节点的数值生成校验用变量节点数值，而校验用变量节点数值则是从中去除对应的校验节点计算得来.既限制了硬件资源的消耗，又提高了纠错效率.
变量节点数据处理表达式为
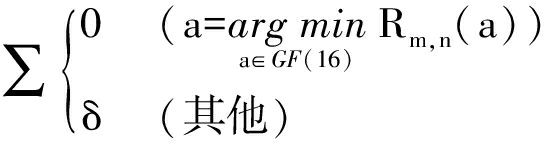
(9)
(10)
(11)
式中：Rm，n为校验节点数据；k为迭代次数；m和n分别为校验节点的行列位置；a为来自校验节点或输入数据的数值；δ为a中的非零值.
校验节点的数据处理过程为：初始输入变量值先与校验矩阵H中对应的符号做GF(16)域下的乘法运算，再经过前向后向算法依次得到校验节点回发给变量节点的数据，最后做GF(16)域下的除法运算，产生从校验节点到变量节点的消息，送到变量节点运算器做信息更新.校验节点数据处理表达式为
(12)
式中：h为校验矩阵H中的数值；⨁为GF(16)加法运算；
为第k-1次迭代后产生的校验信号.LDPC解码模块的吞吐率表达式为
(13)
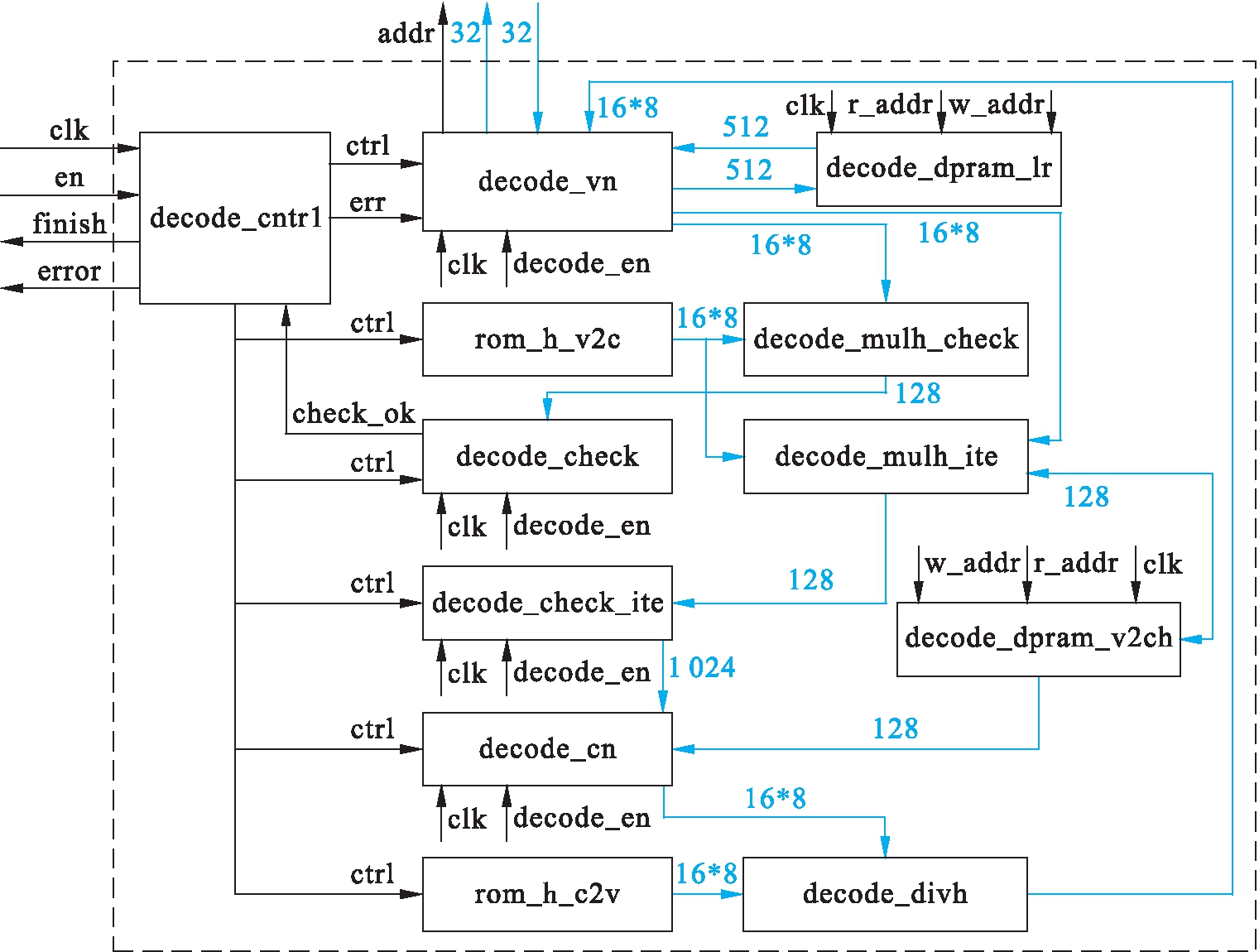
图4 解码模块顶层架构
Fig.4 Top-level architecture of decoding module
式中：N为码长；f为时钟频率；i为最大迭代次数；t为单次迭代过程所需要的时钟周期数.在本次设计中，码长为512 bit，时钟频率为400 MHz，最大迭代次数为10次，单次迭代所需时钟周期数为28，由此计算出的吞吐率约为731.4 Mb/s.
2 时分复用系统架构
本次设计的动态低延迟时分复用系统可以支持最高同时传输640个通道数据，其中每个通道数据位宽为16 bit，共10 240 bit.发送端和接收端各有3级，每级模块之间通过异步FIFO连接.
发送端由8个通道采集模块和1个汇总模块组成.其中每个通道采集模块连接最多10个数据采集模块.采集到的通道数据先在数据前端加上6位通道号后通过异步FIFO传给汇总模块.汇总模块将收到的数据前端再加上4位通道采集模块编号后，送入并行转串行模块和编码模块进行数据编码和串行发送.编码的流水线结构可以保证数据位发送完后立刻发送校验位.为了体现LDPC算法的优势，需要一次传输16个通道数据并进行编码.
接收端由1个数据整合模块和8个数据发送模块构成.开始接到数据后会先通过串行转并行模块将1位数据组成GF(16)的格式即4位数据送入解码模块进行解码，如果数据校验成功可立即读出数据.根据数据的通道采集模块编号将数据存入对应的异步FIFO，进入对应的数据发送模块后通过通道标号将数据传给对应的通道.
3 实验结果及分析
设计基于Xilinx的Kintex Ultra系列FPGA，型号为xcku115-flvb2104-3-e，介绍主要模块的仿真以及最大数据传输的延时.
图5、6为数据传输时间仿真结果，仿真方式为按通道号依次发送数据，测量从第一个发送端通道发出数据到最后一个接收端通道接收数据之间的时间.本文时分复用系统最高可支持8×8×10个16 bit通道的数据传输，因此单次最高可传输10 240 bit数据，从仿真结果可以看出单轮发送10 240 bit数据大概需要43.8 ns.
时序约束结果如图7所示，证明该设计可运行在400 MHz的频率下.图8为LDPC算法纠错效果.通过使用Matlab编写与硬件设计等价的代码测试程序验证LDPC解码算法纠错能力，对编码后的数据进行随机出错后再进行解码纠错检验.由图8可见，解码算法可稳定纠错7位.
对于编解码算法的设计要求通常是在保证较高吞吐率的情况下兼具一定的纠错效率，同时可以工作在较高频率以适应高频系统.
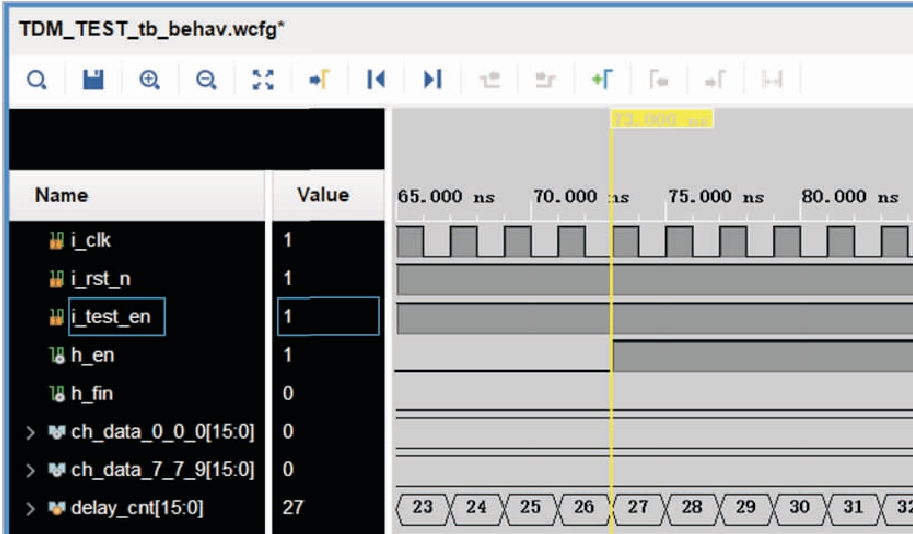
图5 数据传输开始
Fig.5 Beginning of data transmission
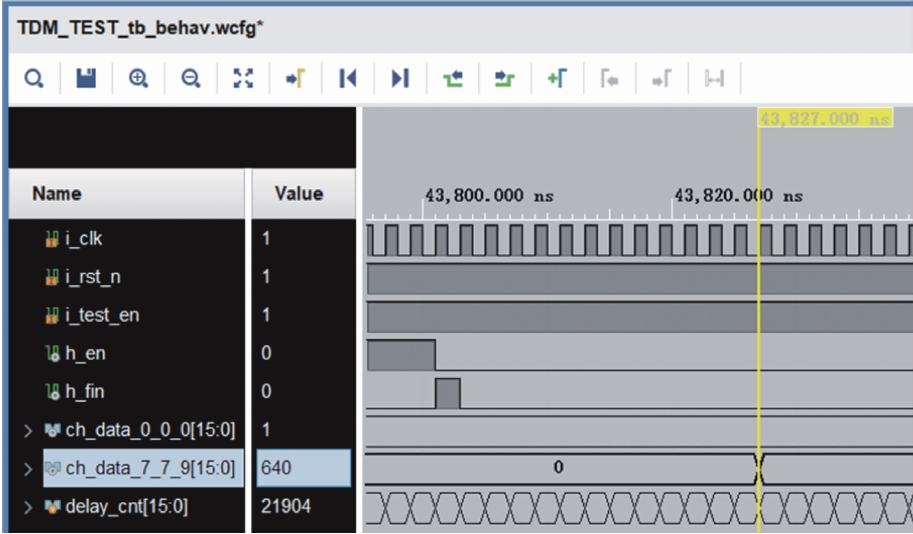
图6 数据传输结束
Fig.6 Ending of data transmission
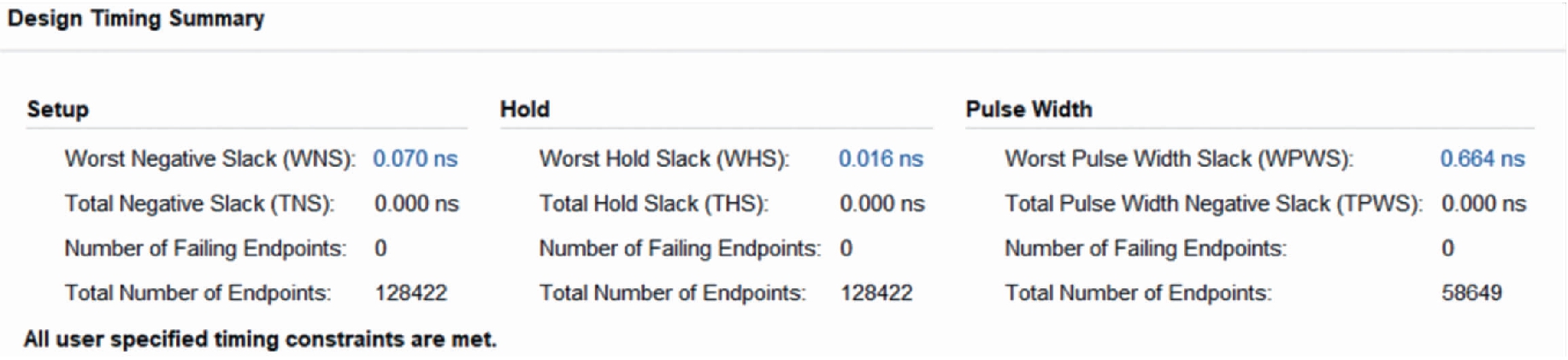
图7 时序约束结果
Fig.7 Timing constraint results
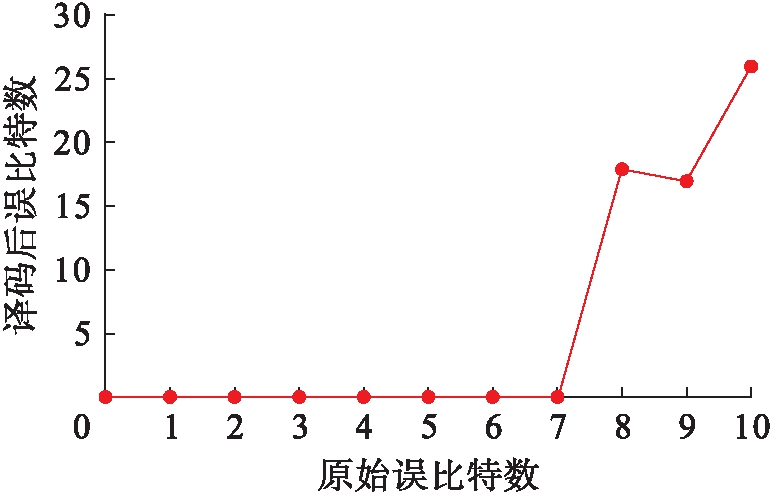
图8 LDPC算法纠错效果
Fig.8 Error correction results by LDPC algorithm
与其他参考文献的设计指标进行对比结果如表2所示，主要对比参数为码长、码率、工作频率和吞吐率.
表2 本设计与其他文献设计的性能比较
Tab.2 Performance comparison of design by this work with other literatures
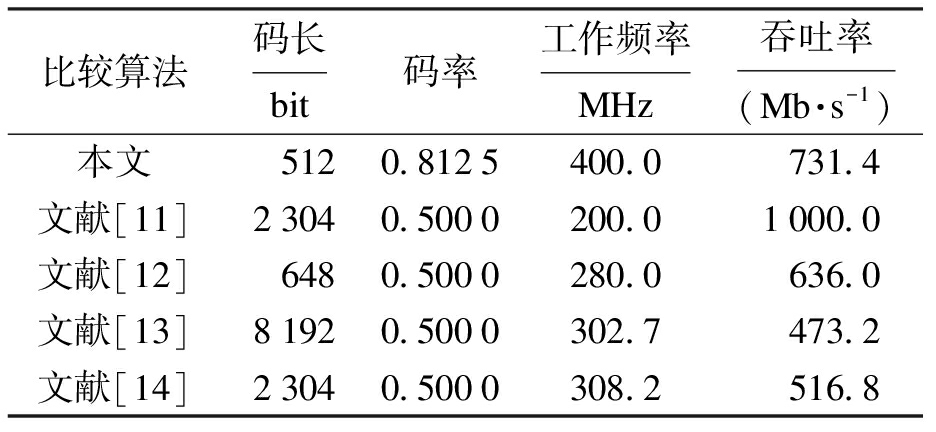
比较算法码长bit码率工作频率MHz吞吐率(Mb·s-1)本文5120.8125400.0 731.4文献[11]23040.5000200.01000.0文献[12]6480.5000280.0636.0文献[13]81920.5000302.7473.2文献[14]23040.5000308.2516.8
码长一般由系统对数据的需求决定，与码率共同影响纠错效率.通常为了提高纠错效率会降低码率，但较低码率代表用于校验的位数更多，单次传输的有效数据更少，可能会造成吞吐率的降低.码长、工作频率与码率共同影响吞吐率，较高吞吐率将会减轻编解码模块对系统的负担.
文献[11]实现了基于最小和算法的MIMAX标准(2 304，1 152)QC-LDPC译码器，侧重高吞吐率，但是码率和工作频率较低；文献[12]采用了分层译码算法；文献[13]设计了一种低复杂度分层全并行结构的译码器；文献[14]采用了与文献[11]同样的编码标准在FPGA上实现算法，文献[12]～[14]均侧重于减少资源占用，但码率和吞吐率不理想.本文设计的LDPC解码模块的吞吐率基本高于其他文献，并且在支持更高的时钟频率同时保持了极高的码率.
4 结 论
本文设计的时分复用系统具有低延时、高数据传输量、高稳定性等优点.采用了基于伽罗华域的LDPC编解码算法，该算法具有高码率、高吞吐率等优势，其中码率0.812 5，吞吐率731.4 Mb/s，在保证数据高速传输的同时，以流水线结构对数据进行判断纠错，对于单次处理的512位数据，可稳定纠错7位.
[1]黄翔，黎勇，张晓琴.基于QR码构造的广义LDPC码 [J].重庆邮电大学学报(自然科学版)，2020，32(6)：961-968.
(HUANG Xiang，LI Yong，ZHANG Xiao-qin.Construction of generalized LDPC codes based on QR codes [J].Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition)，2020，32(6)：961-968.)
[2]陈发堂，刘一帆，唐成.LDPC码的一种低复杂度归一化最小和译码算法 [J].重庆邮电大学学报(自然科学版)，2020，32(1)：92-98.
(CHEN Fa-tang，LIU Yi-fan，TANG Cheng.A low-complexity normalized min-sum decoding algorithm for LDPC codes [J].Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition)，2020，32(1)：92-98.)
[3]Mateusz K，Wojciech S，Dariusz K.FPGA-oriented LDPC decoder for cyber-physical systems [J].Mathematics，2020，8(5)：44-48.
[4]刘华军.LDPC码ADMM译码简单混合投影算法及其硬件实现研究 [D].武汉：华中师范大学，2020.
(LIU Hua-jun.Research on simple Hybrid projection algorithm for ADMM decoding of LDPC codes and its hardware implementation [D].Wuhan：Central China Normal University，2020.)
[5]邓熠.基于短码的LDPC译码算法改进研究及FPGA实现 [D].重庆：西南大学，2020.
(DENG Yi.Research on improvement of LDPC decoding algorithm based on short code and FPGA implementation [D].Chongqing：Southwest University，2020.)
[6]Wang Z X，Liu B J，Zhang M，et al.Research on encoding and decoding algorithms of non-binary LDPC code and FPGA implementation [J].Journal of Computational Methods in Sciences and Engineering，2019，20(1)：167-175.
[7]Cheng K，Shen Q，Liao S K，et al.Implementation of encoder and decoder for LDPC codes based on FPGA [J].Journal of Systems Engineering and Electronics，2019，30(4)：642-650.
[8]王梦.基于流水线译码器结构的LDPC-CC码的译码算法研究与FPGA实现 [D].重庆：西南大学，2020.
(WANG Meng.Research on decoding algorithm and FPGA implementation of LDPC-CC code based on pipeline decoder structure [D].Chongqing：Southwest University，2020.)
[9]杨涛宇.超高清视频无线传输用LDPC编译码器的研究与实现 [D].成都：电子科技大学，2020.
(YANG Tao-yu.Research and implementation of LDPC codec for ultra HD video wireless transmission [D].Chengdu：University of Electronic Science and Technology，2020.)
[10]Yann D，Bertrand L G，Crenne J，et al.Model-based design of flexible and efficient LDPC decoders on FPGA devices [J].Journal of Signal Processing Systems，2020，92：727-745.
[11]李剑凌，陈斌杰.基于最小和算法的QC-LDPC译码器的FPGA实现 [J].应用科技，2020，47(5)：35-40.
(LI Jian-ling，CHEN Bin-jie.FPGA implementation of QC-LDPC decoder based on minimum sum algorithm [J].Applied Technology，2020，47(5)：35-40.)
[12]徐斌，贺玉成.高吞吐率QC-LDPC码分层译码设计 [J].计算机工程，2019，45(7)：121-125.
(XU Bin，HE Yu-cheng.Hierarchical decoding design of high throughput QC-LDPC codes [J].Computer Engineering，2019，45(7)：121-125.)
[13]邱丽鹏.分层全并行QC-LDPC码译码器的研究与实现 [D].泉州：华侨大学，2017.
(QIU Li-peng.Research and implementation of hiera-rchical fully parallel QC-LDPC decoder [D].Quan-zhou：Overseas Chinese University，2017.)
[14]Çalan A，Balc
soy E，Kaya E，et al，FPGA implementa-tion of layered low density parity check error correction codes [C]//Proceedings of the 2017 25th Signal Processing and Communications Applications Conference.Antalya，Turkey，2017：1-4.