由永磁直线同步电机(PMLSM)驱动的H型平台可以在平面实现二维高频运动,广泛应用于数控机床、精密测量和激光打印行业中[1-2].但直驱H型平台三轴之间的机械耦合会影响轮廓控制精度[3],此外,在实际工作中,横梁上工作台频繁加减速运动会对系统动态、稳态性能造成影响,从而增加系统机械耦合程度,大大降低控制精度[4].为提高直驱H型平台的轮廓控制精度,需要采用合理的解耦控制策略解决机械耦合问题,同时选用具有强鲁棒性的控制器抑制不确定性问题,从而实现平台的精密控制.
为提高直驱H型平台跟踪精度,Chen等[5]提出轴间协调运动与冗余执行器同步相结合的轮廓控制方法.该方法在轮廓误差计算中引入转角进行了相应的修正,提高轮廓跟踪性能,但该方法在建立动力学模型时进行了近似估计,仅适合转角较小的情况[6].王丽梅等[7]针对直驱H型平台直线电机参数变化和扰动等不确定因素的影响,建立了含不确定集的直驱H型平台的数学模型,然后在此模型基础上提出了交叉耦合模糊PID控制方法,从而提高了系统的跟踪性和鲁棒性,但该方法在建立模型过程中忽略了机械耦合的影响.
针对运动平台机械耦合对轮廓控制的影响,一些学者通过解耦轮廓误差模型进行控制.Chen等[8]通过将轮廓误差解耦成切线误差和等效轮廓误差进行控制,能够克服跟踪精度不高对轮廓控制的影响.为解决由于轮廓误差累积,系统出现收敛速度降低甚至发散这一问题,王丽梅等[9]提出一种与经验模态分解算法相结合的交叉耦合迭代学习控制方法.该方法首先通过设计交叉耦合迭代学习控制降低轮廓误差,然后利用经验模态学习算法分解控制过程中的轮廓误差,提高系统收敛速度和轮廓精度.
为解决多输入、多输出系统耦合程度高、难控制的问题,肖友刚等[10]利用线性扩张观测器对系统的耦合部分、非线性部分及扰动部分进行估计并补偿,实现各环节的自解耦,但其对整体系统缺乏宏观的解耦控制.许伟[11]将反馈线性化控制策略应用到永磁同步电动机这一强耦合、非线性的系统中,获得精确的控制性能.屈高敏等[12]将反馈线性化解耦理论应用到无人机姿态控制系统中,很好地实现了各自由度之间的解耦,并保证了系统的响应速度.虽然反馈线性化解耦在精密控制上有一系列的成果,但其对于直驱H型平台应用成果却相对较少.
为解决直驱H型平台的机械耦合问题,提高轮廓控制精度,本文设计了基于反馈线性化解耦的轮廓控制算法.采用反馈线性化理论设计解耦控制律,将耦合动力学模型分解为独立的单输入单输出系统.设计了滑模控制器克服系统干扰和未建模动态等不确定性的影响,进一步提高解耦模型的鲁棒性和轮廓跟踪性能.
1 直驱H型平台动力学模型
直驱H型平台集总参数模型如图1所示.其中,y1、y2为平行轴的实际位置,la为横梁长度,θ为横梁与水平位置夹角,x1为工作台到横梁中点的距离(此处忽略了扭转引起的横梁的水平误差),ma为横梁质量(包括y轴电机动子),me为x轴滑动块质量,d为滑动块到横梁中心线的垂直距离,Ja和Je分别为横梁和滑动块质心的旋转惯量,le为横梁上滑动块的长度.k1和k2为扭转刚度系数,μgx、μg1和μg2为x轴、y1和y2轴的粘滞摩擦系数,cx、c1和c2为x轴、y1和y2轴的库伦摩擦系数.
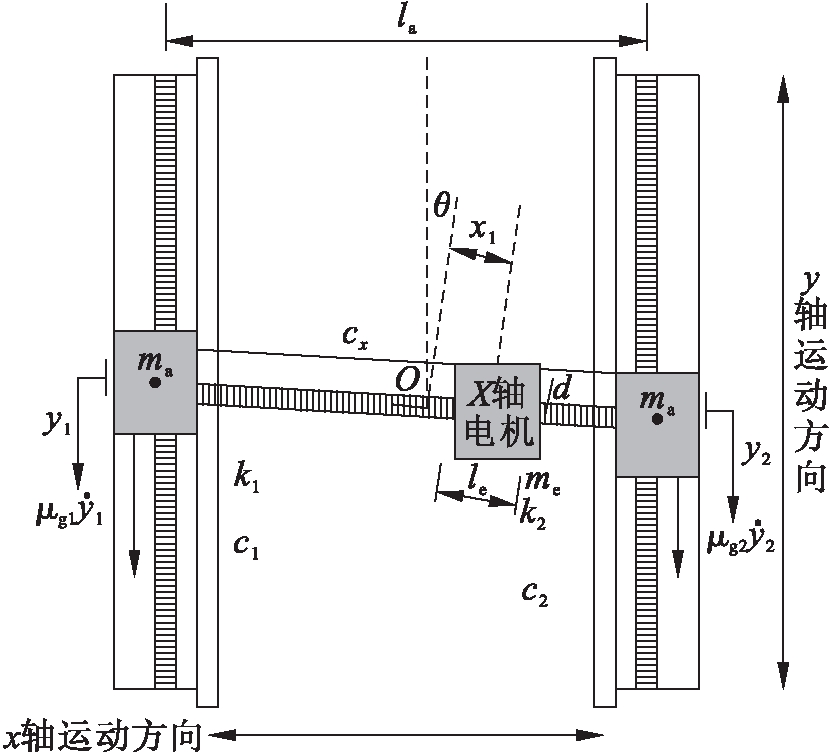
图1 直驱H型平台集总参数模型
Fig.1 Lumped-parameter model of direct drive H-type platform
定义q=[x1,y1,θ],则直驱H型平台的动力学模型[13]可表示为
(1)
式中:M为惯性矩阵;B为摩擦力系数矩阵;K为刚度矩阵;D为前馈余项;Q为相对广义力矩阵.各项分别表示为
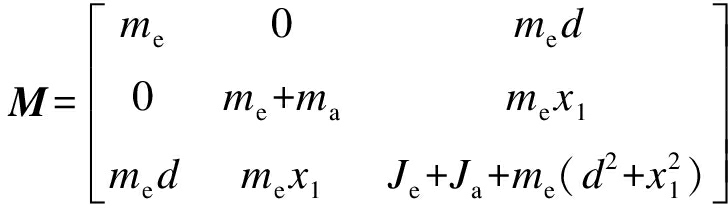
(2)
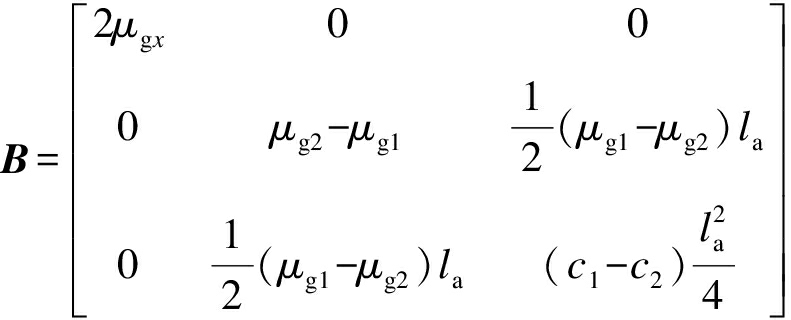
(3)
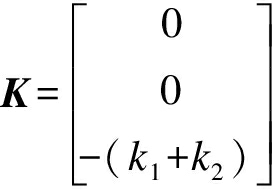
(4)
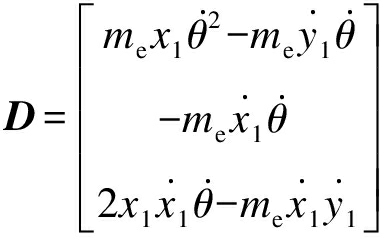
(5)
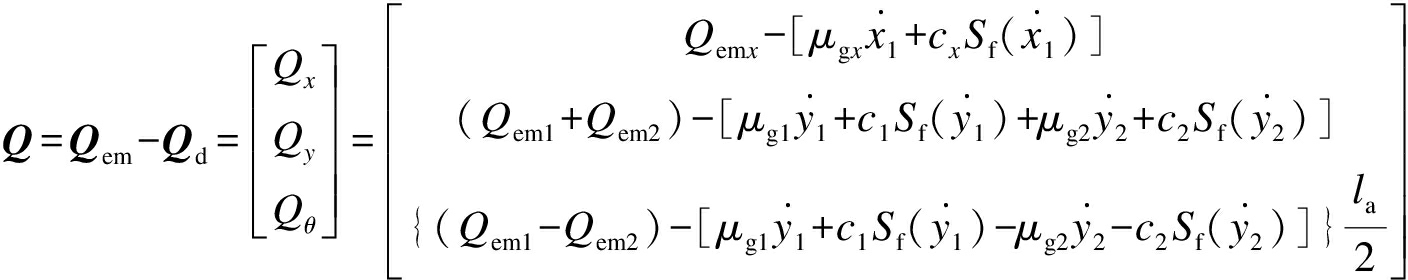
(6)
式中:Qem为在各个自由度上的驱动力;Qd为在各自由度上的阻力;Sf(·)为近似于sgn(·)的连续函数.
根据式(1)可以看出,直驱H型平台动力学模型中的质量矩阵为非对角矩阵,因此,直驱H型平台各个自由度之间存在动力学耦合现象.工作台运动过程中,各轴之间相互作用,影响轮廓控制性能.
2 控制器设计
2.1 反馈线性化解耦理论
为确保系统完全解耦,需使系统每一个输出被一个输入单独控制.一般情况下,多输入多输出非线性系统[14]可描述为
(7)
式中:X∈R2n为状态向量;u∈Rn为控制向量;Y∈Rn为输出向量;f(·)∈R2n、h(·)∈Rn×2n、g(·)∈R2n×n为X的函数,其中,n为伺服系统的自由度.
根据李导数定义,引入李导数算子L.对于平衡点X0,该非线性系统具有相对阶Oi,如果存在:对所有X(X属于X0的一个邻域)以及i,j∈n,k<Oi-1,均有
(8)
且n×n矩阵P(X)在平衡点X0处非奇异,P(X)可表示为
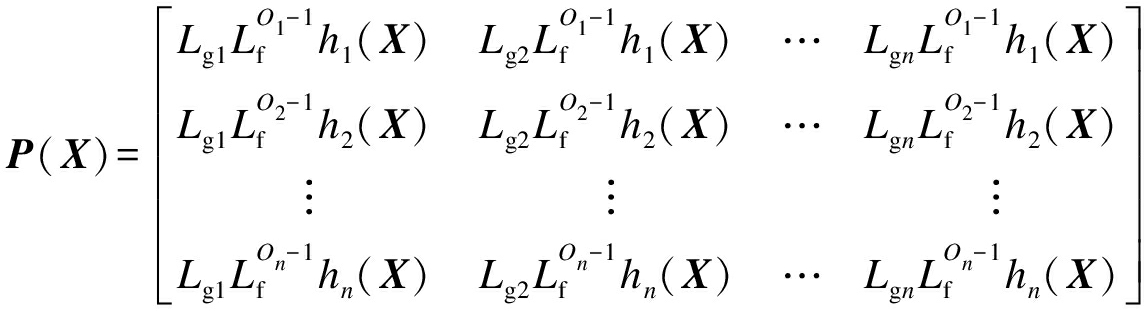
(9)
则系统在控制律u(X)=-P-1(X)b(X)+P-1(X)v的作用下可解耦为基于控制律v的线性系统,v=[v1,v2,v3]T为滑模控制器输出,且
(10)
2.2 直驱H型平台反馈线性化解耦
通过式(1)和(6)可知
(11)
令![]() 定义
定义![]() 在三直线电机直驱H型平台中,n=3,将式(11)表示成式(7)的形式,其中
在三直线电机直驱H型平台中,n=3,将式(11)表示成式(7)的形式,其中
f(X)=[X2,f1(X)X4,f2(X)X6,f3(X)]T
(12)
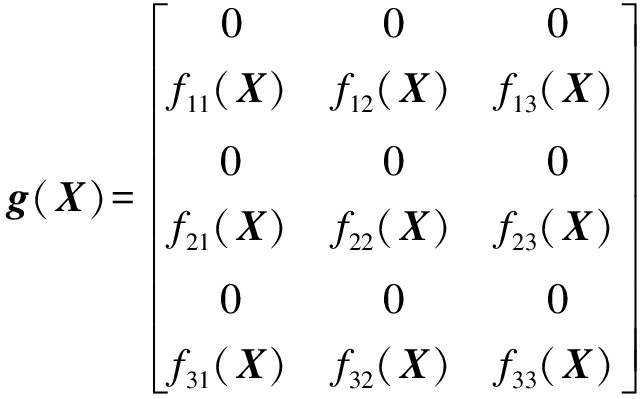
(13)
式中:f1(X),f2(X),f3(X)为x1,y1,θ的耦合函数,则系统输出表示为
Y=[x1,y1,θ]T
(14)
由式(11)可将式(12)、(13)进一步表示为
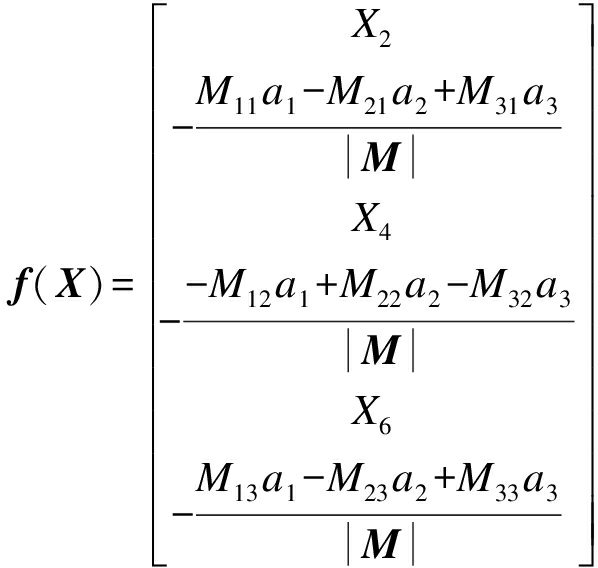
(15)

(16)
由于Lg1h2(X),Lg1h3(X),…,Lg3h3(X),Lg3h1(X)皆为零,满足
(17)
同理,Lfh2=X3,Lfh3=X6,则
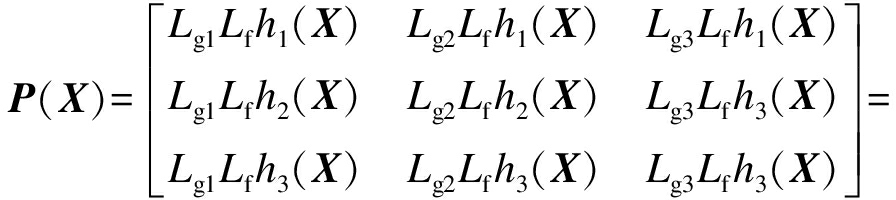
M-1
(18)
由于P(X)为非奇异矩阵,可知该系统的相对阶Oi=2,则
Z(X)=P-1(X)=
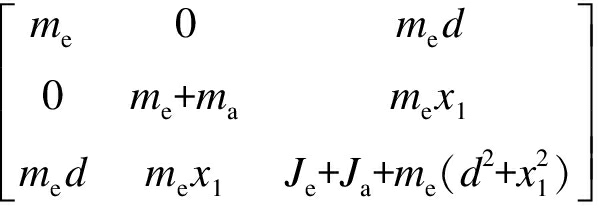
(19)
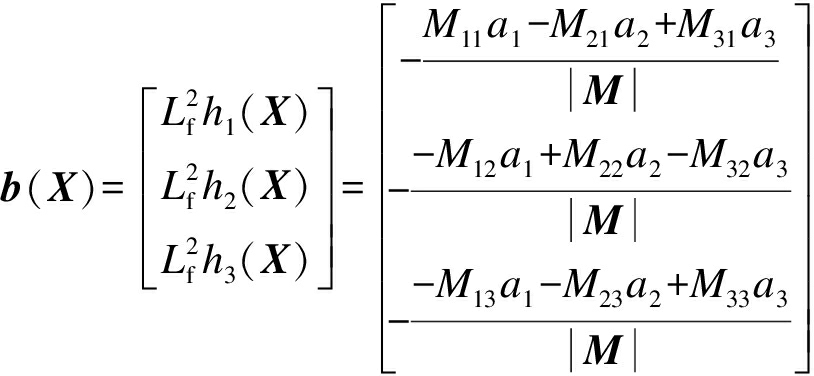
(20)
令
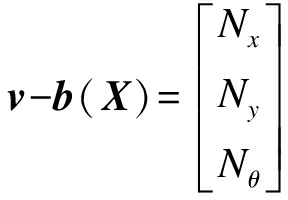
(21)
由式(19)~(21)可知解耦控制律的表达式为
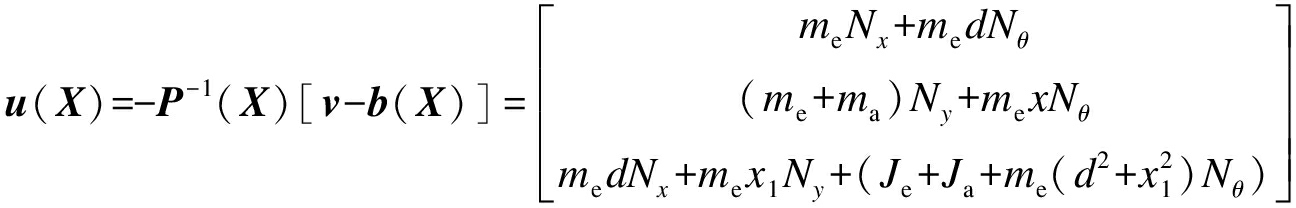
(22)
由式(22)可以看出,多输入多输出的耦合系统通过反馈线性化理论将耦合动力学模型分解为独立的单输入单输出系统,避免了H型平台运行过程中各自由度之间存在耦合而影响轮廓控制精度.
2.3 滑模控制器设计
由于解耦后的系统存在参数变化、外部扰动等不确定项,因此算法必须具备较强鲁棒性.滑模控制对外部扰动和系统参数摄动具有强鲁棒性,有助于减弱反馈线性化控制策略对精确参数的依赖性.本文在控制器设计上采用滑模控制策略,从而实现系统的鲁棒控制.选取线性滑模面为
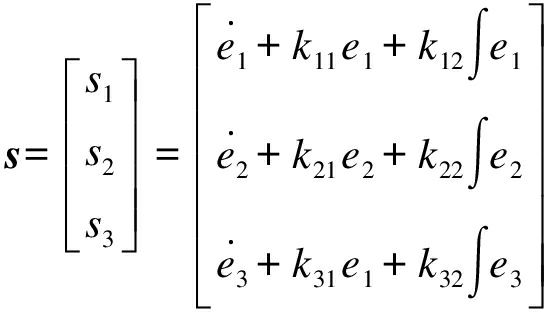
(23)
式中:e1=xd-x为x轴跟踪误差;e2=yd-y为y轴跟踪误差;e3=θd-θ为横梁与水平之间夹角的误差;k11、k12、k21、k22、k31、k32为正常数;xd、yd、θd为参考输入信号.
令![]() 求得等效控制veq为
求得等效控制veq为
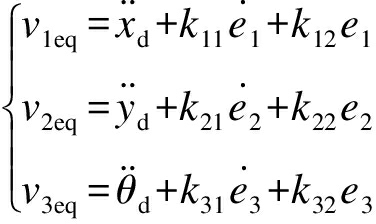
(24)
根据特定的趋近律来设计滑模控制,既能减小抖振又能保持系统的鲁棒性,本文采用指数趋近律vs进行设计,可得
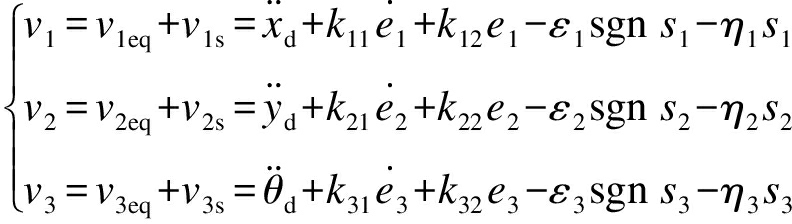
(25)
式中:ε1、ε2、ε3和η1、η2、η3均为正常数;sgn为符号函数.
针对x轴伺服系统,取Lyapunov函数![]() 则
则
s1[-ε1sgn(s1)-η1s1]=
(26)
根据Lyapunov稳定性理论,当s1≠0时,![]() 是负定的,表明Lyapunov函数s1是收敛的,可以确保系统状态在有限时间内到达滑模面,并将按指数规律趋向原点稳定.同理可证,y轴闭环控制系统也是稳定的.将式(25)代入式(22),得到状态反馈律.
是负定的,表明Lyapunov函数s1是收敛的,可以确保系统状态在有限时间内到达滑模面,并将按指数规律趋向原点稳定.同理可证,y轴闭环控制系统也是稳定的.将式(25)代入式(22),得到状态反馈律.
直驱H型平台反馈线性化滑模解耦控制系统框图如图2所示,虚框内为平台解耦后线性系统.
3 实验结果与分析
3.1 实验系统总体结构及参数
本文实验系统如图3所示,主要由上位机、多轴直线电机运动平台控制箱及多轴运动控制平台构成.实验平台及控制器参数如表1、2所示.实验中控制器参数均是经过多次调试选取而得,以保证系统的动、静态性能.
3.2 实验研究
为验证基于反馈线性化解耦滑模轮廓控制算法的可行性和有效性,针对本文提出的解耦控制方法,分别采用PID控制策略及滑模控制策略对解耦前后系统性能进行分析.
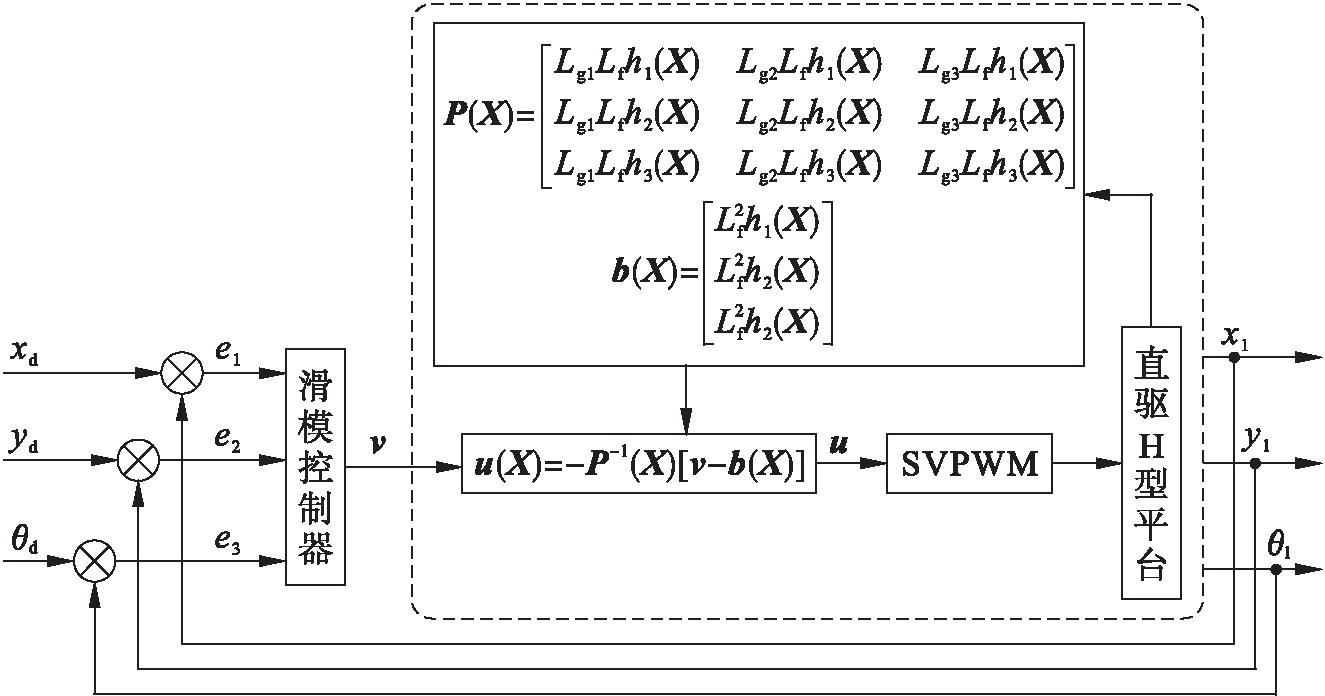
图2 反馈线性化滑模解耦控制结构图
Fig.2 Structure diagram of feedback linear sliding mode decoupling control

图3 实验系统图
Fig.3 Image of experimental system
表1 实验平台参数
Tab.1 Parameters of experimental platform
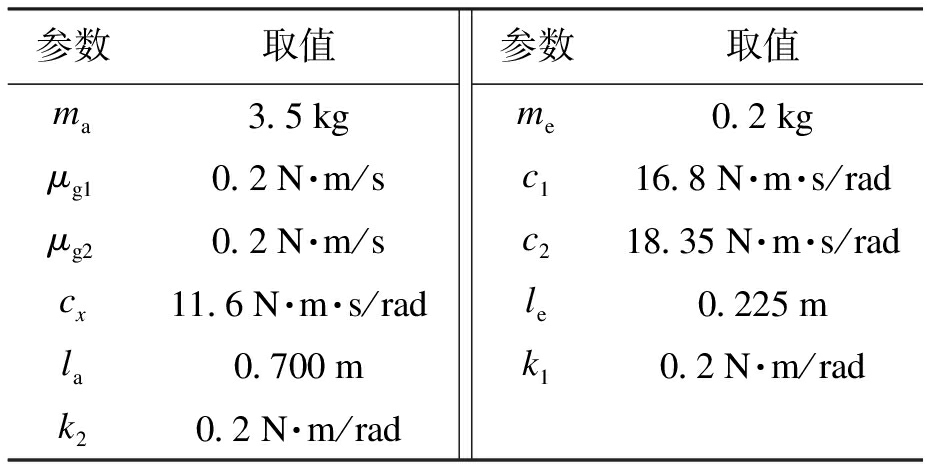
参数取值ma3.5kgμg10.2N·m/sμg20.2N·m/scx11.6N·m·s/radla0.700mk20.2N·m/rad参数取值me0.2kgc116.8N·m·s/radc218.35N·m·s/radle0.225mk10.2N·m/rad
表2 控制器参数
Tab.2 Parameters of controller
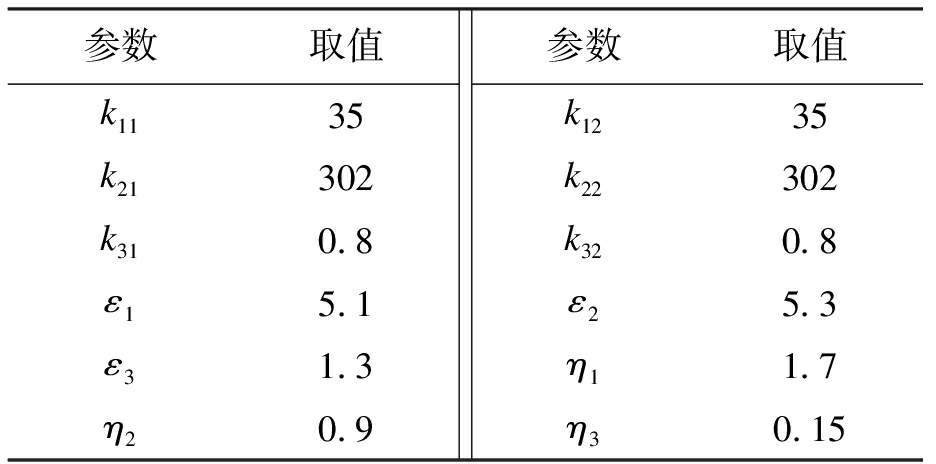
参数取值k1135k21302k310.8ε15.1ε31.3η20.9参数取值k1235k22302k320.8ε25.3η11.7η30.15
3.2.1 单轴跟踪精度对比
直驱H平台给定输入信号为r1=20sin(2πt) mm,r2=20cos(2πt) mm,即给定输入轨迹为圆形轨迹.
实验1:在空载条件下进行单轴的轨迹跟踪实验.基于PID控制器的位置跟踪响应曲线如图4所示.系统解耦前的位置跟踪误差大约在-12.2~12.5 μm,解耦后的误差有所减小,大约为-4.8~4.8 μm.这表明在空载状态下,本文采用的解耦算法可行有效,将跟踪误差减小了58.33%,保证了直驱H平台单轴电机的位置跟踪精度,明显提高跟踪性能.
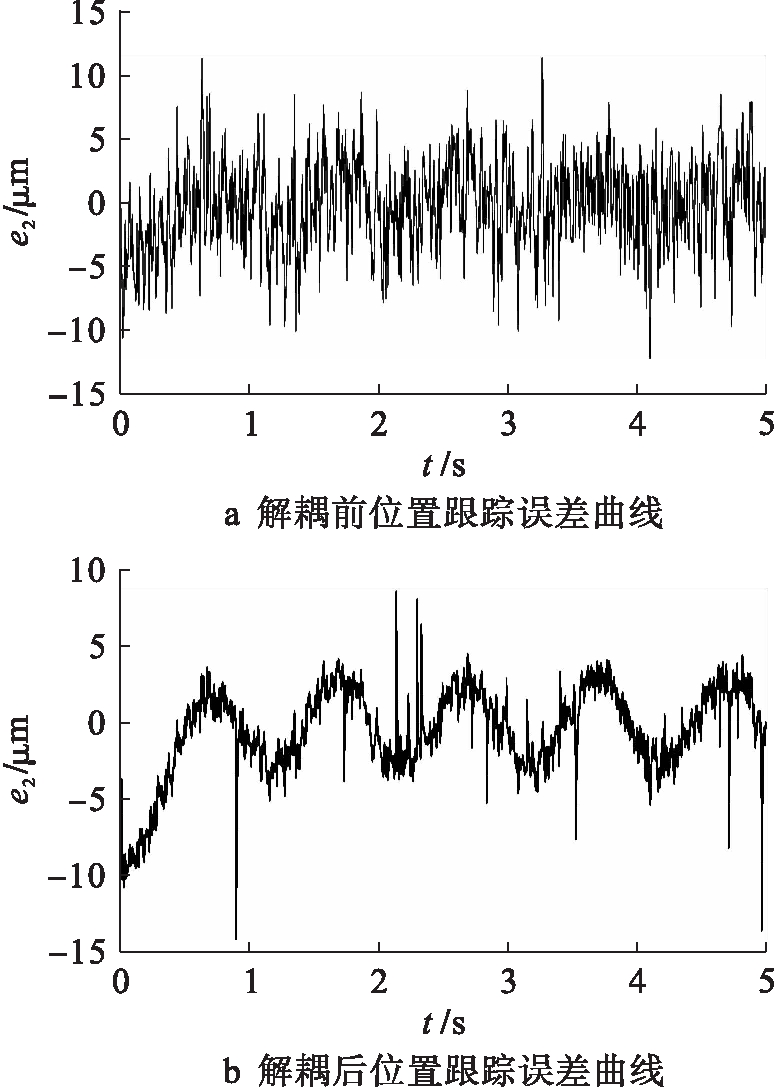
图4 基于PID控制器的y轴电机位置响应曲线
Fig.4 Position response curve of y-axis motor based on PID controller
实验2:由于系统存在参数变化、外部扰动等不确定项的影响,需要控制器具有较强的鲁棒性.在3 s时对系统突加50 N的负载扰动,基于滑模控制的单轴电机位置响应曲线如图5所示.在突加负载扰动时,解耦前的位置跟踪误差约为7.8 μm,而解耦后的误差约为4.2 μm,且在更短的时间内恢复稳定,具有较快的响应速度.对比图4、5两种方法下的位置跟踪误差响应曲线可以看出,尽管存在负载扰动,滑模控制下的系统仍然具有较小的跟踪误差,且解耦后的系统跟踪精度较高.这表明本方法不但可以保证系统单轴跟踪精度,还对不确定性具有较强的鲁棒性.
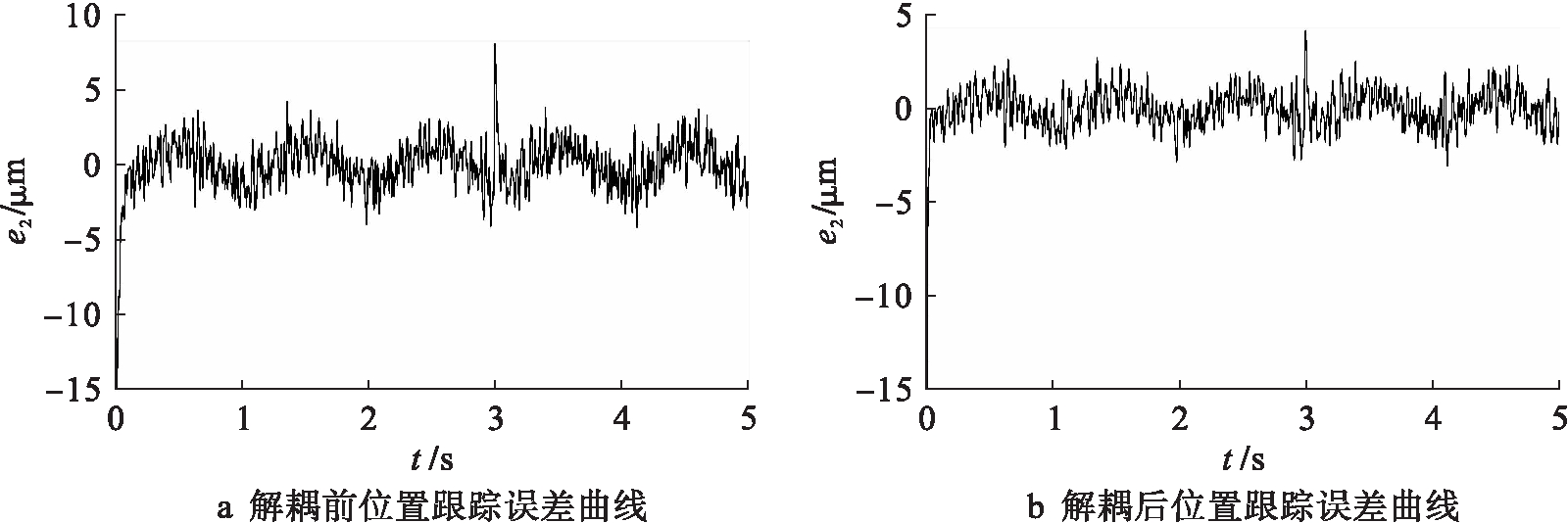
图5 基于滑模控制的y轴电机位置响应曲线
Fig.5 Position response curve of y-axis motor based on sliding mode control
3.2.2 轮廓误差对比
为验证解耦后系统的轮廓跟踪精度,在实验2所述的情况下,解耦前后基于滑模控制的H型平台轮廓误差曲线如图6所示.系统解耦前的轮廓误差约为-1.3~2.1 μm,而在解耦后系统轮廓误差约为-0.7~0.9 μm,相比于解耦前的系统,轮廓跟踪精度大大提高.
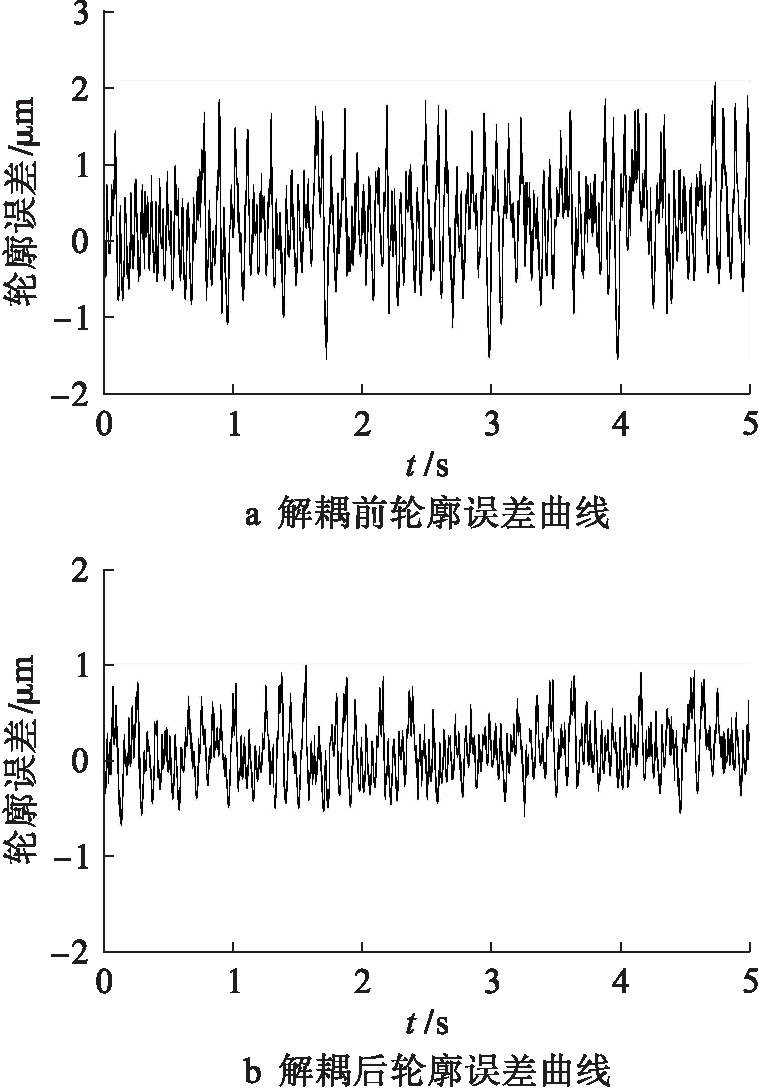
图6 基于滑模控制的H型平台轮廓误差曲线
Fig.6 Contour error curve of H-type platform based on sliding mode control
此外,将本文设计的轮廓控制方法与文献[7]的交叉耦合迭代学习轮廓控制方法进行对比.在相同的输入信号下,交叉耦合迭代学习轮廓控制的轮廓误差曲线如图7所示.从图7可以看出,该方法控制下的直驱H型平台轮廓跟踪误差大约在-1.3~1.5 μm之间波动,同图6b相比,轮廓误差稍大.这表明,对直驱H型平台进行反馈线性化解耦可以很好地改善轮廓跟踪精度.
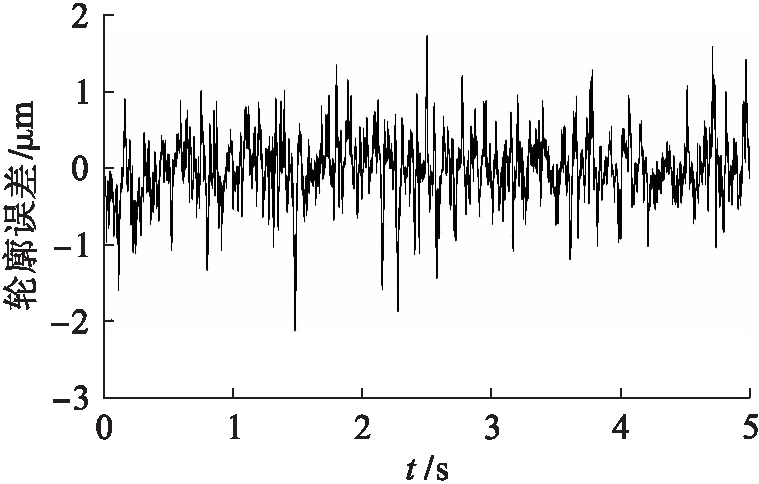
图7 基于经验模态分解法交叉耦合迭代学习控制的H型平台轮廓误差曲线
Fig.7 Contour error curve of H-type platform based on cross coupling and iterative learning control of empirical mode decomposition method
4 结 论
本文针对多输入多输出直驱H型平台的轮廓控制问题,设计了基于动力学耦合模型的反馈线性化解耦控制器;同时,利用滑模控制解决系统存在的外部扰动等不确定影响,保证系统的鲁棒性.通过实验表明,基于反馈线性化解耦的直驱H型平台滑模轮廓控制方法可以有效解决机械耦合问题,克服不确定性对系统的影响,进而提高了系统的轮廓跟踪精度和鲁棒性.
[1]郭庆鼎,王成元.直线交流伺服系统的精密控制技术 [M].北京:机械工业出版社,2000.
(GUO Qing-ding,WANG Cheng-yuan.Precision control technology of linear AC servo system [M].Beijing:China Machine Press,2000.)
[2]张康,王丽梅.基于融合误差的直驱H型平台自适应全局滑模轮廓控制 [J].中国电机工程学报,2020,40(16):5337-5345.
(ZHANG Kang,WANG Li-mei.Adaptive global sliding mode contour control of direct drive H-type platform based on integrated error [J].Proceedings of the CSEE,2020,40(16):5337-5345.)
[3]孙宜标,王亚朋,刘春芳.永磁直线电机自适应区间二型模糊滑模控制 [J].沈阳工业大学学报,2017,39(6):601-606.
(SUN Yi-biao,WANG Ya-peng,LIU Chun-fang.Adaptive interval type-2 fuzzy sliding mode control for permanent magnet linear motor [J].Journal of Shenyang University of Technology,2017,39(6):601-606.)
[4]Ivan G H,Xanier K,Julien G,et al.Model-based decoupling control method for dual-drive gantry stages:a case study with experimental validations [J].Control Engineering Practice,2013,21(3):298-307.
[5]Chen Z,Li C,Yao B,et al.Integrated coordinated/synchronized contouring control of a dual-linear-motor-driven gantry [J].IEEE Transactions on Industrial Electronics,2020,67(5):3944-3954.
[6]郑伟勇,李艳玮,周兵.两自由度机械手臂的交叉耦合模糊逻辑控制 [J].沈阳工业大学学报,2019,41(3):326-331.
(ZHENG Wei-yong,LI Yan-wei,ZHOU Bing.Cross-coupling fuzzy logic control for two-degree-of-freedom robotic arm [J].Journal of Shenyang University of Technology,2019,41(3):326-331.)
[7]王丽梅,张宗雪.H型精密运动平台交叉耦合模糊PID同步控制 [J].沈阳工业大学学报,2018,40(1):1-5.
(WANG Li-mei,ZHANG Zong-xue.Cross-coupled fuzzy PID synchronous control for H-type precision motion platform [J].Journal of Shenyang University of Technology,2018,40(1):1-5.)
[8]Chen S L,Wu K C.Contouring control of smooth paths for multi-axis motion systems based on equivalent errors [J].IEEE Transaction on Control Systems Technology,2007,15(6):1151-1158.
[9]王丽梅,孙璐.基于经验模态分解算法的直驱XY平台交叉耦合迭代学习控制 [J].中国电机工程学报,2016,36(17):4745-4753.
(WANG Li-mei,SUN Lu.Cross-couple iterative learning control of direct drive XY table based on an empirical mode decomposition algorithm [J].Proceedings of the CSEE,2016,36(17):4745-4753.)
[10]肖友刚,卢浩.一类非线性MIMO系统的自解耦控制 [J].哈尔滨工业大学学报,2020,52(9):129-136.
(XIAO You-gang,LU Hao.Self-decoupling control for a class of nonlinear MIMO systems [J].Journal of Harbin Institute of Technology,2020,52(9):129-136.)
[11]许伟.基于微分几何的汽车主动悬架模糊PID控制研究 [J].汽车实用技术,2019(9):77-81.
(XU Wei.Research on fuzzy PID control of vehicle active suspension based on differential geometry [J].Automotive Practical Technology,2019(9):77-81.)
[12]屈高敏,李继广.基于微分几何方法的飞翼无人飞行器解耦飞行控制 [J].弹箭与制导学报,2018,38(2):116-122.
(QU Gao-min,LI Ji-guang.Decoupling flight control of flying wing unmanned aerial vehicle based on differential geometry method [J].Journal of Missile and Guidance,2018,38(2):116-122.)
[13]罗品奎.双直线电机驱动的H型运动平台控制研究 [D].武汉:华中科技大学,2013.
(LUO Pin-kui.Research on H-type motion platform control driven by double linear motor [D].Wuhan:Huazhong University of Science,2013.)
[14]孙云鹏,蓝益鹏,徐泽来,等.数控机床直线同步电动机磁悬浮系统反馈线性化控制的研究 [J].制造技术与机床,2021(10):133-139.
(SUN Yun-peng,LAN Yi-peng,XU Ze-lai,et al.Research on feedback linearization control of magnetic levitation system of linear synchronous motor for CNC machine tool [J].Manufacturing Technology & Machine Tool,2021(10):133-139.)