居民用电的短期负荷预测在电力系统运行中具有重要意义，准确的负荷预测有利于电力市场各方进行交易获利，也便于市场资产的所有者安排生产运营[1-3].经典的负荷预测方法主要通过时间序列建模或模式识别技术完成[4-5].其他算法还包括但不局限于将人工神经网络和模糊专家系统相结合，形成短期负荷预测混合模型[6].算法首先通过人工神经网络提供临时预测，然后由模糊专家系统进行修正[7-8].
近些年，相关研究对传统算法进行了改进，一方面侧重于对多种预测方法的融合，例如Jelena[9]结合3种不同模糊神经网络模型来评估其负荷预测性能；Wang等[10]结合遗传算法和神经网络的短期负荷进行预测，通过遗传算法优化神经网络的参数学习性能，缩短网络的整体训练时间，克服了神经网络算法容易陷入局部最优解的弊端.另一方面，学者依靠先进的计量基础设施，例如通过智能电表进行双向通信和实时电力分析[11-12]，从用户的智能仪表端获取实时测量数据，从而提供更准确的负载预测.然而，大量数据的获取、传输及计算也增加了负荷预测的成本，因此，必须选择适当的测量采样率，以便在合适的数据量下得到所需的预测精度.
本文研究了智能电表的短期负荷预测，使用成型滤波和卡尔曼滤波相结合的算法对居民用电负荷进行预测，并分析测量采样率对预测误差的影响.
1 预测方法
将住宅负荷分为两个独立分量：天气相关分量和生活方式分量.计算方式借鉴了将电力负荷分解为气象敏感和非气象敏感两部分的处理想法[13].生活方式分量部分是负荷的决定性部分，主要取决于居民日常生活的能量消耗.天气相关分量是高斯噪声信号，主要影响空调、新风等负荷.从测量的历史消耗数据中减去住宅负荷的确定性部分，留下一个零均值随机信号，依据后续提及的频谱确定成型滤波器.
1.1 谱分析
采用谱分析方法对住宅负载的随机波动进行建模是一种经典方法，常规方式包括将时间序列建模与专家算子知识相结合的短期负荷预测以及直接适用高斯过程、非高斯过程的短期负荷预测模型辨识[14].假设住宅负荷数据分量随机服从一个高斯
马尔可夫过程模型，本文利用最小二乘法得到住宅负荷数据随机分量的功率谱密度函数.状态空间模型表示为
(1)
Y=αX+V(t)
(2)
式中：α和β为常数；U为单位白噪声输入；X为状态向量；Y为测量值；V为单位高斯白噪声测量值.
1.2 卡尔曼滤波
随机系统的动态行为由简化状态向量和输出向量描述，即
X(t+1)=ΦX(t)+V1(t)
(3)
Y(t)=AX(t)+V2(t)
(4)
式中，Φ、A为状态转换关系矩阵.噪声变量V1(t)与V2(t)是独立的零均值高斯噪声及其协方差矩阵，进一步可得
(5)
式中：δ(k，l)为克罗内克符号；Q为过程噪声协方差矩阵；R为测量噪声协方差矩阵.
卡尔曼滤波是一种递归预测算法，给定初始状态估计
和初始误差协方差矩阵P(0)，本文使用测量矩阵C与测量噪声协方差计算卡尔曼增益，即
K(t)=P(t)CT[CP(t)CT+R]-1
(6)
更新后估计的误差协方差矩阵为
[I-K(t)C]P(t)[I-K(t)C]T+
K(t)RKT(t)
(7)
使用状态方程预测下一个状态，即
(8)
预测状态的误差协方差矩阵为
P(t+1)=ΦP(t)ΦT+Q(t)
(9)
重复校正和预测以产生一系列状态估计，这种渐进分析预测的方法实际上属于一种依据不同阶段进行预测分析的技巧.已有学者提出基于混合模糊神经网络的负荷预测器，方法分为3个阶段：1)利用增长趋势和必要的补偿，将历史负荷更新为当前负荷需求；2)使用Kohonen自组织映射来映射负载配置文件；3)神经网络与模糊并行处理器利用输入变量(如日类型、天气和假日接近度)来预测当前日的负荷.该更新调整的方式与卡尔曼滤波较为相似，本文算法通过卡尔曼滤波更新预测居民用电数据.
2 结果与讨论
本文通过某电网公司提供的居民负荷数据来评价方法的短期负荷预测性能，采集了某电网公司所属供电公司2019年春季500户居民的用电数据.图1实线显示了2019年4月15日一个住宅客户的15 min间隔负载分布图.负载数据被认为是确定性部分与随机部分之和，用一个10阶多项式拟合负荷曲线.采样点的时间间隔为15 min，采样点数为96，其拟合曲线如图1虚线所示.
用实测负荷减去多项式拟合得到的住宅荷载的天气相关分量，然后利用功率谱估计得到的天气相关分量计算成型滤波器.利用最小二乘法最小化误差，并计算高斯马尔科夫过程的功率谱密度参数.
根据2019年4月15日的居民住宅用电负荷数据，利用成型滤波器设计卡尔曼滤波器，预测2019年4月16日的负荷.需要注意的是，用于预测的日期必须具有与获得成型滤波器日期相似的气候特征.卡尔曼滤波的追踪数值均值范围为0.01～0.23 kW·h，滤波观测标准差为0.002 3～0.003 7 kW·h，滤波状态标准差为0.001～0.007 kW·h.作为计算过程中的一个典型示例，可以得到参见式(5)的矩阵数值
计算得到此时迭代生成的估计值
最终获得的测量负载与预测负载对比如图2所示.
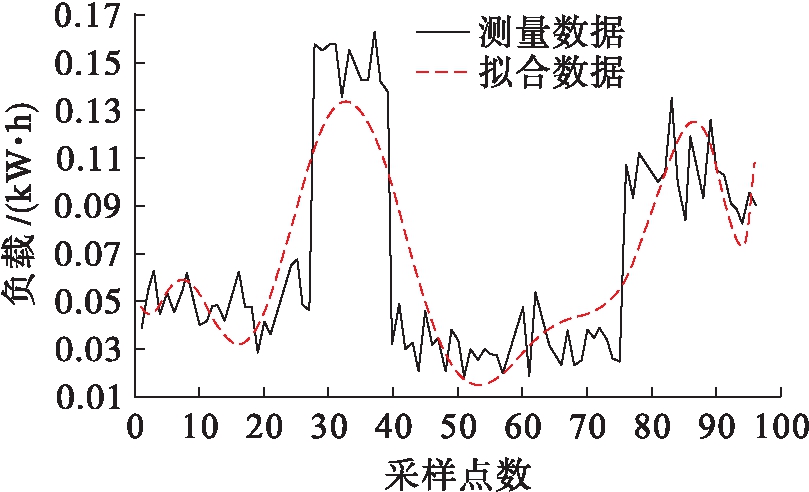
图1 实测负荷数据与拟合数据
Fig.1 Measured load data and fitting data
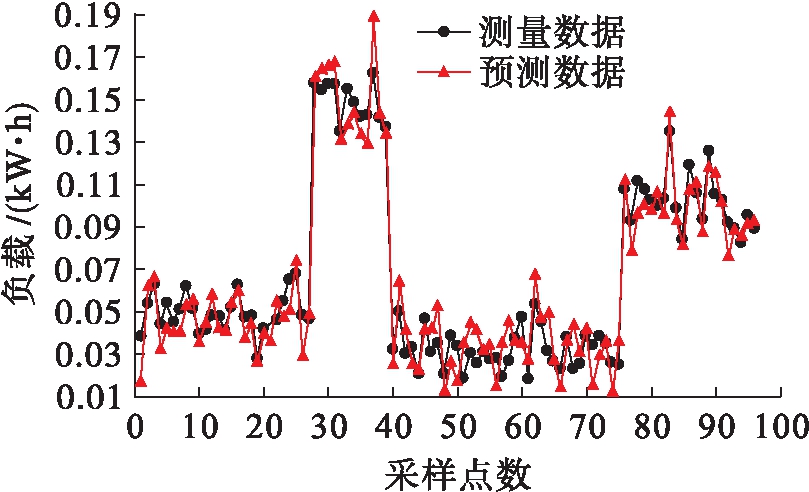
图2 15 min间隔下测量负载与预测负载对比
Fig.2 Comparison between measured and predicted loads at intervals of 15 min
智能电表的通信能力使实时测量数据的获取成为可能，为评价所提出的预测方法在不同采样周期和预测水平下的性能提供了机会.除了15 min的采样周期外，还需考虑更大的30 min和1 h采样周期.图3、4分别展示了30 min和1 h采样周期的住宅测量负载与预测负载对比情况.
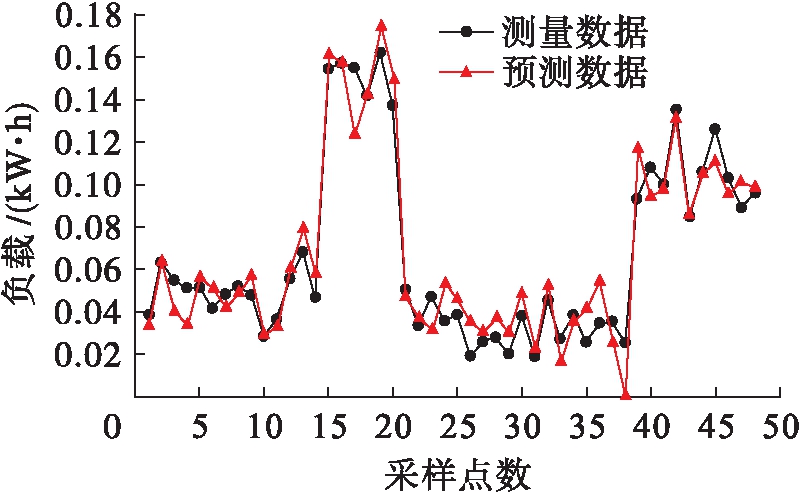
图3 30 min间隔下测量负载与预测负载对比
Fig.3 Comparison between measured and predicted loads at intervals of 30 min
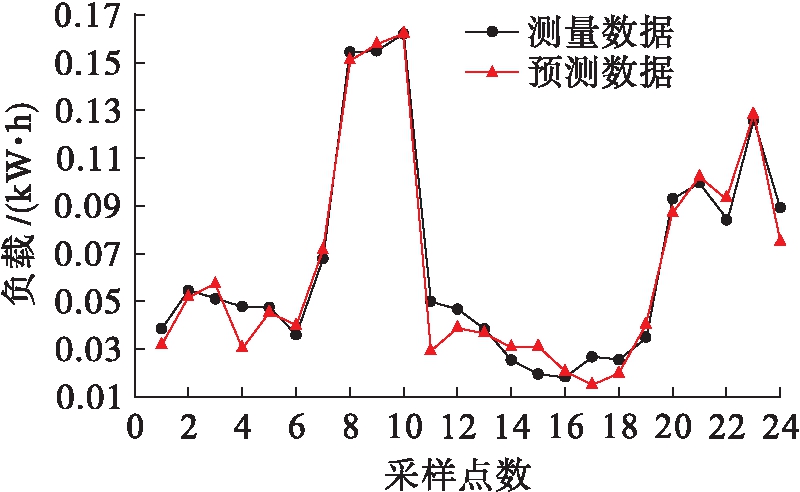
图4 60 min间隔下测量负载与预测负载对比
Fig.4 Comparison between measured and predicted loads at intervals of 60 min
对于30 min间隔预测，卡尔曼滤波的追踪数值均值范围为0～0.2 kW·h，滤波观测标准差为0.001 3～0.006 4 kW·h，滤波状态标准差为0.001 5～0.009 kW·h.可以得到矩阵数值
计算得到此时迭代生成的估计值
对于1 h间隔预测，卡尔曼滤波的追踪数值均值范围为0.012～0.18 kW·h，滤波观测标准差为0.002 3～0.01 kW·h，滤波状态标准差为0.003 5～0.01 kW·h.可以得到矩阵数值为
计算得到此时迭代生成的估计值
本文利用计算平均绝对百分比误差(MAPE)来评价预测精度，表1显示了不同采样周期和预测时段内的MAPE情况.
表1 不同采样周期和预测时段下的MAPE
Tab.1 MAPE at different sampling periods and prediction levels %
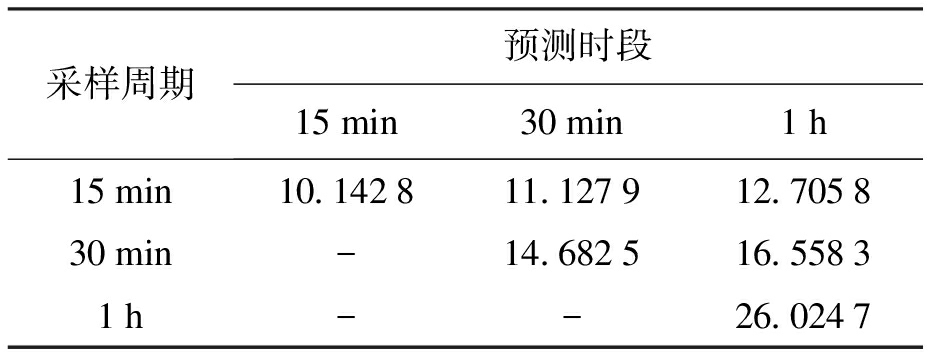
采样周期预测时段15min30min1h15min10.142811.127912.705830min-14.682516.55831h--26.0247
预测结果表明，在采样周期和预测时段均为1 h的情况下，负荷预测不准确，MAPE为26.024 7%.缩短从客户智能电表接收实时测量数据的时间间隔，可以提高方法的准确性，降低MAPE.在30 min、15 min的采样周期内，MAPE分别降低到16.558 3%和12.705 8%.然而，采样周期较短(15 min、30 min)会增加预测的计算负荷，因此，采样率的选择必须在精度与计算量之间进行权衡.
采样率对500户配电馈线预测精度和计算负荷的影响如图5所示.计算负荷是按顺序处理500个测量数据所需的总时间.由图5可以看出，当采样间隔为32 min时，计算效能和精度能够达到最优解.
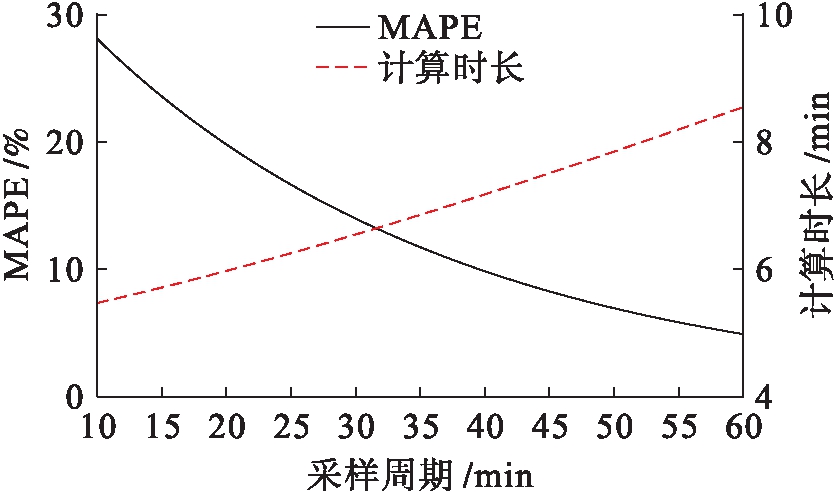
图5 采样率对预测精度和计算负荷的影响
Fig.5 Influence of sampling rate on prediction accuracy and calculation loads
3 结 论
随着智能电表的普及，住宅用户的短期负荷预测可以逐步实现.利用电网公司提供的数据，本文将一个住宅负荷表示为确定性分量和随机高斯扰动的总和，然后，利用卡尔曼滤波器对不同采样周期的住宅负荷进行预测，评估了不同采样周期下负荷预测的准确性.实验结果表明，虽然更快的采样率可以提供更多的实时测量数据，并能大幅度提高负荷预测的准确性，但额外的计算成本可能较高.因此，在限制用于预测的数据量同时，也需要达到预测精度，选择恰当的采样率或周期.
[1]杨德昌，赵肖余，何绍文，等.面向海量用户用电数据的集成负荷预测 [J].电网技术，2018，42(9)：2923-2929.
(YANG De-chang，ZHAO Xiao-yu，HE Shao-wen，et al.Aggregated load forecasting based on massive household smart meter data [J].Power System Technology，2018，42(9)：2923-2929.)
[2]陈璞迪.基于深度神经网络的电力负荷分析方法的研究与实现 [D].北京：北京邮电大学，2019.
(CHEN Pu-di.Research and implementation of power load analysis method based on deep neural network [D].Beijing：Beijing University of Posts and Telecommunications，2019.)
[3]黄宇腾，韩翊，赖尚栋.深度神经网络在配电网公变短期负荷预测中的应用研究 [J].浙江电力，2018，37(5)：1-6.
(HUANG Yu-teng，HAN Yi，LAI Shang-dong.Appli-cation of deep neural network in short-term load prediction of public transformer of power distribution network [J].Zhejiang Electric Power，2018，37(5)：1-6.)
[4]李媛，武岩岩，王思琪.基于混沌时间序列的Elman神经网络工业用电预测 [J].沈阳工业大学学报，2016，38(2)：196-200.
(LI Yuan，WU Yan-yan，WANG Si-qi.Elman neural network for forecasting industrial electricity consumption based on chaotic time series [J].Journal of Shenyang University of Technology，2016，38(2)：196-200.)
[5]翁国庆，朱双双，闫翠萍，等.基于模糊专家系统的电能质量治理决策支持系统 [J].浙江工业大学学报，2019，47(2)：210-218.
(WENG Guo-qing，ZHU Shuang-shuang，YAN Cui-ping，et al.Fuzzy expert system based decision support system for power quality control [J].Journal of Zhejiang University of Technology，2019，47(2)：210-218.)
[6]王栋，邵常宁，费建平，等.基于大客户和地方电厂数据管理预测平台的负荷还原预测方法研究 [J].浙江电力，2015，34(12)：11-15.
(WANG Dong，SHAO Chang-ning，FEI Jian-ping，et al.Research of load reduction forecasting method based on data management and forecasting platform of large-scale consumer and regional power plants [J].Zhejiang Electric Power，2015，34(12)：11-15.)
[7]刘南艳，贺敏，赵建文.基于大数据平台的电力负荷预测 [J].现代电子技术，2018，41(20)：153-156.
(LIU Nan-yan，HE Min，ZHAO Jian-wen.Power load prediction based on big data platform [J].Modern Electronics Technique，2018，41(20)：153-156.)
[8]陈本阳，张成刚，倪鸣，等.基于模糊信息粒化支撑向量机的电网负荷预测 [J].电子设计工程，2018，26(6)：56-59.
(CHEN Ben-yang，ZHANG Cheng-gang，NI Ming，et al.Power load forecasting based on fuzzy information granulation support vector machine [J].Electro-nic Design Engineering，2018，26(6)：56-59.)
[9]Jelena P.Forecasting demand flexibility of aggregated residential load using smart meter data [J].IEEE Transactions on Power Systems，2018，33(5)：5446-5455.
[10]Wang X W，Chen J X，Yuan R M，et al.OOK power model based dynamic error testing for smart electricity meter [J].Measurement Science & Technology，2017，28(2)：25-40.
[11]Ali A W，Wu J Z，Jenkins N.K-means based load estimation of domestic smart meter measurements [J].Applied Energy，2017，5：194-209.
[12]马立新，尹晶晶，郑晓栋.基于特征提取相似日的ELM短期负荷预测研究 [J].电子科技，2015，28(12)：22-25.
(MA Li-xin，YIN Jing-jing，ZHENG Xiao-dong.Short-term load forecasting based on daily feature extraction of similar days and ELM [J].Electronic Science and Technology，2015，28(12)：22-25.)
[13]宫毓斌，滕欢.基于GOA-SVM的短期负荷预测 [J].电测与仪表，2019，56(14)：12-16.
(GONG Yu-bin，TENG Huan.Short-term load forecasting based on GOA-SVM [J].Electrical Measurement & Instrumentation，2019，56(14)：12-16.)
[14]王增平，赵兵，纪维佳，等.基于GRU-NN模型的短期负荷预测方法 [J].电力系统自动化，2019，43(5)：53-62.
(WANG Zeng-ping，ZHAO Bing，JI Wei-jia，et al.Short-term load forecasting method based on GRU-NN model [J].Automation of Electric Power Systems，2019，43(5)：53-62.)