舰船在海上实战中不可避免要遇到鱼雷、水雷、深水炸弹等各种兵器的非接触爆炸攻击.当瞬态高能量冲击波作用于船体后,大部分能量传递到装舰的各种设备上,往往会对舰载设备造成致命的破坏[1-2].在现有冲击试验机能够提供的冲击环境情况下,为冲击试验机添加一种设备,使冲击试验机产生的冲击环境通过该设备放大后作用在被试设备上,以满足被试设备的抗冲击考核冲击载荷要求,这种设备称之为冲击放大器[3].研制性能优异、成本低廉、试验灵活的冲击放大器是开展冲击强化试验研究的一种简单有效的方法.对试验过程进行理论计算研究是此试验行之有效的基础.
Kelly等[3]研究了用于微小尺度元器件的高加速度冲击测试的速度放大器,利用多个连续冲击使被限制在垂直轴上运动的质量递减的系统来放大速度;Rodgers等[4]认为冲击放大器的研究工作主要焦点是通过多个质量之间的成对碰撞来实现速度放大的动力学分析.基于简单的刚体力学,提出了确定这种冲击放大器中间级数量和质量的基础理论.
1 二次冲击系统模型建立
1.1 试验方法原理介绍
利用二次冲击的冲击强化试验是在传统跌落冲击试验机上添加一个冲击放大器实现强化冲击环境的冲击试验[5-6],其结构原理如图1所示.
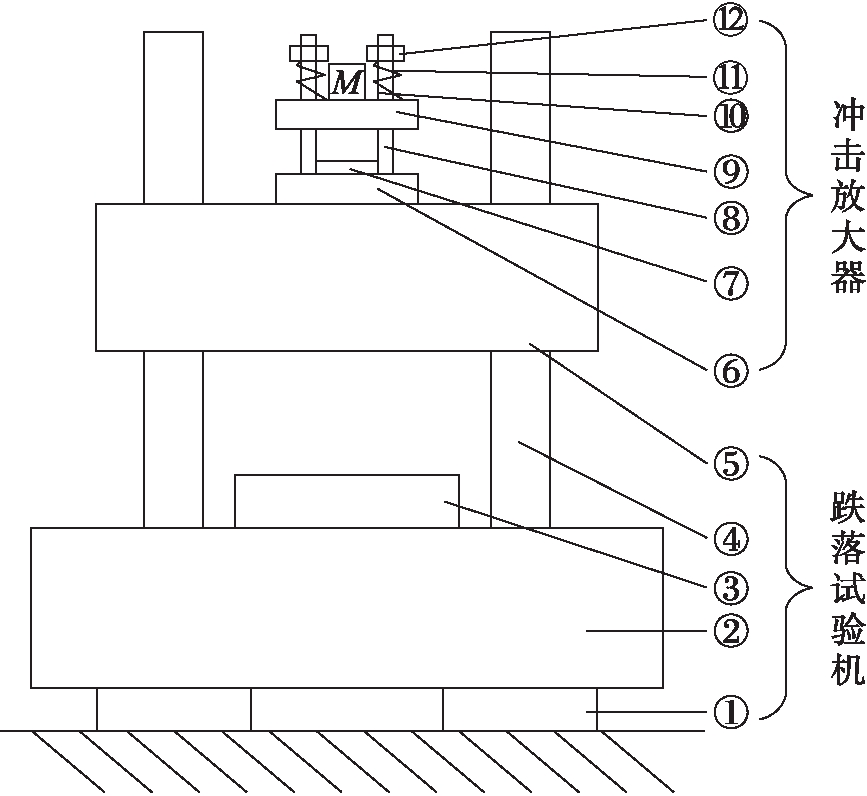
①基础支撑 ②跌落试验机基础 ③跌落试验机波形发生器 ④跌落台导向柱 ⑤跌落台 ⑥冲击放大器安装底座 ⑦冲击放大器波形发生器 ⑧冲击放大器台面导向柱 ⑨冲击放大器台面 ⑩被试件  冲击放大器台面悬挂弹簧
冲击放大器台面悬挂弹簧  悬挂弹簧安装块
悬挂弹簧安装块
图1 强化冲击试验原理图
Fig.1 Schematic principle of enhanced impact test
由图1可知,冲击强化试验原理图主要由跌落试验机和冲击放大器两部分构成.试验时,被试件安装在冲击放大器台面,冲击放大器安装在跌落试验机台面,跌落试验机台面提升至试验要求高度后释放,被试件、冲击放大器连同跌落试验机台面一起向下运动.这个过程冲击放大器台面与跌落试验机台面相对静止.直至跌落试验机台面与跌落试验机波形发生器发生碰撞形成一次冲击.在这个过程中,跌落试验机台面速度快速减小,并发生方向改变,开始向上运动,冲击放大器安装底座和冲击放大器波形发生器随跌落试验机台面向上运动;冲击放大器台面在悬挂弹簧作用下继续减速向下运动.当参数设计合理时,冲击放大器台面将会与冲击放大器波形发生器发生碰撞形成二次冲击,实现冲击强化试验.
1.2 第一次冲击过程分析
当跌落试验机台面与跌落试验机波形发生器接触时,可以将跌落试验机看作一个单自由度弹簧质量系统[7],如图2所示.
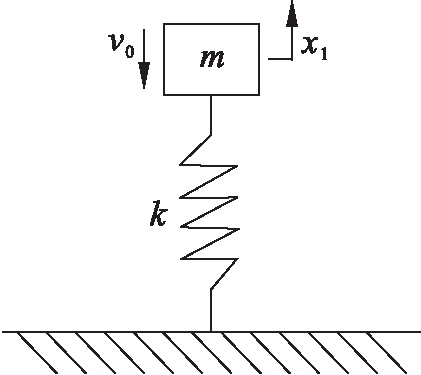
图2 单自由度弹簧质量系统
Fig.2 Spring mass system with single-degree-of-freedom
分析可得,取开始碰撞为t=0时刻,初始条件![]() 一次冲击过程应满足
一次冲击过程应满足
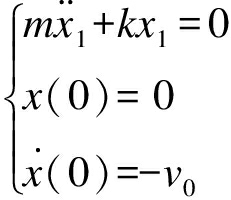
(1)
(2)
式中:![]() 为重力加速度,h为跌落试验机台面跌落高度;
为重力加速度,h为跌落试验机台面跌落高度;![]() 为跌落试验机波形发生器刚度.
为跌落试验机波形发生器刚度.
对式(2)进行二阶求导可得加速度响应为
(3)
当![]() 时,跌落试验机台面与跌落试验机波形发生器分离,则接触持续时间Δt1为
时,跌落试验机台面与跌落试验机波形发生器分离,则接触持续时间Δt1为![]() 的最小正解,即
的最小正解,即
(4)
式中,T为![]() 周期,
周期,![]()
令加速度响应的振幅为A,则
(5)
由式(4)、(5)可知,一次冲击的脉宽与幅值可由跌落试验机台面加冲击放大器质量和m、跌落试验机波形发生器刚度k以及跌落高度h调节.
1.3 第二次冲击过程分析
二次冲击过程可分为冲击放大器台面与冲击放大器波形发生器接触前和接触后两部分,令接触时刻为t1,接触后分离时刻为t2,分析过程如下.
接触前过程(0<t<t1).在这个过程中,跌落试验机台面速度快速减小,然后发生方向改变,开始向上运动,冲击放大器安装底座和冲击放大器波形发生器随跌落试验机台面向上运动;冲击放大器台面在悬挂弹簧作用下继续减速向下运动.系统简化模型如图3所示.
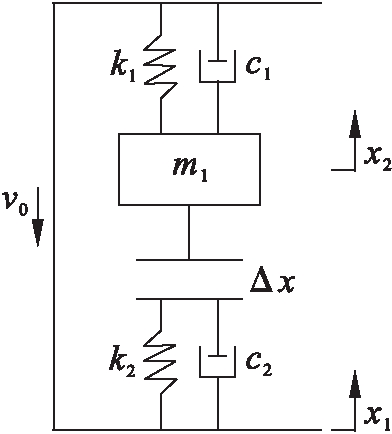
图3 二次冲击过程简化模型
Fig.3 Simplified model of secondary impact process
分析可得,过程中质体m1运动满足
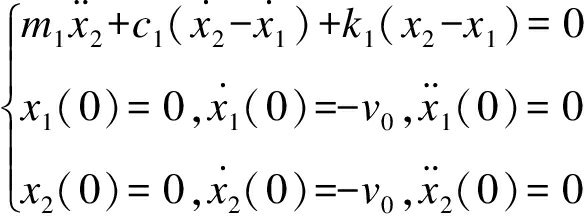
(6)
令z=x2-x1,则
(7)
在振动理论中,杜哈梅积分(Duhamel’s integral)[8]是求解线性系统在任意外载激励下响应的一种方法,利用杜哈梅积分可解得相对位移响应为
sin[ωd1(t-τ)]dτ
(8)

(9)
式中:![]()
冲击载荷作用时间很短,在系统产生最大位移之前,阻尼因素(c1、c2)所吸收的能量很少,因此,冲击载荷作用下的计算,一般不计阻尼的影响.
当ωn1≠ω时,可解得相对位移响应为
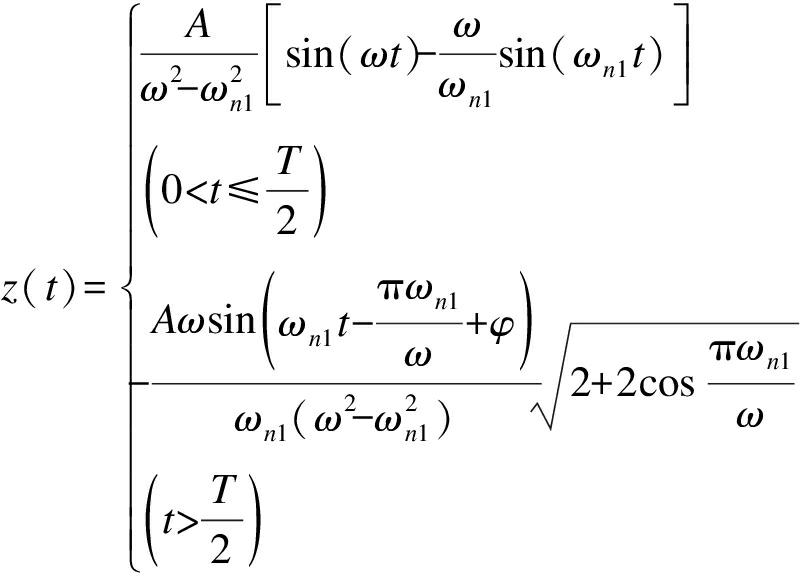
(10)
式中,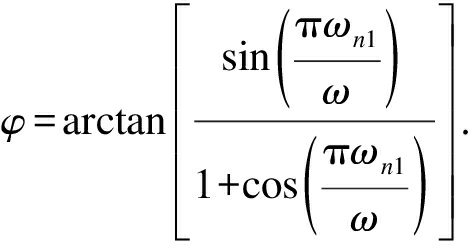
对式(10)进行一阶求导可得相对速度响应为
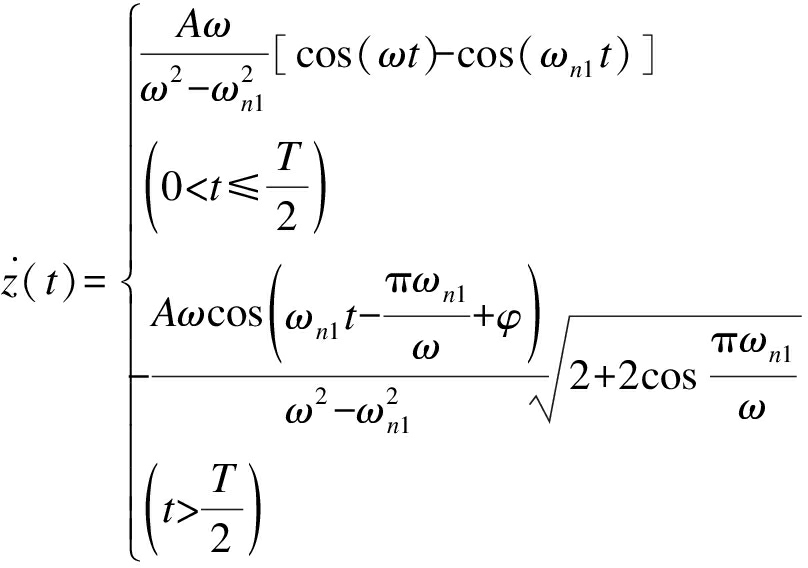
(11)
对式(11)进行一阶求导可得相对加速度响应为
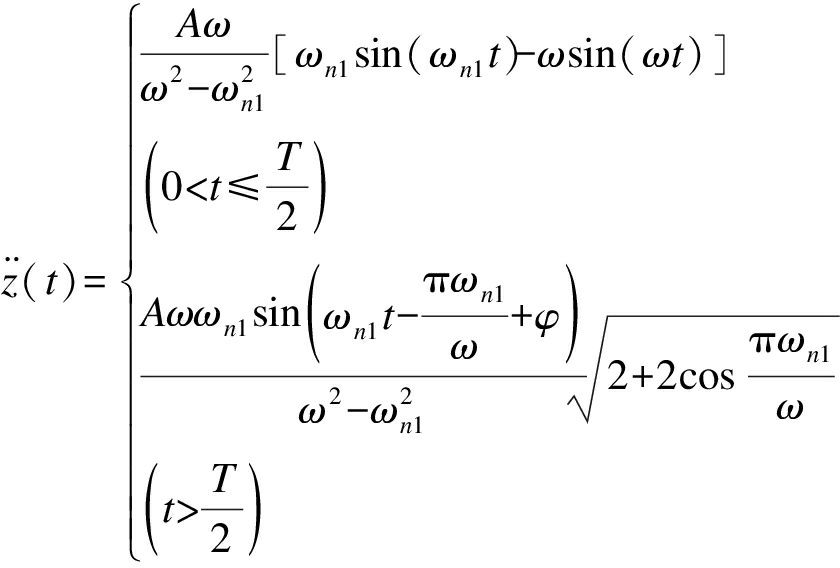
(12)
由于z=x2-x1,则有
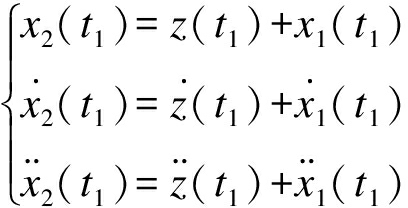
(13)
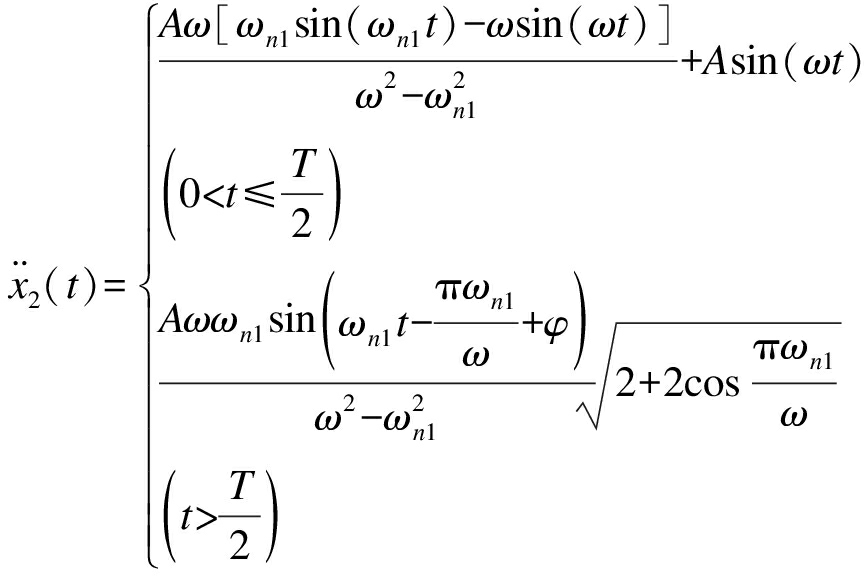
(14)
当z(t1)=Δx时,二次冲击发生,且为使碰撞过程增益最大化,应当在激励正波作用结束后发生二次碰撞,则有
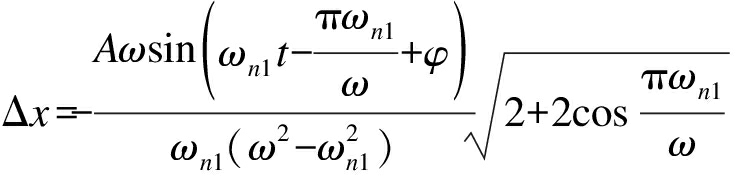
(15)
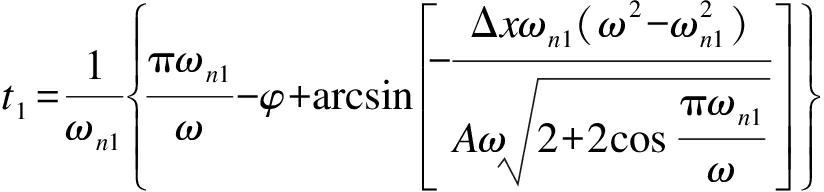
(16)
在t=t1时刻,冲击放大器台面与冲击放大器波形发生器接触,接触期间(t1<t<t2),该接触过程中运动过程满足
(17)
初始状态![]() 均可由式(10)~(12)、(14)求得.
均可由式(10)~(12)、(14)求得.
对于无阻尼情况,可解得相对位移响应为
(18)
式中:![]()
对式(16)进行一阶求导可得相对速度响应为
(19)
对式(12)进行一阶求导可得相对加速度响应为
(20)
二次冲击接触时间Δt2=t2-t1由![]() 的最小正解确定,即
的最小正解确定,即
(21)
(22)
接触后过程(t2<t).该过程中运动过程满足
(23)
可解得
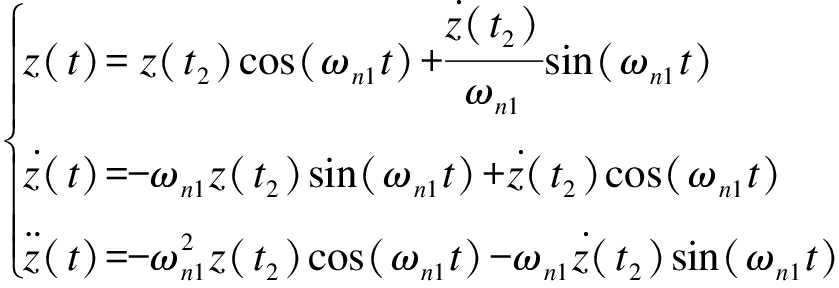
(24)
由上述分析可知,整个冲击过程冲击放大器台面与跌落试验机台面相对位移响应为
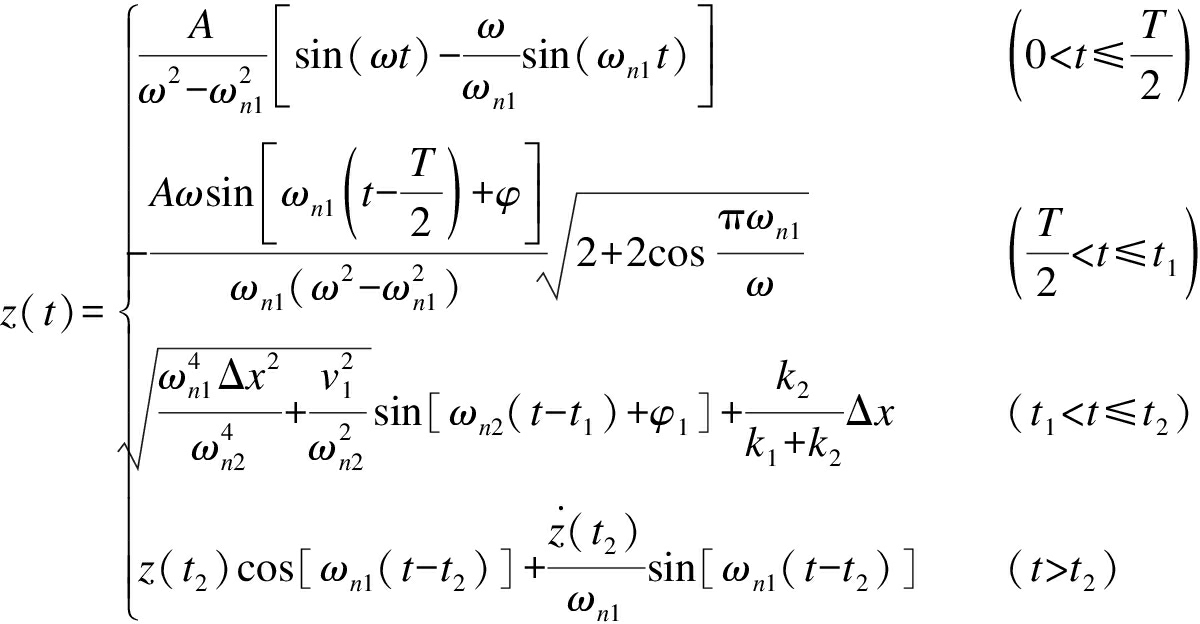
(25)
冲击放大器台面与跌落试验机台面相对速度响应为
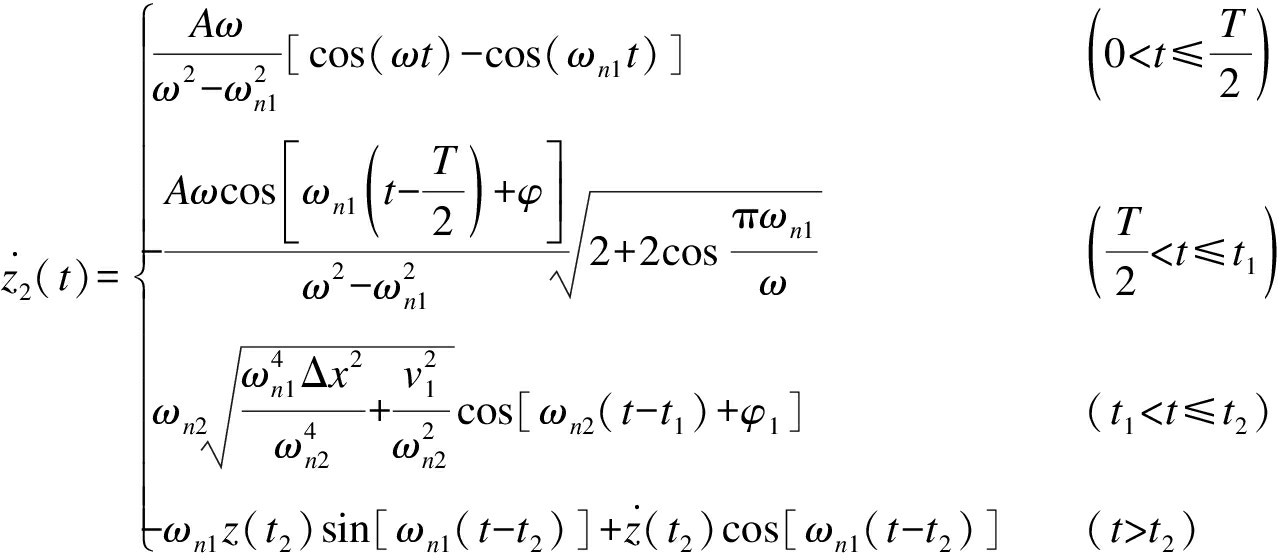
(26)
冲击放大器台面绝对加速度响应为
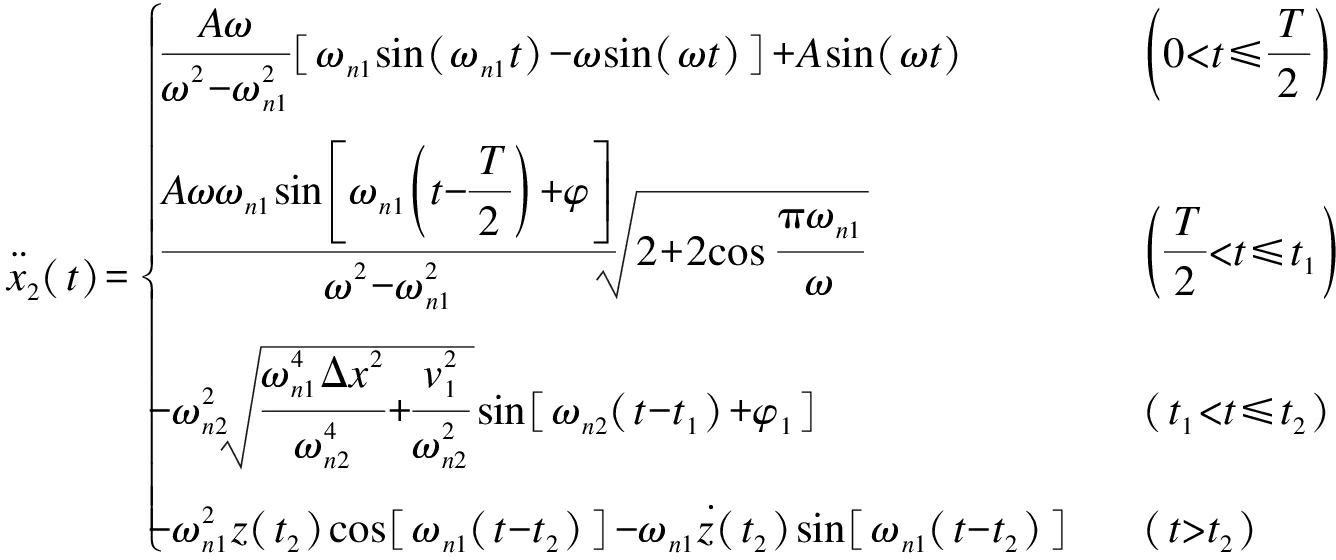
(27)
2 实例计算分析
2.1 计算参数
冲击放大器台面质量为40 kg,冲击放大器安装底座质量为40 kg.跌落试验台台面质量为1 000 kg.波形发生器静态刚度为1.441 kN/mm;悬挂弹簧刚度为0.38 kN/mm;冲击放大器台面与波形发生器安装距离为0.01 m[9-10].
2.2 载荷施加
二次冲击过程在一次冲击发生后发生,并且以一次冲击的输出为二次冲击过程的输入.为简化计算过程,选取加速度设计谱值为250g、速度设计谱值V0为6 m/s、位移设计谱值D0为0.043 m作为二次冲击输入进行计算.根据德国军标BV043-85中对设备冲击考核环境的相关规定,可以将三个设计谱值转换为加载波形,如图4所示.
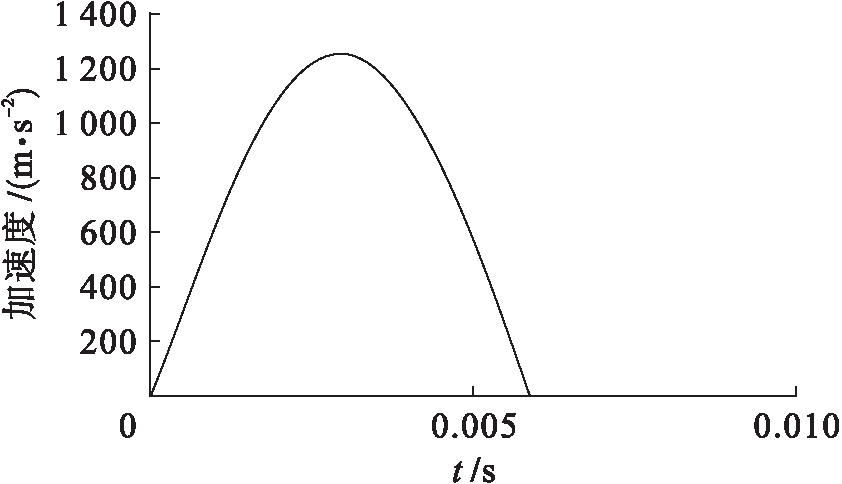
图4 加载波形
Fig.4 Loading waveform
2.3 计算结果分析
2.3.1 时域历程描述方法分析
按照本文建立的模型和参数设置进行仿真计算,加速度响应曲线如图5所示.
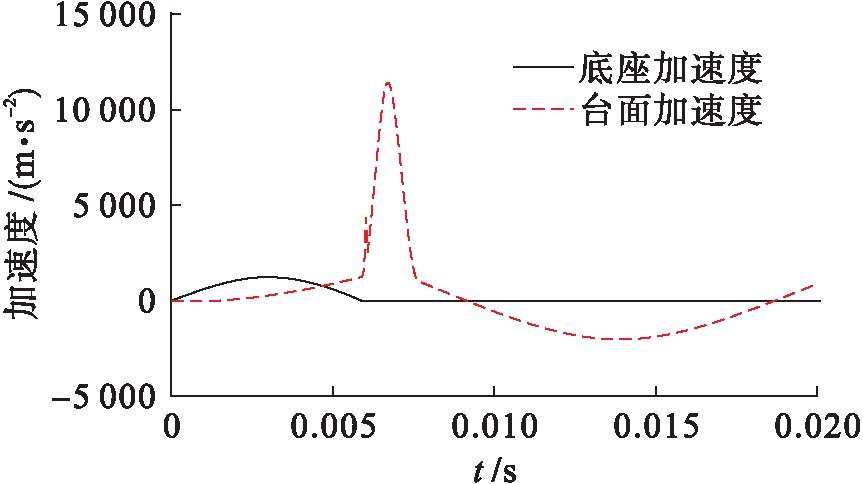
图5 底座与台面加速度对比
Fig.5 Acceleration comparison between base and table-board
由图5可知,冲击放大器台面的加速度曲线为冲击放大器输出的冲击加速度曲线,冲击放大器底座的加速度曲线为冲击放大器输入的冲击加速度曲线.输入的加速度曲线呈半正弦波形,在加载结束后保持为0.输出的加速度曲线整体呈正弦振荡形式,但其在0.006~0.008 s之间出现一个突增的小尖峰,峰值为11 883 m/s2,放大了9.5倍.这个小尖峰的形成是由于突然增加的外力导致的,根据二次冲击过程分析可知,这个突然增加的外力来源于冲击放大器台面与波形发生器的碰撞,即整个试验过程的二次冲击.因此可以确定二次冲击发生在0.006 s,且持续了0.002 s.在0.008 s时,突增的小尖峰结束,表明冲击放大器台面与波形发生器分离,二次冲击结束.冲击放大器台面继续振荡,并在阻尼的作用下衰减直至停止.
由以上分析可知,二次冲击发生在0.006~0.008 s之间.因此,冲击放大器各部分在冲击作用下的位移响应,可以将整个仿真过程分为二次冲击前、二次冲击期间和二次冲击后三个过程.冲击放大器底座和台面位移响应曲线如图6、7所示.
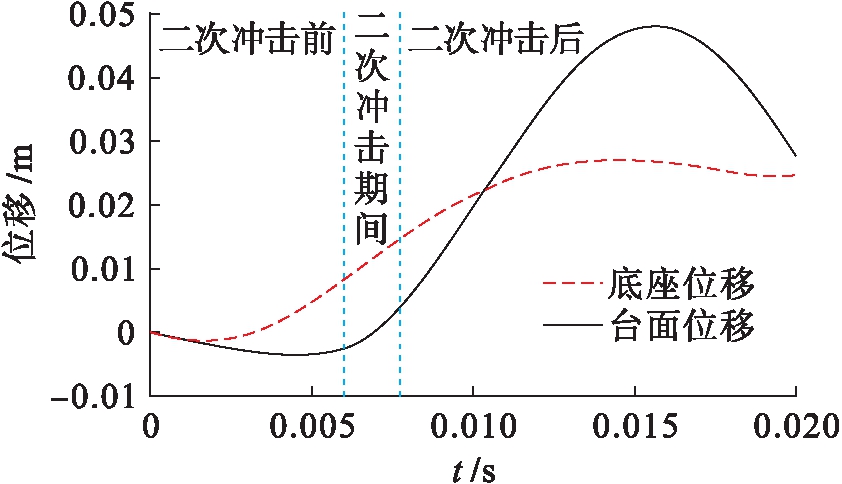
图6 底座与台面位移对比
Fig.6 Displacement comparison between base and table-board
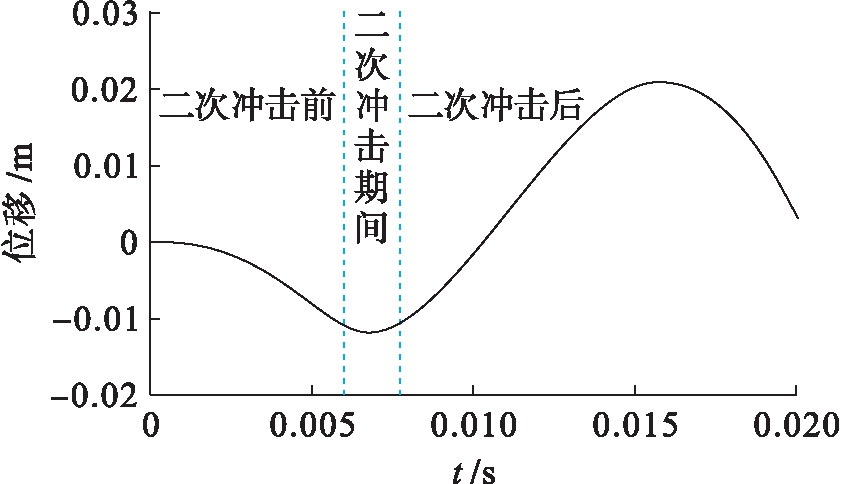
图7 底座与台面相对位移
Fig.7 Relative displacement between base and table-board
结合图6、7可知,二次冲击前底座位移曲线先减小后增大,且减小的趋势逐渐减小,增大的趋势逐渐增大,在0.001 s附近取得最小值,最小值为-0.001 m.表明冲击放大器底座在一次冲击发生后,由于惯性先向下运动,同时在一次冲击作用下,随着时间增加,一次冲击对冲击放大器底座输入能量越多,冲击放大器底座向下运动的趋势逐渐减小,0.001 s时开始向上运动直至0.006 s时发生二次冲击.二次冲击前台面位移曲线先减小后增大,且减小的趋势逐渐减小,增大的趋势逐渐增大.在0.005 s附近取得最小值,最小值为-0.003 m.台面底座相对位移曲线逐渐减小,且减小的趋势逐渐增大.表明冲击放大器台面在一次冲击发生后,由于惯性继续向下运动,且相对于底座向下运动,在该过程中,台面悬挂弹簧开始被拉伸,限制台面继续向下运动.在台面悬挂弹簧作用下,冲击放大器台面向下运动的趋势逐渐减小,0.005 s时开始向上运动直至0.006 s时发生二次冲击.
在二次冲击期间,底座位移曲线和台面位移曲线均逐渐增加,其中底座位移曲线增加趋势基本保持不变,台面位移曲线增加趋势变大.台面底座相对位移曲线先减少后增加,在0.007 s左右取得最小值,最小值为-0.01 m,且减少趋势逐渐减小,增加趋势逐渐增大.这表明在0.006 s时,冲击放大器台面和冲击放大器波形发生碰撞,惯性台面继续向下运动.波形发生器开始被压缩,限制台面继续向下运动,在台面悬挂弹簧和波形发生器共同作用下,冲击放大器台面相对于冲击放大器底座向下运动的趋势逐渐减小,0.007 s时相对于冲击放大器底座开始向上运动.此时,冲击放大器台面在台面悬挂弹簧和波形发生器回复力作用下,向上运动趋势逐渐增大.在0.008 s时冲击放大器台面和波形发生器分离.由图7可知,在二次冲击发生的初始时刻和结束时刻,台面底座相对位移值为-0.01 m,这表明冲击放大器台面与波形发生器之间安装距离为0.01 m,这与实际情况相符.在二次冲击后,底座位移曲线先增加然后趋于稳定,这是因为冲击放大器底座随跌落试验台台面一起被强制约束.由于冲击放大器台面与台面悬挂弹簧组合成一个弹簧质量系统,因此台面位移曲线在二次冲击发生后呈自由振荡形式,在阻尼作用下衰减至静止.
2.3.2 冲击响应谱描述方法分析
将冲击放大器台面和底座的加速度数据做冲击谱,如图8所示.由图8可知,冲击放大器底座冲击响应谱描述的是冲击放大器输入冲击环境,冲击放大器台面冲击响应谱描述的是冲击放大器输出冲击环境,可得输入冲击环境的等速度谱值为5.2 m/s,等加速度谱值为250g,与设计谱值基本一致.输出冲击环境的等速度谱值为10.5 m/s,等加速度谱值为1 400g.在实际工程中,一般以等速度谱值为考核要求.因此,从等速度谱值来看,冲击环境经过冲击放大器放大了2.01倍;从等加速度谱值来看,冲击环境经过冲击放大器放大了5.6倍.
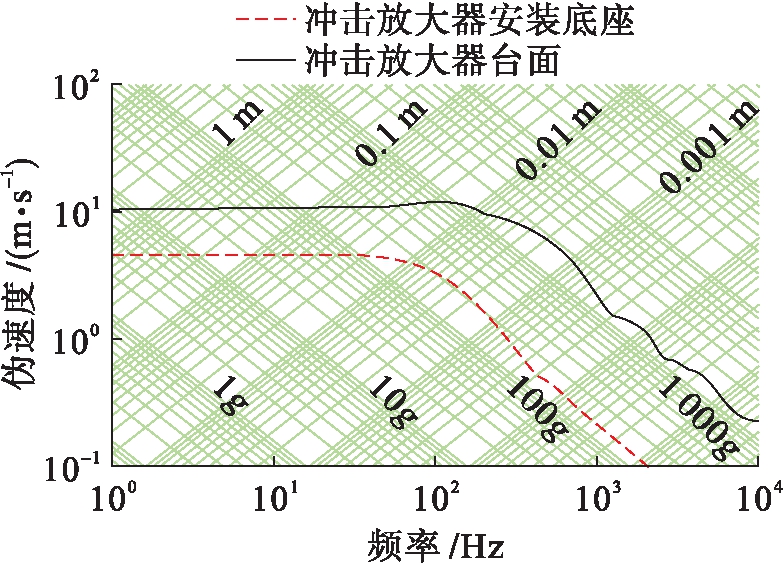
图8 台面和底座冲击响应谱对比
Fig.8 Comparison of impact response spectrum between table-board and base
3 结 论
本文通过分析得出以下结论:
1) 本文提出一种能够强化冲击环境的试验方法.该方法能够在现有抗冲击考核试验基础上强化冲击环境,提供更加严酷的考核条件,并对试验过程进行运动分析,得出了强化冲击试验全过程的运动响应理论解,为分析多过程碰撞振动系统提供了参考.
2) 通过实例计算,进一步验证了该试验方法的有效性.计算结果显示,以时间历程描述方法分析了加速度峰值描述的冲击环境特性,加速度峰值放大了9.5倍.以冲击响应谱描述方法分析了伪速度谱描述的冲击环境特性,等速度谱值放大了2.01倍,等加速度谱值放大了5.6倍.
[1]张磊,汪玉,温肇东,等.舰载设备冲击试验系统研制现状和发展趋势 [J].科技导报,2009,27(1):96-101.
(ZHANG Lei,WANG Yu,WEN Zhao-dong,et al.Progress and trend of shock test system for warship equipment [J].Science & Technology Review,2009,27(1):96-101.)
[2]叶明,范井峰.舰艇抗冲击综合研究初探 [J].船舶,2004,15(6):10-12.
(YE Ming,FAN Jing-feng.The comprehensive research on shock-resistance for warships [J].Ship & Boat,2004,15(6):10-12.)
[3]Kelly G,Punch J,Goyal S,et al.Analysis of shock pulse from a small velocity amplifier [C]//Procee-dings of the 11th International Congress and Exposition.Washington D C,USA,2008:256-278.
[4]Rodgers B,Goyal S,Kelly G,et al.The dynamics of multiple pair-wise collisions in a chain for designing optimal shock amplifiers [J].Shock and Vibration,2009,16(1):99-116.
[5]Zhang A.High acceleration board level reliability drop test using dual mass shock amplifier [C]//2014 IEEE 64th Electronic Components and Technology Conference.Orlando,USA,2014:1441-1448.
[6]Douglas S T.High accelerations produced through secondary impact and its effect on reliability of printed wiring assemblies [D].Washington D C:University of Maryland,2010.
[7]邹晓君,李豪杰.一种高g值大脉宽冲击试验装置的设计与仿真 [J].机械制造与自动化,2012,41(5):101-103.
(ZOU Xiao-jun,LI Hao-jie.Design and simulation of high g-value and long pulse impact test device [J].Machine Building & Automation,2012,41(5):101-103.)
[8]金栋平,胡海岩.碰撞振动与控制 [M].北京:科学出版社,2005.
(JIN Dong-ping,HU Hai-yan.Impact vibration and control [M].Beijing:Science Press,2005.)
[9]杨玉良,秦俊奇,狄长春,等.橡胶波形发生器材料本构模型有限元仿真及试验研究 [J].机械设计,2013,30(9):86-89.
(YANG Yu-liang,QIN Jun-qi,DI Chang-chun,et al.Finite element simulation and experimental study on material constitution model of rubber waveform gene-rator [J].Journal of Machine Design,2013,30(9):86-89.)
[10]吕剑,岳晓红,黄含军.利用数值方法模拟橡胶波形发生器生成半正弦冲击波 [J].橡胶工业,2008,55(1):15-19.
(LÜ Jian,YUE Xiao-hong,HUANG Han-jun.Nume-rical simulation for half-sine pulse generated by rubber waveform generator [J].China Rubber Industry,2008,55(1):15-19.)