管道机器人作为特种机器人研究领域的主要分支之一,已被广泛、深入地研究并使用于油气管道的检修工作中.其中,支撑轮式管道机器人因自身驱动能力强、弯道通过性较好及适应管径变化能力强等特点而被更多地投入到实际的管道检测工作中,但在其通过弯道时不同位置驱动轮与管道内壁的接触点相对于弯道曲率中心距离不等,致使驱动轮所需的实时转速也各有差异.对于无法调节各个驱动轮转速的机器人来说,虽能通过弯道,但各驱动轮会与管道内壁存在打滑现象,由此增大机器人行走的不稳定性,加大驱动电机的负载,甚至会发生堵转现象[1-6].哈尔滨工业大学邓宗全教授首次将基于差速器原理改良的三轴差速系统引入到轮式管道机器人之中,该机器人通过单电机输出动力,经过含有分动器的三轴差速系统将动力分配到三组驱动轮上,机器人在行走时各驱动轮会根据实际经过的轨迹长度调整自身的转动速度,避免了多余的摩擦损耗.但由于三轴差速系统较为复杂,导致机器人的整体体积较大且质量较重,只能适用于管径约为300 mm的中大型油气管道.而对于收集刚经过开采而未经处理的天然气从气田井口装置经集气站到气体处理厂或起点压气站的这类管道,内部气体压力高、管径较小(约为150 mm)且存在转弯,机器人则无法顺利通过[7-8].
基于上述研究,本文提出了一种传动系统更为简单紧凑,可根据各个驱动轮所通过距离不同而自行调节各自转速的机械差速式支撑轮式管道机器人.该机器人不仅能实时调节驱动轮转速,避免驱动轮打滑,还可在较小内径的管道内爬行.
1 机器人结构及驱动原理
1.1 机器人结构组成
机械差速式管道机器人如图1所示.该机器人可在内径由140~150 mm变化的管道内爬行,根据模块化的设计思路,将机器人划分为5个功能模块,即外框模块、变径模块、传动模块、差速器及辅助支撑模块.
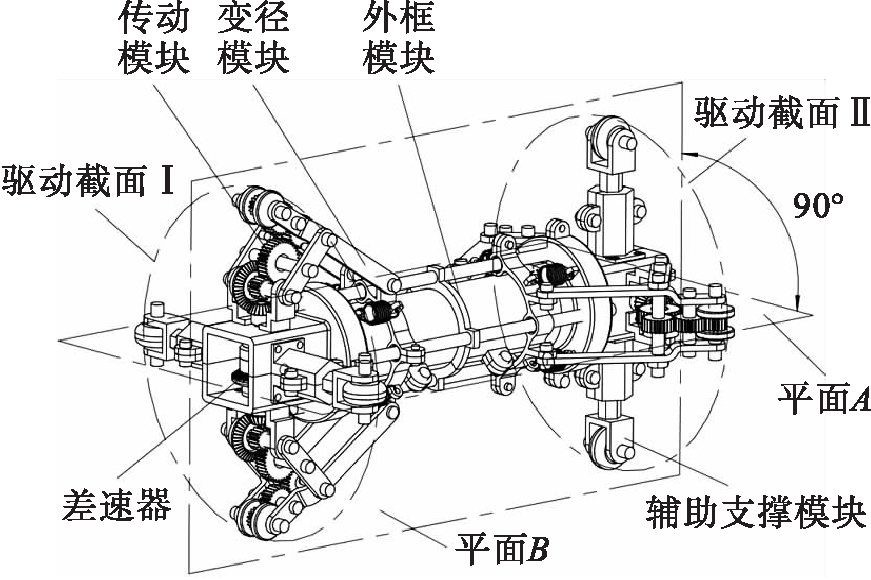
图1 机器人轴侧视图
Fig.1 Side view of robot
从图1中可以看出,机器人具有前后两个驱动截面且前后两组驱动轮所在平面夹角为90°,将机器人分别向着平面A、平面B做投影,得到其传动系统结构图如图2所示.
1.2 机器人驱动原理
机器人前后A、B两个驱动截面的支撑与驱动原理均相同.每个平面中均由单独的直流减速电机提供动力,并将动力传递到差速器,由差速器根据输出轴两侧的驱动轮所通过的实际轨迹长度来调节驱动轮的转速,使驱动轮与管道内壁发生纯滚动,避免打滑.驱动轮交错布置使得机器人的驱动力沿轴向分布更加均匀,而辅助支撑模块可提高机器人自身轴线与管道轴线重合度,增加机器人行走的稳定性.
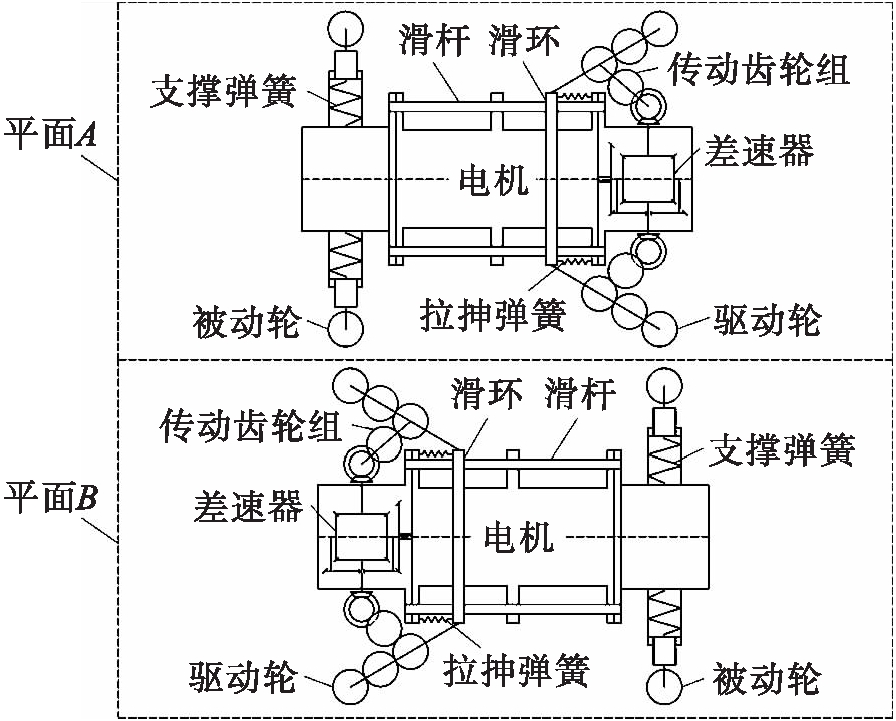
图2 机器人传动系统结构图
Fig.2 Structure diagram of robot transmission system
2 变径支撑及越障能力分析
2.1 机器人变径能力分析
为简化机器人的机械结构,降低机器人对控制系统的需求,该机器人驱动轮与被动轮的支撑均采用被动变径的方式.图3为变径支撑原理图.由图3可以看出,在辅助支撑模块中,每个被动轮均由一根支撑弹簧推动使其与管道内壁接触,其支撑力由弹簧直接提供;每个驱动轮侧的支撑结构类似于“Y”型,同一驱动截面的两个驱动轮由4根相同的拉抻弹簧拉动滑环沿滑杆向机器人首尾两侧移动,支撑杆在弹簧力的作用下将驱动轮抵在管道内壁上.
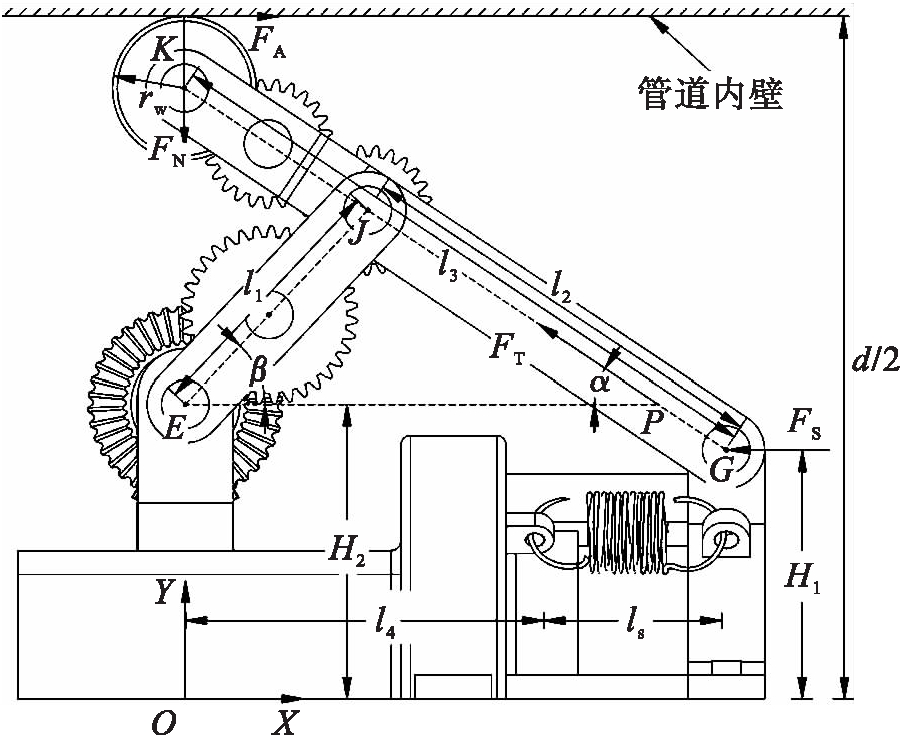
图3 变径支撑原理图
Fig.3 Schematic principle of variable diameter supporting
以任意驱动截面的一侧驱动轮支撑的投影为例进行分析,建立的坐标系如图3所示.其中,点E、G、J、K为支撑杆上的铰点,线段EJ、GJ、GK的长度固定且分别为l1、l2、l3,点P为平行于X轴且过点E的直线与GJ的交点,管道半径为d/2,驱动轮半径为rw,ls为弹簧的有效长度,l4为弹簧与差速器外壳侧的接触点到Y轴的长度,α、β分别为GK、EJ与X轴的夹角,H1、H2分别为点G、E到X轴的距离.
当管道机器人所经过管道的管径d发生变化时,拉抻弹簧的长度ls也将发生改变,并满足
d=2[(ls+l4)tan α+H1+rw]
(1)
机器人驱动轮与管道内壁间产生的接触力全部由拉抻弹簧发生形变而产生的弹簧力提供,对图3中的E点做力矩平衡分析,因点E在坐标系中的坐标为(0,H2),则有
FS=4kΔx
(2)
(3)
FA≤μFN
(4)
FN(l3cos α-l1cos β-l2cos α)-
FAlPKsin α+FTlEPsin α=0
(5)
(6)
lEP=l1cos β+l2cos α-(H2-H1)cot α
(7)
(8)
式中:k为弹簧刚度系数;Δx为弹簧变形量;μ为管道内壁与行走轮间的摩擦系数;FS为弹力;FT为滑环对支撑杆作用力;FA为轴向驱动力;FN为管道内壁对驱动轮的正压力.
2.2 机器人越障条件分析
由于管道内壁附着的杂质或异物会影响机器人的行走性能,因此需要对机器人的越障能力进行分析.对于支撑轮式管道机器人而言,最难越过的障碍类型为均匀分布的环形障碍,因为此时障碍物与行走轮接触最多,阻碍面积最大.为简化分析,假设驱动轮具有足够大的扭矩并忽略重力影响,计算机器人越障所需满足的条件.
图4为机器人的某个驱动截面内行走轮越障分析图.如果机器人此时可以越障,则越障的驱动轮、被动轮与管道内壁的接触力刚好为零,机器人越障需满足
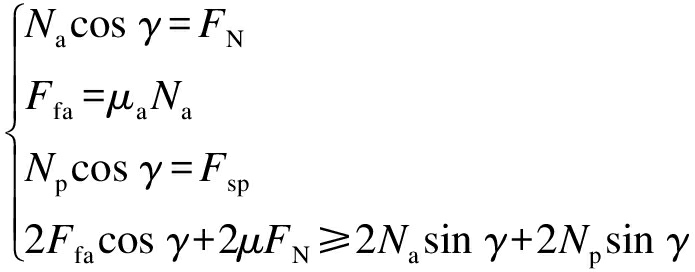
(9)
(10)
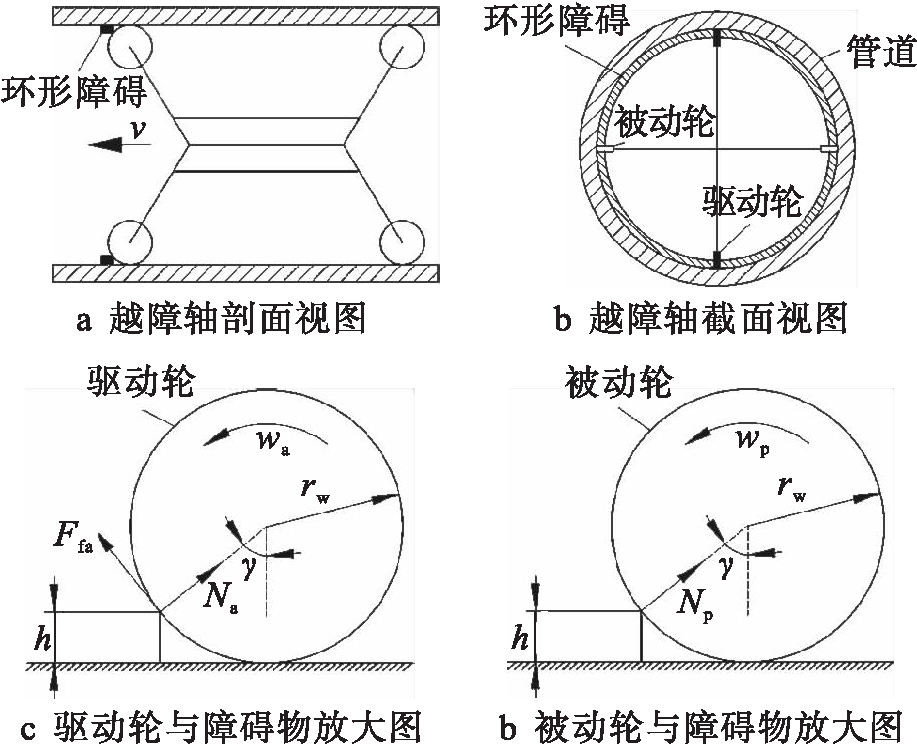
图4 越障分析图
Fig.4 Analysis diagram of obstacle crossing
式中:Na为障碍物对驱动轮的支持力;Ffa为越障驱动轮的驱动力;μa为行走轮与障碍物之间的摩擦系数;h为障碍物高度;Np为障碍物对被动轮的支持力;Fsp为支撑弹簧对被动轮的推力;rw为驱动轮与被动轮的半径;γ为越障角.
3 机器人过弯阶段划分
管道机器人在通过弯道时,由于驱动轮与管道内壁的接触点曲率半径各不相同,则需要驱动轮根据实际需求转动相应的角度才能避免与管道内壁之间发生打滑.
管道机器人的过弯包括过渡阶段与旋转阶段,而过渡阶段又包含入弯和出弯两个过程.其中,过渡阶段是指机器人的一个驱动截面处于弯管而另一驱动截面处于直管中的阶段;旋转阶段是指管道机器人两个驱动截面全部在弯管中行驶的阶段.
由于设计的管道机器人交错对称,故以任意平面进行分析.图5为机器人过弯区域划分图.由图5可知,以90°弯管轴线的圆心建立坐标系,坐标系Z轴垂直于弯管轴线所在平面,Y轴与弯管截止截面夹角为45°,管道直径为d,弯管轴线的弯曲半径为R.
当机器人处于过渡阶段时,前后两个驱动截面处管道的轴线形状不同,机器人自身会发生偏转,而机器人与弯管各自的几何特性不同,导致机器人在过弯过程中其自身质心轨迹与管道轴线并不重合.将弯管圆心到机器人质心的连线与机器人前后两个驱动截面对称面的夹角称为偏转角θ;过弯管轴线上任意一点作该点切线的垂线,将这条垂线与机器人质心轨迹的交点到前文所述切线的距离称为偏移距离δ;弯管圆心到机器人质心的连线与Y轴夹角为σ;A、B、C、D代表机器人的四个驱动轮,机器人的姿态角为λ,机器人两个驱动截面的距离为L,按照图5所示的运动过程,σ值的大小与机器人所处运动阶段的对应关系如式(11)所示,Ⅰ、Ⅱ代表机器人处于入弯阶段,Ⅲ代表机器人处于旋转阶段,Ⅳ、Ⅴ代表机器人处于出弯阶段.
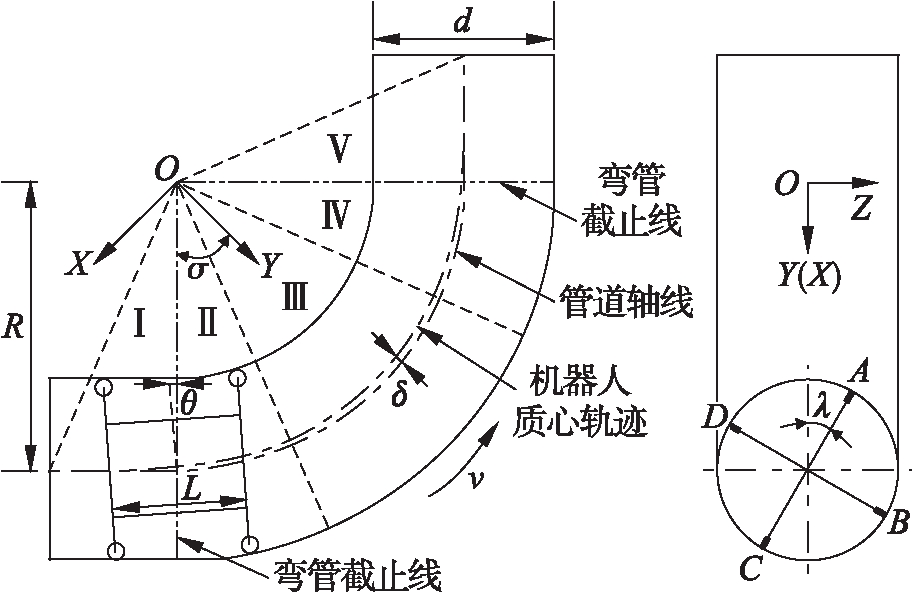
图5 机器人过弯区域划分图
Fig.5 Division diagram of robot bending areas

(11)
由管道机器人与弯管的结构特点可以看出,偏移距离δ在入弯阶段会从0逐渐增大,在旋转阶段保持不变,在出弯阶段又逐渐减小为0,偏转角θ在过渡阶段也会发生变化,这也导致了机器人在过渡阶段各驱动轮的转速并不会像处于旋转阶段一样保持不变.
4 ADAMS仿真分析
首先采用Solidworks软件创建机器人模型,并转存为Parasolid格式,然后导入到ADAMS软件中,即可对其进行虚拟样机仿真分析,导入后示意图如图6所示.
4.1 机器人牵引力仿真分析
对于采用被动变径方式的管道机器人,机器人牵引力的大小主要受摩擦系数和弹簧力这两个因素影响.如果牵引力过低,将导致机器人无法在竖直管道中行走,说明设计的机器人结构或参数不合理.因此,机器人的最小牵引力应能保证机器人在竖直管道中不会发生打滑甚至滑落.

图6 虚拟样机仿真示意图
Fig.6 Schematic diagram of virtual prototype simulation
机器人在竖直管道中行走时,自身的牵引力主要克服自身重力,本文设计的机器人自重M为3 kg.由于机器人的被动轮在机器人行走时只起到辅助支撑作用,所以其内部支撑弹簧作用力较小,而滚动摩擦力又远小于滑动摩擦力,机器人若仍在竖直管道中行走则需满足
Mg<4μFN
(12)
由于机器人在150 mm管径管道中行走时,机器人的拉抻弹簧形变量最小,所以将此时机器人的参数l1=27.75 mm、l2=45 mm、l3=68 mm、α=33.65°、β=46.67°、H2-H1=4.75 mm、μ=0.5代入式(8)及式(12)中.为方便计算,可先将机器人每侧驱动截面的总弹簧拉力FS设为30 N,得到FN的值为17.56 N,即牵引力的理论计算值为35.12 N.为测试机器人在上述条件下的牵引力,在机器人尾部与大地之间添加一作用方向与机器人前进方向相反且预紧力为零的虚拟弹簧力并进行仿真,随着机器人不断前进,虚拟弹簧被拉抻且对机器人的拉力逐渐增大,当机器人直行出现打滑时,此时的虚拟弹簧拉力即为机器人最大牵引力,具体仿真结果如图7所示.
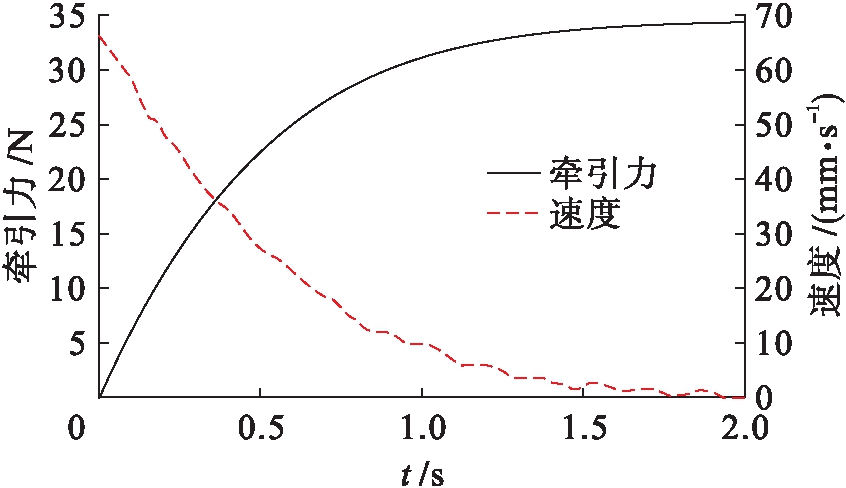
图7 牵引力仿真
Fig.7 Traction simulation
由图7可知,机器人在2 s内前进速度由65 mm/s逐渐降为0,代表牵引力的弹簧拉力大小逐渐增至为34.19 N并保持稳定,此时的牵引力大小略大于重力,而由于机器人辅助支撑模块会带有少许阻力,导致仿真值与理论牵引力值大小存在2.6%的误差,但整体参数设计满足机器人的行走需求.
4.2 机器人越障仿真分析
为求出机器人在越过环形障碍时可越过障碍的最大高度,在ADAMS中将式(10)中提及的μa、μ均设置为0.5,Fsp设为5 N,每一侧的拉抻弹簧力总和FS大小设置为30 N,模型中的行走轮半径rw为7.5 mm,得出可越过障碍的理论高度值为2.64 mm.在仿真过程中通过不断增加环形障碍物的高度,直到机器人驱动轮发生打滑,不能越过为止.仿真结果表明,在上述条件下机器人的越障高度可达3 mm,这是由于机器人自身行走具有一定惯性,使得在仿真过程中可越过的障碍物高度略大于理论计算值.
图8为机器人越过最高障碍物时,拉抻弹簧形变量随时间的变化.由于机器人的前后驱动截面依次越过障碍,所以前后拉抻弹簧会在两个驱动截面分别越障时发生形变,最大形变量为2.7 mm.
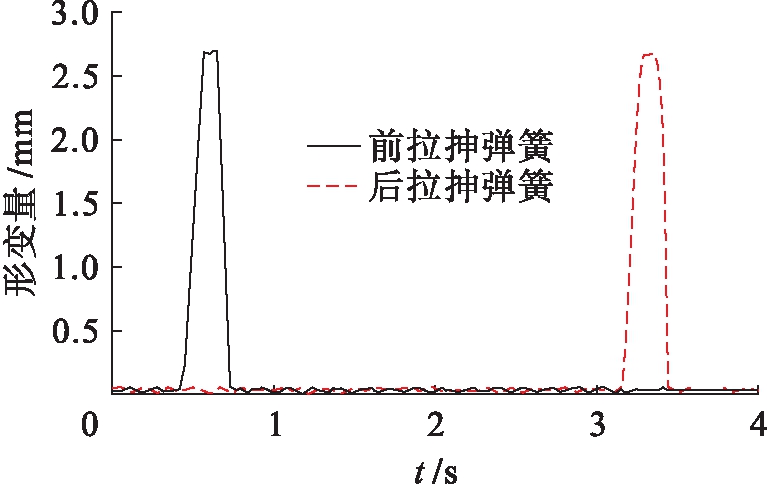
图8 机器人越障时拉抻弹簧形变图
Fig.8 Deformation diagram of stretching spring for robot during obstacle crossing
4.3 机器人过弯仿真分析
机器人在过弯阶段偏转角和各驱动轮转速的变化,可反映出本文提出的机械差速式管道机器人驱动轮在通过弯道时是否为纯滚动.
将机器人通过管径为145 mm管道、轴线曲率半径为250 mm的90°弯管模型导入到ADAMS软件中并进行仿真.在仿真过程中,偏转角θ的变化如图9所示.
当机器人处于式(11)中Ⅰ阶段时,机器人的偏转角θ逐渐增大,当机器人的质心与直管、弯管过渡截面重合时,即对应的σ值为-π/4,偏转角θ值达到最大为5.68°;当机器人运动到Ⅱ阶段时,偏转角θ由峰值逐渐减小,直到Ⅱ阶段结束,θ减小为0,并在Ⅲ阶段时保持不变,在Ⅳ、Ⅴ阶段θ值的变化与Ⅱ、Ⅰ阶段对应互为相反数.
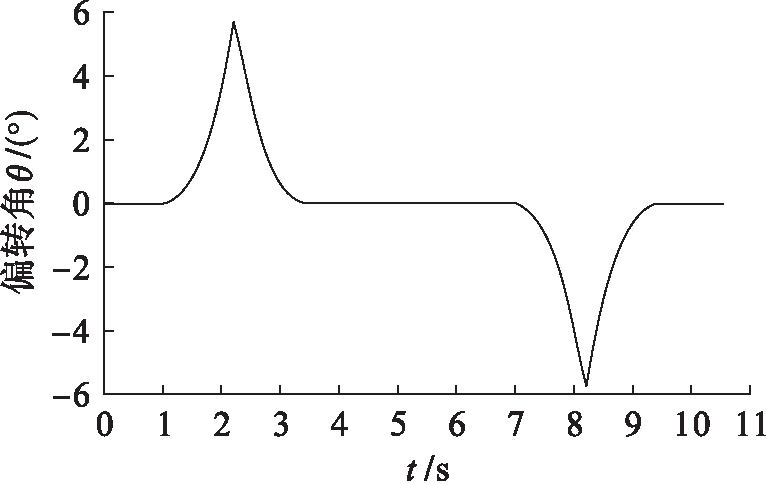
图9 过弯过程中偏转角变化
Fig.9 Change of deflection angle during bending process
机器人在过弯时,各驱动轮的转速比会受到姿态角λ的影响,由于设计的管道机器人前后交错分布,当λ值大于等于90°时,机器人的位姿会出现重复,所以可针对机器人姿态角为0°、30°和45°时的状态进行过弯分析.
各个驱动轮在处于Ⅲ阶段,即旋转阶段的理论转速比与各驱动轮接触点到Z轴的距离之比相同,将实际的R、d、λ代入式(13)中,可得到相应的理论转速比,即
(13)
当机器人处于145 mm管径的管道中,在恒定驱动下,各驱动轮理论转速如表1所示.
表1 旋转阶段不同姿态角各驱动轮转速
Tab.1 Rotating speed of each driving wheel at different
attitude angles in rotation stage
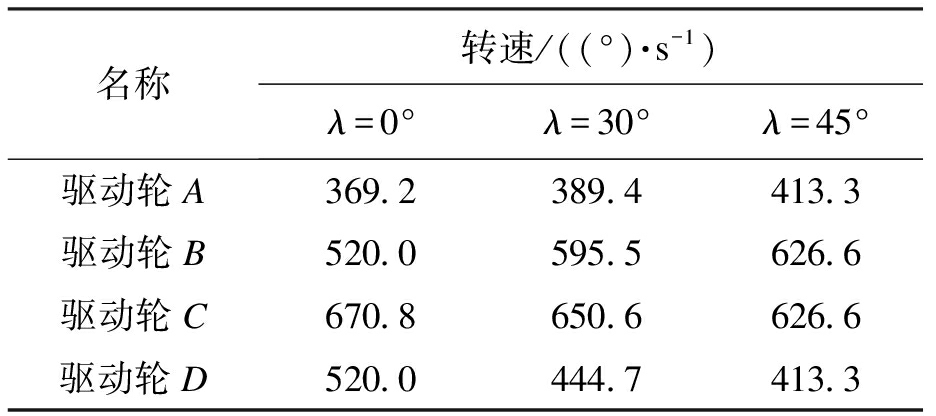
名称转速/((°)·s-1)λ=0°λ=30°λ=45°驱动轮A369.2389.4413.3驱动轮B520.0595.5626.6驱动轮C670.8650.6626.6驱动轮D520.0444.7413.3
对处于不同姿态角的机器人添加相同的驱动速度并分别进行过弯仿真.各驱动轮在仿真中的转速数据如图10所示.图10a、b、c分别为机器人以0°、30°及45°姿态角过弯时,各个驱动轮的转速随时间变化的情况.在直行阶段,差速器内的行走轮不发生转动,各个驱动轮行走路程一致且转速一致;在过弯时,各个行走轮的转速逐渐发生改变,在完全处于旋转阶段时,各驱动轮的转速保持相对稳定.由于在仿真过程中差速及动力传递功能的实现全部由齿轮副完成,因此在机器人行走过程中驱动轮转速会产生小范围波动,但在旋转阶段各个驱动轮转速的均值与理论转速吻合较好,表明差速器起到了调节驱动轮转速的作用.
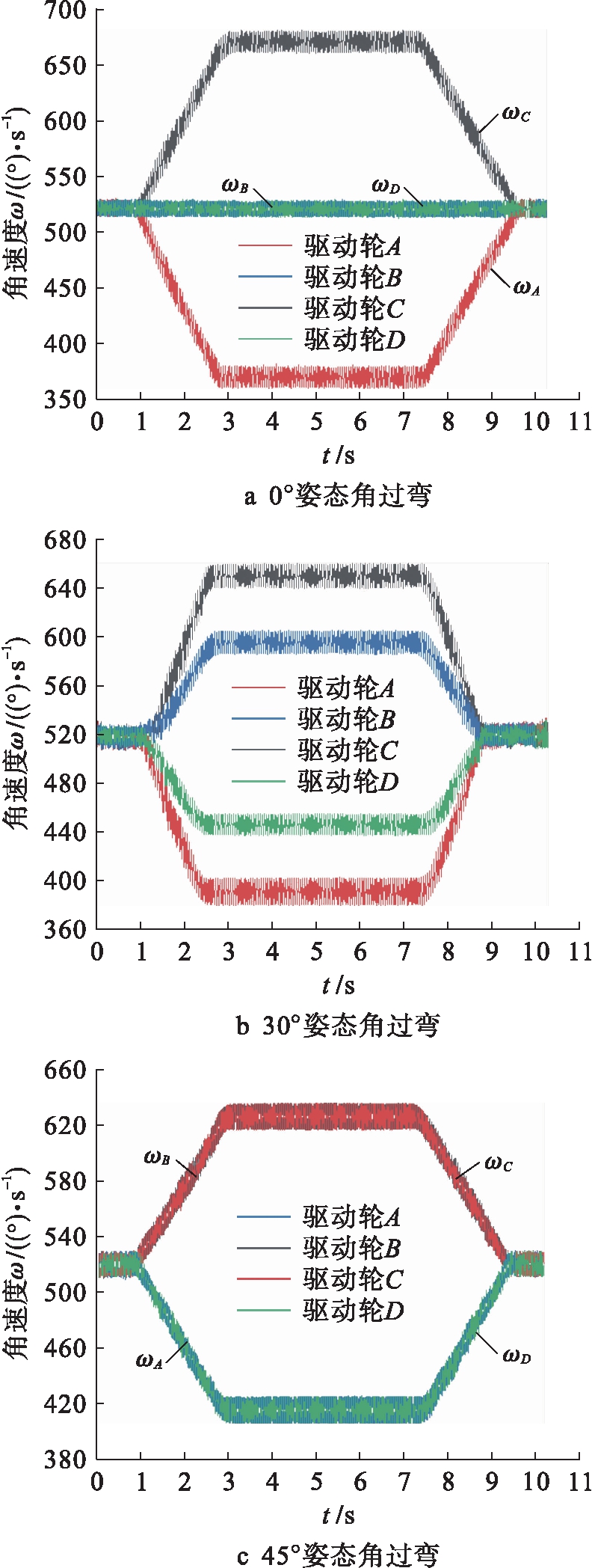
图10 过弯过程中驱动轮转速
Fig.10 Rotation speed of driving wheel during bending process
5 结 论
本文设计了一种可适应140~150 mm内径管道的机械差速式管道机器人,对机器人的支撑、变径、越障及过弯建立了相应的力学、数学模型,在ADAMS中进行虚拟样机运动仿真,仿真结果验证了理论模型的正确性,所设计的机器人驱动轮在过弯时具有差速功能,避免了驱动轮与管道内壁之间的打滑,提高了管道机器人的运动稳定性.
[1]唐德威,梁涛,姜生元,等.机械自适应管道机器人的机构原理与仿真分析 [J].机器人,2008,30(1):29-33.
(TANG De-wei,LIANG Tao,JIANG Sheng-yuan,et al.Mechanism and simulation analysis of mechanical self-adaptive pipe-robot [J].Robot,2008,30(1):29-33.)
[2]曹建树,徐宝东,刘强,等.支承轮式管道机器人变径机构动力学分析 [J].新技术新工艺,2015(2):87-90.
(CAO Jian-shu,XU Bao-dong,LIU Qiang,et al.Dynamics analysis of adjusting mechanism for wall-press pipeline robots [J].New Technology & New Process,2015(2):87-90.)
[3]刘清友.油气管道机器人技术现状及发展趋势 [J].西华大学学报(自然科学版),2016,35(1):1-6.
(LIU Qing-you.Research status and development ten-dency of the oil and gas in-pipe robot [J].Journal of Xihua University (Natural Science Edition),2016,35(1):1-6.)
[4]武洪恩,董洁,潘俊朋,等.基于ADAMS的装车机器人运动分析 [J].科学技术与工程,2019,19(4):121-125.
(WU Hong-en,DONG Jie,PAN Jun-peng,et al.Kinematic analysis of loading robot based on ADAMS [J].Science Technology and Engineering,2019,19(4):121-125.)
[5]陈克,李晓政,周霜霜.动力总成悬置系统优化与减振分析 [J].沈阳工业大学学报,2016,38(1):57-62.
(CHEN Ke,LI Xiao-zheng,ZHOU Shuang-shuang.Optimization and vibration reduction analysis for po-wertrain mounting system [J].Journal of Shenyang University of Technology,2016,38(1):57-62.)
[6]Zagler A,Pfeiffer F.“MORITZ” a pipe crawler for tube junctions [C]//2003 IEEE International Confe-rence on Robotics and Automation.Taipei,China,2003:2954-2959.
[7]李庆凯,唐德威,姜生元,等.三轴差动式管道机器人的驱动特性及仿真研究 [J].哈尔滨工程大学学报,2012,33(6):753-758.
(LI Qing-kai,TANG De-wei,JIANG Sheng-yuan,et al.Research and simulation on the driving property of a tri-axial differential pipeline robot [J].Journal of Harbin Engineering University,2012,33(6):753-758.)
[8]王殿君,李润平,黄光明.管道机器人的研究进展 [J].机床与液压,2008,36(4):185-187.
(WANG Dian-jun,LI Run-ping,HUANG Guang-ming.Progresses in study of pipeline robot [J].Machine Tool & Hydraulics,2008,36(4):185-187.)