库塔法进行仿真计算，研究了限位器参数(刚度比、阻尼比)对冲击响应的影响.结果表明，限位式准零刚度隔离系统能有效降低冲击载荷作用下的相对位移响应，通过匹配合理的限位器刚度及阻尼参数，可有效提高其抗冲击性能.摘 要： 针对准零刚度系统受冲击载荷作用时相对位移响应较大的问题，提出限位式准零刚度隔离系统.分析了限位式准零刚度系统的工作原理，建立其冲击激励下的动力学方程，采用龙格库塔法进行仿真计算，研究了限位器参数(刚度比、阻尼比)对冲击响应的影响.结果表明，限位式准零刚度隔离系统能有效降低冲击载荷作用下的相对位移响应，通过匹配合理的限位器刚度及阻尼参数，可有效提高其抗冲击性能.
低频隔振一直是学者们所关注的热点话题，准零刚度隔振便是其中一种非常具有代表性的低频隔振技术.通过正、负刚度机构并联而成的准零刚度隔振器，在不牺牲承载能力的同时，又能获得较低的隔振频率，从而实现低频甚至超低频隔振.由Ibrahim[1]和陆泽琦等[2]发表的相关综述可以看出，随着国内外学者对低频非线性隔振系统展开的深入研究，准零刚度系统在隔振方面的研究已取得一定进展.
近年来，由于对恶劣坏境下敏感设备的隔离要求不断提高，学者们对非线性系统在冲击隔离方面的研究逐渐增多[3-6].Ledezma-Ramirez等[7]利用非线性刚度特别是低动态刚度实现冲击隔离，表明非线性刚度能减小位移和加速度响应；Liu等[8]研究了准零刚度隔振器在不同基底冲击激励下的隔冲性能，研究表明，准零刚度系统在加速度响应方面具有良好的隔冲效果；Tang等[9]分析了三弹簧准零刚度隔振器在基底激励下的冲击隔离特性，结果表明，准零刚度隔振系统在小振幅激励下的加速度响应与位移响应优于线性隔振器.
由上述文献可知，准零刚度隔振器在受到冲击载荷作用时的加速度响应幅值较小，但相对位移响应幅值较大.设备相对基底的位移幅值过大时，很可能会超过设备与外界连接部件的允许值，甚至会超出隔振元件本身的极限变形范围，因此，在隔振装置的设计过程中如何限制设备的相对位移幅值显得非常重要[10].目前，通过增加限位装置来限制设备的相对位移是简单且有效的方法之一[11-13].
本文为提高准零刚度系统的隔冲性能，提出限位式准零刚度隔离系统.对比分析了有无限位装置的准零刚度系统在半正弦冲击载荷作用下的相对位移响应及加速度响应，研究了限位式准零刚度系统在不同限位器参数(刚度比、阻尼比)下的冲击响应特性，为之后合理设计具有抗冲击性能的低频隔离系统提供理论参考.
图1为限位式准零刚度隔离系统的简化模型，主要由三弹簧准零刚度隔振系统与限位装置并联而成.其中，构成准零刚度系统负刚度结构的是刚度为kh的水平双压缩弹簧，其原长为l0，压缩后长度为l；正刚度结构是刚度为kv的竖直弹簧，阻尼为c1；k2和c2代表限位系统刚度和阻尼；M为被隔离设备的质量；限位器为双向限位，Gap为限位器单侧间隙，设限位器上侧间隙为正值，下侧间隙为负值；x为系统的位移响应.在重力作用下，此时系统处于静平衡位置，两侧弹簧kh处于水平压缩状态.准零刚度隔振系统的上下两端分别与被隔离设备和基座相连，起到支撑和隔振作用.当准零刚度隔振器变形超过单侧间隙时，限位器与设备接触，限制设备产生较大位移.
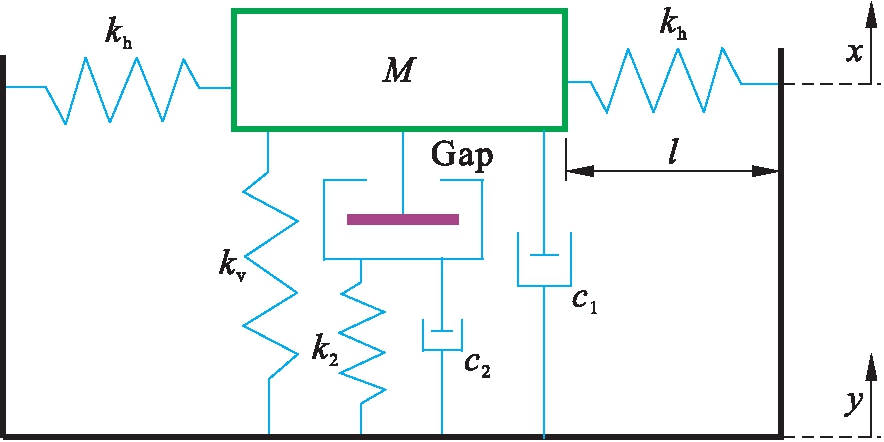
图1 限位式准零刚度系统简化模型
Fig.1 Simplified model of limiter-type QZS system
当设备处于平衡位置或隔离器变形较小，限位器未与设备发生接触时，系统为准零刚度隔振系统，由文献[14]可知，此时系统具有良好的低频隔振效果，在力f的作用下，系统的力位移关系式为
(1)
当隔离器的变形量大于单侧间隙Gap时，被隔离设备与限位器发生接触，限位器限制设备产生过大位移，此时系统的力位移关系式为
(2)
限位式准零刚度隔振器的力学模型如图2所示，其中，虚线为无限位装置的准零刚度隔振系统力学模型.x3与x2分别为限位器作动的上下节点.当x位于|x2x3|段内时，两曲线重合，此时限位器未作动，系统具有准零刚度特性，一般情况下|ox2|=|ox3|=Gap.当x超过此段时，限位器发生作用.
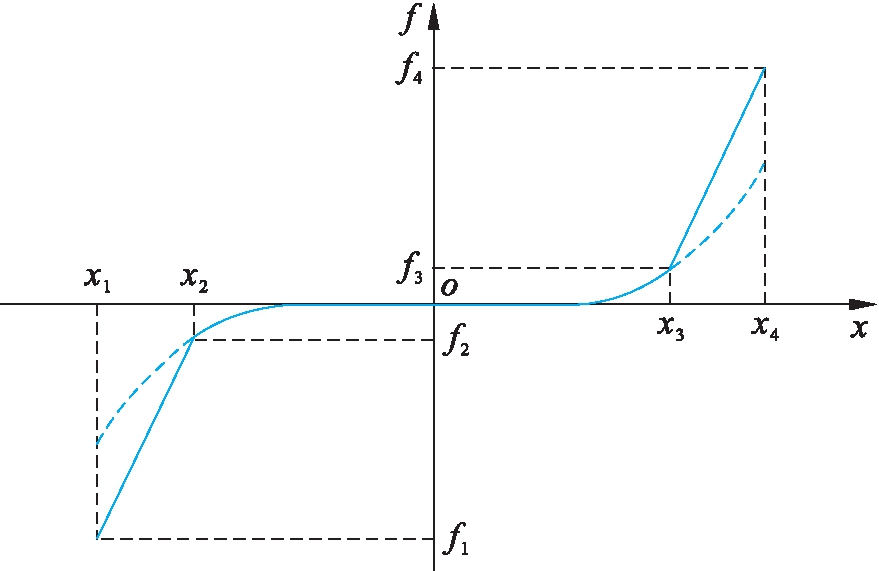
图2 力学模型简图
Fig.2 Schematic diagram of mechanical model
在基底冲击激励的作用下，图1所示的限位式准零刚度系统的运动方程主要分为两部分，本文用z=x-y表示设备的相对位移.
1) 当|z| 2) 当|z|≥Gap时，被隔离设备的相对位移大于限位器的安装间隙，与限位器发生碰撞，此时系统的刚度k为准零刚度系统与限位系统的刚度之和，系统的阻尼为隔振器阻尼c1与限位器阻尼c2之和. 根据以上分析，限位式准零刚度隔振系统在冲击激励作用下的运动方程为 (3) 式中， (4) 其中：A为冲击载荷加速度幅值；t0为冲击持续时间；fs=1/t0为冲击频率. 选取的被隔离设备质量M=9 kg，准零刚度部分的结构参数满足公式(5)所给出的准零刚度设计条件，支撑弹簧kv=12 N/mm，阻尼比ζ1=0.05，负刚度弹簧刚度kh=9 N/mm，负刚度弹簧的原长l0=60 mm，平衡位置的长度l=36 mm.限位器的阻尼比为ζ2，限位器与隔振器支撑弹簧的刚度比为η.采用四阶龙格 (5) (6) (7) 根据已确定的隔离器参数，选取冲击载荷加速度幅值A=50g，脉宽t0=5 ms，g=9.8 m/s2.取限位器两侧限位间隙为5 mm，限位器的阻尼比为ζ2=0.05，刚度比为η=8.系统的相对位移响应及加速度响应曲线分别如图3、4所示.其中，限位系统为图1所示的限位式准零刚度隔离系统；准零系统为无限位器的三弹簧准零刚度系统；线性系统为准零系统去掉负刚度结构后的等效线性系统. 图3 相对位移响应曲线 由图3可以看出，三个系统中设备的相对位移最大峰值均出现在冲击结束后的第一个峰值处，其中，准零系统的最大峰值出现在0.047 8 s处，峰值为48.67 mm；线性系统的最大峰值出现在0.044 2 s处，其峰值为39.76 mm，相对于准零系统降低18.3%；限位系统第一个峰值出现在0.019 8 s，其峰值为18.41 mm，相较于未安装限位器的准零系统，其峰值降低62.2%，相对位移响应峰值大幅降低. 图4 加速度响应曲线 由图4可以看出，限位系统的加速度响应明显增加，其峰值出现在0.018 7 s，峰值为15.34g，是准零系统加速度峰值的2.3倍.同时可以看出，由于限位器压缩时吸收能量，恢复变形时释放能量，使系统受到的冲击能量更快耗散，限位系统的加速度响应更快趋于平稳. 通过对比可知，限位器的加入使相对位移响应得到明显降低，有效限制设备在冲击激励下产生较大位移，同时加速度响应急剧增加.匹配合理的隔离器参数，既使相对位移有效降低，又可以获得相对较低的加速度响应. 限位式准零刚度系统在半正弦冲击载荷作用下，分别选取不同的限位器阻尼比ζ2(0.03～0.57)和刚度比η(1～60).限位器阻尼比ζ2与刚度比η对限位式准零刚度系统相对位移响应峰值的影响规律如图5、6所示. 图5 不同刚度比下相对位移幅值随阻尼比变化曲线 由图5可以看出，当系统的刚度比η为定值时，设备的最大相对位移随限位器阻尼比ζ2的增大而减小，且η较小的设备对阻尼比ζ2更加敏感.同时结合图6可以明显看出，当阻尼比ζ2为定值时，相对位移幅值随着刚度比的增加而逐渐衰减，当η<10时衰减迅速，随刚度比逐渐增大衰减趋势逐渐变缓. 图6 不同阻尼比下相对位移幅值随刚度比变化曲线 限位器阻尼比ζ2与刚度比η对限位式准零刚度系统加速度响应峰值的影响规律如图7、8所示. 图7 不同刚度比下加速度幅值随阻尼比变化曲线 图8 不同阻尼比下加速度幅值随刚度比变化曲线 由图7可以看出，当刚度比η为定值时，加速度幅值随阻尼比ζ2的增加呈现先减小后增大的趋势.为了更加清晰地反应出峰值变化的规律，将不同刚度比η对应的加速度响应峰值的极小值点设为a，将a点所对应的阻尼比设为ζa，并将这些极值点连接起来，如图7中的曲线α所示.对于加速度响应来说，较大刚度比η的设备对阻尼比ζ2的变化更加敏感.结合图8可以看出，系统加速度响应峰值与刚度比η呈正相关，且增加趋势逐渐变缓. 综上所述，当限位器刚度较大时，其相对位移幅值较小，适当减小限位器的阻尼比，可减小其加速度响应幅值；当限位器刚度较小时，其加速度响应幅值较小，此时适当增加其限位器的阻尼比，可以减小相对位移的响应幅值.通过匹配合理的限位器参数既可获得较低相对位移响应，同时系统的加速度响应也可显著减小，有效提升系统的抗冲击性能. 本文通过分析得出以下结论： 1) 相较于无限位的准零刚度系统，限位式准零刚度隔离系统在冲击载荷作用下可有效降低系统的相对位移响应峰值，且该系统在平衡位置附近仍具有准零刚度特性. 2) 在小阻尼比范围内(0<ζ2<ζa)，增大限位器的阻尼可降低设备的相对位移响应幅值和加速度响应幅值；当阻尼比较大时(ζa<ζ2)，相对位移响应幅值继续降低，但加速度响应幅值会随之增大. 3) 限位器刚度比的增加可有效降低系统的相对位移响应幅值，但会导致加速度响应幅值增大. 4) 对于大刚度比限位器而言，系统的相对位移响应较小，适当减小限位器的阻尼比，可减小其加速度响应幅值；小刚度比限位器的加速度幅值较小，此时适当增加其限位器的阻尼比，可降低其相对位移的响应幅值. [1]Ibrahim R A.Recent advances in nonlinear passive vibration isolators [J].Journal of Sound and Vibration，2008，314(3/4/5)：371-452. [2]陆泽琦，陈立群.非线性被动隔振的若干进展 [J].力学学报，2017，49(3)：550-564. (LU Ze-qi，CHEN Li-qun.Some recent progresses in nonlinear passive isolations of vibrations [J].Chinese Journal of Theoretical and Applied Mechanics，2017，49(3)：550-564.) [3]Ledezma-Ramirez D F，Tapia-Gonz [4]闫明，田浩男，刘海超.孔隙式隔振系统非线性阻尼特性 [J].沈阳工业大学学报，2020，42(6)：648-653. (YAN Ming，TIAN Hao-nan，LIU Hai-chao.Nonli-near damping characteristics of pore-type vibration isolation system [J].Journal of Shenyang University of Technology，2020，42(6)：648-653.) [5]刘浩，姜长青.大型复杂机电加工系统缓冲阻尼动力学性能分析 [J].沈阳工业大学学报，2020，42(6)：654-658. (LIU Hao，JIANG Chang-qing.Analysis of buffer damping dynamic performance of large complex electromechanical machining system [J].Journal of Shenyang University of Technology，2020，42(6)：654-658.) [6]陈克，李春萍，李孟宇.基于发动机激励的车内振动和噪声阶次分析 [J].沈阳工业大学学报，2019，41(1)：47-51. (CHEN Ke，LI Chun-ping，LI Meng-yu.Order analysis for vehicle interior vibration and noise based on engine excitation [J].Journal of Shenyang University of Technology，2019，41(1)：47-51.) [7]Ledezma-Ramirez D F，Ferguson N S，Brennan M J，et al.An experimental nonlinear low dynamic stiffness device for shock isolation [J].Journal of Sound and Vibration，2015，347：1-13. [8]Liu X T，Huang X C，Hua H X.Performance of a zero stiffness isolator under shock excitations [J].Journal of Vibration and Control，2014，20(14)：2090-2099. [9]Tang B，Brennan M J.On the shock performance of a nonlinear vibration isolator with high-static-low-dynamic-stiffness [J].International Journal of Mechanical Sciences，2014，81：207-214. [10]刘海超.舰用限位隔离系统隔振抗冲击性能研究 [D].沈阳：沈阳工业大学，2019. (LIU Hai-chao.Research on vibration isolation and shock resistance of vibration isolation system with displacement restrictors for warships [D].Shenyang：Shenyang University of Technology，2019.) [11]张春辉，汪玉，吴一红，等.双限位器隔离系统的冲击响应计算及参数影响分析 [J].振动与冲击，2015，34(9)：125-130. (ZHANG Chun-hui，WANG Yu，WU Yi-hong，et al.Shock response calculation and effects of structural parameters on shock isolation system with double displacement restrictors [J].Journal of Vibration and Shock，2015，34(9)：125-130.) [12]刘海超，闫明，冯麟涵.带限位隔振系统的冲击响应分析 [J].振动与冲击，2019，38(21)：172-177. (LIU Hai-chao，YAN Ming，FENG Lin-han.Shock response of a vibration isolation system with displacement restrictors [J].Journal of Vibration and Shock，2019，38(21)：172-177.) [13]李鹏超，李明.冲击激励下含限位器的气囊 (LI Peng-chao，LI Ming.Dynamic characteristics of an airbag-marine rotating machinery system with displacement restrictor under shock excitation [J].Journal of Vibration and Shock，2020，39(5)：183-187.) [14]Carrella A，Brennan M J，Waters T P，et al.Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness [J].International Journal of Mechanical Sciences，2012，55：22-29.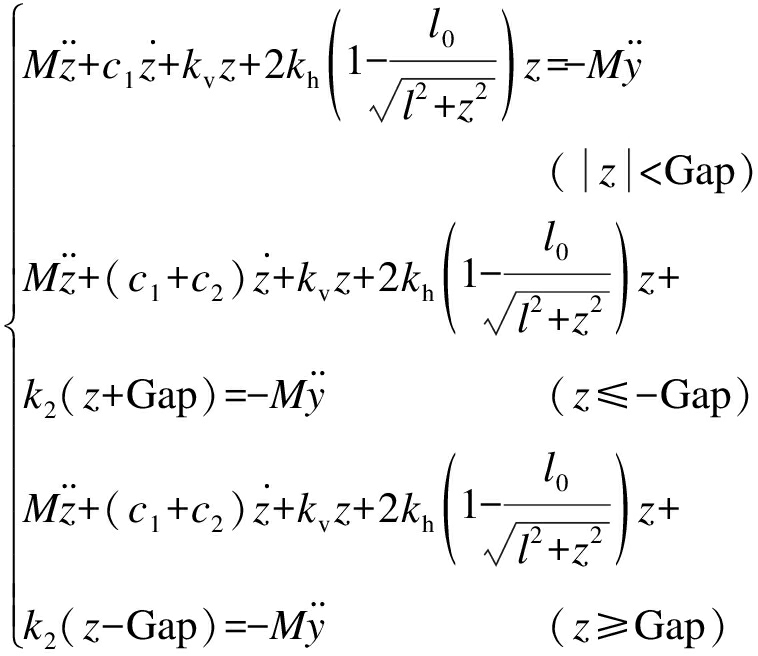
为半正弦加速度冲击激励，其表达式为
3 冲击响应计算及分析
库塔法对式(3)进行求解，即
3.1 限位器对冲击响应的影响
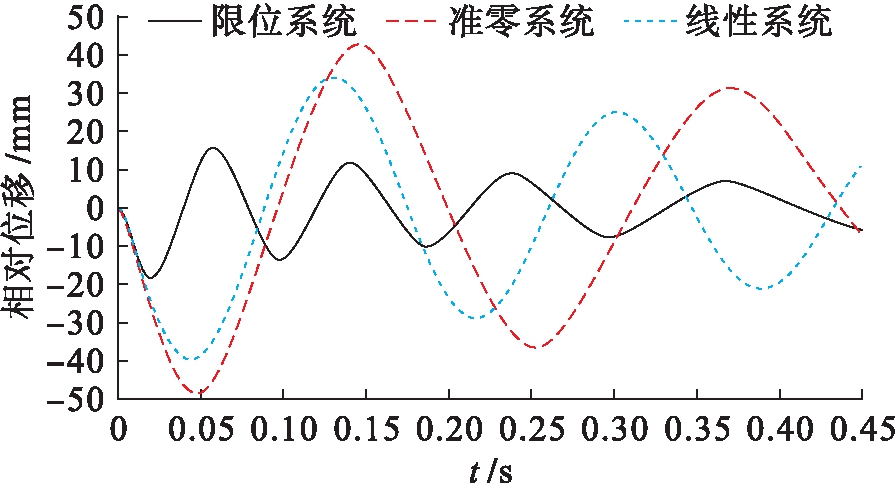
Fig.3 Relative displacement response curves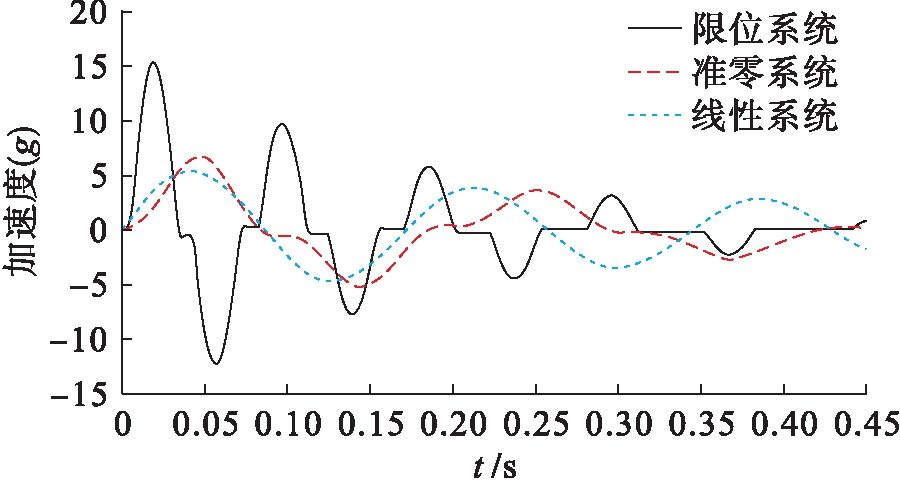
Fig.4 Acceleration response curves3.2 限位器参数对冲击响应的影响
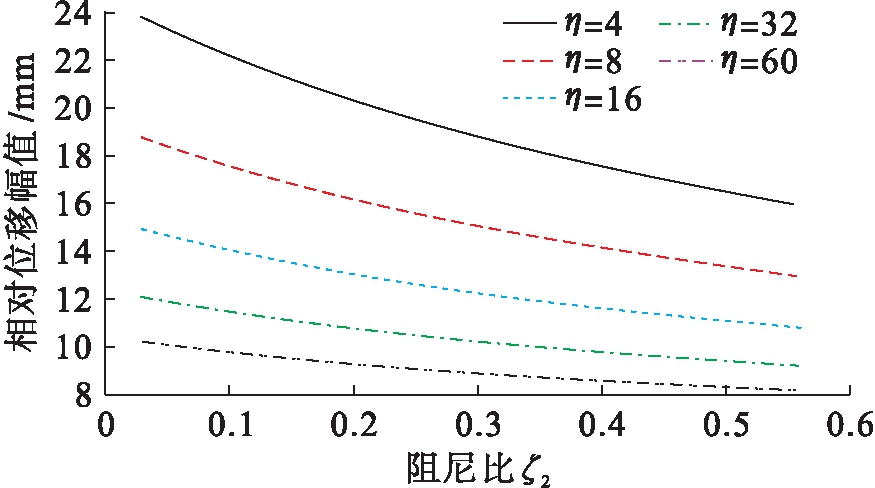
Fig.5 Curves of relative displacement amplitude in relation with damping ratio under different stiffness ratios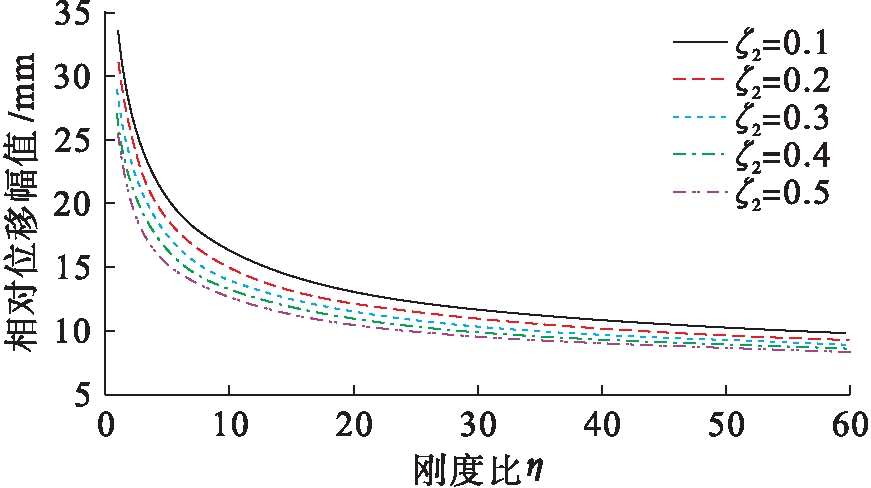
Fig.6 Curves of relative displacement amplitude in relation with stiffness ratio under different damping ratios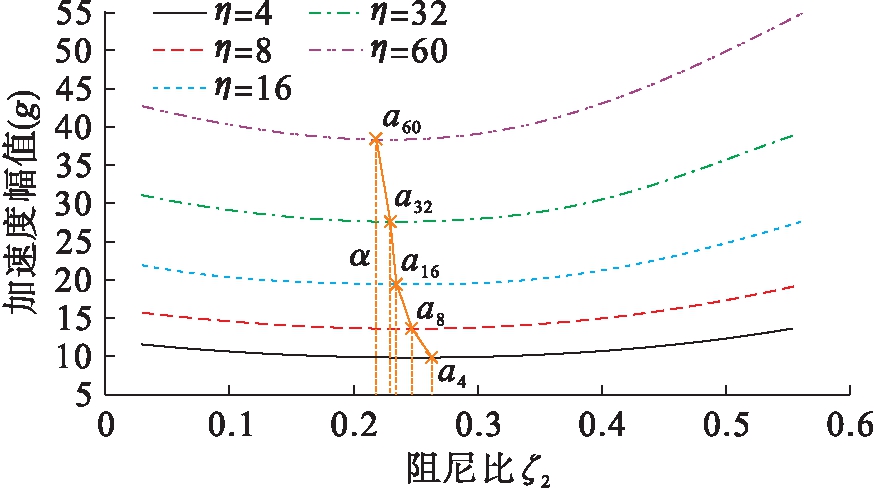
Fig.7 Curves of acceleration amplitude in relation with damping ratio under different stiffness ratios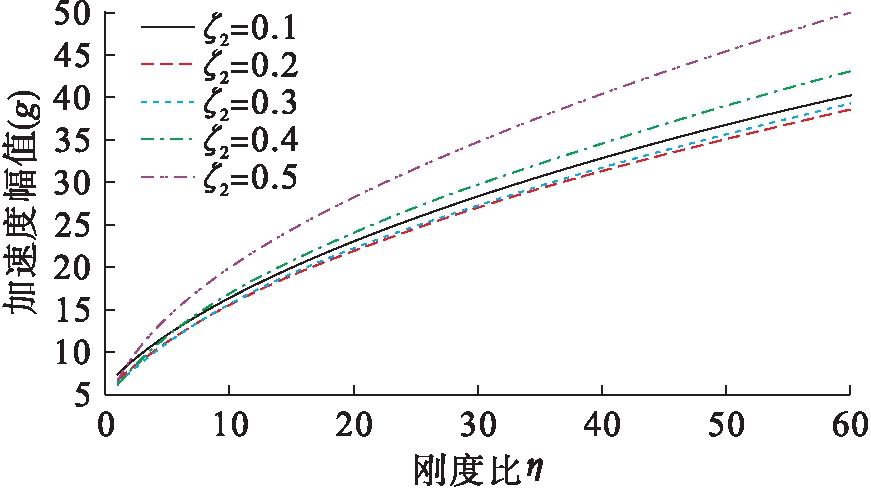
Fig.8 Curves of acceleration amplitude in relation with stiffness ratio under different damping ratios4 结 论
lez P E，Ferguson N，et al.Recent advances in shock vibration isolation：an overview and future possibilities [J].Applied Mechanics Reviews，2019，71(6)：1-13.船用旋转机械系统的动力学特性分析 [J].振动与冲击，2020，39(5)：183-187.