近年来,绿色建筑已经成为建筑业一种新的发展趋势[1-2].燃煤电厂固废的粉煤灰通常作为混凝土中一种替代水泥的掺合料,在建筑工程领域中具有广泛的应用[3].但粉煤灰混凝土也存在一些无法避免的缺点,如抗折强度低、抗裂能力差、易脆性破坏等,严重影响了建筑结构的可靠性[4].为了提高粉煤灰混凝土的抗折强度,解决脆性开裂问题,弥补韧性差的不足,国内外许多学者对其进行了研究.范梦甜等[5]研究发现掺入超细粉煤灰的水泥复合胶凝材料28 d抗压强度明显提高,且粉煤灰粒径越细28 d抗压强度越高;陈峰宾等[6]发现纤维的掺入可以改变混凝土内部孔隙率与孔径分布比,且通过各纤维空间网状分布,增强混凝土整体性,可以显著提高混凝土28 d抗压强度;Abushanab等[7]研究发现掺加玄武岩纤维可以显著改善混凝土梁的延性指数和承载能力.本文通过外掺玄武岩纤维研究超细粉煤灰混凝土力学性质.
玄武岩纤维是一种绿色新型无机纤维材料,具有抗拉强度高、弹性模量大、耐腐蚀、成本低等优点,与粉煤灰混凝土之间具有很好的相容性,明显改善粉煤灰混凝土的脆性问题,延长建筑物的使用寿命[8-9].超细粉煤灰与普通粉煤灰相比,可以增强粉煤灰的活性,提高混凝土的密实度,更具减水效应,显著提高粉煤灰混凝土的力学性能[10].为了研究玄武岩纤维超细粉煤灰混凝土(basalt fiber ultrafine fly ash concrete,BFUFAC)的力学性能,本文通过设计正交试验方案,研究不同因素水平的抗压、劈裂抗拉、抗折强度变化,寻求不同工作条件下相对最优的BFUFAC配合比,为BFUFAC的工程应用提供一定的指导和借鉴意义.
1 正交试验设计
1.1 试验原材料
水泥选用辽宁山水集团生产的P.O42.5普通硅酸盐水泥,性能指标如表1所示.粗骨料选用粒径为8~20 mm的碎石;细骨料选用细度模数为2.68的天然中河砂;超细粉煤灰为华电集团生产的I级粉煤灰加工粉磨后的超细粉煤灰,中位径d50=2.433 μm,且粒径在10 μm以下的粉煤灰占总体积的84.1%,超细粉煤灰的具体粒径分布如表2所示;玄武岩纤维选用河南登电玄武石纤公司制造的短切玄武岩纤维,其密度为2.65 g/cm3,性能指标如表3所示,试验纤维样品如图1所示;减水剂使用奈系高效减水剂;采用洁净自来水.
表1 水泥性能指标
Tab.1 Cement performance indexes

安定性初凝时间/min终凝时间/min28d抗压强度/MPa28d抗折强度/MPa合格175235≥49.0≥8.0
表2 超细粉煤灰粒径分布
Tab.2 Particle size distribution of ultrafine fly ash

粒径/μm体积分数/%0~247.52~416.0粒径/μm体积分数/%4~69.66~86.6粒径/μm体积分数/%8~104.410~2010.3粒径/μm体积分数/%20~404.840~600.8
表3 玄武岩纤维性能指标
Tab.3 Basalt fiber performance indexes

密度/(g·cm-3)单纤直径/μm抗拉强度/MPa弹性模量/GPa极限延伸率/%2.651242501023.2

图1 试验用玄武岩纤维样品
Fig.1 Test samples of basalt fibers used for tests
1.2 试件制作与设备
试验中,抗压和劈裂抗拉试验采用100 mm×100 mm×100 mm立方体试件,抗折试验采用100 mm×100 mm×400 mm棱柱体试件,每组不少于3个.搅拌机采用HY2-60式搅拌机,各组分投料次序如图2所示.将拆模试件放入室温20±2 ℃,相对湿度大于95%的养护室养护,养护28 d.抗压试验采用济南恒瑞金试验机有限公司生产的YAW-1000型微机控制电液伺服压力试验机,劈裂抗拉试验和抗折试验采用时代试金生产的WDW-100型微机控制电子式万能试验机.
1.3 因素、水平的确定
正交试验是研究多因素多水平问题的一种常规有效方法,可以通过试验结果分析各个因素在不同水平下对试验结果的影响程度[11].在不同水平下,超细粉煤灰掺量、玄武岩纤维掺量、玄武岩纤维长度、减水剂掺量会对BFUFAC产生不同程度的力学性能影响[12].本文设计四因素三水平正交试验,正交因素、水平如表4所示.
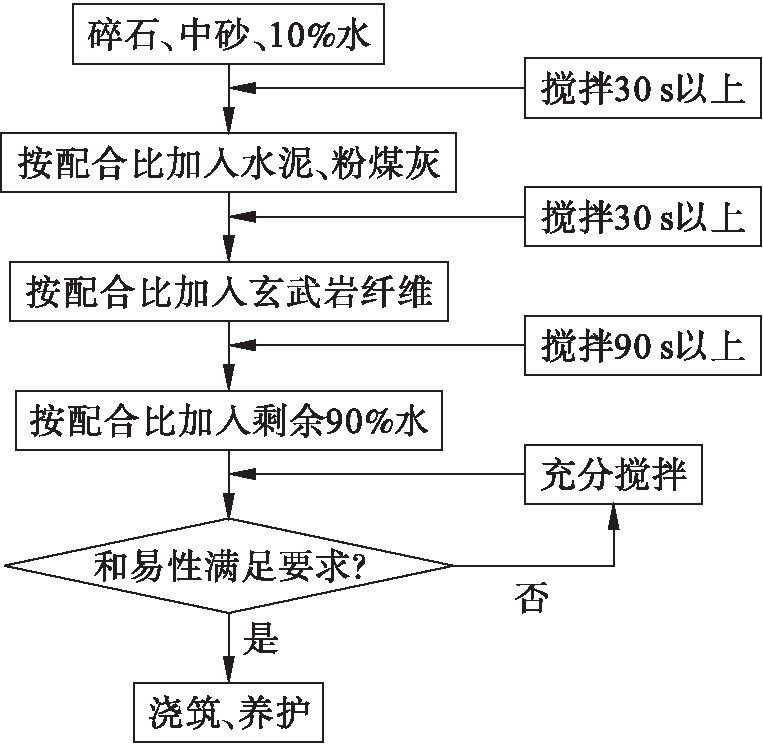
图2 试件制作流程图
Fig.2 Flow chart of sample fabrication
1.4 材料配合比及试验结果
在配制BFUFAC试验中,为弥补粉煤灰对BFUFAC的强度损失,粉煤灰采用超量取代法进行配比,取代系数为1.2[13].试验材料配合比和试验结果如表5所示.
2 正交试验极差分析
2.1 各因素对抗压强度的影响
抗压试验完成后,运用极差法对各组试件结果进行数据分析,极差分析结果如表6所示.各因素在不同水平下的抗压强度曲线如图3所示.
由极差分析法可知,极差Rj数值越大,表明该因素对试验结果影响越大[14].由表6可知,各因素对BFUFAC抗压强度影响程度为:粉煤灰掺量大于玄武岩纤维掺量大于玄武岩纤维长度大于减水剂掺量.其中,粉煤灰掺量对抗压强度的影响最明显.由图3可知,当粉煤灰掺量越高时,混凝土抗压强度越低,且随着掺量增大,抗压强度降低速率越快;当玄武岩纤维掺量增大时,抗压强度降低,掺量为0.1%时,抗压强度最高;当玄武岩纤维长度增大时,抗压强度先增大后减少,其长度为18 mm时,抗压强度最大;当减水剂掺量增大时,抗压强度降低,且减水剂掺量越大,抗压强度降低速率越快.因此,在侧重抗压强度的工程实际应用中,BFUFAC应选择的配合比为A1B1C2D1.
表4 正交因素、水平
Tab.4 Orthogonal factors and levels

水平粉煤灰掺量/%玄武岩纤维掺量/%玄武岩纤维长度/mm减水剂掺量/%1A1(20)B1(0.1)C1(12)D1(0.8)2A2(30)B2(0.2)C2(18)D2(1.2)3A3(40)B3(0.3)C3(24)D3(1.6)
表5 材料配合比及试验结果
Tab.5 Material ratio and test results
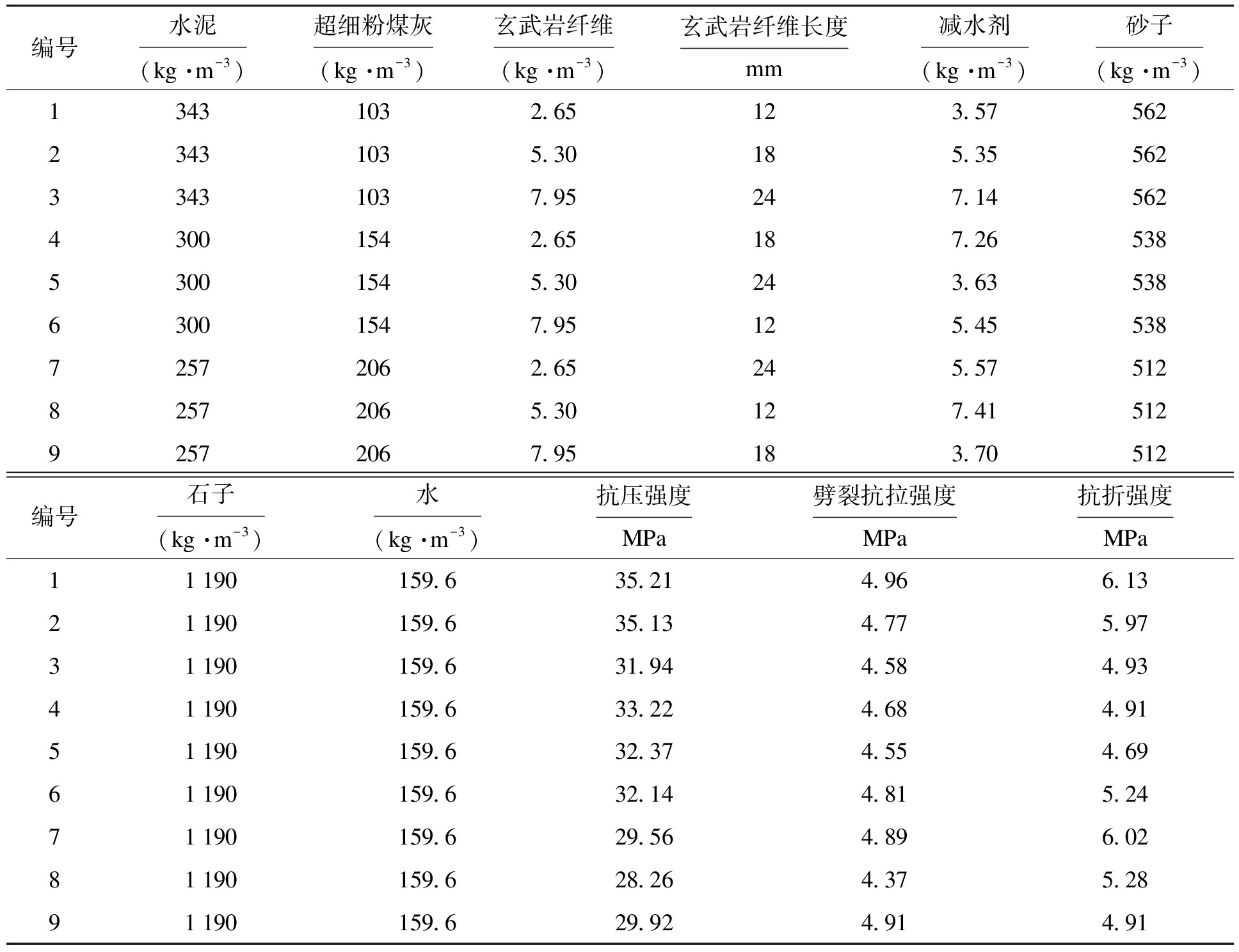
编号水泥(kg·m-3)超细粉煤灰(kg·m-3)玄武岩纤维(kg·m-3)玄武岩纤维长度mm减水剂(kg·m-3)砂子(kg·m-3)13431032.65123.5756223431035.30185.3556233431037.95247.1456243001542.65187.2653853001545.30243.6353863001547.95125.4553872572062.65245.5751282572065.30127.4151292572067.95183.70512编号石子(kg·m-3)水(kg·m-3)抗压强度MPa劈裂抗拉强度MPa抗折强度MPa11190159.635.214.966.1321190159.635.134.775.9731190159.631.944.584.9341190159.633.224.684.9151190159.632.374.554.6961190159.632.144.815.2471190159.629.564.896.0281190159.628.264.375.2891190159.629.924.914.91
表6 抗压强度极差分析
Tab.6 Range analysis of compressive strength
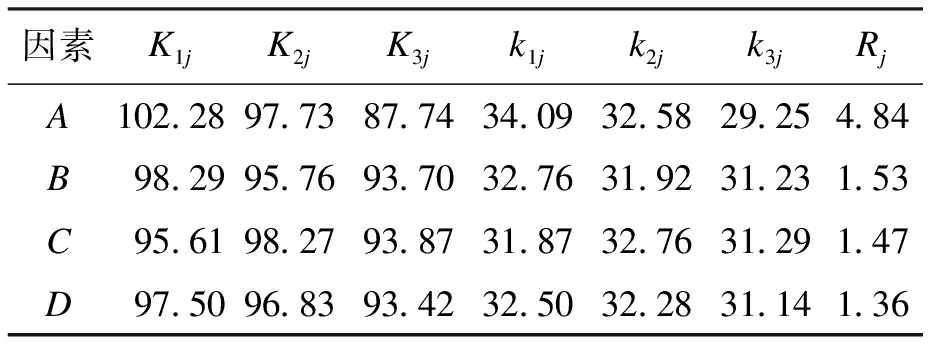
因素K1jK2jK3jk1jk2jk3jRjA102.2897.7387.7434.0932.5829.254.84B98.2995.7693.7032.7631.9231.231.53C95.6198.2793.8731.8732.7631.291.47D97.5096.8393.4232.5032.2831.141.36
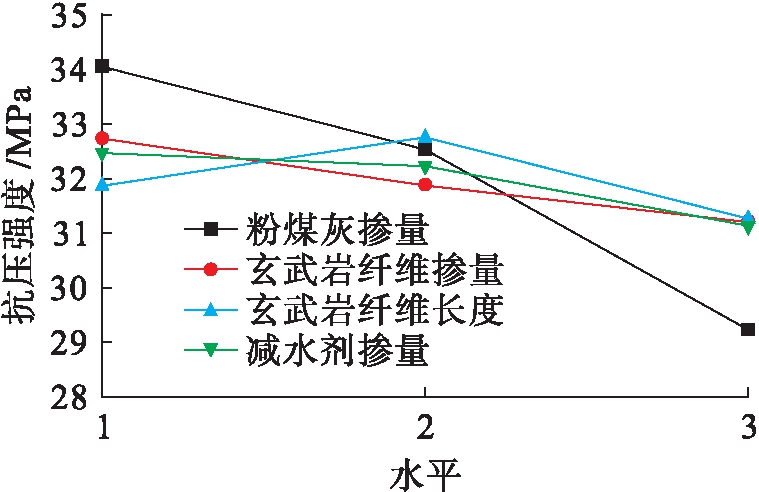
图3 各因素对抗压强度的影响
Fig.3 Influence of various factors on compressive strength
2.2 各因素对劈裂抗拉强度的影响
各组试件的劈裂抗拉试验极差分析表明,各因素对劈裂抗拉强度影响程度不同,具体极差分析结果如表7所示,各因素对劈裂抗拉影响如图4所示.
表7 劈裂抗拉强度极差分析
Tab.7 Range analysis of splitting tensile strength
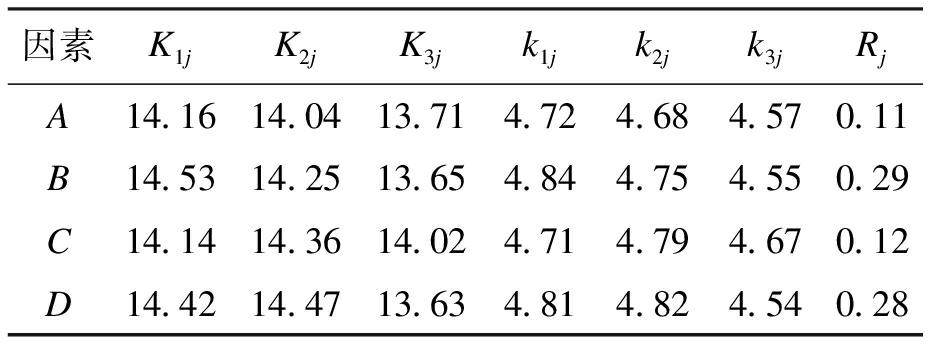
因素K1jK2jK3jk1jk2jk3jRjA14.1614.0413.714.724.684.570.11B14.5314.2513.654.844.754.550.29C14.1414.3614.024.714.794.670.12D14.4214.4713.634.814.824.540.28
由极差Rj可知,对于BFUFAC的劈裂抗拉强度,各因素的影响程度为:玄武岩纤维掺量大于减水剂掺量大于玄武岩纤维长度大于粉煤灰掺量.由图4可知,粉煤灰掺量越大,劈裂抗拉强度越低,且随着掺量增大,降低速率越快;减水剂掺量为1.2 kg/m3时劈裂抗拉强度最大,过量的减水剂掺量会严重影响混凝土的劈裂抗拉强度;玄武岩纤维掺量越大,劈裂抗拉强度越低,且随着掺量增大,降低速率越快;玄武岩纤维长度为18 mm时,劈裂抗拉强度最大,过长的纤维长度会严重影响混凝土的劈裂抗拉强度.因此,在侧重劈裂抗拉强度的工程实际应用中,BFUFAC最优配合比为A1B1C2D2.
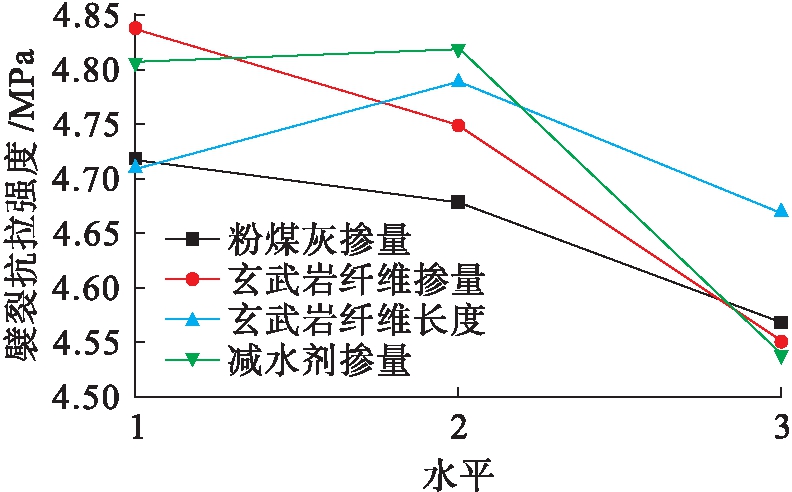
图4 各因素对劈裂抗拉强度的影响
Fig.4 Influence of various factors on splitting tensile strength
2.3 各因素对抗折强度的影响
由各组试件抗折试验极差分析表明,各因素对抗折强度影响程度不同,具体极差分析结果如表8所示,各因素对抗折强度影响程度如图5所示.
表8 抗折强度极差分析
Tab.8 Range analysis of flexural strength
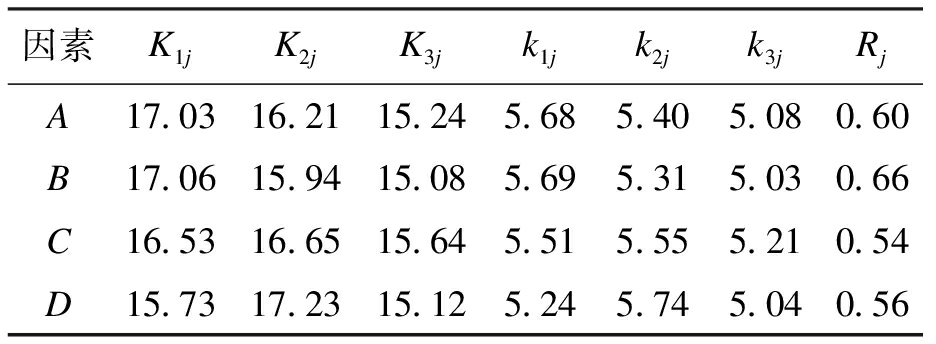
因素K1jK2jK3jk1jk2jk3jRjA17.0316.2115.245.685.405.080.60B17.0615.9415.085.695.315.030.66C16.5316.6515.645.515.555.210.54D15.7317.2315.125.245.745.040.56
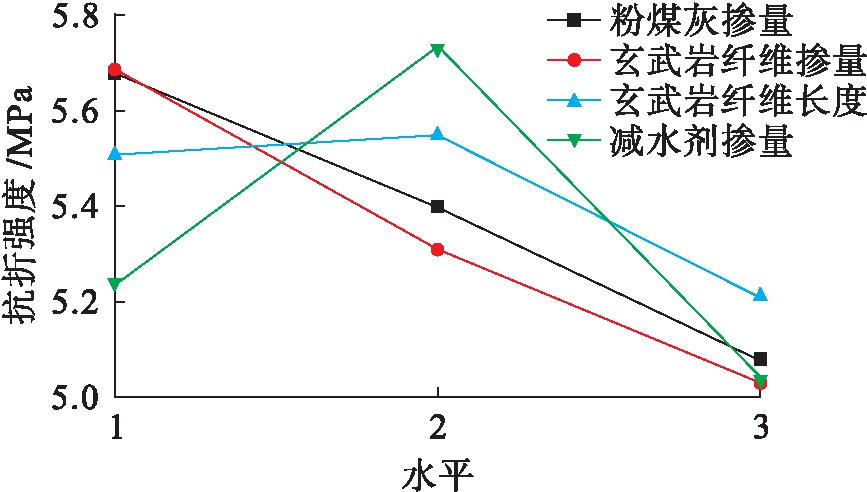
图5 各因素对抗折强度的影响
Fig.5 Influence of various factors on flexural strength
对于BFUFAC的抗折强度,各因素的影响程度为:玄武岩纤维掺量大于粉煤灰掺量大于减水剂掺量大于玄武岩纤维长度.由图5可知,玄武岩纤维掺量越大,抗折强度越低,掺量为0.1%时,抗折强度最大;当粉煤灰掺量越大时,抗折强度越低,20%掺量时,抗折强度最大;减水剂掺量增大时,抗折强度的变化趋势先增大后降低,在掺量1.2%时抗折强度最高;抗折强度随玄武岩纤维长度增长先增加后降低,18 mm的玄武岩纤维能够充分发挥纤维优异的抗拉性能,增强混凝土的抗折性能.因此,在侧重抗折强度的工程实际应用中,BFUFAC抗折强度最优配合比为A1B1C2D2.
2.4 各因素对力学性能影响机理分析
为进一步研究BFUFAC力学性能,现对试验各主要影响因素的作用机理进行分析.粉煤灰在混凝土中的水化反应速度较慢,在28 d的养护周期内,粉煤灰掺量越多,对混凝土的影响越显著,导致混凝土的力学强度越低[15].同时,混凝土强度降低会减小混凝土对玄武岩纤维提供的握裹力,影响玄武岩纤维对混凝土力学性能的加强作用.适量的玄武岩纤维掺加到混凝土中可以起到“微筋”作用,能够从各个方向上有效抑制和约束裂缝的开展和延伸,增强其力学性能,但过高的纤维掺量在混凝土中分散不均匀,极易形成有害孔隙,增大了混凝土的薄弱面,降低了混凝土的力学性能[16].合适的玄武岩纤维长度可以在混凝土中产生较大的握裹力,充分发挥玄武岩纤维的抗拉性能.纤维长度过短时,混凝土浆体对纤维的包裹力较小,不能充分发挥纤维优异的抗拉性能;纤维长度过长时,纤维极易在混凝土中发生团结现象,显著增加了混凝土中的有害孔隙率,降低了玄武岩纤维对混凝土的增强能力.过量地使用减水剂会导致混凝土出现离析、泌水、板结现象,严重影响混凝土的强度.
3 正交试验方差分析
3.1 抗压强度方差分析
极差分析可以直接得出试验的最优方案,但是极差分析具有一定的片面性,不能区分试验结果与试验误差[17].方差分析可以区分各因素水平变化和误差原因导致的试验结果差异,对极差分析结果进一步补充.本试验中,抗压强度方差分析如表9所示.
因在四因素三水平正交试验中无空白列,所以将因素偏差小的偏差平方和代替误差平方和.由表9可以看出,粉煤灰掺量偏差平方和最大,对抗压强度有显著影响的可信度为99%,可认为粉煤灰对抗压强度的影响是第一位的,这也与极差分析的结果相符;其他因素偏差平方和相对较小,对抗压强度的影响不明显,产生显著性影响的可信度很低,可弱化该因素对抗压强度产生的影响,并将这种影响视为试验误差影响.
表9 抗压强度方差分析
Tab.9 Variance analysis of compressive strength
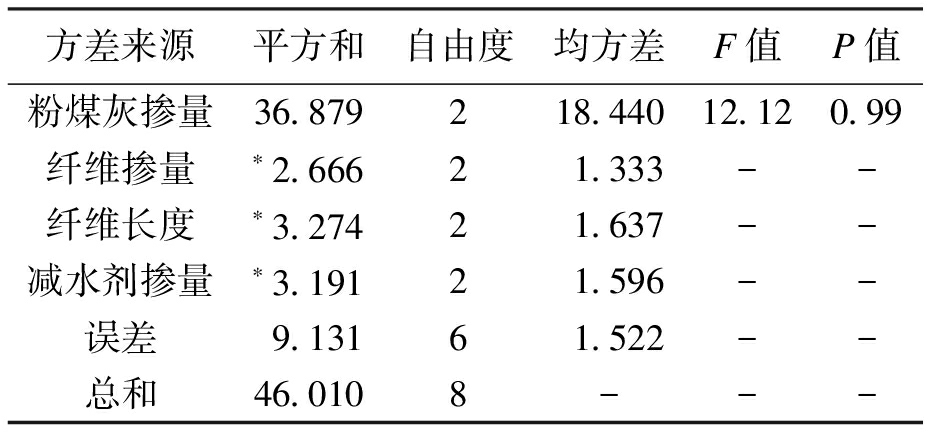
方差来源平方和自由度均方差F值P值粉煤灰掺量36.879218.44012.120.99纤维掺量∗2.66621.333--纤维长度∗3.27421.637--减水剂掺量∗3.19121.596--误差9.13161.522--总和46.0108---
注:带*的项之和归为误差项,下同。
3.2 劈裂抗拉强度方差分析
在劈裂抗拉强度方差分析中,粉煤灰掺量和玄武岩纤维长度偏差平方和最小,弱化该因素影响,将其偏差平方和代替误差平方和,具体方差分析结果如表10所示.
表10 劈裂抗拉强度方差分析
Tab.10 Variance analysis of splitting tensile strength
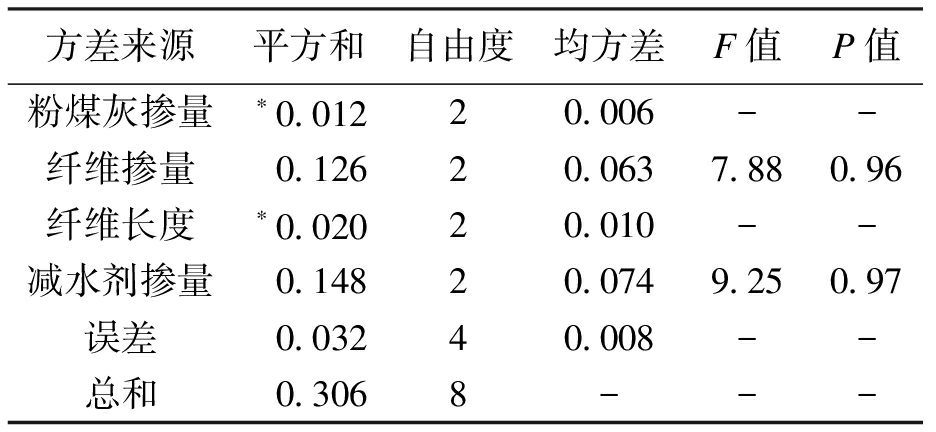
方差来源平方和自由度均方差F值P值粉煤灰掺量∗0.01220.006--纤维掺量0.12620.0637.880.96纤维长度∗0.02020.010--减水剂掺量0.14820.0749.250.97误差0.03240.008--总和0.3068---
由表10可以看出,减水剂掺量和玄武岩纤维掺量对劈裂抗拉强度最具显著性影响,可信度分别达97%和96%.粉煤灰掺量和玄武岩纤维长度不能对劈裂抗拉强度产生明显作用,影响效果相对不显著,与极差分析结果相符.
3.3 抗折强度方差分析
在抗折强度方差分析中,玄武岩纤维长度偏差平方和相对最小,显著性影响程度最低,可将其视作误差,弱化这一因素对试验的作用影响,具体方差分析如表11所示.
表11 抗折强度方差分析
Tab.11 Variance analysis of flexural strength
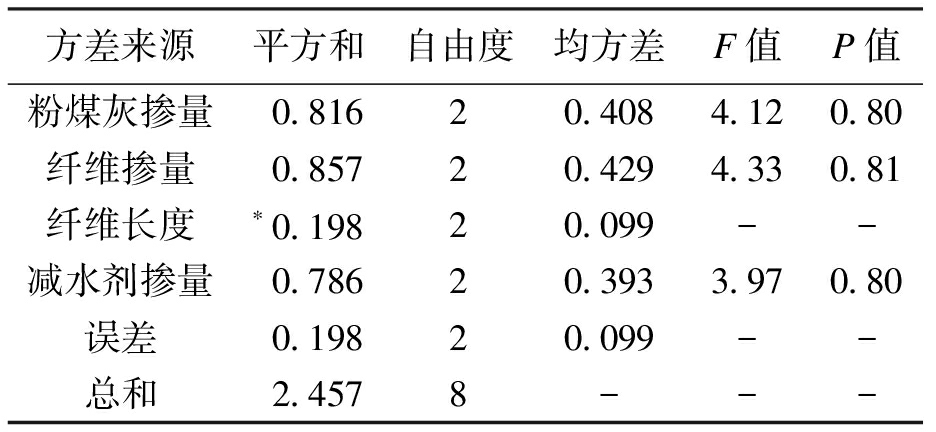
方差来源平方和自由度均方差F值P值粉煤灰掺量0.81620.4084.120.80纤维掺量0.85720.4294.330.81纤维长度∗0.19820.099--减水剂掺量0.78620.3933.970.80误差0.19820.099--总和2.4578---
根据表11方差分析结果可知,玄武岩纤维掺量对抗折强度最具显著性影响,可信度为81%;粉煤灰掺量和减水剂掺量对抗折强度的显著性影响稍低,可信度均达80%,也是试验主要的影响因素;玄武岩纤维长度不能对抗折强度产生明显作用,显著性影响的可信度较低.方差分析结果与极差分析结果基本相符.
玄武岩纤维长度越大,混凝土提供的握裹力越大,可充分发挥纤维的抗拉性能,但纤维在相同体积掺量下,纤维长度越大,混凝土断裂面的纤维相对越少,单一改变纤维长度这一因素变量,对混凝土的抗折性能改善不能起到显著作用,因此在抗折强度中,玄武岩纤维长度最不具显著性影响.
4 试验结果线性回归分析
利用统计软件SPSS26.0对试验结果进行多元线性回归分析,得到了抗压强度、劈裂抗拉强度、抗折强度的模型摘要,如表12所示.
表12 多元线性回归模型数据
Tab.12 Multiple linear regression model data
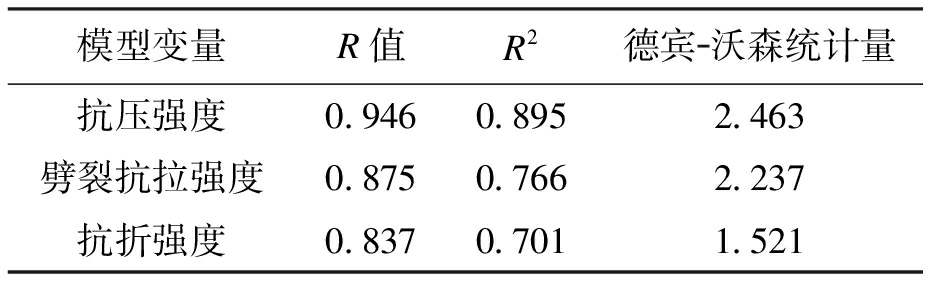
模型变量R值R2德宾沃森统计量抗压强度0.9460.8952.463劈裂抗拉强度0.8750.7662.237抗折强度0.8370.7011.521
由表12可以发现,R2的值为0.895、0.766、0.701,分别表示试验四因素变量(粉煤灰掺量、玄武岩纤维掺量、玄武岩纤维长度、减水剂掺量)引起抗压强度、劈裂抗拉强度、抗折强度变化的比重占所有因素引起抗压强度、劈裂抗拉强度、抗折强度的89.5%、76.6%、70.1%;德宾![]() 沃森统计量2.463、2.237、1.521表明抗压强度、劈裂抗拉强度、抗折强度试验中各组试验是相互独立的,无相互关联干扰.
沃森统计量2.463、2.237、1.521表明抗压强度、劈裂抗拉强度、抗折强度试验中各组试验是相互独立的,无相互关联干扰.
假设线性回归模型为
yi=β0+β1x1+β2x2+β3x3+β4x4
(1)
式中:yi为因变量(y1为抗压强度,y2为劈裂抗拉强度,y3为抗折强度);βi为线性回归系数;xi为自变量(x1为粉煤灰掺量,x2为玄武岩纤维掺量,x3为玄武岩纤维长度,x4为减水剂掺量).将各组试验数据代入线性回归模型中,可得到各因变量的方差分析和回归系数如表13~16所示.
回归方程为
y1=44.260-0.266x1-8.600x2+
0.056x3-1.799x4 (2)
表13 抗压强度线性回归方差分析
Tab.13 Linear regression analysis of variance for compressive strength
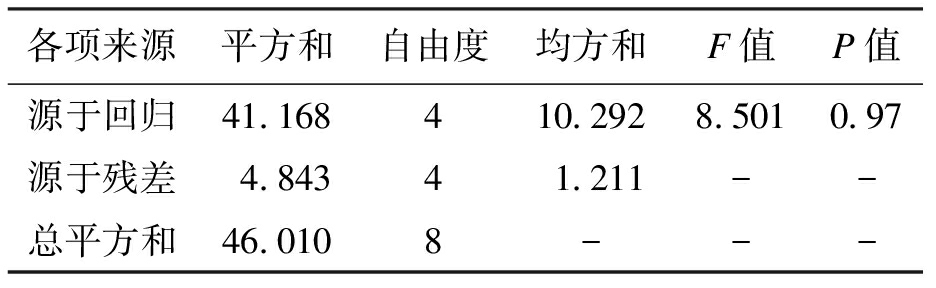
各项来源平方和自由度均方和F值P值源于回归41.168410.2928.5010.97源于残差4.84341.211--总平方和46.0108---
表14 劈裂抗拉强度线性回归方差分析
Tab.14 Linear regression analysis of variance for splitting tensile strength
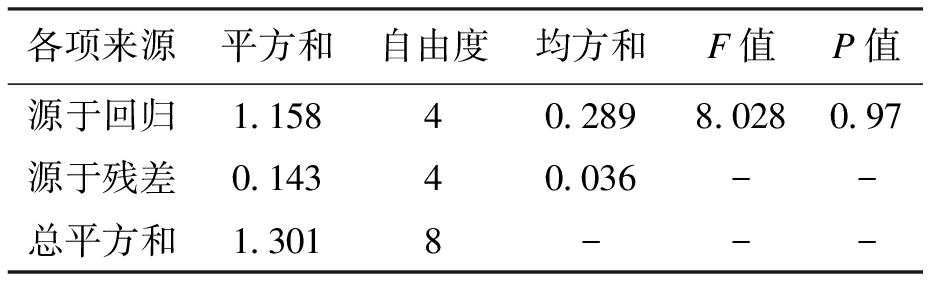
各项来源平方和自由度均方和F值P值源于回归1.15840.2898.0280.97源于残差0.14340.036--总平方和1.3018---
表15 抗折强度线性回归方差分析
Tab.15 Linear regression analysis of variance for flexural strength
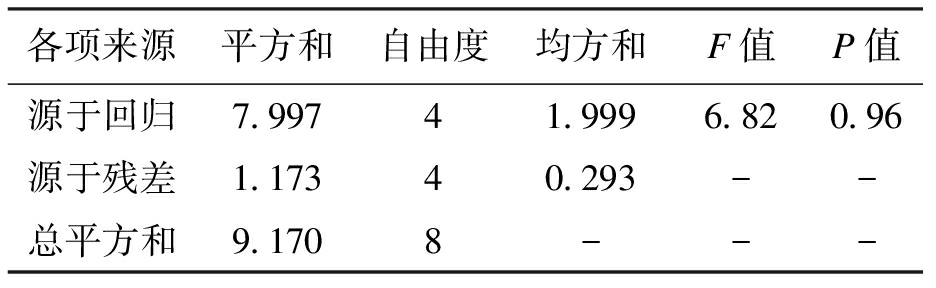
各项来源平方和自由度均方和F值P值源于回归7.99741.9996.820.96源于残差1.17340.293--总平方和9.1708---
表16 线性回归系数
Tab.16 Linear regression coefficients
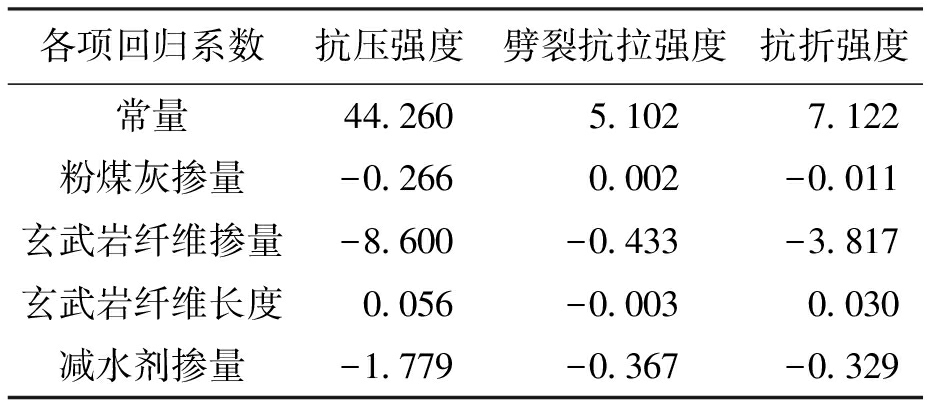
各项回归系数抗压强度劈裂抗拉强度抗折强度常量44.260 5.102 7.122粉煤灰掺量-0.2660.002-0.011玄武岩纤维掺量-8.600-0.433-3.817玄武岩纤维长度0.056-0.0030.030减水剂掺量-1.779-0.367-0.329
y2=5.102+0.002x1-0.433x2-
0.003x3-0.367x4
(3)
y3=7.122-0.011x1-3.817x2+
0.030x3-0.329x4
(4)
试验中,各因素水平变化影响力学性能变化趋势与线性回归方程变化趋势相符.其中,各因素系数反映该因素对力学性能的影响程度[18-20].由于P值分别为0.97、0.97、0.96,可以认为多元线性回归模型合理,因变量和自变量之间的关系均符合线性关系.因此,可以通过线性回归方程对BFUFAC的抗压强度、劈裂抗拉强度和抗折强度进行预测.
5 结 论
本文采用正交试验方法开展各主要组成成份对BFUFAC力学性能的影响研究,得到如下结论:
1) BFUFAC的抗压强度按影响效果显著程度由强及弱的排序为:粉煤灰掺量大于玄武岩纤维掺量大于玄武岩纤维长度大于减水剂掺量,其中只有粉煤灰掺量对抗压强度影响效果最为显著,其他因素影响不显著.
2) BFUFAC的劈裂抗拉强度按影响效果显著程度由强及弱的排序为:玄武岩纤维掺量大于减水剂掺量大于玄武岩纤维长度大于粉煤灰掺量,其中玄武岩纤维掺量和减水剂掺量对劈裂抗拉强度的影响最为显著.
3) BFUFAC的抗折强度按影响效果显著程度由强及弱的排序为:玄武岩纤维掺量大于粉煤灰掺量大于减水剂掺量大于玄武岩纤维长度,其中玄武岩纤维掺量、粉煤灰掺量和减水剂掺量对抗折强度的影响相对显著.
4) 在本研究范围内,优先侧重BFUFAC抗压强度、劈裂抗拉强度和抗折强度要求的工程实际应用中,最优配合比分别为A1B1C2D1、A1B1C2D2和A1B1C2D2.
5) 通过对各组正交试验结果的多元线性回归分析,可得到BFUFAC的力学性能预测模型,根据该模型可以对BFUFAC不同条件下的力学性能进行预测.
[1]Najmi A M,Mariyana A K,Shek P N,et al.Effect of water-cement ratio on mechanical properties of rubbe-rized fly ash concrete [J].IOP Conference Series:Materials Science and Engineering,2021,1144(1):1-8.
[2]姚大立,刘云峰,余芳.预应力自密实再生混凝土梁弹性阶段挠度计算 [J].沈阳工业大学学报,2020,42(3):355-360.
(YAO Da-li,LIU Yun-feng,YU Fang.Deflection cal-culation for elastic stage of prestressed self-compacting recycled concrete beams [J].Journal of Shenyang University of Technology,2020,42(3):355-360.)
[3]孙一民,李忠良,张健.短切BFRC力学性能及机场道面工程应用 [J].沈阳工业大学学报,2019,41(6):699-704.
(SUN Yi-min,LI Zhong-liang,ZHANG Jian.Mechanical properties of chopped BFRC and its application in airport pavement engineering [J].Journal of Shenyang University of Technology,2019,41(6):699-704.)
[4]姚大立,迟金龙,余芳,等.粉煤灰与再生骨料对自密实再生混凝土的影响 [J].沈阳工业大学学报,2020,42(2):236-240.
(YAO Da-li,CHI Jin-long,YU Fang,et al.Influence of fly ash and recycled aggregate on self-compacting recycled aggregate concrete [J].Journal of Shenyang University of Technology,2020,42(2):236-240.)
[5]范梦甜,王迎斌,苏英,等.超细粉煤灰对水泥性能的影响及在混凝土中的应用研究 [J].新型建筑材料,2021,48(8):16-20.
(FAN Meng-tian,WANG Ying-bin,SU Ying,et al.Study on the effect of ultra-fine fly ash on cement performance and its application in concrete [J].New Building Materials,2021,48(8):16-20.)
[6]陈峰宾,许斌,焦华喆,等.玄武岩纤维混凝土纤维分布及孔隙结构表征 [J].中国矿业大学学报,2021,50(2):273-280.
(CHEN Feng-bin,XU Bin,JIAO Hua-zhe,et al.Fiber distribution and pore structure characterization of basalt fiber reinforced concrete [J].Journal of China University of Mining & Technology,2021,50(2):273-280.)
[7]Abushanab A,Alnahhal W,Farraj M.Structural performance and moment redistribution of basalt FRC continuous beams reinforced with basalt FRP bars [J].Engineering Structures,2021,240:1-7.
[8]张吉松,赵颖华.玄武岩纤维超高性能混凝土力学性能试验 [J].沈阳工业大学学报,2018,40(5):595-600.
(ZHANG Ji-song,ZHAO Ying-hua.Experiment on mechanical properties of ultra-high performance concrete with basalt fibers [J].Journal of Shenyang University of Technology,2018,40(5):595-600.)
[9]金生吉,李忠良,张健,等.玄武岩纤维混凝土腐蚀条件下抗冻融性能试验研究 [J].工程力学,2015,32(5):178-183.
(JIN Sheng-ji,LI Zhong-liang,ZHANG Jian,et al.Experimental study on anti-freezing and thawing performance of reinforced concrete of basalt fiber under corrosion condition [J].Engineering Mechanics,2015,32(5):178-183.)
[10]Jaganathan K,Ramesh K G B.An experimental study on polymer impregnated concrete with fly ash [J].Journal of Physics:Conference Series,2021,1964(7):1-8.
[11]陈峰,陈欣.玄武岩纤维混凝土的正交试验研究 [J].福州大学学报(自然科学版),2014,42(1):133-137.
(CHEN Feng,CHEN Xin.Orthogonal experimental research on strength of concrete reinforced by basalt fiber [J].Journal of Fuzhou University (Natural Science Edition),2014,42(1):133-137.)
[12]王钧,马跃,张野,等.短切玄武岩纤维混凝土力学性能试验与分析 [J].工程力学,2014,31(增刊1):99-102.
(WANG Jun,MA Yue,ZHANG Ye,et al.Experimental research and analysis on mechanical properties of chopped basalt fiber reinforced concrete [J].Engineering Mechanics,2014,31(Sup1):99-102.)
[13]Wang K,Guo J J,Liu X J,et al.Effect of dry-wet ratio on pore-structure characteristics of fly ash concrete under sulfate attack [J].Materials and Structures,2021,54(3):100.
[14]刘子璐,陈新明,焦华喆,等.基于正交设计的玄武岩纤维增强混凝土配合比优化研究 [J].混凝土与水泥制品,2017(10):51-55.
(LIU Zi-lu,CHEN Xin-ming,JIAO Hua-zhe,et al.Optimization study on mix proportion of basalt fiber reinforced concrete based on orthogonal design [J].China Concrete and Cement Products,2017(10):51-55.)
[15]Zhang J,Zhou X Z,Zheng J J,et al.Experimental investigation and analytical modeling of chloride diffusivity of fly ash concrete [J].Materials (Basel,Switzerland),2020,13(4):862.
[16]Valovoi A,Eremenko A,Valovoi M,et al.The impact of percentage content of basalt fiber-reinforced polymer and steel reinforcement on the strength indicators of experimental beams with hybrid reinforcement [J].IOP Conference Series:Materials Science and Engineering,2021,1164(1):1-3.
[17]Yang L Y,Xie H Z,Fang S Z,et al.Experimental study on mechanical properties and damage mechanism of basalt fiber reinforced concrete under uniaxial compression [J].Structures,2021,31:330-340.
[18]王晓敏,郑建岚,朱艺婷.粉煤灰颗粒特性对再生混凝土水化性质的影响 [J].福州大学学报(自然科学版),2021,49(2):238-244.
(WANG Xiao-min,ZHENG Jian-lan,ZHU Yi-ting.Effect of particle characteristics of fly ash on hydration properties of recycled concrete [J].Journal of Fuzhou University (Natural Science Edition),2021,49(2):238-244.)
[19]陈四利,李锋,侯芮,等.温度变化对水泥土渗透特性影响试验 [J].沈阳工业大学学报,2020,42(4):453-458.
(CHEN Si-li,LI Feng,HOU Rui,et al.Tests on influence of temperature variation on permeability of cemented soil [J].Journal of Shenyang University of Technology,2020,42(4):453-458.)
[20]吴春扬,马剑,潘志宏,等.非连续级配再生粗骨料自密实混凝土基本力学性能试验研究 [J].建筑结构,2015,45(10):69-73.
(WU Chun-yang,MA Jian,PAN Zhi-hong,et al.Exprimental study on basic mechanical properties of self-compacting recycled concrete with discontinuous graded recycled coarse aggregate [J].Building Structure,2015,45(10):69-73.)