随着我国经济水平的提高以及城镇化进程的加快，有效推动了建筑行业的发展，工地中临时设施也随之不断发展.临时作业棚作为施工现场中重要的临时性设施，为实现绿色施工，其标准化及模数化的研究也越来越多.双拼C型钢梁具有良好的截面力学性能、良好的抗震性能、安全可靠、施工方便等诸多优点，因此成为临时作业棚中的主要承重构件.双拼C型钢梁即将两根带卷面的C型冷弯薄壁型钢以“背靠背”的方式用自攻螺钉将其腹板连接在一起[1]，腹板两侧布置加劲肋焊接成为梁.
目前，国内外学者对双拼C型钢梁构件进行了一定的试验研究和理论分析.Stone等[2]对32个双C型冷弯薄壁型钢构件采用螺栓进行背靠背连接并进行轴压承载力试验研究；Dundu等[3]采用双C型冷弯薄壁型钢利用螺栓连接制成4个门式刚架，对刚架承载力和檐口节点破坏形态进行试验研究；周绪红等[4]通过改变梁跨高比、截面高宽比、螺钉连接间距及腹板开孔对双肢拼合工字截面梁进行受弯性能研究；杨娜等[5]应用有限元软件对考虑接触的C-C梁柱钢板
螺栓节点进行模拟；唐忠平[6]运用有限元软件对双拼C型冷弯薄壁型钢架抗震性能进行了研究.通过阅读相关文献发现，对双拼C型钢梁抗弯性能及其有限元模拟研究较少.
通过对4根双拼C型钢梁的纯弯试验，分析此类双拼梁的承载能力、变形特征、破坏形态等.采用ABAQUS有限元软件建立双拼C型钢梁的有限元分析模型，进行受弯过程分析.通过试验结果对有限元分析模型的准确性进行了验证，研究结果将为此类冷弯薄壁型钢梁设计及实际工程应用提供参考.
1 试验概况
1.1 试件设计
试验共设计了四个试件，试件设计示意图如图1所示(单位为mm).DSC-1、DSC-2自攻螺钉间距为300 mm，DSC-3、DSC-4自攻螺钉间距为600 mm，试件的加工制作在工厂完成.
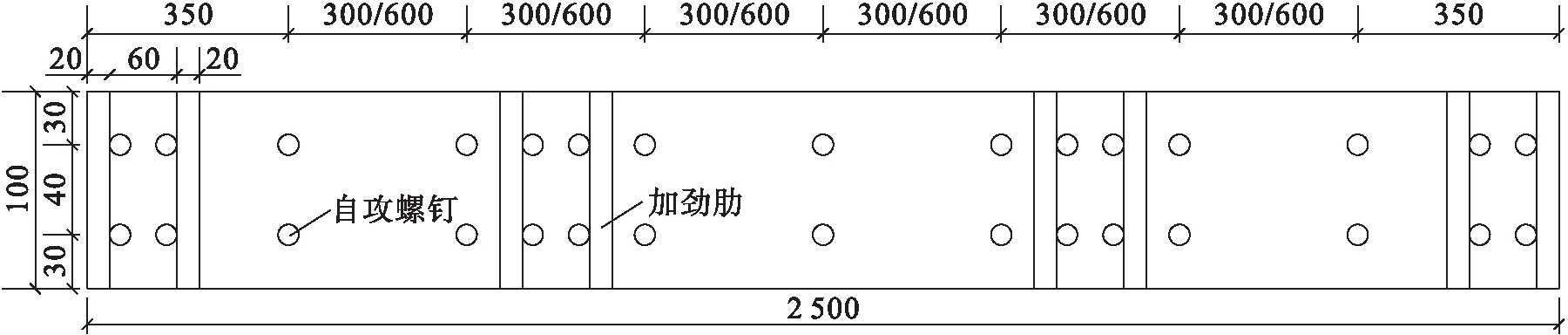
图1 试件设计示意图
Fig.1 Schematic design of specimen
1.2 材性试验
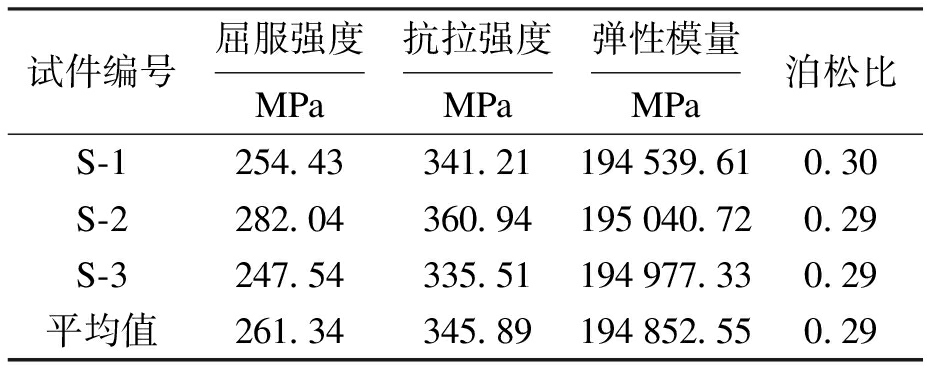
根据国家规范《金属材料拉伸试验：第1部分：室温试验方法》(GB/T 228.1-2010)[7]中的相关规定对所用钢材进行材性试验，结果如表1所示.
表1 材性试验结果
Tab.1 Results of material experiments
试件编号屈服强度MPa抗拉强度MPa弹性模量MPa泊松比S-1254.43341.21194539.610.30S-2282.04360.94195040.720.29S-3247.54335.51194977.330.29平均值261.34345.89194852.550.29
1.3 加载方案
试验在沈阳建筑大学结构工程试验室进行.试验采用三分点加载，试验装置如图2所示.采用手动加载，首先对试件进行预加载，对试件进行检查，保证各部分接触情况良好，各试验装置、采集及观测仪器都进入正常工作状态；然后正式加载，所施加的每级荷载取为预估极限荷载的5%；直至试件开始出现屈曲变形或荷载达到预估极限荷载的80%后开始减小加载幅度；当试件出现较大变形或位移计、应变读数发生突变时，进行更细分级，对各加载阶段数据对应试验现象进行记录，直到荷载达到最大值；为得到试件荷载位移曲线的下降段，在荷载达到最大值后继续加载，直到荷载下降为极限荷载的85%时停止加载.每级荷载施加并持荷60 s后进行数据采集，采用静态电阻应变仪对测点数据进行采集.
图2 试验加载布置图
Fig.2 Experimental loading layout
1.4 测点布置
为测量试件的挠曲变形及支座位移，分别在试件的三分点、跨中及支座处设置位移计，应变片布置如图3所示.
2 试验结果与分析
2.1 破坏模式
试验完成后各试件破坏形态如图4所示，对DSC-1及DSC-4的破坏过程进行分析.
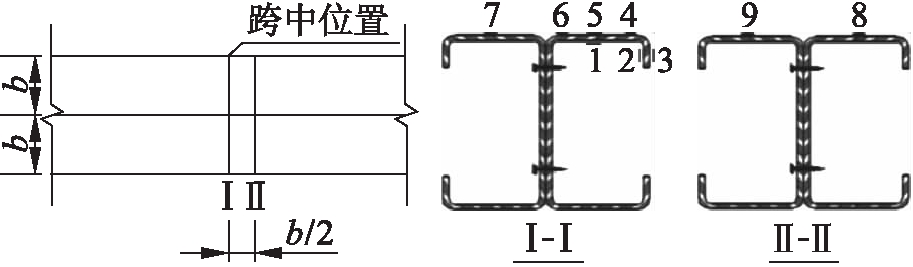
图3 应变片布置图
Fig.3 Strain gauge arrangement
图4 试件整体破坏形态
Fig.4 Overall failure modes of specimens
对于DSC-1，当试件承担的荷载增大时，试件与加载装置的间隙逐渐减小；直到荷载增至18 kN，试件纯弯段上侧受压翼缘处发生局部屈曲，试件开始屈服；荷载增加至26 kN，纯弯段拼接处有开裂迹象；当加载至28 kN，纯弯段受压翼缘出现大面积塑性变形，此后荷载持续增大，直到变形加剧致使试件失稳，发生弯扭破坏，此时达到试件破坏的极限荷载34 kN，最终发生局部屈曲变形、试件整体弯扭失稳的破坏模式，破坏形态如图5a所示.
对于DSC-4，加载初期同DSC-1，直到荷载增至16 kN，试件纯弯段上侧受压翼缘处发生局部屈曲，试件开始屈服；荷载增加至24 kN，纯弯段拼接处有开裂迹象；加载至26 kN，纯弯段拼接处开裂迹象明显，此后荷载持续增大，直到变形加剧致使试件失稳，发生弯扭破坏，此时达到试件破坏的极限荷载32.5 kN，最终发生局部屈曲变形、试件整体弯扭失稳的破坏模式，破坏形态如图5b所示.
图5 试件破坏形态
Fig.5 Failure modes of specimens
2.2 结果分析
2.2.1 荷载位移曲线
双拼C型钢梁的受弯荷载位移曲线如图6所示.由图6可知：在施加荷载初期，各试件整体刚度均未发生改变；当持续施加荷载时，荷载位移曲线的斜率逐渐减小，荷载位移曲线不再保持线性增长关系，试件开始发生破坏，试件的刚度随之减小；当所加荷载达到极限荷载时，荷载位移曲线的增长也达到极限；随着荷载继续施加，构件的受弯承载力不再增加反而急剧下降，此时曲线的斜率变为负值，表明此时构件因整体挠度过大而发生破坏，构件已达到正常使用极限状态.
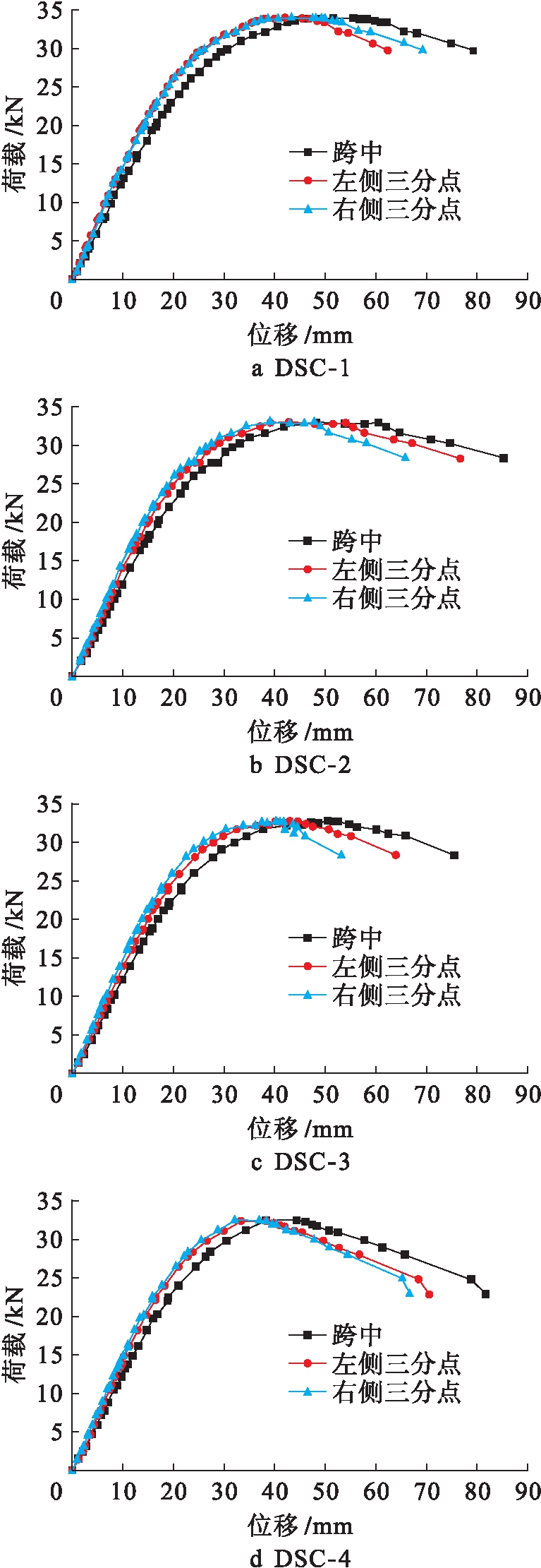
图6 荷载位移曲线
Fig.6 Load-displacement curves
2.2.2 荷载应变曲线
双拼C型钢梁的荷载应变曲线如图7所示.由于试件受压区主要集中在上翼缘，将产生较明显的局部屈曲变形，因此，将应变片设置在纯弯段上部以观察荷载应变曲线的变化，结合荷载位移曲线对其临界屈曲荷载进行确定.当施加荷载较小时，试件表面不会发生局部屈曲，所有应变片的应变同时同向增加，试件所承担的荷载逐渐增大时，试件表面将出现局部屈曲，当所测应变处于屈曲波峰处为正，波谷处为负.此时，曲线将出现反向增长；当试件由局部屈曲发展到整体破坏时，由于受拉导致试件凸侧压应变增加缓慢，而凹侧则因受压而继续保持压应变的快速增长，但最终试件出现拉应变.在荷载应变曲线出现拐点时，可将此荷载近似确定为该试件的局部屈曲临界荷载值.
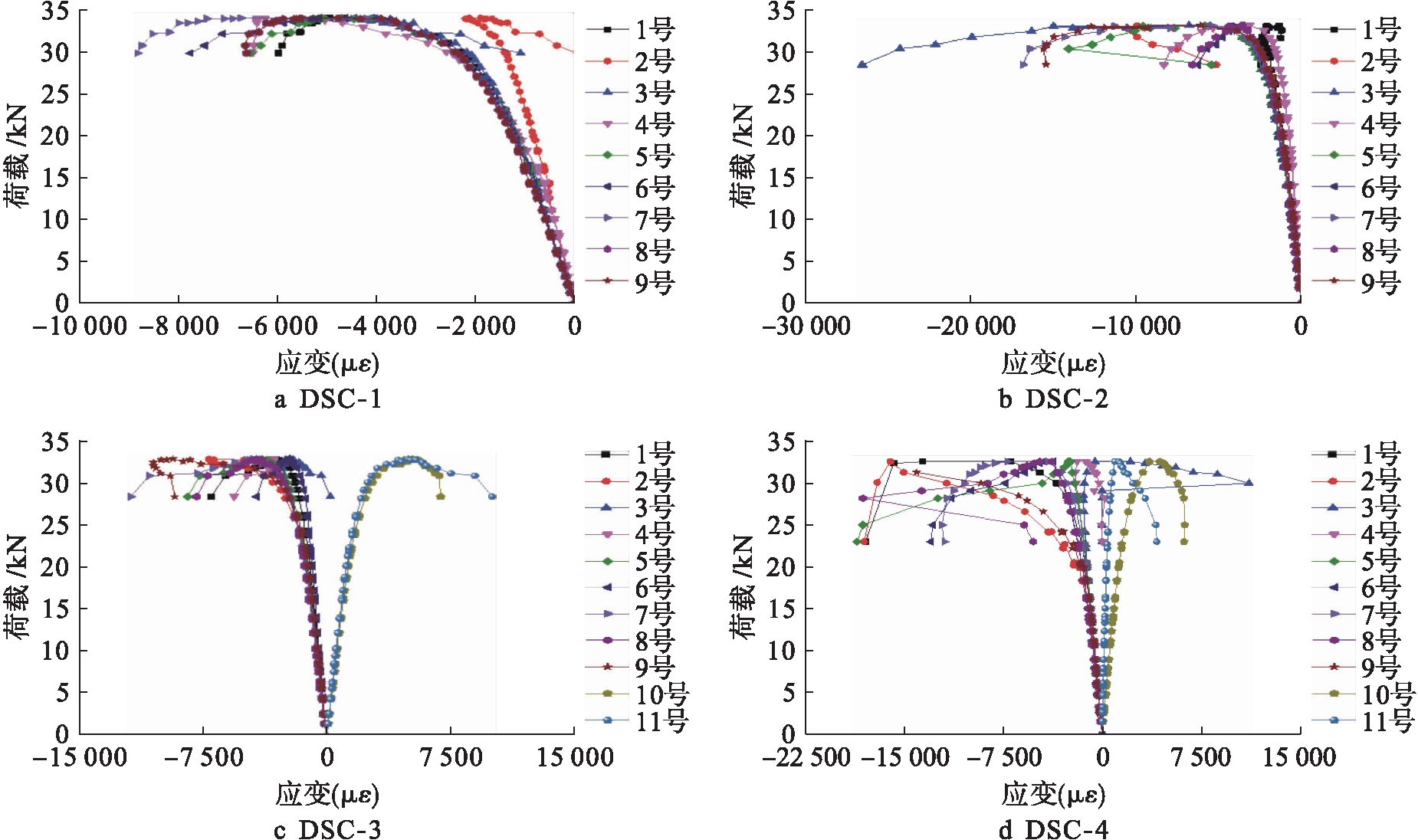
图7 荷载应变曲线
Fig.7 Load-strain curves
3 有限元分析
3.1 模型建立
利用ABAQUS有限元分析软件建立双拼C型钢梁有限元分析模型.有限元模型由刚性加载板、C型钢、加劲肋以及自攻螺钉组成，各部件均采用C3D8R八节点线性三维六面体减缩积分单元进行模拟.根据文献[8]中C型冷弯薄壁型钢截面网格划分方法，确定其网格尺寸为20 mm，最终有限元模型及单元划分如图8所示.
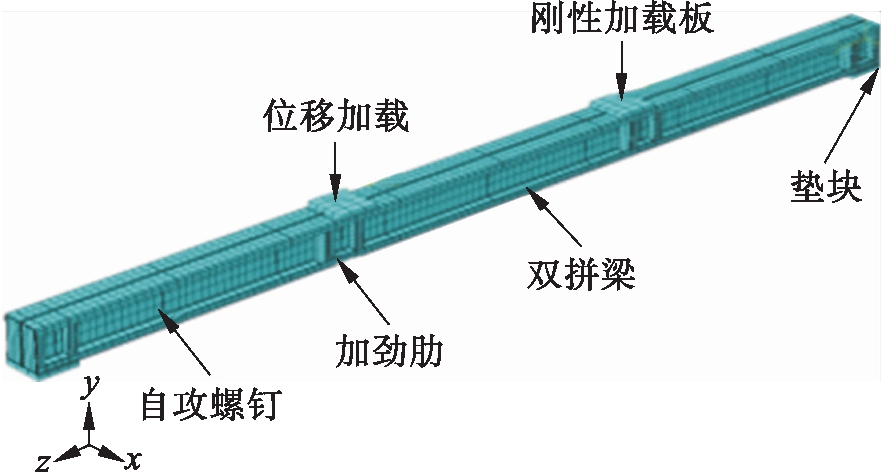
图8 有限元分析模型
Fig.8 Finite element analysis model
模型分析采用如下基本假定：1)假定“背靠背”的两片C型冷弯薄壁型钢能够紧密相贴，两者之间没有间隙.2)忽略C型冷弯薄壁型钢初始缺陷.初始缺陷分为残余应力初始缺陷和几何初始缺陷两类.由于冷弯薄壁型钢在制作过程中进行了冷加工，残余应力呈现“弯曲型”分布，且在构件的角部区域集中.角部构件由于受到冷加工的影响，会提高其屈服强度，两者产生的效应相互抵消，所以在对双拼C型钢梁建模时，未对残余应力初始缺陷对极限承载力产生的影响进行考虑.建模分析时未进行非线性屈曲分析，忽略几何初始缺陷对构件的影响[9].3)假定加劲肋与C型冷弯薄壁型钢焊接可靠，忽略焊接应力对双拼C型钢梁极限承载力的影响.
3.2 材性定义
模型中C型冷弯薄壁型钢及加劲肋材料本构关系采用材性试验中测得的材料属性数值.自攻螺钉采用ST4.8自攻钉，材料为合金钢，材质较硬，应力应变曲线无明显的流幅，应力达到极限强度600 MPa便宣告破坏，之前的塑性变形极小.为了体现极限强度的概念，将自攻螺钉在有限元分析中进行本构关系设定，如图9所示，利用材料“进入塑性产生很大变形”来控制收敛，进而得出极限荷载.事实上，螺钉材料“进入塑性产生很大变形”几乎不可能，因为实际上螺钉一旦达到极限强度就断裂了[10].
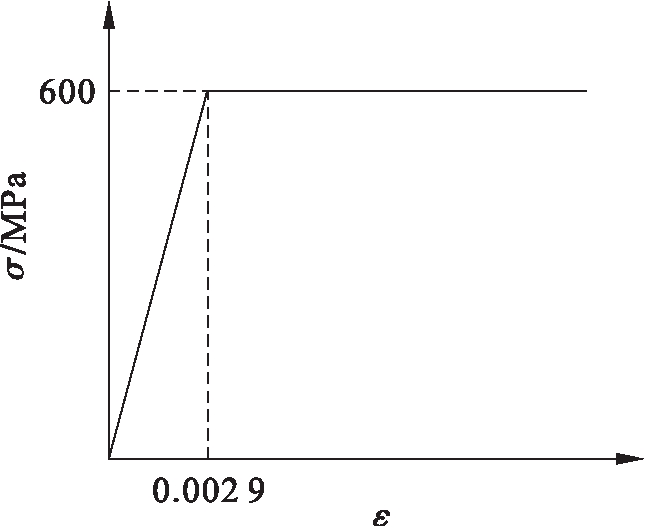
图9 自攻螺钉本构关系
Fig.9 Constitutive relationship of self-tapping screw
3.3 边界条件与加载方式
为避免加载点处应力集中，在三分之一跨处各设置一个宽100 mm、厚10 mm的长方体垫块.将刚体加载面通过Coupling耦合到参考点，在参考点上施加沿Y轴负方向位移，大小为80 mm.试件两端简支，为与试验保持一致，在双拼梁两端设置刚体垫块以模拟实际支座，在支座底部施加边界条件.
对于模型中的接触问题，由于在试验过程中自攻螺钉均未发生明显破坏，故自攻螺钉与C型钢之间采用Tie绑定约束进行模拟即可，加劲肋与C型钢连接采用Tie绑定约束，两C型钢“背靠背”连接采用Tie绑定约束进行模拟.
3.4 试验验证
将双拼梁试验结果与有限元模拟结果进行比较，图10为试件DSC-1及DSC-4的整体破坏模式对比，其中有限元破坏应力云图采用Mises应力云图.图11为其荷载位移曲线对比，其中模拟所得左右三分点荷载位移曲线几乎重合.图12为其荷载应变曲线对比.双拼C型钢梁纯弯试验结果与有限元分析结果基本吻合，由应力云图可得，在试件钢材发生破坏后，自攻螺钉仍处于正常工作状态与试验时相符.同时也验证了有限元分析的准确性与可靠性.
3.5 自攻螺钉间距的影响
为进一步分析自攻螺钉间距对双拼C型钢梁抗弯承载力的影响，自攻螺钉间距按间隔150 mm从150～900 mm进行分析.图13为各模型荷载跨中挠度曲线，各模型对应极限承载力差别极小.考虑到模型基本假设中忽略初始缺陷为理想化模型，且布置有加劲肋存在，故改变螺钉间距对其极限承载力影响较小.图14为跨中受压区荷载应变关系图.随着自攻螺钉间距增大，其变形能力呈下降趋势.自攻螺钉间距为450 mm时因其有自攻螺钉布置于加劲肋间，局部自攻螺钉较密集，故其变形能力略高于间距为300 mm时.综合考虑实际施工的方便性、经济性及双拼梁的承载能力和变形能力，建议双拼C型钢梁采用自攻螺钉间距为600 mm.
图10 试件破坏模式对比
Fig.10 Comparison of specimen failure modes
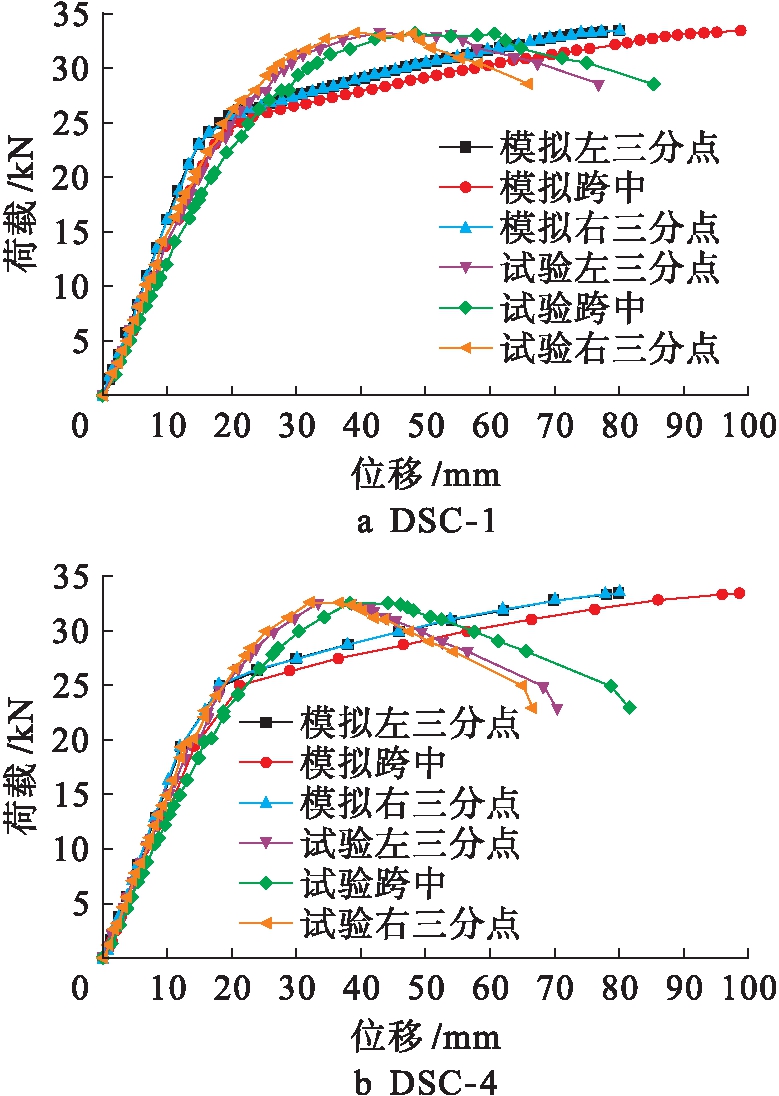
图11 试件的荷载位移曲线对比
Fig.11 Comparison of specimen load-displacement curves
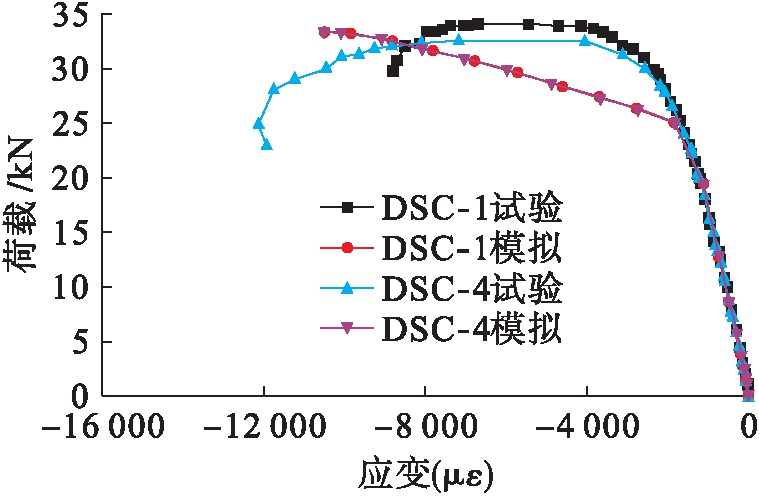
图12 试件的荷载应变曲线对比
Fig.12 Comparison of specimen load-strain curves
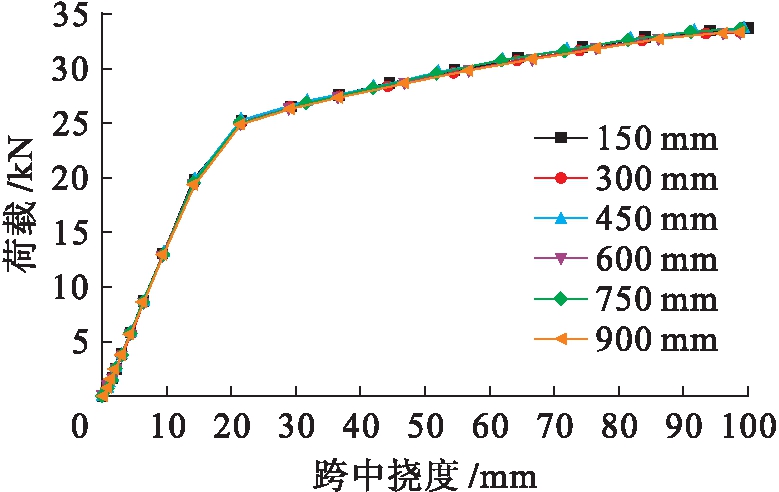
图13 荷载跨中挠度曲线
Fig.13 Load-midspan deflection curves
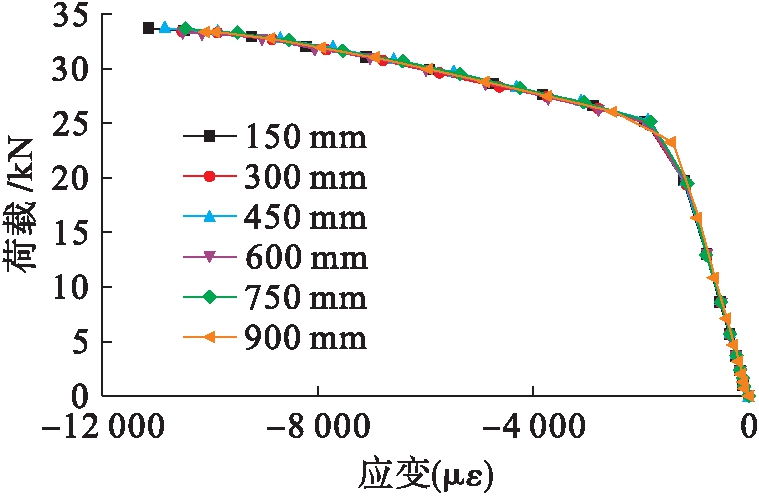
图14 跨中受压区荷载应变曲线
Fig.14 Load-strain curves of midspan compressive zone
4 结 论
本文通过分析得出以下结论：
1) 双拼C型钢梁在加载过程中，无栓钉被剪断，且拼接处未出现较大分离，由于试件厚度较薄，在整体破坏之前，均出现局部屈曲，承载力的下降主要由钢梁上翼缘局部屈曲进而引起构件失稳.
2) 基于ABAQUS建立了双拼C型钢梁有限元分析模型，并改变自攻螺钉间距进行分析.结果表明，有限元分析结果与试验结果吻合较好，有限元模型及分析结果具有一定的准确性，随着自攻螺钉间距增大，双拼C型钢梁极限承载力变化不明显，但变形能力呈下降趋势，考虑到构件加工的便携性，建议实际工程中采用自攻螺钉间距为600 mm.
[1]中华人民共和国住房和城乡建设部.GB50018-2002冷弯薄壁型钢结构技术规范 [S].北京：中国标准出版社，2003.
(Ministry of Housing and Urban-Rural Construction of the People’s Republic of China.GB50018-2002 Technical code of cold-formed thin-wall steel structures [S].Beijing：Standards Press of China，2003.)
[2]Stone T A，LaBoube R A.Behavior of cold-formed steel built-up I-sections [J].Thin-Walled Structures，2005，43(12)：1805-1817.
[3]Dundu M，Kemp A R.Strength requirements of single cold-formed channels connected back-to-back [J].Journal of Constructional Steel Research，2006，62(3)：250-261.
[4]周绪红，管宇，高婷婷，等.双肢拼合冷弯薄壁型钢工字形截面梁受弯性能研究 [J].土木工程学报，2016，49(8)：16-27.
(ZHOU Xu-hong，GUAN Yu，GAO Ting-ting，et al.Study on flexural capacity of cold-formed steel double-limb built-up I-shape beams [J].China Civil Engineering Journal，2016，49(8)：16-27.)
[5]杨娜，钟延营，彭雄.冷弯薄壁型钢钢板螺栓梁柱节点滞回性能与恢复力简化模型研究 [J].工业建筑，2011，41(增刊1)：247-250.
(YANG Na，ZHONG Yan-ying，PENG Xiong.The in-vestigation on cold-formed steel beam-column joints with bolt-plate [J].Industrial Construction，2011，41(Sup 1)：247-250.)
[6]唐忠平.双拼C型冷弯薄壁型钢刚架抗震性能研究 [D].杭州：浙江工业大学，2012.
(TANG Zhong-ping.Study on seismic performance of C-C cold-formed steel frame [D].Hangzhou：Zhejiang University of Technology，2012.)
[7]中华人民共和国国家质量监督检验检疫总局.GB/T 228.1-2010金属材料拉伸试验：第1部分：室温试验方法 [S].北京：中国标准出版社，2011.
(General Administration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China.GB/T 228.1-2010 Metallic materials-tensile testing-part 1：method of test at room temperature [S].Beijing：China Standard Press，2011.)
[8]张莉亚.轻钢龙骨混凝土组合外挂墙板优化设计及力学性能研究 [D].南京：东南大学，2018.
(ZHANG Li-ya.Optimization design and mechanical behaviors of light-gauge steel stud concrete composite external wall panel [D].Nanjing：Southeast University，2018.)
[9]江力强.双肢拼合冷弯薄壁型钢箱型截面梁受弯性能研究 [D].西安：长安大学，2014.
(JIANG Li-qiang.Researchon flexural capacity of cold-formed steel double limbs built-up box beams [D].Xi’an：Chang’an University，2014.)
[10]王小平，房玉松.自攻螺钉连接抗剪承载力的有限元建模方法 [J].武汉大学学报(工学版)，2012，45(1)：75-79.
(WANG Xiao-ping，FANG Yu-song.Finite element modeling method of anti-shear capacity of self-drilling-screw connection [J].Engineering Journal of Wuhan University，2012，45(1)：75-79.)