在太阳能光伏发电系统中，发电状况主要取决于实际的天气情况，但天气情况类型各异、系数数量差异巨大、功能不一，使光伏发电功率的间断性和随机性较强，严重影响着光伏并网发电的安全性和稳定性[1-2].因此，需要对光伏发电功率预测展开探讨，首先得到光伏输出功率曲线[3]，再由电网调度部门协调安排，减少光伏并网给电力系统带来的影响，提高电力系统规划的科学性.
卢舟鑫等[4]提出基于时段综合相似日的光伏发电功率预测方法，分时段对光伏发电功率进行预测，该方法运行简单，但方法功率预测结果与实际结果相差较大；冬雷等[5]提出基于双重筛选的光伏发电功率预测方法，对光伏发电功率和云量、温度等气象因素之间的相关系数进行计算；于秋玲等[6]提出基于模糊聚类的光伏发电功率预测方法，利用气象信息构建模糊相似矩阵，将预测日的气象条件当作预测模型的样本，构建光伏发电功率的预测模型.
上述文献无法同时保证较高的预测精度和低复杂度，为此，本文提出基于改进支持向量机的光伏发电功率预测方法.在分析光伏发电影响因素的基础上，构建光伏电池预测模型，降低以往预测光伏发电功率对历史数据的依赖性，并且避免了整体复杂度较高的问题，提高光伏发电功率预测效率.
1 改进支持向量算法参数
光伏发电功率受气象因素影响较大，在预测光伏发电功率时，需要充分考虑气象因素[7-9].从物理学角度分析光伏发电系统可知：影响光伏发电功率的主要气象因素分别为太阳辐射照度(可分解为晴空指数和日照时数)、云层量、灰尘浓度和环境温度等[10-13].当云量和灰尘达到一定量时，大气可见度和透明度降低，致使太阳对地面的辐射减少.
首先需要判断光伏发电功率预测过程中气象影响因素之间的关联程度，并根据关联程度的大小确定各因素的影响，对支持向量算法的具体参数进行优化.设置X为灰色系统的整体因子集合，x0(k)表示x0序列的第k个数据点，其中k=1，2，…，n，将其作为参考序列表示光伏发电功率数据量；比较数据为系统的自变量，是影响系统变化的因素，可表示不同气象影响因素，其表达式为
xi=(xi(1)，xi(2)，…，xi(n))∈X
(i=1，2，…，m)
(1)
式中，m为比较序列对应的数量.为使系统各因素具有相关性和等级性，用归一化处理对各数据序列进行正向分析比较.考虑到所选取的气象影响因素多数为正值，可利用极大值归一化方法对数据序列进行归一化处理.
极大值归一法可表示为将数据序列的每一项除以该序列的最大值，即
(i=0，1，…，m；k=1，2，…，n)
(2)
定义参考序列与比较序列的差值为Δi(k)，即
Δi(k)=|x′0(k)-x′i(k)|
(i=0，1，…，m；k=1，2，…，n)
(3)
式(3)其实质上是差序列，将差序列中的最小值和最大值分别作为最小极差
和最大极差
则第i个气象影响因素与光伏发电功率的关联系数关系γ0i(k)可表示为
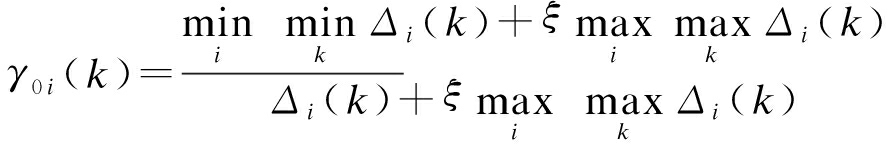
(4)
式中，ξ为分辨系数.得到关联系数γ0i(k)后，进而可以得到灰色关联度为
(5)
灰色关联度
取值范围为0～1，受参考序列、比例序列、关联系数和分辨系数影响.各种比较序列与参考序列的相似程度越高，关联值越接近1.当
时，序列xi与x0是平行的.将灰色关联度归一化，得到第i个比较序列(气象影响因素)的因子权重系数γi为
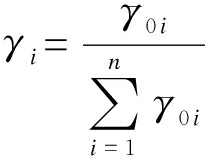
(6)
灰色关联分析方法可以对系统动态变化过程进行量化分析，通过计算参考序列与比较序列曲线的相似度来分析各因素关联程度，对支持向量机算法进行改进，约束参数可表示为
(7)
式中：t为序列处理时间；Bw为各个影响因素阈值.
2 光伏电池等效模型
光伏电池等效电路中电压与电流之间的关系表达式为
(8)
式中：IL为光电流，由太阳的辐射强度来决定；ID为二极管反向饱和电流，受电池串接个数和光电池温度K的影响；Rs、Rsh分别为串联和并联电阻.根据式(8)可知，电池串接个数、电池组件温度以及太阳的辐射强度是影响光伏发电的几个主要因素[14-15].假设电池个数是固定的，并且具有最佳的倾斜角度，则影响光伏发电的主要因素为气象条件.光伏电池等效模型中参数与气象影响因素的关系表达式为
(9)
(10)
(11)
式中：r1和r2分别为太阳辐射和环境温度；r11、r12、r13和r14分别为晴空指数、日照时数、云量和灰尘量；下标ref为标准测试条件；α为光生电流温度系数.
3 光伏发电功率预测
应用支持向量机算法将非线性问题转为线性问题，经过高维线性空间中的拟合，可以获得光伏发电功率，并对其进行降维处理，最终获得光伏发电功率的预测结果.
假设(xi，yi)(i=1，2，…，m)为给定的光伏数据集，xi、yi分别代表输入和输出量.利用非线性函数g(x)将m映射到特征空间l(l>m)中，聚集相似数据的同时，筛选不同数据，对特征空间中的输出预测功率定义为
f(x)=Wg(x)+Te
(12)
式中，W为权变量，可以对不同光伏数据的区域进行划分.预测差值为
|yi-f(xi)|≤ε (ε≥0)
(13)
符合式(13)的数据为正常光伏发电数据，能够用来计算光伏发电输出的有效功率.利用非负松弛变量ξ和ξ′以及惩罚系数C(C>0)来降低误差，利用式(14)建立最优计算结果，将其转为凸二次优化问题，即
s.t. f(xi)-yi≤ε+ξ′i (ξi≥0，ξ′i≥0)
(14)
利用拉格朗日乘子αi和α′i来寻找最优的功率估计值，将式(14)转为相对应的双重问题，即
(15)
最佳估计结果也可以称作回归函数，其表达式为
(16)
确定非线性方程g(x)具有一定难度，本文利用核函数k(xi，x)代替gT(xi)g(x)，至此，基于改进支持向量机算法的光伏发电功率预测模型构建完成.
4 实验结果与分析
为了验证所提方法的有效性，对不同天气情况下的光伏发电功率进行预测.数据来源于某市的光伏电站气象站和并网点，包括24天的光伏发电记录数据，排除天气状况不明显和应用条件受限制的67个数据，共406个数据.在其中随机选取3天光伏发电站数据作为样本数据进行实验对比.
测试方法1(本文方法)、方法2(文献[4]方法)和方法3(文献[5]方法)的光伏发电功率预测结果与实际结果对比如图1所示.
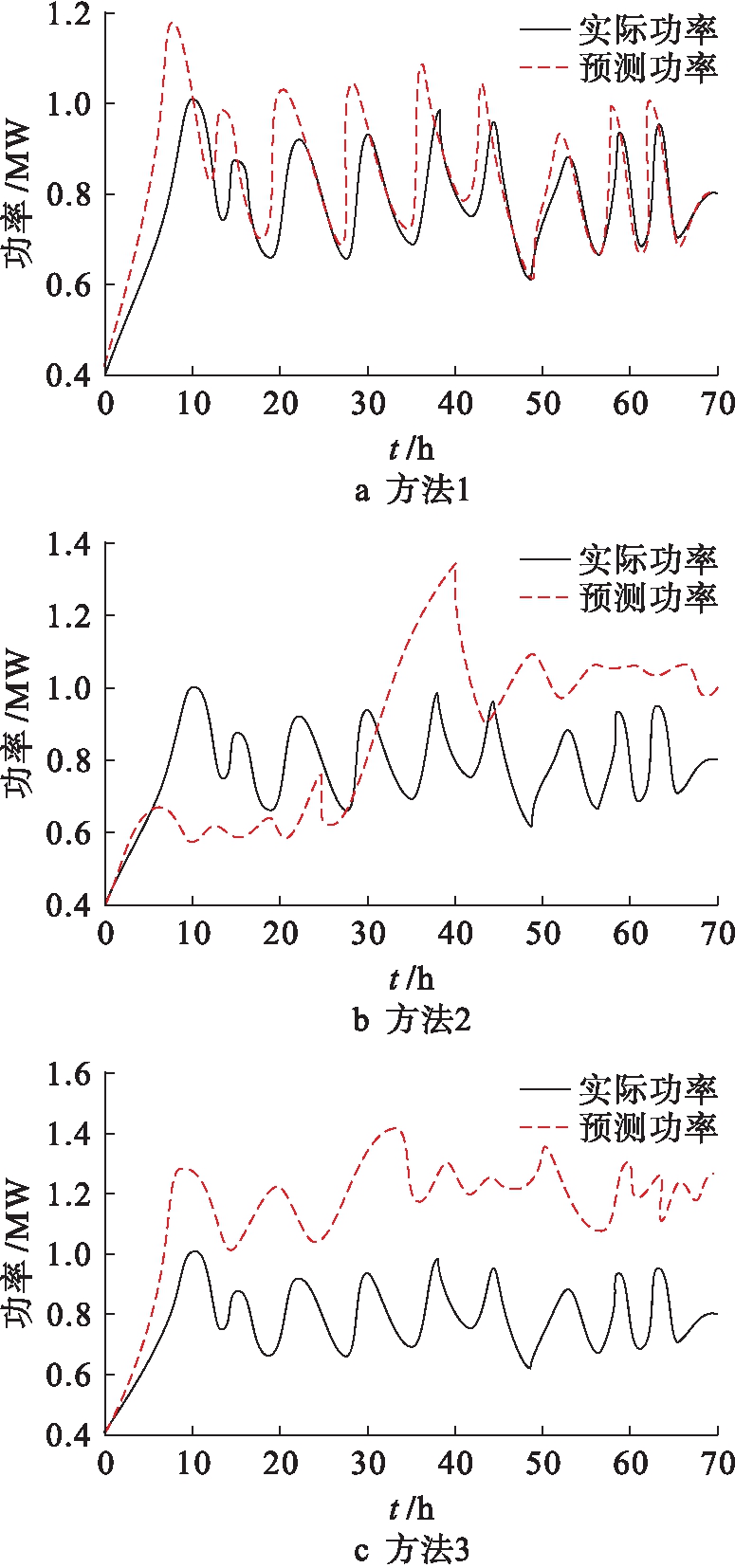
图1 不同方法预测结果与实际结果对比
Fig.1 Comparison between predicted and actual values by different methods
分析图1可知，本文方法光伏发电功率的预测结果与实际结果曲线的变化情况较为贴近；方法2的预测结果与实际结果存在一定的偏差，由于方法2依赖不同时间段的历史数据，一旦历史数据不准确或出现偏差，预测结果将出现更大的误差；方法3的预测结果与实际结果偏离程度较大，这是由于方法3对气象因素具有一定的选择性，其并未考察多种气象因素的影响，而是选择性考察气象因素.
日光辐照计观测到全天候太阳辐照量，按日光辐照强度计的数值进行估算处理，用光伏发电功率预测的绝对误差测试不同方法预测功率的精度.因此在对光伏发电功率预测结果与实际结果对比测试的基础上，进行绝对误差对比测试，测试结果如图2所示.
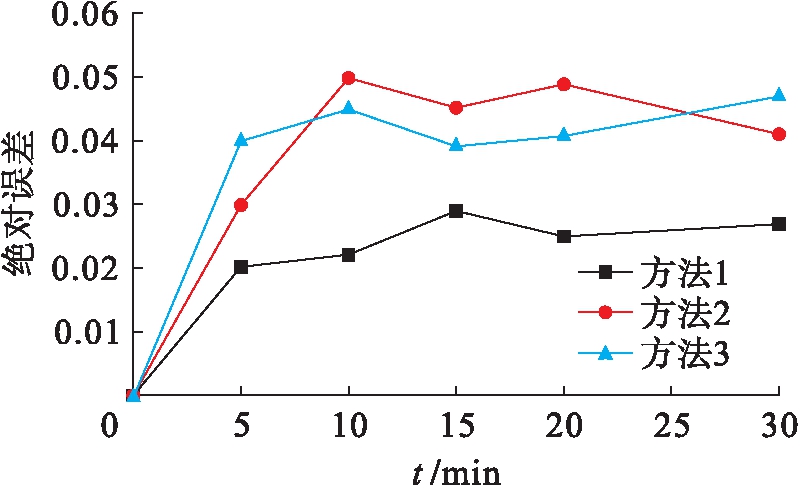
图2 不同方法光伏发电功率预测的绝对误差
Fig.2 Absolute error predicted using different methods for photovoltaic generation power
从图2可以看出，本文方法预测绝对误差整体小于等于0.03，其他方法预测绝对误差整体在0.03～0.06范围内变化.对比可知本文方法功率预测的绝对误差较小，说明本文方法预测精准度较高.
5 结 论
光伏发电功率的预测是增强光伏消耗能力和提高电力系统能源控制的重要方式.本文提出基于改进支持向量机算法的光伏发电功率预测方法，得到结论如下：
1) 利用灰色关联分析方法对不同的气象影响因素进行量化分析比较处理，分析各因素关联程度强弱，实现改进支持向量机算法参数量化分析.
2) 算法不再完全依赖历史数据，提高光伏发电功率的准确性.
3) 利用核函数代替非线性函数，并将非线性问题转换为线性问题，进一步提高光伏发电功率预测的科学性与准确性.
实验发现，使用本文方法得到的光伏发电功率预测结果与实际结果更相符，并且绝对误差较小，验证了本文方法是可行并且有效的.
[1] 李青，孙谊媊，于永军，等.基于EWT-KMPMR组合模型的光伏电站短期功率预测 [J].农业工程学报，2017，33(20)：265-273.
(LI Qing，SUN Yi-qian，YU Yong-jun，et al.Short-term power forecasting of photovoltaic power plants based on EWT-KMPMR combined model [J].Tran-sactions of the Chinese Society of Agricultural Engineering，2017，33(20)：265-273.)
[2] 张程熠，唐雅洁，李永杰，等.适用于小样本的神经网络光伏预测方法 [J].电力自动化设备，2017，37(1)：101-106.
(ZHANG Cheng-yi，TANG Ya-jie，LI Yong-jie，et al.Photovoltaic power forecast based on neural network with a small number of samples [J].Electric Power Automation Equipment，2017，37(1)：101-106.)
[3] 李春来，张海宁，杨立滨，等.基于无迹卡尔曼滤波神经网络的光伏发电预测 [J].重庆大学学报(自然科学版)，2017，40(4)：54-61.
(LI Chun-lai，ZHANG Hai-ning，YANG Li-bin，et al.Photovoltaic power forecasting based on unscented Kalman filtering neural network [J].Journal of Chongqing University (Natural Science Edition)，2017，40(4)：54-61.)
[4] 卢舟鑫，王冰，荣军峰.基于多时段综合相似日的光伏发电功率预测 [J].电源技术，2017，41(1)：103-106.
(LU Zhou-xin，WANG Bing，RONG Jun-feng.Photovoltaic generation power prediction based on multi-period integrated similar days [J].Chinese Journal of Power Sources，2017，41(1)：103-106.)
[5] 冬雷，周晓，郝颖，等.基于样本双重筛选的光伏发电功率预测 [J].太阳能学报，2018，39(4)：1018-1025.
(DONG Lei，ZHOU Xiao，HAO Ying，et al.Photovoltaic power prediction based on sample dual screening [J].Acta Energiae Solaris Sinica，2018，39(4)：1018-1025.)
[6] 于秋玲，许长清，李珊，等.基于模糊聚类和支持向量机的短期光伏功率预测 [J].电力系统及其自动化学报，2016，28(12)：115-118.
(YU Qiu-ling，XU Chang-qing，LI Shan，et al.Application of fuzzy clustering algorithm and support vector machine to short-term forecasting of PV power [J].Proceedings of the CSU-EPSA，2016，28(12)：115-118.)
[7] 徐敏姣，徐青山，袁晓冬.基于改进EMD及Elman算法的短期光伏功率预测研究 [J].现代电力，2016，33(3)：8-13.
(XU Min-jiao，XU Qing-shan，YUAN Xiao-dong.A short-term power forecasting model of photovoltaic system based on improved EMD and Elman neural network [J].Modern Electric Power，2016，33(3)：8-13.)
[8] 侯松宝，王侃宏，石凯波，等.基于相似日和主成分分析的光伏发电系统短期出力预测 [J].可再生能源，2018，36(1)：15-21.
(HOU Song-bao，WANG Kan-hong，SHI Kai-bo，et al.Short-term output power forecast of photovoltaic power generation system based on similar day and principal component analysis [J].Renewable Energy Resources，2018，36(1)：15-21.)
[9] 宋启军，胡翔奎，王腾飞，等.基于GRA-SVM的光伏发电功率预测 [J].水力发电，2016，42(11)：110-113.
(SONG Qi-jun，HU Xiang-kui，WANG Teng-fei，et al.Photovoltaic power forecasting based on GRA-SVM model [J].Water Power，2016，42(11)：110-113.)
[10] 史佳琪，张建华.基于深度学习的超短期光伏精细化预测模型研究 [J].电力建设，2017，38(6)：28-35.
(SHI Jia-qi，ZHANG Jian-hua.Ultra short-term photovoltaic refined forecasting model based on deep learning [J].Electric Power Construction，2017，38(6)：28-35.)
[11] 程启明，张强，程尹曼，等.基于密度峰值层次聚类的短期光伏功率预测模型 [J].高电压技术，2017，43(4)：1214-1222.
(CHENG Qi-ming，ZHANG Qiang，CHENG Yin-man，et al.Short-term photovoltaic power prediction model based on density peak hierarchical clustering [J].High Voltage Engineering，2017，43(4)：1214-1222.)
[12] 付青，单英浩，朱昌亚.基于NARX神经网络的光伏发电功率预测研究 [J].电气传动，2016，46(4)：42-45.
(FU Qing，SHAN Ying-hao，ZHU Chang-ya.Generated power forecasting for photovoltaic system based on NARX neural network [J].Electric Drive，2016，46(4)：42-45.)
[13] 杜川.基于电流预测控制的永磁同步电机矢量控制策略 [J].沈阳工业大学学报，2019，12(6)：616-620.
(DU Chuan.Vector control strategy of PMSM based on current predictive control [J].Journal of Shenyang University of Technology，2019，12(6)：616-620.)
[14] 杨锡运，任杰，肖运启.基于粗糙集的光伏输出功率组合预测模型 [J].中国电力，2016，49(12)：133-138.
(YANG Xi-yun，REN Jie，XIAO Yun-qi.A combined photovoltaic output forecasting method based on rough set theory [J].Electric Power，2016，49(12)：133-138.)
[15] 王昕，黄柯，郑益慧，等.基于萤火虫算法
广义回归神经网络的光伏发电功率组合预测 [J].电网技术，2017，41(2)：125-131.
(WANG Xin，HUANG Ke，ZHENG Yi-hui，et al.Power generation forecasting of photovoltaic generation based on firefly algorithm-generalized regression neural network [J].Power System Technology，2017，41(2)：125-131.)